All Exams >
Commerce >
Online MCQ Tests for Commerce >
All Questions
All questions of Probability for Commerce Exam
One card is drawn from a pack of cards, each of the 52 cards being equally likely to be drawn. The probability that the card drawn is red and a queen is:- a)1/26
- b)1/2
- c)2
- d)1/4
Correct answer is option 'A'. Can you explain this answer?
One card is drawn from a pack of cards, each of the 52 cards being equally likely to be drawn. The probability that the card drawn is red and a queen is:
a)
1/26
b)
1/2
c)
2
d)
1/4
|
Gaurav Kumar answered |
The cards contains 4 Queen from which 2 are black and 2 are red
we need to find the probability that the card drawn is red and a queen is: 2/52
= 1/26
we need to find the probability that the card drawn is red and a queen is: 2/52
= 1/26
Probability of getting a number between 1 and 100, which is divisible by 1 and itself only, is- a)25/99
- b)1/4
- c)25/98
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Probability of getting a number between 1 and 100, which is divisible by 1 and itself only, is
a)
25/99
b)
1/4
c)
25/98
d)
none of these
|
Nandini Iyer answered |
The prime numbers between 1 and 100 are :2, 3, 5, 7, 11,
The probability that a man will live for 10 more years is 1/4 and that his wife will live 10 more years is 1/3. The probability that neither will be alive in 10 years is- a)5/12
- b)1/2
- c)11/12
- d)7/12
Correct answer is option 'B'. Can you explain this answer?
The probability that a man will live for 10 more years is 1/4 and that his wife will live 10 more years is 1/3. The probability that neither will be alive in 10 years is
a)
5/12
b)
1/2
c)
11/12
d)
7/12
|
Mayank Dasgupta answered |
Given probabilities:
- Probability that the man will live for 10 more years = 1/4
- Probability that his wife will live for 10 more years = 1/3
To find: Probability that neither will be alive in 10 years
Solution:
Let A be the event that the man will be alive in 10 years, and B be the event that his wife will be alive in 10 years. Then, the probability that neither will be alive in 10 years is the probability of the complement of the union of A and B, i.e., P((A ∪ B)').
Using the formula for the probability of the union of two events, we have:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
where P(A ∩ B) is the probability that both the man and his wife will be alive in 10 years.
Substituting the given probabilities, we get:
P(A ∪ B) = 1/4 + 1/3 - P(A ∩ B)
Simplifying, we get:
P(A ∩ B) = 7/12 - P((A ∪ B)')
Now, we know that the probability of the man being alive in 10 years is 1/4, which means the probability of him not being alive in 10 years is 3/4. Similarly, the probability of his wife not being alive in 10 years is 2/3.
Using the product rule of probability, we can find the probability of both of them not being alive in 10 years:
P((A ∪ B)') = P(A' ∩ B') = P(A') × P(B') = (3/4) × (2/3) = 1/2
Substituting this value in the above equation, we get:
P(A ∩ B) = 7/12 - 1/2 = 1/12
Therefore, the probability that neither the man nor his wife will be alive in 10 years is:
P((A ∪ B)') = 1 - P(A ∪ B) = 1 - (1/4 + 1/3 - 1/12) = 1/2
Hence, the correct option is (B).
- Probability that the man will live for 10 more years = 1/4
- Probability that his wife will live for 10 more years = 1/3
To find: Probability that neither will be alive in 10 years
Solution:
Let A be the event that the man will be alive in 10 years, and B be the event that his wife will be alive in 10 years. Then, the probability that neither will be alive in 10 years is the probability of the complement of the union of A and B, i.e., P((A ∪ B)').
Using the formula for the probability of the union of two events, we have:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
where P(A ∩ B) is the probability that both the man and his wife will be alive in 10 years.
Substituting the given probabilities, we get:
P(A ∪ B) = 1/4 + 1/3 - P(A ∩ B)
Simplifying, we get:
P(A ∩ B) = 7/12 - P((A ∪ B)')
Now, we know that the probability of the man being alive in 10 years is 1/4, which means the probability of him not being alive in 10 years is 3/4. Similarly, the probability of his wife not being alive in 10 years is 2/3.
Using the product rule of probability, we can find the probability of both of them not being alive in 10 years:
P((A ∪ B)') = P(A' ∩ B') = P(A') × P(B') = (3/4) × (2/3) = 1/2
Substituting this value in the above equation, we get:
P(A ∩ B) = 7/12 - 1/2 = 1/12
Therefore, the probability that neither the man nor his wife will be alive in 10 years is:
P((A ∪ B)') = 1 - P(A ∪ B) = 1 - (1/4 + 1/3 - 1/12) = 1/2
Hence, the correct option is (B).
A box contains 15 red marbles, 15 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?- a)
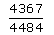
- b)
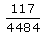
- c) zero
- d)1
Correct answer is option 'A'. Can you explain this answer?
A box contains 15 red marbles, 15 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?
a)
b)
c)
zero
d)
1
|
Shashwat Singh answered |
It's like doing the question orally... (don't get into maths... as I was also stuck in the middle) but by common sense (which is very uncommon) it can be said as 1-probablity of not getting any green in 5 balls... in this case we can see the answer aproaches to 1 which can be seen in option a) .... hope it helps... but with maths a can see a nightmare coming...
The sample space of an experiment is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and A = {TTT}, B = {HTT, THT, TTH}, C = {HHT, HTH, THH, HHH},
then A, B and C form a set of?- a)Mutually exclusive but not exhaustive events
- b)Exhaustive but not mutually exclusive events
- c)Mutually exclusive and exhaustive events
- d)Neither mutually exclusive nor exhaustive events
Correct answer is option 'C'. Can you explain this answer?
The sample space of an experiment is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and A = {TTT}, B = {HTT, THT, TTH}, C = {HHT, HTH, THH, HHH},
then A, B and C form a set of?
then A, B and C form a set of?
a)
Mutually exclusive but not exhaustive events
b)
Exhaustive but not mutually exclusive events
c)
Mutually exclusive and exhaustive events
d)
Neither mutually exclusive nor exhaustive events
|
Suresh Reddy answered |
Above information has no common element in three of them and U of three sets forms sample set . Therefore option C is correct.
If 2/7 is the probability of an event, then the probability of the event ‘not A’ is:- a)5/7
- b)6/7
- c)2/7
- d)3/7
Correct answer is option 'A'. Can you explain this answer?
If 2/7 is the probability of an event, then the probability of the event ‘not A’ is:
a)
5/7
b)
6/7
c)
2/7
d)
3/7
|
|
Geetika Shah answered |
If 2/7 is probability of event A then the probability of an event not A is 1-(2/7) i.e., probability of not A is 5/7
In a simultaneous toss of two coins, the probability of getting no tail is:- a)1/4
- b)1/2
- c)2
- d)0.1
Correct answer is option 'A'. Can you explain this answer?
In a simultaneous toss of two coins, the probability of getting no tail is:
a)
1/4
b)
1/2
c)
2
d)
0.1
|
Om Desai answered |
Sample space = {HH, HT, TH, TT}
n(SS) = 4
No tail = {HH}
n(No tail) = 1
P(No tail) = n(No tail) / n(SS
= 1/4
n(SS) = 4
No tail = {HH}
n(No tail) = 1
P(No tail) = n(No tail) / n(SS
= 1/4
If an event has more than one sample point, it is called a ………- a)Exhaustive event
- b)Compound event
- c)Simple event
- d)Mutually exclusive event
Correct answer is option 'B'. Can you explain this answer?
If an event has more than one sample point, it is called a ………
a)
Exhaustive event
b)
Compound event
c)
Simple event
d)
Mutually exclusive event
|
|
Nandini Patel answered |
b) Compound event
If an event has more than one sample point, it is called a compound event. A sample point is a specific outcome of an experiment, such as rolling a particular number on a die or drawing a particular card from a deck. An event is a collection of one or more sample points.
A compound event is an event that is made up of multiple sample points, which means that there is more than one way for the event to occur. For example, if you roll a die and count the number of dots on the top face, the event "rolling a number greater than 4" is a compound event, because it consists of the sample points "rolling a 5" and "rolling a 6".
A simple event, on the other hand, is an event that consists of a single sample point. For example, if you roll a die, the event "rolling a 3" is a simple event, because it consists of only one sample point.
Exhaustive events and mutually exclusive events are different concepts. An exhaustive event is an event that includes all possible sample points, so that one of the sample points must occur. A mutually exclusive event is an event that cannot occur at the same time as another event. For example, the events "rolling an odd number" and "rolling an even number" are mutually exclusive, because a die cannot show both an odd and an even number at the same time.
8 coins are tossed at a time. The probability of getting 6 heads up is- a)57/64
- b)7/64
- c)37/256
- d)229/256
Correct answer is option 'C'. Can you explain this answer?
8 coins are tossed at a time. The probability of getting 6 heads up is
a)
57/64
b)
7/64
c)
37/256
d)
229/256
|
|
Koyna Jatwar answered |
The required probability =8C6(1/2)^6.(1/2)^2+8C7(1/2)^7(1/2)+8C8(1/2)^8. =1/256(28+8+1)=37/256
Two students Amit and Priyanka appeared in an examination. The probability that Amit will qualify the examination is 0.06 and that Priyanka will qualify the examination is 0.12. The probability that both will qualify the examination is 0.02. Then, the probability that both Amit and Priyanka will not qualify the examination is:- a)0.91
- b)0.12
- c)0.84
- d)0.45
Correct answer is option 'C'. Can you explain this answer?
Two students Amit and Priyanka appeared in an examination. The probability that Amit will qualify the examination is 0.06 and that Priyanka will qualify the examination is 0.12. The probability that both will qualify the examination is 0.02. Then, the probability that both Amit and Priyanka will not qualify the examination is:
a)
0.91
b)
0.12
c)
0.84
d)
0.45
|
|
Naina Sharma answered |
Probability that Amit will qualify the exam(E) = 0.06
Probability that Priyanka will qualify the exam(F) = 0.12
Probability that both will qualify the exam P(E⋂F) = 0.02
P(EUF) = P(E) + P(F) - P(EUF)
= 0.06 + 0.12 - 0.02 = 0.16
P(E’⋂F’) = 1 - P(EUF)
⇒ 1 - 0.16
= 0.84
Probability that Priyanka will qualify the exam(F) = 0.12
Probability that both will qualify the exam P(E⋂F) = 0.02
P(EUF) = P(E) + P(F) - P(EUF)
= 0.06 + 0.12 - 0.02 = 0.16
P(E’⋂F’) = 1 - P(EUF)
⇒ 1 - 0.16
= 0.84
When the sets A and B are two events associated with a sample space, then "A ∩ B " is the event common to
- a)Either A or B or both
- b)Only one of the two, A or B
- c)Both A and B
- d)Neither A nor B
Correct answer is option 'C'. Can you explain this answer?
When the sets A and B are two events associated with a sample space, then "A ∩ B " is the event common to
a)
Either A or B or both
b)
Only one of the two, A or B
c)
Both A and B
d)
Neither A nor B
|
Harsh Rajput answered |
There is a common sample space in between
Five marbles are drawn from a bag which contains 6 blue marbles and 7 green marbles. Then, the probability that 3 will be blue and 2 green is:- a)213/429
- b)140/429
- c)117/429
- d)167/429
Correct answer is option 'B'. Can you explain this answer?
Five marbles are drawn from a bag which contains 6 blue marbles and 7 green marbles. Then, the probability that 3 will be blue and 2 green is:
a)
213/429
b)
140/429
c)
117/429
d)
167/429
|
|
Naina Sharma answered |
Blue = 6
Green = 7
Number of ways 3 blue marbles can be drawn = 6C3
number of ways 2 green marbles can be drawn = 7C2
total ways of drawing 5 marbles = 13C5
=> probability = (6C3 * 7C2)/13C5
= 140/429
Green = 7
Number of ways 3 blue marbles can be drawn = 6C3
number of ways 2 green marbles can be drawn = 7C2
total ways of drawing 5 marbles = 13C5
=> probability = (6C3 * 7C2)/13C5
= 140/429
The events when we have no reason to believe that one is more likely to occur than the other is called:- a)Equally likely events
- b)Independent events
- c)Dependent event
- d)Not equally likely events
Correct answer is option 'A'. Can you explain this answer?
The events when we have no reason to believe that one is more likely to occur than the other is called:
a)
Equally likely events
b)
Independent events
c)
Dependent event
d)
Not equally likely events
|
Vikas Kapoor answered |
Equally Likely Events Events which have the same chance of occurring Probability. Chance that an event will occur. Theoretically for equally likely events, it is the number of ways an event can occur divided by number of outcomes in the sample space.
Both A and B throw a dice. The chance that B throws a number not less than that thrown by A is- a)1/2
- b)15/36
- c)21/36
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Both A and B throw a dice. The chance that B throws a number not less than that thrown by A is
a)
1/2
b)
15/36
c)
21/36
d)
none of these
|
|
Nandini Patel answered |
c) 21/36
If both A and B throw a dice, there are 36 possible outcomes in total: 6 possibilities for what A throws and 6 possibilities for what B throws. Of these 36 outcomes, 15 of them result in B throwing a number that is not less than the number thrown by A. Therefore, the probability that B throws a number not less than that thrown by A is 15/36, which is approximately 41.7%.
To find the probability of this event, we can consider each of the possible outcomes separately. For example, if A throws a 1 and B throws a 2, then B has thrown a number not less than that thrown by A. If A throws a 3 and B throws a 3, then B has thrown a number not less than that thrown by A. If A throws a 4 and B throws a 6, then B has thrown a number not less than that thrown by A. There are a total of 15 such outcomes.
The probability that B throws a number less than that thrown by A is 21/36, or approximately 58.3%. This is the complementary probability to the probability that B throws a number not less than that thrown by A. The complementary probability is the probability of the event not occurring. In this case, the event "B throws a number not less than that thrown by A" is not occurring if B throws a number less than that thrown by A. The sum of the probability of an event occurring and the probability of the event not occurring is always 1, so the probability of an event occurring plus the complementary probability of the event is always equal to 1.
A four digit number is formed by using the digits 1,2,3,4,5,6,7 without repetition. What is the probability that it’s divisible by 2?- a)3/7
- b)4/7
- c)2/7
- d)1/7
Correct answer is option 'A'. Can you explain this answer?
A four digit number is formed by using the digits 1,2,3,4,5,6,7 without repetition. What is the probability that it’s divisible by 2?
a)
3/7
b)
4/7
c)
2/7
d)
1/7
|
Anushka Ahuja answered |
The total number of possible four-digit numbers using the digits 1, 2, 3, 4, 5, 6, 7 without repetition is 7P4 = 7!/3! = 7*6*5*4 = 840.
To find the probability of the number being divisible by 4, we need to find the number of four-digit numbers using these digits that are divisible by 4.
A number is divisible by 4 if the last two digits form a number divisible by 4.
The possible two-digit numbers that are divisible by 4 are 12, 16, 24, 32, 36, 52, 56, 64, 72, and 76.
For each of these two-digit numbers, there are 5 choices for the first digit (excluding the last two digits used), and 4 choices for the remaining digit.
So, the total number of four-digit numbers using these digits that are divisible by 4 is 10 * 5 * 4 = 200.
Therefore, the probability of a random four-digit number using the digits 1, 2, 3, 4, 5, 6, 7 without repetition being divisible by 4 is 200/840 = 5/21.
To find the probability of the number being divisible by 4, we need to find the number of four-digit numbers using these digits that are divisible by 4.
A number is divisible by 4 if the last two digits form a number divisible by 4.
The possible two-digit numbers that are divisible by 4 are 12, 16, 24, 32, 36, 52, 56, 64, 72, and 76.
For each of these two-digit numbers, there are 5 choices for the first digit (excluding the last two digits used), and 4 choices for the remaining digit.
So, the total number of four-digit numbers using these digits that are divisible by 4 is 10 * 5 * 4 = 200.
Therefore, the probability of a random four-digit number using the digits 1, 2, 3, 4, 5, 6, 7 without repetition being divisible by 4 is 200/840 = 5/21.
An experiment involves rolling a pair of dice and recording the number that comes up. Suppose,
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.- a)Random experiment
- b)Mutually exclusive events
- c)Exhaustive events
- d)Favorable events
Correct answer is option 'B'. Can you explain this answer?
An experiment involves rolling a pair of dice and recording the number that comes up. Suppose,
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.
a)
Random experiment
b)
Mutually exclusive events
c)
Exhaustive events
d)
Favorable events
|
Advait Ghoshal answered |
A pair of dice is rolled
Therefore the sample space S will be
Pairs which are mutually exclusive :
A∩B=ϕ⇒ A and B are mutually exclusive.
B∩C=ϕ⇒ B and C are mutually exclusive.
A∩C=ϕ⇒ They are not mutually exclusive.
∴A∩B and B∩C are mutually exclusive.
The letters of the word ‘ASSASSIN ‘ are written at random in a row. The chance that all the similar letters occur together is- a)1/35
- b)1/14
- c)34/35
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The letters of the word ‘ASSASSIN ‘ are written at random in a row. The chance that all the similar letters occur together is
a)
1/35
b)
1/14
c)
34/35
d)
none of these
|
Anjali Sharma answered |
Total number of ways to arrange "ASSASSIN" is 8!/(4!.2!) first we fix the position.
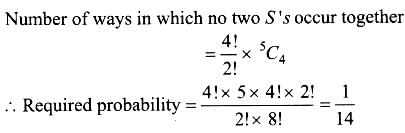
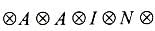
A cubical dice has 3 on three faces, 2 on two faces and 1 on the 6 thth face .It is tossed twice. The chance that both the tosses show an even number is- a)1/4
- b)1/9
- c)1/36
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A cubical dice has 3 on three faces, 2 on two faces and 1 on the 6 thth face .It is tossed twice. The chance that both the tosses show an even number is
a)
1/4
b)
1/9
c)
1/36
d)
none of these
|
|
Priya Mishra answered |
The correct option is B.
Since we have only even number 2,so when the dice is rolled twice we have (2,2) four times which means 2 on first dice pairs with both the twos on the second dice , similarly second two on first dice pairs with both the twos on the second dice
Hence the probability = 4/36 = 1/9
A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. The chance that atleast two balls are black is- a)243/256
- b)67/256
- c)54/256
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. The chance that atleast two balls are black is
a)
243/256
b)
67/256
c)
54/256
d)
none of these
|
|
Riya Banerjee answered |
Let A, B, C, D denote the events of not getting a white ball in first, second, third and fourth draw respectively.
Since the balls are drawn with replacement, therefore, A, B, C, D are independent events such that P (A) = P (B) = P (C) = P (D).
Since out of 16 balls, 11 are not white, therefore, P (A) = 11/16
∴ Required probability = P (A) . P (B) . P (C) . P (D)
=> (11/16) x (11/16) x (11/16) x (11/16) = (11/16)^4.
A possible result of a random experiment is called its ……- a)Favorable outcomes
- b)Event
- c)Outcome
- d)Experiment
Correct answer is option 'C'. Can you explain this answer?
A possible result of a random experiment is called its ……
a)
Favorable outcomes
b)
Event
c)
Outcome
d)
Experiment
|
Mehul Rane answered |
Understanding Random Experiments
In probability theory, a random experiment is any procedure or action that results in one or more outcomes that cannot be predicted with certainty. A key aspect of this is understanding the terminology associated with its possible results.
What is an Outcome?
- An outcome is a specific result of a random experiment.
- For example, when tossing a coin, the possible outcomes are "heads" or "tails."
- Each outcome represents a unique, observable result of the experiment.
Other Terms Explained
- Favorable Outcomes: These refer to outcomes that align with a specific event we are interested in. For instance, if we want to know the probability of rolling an even number on a die, the favorable outcomes would be 2, 4, and 6.
- Event: This is a set of outcomes. An event can consist of one or more outcomes. For example, getting a "head" when tossing a coin is an event consisting of a single outcome.
- Experiment: This is the process or action through which outcomes are generated. The term encompasses the entire procedure, such as rolling a die or drawing a card from a deck.
Conclusion
Given these definitions, the correct answer to the question is option C: an outcome, as it specifically refers to the result of a random experiment. Understanding these terms is crucial for grasping the foundational concepts of probability and statistics, which are essential for success in JEE and other competitive exams.
In probability theory, a random experiment is any procedure or action that results in one or more outcomes that cannot be predicted with certainty. A key aspect of this is understanding the terminology associated with its possible results.
What is an Outcome?
- An outcome is a specific result of a random experiment.
- For example, when tossing a coin, the possible outcomes are "heads" or "tails."
- Each outcome represents a unique, observable result of the experiment.
Other Terms Explained
- Favorable Outcomes: These refer to outcomes that align with a specific event we are interested in. For instance, if we want to know the probability of rolling an even number on a die, the favorable outcomes would be 2, 4, and 6.
- Event: This is a set of outcomes. An event can consist of one or more outcomes. For example, getting a "head" when tossing a coin is an event consisting of a single outcome.
- Experiment: This is the process or action through which outcomes are generated. The term encompasses the entire procedure, such as rolling a die or drawing a card from a deck.
Conclusion
Given these definitions, the correct answer to the question is option C: an outcome, as it specifically refers to the result of a random experiment. Understanding these terms is crucial for grasping the foundational concepts of probability and statistics, which are essential for success in JEE and other competitive exams.
The letters of the word ‘MALENKOV‘are arranged in all possible ways. The chance that there are exactly four letters between M and E is- a)3/28
- b)3/14
- c)1/14
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The letters of the word ‘MALENKOV‘are arranged in all possible ways. The chance that there are exactly four letters between M and E is
a)
3/28
b)
3/14
c)
1/14
d)
none of these
|
Shilpa Rane answered |
"algorithm" can be rearranged in 9! (362,880) different ways.
A coin is tossed. If head comes up a die is thrown but if tail comes up, the coin is tossed again. The probability of obtaining head and number 6 is:- a)1/8
- b)5/8
- c)7/8
- d)3/8
Correct answer is option 'A'. Can you explain this answer?
A coin is tossed. If head comes up a die is thrown but if tail comes up, the coin is tossed again. The probability of obtaining head and number 6 is:
a)
1/8
b)
5/8
c)
7/8
d)
3/8
|
|
Sanchita Mukherjee answered |
Sample space = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, H), (T, T)}
n(Sample space) = 8
P(obtaining head and number 6) = P(H, 6) = 1/8
n(Sample space) = 8
P(obtaining head and number 6) = P(H, 6) = 1/8
The probability on the basis of observations and collected data is called:- a)Axiomatic approach of probability
- b)Empirical probability
- c)Statistical approach of probability
- d)Classical approach of probability
Correct answer is option 'C'. Can you explain this answer?
The probability on the basis of observations and collected data is called:
a)
Axiomatic approach of probability
b)
Empirical probability
c)
Statistical approach of probability
d)
Classical approach of probability
|
|
Shreya Gupta answered |
The basic approach statistical methods adopt to deal with uncertainty is via the axioms of probability: Probabilities are (real) numbers in the range 0 to 1. A probability of P(A) = 0 indicates total uncertainty in A, P(A) = 1 total certainty and values in between some degree of (un)certainty.
Non detects or “less than" values are technically known as “left-censored" values. Data censoring complicates statistical evaluations, especially when a large portion of a data set is non detect. Uncertain measurements lead to data sets with varying analytical precision, also complicating statistical analysis.
A drawer contains 5 black socks and 4 blue socks well mixed. A person searches the drawer and pulls out 2 socks at random. The probability that they match is- a)41/81
- b)5/8
- c)4/9
- d)5/9
Correct answer is option 'C'. Can you explain this answer?
A drawer contains 5 black socks and 4 blue socks well mixed. A person searches the drawer and pulls out 2 socks at random. The probability that they match is
a)
41/81
b)
5/8
c)
4/9
d)
5/9
|
|
Jaya Deshpande answered |
Out of 9 socks, 2 can be drawn in 9C2 ways.
Therefore, the total number of cases is 9C2.
Two socks drawn from the drawer will match if either both are black or both are blue.
Therefore, favorable number of cases is 5C2+ 4C2.
Hence, the required probability is
(5C2+ 4C2.)/ 9C2
= 4/9
From a pack of 52 cards, the cards are drawn one by one till an ace appears. The chance that an ace does not come up in first 26 cards is- a)109/153
- b)23/27
- c)46/153
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
From a pack of 52 cards, the cards are drawn one by one till an ace appears. The chance that an ace does not come up in first 26 cards is
a)
109/153
b)
23/27
c)
46/153
d)
none of these
|
|
Madhavan Chatterjee answered |
There are 4 aces in a pack. So, the probability of drawing an ace = 4/52
= 1/13
and the probability of drawing a card other than ace = 12/13.
Hence, the probability that ace doesn't appear in first 26 draws = (12/13)26
= 1/13
and the probability of drawing a card other than ace = 12/13.
Hence, the probability that ace doesn't appear in first 26 draws = (12/13)26
A fair coin is tossed a fixed number of times. If the probability of getting 4 heads is equal to the probability of getting 7 heads, then the probability of getting 2 heads is- a)55/2048
- b)3/4096
- c)1/1024
- d)3/1024
Correct answer is option 'A'. Can you explain this answer?
A fair coin is tossed a fixed number of times. If the probability of getting 4 heads is equal to the probability of getting 7 heads, then the probability of getting 2 heads is
a)
55/2048
b)
3/4096
c)
1/1024
d)
3/1024
|
Sanchita Khanna answered |
Given, probability of getting 4 heads = probability of getting 7 heads
Let the number of tosses be n. Then,
Probability of getting 4 heads = Probability of getting (n-4) tails = (1/2)^n * nC4
Probability of getting 7 heads = Probability of getting (n-7) tails = (1/2)^n * nC7
Equating the two probabilities, we get
nC4 = nC7/35
Solving this equation, we get n = 11
So, the number of tosses is 11.
Now, we need to find the probability of getting 2 heads.
Probability of getting 2 heads = Probability of getting (11-2) tails = (1/2)^11 * nC2
= (1/2)^11 * 55
= 55/2048
Therefore, the correct option is A) 55/2048.
Let the number of tosses be n. Then,
Probability of getting 4 heads = Probability of getting (n-4) tails = (1/2)^n * nC4
Probability of getting 7 heads = Probability of getting (n-7) tails = (1/2)^n * nC7
Equating the two probabilities, we get
nC4 = nC7/35
Solving this equation, we get n = 11
So, the number of tosses is 11.
Now, we need to find the probability of getting 2 heads.
Probability of getting 2 heads = Probability of getting (11-2) tails = (1/2)^11 * nC2
= (1/2)^11 * 55
= 55/2048
Therefore, the correct option is A) 55/2048.
The sample space associated to thrown a dice is- a)(1, 2, 3)
- b)(1, 2, 3, 4, 5, 6)
- c)(1, 3, 5)
- d)(2, 4, 6)
Correct answer is option 'B'. Can you explain this answer?
The sample space associated to thrown a dice is
a)
(1, 2, 3)
b)
(1, 2, 3, 4, 5, 6)
c)
(1, 3, 5)
d)
(2, 4, 6)
|
Kamali Anandbabu answered |
The size of the sample space is the total number of possible outcomes. So one dice has 6 sides which has sample space of 1,2,3,4,5 and 6.
The probability that a card drawn at random from a pack of 52 cards is a king or a heart is- a)16/52
- b)1/13
- c)1/52
- d)1/4
Correct answer is option 'A'. Can you explain this answer?
The probability that a card drawn at random from a pack of 52 cards is a king or a heart is
a)
16/52
b)
1/13
c)
1/52
d)
1/4
|
Er Aarif answered |
The number of kings in a deck are 4
Number of hearts in the deck are 13, including the king of hearts
Probability of getting either a king or a heart is, P = 4+(13–1) / 52
P = 16/52
Number of hearts in the deck are 13, including the king of hearts
Probability of getting either a king or a heart is, P = 4+(13–1) / 52
P = 16/52
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is square.- a)4/9
- b)5/9
- c)1/3
- d)5/18
Correct answer is option 'B'. Can you explain this answer?
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is square.
a)
4/9
b)
5/9
c)
1/3
d)
5/18
|
|
Varun Kapoor answered |
Number of favourable outcomes for the events that squares is lost, i.e.,
F(E) = 10
T(E) = 8 + 10 = 18
P(getting a square), P(E) = 10/18 = 5/9
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is a triangle.- a)4/9
- b)5/9
- c)1/3
- d)5/18
Correct answer is option 'A'. Can you explain this answer?
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is a triangle.
a)
4/9
b)
5/9
c)
1/3
d)
5/18
|
|
Jatin More answered |
Answer ( A ) 4/9
Three of the 6 vertices of a regular hexagon are chosen at random.The probability that the triangle with these vertices is equilateral is- a)1/10
- b)1/20
- c)1/5
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Three of the 6 vertices of a regular hexagon are chosen at random.The probability that the triangle with these vertices is equilateral is
a)
1/10
b)
1/20
c)
1/5
d)
1/2
|
|
Kurakula Suryateja answered |
Rules of Triangle …..
Total possible cases = 6 C 3
Favourable cases =2
So the probability is = 2/6 C 3 =1/10.
Because there can be 2 22 equilateral triangles possible and total number of triangles possible would be (6/3) the answer is 1/10.
Total possible cases = 6 C 3
Favourable cases =2
So the probability is = 2/6 C 3 =1/10.
Because there can be 2 22 equilateral triangles possible and total number of triangles possible would be (6/3) the answer is 1/10.
If three dice are thrown, then the probability that they show the numbers in A.P. is- a)1/12
- b)7/36
- c)1/36
- d)1/18
Correct answer is option 'D'. Can you explain this answer?
If three dice are thrown, then the probability that they show the numbers in A.P. is
a)
1/12
b)
7/36
c)
1/36
d)
1/18
|
Anagha Dey answered |
A.P. with common diff one are =4=(123)(234)(345)(456)
A.P. with common diff 2 are =2=(135)(246)
A.P. with common diff 0 are =6
⇒P=2+4+6/216=1/18
A.P. with common diff 2 are =2=(135)(246)
A.P. with common diff 0 are =6
⇒P=2+4+6/216=1/18
Two players toss four coins each. The probability that both obtain the same number of heads is- a)1/16
- b)5/256
- c)35/128
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Two players toss four coins each. The probability that both obtain the same number of heads is
a)
1/16
b)
5/256
c)
35/128
d)
none of these
|
Rahul Chaudhary answered |
The tossing of coin by each of the two players is independent. So we can multiply the respective probabilities and get the required probability.
There are five cases:
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Ritapromoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John's promotion is the same as that of Gurpreet, Rita's chances of promotion are twice as likely as Johns. Aslam's chances are four times that of John.
Sol. Let Event :J = John promotedR = Rita promotedA = Aslam promotedG = Gurpreet promoted Given sample space, S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}i.e., S ={J, R, A, G)It is given that, chances of John’s promotion is same as that of Gurpreet.P(J) = P(G)Rita’s chances of promotion are twice as likely as John.P(R) = 2P(J)and Aslam’s chances of promotion are four times that of John.P(A) = 4P(J)Q. What is the probability that Aslam got a promotion?- a)1/8
- b)1/4
- c)1/2
- d)1/6
Correct answer is option 'C'. Can you explain this answer?
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Rita
promoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John's promotion is the same as that of Gurpreet, Rita's chances of promotion are twice as likely as Johns. Aslam's chances are four times that of John.
Sol. Let Event :
J = John promoted
R = Rita promoted
A = Aslam promoted
G = Gurpreet promoted Given sample space, S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}
i.e., S ={J, R, A, G)
It is given that, chances of John’s promotion is same as that of Gurpreet.
P(J) = P(G)
Rita’s chances of promotion are twice as likely as John.
P(R) = 2P(J)
and Aslam’s chances of promotion are four times that of John.
P(A) = 4P(J)
Q. What is the probability that Aslam got a promotion?
a)
1/8
b)
1/4
c)
1/2
d)
1/6
|
|
Varun Kapoor answered |
P(Aslam promoted) = 4P(J)
4P(J) = 4 × 1/8 = 1/2
Two dice are thrown simultaneously. The probability of getting an even number as the sum is:
- a)1/2
- b)3/4
- c)1/4
- d)1/3
Correct answer is option 'A'. Can you explain this answer?
Two dice are thrown simultaneously. The probability of getting an even number as the sum is:
a)
1/2
b)
3/4
c)
1/4
d)
1/3
|
|
Nandini Iyer answered |
each dice can show 1,3 or 5..so ways of getting ODD product= 3∗3=93∗3=9Total ways to ch
What is the sample space for an experiment when a coin is tossed and then a dice is thrown?- a){1H,2H3H,4H,5H,6H,T1,T2,T3,T4,T5,T6}
- b){H1,T1,H6,T6}
- c){H1,T1,H2,T2,H3,T3,H4,T4,H5,T5,H6,T6}
- d){HT,TH,TT,HH,1,2,3,4,5,6}
Correct answer is option 'C'. Can you explain this answer?
What is the sample space for an experiment when a coin is tossed and then a dice is thrown?
a)
{1H,2H3H,4H,5H,6H,T1,T2,T3,T4,T5,T6}
b)
{H1,T1,H6,T6}
c)
{H1,T1,H2,T2,H3,T3,H4,T4,H5,T5,H6,T6}
d)
{HT,TH,TT,HH,1,2,3,4,5,6}
|
Aniket Joshi answered |
Sample Space for Coin Toss and Dice Throw Experiment
The sample space of an experiment refers to the set of all possible outcomes of that experiment. In this case, the experiment involves tossing a coin and then throwing a dice. Let's analyze the given options and determine which one represents the correct sample space.
a) {1H, 2H, 3H, 4H, 5H, 6H, T1, T2, T3, T4, T5, T6}
b) {H1, T1, H6, T6}
c) {H1, T1, H2, T2, H3, T3, H4, T4, H5, T5, H6, T6}
d) {HT, TH, TT, HH, 1, 2, 3, 4, 5, 6}
To determine the correct sample space, we need to consider the possible outcomes of each individual event (coin toss and dice throw) and combine them in all possible ways.
1. Coin Toss:
The coin can either land on heads (H) or tails (T). So, the sample space for the coin toss is {H, T}.
2. Dice Throw:
The dice has six faces numbered 1 to 6. So, the sample space for the dice throw is {1, 2, 3, 4, 5, 6}.
Combining the outcomes of the coin toss and dice throw:
To find the sample space for both events combined, we need to take all possible combinations of outcomes from the coin toss and dice throw.
For each outcome of the coin toss, we can pair it with each outcome of the dice throw. This results in the following combinations:
- H1, H2, H3, H4, H5, H6 (coin landed on heads, dice showed 1, 2, 3, 4, 5, 6 respectively)
- T1, T2, T3, T4, T5, T6 (coin landed on tails, dice showed 1, 2, 3, 4, 5, 6 respectively)
Therefore, the correct sample space is:
{H1, T1, H2, T2, H3, T3, H4, T4, H5, T5, H6, T6}
Option c) {H1, T1, H2, T2, H3, T3, H4, T4, H5, T5, H6, T6} represents the correct sample space for the given experiment.
Note: The other options do not include all possible combinations of outcomes from the coin toss and dice throw, making them incorrect.
The sample space of an experiment refers to the set of all possible outcomes of that experiment. In this case, the experiment involves tossing a coin and then throwing a dice. Let's analyze the given options and determine which one represents the correct sample space.
a) {1H, 2H, 3H, 4H, 5H, 6H, T1, T2, T3, T4, T5, T6}
b) {H1, T1, H6, T6}
c) {H1, T1, H2, T2, H3, T3, H4, T4, H5, T5, H6, T6}
d) {HT, TH, TT, HH, 1, 2, 3, 4, 5, 6}
To determine the correct sample space, we need to consider the possible outcomes of each individual event (coin toss and dice throw) and combine them in all possible ways.
1. Coin Toss:
The coin can either land on heads (H) or tails (T). So, the sample space for the coin toss is {H, T}.
2. Dice Throw:
The dice has six faces numbered 1 to 6. So, the sample space for the dice throw is {1, 2, 3, 4, 5, 6}.
Combining the outcomes of the coin toss and dice throw:
To find the sample space for both events combined, we need to take all possible combinations of outcomes from the coin toss and dice throw.
For each outcome of the coin toss, we can pair it with each outcome of the dice throw. This results in the following combinations:
- H1, H2, H3, H4, H5, H6 (coin landed on heads, dice showed 1, 2, 3, 4, 5, 6 respectively)
- T1, T2, T3, T4, T5, T6 (coin landed on tails, dice showed 1, 2, 3, 4, 5, 6 respectively)
Therefore, the correct sample space is:
{H1, T1, H2, T2, H3, T3, H4, T4, H5, T5, H6, T6}
Option c) {H1, T1, H2, T2, H3, T3, H4, T4, H5, T5, H6, T6} represents the correct sample space for the given experiment.
Note: The other options do not include all possible combinations of outcomes from the coin toss and dice throw, making them incorrect.
A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of the determinant chosen is positive is- a)1/4
- b)1/16
- c)2/16
- d)3/16
Correct answer is option 'D'. Can you explain this answer?
A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of the determinant chosen is positive is
a)
1/4
b)
1/16
c)
2/16
d)
3/16
|
Hansa Sharma answered |
Total number of determinant =2 ^ 4 =16
The positive determinants are [1 1 0 1 ], [1 0 1 1], [1 0 0 1]
Therefore required probability = 3/16
In a certain town, 40% persons have brown hair, 25% have brown eyes, and 15% have both. If a person selected at random has brown hair, the chance that a person selected at random with brown hair is with brown eyes- a)3/8
- b)1/3
- c)3/20
- d)2/3
Correct answer is option 'A'. Can you explain this answer?
In a certain town, 40% persons have brown hair, 25% have brown eyes, and 15% have both. If a person selected at random has brown hair, the chance that a person selected at random with brown hair is with brown eyes
a)
3/8
b)
1/3
c)
3/20
d)
2/3
|
|
Rhea Basak answered |
Solution:
Given that 40% of persons have brown hair, 25% have brown eyes, and 15% have both.
Let A be the event that a person has brown hair, and B be the event that a person has brown eyes.
Then, P(A) = 0.40, P(B) = 0.25, and P(A ∩ B) = 0.15.
We are asked to find the probability that a person selected at random with brown hair is also with brown eyes, i.e., P(B|A).
Using Bayes' theorem, we have:
P(B|A) = P(A ∩ B) / P(A)
Substituting the given values, we get:
P(B|A) = 0.15 / 0.40
Simplifying, we get:
P(B|A) = 3/8
Therefore, the answer is option (A).
Given that 40% of persons have brown hair, 25% have brown eyes, and 15% have both.
Let A be the event that a person has brown hair, and B be the event that a person has brown eyes.
Then, P(A) = 0.40, P(B) = 0.25, and P(A ∩ B) = 0.15.
We are asked to find the probability that a person selected at random with brown hair is also with brown eyes, i.e., P(B|A).
Using Bayes' theorem, we have:
P(B|A) = P(A ∩ B) / P(A)
Substituting the given values, we get:
P(B|A) = 0.15 / 0.40
Simplifying, we get:
P(B|A) = 3/8
Therefore, the answer is option (A).
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is a square of blue colour.- a)4/9
- b)5/9
- c)1/3
- d)5/18
Correct answer is option 'C'. Can you explain this answer?
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is a square of blue colour.
a)
4/9
b)
5/9
c)
1/3
d)
5/18
|
|
Varun Kapoor answered |
Number of favourable outcomes for the events that lost figure is square of blue colour,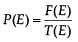
i.e., F(E) = 6 and T(E) = 18
∴ P(getting a blue square),
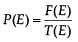
=6/18 = 1/3
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is a triangle of red colour.- a)4/9
- b)5/9
- c)1/3
- d)5/18
Correct answer is option 'D'. Can you explain this answer?
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. Find the probability that the lost piece is a triangle of red colour.
a)
4/9
b)
5/9
c)
1/3
d)
5/18
|
|
Varun Kapoor answered |
Number of favourable outcomes for the event that lost figure is triangle of red colour = 5,
i.e., F(E) = 5 and
T(E) = 18
∴ P(lost figure is red triangle), P(E) = 5/18
What is the probability of getting a sum of eight if two dice are thrown at once?- a)5/216
- b)5/36
- c)1/6
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
What is the probability of getting a sum of eight if two dice are thrown at once?
a)
5/216
b)
5/36
c)
1/6
d)
none of these
|
|
Hansa Sharma answered |
Explanation : (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,1) (2,2) (2,3) (2,4)
so on upto (6,6) are the total numbers we get when we throw a pair of dice that is, 36
In the question they are asking the probability of getting a sum of 8
(2,6) (3,5) (4,4) (5,3) (6,2) are the pairs which upon adding we get 8
Therefore, 5/36 is your answer
The odds in favour of an event are 6 : 5. The probability of occurrence of this event:- a)6/11
- b)5/11
- c)3/11
- d)2/11
Correct answer is option 'A'. Can you explain this answer?
The odds in favour of an event are 6 : 5. The probability of occurrence of this event:
a)
6/11
b)
5/11
c)
3/11
d)
2/11
|
Akash Ghoshal answered |
The odds in favor of an event are 6:5.
The odds in favor of an event represent the ratio of the number of favorable outcomes to the number of unfavorable outcomes. In this case, the odds are given as 6:5, which means that for every 6 favorable outcomes, there are 5 unfavorable outcomes.
Probability of occurrence of the event:
The probability of an event occurring is defined as the ratio of the number of favorable outcomes to the total number of possible outcomes. In this case, we need to determine the probability of the event occurring.
To find the probability, we can use the formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Calculating the probability:
Let's assume that the number of favorable outcomes is 6x and the number of unfavorable outcomes is 5x. Therefore, the total number of possible outcomes would be 6x + 5x = 11x.
Now, we can substitute these values into the probability formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 6x / 11x
Simplifying the expression by canceling out the common factor of x, we get:
Probability = 6 / 11
Therefore, the probability of the event occurring is 6/11.
Conclusion:
The correct answer is option A) 6/11. This is because the probability of the event occurring is given by the ratio of the number of favorable outcomes (6) to the total number of possible outcomes (11), which simplifies to 6/11.
The odds in favor of an event represent the ratio of the number of favorable outcomes to the number of unfavorable outcomes. In this case, the odds are given as 6:5, which means that for every 6 favorable outcomes, there are 5 unfavorable outcomes.
Probability of occurrence of the event:
The probability of an event occurring is defined as the ratio of the number of favorable outcomes to the total number of possible outcomes. In this case, we need to determine the probability of the event occurring.
To find the probability, we can use the formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Calculating the probability:
Let's assume that the number of favorable outcomes is 6x and the number of unfavorable outcomes is 5x. Therefore, the total number of possible outcomes would be 6x + 5x = 11x.
Now, we can substitute these values into the probability formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 6x / 11x
Simplifying the expression by canceling out the common factor of x, we get:
Probability = 6 / 11
Therefore, the probability of the event occurring is 6/11.
Conclusion:
The correct answer is option A) 6/11. This is because the probability of the event occurring is given by the ratio of the number of favorable outcomes (6) to the total number of possible outcomes (11), which simplifies to 6/11.
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. How many triangles are of red colour and how many squares are of red colour?- a)5, 4
- b)4, 5
- c)5, 5
- d)8, 6
Correct answer is option 'A'. Can you explain this answer?
A child's game has 8 triangles of which 3 are blue and the rest are red, and 10 squares of which 6 are blue and the rest are red. One piece is lost at random.
Q. How many triangles are of red colour and how many squares are of red colour?
a)
5, 4
b)
4, 5
c)
5, 5
d)
8, 6
|
|
Varun Kapoor answered |
Since, total no. of triangles = 8
Triangles with blue colour = 3
Triangles with red colour = 8 – 3 = 5
and total no. of squares = 10
Squares with blue colour = 6
Squares with red colour = 10 – 6 = 4
An urn contains 9 red, 7 white and 4 black balls. If two balls are drawn at random, then the probability that one ball is white is:- a)21/170
- b)81/190
- c)87/190
- d)91/190
Correct answer is option 'D'. Can you explain this answer?
An urn contains 9 red, 7 white and 4 black balls. If two balls are drawn at random, then the probability that one ball is white is:
a)
21/170
b)
81/190
c)
87/190
d)
91/190
|
Seelam Yogitha answered |
N(S)=20C2=190,N(A)=13C1*7C1=91==> P(A)=N(A)/N(S)=91/190
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Ritapromoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John's promotion is the same as that of Gurpreet, Rita's chances of promotion are twice as likely as Johns. Aslam's chances are four times that of John.
Sol. Let Event :J = John promotedR = Rita promotedA = Aslam promotedG = Gurpreet promoted Given sample space, S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}i.e., S ={J, R, A, G)It is given that, chances of John’s promotion is same as that of Gurpreet.P(J) = P(G)Rita’s chances of promotion are twice as likely as John.P(R) = 2P(J)and Aslam’s chances of promotion are four times that of John.P(A) = 4P(J)Q. What is the probability that Gurpreet got a promotion?- a)1/8
- b)1/4
- c)1/2
- d)1/6
Correct answer is option 'A'. Can you explain this answer?
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Rita
promoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John's promotion is the same as that of Gurpreet, Rita's chances of promotion are twice as likely as Johns. Aslam's chances are four times that of John.
Sol. Let Event :
J = John promoted
R = Rita promoted
A = Aslam promoted
G = Gurpreet promoted Given sample space, S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}
i.e., S ={J, R, A, G)
It is given that, chances of John’s promotion is same as that of Gurpreet.
P(J) = P(G)
Rita’s chances of promotion are twice as likely as John.
P(R) = 2P(J)
and Aslam’s chances of promotion are four times that of John.
P(A) = 4P(J)
Q. What is the probability that Gurpreet got a promotion?
a)
1/8
b)
1/4
c)
1/2
d)
1/6
|
|
Anjali Sharma answered |
P(Gurpreet promoted) = P(G) = P(J) = 1/8
If the letters of the word ‘ INDEPENDENCE ‘ are written down at random in a row, then the chance that no two E’s occur together is- a)14/55
- b)1/55
- c)54/55
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If the letters of the word ‘ INDEPENDENCE ‘ are written down at random in a row, then the chance that no two E’s occur together is
a)
14/55
b)
1/55
c)
54/55
d)
none of these
|
|
Ankita Kaur answered |
There is no word given in the question for which the letters need to be arranged. Please provide more information.
The numbers 2, 4, 6, 8 and 10 are written separately on five slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Then, the sample space for the experiment is:- a)
- b)
- c)
- d)
Correct answer is option 'C'. Can you explain this answer?
The numbers 2, 4, 6, 8 and 10 are written separately on five slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Then, the sample space for the experiment is:
a)
b)
c)
d)
|
Vivek Saxena answered |
Select one of the numbers for the first draw and then any number except that one can appear in the second draw. do this for all the numbers one by one
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Ritapromoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John's promotion is the same as that of Gurpreet, Rita's chances of promotion are twice as likely as Johns. Aslam's chances are four times that of John.
Sol. Let Event :J = John promotedR = Rita promotedA = Aslam promotedG = Gurpreet promoted Given sample space, S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}i.e., S ={J, R, A, G)It is given that, chances of John’s promotion is same as that of Gurpreet.P(J) = P(G)Rita’s chances of promotion are twice as likely as John.P(R) = 2P(J)and Aslam’s chances of promotion are four times that of John.P(A) = 4P(J)Q. What is the probability that John got a promotion?- a)1/8
- b)1/4
- c)1/2
- d)1/6
Correct answer is option 'A'. Can you explain this answer?
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Rita
promoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John's promotion is the same as that of Gurpreet, Rita's chances of promotion are twice as likely as Johns. Aslam's chances are four times that of John.
Sol. Let Event :
J = John promoted
R = Rita promoted
A = Aslam promoted
G = Gurpreet promoted Given sample space, S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}
i.e., S ={J, R, A, G)
It is given that, chances of John’s promotion is same as that of Gurpreet.
P(J) = P(G)
Rita’s chances of promotion are twice as likely as John.
P(R) = 2P(J)
and Aslam’s chances of promotion are four times that of John.
P(A) = 4P(J)
Q. What is the probability that John got a promotion?
a)
1/8
b)
1/4
c)
1/2
d)
1/6
|
|
Rohini Desai answered |
Now, P(J) + P(R) + P(A) + P(G) = 1
⇒ P(J) + 2P(J) + 4P(J) + P(J) = 1
⇒ 8P(J) = 1
P(J) = P(John Promoted)= 1/8
The probability of having atleast one head in 5 throws of a coin is- a)1/32
- b)5/32
- c)31/32
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The probability of having atleast one head in 5 throws of a coin is
a)
1/32
b)
5/32
c)
31/32
d)
none of these
|
|
Jyoti Tiwari answered |
**Solution:**
When we toss a coin, the possible outcomes are head (H) or tail (T).
- The probability of getting a head on any one toss of a fair coin is 1/2.
So, the probability of getting a tail on any one toss of a fair coin is also 1/2.
**Finding the probability of having at least one head in 5 throws:**
To find the probability of having at least one head in 5 throws of a coin, we can use the concept of complementary events.
- The complementary event of having at least one head in 5 throws is having no heads in 5 throws.
The probability of having no heads in 5 throws is:
- (1/2) x (1/2) x (1/2) x (1/2) x (1/2) = 1/32
Therefore, the probability of having at least one head in 5 throws is:
- 1 - 1/32 = 31/32
Hence, the correct option is (c) 31/32.
When we toss a coin, the possible outcomes are head (H) or tail (T).
- The probability of getting a head on any one toss of a fair coin is 1/2.
So, the probability of getting a tail on any one toss of a fair coin is also 1/2.
**Finding the probability of having at least one head in 5 throws:**
To find the probability of having at least one head in 5 throws of a coin, we can use the concept of complementary events.
- The complementary event of having at least one head in 5 throws is having no heads in 5 throws.
The probability of having no heads in 5 throws is:
- (1/2) x (1/2) x (1/2) x (1/2) x (1/2) = 1/32
Therefore, the probability of having at least one head in 5 throws is:
- 1 - 1/32 = 31/32
Hence, the correct option is (c) 31/32.
A person throws successively with a pair of dice. The chance that he throws 9 before he throws 7 is- a)1/9
- b)2/45
- c)1/81
- d)2/5
Correct answer is option 'D'. Can you explain this answer?
A person throws successively with a pair of dice. The chance that he throws 9 before he throws 7 is
a)
1/9
b)
2/45
c)
1/81
d)
2/5
|
|
Dhruv Saha answered |
Solution:
The possible outcomes of the throw of a pair of dice are given below:
{1,1}, {1,2}, {1,3}, {1,4}, {1,5}, {1,6}, {2,1}, {2,2}, {2,3}, {2,4}, {2,5}, {2,6}, {3,1}, {3,2}, {3,3}, {3,4}, {3,5}, {3,6}, {4,1}, {4,2}, {4,3}, {4,4}, {4,5}, {4,6}, {5,1}, {5,2}, {5,3}, {5,4}, {5,5}, {5,6}, {6,1}, {6,2}, {6,3}, {6,4}, {6,5}, {6,6}
There are 6 ways to throw a 7 and 4 ways to throw a 9. Therefore, the probability of throwing a 7 before a 9 is 6/10 or 3/5.
To throw a 9 before a 7, the person must throw a 9 on the first roll, which has a probability of 4/36 or 1/9. If he does not throw a 9 on the first roll, he must throw non-7 numbers until he throws a 9 or a 7. The probability of throwing a non-7 number on any roll is 30/36 or 5/6. Therefore, the probability of throwing a 9 before a 7 is:
P(9 before 7) = P(throw 9 on first roll) + P(throw non-7 number on first roll) × P(throw 9 before 7 on subsequent rolls)
P(9 before 7) = 1/9 + 5/6 × P(9 before 7)
Solving for P(9 before 7), we get:
P(9 before 7) = 2/5
Therefore, the chance that he throws 9 before he throws 7 is 2/5.
The possible outcomes of the throw of a pair of dice are given below:
{1,1}, {1,2}, {1,3}, {1,4}, {1,5}, {1,6}, {2,1}, {2,2}, {2,3}, {2,4}, {2,5}, {2,6}, {3,1}, {3,2}, {3,3}, {3,4}, {3,5}, {3,6}, {4,1}, {4,2}, {4,3}, {4,4}, {4,5}, {4,6}, {5,1}, {5,2}, {5,3}, {5,4}, {5,5}, {5,6}, {6,1}, {6,2}, {6,3}, {6,4}, {6,5}, {6,6}
There are 6 ways to throw a 7 and 4 ways to throw a 9. Therefore, the probability of throwing a 7 before a 9 is 6/10 or 3/5.
To throw a 9 before a 7, the person must throw a 9 on the first roll, which has a probability of 4/36 or 1/9. If he does not throw a 9 on the first roll, he must throw non-7 numbers until he throws a 9 or a 7. The probability of throwing a non-7 number on any roll is 30/36 or 5/6. Therefore, the probability of throwing a 9 before a 7 is:
P(9 before 7) = P(throw 9 on first roll) + P(throw non-7 number on first roll) × P(throw 9 before 7 on subsequent rolls)
P(9 before 7) = 1/9 + 5/6 × P(9 before 7)
Solving for P(9 before 7), we get:
P(9 before 7) = 2/5
Therefore, the chance that he throws 9 before he throws 7 is 2/5.
Chapter doubts & questions for Probability - Online MCQ Tests for Commerce 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - Online MCQ Tests for Commerce in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily