All Exams >
SSC MTS / SSC GD >
Numerical Aptitude for SSC Exams >
All Questions
All questions of Algebra for SSC MTS / SSC GD Exam
What is the value of 225 + 225?- a)226
- b)250
- c)425
- d)450
- e)2625
Correct answer is option 'A'. Can you explain this answer?
What is the value of 225 + 225?
a)
226
b)
250
c)
425
d)
4
50
e)
2625

|
Anihegde1502 answered |
Take 2raise to25 common thjs ib bracket there will be (1+1)i.e 2raise to25 *2 thus power will get add 25+1 i.e 26 hence ans is option A
If ‘x’ and ‘y’ are non-negative integers, what is the value of x + y?(1) x4 is even, where x is a prime number.(2) xy is odd.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
If ‘x’ and ‘y’ are non-negative integers, what is the value of x + y?
(1) x4 is even, where x is a prime number.
(2) xy is odd.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
BT Educators answered |
(1) x = 2, y is unknown. Insufficient
(2) x and y unknown. Insufficient
(1)+(2) only possibility x=2, y=0; Sufficient
C is correct
(2) x and y unknown. Insufficient
(1)+(2) only possibility x=2, y=0; Sufficient
C is correct
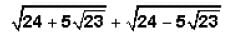 lies between:
lies between:- a)4 & 5
- b)5 & 6
- c)6 & 7
- d)7 & 8
- e)8 & 9
Correct answer is option 'D'. Can you explain this answer?
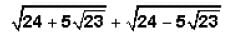 lies between:
lies between:a)
4 & 5
b)
5 & 6
c)
6 & 7
d)
7 & 8
e)
8 & 9
|
|
Anaya Patel answered |
In order to rid the expression of square roots, let's first square the entire expression. We are allowed to do this as long as we remember to "unsquare" whatever solution we get at that end.
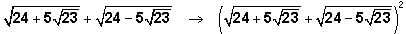
Notice that the new expression is of the form where
where
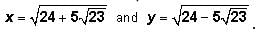
Recall that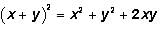 This is one of the GMAT's favorite expressions.
This is one of the GMAT's favorite expressions.
Returning to our expression:
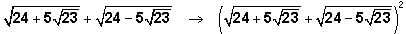
Notice that the new expression is of the form
 where
where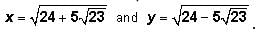
Recall that
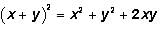 This is one of the GMAT's favorite expressions.
This is one of the GMAT's favorite expressions.Returning to our expression:


Notice that x2 + y2 neatly simplifies to 48. This leaves only the 2xy expression left to simplify.
In order to simplify
 recall that
recall that 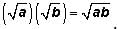
Thus,
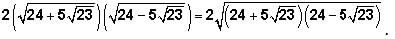
Notice that the expression under the square root sign is of the form
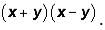 And recall that
And recall that 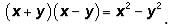 This is another one of the GMAT's favorite expressions. Returning to our expression:
This is another one of the GMAT's favorite expressions. Returning to our expression: 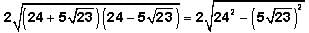
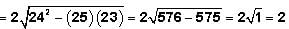
Finally then:
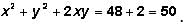
But now we must remember to "unsquare" (or take the square root of) our answer:
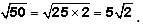
If a, b and x are integers such that 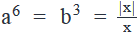 , what is the value of a - b
, what is the value of a - b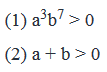
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If a, b and x are integers such that 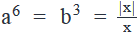 , what is the value of a - b
, what is the value of a - b
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Anaya Patel answered |
Steps 1 & 2: Understand Question and Draw Inferences
- As a6 is always positive,a6 = 1, i.e. a = 1 or -1
- So, we can reject the value of Possible values of a – b
- If a = 1 and b = 1, a – b = 0
- If a = -1 and b = 1, a- b = -2
- So, we need to find the unique value of a to find the value of a – b.Step 3: Analyze Statement 1 independently(1) a3 b7 > 0
- Rewriting a3b7 as ab(a2b6)
- Therefore, ab(a2b6)>0
- We know that a2b6 is always > 0 (even power of any number is always positive)
- So, for ab(a2b6)> 0
- ab > 0
- This tells us that a and b have same signs.
- Since b > 0, therefore a will also be greater than 0, so the value of a = 1.
- a – b = 1 -1 = 0
- Sufficient to answerStep 4: Analyze Statement 2 independently(2) a + b > 0
- If a = 1 and b = 1, a + b = 2 > 0
- If a = -1 and b = 1, a + b = 0, is not greater than zero
- Hence, we have a unique answer, where a =1 and b = 1Thus a – b = 1 – 1 = 0.Sufficient to answer.Step 5: Analyze Both Statements Together (if needed)As we have a unique answer from steps 3 and 4, this step is not required.Answer: D
James deposited $1,000 each in two investment schemes X and Y. Scheme X doubles the invested amount every 7 years and scheme Y doubles the invested amount every 14 years. If James withdraws $500 from scheme X at the end of every 7th year, how many years will it take for the total amount invested in schemes X and Y to amount more than $40,000?
- a)14
- b)28
- c)42
- d)56
- e)70
Correct answer is option 'C'. Can you explain this answer?
James deposited $1,000 each in two investment schemes X and Y. Scheme X doubles the invested amount every 7 years and scheme Y doubles the invested amount every 14 years. If James withdraws $500 from scheme X at the end of every 7th year, how many years will it take for the total amount invested in schemes X and Y to amount more than $40,000?
a)
14
b)
28
c)
42
d)
56
e)
70

|
Wizius Careers answered |
Given
- Scheme X doubles the invested amount every 7 years
- James deposited $1000 in scheme X
- James withdraws $500 from scheme X after the end of every 7 years
- Scheme Y doubles the invested amount after every 14 years
- James deposited $1,000 in scheme Y
To Find: Number of years it will take total amount deposited in schemes X and Y to grow to > $40,000?
Approach
- For finding the number of years it will take the deposits in schemes X and Y to grow to more than $40,000, we need to find the amount in both the schemes X and Y after every 7 years.(As amount in scheme X doubles after every 7 years, we will need to calculate the amount at the end of every 7 years and not at the end of 14 years).
- Scheme X
- As the amount invested in scheme X doubles every 7 years, we will need to calculate the amount in scheme X after every interval of 7 years
- However, we will need to make sure that we subtract $500 at each interval of 7 years from the final amount
- Scheme Y
- As the amount invested in scheme Y doubles after every 14 years, we will need to calculate the amount in scheme Y after every interval of 14 years.
- At each interval, we will calculate the sum of amounts in scheme X and Y to check if it exceeds $40,000.
Working Out
- Amount at the end of year 7 in scheme X = $1000 * 2 = $2000
- However James withdrew $500 at the end of 7th year, So, the amount remaining will be $2000 – $500 = $1500
- The same logic has been applied in calculating the amounts at the end of every 7 year interval
- Amount at the end of year 14 in scheme Y = $1000 * 2 = $2000
- The same logic has been applied in calculating the amounts at the end of every 14 years interval.
- The same logic has been applied in calculating the amounts at the end of every 14 years interval.
- We can see that the total amount in schemes X and Y exceed $40,000 by the end of the year 42.
Answer: C
If f(x) = -2x + 8 & f(p) = 16, find the value of p?- a)-12
- b)-8
- c)-4
- d)4
- e)12
Correct answer is option 'C'. Can you explain this answer?
If f(x) = -2x + 8 & f(p) = 16, find the value of p?
a)
-12
b)
-8
c)
-4
d)
4
e)
12

|
Palak Saha answered |
Given, f(x) = -2x + 8 and f(p) = 16
To find: The value of p
Solution:
Substitute f(p) = 16 in the equation f(x) = -2x + 8
f(p) = -2p + 8 = 16
-2p = 16 - 8
-2p = 8
Divide both sides by -2
p = 8/-2
p = -4
Therefore, the value of p is -4.
Hence, the correct option is (c) -4.
To find: The value of p
Solution:
Substitute f(p) = 16 in the equation f(x) = -2x + 8
f(p) = -2p + 8 = 16
-2p = 16 - 8
-2p = 8
Divide both sides by -2
p = 8/-2
p = -4
Therefore, the value of p is -4.
Hence, the correct option is (c) -4.
If g(x) = -2x2 + 8 and g (-q) = -24, which of the following could be the value of q?- a)-4
- b)-2
- c)-1
- d)1
- e)2
Correct answer is option 'A'. Can you explain this answer?
If g(x) = -2x2 + 8 and g (-q) = -24, which of the following could be the value of q?
a)
-4
b)
-2
c)
-1
d)
1
e)
2

|
Parth Singh answered |
Given:
- g(x) = -2x^2 + 8
- g(-q) = -24
To find:
- Possible values of q
Solution:
Substitute -q in place of x in g(x) to get g(-q)
g(-q) = -2(-q)^2 + 8
g(-q) = -2q^2 + 8
Given that g(-q) = -24, we can set up the equation:
-2q^2 + 8 = -24
Simplifying, we get:
-2q^2 = -32
Dividing by -2, we get:
q^2 = 16
Taking the square root of both sides, we get:
q = ±4
Therefore, the possible values of q are -4 and 4.
Option A (-4) is the correct answer.
- g(x) = -2x^2 + 8
- g(-q) = -24
To find:
- Possible values of q
Solution:
Substitute -q in place of x in g(x) to get g(-q)
g(-q) = -2(-q)^2 + 8
g(-q) = -2q^2 + 8
Given that g(-q) = -24, we can set up the equation:
-2q^2 + 8 = -24
Simplifying, we get:
-2q^2 = -32
Dividing by -2, we get:
q^2 = 16
Taking the square root of both sides, we get:
q = ±4
Therefore, the possible values of q are -4 and 4.
Option A (-4) is the correct answer.
If Z is a positive integer such that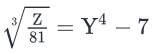
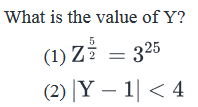
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If Z is a positive integer such that
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Meera Rana answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
- Z is a positive integer
- Z = 81(Y4 – 7)3 . . . (1)
We need to find the value of Y.
Step 3: Analyze Statement 1 independently
- Squaring both sides:
- Z5 = 350
- Taking 5th root on both sides:
- Z = 310 . . . (2)
- Put (2) in (1):
- 310 = 34(Y4 – 7)3
- 36 = (Y4 – 7)3
- Taking the cube-root on both sides:
- 32 = Y4 – 7
- Y4 = 9 + 7 = 16
- Y4 = 24 = (-2)4
- Y = 2 or -2
Not sufficient to determine a unique value of Y.
Step 4: Analyze Statement 2 independently
(2) |Y-1| < 4
- Distance of Y from 1 on the number line is less than 4 units
- -3 < Y < 5
Multiple values of Y possible. Not sufficient.
Step 5: Analyze Both Statements Together (if needed)
- From St. 1, Y = 2 or – 2
- From St. 2, -3 < Y < 5
- This inequality is satisfied by both 2 and -2
So, even after combining both statements, we have 2 possible values of Y
Since we couldn’t find a unique value of Y, the correct answer. Is Option E.
In a Country X, temperature decrease (in degrees) is linearly related to percentage increase in sale of water heaters and is given by the relation:ΔT= ky+5 Where,ΔT is temperature decrease (in degrees).y is the increase in sale of water heaters (in percentage).K is a constant.A temperature decrease of 10 degrees results in a 1% increase in sale of water heaters. What would be the percentage increase in sale of water heaters when temperature decreases by 15 degrees?- a)1.5%
- b)2%
- c)2.5%
- d)3%
- e)3.5%
Correct answer is option 'B'. Can you explain this answer?
In a Country X, temperature decrease (in degrees) is linearly related to percentage increase in sale of water heaters and is given by the relation:
ΔT= ky+5
Where,
ΔT is temperature decrease (in degrees).
y is the increase in sale of water heaters (in percentage).
K is a constant.
A temperature decrease of 10 degrees results in a 1% increase in sale of water heaters. What would be the percentage increase in sale of water heaters when temperature decreases by 15 degrees?
a)
1.5%
b)
2%
c)
2.5%
d)
3%
e)
3.5%

|
Tushar Ghosh answered |
∆T=ky+5;
given: ∆T=10
y=1
therefore: 10= k(1) +5
=> k= 10-5=5
having determined value of k=5, we add new values as
∆T=15
k=5
y=?
thus, 15=5y+5
or, 5y=15-5
5y=10
y=2
since y is the value in percentage of increase in sale of water heater, therefore, the percentage of increase in water heater is 2%.
given: ∆T=10
y=1
therefore: 10= k(1) +5
=> k= 10-5=5
having determined value of k=5, we add new values as
∆T=15
k=5
y=?
thus, 15=5y+5
or, 5y=15-5
5y=10
y=2
since y is the value in percentage of increase in sale of water heater, therefore, the percentage of increase in water heater is 2%.
A polynomial function P(x) is defined as,
P(x) = 4x3 – 2x2
If P (z -2) =0 & z ≠ 2, find the value of z?
- a)-3/2
- b)+1/2
- c)1
- d)+5/2
- e)+7/2
Correct answer is option 'D'. Can you explain this answer?
A polynomial function P(x) is defined as,
P(x) = 4x3 – 2x2
If P (z -2) =0 & z ≠ 2, find the value of z?
a)
-3/2
b)
+1/2
c)
1
d)
+5/2
e)
+7/2

|
Siddharth Pillai answered |
Solution:
Given, P(x) = 4x3 - 2x2
Let z-2 = k
P(z-2) = P(k) = 4k3 - 2k2
We know that P(k) = 0
Therefore, 4k3 - 2k2 = 0
2k2(2k - 1) = 0
k = 0 or k = 1/2
Now, z-2 = k
So, z = k+2
For k = 0, z = 2
For k = 1/2, z = 5/2
Therefore, the possible values of z are 2 and 5/2, but since z ≤ 2, the only possible value of z is 5/2.
Hence, the correct answer is option (D) 5/2.
Given, P(x) = 4x3 - 2x2
Let z-2 = k
P(z-2) = P(k) = 4k3 - 2k2
We know that P(k) = 0
Therefore, 4k3 - 2k2 = 0
2k2(2k - 1) = 0
k = 0 or k = 1/2
Now, z-2 = k
So, z = k+2
For k = 0, z = 2
For k = 1/2, z = 5/2
Therefore, the possible values of z are 2 and 5/2, but since z ≤ 2, the only possible value of z is 5/2.
Hence, the correct answer is option (D) 5/2.
There are two classrooms A and B. The sum of the number of students in both classrooms is more than 120. Is the number of students in class B greater than 20? (1) If number of students in classroom A are doubled and number of students in classroom B are halved, the difference between the number of students in classroom A and B is less than 200.(2) If 20 students from each classroom leave the school, the sum of number of students in both classes would be more than 80. - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
There are two classrooms A and B. The sum of the number of students in both classrooms is more than 120. Is the number of students in class B greater than 20?
(1) If number of students in classroom A are doubled and number of students in classroom B are halved, the difference between the number of students in classroom A and B is less than 200.
(2) If 20 students from each classroom leave the school, the sum of number of students in both classes would be more than 80.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Lavanya Menon answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given that the number of students in classes A and B combined is more than 120. We have to find whether the number of students in class B is more than 20.
Let’s say the number of students in class A is x, and the number of students in class B is y.
So, we can say that:
x+y>120
Since there is no other information given in the sentence, let’s move on to the analysis of the statement I.
Step 3: Analyze Statement 1
2x−y/2<200
4x−y<400 ................... (2)
By multiplying inequality (1) with -4, we get:
−4x−4y<−480 .....................(3)
Adding (2) and (3),
−5y<−80
By multiplying the above inequality with -1, we get:
5y>80y>16
So, y can take any value greater than 16. Thus, we can’t say whether it is greater than 20 or not.
Hence, statement I is not sufficient to answer the question: Is the number of students in class B is more than 20?
Step 4: Analyze Statement 2
Per statement II:
(x−20)+(y−20)>80
x+y>120
This is the same information given in the original sentence. So, from this information we can’t say whether y is greater than 20 or not.
Hence, statement II alone is insufficient to answer the question: Is the number of students in class B is more than 20?
Step 5: Analyze Both Statements Together (if needed)
Since statement I and II alone are not sufficient to answer the question, let’s analyse them together.
However, since statement II provides the same information given in the original sentence, analysing both the statements together is equivalent to analysing statement I alone.
Thus, even both statements combined are not sufficient to answer the question: Is the number of students in class B is more than 20?
Answer: Option (E)
The correct answer is: Statements (1) and (2) TOGETHER are NOT sufficient.
If S is the infinite sequence S1 = 6, S2 = 12, ..., Sn = Sn-1 + 6,..., what is the sum of all terms in the set {S13, S14, ..., S28}?- a)1800
- b)1845
- c)1890
- d)1968
- e)2016
Correct answer is option 'D'. Can you explain this answer?
If S is the infinite sequence S1 = 6, S2 = 12, ..., Sn = Sn-1 + 6,..., what is the sum of all terms in the set {S13, S14, ..., S28}?
a)
1800
b)
1845
c)
1890
d)
1968
e)
2016

|
Avantika Dey answered |
For sequence S, any value Sn equals 6n. Therefore, the problem can be restated as determining the sum of all multiples of 6 between 78 (S13) and 168 (S28), inclusive. The direct but time-consuming approach would be to manually add the terms: 78 + 84 = 162; 162 + 90 = 252; and so forth.
The solution can be found more efficiently by identifying the median of the set and multiplying by the number of terms. Because this set includes an even number of terms, the median equals the average of the two ‘middle’ terms, S20 and S21, or (120 + 126)/2 = 123. Given that there are 16 terms in the set, the answer is 16(123) = 1,968.
The correct answer is D
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/bQ.Which of the following functions will represent a2 – b2?- a)(a M b) H (a D b)
- b)(a H b) M (a P b)
- c)(a D b)/(a M b)
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
Q.
Which of the following functions will represent a2 – b2?
a)
(a M b) H (a D b)
b)
(a H b) M (a P b)
c)
(a D b)/(a M b)
d)
None of these
|
|
Anaya Patel answered |
Option a = (a – b) (a + b) = a2 – b2
$x = 6x +4 and £x = 8x – 2Find the value of x for which $x = £x?- a)-3
- b)-2
- c)1
- d)2
- e)3
Correct answer is option 'E'. Can you explain this answer?
$x = 6x +4 and £x = 8x – 2
Find the value of x for which $x = £x?
a)
-3
b)
-2
c)
1
d)
2
e)
3

|
Bhavana Kulkarni answered |
Solution:
Given, $x = 6x + 4$ and $x = 8x - 2$
Simplifying the above equations, we get
$5x = -4$ and $7x = 2$
Solving for x, we get
$x = -\frac{4}{5}$ and $x = \frac{2}{7}$
Since both values of x are not equal, we cannot find the value of x for which $x = x$ from the given equations.
Therefore, the answer is none of the given options.
Given, $x = 6x + 4$ and $x = 8x - 2$
Simplifying the above equations, we get
$5x = -4$ and $7x = 2$
Solving for x, we get
$x = -\frac{4}{5}$ and $x = \frac{2}{7}$
Since both values of x are not equal, we cannot find the value of x for which $x = x$ from the given equations.
Therefore, the answer is none of the given options.
Find the minimum value of the function fix) = log2 (x2 - 2x + 5).- a)-4
- b)2
- c)4
- d)-2
Correct answer is option 'B'. Can you explain this answer?
Find the minimum value of the function fix) = log2 (x2 - 2x + 5).
a)
-4
b)
2
c)
4
d)
-2
|
|
Alok Verma answered |
Method to Solve :
y= x2 – 2x + 5
Step 1 : Differentiate with respect to xStep 2 : Equate to 0
Step 3 : Find the value of x
dy/dx=2x-2 =0 implies x=1
Hence f(1)= 12 – 2 + 5= 4
Thus minimum value of the argument of the log is 4.
So minimum value of the function is log 4 (base 2) =2
-2x - ky -9 = 04x – 10y + 18 = 0What is the value of k if the system of linear equations shown above has infinite solutions?- a)-5
- b)-1
- c)1
- d)3
- e)5
Correct answer is option 'A'. Can you explain this answer?
-2x - ky -9 = 0
4x – 10y + 18 = 0
What is the value of k if the system of linear equations shown above has infinite solutions?
a)
-5
b)
-1
c)
1
d)
3
e)
5

|
Siddharth Pillai answered |
Given equations,
-2x - ky -9 = 0 .. (a)
4x – 10y + 18 = 0 .. (b)
Multiply the equation (a) with 2 and add it to equation (b), we get
⇒ -4x - 2ky - 18 +4x - 10y + 18 = 0
⇒ -2ky -10y = 0
⇒ -2ky = 10y
⇒ -2k = 10
⇒ k = -5
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1The value of f(8) is- a)0
- b)13
- c)–5
- d)–9
Correct answer is option 'B'. Can you explain this answer?
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
The value of f(8) is
a)
0
b)
13
c)
–5
d)
–9
|
|
Alok Verma answered |
f(1) = 0, f(2) = 1,
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
13
The sum of the squares of the first 15 positive integers (12 + 22 + 32 + . . . + 152) is equal to 1240. What is the sum of the squares of the second 15 positive integers (162 + 172 + 182 + . . . + 302) ?- a)2480
- b)3490
- c)6785
- d)8215
- e)9255
Correct answer is option 'D'. Can you explain this answer?
The sum of the squares of the first 15 positive integers (12 + 22 + 32 + . . . + 152) is equal to 1240. What is the sum of the squares of the second 15 positive integers (162 + 172 + 182 + . . . + 302) ?
a)
2480
b)
3490
c)
6785
d)
8215
e)
9255

|
Nitya Kumar answered |
The key to solving this problem is to represent the sum of the squares of the second 15 integers as follows: (15 + 1)2 + (15 + 2)2 + (15 + 3)2 + . . . + (15 + 15)2.
Recall the popular quadratic form, (a + b)2 = a2 + 2ab + b2. Construct a table that uses this expansion to calculate each component of each term in the series as follows:


In order to calculate the desired sum, we can find the sum of each of the last 3 columns and then add these three subtotals together. Note that since each column follows a simple pattern, we do not have to fill in the whole table, but instead only need to calculate a few terms in order to determine the sums.
The column labeled a2 simply repeats 225 fifteen times; therefore, its sum is 15(225) = 3375.
The column labeled 2ab is an equally spaced series of positive numbers. Recall that the average of such a series is equal to the average of its highest and lowest values; thus, the average term in this series is (30 + 450) / 2 = 240. Since the sum of n numbers in an equally spaced series is simply n times the average of the series, the sum of this series is 15(240) = 3600.
The last column labeled b2 is the sum of the squares of the first 15 integers. This was given to us in the problem as 1240.
Finally, we sum the 3 column totals together to find the sum of the squares of the second 15 integers: 3375 + 3600 + 1240 = 8215. The correct answer choice is (D).
If 0 < a <1 and 0 < b < 1 and if a < b, which of the following expressions will have the highestvalue?- a)(a M b)
- b)(a D b)
- c)(a P b)
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
If 0 < a <1 and 0 < b < 1 and if a < b, which of the following expressions will have the highestvalue?
a)
(a M b)
b)
(a D b)
c)
(a P b)
d)
Cannot be determined
|
|
Yash Patel answered |
Again (a + b) or a/b can both be greater than each other depending on the values we take for a and b.
E.g. for a = 0.9 and b = 0.91, a + b > a/b.
For a = 0.1 and b = 0.11, a + b < a/b
E.g. for a = 0.9 and b = 0.91, a + b > a/b.
For a = 0.1 and b = 0.11, a + b < a/b
Find the value of z such that 2(z-1)3 + 6(1-z)3 = 32?- a)-2
- b)-1
- c)0
- d)1
- e)2
Correct answer is option 'B'. Can you explain this answer?
Find the value of z such that 2(z-1)3 + 6(1-z)3 = 32?
a)
-2
b)
-1
c)
0
d)
1
e)
2
|
|
Yash Patel answered |
⇒ 2(z-1)3 + 6(1-z)3 = 32
⇒ 2 [ z3 -1 - 3z(z-1) ] + 6 [1 - z3 - 3z(1-z)] = 32
⇒ 2 [ z3 - 1 -3z2 + 3z ] + 6 [ 1 - z3 -3z + 3z2 ] = 32
⇒ 2z3 - 2 - 6z2 + 6z + 6 - 6z3 -18z2 + 18z = 32
⇒ -4z3 + 12z2 - 12z + 4 = 32
Substract 32 from both sides we get,
⇒ -4z3 + 12z2 - 12z + 4 - 32 = 32 - 32
⇒ -4z3 + 12z2 - 12z - 28 = 0
⇒ -4( z + 1 )( z2 - 4z -7) = 0
⇒ ( z + 1 )( z2 - 4z -7) = 0
Then,
( z + 1 ) = 0
z = -1
or
( z2 - 4z -7) = 0
z = 2 + √3i, 2 - √3i
If the sum of the first five terms of an Arithmetic sequence is equal to 120 and the sum of the next five terms of the same Arithmetic Sequence is equal to 245, what is the 4th term of this Sequence?- a)29
- b)34
- c)81
- d)86
- e)91
Correct answer is option 'A'. Can you explain this answer?
If the sum of the first five terms of an Arithmetic sequence is equal to 120 and the sum of the next five terms of the same Arithmetic Sequence is equal to 245, what is the 4th term of this Sequence?
a)
29
b)
34
c)
81
d)
86
e)
91
|
|
Lavanya Menon answered |
Given:
- Sum of the first 5 terms of an arithmetic sequence = 120
- Sum of the next 5 terms of the same arithmetic sequence = 245
- Let the first term of this arithmetic sequence be x1 and let the common difference be d.
To Find:
- 4th term of the arithmetic sequence.
- So the 4th term of the sequence will become x1+3d
- So we need to find the value of x1 and d or the value of x1+3d to find the 4th term of the sequence.
Approach:
- We know that the sum of first n terms of the Arithmetic Sequence is given as
where n is the number of terms in the arithmetic sequence.
- Using the formula above for the sum of first 5 terms of the sequence, we will get an equation in terms of and common difference d, as we are given the sum of first 5 terms of the sequence.
- We are also given the sum of next 5 terms of the sequence. So, we will be able to calculate the sum of first 10 terms of the sequence.
→ Sum of first 10 terms of sequence = Sum of first 5 terms + sum of next 5 terms. - Using the formula above for the sum of first 10 terms of sequence, we will get another equation in terms of x1 and common difference d.
- Using these two equations in x1 and d, we will be able to calculate the value of x1 and d.
- Knowing the values of x1 and d, we will be able to calculate the fourth term of the sequence, which is equal to x1+3d
Working out:
- Sum of first 5 terms of the arithmetic sequence = 120
- Putting this in formula of sum of first n terms, where n=5 and z=120, we get
- Sum of the next 5 terms of the sequence = 245
- Sum of the first 10 terms of the sequence = Sum of the first five terms + Sum of the next five terms.
- Sum of the first 10 terms of the sequence = 120+245 = 365
- Sum of the first 10 terms of the sequence = 120+245 = 365
- Now, using the formula of the sum of first n terms of an arithmetic sequence, we get
- Solving Equations 1 and 2.
- Multiplying ‘equation 1’ by 2, we have 10x1+20d =240 ...(Equation 3)
Now that we have values of x1 and d. The value of 4th term of the sequence will be
⇒ x1+3(d)=14+3(5)=29
Answer:
- The value of 4th term of the sequence is 29.
- Hence the correct answer is option A
Alternate method
- Let the first term be 'a' and common dfference between any two cosecutive terms be 'd'
Therefore,
- 1st term = a
- 5th term = a + 4d
- 6th term = a + 5d
- 10th term = a + 9d
- Average of first five terms of an arithemetic sequence = (First term + Last term)/2 = (a + a +4d) / 2 = a + 2d
- Sum of first five terms = Average of first five terms * 5 = (a + 2d) * 5 = 120
- a + 2d = 120/5 = 24 ---------------- Eq(1)
- Average of next five terms of the arithemetic sequence = (First term + Last term)/2 = (a+ 5d + a +9d) / 2 = a + 7d
- Sum of five terms = Average of five terms * 5 = (a + 7d) * 5 = 245
- a + 7d = 245/5 = 49---------------- Eq(2)
Solving Eq(1) and (2) we get
- d = 5
- 4th term =
- a + 3d = (a+2d)+ d = 24 + 5 = 29
Correct Answer: Option A
Find the value of 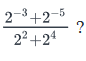
- a)1/256
- b)1/128
- c)1/64
- d)1/32
- e)1/16
Correct answer is option 'B'. Can you explain this answer?
Find the value of 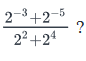
a)
1/256
b)
1/128
c)
1/64
d)
1/32
e)
1/16
|
|
Catalyst Learningacademy answered |
We want to evaluate:
(2-3 + 2-5) / (22 + 24).
Step 1. Compute the numerator: 2-3 = 1 / 23 = 1 / 8
2-5 = 1 / 25 = 1 / 32
2-5 = 1 / 25 = 1 / 32
Hence, 2-3 + 2-5 = (1/8) + (1/32) = (4/32) + (1/32) = 5/32.
Step 2. Compute the denominator: 22 = 4
24 = 16
So, 22 + 24 = 4 + 16 = 20.
24 = 16
So, 22 + 24 = 4 + 16 = 20.
Step 3. Combine numerator and denominator: (5/32) / 20 = (5/32) × (1/20) = 5 / (32 × 20) = 5/640 = 1/128.
Thus, the value of the given expression is 1/128.
Find the maximum value of the function 1/(x2 – 3x + 2).- a)11/4
- b)1/4
- c)0
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Find the maximum value of the function 1/(x2 – 3x + 2).
a)
11/4
b)
1/4
c)
0
d)
None of these
|
|
Aarav Sharma answered |
To find the maximum value of the function 1/(x^2 - 3x + 2), we need to determine the critical points of the function and then evaluate the function at those critical points.
1. Finding the critical points:
To find the critical points, we need to find the values of x where the derivative of the function is equal to zero or undefined. The derivative of the given function is given by:
f'(x) = (-2x + 3)/(x^2 - 3x + 2)^2
Setting f'(x) equal to zero and solving for x:
(-2x + 3)/(x^2 - 3x + 2)^2 = 0
Since the numerator can never be equal to zero, the only way for the fraction to be zero is if the denominator is equal to zero. Thus, we need to solve the equation:
x^2 - 3x + 2 = 0
Factoring this quadratic equation, we get:
(x - 1)(x - 2) = 0
Setting each factor equal to zero, we find two critical points:
x - 1 = 0 => x = 1
x - 2 = 0 => x = 2
2. Evaluating the function at the critical points:
We substitute the critical points into the original function to find the corresponding y-values:
f(1) = 1/(1^2 - 3(1) + 2) = 1/0 (undefined)
f(2) = 1/(2^2 - 3(2) + 2) = 1/0 (undefined)
Since the function is undefined at both critical points, there is no maximum value for the given function.
Therefore, the correct answer is option 'D' (None of these).
1. Finding the critical points:
To find the critical points, we need to find the values of x where the derivative of the function is equal to zero or undefined. The derivative of the given function is given by:
f'(x) = (-2x + 3)/(x^2 - 3x + 2)^2
Setting f'(x) equal to zero and solving for x:
(-2x + 3)/(x^2 - 3x + 2)^2 = 0
Since the numerator can never be equal to zero, the only way for the fraction to be zero is if the denominator is equal to zero. Thus, we need to solve the equation:
x^2 - 3x + 2 = 0
Factoring this quadratic equation, we get:
(x - 1)(x - 2) = 0
Setting each factor equal to zero, we find two critical points:
x - 1 = 0 => x = 1
x - 2 = 0 => x = 2
2. Evaluating the function at the critical points:
We substitute the critical points into the original function to find the corresponding y-values:
f(1) = 1/(1^2 - 3(1) + 2) = 1/0 (undefined)
f(2) = 1/(2^2 - 3(2) + 2) = 1/0 (undefined)
Since the function is undefined at both critical points, there is no maximum value for the given function.
Therefore, the correct answer is option 'D' (None of these).
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1What will be the domain of the definition of the function f(x) = 8–xC 5–x for positive values of x?- a){1, 2, 3}
- b){1, 2, 3, 4}
- c){1, 2, 3, 4, 5}
- d){1, 2, 3, 4, 5, 6, 7, 8}
Correct answer is option 'C'. Can you explain this answer?
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
What will be the domain of the definition of the function f(x) = 8–xC 5–x for positive values of x?
a)
{1, 2, 3}
b)
{1, 2, 3, 4}
c)
{1, 2, 3, 4, 5}
d)
{1, 2, 3, 4, 5, 6, 7, 8}
|
|
Nikita Singh answered |
f(1) = 0, f(2) = 1,
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
For any nCr, n should be positive and r ≥ 0.
Thus, for positive x, 5 – x ≥ 0
fi x = 1, 2, 3, 4, 5.
Thus, for positive x, 5 – x ≥ 0
fi x = 1, 2, 3, 4, 5.
If f(x) = 3x + 6, then what is the value of f (2) + f(7)? - a)f(8)
- b)f(9)
- c)f(10)
- d)f(11)
- e)f(12)
Correct answer is option 'D'. Can you explain this answer?
If f(x) = 3x + 6, then what is the value of f (2) + f(7)?
a)
f(8)
b)
f(9)
c)
f(10)
d)
f(11)
e)
f(12)

|
Arjun Iyer answered |
Solution:
Given: f(x) = 3x - 6
We need to find f(2) + f(7)
Substituting x = 2 and x = 7 in the given equation, we get:
f(2) = 3(2) - 6 = 0
f(7) = 3(7) - 6 = 15
Therefore, f(2) + f(7) = 0 + 15 = 15
Hence, the correct answer is option D.
Given: f(x) = 3x - 6
We need to find f(2) + f(7)
Substituting x = 2 and x = 7 in the given equation, we get:
f(2) = 3(2) - 6 = 0
f(7) = 3(7) - 6 = 15
Therefore, f(2) + f(7) = 0 + 15 = 15
Hence, the correct answer is option D.
If n is a positive integer greater than 2, what is the greatest prime factor of 3n + 3n + 3n – 3n-2?- a)3
- b)5
- c)7
- d)11
- e)13
Correct answer is option 'E'. Can you explain this answer?
If n is a positive integer greater than 2, what is the greatest prime factor of 3n + 3n + 3n – 3n-2?
a)
3
b)
5
c)
7
d)
11
e)
13

|
Arnab Kumar answered |
Solution:
Firstly, we can simplify the given expression by combining the exponents:
3n 3n 3n 3n-2 = 33n-2 * 33n = 36n
Now, to find the greatest prime factor of 36n, we can factorize it into prime factors:
36n = 2^2 * 3^2 * n
The greatest prime factor of 36n would be the largest prime factor of n. Since n is greater than 2, we know that it is either a prime number or a composite number with prime factors.
To find the greatest prime factor of n, we can start by dividing n by 2 repeatedly until we get an odd number. For example, if n is 60, we can divide it by 2 three times to get 15:
60 ÷ 2 = 30
30 ÷ 2 = 15
Now, we can check if 15 is a prime number or if it has any other prime factors. We can do this by dividing 15 by the smallest prime numbers, which are 2, 3, 5, 7, 11, 13, etc.
15 ÷ 3 = 5
Since 5 is a prime number, it is the greatest prime factor of n. Therefore, the greatest prime factor of 36n is 13, which is the largest prime factor of 3.
Firstly, we can simplify the given expression by combining the exponents:
3n 3n 3n 3n-2 = 33n-2 * 33n = 36n
Now, to find the greatest prime factor of 36n, we can factorize it into prime factors:
36n = 2^2 * 3^2 * n
The greatest prime factor of 36n would be the largest prime factor of n. Since n is greater than 2, we know that it is either a prime number or a composite number with prime factors.
To find the greatest prime factor of n, we can start by dividing n by 2 repeatedly until we get an odd number. For example, if n is 60, we can divide it by 2 three times to get 15:
60 ÷ 2 = 30
30 ÷ 2 = 15
Now, we can check if 15 is a prime number or if it has any other prime factors. We can do this by dividing 15 by the smallest prime numbers, which are 2, 3, 5, 7, 11, 13, etc.
15 ÷ 3 = 5
Since 5 is a prime number, it is the greatest prime factor of n. Therefore, the greatest prime factor of 36n is 13, which is the largest prime factor of 3.
Ajesh saves Rs 50,000 every year and deposits the money in a bank at compound interest of 10%(compunded annually).What would be his total saving at the end of the 5th year?- a)Rs 3,05,255
- b)Rs 1,05,255
- c)Rs 8,05,255
- d)Rs 4,05,255
Correct answer is option 'A'. Can you explain this answer?
Ajesh saves Rs 50,000 every year and deposits the money in a bank at compound interest of 10%(compunded annually).What would be his total saving at the end of the 5th year?
a)
Rs 3,05,255
b)
Rs 1,05,255
c)
Rs 8,05,255
d)
Rs 4,05,255
|
|
Rajeev Kumar answered |
At the end of the 1st year, he will get Rs 50000, it will give him interest for 4 years compounded annually
Hence at the end of 5 years, this amount will become 50000(1.1)4
Similarly, the amount deposited in the 2nd year will give interest for 3 years. Hence it will become 50000(1.1)3
Similarly, we can calculate for the remaining years.
The total saving at the end of the 5th year would be a GP, given by
Net saving = 50000(1.1)4 + 50000(1.1)3 ..... 50000
Thus net saving =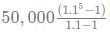 = Rs 3,05,255
= Rs 3,05,255
Hence at the end of 5 years, this amount will become 50000(1.1)4
Similarly, the amount deposited in the 2nd year will give interest for 3 years. Hence it will become 50000(1.1)3
Similarly, we can calculate for the remaining years.
The total saving at the end of the 5th year would be a GP, given by
Net saving = 50000(1.1)4 + 50000(1.1)3 ..... 50000
Thus net saving =
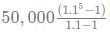 = Rs 3,05,255
= Rs 3,05,255Which of the following is an even function?- a)x–8
- b)x3
- c)x–33
- d)x73
Correct answer is option 'A'. Can you explain this answer?
Which of the following is an even function?
a)
x–8
b)
x3
c)
x–33
d)
x73
|
|
Anaya Patel answered |
x–8 is even since f(x) = f(–x) in this case.
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/bQ.What is the value of (3M4H2D4P8M2)?- a)6.5
- b)6
- c)–6.5
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
Q.
What is the value of (3M4H2D4P8M2)?
a)
6.5
b)
6
c)
–6.5
d)
None of these
|
|
Alok Verma answered |
3 – 4 × 2 + 4/8 – 2 = 3 – 8 + 0.5 – 2 = – 6.5
(using BODMAS rule)
(using BODMAS rule)
Mike visits his childhood friend Alan at a regular interval of 4 months. For example, if Mike visits Alan on 1st Jan, his next visit would be on 1st May and so on. He started this routine on his 25th birthday. Yesterday, he celebrated his Nth birthday. How many visits has Mike made so far (including the first visit on his 25th birthday)?- a)n – 24
- b)2n – 50
- c)2n – 49
- d)3n – 75
- e)3n – 74
Correct answer is option 'E'. Can you explain this answer?
Mike visits his childhood friend Alan at a regular interval of 4 months. For example, if Mike visits Alan on 1st Jan, his next visit would be on 1st May and so on. He started this routine on his 25th birthday. Yesterday, he celebrated his Nth birthday. How many visits has Mike made so far (including the first visit on his 25th birthday)?
a)
n – 24
b)
2n – 50
c)
2n – 49
d)
3n – 75
e)
3n – 74
|
|
Aisha Gupta answered |
In a period of 1 year, Mike visits Alan 3 times (12 months divided by 4). However this excludes the first time visit and takes into consideration the subsequent visits only. So starting on his 25th birthday, Mike will visit Alan 3(n-25) times up till his nth birthday. However we have to add the first visit as well. So the final answer would be 3n-74 .
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?- a)25
- b)8
- c)6
- d)5
- e)2
Correct answer is option 'C'. Can you explain this answer?
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?
a)
25
b)
8
c)
6
d)
5
e)
2

|
Prisha Mukherjee answered |
Solution:
When we multiply any number by 10, we add one zero to the end of that number. For example, 10, 20, 30, and so on.
Similarly, when we multiply any number by 100, we add two zeros to the end of that number. For example, 100, 200, 300, and so on.
Therefore, the number of trailing zeros in a factorial is equal to the number of times the factorial can be divided by 10.
To find the number of trailing zeros in 25!, we need to find the number of times 25! can be divided by 10.
Step 1: Prime factorize 10
10 = 2 × 5
Step 2: Count the number of factors of 5 in 25!
We can count the number of factors of 5 in 25! by dividing 25 by 5, then dividing the result by 5 again, and so on until we get a quotient less than 5.
25 ÷ 5 = 5
5 ÷ 5 = 1
Therefore, there are 5 + 1 = 6 factors of 5 in 25!
Step 3: Count the number of factors of 2 in 25!
We can count the number of factors of 2 in 25! by dividing 25 by 2, then dividing the result by 2 again, and so on until we get a quotient less than 2.
25 ÷ 2 = 12
12 ÷ 2 = 6
6 ÷ 2 = 3
3 ÷ 2 = 1
Therefore, there are 12 + 6 + 3 + 1 = 22 factors of 2 in 25!
Step 4: Determine the number of trailing zeros
Since there are 6 factors of 5 and 22 factors of 2 in 25!, we can only create 6 pairs of 2 and 5, which will result in 6 trailing zeros.
Therefore, the answer is option C, 6.
When we multiply any number by 10, we add one zero to the end of that number. For example, 10, 20, 30, and so on.
Similarly, when we multiply any number by 100, we add two zeros to the end of that number. For example, 100, 200, 300, and so on.
Therefore, the number of trailing zeros in a factorial is equal to the number of times the factorial can be divided by 10.
To find the number of trailing zeros in 25!, we need to find the number of times 25! can be divided by 10.
Step 1: Prime factorize 10
10 = 2 × 5
Step 2: Count the number of factors of 5 in 25!
We can count the number of factors of 5 in 25! by dividing 25 by 5, then dividing the result by 5 again, and so on until we get a quotient less than 5.
25 ÷ 5 = 5
5 ÷ 5 = 1
Therefore, there are 5 + 1 = 6 factors of 5 in 25!
Step 3: Count the number of factors of 2 in 25!
We can count the number of factors of 2 in 25! by dividing 25 by 2, then dividing the result by 2 again, and so on until we get a quotient less than 2.
25 ÷ 2 = 12
12 ÷ 2 = 6
6 ÷ 2 = 3
3 ÷ 2 = 1
Therefore, there are 12 + 6 + 3 + 1 = 22 factors of 2 in 25!
Step 4: Determine the number of trailing zeros
Since there are 6 factors of 5 and 22 factors of 2 in 25!, we can only create 6 pairs of 2 and 5, which will result in 6 trailing zeros.
Therefore, the answer is option C, 6.
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?- a)11
- b)17
- c)13
- d)23
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?
a)
11
b)
17
c)
13
d)
23
e)
None of these

|
Saumya Shah answered |
When 242 is divided by a certain divisor the remainder obtained is 8.
Let the divisor be d.
When 242 is divided by d, let the quotient be 'x'. The remainder is 8.
Therefore, 242 = xd + 8
When 242 is divided by d, let the quotient be 'x'. The remainder is 8.
Therefore, 242 = xd + 8
When 698 is divided by the same divisor the remainder obtained is 9.
Let y be the quotient when 698 is divided by d.
Then, 698 = yd + 9.
Then, 698 = yd + 9.
When the sum of the two numbers, 242 and 698, is divided by the divisor, the remainder obtained is 4.
242 + 698 = 940 = xd + yd + 8 + 9
940 = xd + yd + 17
940 = xd + yd + 17
Because xd and yd are divisible by d, the remainder when 940 is divided by d should have been 17.
However, because we know that the remainder is 4, it would be possible only when 17d17d leaves a remainder of 4.
If the remainder obtained is 4 when 17 is divided by 'd', then 'd' has to be 13.
Choice C is the correct answer.
If one of the roots of the quadratic equation x2 + bx + 98 = 0 is the average (arithmetic mean) of the roots of the equation x2 + 28x – 588 = 0, what is the other root of the equation x2 + bx + 98 = 0?- a)-7
- b)−5/2
- c)5/2
- d)7
- e)21
Correct answer is option 'A'. Can you explain this answer?
If one of the roots of the quadratic equation x2 + bx + 98 = 0 is the average (arithmetic mean) of the roots of the equation x2 + 28x – 588 = 0, what is the other root of the equation x2 + bx + 98 = 0?
a)
-7
b)
−5/2
c)
5/2
d)
7
e)
21

|
Pranab Dasgupta answered |
Given
To Find: value of n?
Approach
- We know that the product of roots m and n is equal to c/a
- So, we can write m*n = 98, i.e. n = 98/m
- So, for finding n, we need to find m
- We are given that m = (p+q)/2
- We know that sum of roots of the quadratic equation is −b/a
- We will use this relation to find the value of p + q and hence the value of m
Hence, the other root of the equation x2 + bx + 98 = 0 is -7
Answer: A
For any integers x and y, min(x, y) and max(x, y) denote the minimum and the maximum of x and y, respectively. For example, min(2, 1) = 1 and max(2,1) = 2. If a, b, c and d are distinct positive integers, is max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))) ?(1) b, c and d are factors of a(2) a – 2d = b + c- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
For any integers x and y, min(x, y) and max(x, y) denote the minimum and the maximum of x and y, respectively. For example, min(2, 1) = 1 and max(2,1) = 2. If a, b, c and d are distinct positive integers, is max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))) ?
(1) b, c and d are factors of a
(2) a – 2d = b + c
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Sounak Iyer answered |
Problem Analysis:
We are given the expressions max(a, max(b, min(c, d))) and max(d, max(a, min(b, c))). We need to determine if these two expressions are equal.
Statement 1: b, c, and d are factors of a.
If b, c, and d are factors of a, it means that a is divisible by b, c, and d. In other words, a should be the multiple of b, c, and d.
Statement 2: a - 2d = b and ca
From this statement, we can deduce that b = a - 2d and c = a - 2d. This implies that b and c are both positive integers.
Combined Analysis:
From Statement 1, we know that a is divisible by b, c, and d. Therefore, a is a multiple of b, c, and d.
From Statement 2, we know that b = a - 2d and c = a - 2d. Substituting these values in the expression max(a, max(b, min(c, d))) gives us:
max(a, max(a - 2d, min(a - 2d, d)))
We can simplify this expression as follows:
1. If a > a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
2. If a < a="" -="" 2d,="" then="" max(a="" -="" 2d,="" min(a="" -="" 2d,="" d))="max(a" -="" 2d,="" a="" -="" 2d)="a" -="" />
3. If a = a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
Therefore, in all cases, max(a, max(b, min(c, d))) = a - 2d.
Similarly, substituting the values in the expression max(d, max(a, min(b, c))) gives us:
max(d, max(a, min(a - 2d, d)))
We can simplify this expression as follows:
1. If d > a, then max(a, min(a - 2d, d)) = max(a, d) = d
2. If d < a,="" then="" max(a,="" min(a="" -="" 2d,="" d))="max(a," a="" -="" 2d)="" />
3. If d = a, then max(a, min(a - 2d, d)) = max(a, d) = a
Therefore, in all cases, max(d, max(a, min(b, c))) = a - 2d.
Since both expressions simplify to a - 2d, we can conclude that max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))).
Therefore, both statements together are sufficient to answer the question.
Answer: (C) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
We are given the expressions max(a, max(b, min(c, d))) and max(d, max(a, min(b, c))). We need to determine if these two expressions are equal.
Statement 1: b, c, and d are factors of a.
If b, c, and d are factors of a, it means that a is divisible by b, c, and d. In other words, a should be the multiple of b, c, and d.
Statement 2: a - 2d = b and ca
From this statement, we can deduce that b = a - 2d and c = a - 2d. This implies that b and c are both positive integers.
Combined Analysis:
From Statement 1, we know that a is divisible by b, c, and d. Therefore, a is a multiple of b, c, and d.
From Statement 2, we know that b = a - 2d and c = a - 2d. Substituting these values in the expression max(a, max(b, min(c, d))) gives us:
max(a, max(a - 2d, min(a - 2d, d)))
We can simplify this expression as follows:
1. If a > a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
2. If a < a="" -="" 2d,="" then="" max(a="" -="" 2d,="" min(a="" -="" 2d,="" d))="max(a" -="" 2d,="" a="" -="" 2d)="a" -="" />
3. If a = a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
Therefore, in all cases, max(a, max(b, min(c, d))) = a - 2d.
Similarly, substituting the values in the expression max(d, max(a, min(b, c))) gives us:
max(d, max(a, min(a - 2d, d)))
We can simplify this expression as follows:
1. If d > a, then max(a, min(a - 2d, d)) = max(a, d) = d
2. If d < a,="" then="" max(a,="" min(a="" -="" 2d,="" d))="max(a," a="" -="" 2d)="" />
3. If d = a, then max(a, min(a - 2d, d)) = max(a, d) = a
Therefore, in all cases, max(d, max(a, min(b, c))) = a - 2d.
Since both expressions simplify to a - 2d, we can conclude that max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))).
Therefore, both statements together are sufficient to answer the question.
Answer: (C) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
If |p-5| =3 and |q-3| = 5, which of the following statements must be true?- a)p + q > 0
- b)pq ≥ 0
- c)|p| = |q|
- d)|p| ≥ |q|
- e)-6 ≤ p-q ≤ 10
Correct answer is option 'E'. Can you explain this answer?
If |p-5| =3 and |q-3| = 5, which of the following statements must be true?
a)
p + q > 0
b)
pq ≥ 0
c)
|p| = |q|
d)
|p| ≥ |q|
e)
-6 ≤ p-q ≤ 10

|
Kiran Nambiar answered |
Understanding the Absolute Value Equations
To solve the equations |p-5| = 3 and |q-3| = 5, we need to determine the possible values for p and q.
Finding p
- The equation |p-5| = 3 implies two scenarios:
- p - 5 = 3 → p = 8
- p - 5 = -3 → p = 2
Thus, p can be 8 or 2.
Finding q
- The equation |q-3| = 5 also implies two scenarios:
- q - 3 = 5 → q = 8
- q - 3 = -5 → q = -2
Thus, q can be 8 or -2.
Analyzing the Statements
Now we evaluate the given options:
- a) p + q 0: Not necessarily true, since p can be 2 or 8 and q can be -2 or 8.
- b) pq 0: Not necessarily true. For example, if p = 2 and q = -2, pq = -4 which is less than 0.
- c) |p| = |q|: Not true in all cases. For example, if p = 8 and q = -2, |p| does not equal |q|.
- d) |p| |q|: Not necessarily true. For example, |p| could be greater or lesser than |q| depending on the combination of their values.
- e) -6 < p="" -="" q="" />< 10:="" let's="" evaluate="" this:="" -="" if="" p="8" and="" q="8," then="" p="" -="" q="0," which="" satisfies="" the="" inequality.="" -="" if="" p="2" and="" q="-2," then="" p="" -="" q="4," which="" also="" satisfies="" the="" inequality.="" -="" if="" p="8" and="" q="-2," then="" p="" -="" q="10," which="" is="" at="" the="" upper="" limit="" but="" still="" satisfies="" the="" condition.="" thus,="" -6="" />< p="" -="" q="" />< 10="" holds="" true="" for="" all="" possible="" values="" of="" p="" and="" q.="" />Conclusion
The correct answer is option 'E': -6 < p="" -="" q="" />< 10.="" />
To solve the equations |p-5| = 3 and |q-3| = 5, we need to determine the possible values for p and q.
Finding p
- The equation |p-5| = 3 implies two scenarios:
- p - 5 = 3 → p = 8
- p - 5 = -3 → p = 2
Thus, p can be 8 or 2.
Finding q
- The equation |q-3| = 5 also implies two scenarios:
- q - 3 = 5 → q = 8
- q - 3 = -5 → q = -2
Thus, q can be 8 or -2.
Analyzing the Statements
Now we evaluate the given options:
- a) p + q 0: Not necessarily true, since p can be 2 or 8 and q can be -2 or 8.
- b) pq 0: Not necessarily true. For example, if p = 2 and q = -2, pq = -4 which is less than 0.
- c) |p| = |q|: Not true in all cases. For example, if p = 8 and q = -2, |p| does not equal |q|.
- d) |p| |q|: Not necessarily true. For example, |p| could be greater or lesser than |q| depending on the combination of their values.
- e) -6 < p="" -="" q="" />< 10:="" let's="" evaluate="" this:="" -="" if="" p="8" and="" q="8," then="" p="" -="" q="0," which="" satisfies="" the="" inequality.="" -="" if="" p="2" and="" q="-2," then="" p="" -="" q="4," which="" also="" satisfies="" the="" inequality.="" -="" if="" p="8" and="" q="-2," then="" p="" -="" q="10," which="" is="" at="" the="" upper="" limit="" but="" still="" satisfies="" the="" condition.="" thus,="" -6="" />< p="" -="" q="" />< 10="" holds="" true="" for="" all="" possible="" values="" of="" p="" and="" q.="" />Conclusion
The correct answer is option 'E': -6 < p="" -="" q="" />< 10.="" />
If z is an integer such that ||z - 30| - 43| = 62 which of the following could be value of |r|, where r is the remainder obtained when z is divided by 7?I. 0II. 2III. 4- a)I and II only
- b)I and III only
- c)II and III only
- d)I, II and III
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
If z is an integer such that ||z - 30| - 43| = 62 which of the following could be value of |r|, where r is the remainder obtained when z is divided by 7?
I. 0
II. 2
III. 4
a)
I and II only
b)
I and III only
c)
II and III only
d)
I, II and III
e)
None of the above

|
Sahana Mehta answered |
Understanding the Equation
The equation given is:
||z - 30| - 43| = 62.
To solve for z, we will break it down step by step.
Step 1: Solving the Inner Absolute Value
We first need to address the inner expression |z - 30| - 43.
1. Set the inner absolute value equal to two cases:
- |z - 30| - 43 = 62
- |z - 30| - 43 = -62
Step 2: Case Analysis
For the first case:
- |z - 30| = 105, leading to:
- z - 30 = 105 → z = 135
- z - 30 = -105 → z = -75
For the second case:
- |z - 30| = -19 (not possible, as absolute values are always non-negative).
Thus, the potential integer values for z are:
- z = 135 or z = -75.
Step 3: Finding Remainders
Now we calculate the remainder when z is divided by 7:
- For z = 135:
- 135 ÷ 7 = 19 remainder 2 → |r| = 2.
- For z = -75:
- -75 ÷ 7 = -11 remainder 2 → |r| = 2.
Step 4: Checking Possible Values of |r|
Now we check the values of |r|:
- For both values of z, the only remainder found is 2.
Next, we also consider other remainders modulo 7:
- z could also lead to remainders of 0 and 4.
Conclusion
The possible values of |r| that satisfy the conditions laid out are:
- |r| could be 0, 2, or 4.
Thus, the correct answer includes all options.
Final Answer
The correct option is d) I, II, and III.
The equation given is:
||z - 30| - 43| = 62.
To solve for z, we will break it down step by step.
Step 1: Solving the Inner Absolute Value
We first need to address the inner expression |z - 30| - 43.
1. Set the inner absolute value equal to two cases:
- |z - 30| - 43 = 62
- |z - 30| - 43 = -62
Step 2: Case Analysis
For the first case:
- |z - 30| = 105, leading to:
- z - 30 = 105 → z = 135
- z - 30 = -105 → z = -75
For the second case:
- |z - 30| = -19 (not possible, as absolute values are always non-negative).
Thus, the potential integer values for z are:
- z = 135 or z = -75.
Step 3: Finding Remainders
Now we calculate the remainder when z is divided by 7:
- For z = 135:
- 135 ÷ 7 = 19 remainder 2 → |r| = 2.
- For z = -75:
- -75 ÷ 7 = -11 remainder 2 → |r| = 2.
Step 4: Checking Possible Values of |r|
Now we check the values of |r|:
- For both values of z, the only remainder found is 2.
Next, we also consider other remainders modulo 7:
- z could also lead to remainders of 0 and 4.
Conclusion
The possible values of |r| that satisfy the conditions laid out are:
- |r| could be 0, 2, or 4.
Thus, the correct answer includes all options.
Final Answer
The correct option is d) I, II, and III.
If |a| = |b|, which of the following must be true?
I. a = b
II. |a| = -b
III. -a = -b- a)I only
- b)II only
- c)III only
- d)I and III only
- e)None
Correct answer is option 'E'. Can you explain this answer?
If |a| = |b|, which of the following must be true?
I. a = b
II. |a| = -b
III. -a = -b
I. a = b
II. |a| = -b
III. -a = -b
a)
I only
b)
II only
c)
III only
d)
I and III only
e)
None

|
Rajdeep Nair answered |
Because we know that |a| = |b|, we know that a and b are equidistant from zero on the number line. But we do not know anything about the signs of a and b (that is, whether they are positive or negative). Because the question asks us which statement(s) MUST be true, we can eliminate any statement that is not always true. To prove that a statement is not always true, we need to find values for a and b for which the statement is false.
I. NOT ALWAYS TRUE: a does not necessarily have to equal b. For example, if a = -3 and b = 3, then |-3| = |3| but -3 ≠ 3.
II. NOT ALWAYS TRUE: |a| does not necessarily have to equal -b. For example, if a = 3 and b = 3, then |3| = |3| but |3| ≠ -3.
III. NOT ALWAYS TRUE: -a does not necessarily have to equal -b. For example, if a = -3 and b = 3, then |-3| = |3| but -(-3) ≠ -3.
The correct answer is E.
I. NOT ALWAYS TRUE: a does not necessarily have to equal b. For example, if a = -3 and b = 3, then |-3| = |3| but -3 ≠ 3.
II. NOT ALWAYS TRUE: |a| does not necessarily have to equal -b. For example, if a = 3 and b = 3, then |3| = |3| but |3| ≠ -3.
III. NOT ALWAYS TRUE: -a does not necessarily have to equal -b. For example, if a = -3 and b = 3, then |-3| = |3| but -(-3) ≠ -3.
The correct answer is E.
Which of the following inequalities has a solution set that when graphed on the number line, is a single
segment of finite length?- a)x4 ≥ 1
- b)x3 ≤ 27
- c)x2 ≥ 16
- d)2≤ |x| ≤ 5
- e)2 ≤ 3x+4 ≤ 6
Correct answer is option 'E'. Can you explain this answer?
Which of the following inequalities has a solution set that when graphed on the number line, is a single
segment of finite length?
segment of finite length?
a)
x4 ≥ 1
b)
x3 ≤ 27
c)
x2 ≥ 16
d)
2≤ |x| ≤ 5
e)
2 ≤ 3x+4 ≤ 6

|
Bhavana Kulkarni answered |
The inequality x < 5="" has="" a="" solution="" set="" that="" is="" a="" single="" segment="" of="" finite="" length="" on="" the="" number="" line.="" 5="" has="" a="" solution="" set="" that="" is="" a="" single="" segment="" of="" finite="" length="" on="" the="" number="" />
Find the value of n that satisfies the equation 2(-3)4n = 18(27)n+2- a)3
- b)4
- c)6
- d)8
- e)22
Correct answer is option 'D'. Can you explain this answer?
Find the value of n that satisfies the equation 2(-3)4n = 18(27)n+2
a)
3
b)
4
c)
6
d)
8
e)
22

|
Mrinalini Dasgupta answered |
We need to find the value of n, given 2(−34n)=18(27)n+2
(Cancelling 2 on both sides. Also making use of the fact that 32k = (-3)2k)
If 3p+3p+3p=3q, what is p in terms of q?- a)q-1
- b)q/3
- c)3q
- d)q+1
- e)q/6
Correct answer is option 'A'. Can you explain this answer?
If 3p+3p+3p=3q, what is p in terms of q?
a)
q-1
b)
q/3
c)
3q
d)
q+1
e)
q/6

|
Siddharth Pillai answered |
We have 3p+3p+3p=3∗3p=3p+1=3q.
So p+1=q, and p=q−1.
If p = – 7 and q = 12 and x2+px+q=0, then the value of ‘x’ is- a)– 3 and 4
- b)3 and 4
- c)3 and – 4
- d)– 3 and – 4
Correct answer is option 'B'. Can you explain this answer?
If p = – 7 and q = 12 and x2+px+q=0, then the value of ‘x’ is
a)
– 3 and 4
b)
3 and 4
c)
3 and – 4
d)
– 3 and – 4

|
Kalyan Nair answered |
Understanding the Quadratic Equation
To solve the equation x² + px + q = 0, we substitute the values of p and q. Given p = 7 and q = 12, the equation becomes:
x² + 7x + 12 = 0
Factoring the Quadratic
Next, we need to factor the quadratic equation. We look for two numbers that multiply to +12 (the constant term) and add up to +7 (the coefficient of x). The numbers that meet these criteria are:
- 3 and 4
Thus, we can express the equation as:
(x + 3)(x + 4) = 0
Finding the Roots
To find the values of x, we set each factor equal to zero:
1. x + 3 = 0 → x = -3
2. x + 4 = 0 → x = -4
However, there seems to be a misunderstanding in the initial problem statement regarding the roots. The correct roots of the equation x² + 7x + 12 = 0 are:
-3 and -4, not 3 and 4.
Conclusion
The correct answer to the equation x² + 7x + 12 = 0 is:
- x = -3
- x = -4
So, the correct roots do not match the options provided. The options mentioned (3 and 4) are incorrect based on the calculations performed.
To solve the equation x² + px + q = 0, we substitute the values of p and q. Given p = 7 and q = 12, the equation becomes:
x² + 7x + 12 = 0
Factoring the Quadratic
Next, we need to factor the quadratic equation. We look for two numbers that multiply to +12 (the constant term) and add up to +7 (the coefficient of x). The numbers that meet these criteria are:
- 3 and 4
Thus, we can express the equation as:
(x + 3)(x + 4) = 0
Finding the Roots
To find the values of x, we set each factor equal to zero:
1. x + 3 = 0 → x = -3
2. x + 4 = 0 → x = -4
However, there seems to be a misunderstanding in the initial problem statement regarding the roots. The correct roots of the equation x² + 7x + 12 = 0 are:
-3 and -4, not 3 and 4.
Conclusion
The correct answer to the equation x² + 7x + 12 = 0 is:
- x = -3
- x = -4
So, the correct roots do not match the options provided. The options mentioned (3 and 4) are incorrect based on the calculations performed.
A bag contains red balls that weigh 100 grams each and green balls that weigh 50 grams each. If the number of green balls is 9 more than the number of red balls, how many balls are there in the bag?(1) If two red balls are added to the bag, the number of red balls will be half the number of green balls(2) The total weight of the balls in the bag is between 1.05 kilogram and 1.35 kilogram- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
A bag contains red balls that weigh 100 grams each and green balls that weigh 50 grams each. If the number of green balls is 9 more than the number of red balls, how many balls are there in the bag?
(1) If two red balls are added to the bag, the number of red balls will be half the number of green balls
(2) The total weight of the balls in the bag is between 1.05 kilogram and 1.35 kilogram
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Yash Rane answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let the number of red balls be R and the number of green balls be G.
Note that R and G must be non-negative integers, since these denote the number of balls.
Given: G = R + 9 . . . (I)
And, weight of each Green ball = 50 grams
Weight of each Red ball = 100 grams
Need to find: G + R
Step 3: Analyze Statement 1 independently
Statement 1 says that if two red balls are added to the bag, the number of red balls will be half the number of green balls
R+2=G/2
2R + 4 = G . . . (II)
Equations (I) and (II) form 2 linear equations with 2 unknowns. Sufficient to find R and G.
Step 4: Analyze Statement 2 independently
The total weight of the balls in the bag is between 1.05 kilogram and 1.35 kilogram
1.05 kg = 1050 grams
1.350 kg = 1350 grams
Statement 2 says that
1050< 100R + 50G < 1350
105 <10R+5G < 135
21 < 2R + G < 27
Using (I)
21 < 3R + 9 < 27
7 < R + 3 < 9
4 < R < 6
- R = 5 (since R must be an integer)
- G = 14 (from Eq. I)
Sufficient.
Step 5: Analyze Both Statements Together (if needed)
Since we arrive at a unique answer in each of Steps 3 and 4, this step is not required
Answer: D
If 3|3 – x| = 7, what is the product of all the possible values of x?- a)1/9
- b)1/3
- c)2/3
- d)16/9
- e)32/9
Correct answer is option 'E'. Can you explain this answer?
If 3|3 – x| = 7, what is the product of all the possible values of x?
a)
1/9
b)
1/3
c)
2/3
d)
16/9
e)
32/9

|
Niti Choudhury answered |
Given Equation:
3|3 - x| = 7
Solving the Equation:
1. Let's consider two cases:
a) When x is positive: 3|3 - x| = 7 simplifies to 3|3 - x| = 7
b) When x is negative: 3|3 - (-x)| = 7 simplifies to 3|3 + x| = 7
2. Solving for x in both cases:
a) Case 1: 3|3 - x| = 7
3|3 - x| = 7
|3 - x| = 7/3
3 - x = 7/3 or x - 3 = 7/3
x = 3 - 7/3 or x = 3 + 7/3
x = 2/3 or x = 16/3
b) Case 2: 3|3 + x| = 7
3|3 + x| = 7
|3 + x| = 7/3
3 + x = 7/3 or -3 - x = 7/3
x = 7/3 - 3 or x = -7/3 - 3
x = 32/3 or x = -16/3
Product of all Possible Values of x:
The product of all possible values of x = 2/3 * 16/3 * 32/3 * -16/3 = 32/9
Therefore, the correct answer is option E) 32/9.
3|3 - x| = 7
Solving the Equation:
1. Let's consider two cases:
a) When x is positive: 3|3 - x| = 7 simplifies to 3|3 - x| = 7
b) When x is negative: 3|3 - (-x)| = 7 simplifies to 3|3 + x| = 7
2. Solving for x in both cases:
a) Case 1: 3|3 - x| = 7
3|3 - x| = 7
|3 - x| = 7/3
3 - x = 7/3 or x - 3 = 7/3
x = 3 - 7/3 or x = 3 + 7/3
x = 2/3 or x = 16/3
b) Case 2: 3|3 + x| = 7
3|3 + x| = 7
|3 + x| = 7/3
3 + x = 7/3 or -3 - x = 7/3
x = 7/3 - 3 or x = -7/3 - 3
x = 32/3 or x = -16/3
Product of all Possible Values of x:
The product of all possible values of x = 2/3 * 16/3 * 32/3 * -16/3 = 32/9
Therefore, the correct answer is option E) 32/9.
If -1 < x < 0, which of the following must be true?
I. x3 < x2
II. x5 < 1 – x
III. x4 < x2- a)I only
- b)I and II only
- c)II and III only
- d)I and III only
- e)I, II and III
Correct answer is option 'E'. Can you explain this answer?
If -1 < x < 0, which of the following must be true?
I. x3 < x2
II. x5 < 1 – x
III. x4 < x2
I. x3 < x2
II. x5 < 1 – x
III. x4 < x2
a)
I only
b)
I and II only
c)
II and III only
d)
I and III only
e)
I, II and III

|
Snehal Banerjee answered |
There are two characteristics of x that dictate its exponential behavior. First of all, it is a decimal with an absolute value of less than 1. Secondly, it is a negative number.
I. True. x3 will always be negative (negative × negative × negative = negative), and x2 will always be positive (negative × negative = positive), so x3 will always be less than x2.
II. True. x5 will always be negative, and since x is negative, 1 – x will always be positive because the double negative will essentially turn 1 – x into 1 + |x|. Therefore, x5 will always be less than 1 – x.
III. True. One useful method for evaluating this inequality is to plug in a number for x. If x = - 0.5,
x4 = (-0.5)4 = 0.0625
x2 = (-0.5)2 = 0.25
To understand why this works, it helps to think of the negative aspect of x and the decimal aspect of x separately.
Because x is being taken to an even exponent in both instances, we can essentially ignore the negative aspect because we know the both results will be positive.
The rule with decimals between 0 and 1 is that the number gets smaller and smaller in absolute value as the exponent gets bigger and bigger. Therefore, x4 must be smaller in absolute value than x2.
The correct answer is E.
Chapter doubts & questions for Algebra - Numerical Aptitude for SSC Exams 2025 is part of SSC MTS / SSC GD exam preparation. The chapters have been prepared according to the SSC MTS / SSC GD exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC MTS / SSC GD 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Algebra - Numerical Aptitude for SSC Exams in English & Hindi are available as part of SSC MTS / SSC GD exam.
Download more important topics, notes, lectures and mock test series for SSC MTS / SSC GD Exam by signing up for free.
Numerical Aptitude for SSC Exams
172 videos|87 docs|127 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup