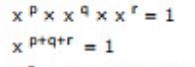All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of Number System for CDS Exam
In the examination a candidate must get 2/5 marks to pass, out of total marks.Shiyam appeared in the exam ang got 198 marks and still failed by 36 marks.The maximum mark is
- a)560
- b)610
- c)585
- d)480
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In the examination a candidate must get 2/5 marks to pass, out of total marks.Shiyam appeared in the exam ang got 198 marks and still failed by 36 marks.The maximum mark is
a)
560
b)
610
c)
585
d)
480
e)
None of these

|
Quantronics answered |
2x = 198+36 = 234
Max = 234*5/2 = 585
Max = 234*5/2 = 585
In a three digit number the digit in the unit’s place is twice the digit in the ten’s place and 1.5 times the digit in the hundred’s place. If the sum of all the three digits of the number is 13, what is the number?- a)356
- b)456
- c)436
- d)626
- e)516
Correct answer is option 'C'. Can you explain this answer?
In a three digit number the digit in the unit’s place is twice the digit in the ten’s place and 1.5 times the digit in the hundred’s place. If the sum of all the three digits of the number is 13, what is the number?
a)
356
b)
456
c)
436
d)
626
e)
516

|
Bank Exams India answered |
100a + 10b + c
c = 2b → b = c/2
c = 1.5a → a = c/1.5
c/1.5 + c/2 + c = 13
6.5c = 39
c = 6, b = 3, a = 4 ⇒ 436
c = 2b → b = c/2
c = 1.5a → a = c/1.5
c/1.5 + c/2 + c = 13
6.5c = 39
c = 6, b = 3, a = 4 ⇒ 436
Sum of three consecutive odd numbers & three consecutive even numbers together is 231. Difference between the smallest odd number and the smallest even number is 11. What is the sum of the largest even number and largest odd number?- a)71
- b)91
- c)101
- d)81
- e)Can not be determined
Correct answer is option 'D'. Can you explain this answer?
Sum of three consecutive odd numbers & three consecutive even numbers together is 231. Difference between the smallest odd number and the smallest even number is 11. What is the sum of the largest even number and largest odd number?
a)
71
b)
91
c)
101
d)
81
e)
Can not be determined
|
|
Kendrika answered |
Let the three odd numbers be x, (x + 2), (x + 4) and
The three even numbers be (x + 11), (x + 13) and (x + 15)
Then,
⇔ x + (x + 2) + (x + 4) + (x + 11) + (x + 13) + (x + 15) = 231
⇔ 6x + 45 = 231
⇔ 6x = 186
⇔ x = 31
∴ Required sum :
= (x + 4) + (x + 15)
= 2x + 19
= 2 × 31 + 19
= 62 + 19
= 81
The three even numbers be (x + 11), (x + 13) and (x + 15)
Then,
⇔ x + (x + 2) + (x + 4) + (x + 11) + (x + 13) + (x + 15) = 231
⇔ 6x + 45 = 231
⇔ 6x = 186
⇔ x = 31
∴ Required sum :
= (x + 4) + (x + 15)
= 2x + 19
= 2 × 31 + 19
= 62 + 19
= 81
A number when divided by 143 leaves 31 as remainder. What will be the remainder
when the same number is divided by 13 ?- a)0
- b)1
- c)3
- d)5
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A number when divided by 143 leaves 31 as remainder. What will be the remainder
when the same number is divided by 13 ?
when the same number is divided by 13 ?
a)
0
b)
1
c)
3
d)
5
e)
None of these

|
Abhishek answered |
Number is = x
x = divisor + remainder
x = 143 + 31
x = 174
when the same number is decided by 13
remainder= 174÷13
= 5 Ans.
x = divisor + remainder
x = 143 + 31
x = 174
when the same number is decided by 13
remainder= 174÷13
= 5 Ans.
The sum of two even numbers is six more than twice of the smaller number. If the difference between these two numbers is 6, If the larger number lies between 15 to 25 Which is the smaller number?
- a)16
- b)6
- c)24
- d)12
- e)Can not be determined
Correct answer is option 'D'. Can you explain this answer?
The sum of two even numbers is six more than twice of the smaller number. If the difference between these two numbers is 6, If the larger number lies between 15 to 25 Which is the smaller number?
a)
16
b)
6
c)
24
d)
12
e)
Can not be determined
|
|
Kavya Saxena answered |
If 12 is smaller number then larger number is 18
Sum = (12+18) = 30
Twice of the smaller number = 24.
The sum of two even numbers is six more than twice of the smaller number.
Therefore Number 12 satisfy both the conditions.
Sum = (12+18) = 30
Twice of the smaller number = 24.
The sum of two even numbers is six more than twice of the smaller number.
Therefore Number 12 satisfy both the conditions.
There are some Parrots and Some Lions in a forest.If the total number of animals head in forest are 840 and total no of animal legs are 1760.What is the number of Parots in the forest ?- a)800
- b)740
- c)620
- d)590
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
There are some Parrots and Some Lions in a forest.If the total number of animals head in forest are 840 and total no of animal legs are 1760.What is the number of Parots in the forest ?
a)
800
b)
740
c)
620
d)
590
e)
None of these

|
Naroj Boda answered |
2x+4(840-x) = 1760
2x+3360-4x = 1760
-2x = 1600
X = 1600/2 = 800
2x+3360-4x = 1760
-2x = 1600
X = 1600/2 = 800
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the difference between numerator and denominator is- a)20
- b)21
- c)22
- d)24
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the difference between numerator and denominator is
a)
20
b)
21
c)
22
d)
24
e)
None of these
|
|
Aisha Gupta answered |
(a +4)/b = 1/3 and a/(b+3) = 1/6 solve both the equations, u will get a = 5 and b = 27
The sum of digits of a two digit number is 6. The ratio of the original number to the number formed by interchanging its digits is 4 : 7. Find the number.- a)60
- b)15
- c)42
- d)33
- e)24
Correct answer is option 'E'. Can you explain this answer?
The sum of digits of a two digit number is 6. The ratio of the original number to the number formed by interchanging its digits is 4 : 7. Find the number.
a)
60
b)
15
c)
42
d)
33
e)
24

|
Target Study Academy answered |
Let the number is 10x+y
So x+y = 6
And (10x+y)/(10y+x) = 4/7
Solve, 2x = y and from above we have x+y = 6
Solve both equations, x = 2, y = 4
So x+y = 6
And (10x+y)/(10y+x) = 4/7
Solve, 2x = y and from above we have x+y = 6
Solve both equations, x = 2, y = 4
A certain number of two digits is three times the sum of its digits. If 45 is added to it, the digits are reversed. The number is _______
- a)16
- b)72
- c)63
- d)27
- e)Can not be determined
Correct answer is option 'D'. Can you explain this answer?
A certain number of two digits is three times the sum of its digits. If 45 is added to it, the digits are reversed. The number is _______
a)
16
b)
72
c)
63
d)
27
e)
Can not be determined

|
KS Coaching Center answered |
A certain number of two digits is three times the sum of its digits only 27 satisfies this condition.
27 + 45 = 72
Therefore Ans is – 27
27 + 45 = 72
Therefore Ans is – 27
When a number is added to 20 percent of the second number, we get 150 percent of the second number. Find the ratio between the first and second number?- a)13:9
- b)12:10
- c)13:10
- d)17:10
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
When a number is added to 20 percent of the second number, we get 150 percent of the second number. Find the ratio between the first and second number?
a)
13:9
b)
12:10
c)
13:10
d)
17:10
e)
None of these

|
Bank Exams India answered |
a + (20/100)*b = (150/100)*b
a:b = 13:10
a:b = 13:10
The sum of the digits of two-digit number is 5. If the digit is reversed, the number is decreased by 27. Find the numbers ?
- a)15,51
- b)41, 14
- c)30, 31
- d)32, 23
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The sum of the digits of two-digit number is 5. If the digit is reversed, the number is decreased by 27. Find the numbers ?
a)
15,51
b)
41, 14
c)
30, 31
d)
32, 23
e)
None of these

|
Naroj Boda answered |
Let the number be (10a + b)
given, a +b = 5 and (10a + b) – (10b +a) = 27
a – b = 3 and a +b = 5
given, a +b = 5 and (10a + b) – (10b +a) = 27
a – b = 3 and a +b = 5
If the sum and the product of 2 numbers are 25 and 144 respectively then the difference of the number should be- a)11
- b)9
- c)7
- d)15
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If the sum and the product of 2 numbers are 25 and 144 respectively then the difference of the number should be
a)
11
b)
9
c)
7
d)
15
e)
None of these
|
|
Anaya Patel answered |
A+B = 25
AB = 24
(a-b)2 = (a+b)2 – 4ab
(a-b)2 = 25 – 4(144)
(a-b)2 = 625 – 576
(a-b)2 = 49
a-b = 7
AB = 24
(a-b)2 = (a+b)2 – 4ab
(a-b)2 = 25 – 4(144)
(a-b)2 = 625 – 576
(a-b)2 = 49
a-b = 7
If the positions of the digits of a two digit number are interchanged, the number obtained is smaller than the original number by 27. If the digits of the number are in the ratio of 1:2, what is the original number?
- a)16
- b)32
- c)63
- d)48
- e)Can not be determined
Correct answer is option 'C'. Can you explain this answer?
If the positions of the digits of a two digit number are interchanged, the number obtained is smaller than the original number by 27. If the digits of the number are in the ratio of 1:2, what is the original number?
a)
16
b)
32
c)
63
d)
48
e)
Can not be determined

|
Divey Sethi answered |
original number – 10x + y
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
y/x = 1/2
x = 2y
y = 3, x = 6 →63
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
y/x = 1/2
x = 2y
y = 3, x = 6 →63
When a number is subtracted from the number 8,12 and 20, the remainders are in continued proportion, Find the number ?- a)3
- b)4
- c)2
- d)6
Correct answer is option 'B'. Can you explain this answer?
When a number is subtracted from the number 8,12 and 20, the remainders are in continued proportion, Find the number ?
a)
3
b)
4
c)
2
d)
6

|
Target Study Academy answered |
8-x / 12 –x = 12-x /20 –x
(8-x)(20-x) = (12 – x)(12 –x)
160 – 8x – 20x + x2 = 144 – 12x – 12x + x2
4x = 16
x = 4
(8-x)(20-x) = (12 – x)(12 –x)
160 – 8x – 20x + x2 = 144 – 12x – 12x + x2
4x = 16
x = 4
When 1 is added to the numerator of a fraction it becomes 1/4 and 1 is subtracted from the denominator of that fraction it becomes 1/5. Find the fraction.- a)4/19
- b)3/16
- c)5/17
- d)2/15
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
When 1 is added to the numerator of a fraction it becomes 1/4 and 1 is subtracted from the denominator of that fraction it becomes 1/5. Find the fraction.
a)
4/19
b)
3/16
c)
5/17
d)
2/15
e)
None of these

|
KS Coaching Center answered |
Let fraction = x/y
Then (x+1)/y = 1/4
And x/(y-1) = 1/5
Solve both equations, x = 3, y = 16
Then (x+1)/y = 1/4
And x/(y-1) = 1/5
Solve both equations, x = 3, y = 16
If three numbers are added in pairs, the sums equal to 11,16 and 23.Find the three numbers
- a)8,6,16
- b)9,2,14
- c)9,5,14
- d)7,2,8
Correct answer is option 'B'. Can you explain this answer?
If three numbers are added in pairs, the sums equal to 11,16 and 23.Find the three numbers
a)
8,6,16
b)
9,2,14
c)
9,5,14
d)
7,2,8
|
|
Preeti Khanna answered |
X+y = 11 - (1)
Y+z = 16 - (2)
Z+x = 23 -(3)
Y+z = 16 - (2)
Z+x = 23 -(3)
Add (1), (2), and (3)
2(x + y + z) = 50
X+y+z = 25
X = 25 – 16 = 9
y = 25 – 23 = 2
z = 25 – 11 = 14
X+y+z = 25
X = 25 – 16 = 9
y = 25 – 23 = 2
z = 25 – 11 = 14
Sum of eight consecutive odd numbers is 656. Average of four consecutive even numbers is 87. What is the sum of the largest even number and largest odd number?- a)171
- b)191
- c)101
- d)181
- e)179
Correct answer is option 'E'. Can you explain this answer?
Sum of eight consecutive odd numbers is 656. Average of four consecutive even numbers is 87. What is the sum of the largest even number and largest odd number?
a)
171
b)
191
c)
101
d)
181
e)
179
|
|
Preeti Khanna answered |
odd numbers — x-8, x-6, x-4, x-2, x, x+2, x+4, x+6
x-8 + x-6 + x-4 + x-2 + x + x+2 + x+4 + x+6 = 656
8x – 8 =656
x = 83
Even numbers — y-2, y, y+2, y+4
4y + 4 = 87 * 4
y = 86
sum of the largest even number and odd number = 89 + 90 = 179
x-8 + x-6 + x-4 + x-2 + x + x+2 + x+4 + x+6 = 656
8x – 8 =656
x = 83
Even numbers — y-2, y, y+2, y+4
4y + 4 = 87 * 4
y = 86
sum of the largest even number and odd number = 89 + 90 = 179
A number is divided by 2, 3, 4, 5 or 6, reminder in each case is one. But the number is exactly divisible by 7. The number lies between 250 and 350, the sum of digits of the number will be
- a)4
- b)7
- c)6
- d)10
- e)Can not be determined
Correct answer is option 'A'. Can you explain this answer?
A number is divided by 2, 3, 4, 5 or 6, reminder in each case is one. But the number is exactly divisible by 7. The number lies between 250 and 350, the sum of digits of the number will be
a)
4
b)
7
c)
6
d)
10
e)
Can not be determined
|
|
Preeti Khanna answered |
To solve this problem, we need to find a number that satisfies the following conditions:
- When divided by 2, 3, 4, 5, or 6, the remainder is 1.
- The number is divisible by 7.
- The number lies between 250 and 350.
Let's start by finding the least common multiple (LCM) of 2, 3, 4, 5, and 6, which is the smallest number divisible by all of these numbers.
LCM(2, 3, 4, 5, 6) = 60
We need to find a number of the form 7k, where k is an integer, that leaves a remainder of 1 when divided by 60. The numbers in this sequence can be expressed as 60n + 1, where n is an integer.
Now, let's find the first few numbers of the form 60n + 1 that are divisible by 7 and lie between 250 and 350:
- For n = 4: 60(4) + 1 = 241 (not divisible by 7)
- For n = 5: 60(5) + 1 = 301 (divisible by 7)
So, the number we're looking for is 301.
Now, let's find the sum of its digits: 3 + 0 + 1 = 4
Therefore, the sum of the digits of the number is 4.
Two numbers such that the sum of twice the first number and thrice the second number is 100 and the sum of thrice the first number and twice the second number is 120. Which is larger number?- a)64
- b)72
- c)65
- d)32
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
Two numbers such that the sum of twice the first number and thrice the second number is 100 and the sum of thrice the first number and twice the second number is 120. Which is larger number?
a)
64
b)
72
c)
65
d)
32
e)
None of the Above
|
|
Anaya Patel answered |
2x + 3y = 100 –(i)
3x + 2y = 120 –(ii)
By Solving eqn (i) and (ii)
x = 32, y = 12
3x + 2y = 120 –(ii)
By Solving eqn (i) and (ii)
x = 32, y = 12
A number is multiplied by 561, and the result obtained is 32,582. But it was found that both 2 in the number are wrong, what should be the correct answer?- a)33,583
- b)37,587
- c)39,589
- d)36,586
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A number is multiplied by 561, and the result obtained is 32,582. But it was found that both 2 in the number are wrong, what should be the correct answer?
a)
33,583
b)
37,587
c)
39,589
d)
36,586
e)
None of these

|
Saktiprasad Behera answered |
561 is divisible by 11 and 3 but it's multiple
which is given by the qs is 32582 is only divisible by 11 so it's digits sum also can b devide by 3 it's right answer is 37587
which is given by the qs is 32582 is only divisible by 11 so it's digits sum also can b devide by 3 it's right answer is 37587
The difference between the digits of a two digit number is 5. Also the original number is 18 more than two times the number obtained by reversing its digits. Find the original number.- a)94
- b)61
- c)72
- d)49
- e)27
Correct answer is option 'C'. Can you explain this answer?
The difference between the digits of a two digit number is 5. Also the original number is 18 more than two times the number obtained by reversing its digits. Find the original number.
a)
94
b)
61
c)
72
d)
49
e)
27
|
|
Ravi Singh answered |
Let number is 10x+y
Then x-y = 5 or y-x = 5
Now given that, 10x+y = 2(10y+x) + 18 Solve, 8x – 19y = 18
Now solve: 8x – 19y = 18 and x-y = 5. In this y = 2, x = 7
And also solve; 8x – 19y = 18 and y-x = 5. In this y come to be negative which is not possible so discard this
So number is 10*7 + 2
Then x-y = 5 or y-x = 5
Now given that, 10x+y = 2(10y+x) + 18 Solve, 8x – 19y = 18
Now solve: 8x – 19y = 18 and x-y = 5. In this y = 2, x = 7
And also solve; 8x – 19y = 18 and y-x = 5. In this y come to be negative which is not possible so discard this
So number is 10*7 + 2
Sum of the three consecutive number is 1956. What is 23% of the highest number ?- a)150.19
- b)105.19
- c)159.50
- d)150.50
Correct answer is option 'A'. Can you explain this answer?
Sum of the three consecutive number is 1956. What is 23% of the highest number ?
a)
150.19
b)
105.19
c)
159.50
d)
150.50
|
|
Kavya Saxena answered |
X+x+1+x+2 = 1956
3x = 1956 – 3 = 1953
X = 1953/3 = 651
X+3 = 653
23% of largest num = 23*653/100 = 150.19
3x = 1956 – 3 = 1953
X = 1953/3 = 651
X+3 = 653
23% of largest num = 23*653/100 = 150.19
Three numbers are in the ratio 4:3:5. If the difference between thrice the third number and the sum of first and second number is 64. Find the difference between the first and third number?- a)4
- b)8
- c)12
- d)16
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Three numbers are in the ratio 4:3:5. If the difference between thrice the third number and the sum of first and second number is 64. Find the difference between the first and third number?
a)
4
b)
8
c)
12
d)
16
e)
None of these

|
Cstoppers Instructors answered |
15x – (7x) = 64, we get x = 8
difference between first and third number = 5x – 4x = x = 8
difference between first and third number = 5x – 4x = x = 8
If the divisor is five times the quotient and six times the remainder, if the remainder is 5 then the dividend is- a)225
- b)300
- c)185
- d)412
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If the divisor is five times the quotient and six times the remainder, if the remainder is 5 then the dividend is
a)
225
b)
300
c)
185
d)
412
e)
None of these
|
|
Aarav Sharma answered |
Let's use the formula for division: dividend = divisor × quotient + remainder
Given: divisor = 5 × quotient and divisor = 6 × remainder
Substituting the first equation into the second equation, we get:
5 × quotient = 6 × remainder
quotient = (6/5) × remainder
Substituting this value of quotient into the formula for division, we get:
dividend = 5 × (6/5) × remainder + remainder
dividend = 6 × remainder + remainder
dividend = 7 × remainder
Since the remainder is 5, we can substitute that value into the formula to get:
dividend = 7 × 5 = 35
Therefore, the correct answer is option C) 185, as it is the only option that has a remainder of 5 when divided by a divisor that is five times the quotient and six times the remainder.
Given: divisor = 5 × quotient and divisor = 6 × remainder
Substituting the first equation into the second equation, we get:
5 × quotient = 6 × remainder
quotient = (6/5) × remainder
Substituting this value of quotient into the formula for division, we get:
dividend = 5 × (6/5) × remainder + remainder
dividend = 6 × remainder + remainder
dividend = 7 × remainder
Since the remainder is 5, we can substitute that value into the formula to get:
dividend = 7 × 5 = 35
Therefore, the correct answer is option C) 185, as it is the only option that has a remainder of 5 when divided by a divisor that is five times the quotient and six times the remainder.
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the numerator and denominator is
- a)5/26
- b)25/4
- c)6/17
- d)5/27
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the numerator and denominator is
a)
5/26
b)
25/4
c)
6/17
d)
5/27
e)
None of these
|
|
Aarav Sharma answered |
Given information:
- Adding 4 to the numerator of a fraction gives 1/3.
- Adding 3 to the denominator of the same fraction gives 1/6.
Let's start by setting up equations to represent the given information:
- (numerator + 4) / denominator = 1/3
- numerator / (denominator + 3) = 1/6
We can simplify these equations by cross-multiplying and solving for the numerator and denominator separately.
- 3(numerator + 4) = denominator
- 6numerator = denominator + 3
Now we have two equations with two variables (numerator and denominator). We can use substitution or elimination to solve for these variables.
Using substitution:
- From the first equation, denominator = 3(numerator + 4)
- Substitute this into the second equation: 6numerator = 3(numerator + 4) + 3
- Simplifying: 3numerator = 15
- Solving for numerator: numerator = 5
Now we can substitute this value back into either of the original equations to find the denominator:
- From the first equation: 3(numerator + 4) = denominator
- Substituting numerator = 5: 3(5 + 4) = denominator
- Simplifying: denominator = 27
Therefore, the fraction is 5/27. The correct answer is option D.
- Adding 4 to the numerator of a fraction gives 1/3.
- Adding 3 to the denominator of the same fraction gives 1/6.
Let's start by setting up equations to represent the given information:
- (numerator + 4) / denominator = 1/3
- numerator / (denominator + 3) = 1/6
We can simplify these equations by cross-multiplying and solving for the numerator and denominator separately.
- 3(numerator + 4) = denominator
- 6numerator = denominator + 3
Now we have two equations with two variables (numerator and denominator). We can use substitution or elimination to solve for these variables.
Using substitution:
- From the first equation, denominator = 3(numerator + 4)
- Substitute this into the second equation: 6numerator = 3(numerator + 4) + 3
- Simplifying: 3numerator = 15
- Solving for numerator: numerator = 5
Now we can substitute this value back into either of the original equations to find the denominator:
- From the first equation: 3(numerator + 4) = denominator
- Substituting numerator = 5: 3(5 + 4) = denominator
- Simplifying: denominator = 27
Therefore, the fraction is 5/27. The correct answer is option D.
A number gets reduced to its two-third when 24 is subtracted from it. Find oneeighth of the number?- a)7
- b)8
- c)9
- d)10
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A number gets reduced to its two-third when 24 is subtracted from it. Find oneeighth of the number?
a)
7
b)
8
c)
9
d)
10
e)
None of these
|
|
Yash Patel answered |
a – 24 = 2a/3
we get a = 72
so one-eighth of the number = 72/8 = 9
we get a = 72
so one-eighth of the number = 72/8 = 9
The number obtained by interchanging the two digits of a two digit number is less than the original number by 27. If the difference between the two digits of the number is 3, then what is the original number?- a)64
- b)72
- c)65
- d)73
- e)None of the Above
Correct answer is option 'E'. Can you explain this answer?
The number obtained by interchanging the two digits of a two digit number is less than the original number by 27. If the difference between the two digits of the number is 3, then what is the original number?
a)
64
b)
72
c)
65
d)
73
e)
None of the Above
|
|
Kavya Saxena answered |
original number – 10x + y
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
All the given options not follow the condition.
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
All the given options not follow the condition.
If the numerator of a fraction is increased by 100% and the denominator is increased by 200%. The resultant fraction is 1 (1/15), What was the original fraction ?- a)1(4/3)
- b)1(5/3)
- c)1(3/5)
- d)1(3/2)
Correct answer is option 'C'. Can you explain this answer?
If the numerator of a fraction is increased by 100% and the denominator is increased by 200%. The resultant fraction is 1 (1/15), What was the original fraction ?
a)
1(4/3)
b)
1(5/3)
c)
1(3/5)
d)
1(3/2)
|
|
Aarav Sharma answered |
Given:
- Numerator of a fraction increased by 100%
- Denominator of the same fraction increased by 200%
- Resultant fraction is 1 (1/15)
To find: Original fraction
Approach:
1. Let the original fraction be x/y
2. According to the given condition, (2x/y) / (3y) = 1(1/15)
3. Simplifying the above equation, we get 2x = 5y
4. Dividing both sides by y, we get 2x/y = 5
5. Therefore, the original fraction is 1(3/5)
Answer: Option C (1(3/5))
- Numerator of a fraction increased by 100%
- Denominator of the same fraction increased by 200%
- Resultant fraction is 1 (1/15)
To find: Original fraction
Approach:
1. Let the original fraction be x/y
2. According to the given condition, (2x/y) / (3y) = 1(1/15)
3. Simplifying the above equation, we get 2x = 5y
4. Dividing both sides by y, we get 2x/y = 5
5. Therefore, the original fraction is 1(3/5)
Answer: Option C (1(3/5))
The sum of square of 2 number is 1972 and the difference of their square is 620. Find the number ?- a)33,26
- b)34,25
- c)36,26
- d)38,28
Correct answer is option 'C'. Can you explain this answer?
The sum of square of 2 number is 1972 and the difference of their square is 620. Find the number ?
a)
33,26
b)
34,25
c)
36,26
d)
38,28
|
|
Aisha Gupta answered |
X2 + y2 = 1972
X2 – y2 = 620
Solve this
2x2 = 2592
x = 1296
x = 36
y2 = 1972 – 1296
y2 = 676
y = 26
X2 – y2 = 620
Solve this
2x2 = 2592
x = 1296
x = 36
y2 = 1972 – 1296
y2 = 676
y = 26
a+b = c and abc = 30, then what is the value of a3 + b3 – c3 ?- a)60
- b)90
- c)-90
- d)-60
Correct answer is option 'C'. Can you explain this answer?
a+b = c and abc = 30, then what is the value of a3 + b3 – c3 ?
a)
60
b)
90
c)
-90
d)
-60

|
Amal P answered |
Given a+b =c
also abc = 30, Now substitute c as a+b in ABC = 30
ab(a+b) = 30 factorize 30, 30 can be (30 *1 ) or (15*2) or (6*5)
Iam taking 30 = 6 * 5 = ( 3 *2 ) (3 +2) Compare with
we can conclude a =3, b=2 and c= a+b = 2+3 =5
There fore
= 27 + 8 - 125
= 35 - 125 = -90
also abc = 30, Now substitute c as a+b in ABC = 30
ab(a+b) = 30 factorize 30, 30 can be (30 *1 ) or (15*2) or (6*5)
Iam taking 30 = 6 * 5 = ( 3 *2 ) (3 +2) Compare with
ab(a+b) = 30
we can conclude a =3, b=2 and c= a+b = 2+3 =5
There fore
a^3 + b^3 – c^3 = 3^3 + 2^3 -5^3
= 27 + 8 - 125
= 35 - 125 = -90
When a number is multiplied by 13 and 13 is added to the product, the resultant is divisible by 5. Find the smallest product possible?- a)85
- b)130
- c)65
- d)90
- e)105
Correct answer is option 'C'. Can you explain this answer?
When a number is multiplied by 13 and 13 is added to the product, the resultant is divisible by 5. Find the smallest product possible?
a)
85
b)
130
c)
65
d)
90
e)
105
|
|
Alok Verma answered |
13x + 13 which is divisible by 5, or 13(x+1) should be divisible by 5. The smallest value of x = 4 to be put here to make it divisible by 5. So the number is 13(4+1)
The sum of three consecutive multiple of 4 is 72 .What is the largest number ?- a)26
- b)20
- c)28
- d)14
Correct answer is option 'C'. Can you explain this answer?
The sum of three consecutive multiple of 4 is 72 .What is the largest number ?
a)
26
b)
20
c)
28
d)
14

|
KS Coaching Center answered |
4x+(4x+4)+(4x+8) = 72
12x+12 = 72
X=(72-12)/12
X=5
Largest number = 4(5)+8 = 20+8 = 28
12x+12 = 72
X=(72-12)/12
X=5
Largest number = 4(5)+8 = 20+8 = 28
The sum of the number and its square is 1406. What is the number ?- a)47
- b)42
- c)32
- d)37
Correct answer is option 'D'. Can you explain this answer?
The sum of the number and its square is 1406. What is the number ?
a)
47
b)
42
c)
32
d)
37
|
|
Rhea Reddy answered |
See the last digit 06…..go for 7
Last digit ..37+(37*37) = 7+49 = 16
So ans: 37
Last digit ..37+(37*37) = 7+49 = 16
So ans: 37
When all the students in a school are made to stand in row of 68, 40 such rows are formed.If the students are made to stand in the row of 20, how many such rows can be formed ?- a)85
- b)136
- c)129
- d)97
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
When all the students in a school are made to stand in row of 68, 40 such rows are formed.If the students are made to stand in the row of 20, how many such rows can be formed ?
a)
85
b)
136
c)
129
d)
97
e)
None of these
|
|
Aarav Sharma answered |
Given:
Number of students in each row = 68
Number of rows = 40
To find:
Number of rows when the students are made to stand in the row of 20
Solution:
Let the total number of students be N
Number of students in each row = 68
Number of rows = 40
So, N = 68 x 40 = 2720
Number of rows when the students are made to stand in the row of 20
Let the number of rows be n
Number of students in each row = 20
So, N = 20 x n
n = N/20 = 2720/20 = 136
Therefore, the number of rows that can be formed when the students are made to stand in the row of 20 is 136.
Hence, the correct option is (b) 136.
Number of students in each row = 68
Number of rows = 40
To find:
Number of rows when the students are made to stand in the row of 20
Solution:
Let the total number of students be N
Number of students in each row = 68
Number of rows = 40
So, N = 68 x 40 = 2720
Number of rows when the students are made to stand in the row of 20
Let the number of rows be n
Number of students in each row = 20
So, N = 20 x n
n = N/20 = 2720/20 = 136
Therefore, the number of rows that can be formed when the students are made to stand in the row of 20 is 136.
Hence, the correct option is (b) 136.
The average of 7 consecutive number is n, if the next 2 number also included then the new average will be increased by ?- a)0
- b)1
- c)2
- d)3
Correct answer is option 'B'. Can you explain this answer?
The average of 7 consecutive number is n, if the next 2 number also included then the new average will be increased by ?
a)
0
b)
1
c)
2
d)
3
|
|
Yash Patel answered |
Avg of 7 no= (7+1)/2 = 8/2 = 4
Avg of 9 no = (9+1)/2 = 5
5- 4 = 1
Hence increased by 1
Avg of 9 no = (9+1)/2 = 5
5- 4 = 1
Hence increased by 1
If the number 10*47* is divisible by both 5 and 11, then the missing digits are respectively- a)1 and 5
- b)6 and 0
- c)5 and 0
- d)2 and 5
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If the number 10*47* is divisible by both 5 and 11, then the missing digits are respectively
a)
1 and 5
b)
6 and 0
c)
5 and 0
d)
2 and 5
e)
None of these

|
Cstoppers Instructors answered |
Check the options in the number 10x47y
all numbers will be divisible by 5 because in end it is 5 and 0
for number to be divisible by 11, (y+4+0) – (7+x+1) should be divisible by 11
from option A, y = 5, x = 1 gives (y+4+0) – (7+x+1) as 0 which is divisible by 11
all numbers will be divisible by 5 because in end it is 5 and 0
for number to be divisible by 11, (y+4+0) – (7+x+1) should be divisible by 11
from option A, y = 5, x = 1 gives (y+4+0) – (7+x+1) as 0 which is divisible by 11
(a-b) = 1, (b-c) = 2 and (c-a) = 3 then the value of (a3 +b3 +c3 -3abc)/(a+b+c) is
- a)5
- b)6
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
(a-b) = 1, (b-c) = 2 and (c-a) = 3 then the value of (a3 +b3 +c3 -3abc)/(a+b+c) is
a)
5
b)
6
c)
7
d)
8
|
|
Rhea Reddy answered |
a3 + b3 + c3 - 3 a b c = ( a + b + c ) ( a2 + b2 + c2 - bc - ab - ac ) .
(a3 +b3 +c3 -3abc)/(a+b+c)
= 1/2[(a-b) 2+(b-c)2 +(c-a)2]
= ½(1+4+9)
= 14/2 = 7
(a3 +b3 +c3 -3abc)/(a+b+c)
= 1/2[(a-b) 2+(b-c)2 +(c-a)2]
= ½(1+4+9)
= 14/2 = 7
Micael gets 3 marks for each correct questions and loses 2 marks for each wrong answers.He attempts 30 sum and obtain 30 marks.Find the no of Questions he answered correctly ?
- a)18
- b)12
- c)23
- d)20
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Micael gets 3 marks for each correct questions and loses 2 marks for each wrong answers.He attempts 30 sum and obtain 30 marks.Find the no of Questions he answered correctly ?
a)
18
b)
12
c)
23
d)
20
e)
None of these
|
|
Anaya Patel answered |
let x be the no of correct answer
x+y=30
3x-2y=30
2x+2y=60
5x=90
x=18
x+y=30
3x-2y=30
2x+2y=60
5x=90
x=18
Find the 5 digit number, 5th digit is one fourth of the 3rd digit and one half of the 4th digit. 3rd digit is one half of the 1st digit. 2nd digit is 5 more than the 5th digit.- a)12786
- b)86421
- c)46218
- d)24675
Correct answer is option 'B'. Can you explain this answer?
Find the 5 digit number, 5th digit is one fourth of the 3rd digit and one half of the 4th digit. 3rd digit is one half of the 1st digit. 2nd digit is 5 more than the 5th digit.
a)
12786
b)
86421
c)
46218
d)
24675
|
|
Anaya Patel answered |
5th digit – 1
Second – 1+5 = 6
Third = 4
Four = 2
First = 4*2 = 8
Second – 1+5 = 6
Third = 4
Four = 2
First = 4*2 = 8
What is the number if 60% of it added to 60 gives the number itself ?- a)150
- b)160
- c)170
- d)180
Correct answer is option 'A'. Can you explain this answer?
What is the number if 60% of it added to 60 gives the number itself ?
a)
150
b)
160
c)
170
d)
180
|
|
Yash Patel answered |
From ans…150
40% of numb = 60
60% of 150 = 90
90+60 = 150
40% of numb = 60
60% of 150 = 90
90+60 = 150
A number when divided by 5 leaves a remainder 4. What is the remainder when the square of the same number is divided by 5?- a)1
- b)2
- c)4
- d)3
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A number when divided by 5 leaves a remainder 4. What is the remainder when the square of the same number is divided by 5?
a)
1
b)
2
c)
4
d)
3
e)
None of these
|
|
Preeti Khanna answered |
Le the number be 5a + 4
square of the number = 25a2 + 16 + 40a
so remainder = 1 (16 divided by 5 leaves a remainder 1)
square of the number = 25a2 + 16 + 40a
so remainder = 1 (16 divided by 5 leaves a remainder 1)
When a number is divided by 527 gives the remainder as 21. When the same number is divided by 17, the remainder will be?- a)2
- b)3
- c)4
- d)7
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
When a number is divided by 527 gives the remainder as 21. When the same number is divided by 17, the remainder will be?
a)
2
b)
3
c)
4
d)
7
e)
None of these

|
P K Kushwaha answered |
527 os divisible by 17 hence no remainder
when 21 is devided by 17
remainder is 4
when 21 is devided by 17
remainder is 4
Chapter doubts & questions for Number System - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Number System - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup