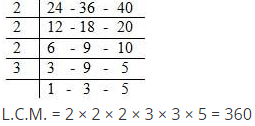All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of HCF & LCM for CDS Exam
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "HCF and LCM" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. Find the greatest number that will divide 43, 91 and 183 so as to leave the same remainder in each case.- a)4
- b)7
- c)9
- d)13
Correct answer is option 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "HCF and LCM" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. Find the greatest number that will divide 43, 91 and 183 so as to leave the same remainder in each case.
a)
4
b)
7
c)
9
d)
13
|
Pallabi Deshpande answered |
Required number = H.C.F. of (91 - 43), (183 - 91) and (183 - 43)
= H.C.F. of 48, 92 and 140 = 4.
What will be the least number which when doubled will be exactly divisible by 12, 18, 21 and 30 ?- a)196
- b)630
- c)1260
- d)2520
Correct answer is option 'B'. Can you explain this answer?
What will be the least number which when doubled will be exactly divisible by 12, 18, 21 and 30 ?
a)
196
b)
630
c)
1260
d)
2520
|
Aditya Kumar answered |
L.C.M. of 12, 18, 21 30 2 | 12 - 18 - 21 - 30
----------------------------
= 2 x 3 x 2 x 3 x 7 x 5 = 1260. 3 | 6 - 9 - 21 - 15
----------------------------
Required number = (1260 � 2) | 2 - 3 - 7 - 5
= 630.
The Greatest Common Divisor of 1.08, 0.36 and 0.9 is:
- a)0.03
- b)0.9
- c)0.18
- d)0.108
Correct answer is option 'C'. Can you explain this answer?
The Greatest Common Divisor of 1.08, 0.36 and 0.9 is:
a)
0.03
b)
0.9
c)
0.18
d)
0.108
|
Faizan Khan answered |
Given numbers are 1.08 , 0.36 and 0.90
G.C.D. i.e. H.C.F of 108, 36 and 90 is 18
Therefore, H.C.F of given numbers = 0.18
G.C.D. i.e. H.C.F of 108, 36 and 90 is 18
Therefore, H.C.F of given numbers = 0.18
Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10 and 12 seconds respectively. In 30 minutes, how many times do they toll together ?- a)4
- b)10
- c)15
- d)16
Correct answer is option 'D'. Can you explain this answer?
Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10 and 12 seconds respectively. In 30 minutes, how many times do they toll together ?
a)
4
b)
10
c)
15
d)
16
|
|
Pallabi Deshpande answered |
LCM of 2, 4, 6, 8 10 and 12 is 120.
So, after each 120 seconds, they would toll together.
Hence, in 30 minutes, they would toll 30*60 seconds / 120 seconds = 15 times
But then the question says they commence tolling together. So, they basically also toll at the "beginning" ("0" second).
So, total tolls together = 15+1 = 16
The least number which when divided by 5, 6 , 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder, is:- a)1677
- b)1683
- c)2523
- d)3363
Correct answer is option 'B'. Can you explain this answer?
The least number which when divided by 5, 6 , 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder, is:
a)
1677
b)
1683
c)
2523
d)
3363
|
Manoj Ghosh answered |
LCM of 5, 6, 7 and 8 = 840.
Hence the number can be written in the form (840k + 3) which is divisible by 9.
If k = 1, number = (840 x 1) + 3 = 843 which is not divisible by 9.
If k = 2, number = (840 x 2) + 3 = 1683 which is divisible by 9.
Hence, 1683 is the least number which when divided by 5, 6, 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder.
Let N be the greatest number that will divide 1305, 4665 and 6905, leaving the same remainder in each case. Then sum of the digits in N is:- a)4
- b)5
- c)6
- d)8
Correct answer is option 'A'. Can you explain this answer?
Let N be the greatest number that will divide 1305, 4665 and 6905, leaving the same remainder in each case. Then sum of the digits in N is:
a)
4
b)
5
c)
6
d)
8
|
Sameer Rane answered |
N = H.C.F. of (4665 - 1305), (6905 - 4665) and (6905 - 1305)
= H.C.F. of 3360, 2240 and 5600 = 1120.
Sum of digits in N = ( 1 + 1 + 2 + 0 ) = 4
The least multiple of 7, which leaves a remainder of 4, when divided by 6, 9, 15 and 18 is:- a)74
- b)94
- c)184
- d)364
Correct answer is option 'D'. Can you explain this answer?
The least multiple of 7, which leaves a remainder of 4, when divided by 6, 9, 15 and 18 is:
a)
74
b)
94
c)
184
d)
364
|
Ishani Rane answered |
7x = 6a+4 = 9b+4 = 15c+4 = 18d+4
7x - 4 = 6a = 9b = 15c = 18d
LCM(6,9,15,18) = 90
7x - 4 = 90y
7x = 90y + 4 = 84y + 6y + 4
7x’ = 6y+4
6x’ + x’ = 6y+4
x’ = 6y’ + 4
y’ = 0 → x’ = 4 → y = 4 → x = 364/7 = 52
Ans: 52*7 = 364
The greatest number of four digits which is divisible by 15, 25, 40 and 75 is:
- a)9000
- b)9400
- c)9600
- d)9800
Correct answer is option 'C'. Can you explain this answer?
The greatest number of four digits which is divisible by 15, 25, 40 and 75 is:
a)
9000
b)
9400
c)
9600
d)
9800
|
Sagar Sharma answered |
To find the greatest number of four digits that is divisible by 15, 25, 40, and 75, we need to find the least common multiple (LCM) of these numbers.
Finding the LCM:
1. Prime factorize each number:
- 15 = 3 × 5
- 25 = 5 × 5
- 40 = 2 × 2 × 2 × 5
- 75 = 3 × 5 × 5
2. Identify the highest power of each prime factor:
- 3 occurs once
- 5 occurs twice
- 2 occurs three times
3. Multiply these prime factors together:
LCM = 3 × 5 × 5 × 2 × 2 × 2 = 600
Finding the greatest number of four digits divisible by 600:
To find the greatest number of four digits divisible by 600, we need to find the largest multiple of 600 that is less than 10,000.
Divide 10,000 by 600:
10,000 ÷ 600 = 16 remainder 400
Subtract the remainder from 10,000:
10,000 - 400 = 9,600
Therefore, the greatest number of four digits divisible by 15, 25, 40, and 75 is 9600 (option C).
Finding the LCM:
1. Prime factorize each number:
- 15 = 3 × 5
- 25 = 5 × 5
- 40 = 2 × 2 × 2 × 5
- 75 = 3 × 5 × 5
2. Identify the highest power of each prime factor:
- 3 occurs once
- 5 occurs twice
- 2 occurs three times
3. Multiply these prime factors together:
LCM = 3 × 5 × 5 × 2 × 2 × 2 = 600
Finding the greatest number of four digits divisible by 600:
To find the greatest number of four digits divisible by 600, we need to find the largest multiple of 600 that is less than 10,000.
Divide 10,000 by 600:
10,000 ÷ 600 = 16 remainder 400
Subtract the remainder from 10,000:
10,000 - 400 = 9,600
Therefore, the greatest number of four digits divisible by 15, 25, 40, and 75 is 9600 (option C).
The least number which should be added to 2497 so that the sum is exactly divisible by 5, 6, 4 and 3 is:- a)3
- b)13
- c)23
- d)33
Correct answer is option 'C'. Can you explain this answer?
The least number which should be added to 2497 so that the sum is exactly divisible by 5, 6, 4 and 3 is:
a)
3
b)
13
c)
23
d)
33
|
Gowri Chakraborty answered |
L.C.M. of 5, 6, 4 and 3 = 60.
On dividing 2497 by 60, the remainder is 37.
Therefore, L.C.M. of 5, 6, 4 and 3 = 60. Number to be added = (60 - 37) = 23.
The smallest number which when diminished by 7, is divisible 12, 16, 18, 21 and 28 is:- a)1008
- b)1015
- c)1022
- d)1032
Correct answer is option 'B'. Can you explain this answer?
The smallest number which when diminished by 7, is divisible 12, 16, 18, 21 and 28 is:
a)
1008
b)
1015
c)
1022
d)
1032
|
|
Pallabi Deshpande answered |
Required Number = (L.C.M of 12, 16, 18,21,28)+7
= 1008 + 7
= 1015
A, B and C start at the same time in the same direction to run around a circular stadium. A completes a round in 252 seconds, B in 308 seconds and c in 198 seconds, all starting at the same point. After what time will they again at the starting point ?- a)26 minutes and 18 seconds
- b)42 minutes and 36 seconds
- c)45 minutes
- d)46 minutes and 12 seconds
Correct answer is option 'D'. Can you explain this answer?
A, B and C start at the same time in the same direction to run around a circular stadium. A completes a round in 252 seconds, B in 308 seconds and c in 198 seconds, all starting at the same point. After what time will they again at the starting point ?
a)
26 minutes and 18 seconds
b)
42 minutes and 36 seconds
c)
45 minutes
d)
46 minutes and 12 seconds
|
|
Aarav Sharma answered |
Given:
- A completes a round in 252 seconds
- B completes a round in 308 seconds
- C completes a round in 198 seconds
To find:
- After what time will they again at the starting point?
Solution:
To find the time at which they will again meet at the starting point, we need to find the least common multiple (LCM) of the given times taken by A, B, and C to complete one round.
Step 1: Prime factorization of the given times:
- 252 = 2 * 2 * 3 * 3 * 7
- 308 = 2 * 2 * 7 * 11
- 198 = 2 * 3 * 3 * 11
Step 2: Finding the LCM:
The LCM is obtained by taking the highest powers of all prime factors involved.
- LCM = 2 * 2 * 3 * 3 * 7 * 11 = 2772 seconds
Step 3: Converting the LCM to minutes and seconds:
- 2772 seconds = 2772 / 60 minutes (quotient) + 2772 % 60 seconds (remainder)
- 2772 seconds = 46 minutes + 12 seconds
Therefore, they will meet again at the starting point after 46 minutes and 12 seconds. Hence, the correct answer is option D.
- A completes a round in 252 seconds
- B completes a round in 308 seconds
- C completes a round in 198 seconds
To find:
- After what time will they again at the starting point?
Solution:
To find the time at which they will again meet at the starting point, we need to find the least common multiple (LCM) of the given times taken by A, B, and C to complete one round.
Step 1: Prime factorization of the given times:
- 252 = 2 * 2 * 3 * 3 * 7
- 308 = 2 * 2 * 7 * 11
- 198 = 2 * 3 * 3 * 11
Step 2: Finding the LCM:
The LCM is obtained by taking the highest powers of all prime factors involved.
- LCM = 2 * 2 * 3 * 3 * 7 * 11 = 2772 seconds
Step 3: Converting the LCM to minutes and seconds:
- 2772 seconds = 2772 / 60 minutes (quotient) + 2772 % 60 seconds (remainder)
- 2772 seconds = 46 minutes + 12 seconds
Therefore, they will meet again at the starting point after 46 minutes and 12 seconds. Hence, the correct answer is option D.
Three number are in the ratio of 3 : 4 : 5 and their L.C.M. is 2400. Their H.C.F. is:- a)40
- b)80
- c)120
- d)200
Correct answer is option 'A'. Can you explain this answer?
Three number are in the ratio of 3 : 4 : 5 and their L.C.M. is 2400. Their H.C.F. is:
a)
40
b)
80
c)
120
d)
200
|
|
Pallabi Deshpande answered |
Let the numbers be 3x, 4x and 5x.
Then, their L.C.M. = 60x.
So, 60x = 2400 or x = 40.
The numbers are (3 x 40), (4 x 40) and (5 x 40).
Hence, required H.C.F. = 40.
The product of two numbers is 2028 and their H.C.F. is 13. The number of such pairs is:- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
The product of two numbers is 2028 and their H.C.F. is 13. The number of such pairs is:
a)
1
b)
2
c)
3
d)
4
|
|
Aarav Sharma answered |
Solution:
Given, the product of two numbers is 2028 and their H.C.F. is 13.
Let the two numbers be 13a and 13b (where a and b are co-primes)
Therefore, 13a × 13b = 2028
=> ab = 12
So, the possible pairs of (a, b) are (1, 12) and (3, 4)
Hence, the possible pairs of numbers are (13 × 1, 13 × 12) and (13 × 3, 13 × 4)
Therefore, there are two pairs of numbers whose product is 2028 and H.C.F. is 13.
Therefore, option 'B' is the correct answer.
Given, the product of two numbers is 2028 and their H.C.F. is 13.
Let the two numbers be 13a and 13b (where a and b are co-primes)
Therefore, 13a × 13b = 2028
=> ab = 12
So, the possible pairs of (a, b) are (1, 12) and (3, 4)
Hence, the possible pairs of numbers are (13 × 1, 13 × 12) and (13 × 3, 13 × 4)
Therefore, there are two pairs of numbers whose product is 2028 and H.C.F. is 13.
Therefore, option 'B' is the correct answer.
The product of two numbers is 4107. If the H.C.F. of these numbers is 37, then the greater number is:- a)101
- b)107
- c)111
- d)185
Correct answer is option 'C'. Can you explain this answer?
The product of two numbers is 4107. If the H.C.F. of these numbers is 37, then the greater number is:
a)
101
b)
107
c)
111
d)
185
|
|
Gowri Chakraborty answered |
Let the numbers be 37a and 37b.
Then, 37a x 37b = 4107
ab = 3.
Now, co-primes with product 3 are (1, 3).
So, the required numbers are (37 x 1, 37 x 3) i.e., (37, 111).
Greater number = 111.
The ratio of two numbers is 3 : 4 and their H.C.F. is 4. Their L.C.M. is:- a)12
- b)16
- c)24
- d)48
Correct answer is option 'D'. Can you explain this answer?
The ratio of two numbers is 3 : 4 and their H.C.F. is 4. Their L.C.M. is:
a)
12
b)
16
c)
24
d)
48
|
Dhruv Mehra answered |
Let the numbers be 3x and 4x . Then their H.C.F = x. So, x=4
Therefore, The numbers are 12 and 16
L.C.M of 12 and 16 = 48
Chapter doubts & questions for HCF & LCM - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of HCF & LCM - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup