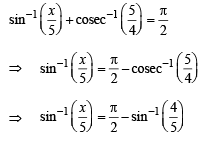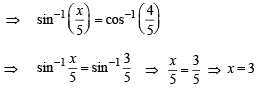All Exams >
Airforce X Y / Indian Navy SSR >
Physics for Airmen Group X >
All Questions
All questions of Trigonometric & Inverse Trigonometric functions for Airforce X Y / Indian Navy SSR Exam
In which quadrant are sin, cos and tan positive?a)... moreIInd quadrantb)IVth quadrantc)IIIrd quadrantd)Ist quadrantCorrect answer is 'D'. Can you explain this answer?

|
Anshu Joshi answered |
- All three of them are positive in Quadrant I
- Sine only is positive in Quadrant II
- Tangent only is positive in Quadrant III
- Cosine only is positive in Quadrant IV

Can you explain the answer of this question below:tan x = - 5/12, x lies in the second quadrant. So sinx=?
- A:
5/13
- B:
-5/13
- C:
-12/13
- D:
12/13
The answer is a.
tan x = - 5/12, x lies in the second quadrant. So sinx=?
5/13
-5/13
-12/13
12/13
|
|
Krishna Iyer answered |
tanx = -5/12
Therefore perpendicular = -5, base = 12
Applying pythagoras theorem,
(hyp)2 = (per)2 + (base)2
⇒ (-5)2 + (12)2
hyp = [25+144]1/2
hyp = (169)1/2
hyp = 13
sinx = perpendicular/hypotenous
= -5/13
In second quadrant, only sin x, cosec x are positive
So. sinx = 5/13
Therefore perpendicular = -5, base = 12
Applying pythagoras theorem,
(hyp)2 = (per)2 + (base)2
⇒ (-5)2 + (12)2
hyp = [25+144]1/2
hyp = (169)1/2
hyp = 13
sinx = perpendicular/hypotenous
= -5/13
In second quadrant, only sin x, cosec x are positive
So. sinx = 5/13
SinA = 1/√10 , SinB= 1/√5 If A and B are both acute angles,then , A+B=?- a)300
- b)750
- c)600
- d)450
Correct answer is option 'D'. Can you explain this answer?
SinA = 1/√10 , SinB= 1/√5 If A and B are both acute angles,then , A+B=?
a)
300
b)
750
c)
600
d)
450
|
|
Riya Banerjee answered |
We know that:
Sin θ = Opposite / Hypotenuse
Sin θ = Opposite / Hypotenuse
∴ SinA = 1/√10
CosA= 3/√10
similarly, SinB = 1/√5
CosB= 2/√5
CosA= 3/√10
similarly, SinB = 1/√5
CosB= 2/√5
⇒ Multiply:
Cos(A+B)= CosA x CosB - SinA x SinB
Cos(A+B)= CosA x CosB - SinA x SinB
Substituting the value in above equation we get:
= 3/√10 x 2/√5 - 1/√10 x 1/√5
= 6/√50 - 1/√50
= 6-1/5√2. ........(√50=5√2)
= 1/ √2
= 6/√50 - 1/√50
= 6-1/5√2. ........(√50=5√2)
= 1/ √2
we know that, sin 45 = 1/ √ 2 therefore
sinθ / cosθ = 45
sinθ / cosθ = 45
Can you explain the answer of this question below: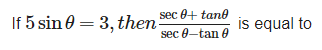
- A:
4
- B:
1/4
- C:
2
- D:
none of these.
The answer is a.
4
1/4
2
none of these.

|
Divey Sethi answered |
sin θ is 3/5.
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
What is the value of sin 7π ?
- a)1
- b)-1
- c)-1/2
- d)0
Correct answer is option 'D'. Can you explain this answer?
What is the value of sin 7π ?
a)
1
b)
-1
c)
-1/2
d)
0
|
|
Om Desai answered |
Sin 7π = Sin 7*180 = Sin 2π * 7 = 0
# Remember Sin nπ =0
# Remember Sin nπ =0
The value of tan 660° cot 1200° is- a)-1/√3
- b)1
- c)1/√3
- d)-1
Correct answer is option 'B'. Can you explain this answer?
The value of tan 660° cot 1200° is
a)
-1/√3
b)
1
c)
1/√3
d)
-1

|
Ciel Knowledge answered |
tan(660o) cot(1200o)
⇒ tan(720 - 60o) cot(1080+120o)
⇒ - tan60o cot120o
⇒ - tan60o (-cot60o)
⇒ 1
⇒ tan(720 - 60o) cot(1080+120o)
⇒ - tan60o cot120o
⇒ - tan60o (-cot60o)
⇒ 1
cos 68° cos 8° + sin 68° sin 8° = ?
- a)1/2
- b)1/4
- c)1
- d)0
Correct answer is option 'A'. Can you explain this answer?
cos 68° cos 8° + sin 68° sin 8° = ?
a)
1/2
b)
1/4
c)
1
d)
0
|
|
Lavanya Menon answered |
We know,
cosA cosB + sinA sinB = cos(A-B)
cosA cosB + sinA sinB = cos(A-B)
cos 68° cos 8° + sin 68° sin 8° = Cos (68-8) = Cos60°
=1/2
=1/2
In which quadrant are sin, cos and tan positive?- a)IInd quadrant
- b)IVth quadrant
- c)IIIrd quadrant
- d)Ist quadrant
Correct answer is option 'B'. Can you explain this answer?
In which quadrant are sin, cos and tan positive?
a)
IInd quadrant
b)
IVth quadrant
c)
IIIrd quadrant
d)
Ist quadrant
|
|
Nandini Patel answered |
For an angle in the fourth quadrant the point P has positive x coordinate and negative y coordinate. Therefore: In Quadrant IV, cos(θ) > 0, sin(θ) < 0 and tan(θ) < 0 (Cosine positive). The quadrants in which cosine, sine and tangent are positive are often remembered using a favorite mnemonic.
tan 15° =- a)√3 - 1
- b)√3 + 1
- c)
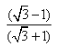
- d)
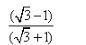
Correct answer is option 'C'. Can you explain this answer?
tan 15° =
a)
√3 - 1
b)
√3 + 1
c)
d)
|
|
Preeti Iyer answered |
In any traingle The sum of 3 sides of a traingle is equal to 180°
Given
A=72°
B=48°
A+B+C=180°
72°+48°+C=180°
C=180°-120°
C=60°
Can you explain the answer of this question below:What is the value of 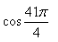
- A:√3/2
- B:1/2
- C:1
- D:1/√2
The answer is d.
What is the value of 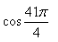
A:
√3/2
B:
1/2
C:
1
D:
1/√2
|
|
Harshitha Mehta answered |
We know ,π = 180deg
So cos 41π/4 = Cos( 41*180/4)
= Cos (1845deg)
= Cos (1800 + 45)
= Cos (10π + π/4)
= Cos (π/4)
= 1/√2
The number of solution of tan x + sec x = 2cos x in [0, 2π) is [2002]- a)2
- b)3
- c)0
- d)1
Correct answer is option 'B'. Can you explain this answer?
The number of solution of tan x + sec x = 2cos x in [0, 2π) is [2002]
a)
2
b)
3
c)
0
d)
1

|
Notes Wala answered |
The given equation is tanx + secx = 2 cos x;
⇒ sin x + 1 = 2cos2 x ⇒ sin x + 1 = 2(1 – sin2 x);
⇒ 2sin2x + sin x – 1= 0;
⇒ (2sin x – 1)(sin x + 1) = 0 ⇒ sin x =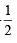 , –1.;
, –1.;
⇒ x = 30°, 150°, 270°
⇒ sin x + 1 = 2cos2 x ⇒ sin x + 1 = 2(1 – sin2 x);
⇒ 2sin2x + sin x – 1= 0;
⇒ (2sin x – 1)(sin x + 1) = 0 ⇒ sin x =
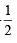 , –1.;
, –1.;⇒ x = 30°, 150°, 270°
cos(π/4 -x) cos ( π/4 -y)-sin(π/4-x) sin( π/4 -y)=- a)cos(x-y)
- b)sin(x-y)
- c)cos(x+y)
- d)sin(x+y)
Correct answer is option 'D'. Can you explain this answer?
cos(π/4 -x) cos ( π/4 -y)-sin(π/4-x) sin( π/4 -y)=
a)
cos(x-y)
b)
sin(x-y)
c)
cos(x+y)
d)
sin(x+y)

|
Infinity Academy answered |
Cos(π/4-x)cos (π/4-y) - sin (π/4-x) sin(π/4-y)
= CosA*Cos B - Sin A*Sin B
= Cos (A+B)
= cos(π/4-x+π/4-y)
= cos(π/2-x-y)
= cos{π/2 - (x+y)}
= sin(x+y)
= Cos (A+B)
= cos(π/4-x+π/4-y)
= cos(π/2-x-y)
= cos{π/2 - (x+y)}
= sin(x+y)
Value of 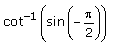
- a)
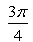
- b)
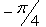
- c)-1
- d)
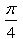
Correct answer is option 'A'. Can you explain this answer?
Value of 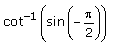
a)
b)
c)
-1
d)
|
|
Aravind Rane answered |
Cot-1[sin(-90)] =cot-1(-1) =π-cot-1(1) =π-π/4 =3π/4
If xy + yz + zx = 1, then, tan–1x + tan–1y + tan–1z =- a)π
- b)π/2
- c)1
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If xy + yz + zx = 1, then, tan–1x + tan–1y + tan–1z =
a)
π
b)
π/2
c)
1
d)
None of these
|
|
Aryan Khanna answered |
If xy + yz + zx = 1,
Then, 1 – xy – yz – zx = 0 ----- eqn1
tan-1x + tan-1y = tan-1((x+y)/(1-xy))
tan-1x + tan-1y + tan-1z = tan-1((x+y)/(1-xy)) + tan-1z
= tan-1( ( ((x+y)/(1-xy)) + z ) / (1 – ((x+y)*z)/(1+xy)))
= tan-1((x+y+z-xyz)/(1-xy-yz-zx))
= tan-1((x+y+z-xyz)/0) [From eqn1]
= π/2
Then, 1 – xy – yz – zx = 0 ----- eqn1
tan-1x + tan-1y = tan-1((x+y)/(1-xy))
tan-1x + tan-1y + tan-1z = tan-1((x+y)/(1-xy)) + tan-1z
= tan-1( ( ((x+y)/(1-xy)) + z ) / (1 – ((x+y)*z)/(1+xy)))
= tan-1((x+y+z-xyz)/(1-xy-yz-zx))
= tan-1((x+y+z-xyz)/0) [From eqn1]
= π/2
What is the range of cos function?
- a)[-1,0]
- b)[0,1]
- c)[-1,1]
- d)[-2,2]
Correct answer is option 'C'. Can you explain this answer?
What is the range of cos function?
a)
[-1,0]
b)
[0,1]
c)
[-1,1]
d)
[-2,2]
|
|
Om Desai answered |
Just look at the graph of cosine.
We know , Range of a function is the set of all possible outputs for that function. If you look at any 2π interval, the cosine function is periodic after every 2π. as you can see it value range between -1 to 1 along the y-axis . So the range for cos function is [-1,1]
The simplest form of 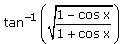 for x > 0 is …
for x > 0 is …- a)x
- b)-x/2
- c)2x
- d)x/2
Correct answer is option 'D'. Can you explain this answer?
The simplest form of 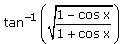 for x > 0 is …
for x > 0 is …
a)
x
b)
-x/2
c)
2x
d)
x/2
|
|
Mira Joshi answered |
tan-1(1-cosx/1+cosx)½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}
= tan-1(tan x/2)
= x/2
= tan-1{(2sin2 x/2) / (2cos2 x/2)}½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}
= tan-1(tan x/2)
= x/2
The value of tan 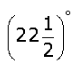
- a)√2 + 1
- b)√2 – 1
- c)±√2 – 1
- d)-√2 – 1
Correct answer is option 'B'. Can you explain this answer?
The value of tan 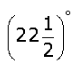
a)
√2 + 1
b)
√2 – 1
c)
±√2 – 1
d)
-√2 – 1
|
|
Krishna Iyer answered |
tan(45°) = tan(45°/2 + 45°/2)
= 2tan(45°/2)/(1 - tan2(45°/2))
(Using expansion for tan(2x))
This implies, 1 = 2tan(45°/2)/(1 - tan2(45°/2))
Rearranging terms, tan2(45°/2) + 2tan(45°/2) - 1 = 0
Solving the quadratic equation x2 + 2x - 1 = 0 gives
x = (√2 - 1) or (-√2 - 1)
But tan(45°/2) lies in the first quadrant, therefore it should be positive.
tan(45°/2) = (√2 - 1)
= 2tan(45°/2)/(1 - tan2(45°/2))
(Using expansion for tan(2x))
This implies, 1 = 2tan(45°/2)/(1 - tan2(45°/2))
Rearranging terms, tan2(45°/2) + 2tan(45°/2) - 1 = 0
Solving the quadratic equation x2 + 2x - 1 = 0 gives
x = (√2 - 1) or (-√2 - 1)
But tan(45°/2) lies in the first quadrant, therefore it should be positive.
tan(45°/2) = (√2 - 1)
Sin(n+1)A sin(n+2)A + cos(n+1)A cos(n+2)A=- a)sinA
- b)sin2A
- c)cosA
- d)cos2A
Correct answer is option 'C'. Can you explain this answer?
Sin(n+1)A sin(n+2)A + cos(n+1)A cos(n+2)A=
a)
sinA
b)
sin2A
c)
cosA
d)
cos2A
|
|
Gaurav Kumar answered |
sin(n+1)Asin(n+2)A + cos(n+1)Acos(n+2)A = cos (n+1)Acos(n+2)A + sin(n+1)Asin(n+2)A = cos{A(n+2-n-1)} = cos (A.1) = cos A
Evaluate sin(3 sin–10.4)a)0.56b)0.31c)0.64d)0.9Correct answer is 'D'. Can you explain this answer?
|
|
Subhankar Choudhary answered |
3sin^-1(x) = sin^-1(3x - 4x^3) when -1/2<=x<=1/2
Definitely 0.4 comes in this range of x and so
Definitely 0.4 comes in this range of x and so
3sin^-1(0.4) = sin^-1[3*0.4 - 4*0.4^3]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
Finally , sin(3sin^-1(0.4)) = sin{sin^-1(0.944)} = 0.944
Which of the following cannot be the value of cos θ .- a)1
- b)-1
- c)√2
- d)0
Correct answer is option 'C'. Can you explain this answer?
Which of the following cannot be the value of cos θ .
a)
1
b)
-1
c)
√2
d)
0
|
|
Naina Sharma answered |
√2 cannot be the value for Cosθ.
The values of Cos θ at different angles are given below :
Cos0°=1
Cos30°=√3/2
Cos45°=1/√2
Cos60°=1/2
Cos90°=0
The value of tan–1(1) + cos–1(–1/2) + sin–1(–1/2) is equal to -
- a)3π/4
- b)5π/12
- c)π/4
- d)13π/12
Correct answer is option 'C'. Can you explain this answer?
The value of tan–1(1) + cos–1(–1/2) + sin–1(–1/2) is equal to -
a)
3π/4
b)
5π/12
c)
π/4
d)
13π/12

|
Bs Academy answered |
Since, here we are considering only principle solutions
tan-1(1) = π/4
cos-1(-1/2) = 2π/3
sin-1(-1/2) = -π/6
Sol : π/4 +2π/3 -π/6
: 3π/4
sin (n+1)x cos(n+2)x-cos(n+1)x sin(n+2)x=- a)cosx
- b)sinx
- c)-cosx
- d)-sinx
Correct answer is option 'D'. Can you explain this answer?
sin (n+1)x cos(n+2)x-cos(n+1)x sin(n+2)x=
a)
cosx
b)
sinx
c)
-cosx
d)
-sinx
|
|
Neha Joshi answered |
sin(n+1)x cos(n+2)x - cos(n+1)x sin(n+2)x
⇒ sin[(n+1)x - (n+2)x]
As we know that sin(A-B) = sinA cosB - cosA sinB
⇒ sin(n+1-n-2)
sin(-x)
= -sinx
⇒ sin[(n+1)x - (n+2)x]
As we know that sin(A-B) = sinA cosB - cosA sinB
⇒ sin(n+1-n-2)
sin(-x)
= -sinx
What is the sign of the sec θ and cosec θ in second quadrant respectively?- a)positive and negative
- b)positive and positive
- c)negative and negative
- d)negative and positive
Correct answer is option 'D'. Can you explain this answer?
What is the sign of the sec θ and cosec θ in second quadrant respectively?
a)
positive and negative
b)
positive and positive
c)
negative and negative
d)
negative and positive
|
|
Preeti Iyer answered |
In quadrant sin, cos tan, cot, sec, cosec all +ve .In second quadrant sin and cosec are +ve. in 3rd quadrant tan and cot are positive.And in 4th cos and sec are +ve. 

Can you explain the answer of this question below:Value of 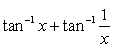 is
is
- A:
π/2
- B:
1/x
- C:
x
- D:
π
The answer is a.
Value of is
π/2
1/x
x
π

|
Case Studies answered |
Tan-1(1/x) = cot-1(x) and tan-1(x) + cot-1(x) =90degree
If sin-1 x + sin-1 y + sin-1z = 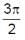 , then
, then - a)

- b)x22 + y42 + z62 - x220- y420 - z620 = 0
- c)x50 + y25 + z5 = 0
- d)
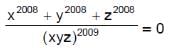
Correct answer is option 'A,B'. Can you explain this answer?
If sin-1 x + sin-1 y + sin-1z = 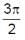 , then
, then
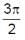 , then
, then a)

b)
x22 + y42 + z62 - x220- y420 - z620 = 0
c)
x50 + y25 + z5 = 0
d)
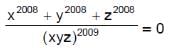

|
Vikash Yadav answered |
Put x = y = z = 1
This will satisfy the eqns
The largest value of sin θ cosθ is- a)
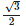
- b)

- c)1/2
- d)1
Correct answer is option 'C'. Can you explain this answer?
The largest value of sin θ cosθ is
a)
b)
c)
1/2
d)
1
|
|
Raghav Bansal answered |
1/root 2 ; root 2 is largest value of sin theta and cos thetha
A wire of length 15 cm is bent to form an arc of a circle with radius 6 cm. Find in radians the angle subtended at the centre.- a)2.5 radians
- b)3.5 radians
- c)4 radians
- d)3 radians
Correct answer is option 'A'. Can you explain this answer?
A wire of length 15 cm is bent to form an arc of a circle with radius 6 cm. Find in radians the angle subtended at the centre.
a)
2.5 radians
b)
3.5 radians
c)
4 radians
d)
3 radians
|
|
Neha Joshi answered |
Length of arc = 15 cm
Radius: R = 6 cm
Arc length = R*θ
(θ is the angle subtended by the arc)
15 = 6*θ
θ = 5/2 radians
Radius: R = 6 cm
Arc length = R*θ
(θ is the angle subtended by the arc)
15 = 6*θ
θ = 5/2 radians
Can you explain the answer of this question below:Domain of f(x) = cos–1 x + cot–1 x + cosec–1 x is
- A:
[–1, 1]
- B:
R
- C:
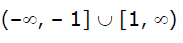
- D:
{–1, 1}
The answer is D.
Domain of f(x) = cos–1 x + cot–1 x + cosec–1 x is
[–1, 1]
R
{–1, 1}
|
|
Suresh Iyer answered |
Domain of cos-1x = [-1 ,1]
Domain of cot-1x = R
Domain of cosec-1x = R - (-1,1)
So taking intersection of domains of all three we have only {-1 ,1}
As cos-1x is confined between [-1,1] and cosec-1x is not defined between (-1,1), So only -1 and 1 are left.
Domain of cot-1x = R
Domain of cosec-1x = R - (-1,1)
So taking intersection of domains of all three we have only {-1 ,1}
As cos-1x is confined between [-1,1] and cosec-1x is not defined between (-1,1), So only -1 and 1 are left.
If sinθ+cosecθ = 2, then sin2θ+cosec2θ =- a)4
- b)1
- c)2
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If sinθ+cosecθ = 2, then sin2θ+cosec2θ =
a)
4
b)
1
c)
2
d)
none of these
|
|
Om Desai answered |
sinθ+cscθ=2
⇒ sinθ+1/sinθ=2
⇒ sin2θ−2sinθ+1=0
⇒ (sinθ−1)2 = 0
⇒ sinθ=1
⇒ sin2θ + csc2θ
= sin2θ + 1/sin2θ
= 1+1
= 2
⇒ sinθ+1/sinθ=2
⇒ sin2θ−2sinθ+1=0
⇒ (sinθ−1)2 = 0
⇒ sinθ=1
⇒ sin2θ + csc2θ
= sin2θ + 1/sin2θ
= 1+1
= 2
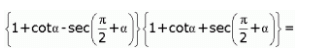
- a)2cot α
- b)2cosec α
- c)cot α
- d)cosec α
Correct answer is option 'A'. Can you explain this answer?
a)
2cot α
b)
2cosec α
c)
cot α
d)
cosec α
|
|
Pooja Shah answered |
Correct Answer : a
Explanation : {1 + cotα - sec(π/2 + α)} {1 + cotα + sec(π/2 + α)}
As we know that (a-b)(a+b) = a2 - b2
(1 + cotα)2 - [sec(π/2 + α)]2
1 + 2cotα + cot2α - (-cosecα)2
2cotα + 1 + cot2α - cosec2α
As we know that 1 + cot2α = cosec2α
= 2cotα + cosec2α - cosec2α
= 2cotα
Find the value of sin θ/3- a)

- b)
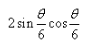
- c)
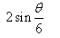
- d)
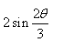
Correct answer is option 'B'. Can you explain this answer?
Find the value of sin θ/3
a)
b)
c)
d)

|
Top Rankers answered |
sin θ/3
Multiply and divide it by '2'
sin2(θ/3*2) = sin2(θ/6)
As we know that sin2θ = 2sinθcosθ
=> 2 sin(θ/6) cos(θ/6)
Multiply and divide it by '2'
sin2(θ/3*2) = sin2(θ/6)
As we know that sin2θ = 2sinθcosθ
=> 2 sin(θ/6) cos(θ/6)
cosA + cos (120° + A) + cos(120° – A) =- a)-1/2
- b)1/2
- c)1
- d)0
Correct answer is option 'D'. Can you explain this answer?
cosA + cos (120° + A) + cos(120° – A) =
a)
-1/2
b)
1/2
c)
1
d)
0
|
|
Raghav Bansal answered |
CosA + Cos(120o-A) + Cos(120°+A)
cosA + 2cos(120° - a + 120° + a)/(2cos(120° - a - 120° - a)
we know that formula
(cos C+ cosD = 2cos (C+D)/2.cos (C-D) /2)
⇒ cosA + 2cos120° cos(-A)
⇒ cosA+ 2cos (180° - 60°) cos(-A)
⇒ cosA + 2(-cos60°) cosA
⇒ cos A - 2 * 1/2cos A
⇒ cosA-cosA
⇒ 0
cosA + 2cos(120° - a + 120° + a)/(2cos(120° - a - 120° - a)
we know that formula
(cos C+ cosD = 2cos (C+D)/2.cos (C-D) /2)
⇒ cosA + 2cos120° cos(-A)
⇒ cosA+ 2cos (180° - 60°) cos(-A)
⇒ cosA + 2(-cos60°) cosA
⇒ cos A - 2 * 1/2cos A
⇒ cosA-cosA
⇒ 0
A train is travelling on a curve of 350 m radius at 7 Km/hr. Through what angle will it turn in one minute?- a)50 radian
- b)3 radian
- c)1/20 radian
- d)1/3 radian
Correct answer is option 'D'. Can you explain this answer?
A train is travelling on a curve of 350 m radius at 7 Km/hr. Through what angle will it turn in one minute?
a)
50 radian
b)
3 radian
c)
1/20 radian
d)
1/3 radian
|
|
Suresh Reddy answered |
length of arc = 350m
Speed = 7km/hr
In one minute = (7*5/18*60)
=> (35*20)/6
= length of arc/radius
θ = (35*20)/(6*350)
θ = 1/3 radian
Speed = 7km/hr
In one minute = (7*5/18*60)
=> (35*20)/6
= length of arc/radius
θ = (35*20)/(6*350)
θ = 1/3 radian
If cos A + cos B =  , then the sides of the triangle ABC are in
, then the sides of the triangle ABC are in- a)H. P.
- b)A. P.
- c)G. P.
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If cos A + cos B =  , then the sides of the triangle ABC are in
, then the sides of the triangle ABC are in
a)
H. P.
b)
A. P.
c)
G. P.
d)
none of these
|
|
Aryan Khanna answered |
cos A + cos B = 4 sin2(C/2)
⇒ 2 cos (A+B)/2 cos (A−B)/2 = 4 sin2(C/2)
⇒ 2 cos (A+B)/2 cos (A−B)/2 = 4 sin2(C/2)
∵ A + B + C = π ⇒ A + B = π − C
⇒ cos (π−C)/2 cos (A−B)/2 = 2 sin2(C/2)
⇒ sin C/2 cos (A−B)/2 = 2 sin2(C/2)
⇒ cos (A−B)/2 = 2 sin (C/2)
⇒ cos C/2 cos (A−B)/2 = 2 sin (C/2) cos (C/2)
⇒ cos (π−(A+B))/2 cos (A−B)/2 = sin C
⇒ 2 sin (A+B)/2 cos (A−B)/2 = sin C
⇒ sin A + sin B = 2 sin C
⇒ sin C/2 cos (A−B)/2 = 2 sin2(C/2)
⇒ cos (A−B)/2 = 2 sin (C/2)
⇒ cos C/2 cos (A−B)/2 = 2 sin (C/2) cos (C/2)
⇒ cos (π−(A+B))/2 cos (A−B)/2 = sin C
⇒ 2 sin (A+B)/2 cos (A−B)/2 = sin C
⇒ sin A + sin B = 2 sin C
∵ a/sinA = b/sinB = c/sinC = k
⇒sinA = ak, sin B = bk , sin C = ck
⇒sinA = ak, sin B = bk , sin C = ck
⇒ ak + bk = 2(ck)
⇒ a+b=2c
⇒ a+b=2c
Therefore the sides of triangle a,b,c are in A.P.
A wheel makes 360 revolutions in 1 minute. Through how many radians does it turn in 3 seconds?- a)6π
- b)36π
- c)10π
- d)12π
Correct answer is option 'B'. Can you explain this answer?
A wheel makes 360 revolutions in 1 minute. Through how many radians does it turn in 3 seconds?
a)
6π
b)
36π
c)
10π
d)
12π

|
Ayush Joshi answered |
Number of revolutions made by the wheel in 1 minute = 360
∴Number of revolutions made by the wheel in 1 second =360/60 = 6
In one complete revolution, the wheel turns an angle of 2π radian.
Hence, in 6 complete revolutions, it will turn an angle of 6 * 2π radian, i.e.,
12 π radian
Thus, in one second, the wheel turns an angle of 12π radian.
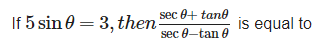
- a)4
- b)1/4
- c)2
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
a)
4
b)
1/4
c)
2
d)
none of these.
|
|
Krishna Iyer answered |
sin θ is 3/5.
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
Two ships A and B, lies 33 m apart on the sea surface. There is submarine ‘C’ on the sea bed. The angle of depression of C from A is 600 and the distance AC is 40 m. Calculate the distance BC.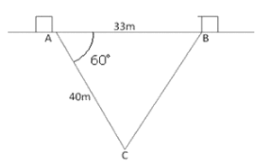
- a)51.9m
- b)37.0m
- c)20.1m
- d)63.3m
Correct answer is option 'B'. Can you explain this answer?
Two ships A and B, lies 33 m apart on the sea surface. There is submarine ‘C’ on the sea bed. The angle of depression of C from A is 600 and the distance AC is 40 m. Calculate the distance BC.
a)
51.9m
b)
37.0m
c)
20.1m
d)
63.3m
|
|
Poonam Reddy answered |
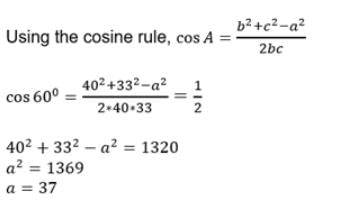
What is the length of side c 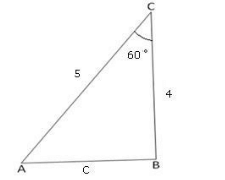
- a)3.58
- b)4.58
- c)4.89
- d)4.56
Correct answer is option 'B'. Can you explain this answer?
What is the length of side c
a)
3.58
b)
4.58
c)
4.89
d)
4.56
|
|
Neha Joshi answered |
a = 4, b = 5
angle c = 60o
cos c = (a2 + b2 - c2)/2ab
= 1/2 = (16 + 25 - c2)/40
⇒ 20 = 41 - c2
c2 = 21
⇒ c = (21)1/2
⇒ c = 4.58
angle c = 60o
cos c = (a2 + b2 - c2)/2ab
= 1/2 = (16 + 25 - c2)/40
⇒ 20 = 41 - c2
c2 = 21
⇒ c = (21)1/2
⇒ c = 4.58
if cosθ = √3/2How many solutions does this equation have between -π and π ?- a)2
- b)1
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
if cosθ = √3/2
How many solutions does this equation have between -π and π ?
a)
2
b)
1
c)
3
d)
4
|
|
Gaurav Kumar answered |
The general solution of the given question is theta= 2nπ± π/6 but it is mentioned that they are lies between -π to π. So when we put n=0 we get theta =±π/6. And when we put n= 1 we get theta does not lies between -π to ÷π. So we get only two values of theta.
Chapter doubts & questions for Trigonometric & Inverse Trigonometric functions - Physics for Airmen Group X 2025 is part of Airforce X Y / Indian Navy SSR exam preparation. The chapters have been prepared according to the Airforce X Y / Indian Navy SSR exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Airforce X Y / Indian Navy SSR 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Trigonometric & Inverse Trigonometric functions - Physics for Airmen Group X in English & Hindi are available as part of Airforce X Y / Indian Navy SSR exam.
Download more important topics, notes, lectures and mock test series for Airforce X Y / Indian Navy SSR Exam by signing up for free.
Physics for Airmen Group X
201 videos|410 docs|280 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

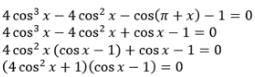

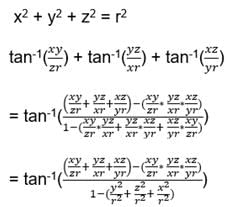
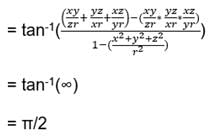




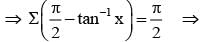
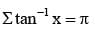

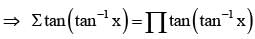



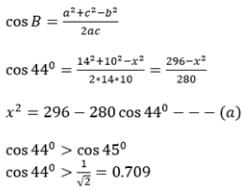
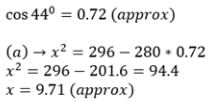

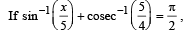 then the values of x is
then the values of x is