All Exams >
ACT >
Science for ACT >
All Questions
All questions of Motion in a plane for ACT Exam
A unit vector has the magnitude of ___- a)5
- b)1
- c)10
- d)0
Correct answer is option 'B'. Can you explain this answer?
A unit vector has the magnitude of ___
a)
5
b)
1
c)
10
d)
0
|
|
Riley Reid answered |
Unit Vector and its Magnitude
Unit vector is a vector with a magnitude of 1. It is commonly used in mathematics and physics to indicate direction without specifying a specific distance or scale. When we talk about the magnitude of a unit vector, it is always equal to 1.
Explanation of Correct Answer
- The correct answer is option 'B' which is 1. This is because a unit vector by definition has a magnitude of 1.
- The magnitude of a vector is calculated using the formula: magnitude = sqrt(a^2 + b^2), where 'a' and 'b' are the components of the vector.
- For a unit vector, the magnitude will be 1. So, in this case, the magnitude of the unit vector is 1.
- Therefore, the correct answer is option 'B' which corresponds to a magnitude of 1.
Unit vector is a vector with a magnitude of 1. It is commonly used in mathematics and physics to indicate direction without specifying a specific distance or scale. When we talk about the magnitude of a unit vector, it is always equal to 1.
Explanation of Correct Answer
- The correct answer is option 'B' which is 1. This is because a unit vector by definition has a magnitude of 1.
- The magnitude of a vector is calculated using the formula: magnitude = sqrt(a^2 + b^2), where 'a' and 'b' are the components of the vector.
- For a unit vector, the magnitude will be 1. So, in this case, the magnitude of the unit vector is 1.
- Therefore, the correct answer is option 'B' which corresponds to a magnitude of 1.
A ball is being rotated in a circle of radius 5 m with a constant tangential velocity of 20 m/s. A stone is also being rotated in a circle of radius 4 m with a constant tangential velocity of 16 m/s. Which one of the following choices is true about both the circular motions?- a)Both have same angular velocity
- b)Both have different angular velocity
- c)Angular velocity of ball > angular velocity of stone
- d)Angular velocity of stone > angular velocity of ball
Correct answer is option 'A'. Can you explain this answer?
A ball is being rotated in a circle of radius 5 m with a constant tangential velocity of 20 m/s. A stone is also being rotated in a circle of radius 4 m with a constant tangential velocity of 16 m/s. Which one of the following choices is true about both the circular motions?
a)
Both have same angular velocity
b)
Both have different angular velocity
c)
Angular velocity of ball > angular velocity of stone
d)
Angular velocity of stone > angular velocity of ball

|
Orion Classes answered |
Angular velocity = Tangential velocity/Radius. When we put in the values and calculate the angular velocities for each of the circular motions, we see that both the angular velocities are equal to each other and the value is 4 rad/s.
Eleven times unit vector along X added to 7 times unit vector along Y gives ______- a)11î + 7ĵ
- b)7î + 11ĵ
- c)7î + 7ĵ
- d)11î + 11ĵ
Correct answer is option 'A'. Can you explain this answer?
Eleven times unit vector along X added to 7 times unit vector along Y gives ______
a)
11î + 7ĵ
b)
7î + 11ĵ
c)
7î + 7ĵ
d)
11î + 11ĵ
|
|
Jasmine Johnson answered |
Eleven times the unit vector along the X-axis added to 7 times the unit vector along the Y-axis gives us a vector in the XY-plane. The resultant vector can be found by adding the components along the X-axis and Y-axis separately.
The X-component of the resultant vector is 11 times the X-component of the unit vector along the X-axis, which is 11 times 1, giving us 11.
The Y-component of the resultant vector is 7 times the Y-component of the unit vector along the Y-axis, which is 7 times 1, giving us 7.
Therefore, the resultant vector is (11, 7).
So the answer is a) 11.
The X-component of the resultant vector is 11 times the X-component of the unit vector along the X-axis, which is 11 times 1, giving us 11.
The Y-component of the resultant vector is 7 times the Y-component of the unit vector along the Y-axis, which is 7 times 1, giving us 7.
Therefore, the resultant vector is (11, 7).
So the answer is a) 11.
A body is moving with a constant acceleration of 11î + 7ĵ, starting from the origin. What will be the position of the body after 10s?- a)550î + 350ĵ
- b)350î + 550ĵ
- c)350î – 550ĵ
- d)550î – 350ĵ
Correct answer is option 'A'. Can you explain this answer?
A body is moving with a constant acceleration of 11î + 7ĵ, starting from the origin. What will be the position of the body after 10s?
a)
550î + 350ĵ
b)
350î + 550ĵ
c)
350î – 550ĵ
d)
550î – 350ĵ

|
Orion Classes answered |
The body’s displacement is given by s = (1/2)at2. The body starts from the origin hence, the total displacement is the final position of the body. Therefore, after putting in the values, we get, s = (1/2)(11î + 7ĵ)*102 = 550î + 350ĵ.
A car travels 5m in X direction and then 7m in Y direction. What is the final vector position of the car with respect to the origin?- a)5î + 7ĵ
- b)7î + 5ĵ
- c)7î + 7ĵ
- d)5î + 5ĵ
Correct answer is option 'A'. Can you explain this answer?
A car travels 5m in X direction and then 7m in Y direction. What is the final vector position of the car with respect to the origin?
a)
5î + 7ĵ
b)
7î + 5ĵ
c)
7î + 7ĵ
d)
5î + 5ĵ

|
Flembe Academy answered |
Unit vector along X is î and that along Y is ĵ. Hence, when the car travels 5m in X direction and 7m in y direction, the final position becomes 5î + 7ĵ.
Calculating the relative velocity is an example of ______- a)Vector addition
- b)Vector subtraction
- c)Vector multiplication
- d)Vector division
Correct answer is option 'B'. Can you explain this answer?
Calculating the relative velocity is an example of ______
a)
Vector addition
b)
Vector subtraction
c)
Vector multiplication
d)
Vector division
|
|
Xavier Hughes answered |
Understanding Relative Velocity
Relative velocity refers to the velocity of one object as observed from another object. To calculate it, we often need to consider the velocities of both objects in a specific frame of reference.
Vector Subtraction in Relative Velocity
- Relative velocity is fundamentally about determining how fast one object is moving compared to another.
- To find the relative velocity of Object A with respect to Object B, you use the formula:
- **VAB = VA - VB**
- Here, **VAB** is the velocity of A relative to B, **VA** is the velocity of A, and **VB** is the velocity of B.
Why is it Vector Subtraction?
- The reason we use subtraction rather than addition is that we are interested in the difference in the velocities.
- For example, if Object A moves north at 10 m/s and Object B moves north at 5 m/s, the relative velocity of A with respect to B is:
- **VAB = 10 m/s (north) - 5 m/s (north) = 5 m/s (north)**
- This subtraction reflects how much faster A is moving compared to B in the same direction.
Conclusion
- Thus, calculating relative velocity is an example of vector subtraction, as it involves determining the difference in motion between two objects in a given frame of reference.
Relative velocity refers to the velocity of one object as observed from another object. To calculate it, we often need to consider the velocities of both objects in a specific frame of reference.
Vector Subtraction in Relative Velocity
- Relative velocity is fundamentally about determining how fast one object is moving compared to another.
- To find the relative velocity of Object A with respect to Object B, you use the formula:
- **VAB = VA - VB**
- Here, **VAB** is the velocity of A relative to B, **VA** is the velocity of A, and **VB** is the velocity of B.
Why is it Vector Subtraction?
- The reason we use subtraction rather than addition is that we are interested in the difference in the velocities.
- For example, if Object A moves north at 10 m/s and Object B moves north at 5 m/s, the relative velocity of A with respect to B is:
- **VAB = 10 m/s (north) - 5 m/s (north) = 5 m/s (north)**
- This subtraction reflects how much faster A is moving compared to B in the same direction.
Conclusion
- Thus, calculating relative velocity is an example of vector subtraction, as it involves determining the difference in motion between two objects in a given frame of reference.
A vector can be resolved along ______- a)Only one direction
- b)Only two directions
- c)Only three directions
- d)Only in independent directions
Correct answer is option 'D'. Can you explain this answer?
A vector can be resolved along ______
a)
Only one direction
b)
Only two directions
c)
Only three directions
d)
Only in independent directions
|
|
Evan Parker answered |
Understanding Vector Resolution
Vector resolution is a fundamental concept in physics and mathematics that involves breaking down a vector into its components along specified directions.
Independent Directions
Vectors can be resolved along multiple directions, but the key point is that these directions must be independent of each other. Independent directions are those that do not affect each other’s magnitude or direction.
Why Only Independent Directions?
- **Dimensionality**: In a three-dimensional space, any vector can be resolved along three independent axes (x, y, z). However, vectors can also be resolved in two dimensions or even one dimension, depending on the situation.
- **Linear Independence**: Directions like x and y in a 2D plane are independent. Resolving a vector along these axes allows for a complete representation of the vector's effects in that plane.
- **Mathematical Representation**: A vector, represented as **V**, can be expressed as **V = Vx + Vy + Vz**, where Vx, Vy, and Vz are the components along independent axes. This principle applies in any dimensional space.
Applications of Vector Resolution
- **Physics**: Used in analyzing forces, motion, and other physical phenomena.
- **Engineering**: Essential for resolving forces in structures and mechanical systems.
- **Computer Graphics**: Used to render movements and transformations in a 3D space.
In summary, vectors can indeed be resolved along only independent directions, allowing for a complete understanding of their behavior in any given space. This resolution is crucial for accurate analysis in various fields.
Vector resolution is a fundamental concept in physics and mathematics that involves breaking down a vector into its components along specified directions.
Independent Directions
Vectors can be resolved along multiple directions, but the key point is that these directions must be independent of each other. Independent directions are those that do not affect each other’s magnitude or direction.
Why Only Independent Directions?
- **Dimensionality**: In a three-dimensional space, any vector can be resolved along three independent axes (x, y, z). However, vectors can also be resolved in two dimensions or even one dimension, depending on the situation.
- **Linear Independence**: Directions like x and y in a 2D plane are independent. Resolving a vector along these axes allows for a complete representation of the vector's effects in that plane.
- **Mathematical Representation**: A vector, represented as **V**, can be expressed as **V = Vx + Vy + Vz**, where Vx, Vy, and Vz are the components along independent axes. This principle applies in any dimensional space.
Applications of Vector Resolution
- **Physics**: Used in analyzing forces, motion, and other physical phenomena.
- **Engineering**: Essential for resolving forces in structures and mechanical systems.
- **Computer Graphics**: Used to render movements and transformations in a 3D space.
In summary, vectors can indeed be resolved along only independent directions, allowing for a complete understanding of their behavior in any given space. This resolution is crucial for accurate analysis in various fields.
Multiplying 2î + 7ĵ by 5 gives ______- a)10î + 35ĵ
- b)2î + 35ĵ
- c)10î + 7ĵ
- d)2î + 7ĵ
Correct answer is option 'A'. Can you explain this answer?
Multiplying 2î + 7ĵ by 5 gives ______
a)
10î + 35ĵ
b)
2î + 35ĵ
c)
10î + 7ĵ
d)
2î + 7ĵ
|
|
Isabella Iqbal answered |
Understanding the Expression
When we multiply the expression (2i + 7) by 5, we need to apply the distributive property. This means we will multiply each term inside the parentheses by 5.
Step-by-Step Calculation
- Distributing the 5:
- Multiply 5 by 2i:
- 5 * 2i = 10i
- Multiply 5 by 7:
- 5 * 7 = 35
- Combining the Results:
- Now, combine the results of these multiplications:
- 10i + 35
Final Result
The result of multiplying (2i + 7) by 5 is:
- 10i + 35
Conclusion
Thus, the correct answer is option 'A':
- 10i + 35
This shows how the distributive property works in algebra, allowing us to efficiently expand expressions by multiplying each term individually.
When we multiply the expression (2i + 7) by 5, we need to apply the distributive property. This means we will multiply each term inside the parentheses by 5.
Step-by-Step Calculation
- Distributing the 5:
- Multiply 5 by 2i:
- 5 * 2i = 10i
- Multiply 5 by 7:
- 5 * 7 = 35
- Combining the Results:
- Now, combine the results of these multiplications:
- 10i + 35
Final Result
The result of multiplying (2i + 7) by 5 is:
- 10i + 35
Conclusion
Thus, the correct answer is option 'A':
- 10i + 35
This shows how the distributive property works in algebra, allowing us to efficiently expand expressions by multiplying each term individually.
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string at the highest point?- a)30 N
- b)50 N
- c)20 N
- d)25 N
Correct answer is option 'A'. Can you explain this answer?
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string at the highest point?
a)
30 N
b)
50 N
c)
20 N
d)
25 N

|
Orion Classes answered |
At the highest point, the tension and the weight are in the same direction but the centrifugal force is in the opposite direction. Centrifugal force can be calculated as mv2/r = 50 N. Hence the tension = centrifugal force-weight = 30 N.
What is the dot product of two vectors, vector A and vector B? The angle between both the vector is θ.- a)A B Sinθ
- b)A B Cosθ
- c)A B tanθ
- d)A B Secθ
Correct answer is option 'B'. Can you explain this answer?
What is the dot product of two vectors, vector A and vector B? The angle between both the vector is θ.
a)
A B Sinθ
b)
A B Cosθ
c)
A B tanθ
d)
A B Secθ
|
|
Charlotte Chen answered |
The dot product of two vectors, vector A and vector B, is a scalar quantity defined as the product of the magnitudes of the vectors and the cosine of the angle between them. Mathematically, it is denoted as A · B.
If the angle between vector A and vector B is θ (theta) in radians, then the dot product can be calculated using the formula:
A · B = |A| |B| cos(θ)
Here, |A| represents the magnitude (or length) of vector A, and |B| represents the magnitude of vector B.
Note that the dot product is commutative, which means A · B = B · A.
If the angle between vector A and vector B is θ (theta) in radians, then the dot product can be calculated using the formula:
A · B = |A| |B| cos(θ)
Here, |A| represents the magnitude (or length) of vector A, and |B| represents the magnitude of vector B.
Note that the dot product is commutative, which means A · B = B · A.
Give an example of motion in two dimensions _________- a)Motion along a straight line in any direction
- b)Bird flying
- c)A flying kite
- d)Projectile motion
Correct answer is option 'D'. Can you explain this answer?
Give an example of motion in two dimensions _________
a)
Motion along a straight line in any direction
b)
Bird flying
c)
A flying kite
d)
Projectile motion
|
|
Aubrey Hayes answered |
Projectile Motion:
Projectile motion is a classic example of motion in two dimensions. It involves an object being thrown or projected into the air and moving in both the horizontal and vertical directions simultaneously.
Key Points:
- In projectile motion, an object moves under the influence of gravity only after an initial force has been applied to set it in motion.
- The object follows a curved path known as a projectile trajectory.
- The horizontal component of motion remains constant, while the vertical component is influenced by the force of gravity.
- The object reaches a maximum height at the peak of its trajectory before falling back to the ground.
- Examples of projectile motion include a thrown baseball, a launched rocket, or even a ball kicked into the air.
Importance of Understanding Projectile Motion:
Understanding projectile motion is crucial in various fields such as physics, engineering, sports, and even military applications. By analyzing the motion of projectiles, scientists and engineers can predict their trajectory, range, and impact point with precision. This knowledge is essential for designing efficient systems like artillery, missiles, or sports equipment.
In conclusion, projectile motion serves as a fundamental example of motion in two dimensions, showcasing the interaction between horizontal and vertical motion components. Mastering the principles of projectile motion is essential for various real-world applications and scientific advancements.
Which one of the following operations is valid?- a)Vector multiplied by scalar
- b)Vector added to scalar
- c)Vector subtracted from scalar
- d)Vector divided by vector
Correct answer is option 'A'. Can you explain this answer?
Which one of the following operations is valid?
a)
Vector multiplied by scalar
b)
Vector added to scalar
c)
Vector subtracted from scalar
d)
Vector divided by vector
|
|
Victoria Walsh answered |
Vector multiplied by scalar
Vectors can be multiplied by scalars, which results in a new vector. This operation involves multiplying each component of the vector by the scalar. The resulting vector has the same direction as the original vector but its magnitude is scaled by the scalar. This operation is commonly used in physics and mathematics to scale vectors by a certain factor.
For example, if we have a vector v = (2, 4, 6) and we multiply it by a scalar k = 3, the resulting vector would be kv = (2*3, 4*3, 6*3) = (6, 12, 18).
This operation is valid and commonly used in various applications such as physics, engineering, and computer graphics. It allows us to scale vectors to represent different quantities or magnitudes.
The position of a body, moving in a plane, changes from origin to 14î + 11ĵ in 20s. What is the velocity of the body?- a)0.7î + 0.55ĵ
- b)0.55î + 0.7ĵ
- c)0.3î + 0.7ĵ
- d)0.3î
Correct answer is option 'A'. Can you explain this answer?
The position of a body, moving in a plane, changes from origin to 14î + 11ĵ in 20s. What is the velocity of the body?
a)
0.7î + 0.55ĵ
b)
0.55î + 0.7ĵ
c)
0.3î + 0.7ĵ
d)
0.3î
|
|
Ethan Cooper answered |
Given Data:
Position of the body changes from origin to 14î + 11 in 20s.
Formula:
Velocity (v) = Change in position / Time taken
Calculations:
- Change in position = Final position - Initial position
- Final position = 14î + 11
- Initial position = 0 (as the body starts from the origin)
- Change in position = 14î + 11 - 0 = 14î + 11
- Time taken = 20s
- Velocity (v) = (14î + 11) / 20
- Velocity (v) = 0.7î + 0.55
Therefore, the velocity of the body is:
0.7î + 0.55
Therefore, the correct answer is option A) 0.7î + 0.55.
Position of the body changes from origin to 14î + 11 in 20s.
Formula:
Velocity (v) = Change in position / Time taken
Calculations:
- Change in position = Final position - Initial position
- Final position = 14î + 11
- Initial position = 0 (as the body starts from the origin)
- Change in position = 14î + 11 - 0 = 14î + 11
- Time taken = 20s
- Velocity (v) = (14î + 11) / 20
- Velocity (v) = 0.7î + 0.55
Therefore, the velocity of the body is:
0.7î + 0.55
Therefore, the correct answer is option A) 0.7î + 0.55.
At which position in vertical circular motion is the tension in the string minimum?- a)At the highest position
- b)At the lowest position
- c)When the string is horizontal
- d)At an angle of 35° from the horizontal
Correct answer is option 'A'. Can you explain this answer?
At which position in vertical circular motion is the tension in the string minimum?
a)
At the highest position
b)
At the lowest position
c)
When the string is horizontal
d)
At an angle of 35° from the horizontal

|
Orion Classes answered |
When the body is at the highest point of its motion. This is because at the highest point the tension = centrifugal force – weight. This is the minimum value for tension throughout the motion.
A car moves 25 units in the positive X direction and 75 units in negative Y direction starting from the origin in 25 seconds. What is the velocity vector of the car?- a)î – 3ĵ
- b)3î – ĵ
- c)î + 3ĵ
- d)3î + ĵ
Correct answer is option 'A'. Can you explain this answer?
A car moves 25 units in the positive X direction and 75 units in negative Y direction starting from the origin in 25 seconds. What is the velocity vector of the car?
a)
î – 3ĵ
b)
3î – ĵ
c)
î + 3ĵ
d)
3î + ĵ

|
Orion Classes answered |
The initial position of the car is at the origin and the final position is 25î – 75ĵ. Hence the displacement is 25î – 75ĵ. The total time taken is 25 s. Hence, the velocity = change in position/time = î – 3ĵ.
A vector, 5 units from the origin, along the X axis, is added to vector 2 units from the origin along the Y axis. What is the resultant vector?- a)3î + 8ĵ
- b)5î + 2ĵ
- c)2î + 5ĵ
- d)2î + 7ĵ
Correct answer is option 'B'. Can you explain this answer?
A vector, 5 units from the origin, along the X axis, is added to vector 2 units from the origin along the Y axis. What is the resultant vector?
a)
3î + 8ĵ
b)
5î + 2ĵ
c)
2î + 5ĵ
d)
2î + 7ĵ
|
|
Madison Butler answered |
To find the resultant vector, we can add the x-components and the y-components separately.
The vector along the X-axis has an x-component of 5 and a y-component of 0.
The vector along the Y-axis has an x-component of 0 and a y-component of 2.
Adding the x-components, we get 5 + 0 = 5.
Adding the y-components, we get 0 + 2 = 2.
So the resultant vector has an x-component of 5 and a y-component of 2.
Thus, the resultant vector is (5, 2).
The vector along the X-axis has an x-component of 5 and a y-component of 0.
The vector along the Y-axis has an x-component of 0 and a y-component of 2.
Adding the x-components, we get 5 + 0 = 5.
Adding the y-components, we get 0 + 2 = 2.
So the resultant vector has an x-component of 5 and a y-component of 2.
Thus, the resultant vector is (5, 2).
A velocity vector (5m/s) is making and angle of 60 degrees with X axis has a horizonal component of magnitude ___- a)2.5
- b)5.5
- c)5
- d)10/√3
Correct answer is option 'A'. Can you explain this answer?
A velocity vector (5m/s) is making and angle of 60 degrees with X axis has a horizonal component of magnitude ___
a)
2.5
b)
5.5
c)
5
d)
10/√3

|
Orion Classes answered |
The horizontal component of any vector with magnitude a is a cos θ. Here θ = 60. cos θ = ½. Hence the answer is 5/2 = 2.5 m/s.
Which of the following is not true about projectile motion?- a)It is an example of motion in a plane
- b)It is an example of motion along a curve
- c)It is not an example of motion in space
- d)The acceleration keeps changing in projectile motion
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not true about projectile motion?
a)
It is an example of motion in a plane
b)
It is an example of motion along a curve
c)
It is not an example of motion in space
d)
The acceleration keeps changing in projectile motion

|
Orion Classes answered |
The only acceleration in projectile motion is the acceleration due to gravity. If the maximum height of the projectile motion is not large, and can be neglected with respect to the radius of earth (which usually is the case), the acceleration due to gravity remains constant. Hence, the acceleration in projectile motion remains constant.
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string when is horizontal?- a)30 N
- b)50 N
- c)20 N
- d)25 N
Correct answer is option 'B'. Can you explain this answer?
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string when is horizontal?
a)
30 N
b)
50 N
c)
20 N
d)
25 N

|
Orion Classes answered |
When the string is horizontal, the tension in the string and the centrifugal force are opposite to each other. Centrifugal force can be calculated as mv2/r = 50 N. Hence the tension = centrifugal force = 50 N.
The velocity of a body, moving in a plane, changes from 3î to 3î + 7ĵ in 10s. What is the acceleration of the body?- a)0.7ĵ
- b)0.7î
- c)0.33î + 7ĵ
- d)0.3î + 7ĵ
Correct answer is option 'A'. Can you explain this answer?
The velocity of a body, moving in a plane, changes from 3î to 3î + 7ĵ in 10s. What is the acceleration of the body?
a)
0.7ĵ
b)
0.7î
c)
0.33î + 7ĵ
d)
0.3î + 7ĵ
|
|
Wyatt Turner answered |
The velocity of a body, moving in a plane, changes from 3 m/s to 5 m/s in a time interval of 2 seconds.
Adding î + 77ĵ and 7î + ĵ gives ______- a)8î + 78ĵ
- b)0î + 76ĵ
- c)î + 74ĵ
- d)78î + 8ĵ
Correct answer is option 'A'. Can you explain this answer?
Adding î + 77ĵ and 7î + ĵ gives ______
a)
8î + 78ĵ
b)
0î + 76ĵ
c)
î + 74ĵ
d)
78î + 8ĵ

|
Orion Classes answered |
When î + 77ĵ is added to 7î + ĵ, the corresponding components get added. Hence, the answer is 8î + 78ĵ.
If S = 3t2 - 5t + 7 find initial velocity.- a)2
- b)5
- c)-2
- d)-5
Correct answer is option 'D'. Can you explain this answer?
If S = 3t2 - 5t + 7 find initial velocity.
a)
2
b)
5
c)
-2
d)
-5
|
|
Harper Phillips answered |
Understanding the Problem
To find the initial velocity from the given equation of motion, we focus on the position equation:
S = 3t² - 5t + 7
Here, S represents the position, and t represents time.
Identifying Initial Conditions
- The initial velocity refers to the velocity of the object at time t = 0.
- We can find the velocity by taking the derivative of the position function S with respect to time t.
Calculating the Velocity Function
- The velocity (v) is given by the derivative of S:
v(t) = dS/dt
- Taking the derivative of the equation S = 3t² - 5t + 7:
* v(t) = d(3t²)/dt - d(5t)/dt + d(7)/dt
* v(t) = 6t - 5
Finding Initial Velocity
- To find the initial velocity, substitute t = 0 into the velocity equation:
v(0) = 6(0) - 5
v(0) = -5
Conclusion
- The initial velocity of the object is -5.
- Therefore, the correct answer is option 'D'.
This detailed breakdown clarifies how to derive the initial velocity from the given position equation.
To find the initial velocity from the given equation of motion, we focus on the position equation:
S = 3t² - 5t + 7
Here, S represents the position, and t represents time.
Identifying Initial Conditions
- The initial velocity refers to the velocity of the object at time t = 0.
- We can find the velocity by taking the derivative of the position function S with respect to time t.
Calculating the Velocity Function
- The velocity (v) is given by the derivative of S:
v(t) = dS/dt
- Taking the derivative of the equation S = 3t² - 5t + 7:
* v(t) = d(3t²)/dt - d(5t)/dt + d(7)/dt
* v(t) = 6t - 5
Finding Initial Velocity
- To find the initial velocity, substitute t = 0 into the velocity equation:
v(0) = 6(0) - 5
v(0) = -5
Conclusion
- The initial velocity of the object is -5.
- Therefore, the correct answer is option 'D'.
This detailed breakdown clarifies how to derive the initial velocity from the given position equation.
A body moves from point A (3,6) to point B (11,12) to point C (15,15). What is the average speed of the body along the given path if the total time taken is 100s?- a)0.15 units/s
- b)1.5 units/s
- c)15 units/s
- d)0.0015 units/s
Correct answer is option 'A'. Can you explain this answer?
A body moves from point A (3,6) to point B (11,12) to point C (15,15). What is the average speed of the body along the given path if the total time taken is 100s?
a)
0.15 units/s
b)
1.5 units/s
c)
15 units/s
d)
0.0015 units/s

|
Orion Classes answered |
The distance between A and B is 10 units. The distance between B and C is 5 units. Hence, the total distance is 15 units. The total time taken is 100 s. Average speed = total distance/total time taken = 15/100 = 0.15 units/s.
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 2 m/s. What is the tension in the string at the lowest point?- a)28 N
- b)20 N
- c)8 N
- d)15 N
Correct answer is option 'A'. Can you explain this answer?
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 2 m/s. What is the tension in the string at the lowest point?
a)
28 N
b)
20 N
c)
8 N
d)
15 N

|
Orion Classes answered |
At the lowest point, the body experiences centrifugal force and the weight in the same direction, opposite to the direction of tension in the string. Centrifugal force can be calculated as mv2/r = 8 N. Hence the tension = weight + centrifugal force = 28 N.
A vector, 7 units from the origin, along the X axis, is added to vector 11 units from the origin along the Y axis. What is the resultant vector?- a)3î + 8ĵ
- b)7î + 11ĵ
- c)11î + 7ĵ
- d)2î + 7ĵ
Correct answer is option 'B'. Can you explain this answer?
A vector, 7 units from the origin, along the X axis, is added to vector 11 units from the origin along the Y axis. What is the resultant vector?
a)
3î + 8ĵ
b)
7î + 11ĵ
c)
11î + 7ĵ
d)
2î + 7ĵ

|
Orion Classes answered |
The vector 7 units from the origin and along X axis is 7î. The vector 11 units from the origin and along Y axis is 11ĵ. Hence the sum is 7î + 11ĵ.
The angular velocity of a stone being rotated is 11 rad/s. What is the angular displacement covered in 0.5s?- a)5.5 rad
- b)0.55 rad
- c)55 rad
- d)0.5 rad
Correct answer is option 'A'. Can you explain this answer?
The angular velocity of a stone being rotated is 11 rad/s. What is the angular displacement covered in 0.5s?
a)
5.5 rad
b)
0.55 rad
c)
55 rad
d)
0.5 rad
|
|
Amelia Martin answered |
Angular Displacement Calculation:
Angular displacement is calculated using the formula:
\[ \text{Angular Displacement} = \text{Angular Velocity} \times \text{Time} \]
Given:
- Angular velocity = 11 rad/s
- Time = 0.5s
Calculation:
\[ \text{Angular Displacement} = 11 \text{ rad/s} \times 0.5 \text{ s} \]
\[ \text{Angular Displacement} = 5.5 \text{ rad} \]
Therefore, the angular displacement covered in 0.5s is 5.5 radians, which corresponds to option (a).
Angular displacement is calculated using the formula:
\[ \text{Angular Displacement} = \text{Angular Velocity} \times \text{Time} \]
Given:
- Angular velocity = 11 rad/s
- Time = 0.5s
Calculation:
\[ \text{Angular Displacement} = 11 \text{ rad/s} \times 0.5 \text{ s} \]
\[ \text{Angular Displacement} = 5.5 \text{ rad} \]
Therefore, the angular displacement covered in 0.5s is 5.5 radians, which corresponds to option (a).
A body is moving in a vertical circular motion. Which one of the following forces does it not experience?- a)Force of gravity
- b)Centripetal force
- c)Normal reaction force
- d)Centrifugal force
Correct answer is option 'C'. Can you explain this answer?
A body is moving in a vertical circular motion. Which one of the following forces does it not experience?
a)
Force of gravity
b)
Centripetal force
c)
Normal reaction force
d)
Centrifugal force
|
|
Scarlett Reed answered |
Explanation:
In a vertical circular motion, a body moves in a circular path in a vertical plane. This motion can be observed in various scenarios such as a roller coaster or a swing. When analyzing the forces acting on the body during this motion, we can identify four main forces: force of gravity, centripetal force, normal reaction force, and centrifugal force.
1. Force of gravity: The force of gravity acts vertically downwards, towards the center of the Earth. It is responsible for pulling the body towards the Earth and giving it weight.
2. Centripetal force: The centripetal force is the force that keeps the body moving in a circular path. It always acts towards the center of the circle and is responsible for changing the direction of the body's velocity. In the case of vertical circular motion, the centripetal force can be provided by tension in a rope or the normal reaction force.
3. Normal reaction force: The normal reaction force is the force exerted by a surface to support the weight of an object resting on it. In the case of vertical circular motion, the normal reaction force acts perpendicular to the surface the body is moving on. It is responsible for preventing the body from falling through the surface.
4. Centrifugal force: The centrifugal force is often referred to as a "fictitious" or "pseudo" force. It is an apparent force that acts in the opposite direction to the centripetal force. In reality, it is not a true force but rather a result of inertia. In vertical circular motion, the centrifugal force would act away from the center of the circle and would be felt by the body as an outward force.
Answer:
The force that the body does not experience in vertical circular motion is the normal reaction force (Option C). This is because the normal reaction force only acts perpendicular to the surface the body is moving on, and in this case, the body is not in contact with any surface. In vertical circular motion, the body is typically suspended or held by a rope, and the centripetal force is provided by tension in the rope. Therefore, the body does not exert any force on a surface, and hence there is no normal reaction force.
It is important to note that the absence of the normal reaction force does not imply that the body is not experiencing any other forces. The force of gravity and the centripetal force are still acting on the body, ensuring its motion in a circular path.
In a vertical circular motion, a body moves in a circular path in a vertical plane. This motion can be observed in various scenarios such as a roller coaster or a swing. When analyzing the forces acting on the body during this motion, we can identify four main forces: force of gravity, centripetal force, normal reaction force, and centrifugal force.
1. Force of gravity: The force of gravity acts vertically downwards, towards the center of the Earth. It is responsible for pulling the body towards the Earth and giving it weight.
2. Centripetal force: The centripetal force is the force that keeps the body moving in a circular path. It always acts towards the center of the circle and is responsible for changing the direction of the body's velocity. In the case of vertical circular motion, the centripetal force can be provided by tension in a rope or the normal reaction force.
3. Normal reaction force: The normal reaction force is the force exerted by a surface to support the weight of an object resting on it. In the case of vertical circular motion, the normal reaction force acts perpendicular to the surface the body is moving on. It is responsible for preventing the body from falling through the surface.
4. Centrifugal force: The centrifugal force is often referred to as a "fictitious" or "pseudo" force. It is an apparent force that acts in the opposite direction to the centripetal force. In reality, it is not a true force but rather a result of inertia. In vertical circular motion, the centrifugal force would act away from the center of the circle and would be felt by the body as an outward force.
Answer:
The force that the body does not experience in vertical circular motion is the normal reaction force (Option C). This is because the normal reaction force only acts perpendicular to the surface the body is moving on, and in this case, the body is not in contact with any surface. In vertical circular motion, the body is typically suspended or held by a rope, and the centripetal force is provided by tension in the rope. Therefore, the body does not exert any force on a surface, and hence there is no normal reaction force.
It is important to note that the absence of the normal reaction force does not imply that the body is not experiencing any other forces. The force of gravity and the centripetal force are still acting on the body, ensuring its motion in a circular path.
A body is moving with a constant acceleration of 4î + 3ĵ, starting from the origin. What will be the position of the body after 5s?- a)50î + 37.5ĵ
- b)37.5î + 50ĵ
- c)37.5î – 50ĵ
- d)50î – 37.5ĵ
Correct answer is option 'A'. Can you explain this answer?
A body is moving with a constant acceleration of 4î + 3ĵ, starting from the origin. What will be the position of the body after 5s?
a)
50î + 37.5ĵ
b)
37.5î + 50ĵ
c)
37.5î – 50ĵ
d)
50î – 37.5ĵ
|
|
Joseph Simmons answered |
Understanding the Problem
The body is moving with a constant acceleration, given as 4i + 3j. We need to find its position after 5 seconds, starting from the origin.
Given Variables
- Initial position (s0) = 0 (origin)
- Initial velocity (u) = 0 (since it starts from rest)
- Acceleration (a) = 4i + 3j
- Time (t) = 5 seconds
Using the Equation of Motion
The position vector (s) after time t under constant acceleration can be calculated using the formula:
s = s0 + ut + (1/2)at²
Since the initial position and velocity are both zero, the equation simplifies to:
s = (1/2)at²
Calculating the Position
- Substitute the acceleration and time into the formula:
s = (1/2)(4i + 3j)(5)²
- Calculate (5)²:
(5)² = 25
- Now, plug this value into the equation:
s = (1/2)(4i + 3j)(25)
s = (1/2)(100i + 75j)
- Simplifying further:
s = 50i + 37.5j
Final Result
After 5 seconds, the position of the body will be:
s = 50i + 37.5j
Thus, the correct answer is option A: 50i + 37.5j.
This detailed calculation confirms that option A is indeed the correct choice.
The body is moving with a constant acceleration, given as 4i + 3j. We need to find its position after 5 seconds, starting from the origin.
Given Variables
- Initial position (s0) = 0 (origin)
- Initial velocity (u) = 0 (since it starts from rest)
- Acceleration (a) = 4i + 3j
- Time (t) = 5 seconds
Using the Equation of Motion
The position vector (s) after time t under constant acceleration can be calculated using the formula:
s = s0 + ut + (1/2)at²
Since the initial position and velocity are both zero, the equation simplifies to:
s = (1/2)at²
Calculating the Position
- Substitute the acceleration and time into the formula:
s = (1/2)(4i + 3j)(5)²
- Calculate (5)²:
(5)² = 25
- Now, plug this value into the equation:
s = (1/2)(4i + 3j)(25)
s = (1/2)(100i + 75j)
- Simplifying further:
s = 50i + 37.5j
Final Result
After 5 seconds, the position of the body will be:
s = 50i + 37.5j
Thus, the correct answer is option A: 50i + 37.5j.
This detailed calculation confirms that option A is indeed the correct choice.
A force is inclined at 60° to the horizontal. If its rectangular component in horizontal direction is 50 N. Find the magnitude of the force and its vertical components respectively.- a)100 N, 50 N
- b)50√3 N, 100 N
- c)100 N, 50√3 N
- d)100 N, 100 N
Correct answer is option 'B'. Can you explain this answer?
A force is inclined at 60° to the horizontal. If its rectangular component in horizontal direction is 50 N. Find the magnitude of the force and its vertical components respectively.
a)
100 N, 50 N
b)
50√3 N, 100 N
c)
100 N, 50√3 N
d)
100 N, 100 N
|
|
Xavier Hughes answered |
Degrees to the horizontal. This means that the force vector makes a 60 degree angle with the horizontal axis. In other words, the force is not acting directly vertical or horizontal, but at an angle of 60 degrees from the horizontal.
A child pulls a rope attached to a stone with a force of 60 N. The rope makes an angle of 60 degrees to the ground. What is the effective force along the horizontal direction?- a)45.96 N
- b)40.3 N
- c)28 N
- d)30 N
Correct answer is option 'D'. Can you explain this answer?
A child pulls a rope attached to a stone with a force of 60 N. The rope makes an angle of 60 degrees to the ground. What is the effective force along the horizontal direction?
a)
45.96 N
b)
40.3 N
c)
28 N
d)
30 N

|
Orion Classes answered |
Concept:
Resolution of vectors into components: We have a vector (F) where the magnitude of the vector is F and the angle with horizontal is θ.
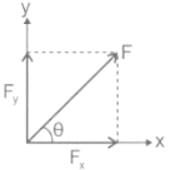

The vector has two components: 1. Vertical component and 2. Horizontal component
Vertical component (Fy) = F Sinθ
Horizontal component (Fx) = F Cosθ
Calculation:
The horizontal component is responsible to move the stone along the ground.
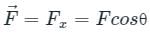
Calculation:
The horizontal component is responsible to move the stone along the ground.
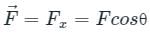
Fx = 60cos60° = 30 N
Hence, the effective value of the pull tending to move the stone on the ground is 30 N.
What is the standard form for the resolution of a vector having magnitude ‘a’ and is inclined at an angle θ to the X-axis?- a)a(cos θ î + sin θ ĵ)
- b)a(sin θ î + cos θ ĵ)
- c)a(sin θ î + sin θ ĵ)
- d)a(cos θ î + cos θ ĵ)
Correct answer is option 'A'. Can you explain this answer?
What is the standard form for the resolution of a vector having magnitude ‘a’ and is inclined at an angle θ to the X-axis?
a)
a(cos θ î + sin θ ĵ)
b)
a(sin θ î + cos θ ĵ)
c)
a(sin θ î + sin θ ĵ)
d)
a(cos θ î + cos θ ĵ)

|
Orion Classes answered |
The correct answer is a(cos θ î + sin θ ĵ). This is obtained by constructing a right-angled triangle with the distance of the point from the origin with either of the axes and then finding out the corresponding values for X and Y components.
Which of the following affects the angular velocity with its rate of change?- a)Angular acceleration
- b)Angular Distance
- c)Angular Displacement
- d)Torque
Correct answer is option 'C'. Can you explain this answer?
Which of the following affects the angular velocity with its rate of change?
a)
Angular acceleration
b)
Angular Distance
c)
Angular Displacement
d)
Torque

|
Orion Classes answered |
Angular velocity is the time rate at which an object rotates, or revolves, about an axis, or at which the angular displacement between two bodies changes. Thus the rate of change of angular velocity depends on angular displacement.
Velocity of a man is 25 units in the positive X direction and 75 units in negative Y direction starting from the origin. Velocity of a woman is 25 units in the positive Y direction and 75 units in the negative X direction starting from the origin. What is the relative velocity of the man with respect to the woman?- a)100î – 100ĵ
- b)100î + 100ĵ
- c)-100î – 100ĵ
- d)0î + 0ĵ
Correct answer is option 'A'. Can you explain this answer?
Velocity of a man is 25 units in the positive X direction and 75 units in negative Y direction starting from the origin. Velocity of a woman is 25 units in the positive Y direction and 75 units in the negative X direction starting from the origin. What is the relative velocity of the man with respect to the woman?
a)
100î – 100ĵ
b)
100î + 100ĵ
c)
-100î – 100ĵ
d)
0î + 0ĵ
|
|
Josephine Myers answered |
Relative Velocity Calculation:
- The velocity of the man (M) with respect to the woman (W) can be calculated by subtracting the velocity of the woman from the velocity of the man.
- Given that the velocity of the man (M) is 25 units in the positive X direction and 75 units in the negative Y direction, represented as M = 25î - 75ĵ.
- The velocity of the woman (W) is 25 units in the positive Y direction and 75 units in the negative X direction, represented as W = -75î + 25ĵ.
- Subtracting the velocity of the woman from the velocity of the man, we get the relative velocity of the man with respect to the woman as M - W = (25î - 75ĵ) - (-75î + 25ĵ) = 25î - 75ĵ + 75î - 25ĵ = 100î - 100ĵ.
- Therefore, the relative velocity of the man with respect to the woman is 100î - 100ĵ, which corresponds to option 'A'.
- The velocity of the man (M) with respect to the woman (W) can be calculated by subtracting the velocity of the woman from the velocity of the man.
- Given that the velocity of the man (M) is 25 units in the positive X direction and 75 units in the negative Y direction, represented as M = 25î - 75ĵ.
- The velocity of the woman (W) is 25 units in the positive Y direction and 75 units in the negative X direction, represented as W = -75î + 25ĵ.
- Subtracting the velocity of the woman from the velocity of the man, we get the relative velocity of the man with respect to the woman as M - W = (25î - 75ĵ) - (-75î + 25ĵ) = 25î - 75ĵ + 75î - 25ĵ = 100î - 100ĵ.
- Therefore, the relative velocity of the man with respect to the woman is 100î - 100ĵ, which corresponds to option 'A'.
The velocity of a car A is to 5î + 11ĵ. The velocity of another car B is 11î + 5ĵ. What is the relative velocity of B with respect to A?- a)6î – 6ĵ
- b)11î + 5ĵ
- c)6î + 6ĵ
- d)5î + 5ĵ
Correct answer is option 'A'. Can you explain this answer?
The velocity of a car A is to 5î + 11ĵ. The velocity of another car B is 11î + 5ĵ. What is the relative velocity of B with respect to A?
a)
6î – 6ĵ
b)
11î + 5ĵ
c)
6î + 6ĵ
d)
5î + 5ĵ
|
|
Savannah Mitchell answered |
Understanding Relative Velocity
Relative velocity is the velocity of one object as observed from another object. To find the relative velocity of car B with respect to car A, we use the formula:
Relative Velocity of B with respect to A = Velocity of B - Velocity of A
Given Velocities
- Velocity of Car A: 5i + 11j
- Velocity of Car B: 11i + 5j
Calculating Relative Velocity
Let's subtract the velocity of car A from the velocity of car B:
- Relative Velocity (B relative to A) = (11i + 5j) - (5i + 11j)
Step-by-Step Calculation
1. Subtract the i-components:
- 11i - 5i = 6i
2. Subtract the j-components:
- 5j - 11j = -6j
Combining these results gives:
Relative Velocity = 6i - 6j
Final Result
Thus, the relative velocity of car B with respect to car A is:
6i - 6j
Conclusion
The correct answer is option 'A': 6i - 6j. This calculation shows that car B is moving 6 units in the i direction and 6 units in the negative j direction relative to car A.
Relative velocity is the velocity of one object as observed from another object. To find the relative velocity of car B with respect to car A, we use the formula:
Relative Velocity of B with respect to A = Velocity of B - Velocity of A
Given Velocities
- Velocity of Car A: 5i + 11j
- Velocity of Car B: 11i + 5j
Calculating Relative Velocity
Let's subtract the velocity of car A from the velocity of car B:
- Relative Velocity (B relative to A) = (11i + 5j) - (5i + 11j)
Step-by-Step Calculation
1. Subtract the i-components:
- 11i - 5i = 6i
2. Subtract the j-components:
- 5j - 11j = -6j
Combining these results gives:
Relative Velocity = 6i - 6j
Final Result
Thus, the relative velocity of car B with respect to car A is:
6i - 6j
Conclusion
The correct answer is option 'A': 6i - 6j. This calculation shows that car B is moving 6 units in the i direction and 6 units in the negative j direction relative to car A.
An object makes a displacement of 4 m due East from a point P and then makes displacement of 3 m due North. Its resultant displacement from P.- a)7 m
- b)1 m
- c)5 m
- d)1.2 m
Correct answer is option 'C'. Can you explain this answer?
An object makes a displacement of 4 m due East from a point P and then makes displacement of 3 m due North. Its resultant displacement from P.
a)
7 m
b)
1 m
c)
5 m
d)
1.2 m
|
|
Sebastian Diaz answered |
Understanding the Problem
The object moves in two perpendicular directions: first 4 m due East and then 3 m due North. To find the resultant displacement, we can visualize this scenario as a right-angled triangle.
Displacement Breakdown
- First Displacement: 4 m East
- Second Displacement: 3 m North
Visualizing the Triangle
- The Eastward displacement forms one side of the triangle (4 m).
- The Northward displacement forms the other side of the triangle (3 m).
- The resultant displacement is the hypotenuse of this right triangle.
Calculating the Resultant Displacement
To find the hypotenuse (resultant displacement), we can apply the Pythagorean theorem:
- Resultant Displacement = √(East Displacement² + North Displacement²)
Substituting the values:
- Resultant Displacement = √(4² + 3²)
- Resultant Displacement = √(16 + 9)
- Resultant Displacement = √25
- Resultant Displacement = 5 m
Conclusion
The resultant displacement from point P is indeed 5 m. Therefore, the correct answer is option 'C'.
The object moves in two perpendicular directions: first 4 m due East and then 3 m due North. To find the resultant displacement, we can visualize this scenario as a right-angled triangle.
Displacement Breakdown
- First Displacement: 4 m East
- Second Displacement: 3 m North
Visualizing the Triangle
- The Eastward displacement forms one side of the triangle (4 m).
- The Northward displacement forms the other side of the triangle (3 m).
- The resultant displacement is the hypotenuse of this right triangle.
Calculating the Resultant Displacement
To find the hypotenuse (resultant displacement), we can apply the Pythagorean theorem:
- Resultant Displacement = √(East Displacement² + North Displacement²)
Substituting the values:
- Resultant Displacement = √(4² + 3²)
- Resultant Displacement = √(16 + 9)
- Resultant Displacement = √25
- Resultant Displacement = 5 m
Conclusion
The resultant displacement from point P is indeed 5 m. Therefore, the correct answer is option 'C'.
In how many independent directions can a vector in a plane be resolved?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
In how many independent directions can a vector in a plane be resolved?
a)
1
b)
2
c)
3
d)
4
|
|
Liam Curry answered |
Understanding Vector Resolution in a Plane
When we talk about resolving a vector in a plane, we refer to breaking it down into its components along specific independent directions.
Independent Directions in a Plane
In a two-dimensional space (or plane), there are two key independent directions:
- Horizontal (x-axis): This represents the direction along the width of the plane.
- Vertical (y-axis): This represents the direction along the height of the plane.
These two directions are perpendicular to each other, meaning they do not affect each other’s measurements, making them independent.
Importance of Resolution
Resolving a vector into its components is crucial for simplifying complex problems in physics and engineering. Each component can be analyzed separately, allowing for:
- Easier calculations: By dealing with two simpler one-dimensional problems instead of one complicated two-dimensional problem.
- Clear understanding: Understanding how a vector behaves in each independent direction.
Conclusion
Thus, in a plane, a vector can be resolved into two independent directions – the horizontal and vertical components. This is why the correct answer to the question is option 'B'.
When we talk about resolving a vector in a plane, we refer to breaking it down into its components along specific independent directions.
Independent Directions in a Plane
In a two-dimensional space (or plane), there are two key independent directions:
- Horizontal (x-axis): This represents the direction along the width of the plane.
- Vertical (y-axis): This represents the direction along the height of the plane.
These two directions are perpendicular to each other, meaning they do not affect each other’s measurements, making them independent.
Importance of Resolution
Resolving a vector into its components is crucial for simplifying complex problems in physics and engineering. Each component can be analyzed separately, allowing for:
- Easier calculations: By dealing with two simpler one-dimensional problems instead of one complicated two-dimensional problem.
- Clear understanding: Understanding how a vector behaves in each independent direction.
Conclusion
Thus, in a plane, a vector can be resolved into two independent directions – the horizontal and vertical components. This is why the correct answer to the question is option 'B'.
Vectors lying in the same or parallel to the same plane are called _____- a)Coplanar vectors
- b)Equal vector
- c)Unit Vector
- d)Displacement vector
Correct answer is option 'A'. Can you explain this answer?
Vectors lying in the same or parallel to the same plane are called _____
a)
Coplanar vectors
b)
Equal vector
c)
Unit Vector
d)
Displacement vector

|
Orion Classes answered |
Coplanar vectors lie in the same or parallel to the same plane.
What happens when a vector is multiplied by a scalar?- a)Its magnitude gets multiplied by that much amount
- b)Its direction rotates in XY plane by that much angle
- c)Its direction rotates in YZ plane by that much angle
- d)Its direction rotates in ZX plane by that much angle
Correct answer is option 'A'. Can you explain this answer?
What happens when a vector is multiplied by a scalar?
a)
Its magnitude gets multiplied by that much amount
b)
Its direction rotates in XY plane by that much angle
c)
Its direction rotates in YZ plane by that much angle
d)
Its direction rotates in ZX plane by that much angle

|
Flembe Academy answered |
Any vector a, can be written as a =  Hence, when we multiply it by a scalar, the magnitude multiplies by that much amount.
Hence, when we multiply it by a scalar, the magnitude multiplies by that much amount.
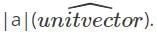 Hence, when we multiply it by a scalar, the magnitude multiplies by that much amount.
Hence, when we multiply it by a scalar, the magnitude multiplies by that much amount.A vector is represented as 4î + 3ĵ. What is its magnitude?- a)5
- b)10
- c)4
- d)3
Correct answer is option 'A'. Can you explain this answer?
A vector is represented as 4î + 3ĵ. What is its magnitude?
a)
5
b)
10
c)
4
d)
3

|
Orion Classes answered |
The magnitude of any vector can be found by taking the square root of sum of the squares of its two components. Hence, the sum of the squares of components is equal to 42 + 32 = 25. Square root of 25 = 5. Hence, the answer is 5.
Which theorem states that “If a particle under the simultaneous action of three forces is in equilibrium, then each force has a constant ratio with the sine of the angle between the other two forces”?- a)Lay’s theorem
- b)Lami’s Theorem
- c)Newton’s law
- d)Faraday’s theorem
Correct answer is option 'B'. Can you explain this answer?
Which theorem states that “If a particle under the simultaneous action of three forces is in equilibrium, then each force has a constant ratio with the sine of the angle between the other two forces”?
a)
Lay’s theorem
b)
Lami’s Theorem
c)
Newton’s law
d)
Faraday’s theorem

|
Orion Classes answered |
Lami’s Theorem states that if f a particle under the simultaneous action of three forces is in equilibrium, then each force has a constant ratio with the sine of the angle between the other two forces.
The splitting of a vector into two component vectors is called ______- a)Vector resolution
- b)Vector sum
- c)Vector decomposition
- d)Vector difference
Correct answer is option 'A'. Can you explain this answer?
The splitting of a vector into two component vectors is called ______
a)
Vector resolution
b)
Vector sum
c)
Vector decomposition
d)
Vector difference

|
Orion Classes answered |
The splitting of a vector into two component vectors is called vector resolution. The vector can be resolved into as many components as there are independent directions.
What is a scalar?- a)A quantity with only magnitude
- b)A quantity with only direction
- c)A quantity with both magnitude and direction
- d)A quantity without magnitude
Correct answer is option 'A'. Can you explain this answer?
What is a scalar?
a)
A quantity with only magnitude
b)
A quantity with only direction
c)
A quantity with both magnitude and direction
d)
A quantity without magnitude

|
Orion Classes answered |
A scalar quantity is one which only has a magnitude. Examples of scalar quantities are mass, volume, work, energy etc.
What is a vector quantity?- a)A quantity with only magnitude
- b)A quantity with only direction
- c)A quantity with both magnitude and direction
- d)A quantity without direction
Correct answer is option 'C'. Can you explain this answer?
What is a vector quantity?
a)
A quantity with only magnitude
b)
A quantity with only direction
c)
A quantity with both magnitude and direction
d)
A quantity without direction

|
Orion Classes answered |
A vector quantity is one which has both magnitude and direction. Unlike scalars, it can also tell the direction in which is the entity is acting. Examples of vector quantities are force, velocity, displacement etc.
The force that keeps the body moving in circular motion is _______- a)Centripetal force
- b)Centrifugal force
- c)Force of gravity
- d)Reaction forces
Correct answer is option 'A'. Can you explain this answer?
The force that keeps the body moving in circular motion is _______
a)
Centripetal force
b)
Centrifugal force
c)
Force of gravity
d)
Reaction forces

|
Orion Classes answered |
Centripetal force is responsible for keeping bodies moving in circular motion. The centripetal force is directly proportional to the square of the tangential velocity and inversely to the radius of circle.
Velocity of a dog is 15 units in the positive X direction and 3 units in positive Y direction starting from the origin. Velocity of a pig is 7 units in the positive Y direction and 17 units in the positive X direction starting from the origin. What is the relative velocity of the dog with respect to the pig?- a)-2î – 4ĵ
- b)-3î – 2ĵ
- c)-4î – 2ĵ
- d)7î + 4ĵ
Correct answer is option 'A'. Can you explain this answer?
Velocity of a dog is 15 units in the positive X direction and 3 units in positive Y direction starting from the origin. Velocity of a pig is 7 units in the positive Y direction and 17 units in the positive X direction starting from the origin. What is the relative velocity of the dog with respect to the pig?
a)
-2î – 4ĵ
b)
-3î – 2ĵ
c)
-4î – 2ĵ
d)
7î + 4ĵ

|
Orion Classes answered |
The velocity of the man is 15î+3ĵ and that of the woman is 17î + 7ĵ. Relative velocity = velocity of dog – velocity of pig = -2î – 4ĵ.
When two bodies move uniformly towards each other, the distance decrease by 6 m/s. If both the bodies moves (as above) in the same direction with the same speed, the distance between them increases by 4 m/s. Then the speed of the two bodies are- a)7 m/s, 3 m/s
- b)5 m/s, 1 m/s
- c)4 m/s, 2 m/s
- d)3 m/s, 3 m/s
Correct answer is option 'B'. Can you explain this answer?
When two bodies move uniformly towards each other, the distance decrease by 6 m/s. If both the bodies moves (as above) in the same direction with the same speed, the distance between them increases by 4 m/s. Then the speed of the two bodies are
a)
7 m/s, 3 m/s
b)
5 m/s, 1 m/s
c)
4 m/s, 2 m/s
d)
3 m/s, 3 m/s

|
Orion Classes answered |
Concept:
A) When two bodies move uniformly in opposite direction, the velocities gets added up.
B) When two bodies move uniformly in same direction, the velocities gets subtracted.
Calculation:
Given:
Let one bodies be A and B, and theor speed be V and U respectively.
As per the problem;
VA + VB = 6 ------(i)
VA - VB = 4 ------(ii)
Adding eq (i) and eq (ii)
2VA = 10
∴ VA = 5 m/s
Similarly
VA + VB = 6
5 + VB = 6
∴ VB = 1 m/s
A body is moving with a constant velocity of 4î + 3ĵ, starting from the origin. What will be the position of the body after 10s?- a)40î + 30ĵ
- b)30î + 40ĵ
- c)30î – 40ĵ
- d)40î – 30ĵ
Correct answer is option 'A'. Can you explain this answer?
A body is moving with a constant velocity of 4î + 3ĵ, starting from the origin. What will be the position of the body after 10s?
a)
40î + 30ĵ
b)
30î + 40ĵ
c)
30î – 40ĵ
d)
40î – 30ĵ

|
Orion Classes answered |
The body’s displacement is given by s = vt. The body starts from the origin hence, the total displacement is the final position of the body. Therefore, after putting in the values, we get, s = (4î + 3ĵ)*10 = 40î + 30ĵ.
What is the name given to a path followed by a projectile?- a)Territory
- b)Treasury
- c)Tractor
- d)Trajectory
Correct answer is option 'D'. Can you explain this answer?
What is the name given to a path followed by a projectile?
a)
Territory
b)
Treasury
c)
Tractor
d)
Trajectory

|
Orion Classes answered |
The path that an object with mass in motion follows through space as a function of time is called a trajectory or flight path. The total distance between the source and the target position is called the slant range. The angle formed between them is called the Inclination Angle.
On adding two vectors we get _____- a)A vector
- b)A scalar
- c)A number
- d)An operation
Correct answer is option 'A'. Can you explain this answer?
On adding two vectors we get _____
a)
A vector
b)
A scalar
c)
A number
d)
An operation

|
Orion Classes answered |
Addition of two vectors gives a vector as the result. The same goes for subtraction and cross multiplication. It is only when two vectors are operated through dot product, we get a scalar as the result.
The process of splitting a vector into two or more vectors in such a way that their combined effect is same as that of the given vector called-- a)Resolution of Vector
- b)Unit vector
- c)Uniqueness of resolution
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
The process of splitting a vector into two or more vectors in such a way that their combined effect is same as that of the given vector called-
a)
Resolution of Vector
b)
Unit vector
c)
Uniqueness of resolution
d)
None of the above

|
Orion Classes answered |
Concept:
- Resolution of vectors is the process of splitting a vector into two or more vectors in such a way that their combined effect is the same as that of the given vectors.
- The vectors into which the given vector is split are called Components of vectors.
Explanation:
- Resolution of vectors into components: We have a vector (F) where the magnitude of the vector is F and the angle with horizontal is θ.
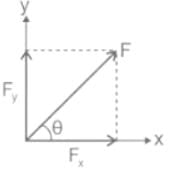
The vector has two components: 1. Vertical component and 2. Horizontal component
Vertical component (Fy) = F Sinθ
Horizontal component (Fx) = F Cosθ
Chapter doubts & questions for Motion in a plane - Science for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Motion in a plane - Science for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Science for ACT
504 videos|539 docs|348 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









