All Exams >
ACT >
Science for ACT >
All Questions
All questions of Solids for ACT Exam
The materials which have the same elastic properties in all directions are called __________.- a)Isotropic
- b)Brittle
- c)Homogeneous
- d)Hard
Correct answer is option 'A'. Can you explain this answer?
The materials which have the same elastic properties in all directions are called __________.
a)
Isotropic
b)
Brittle
c)
Homogeneous
d)
Hard
|
|
Pooja Shah answered |
Same elastic properties in all direction is called the homogenity of a material.
If we compress or elongate the solids, what happens to their potential energy?- a)P.E. of solid decreases whether it is compressed or elongated
- b)P.E. of solid increases if it is elongated
- c)P.E. of solid increases whether it is compressed or elongated
- d)P.E. of solid increases if it is compressed
Correct answer is option 'C'. Can you explain this answer?
If we compress or elongate the solids, what happens to their potential energy?
a)
P.E. of solid decreases whether it is compressed or elongated
b)
P.E. of solid increases if it is elongated
c)
P.E. of solid increases whether it is compressed or elongated
d)
P.E. of solid increases if it is compressed
|
|
Anjali Iyer answered |
When a soild is compressed or elongated, it's P.E increases. Potential energy increases because work has to be done against force of repulsion during compression and against force of attraction during elongation.
Which of the following represents Hooke’s Law?- a)Stress = k x strain
- b)

- c)Stress = k x (strain)2
- d)Stress2 = k x strain
Correct answer is option 'A'. Can you explain this answer?
Which of the following represents Hooke’s Law?
a)
Stress = k x strain
b)
c)
Stress = k x (strain)2
d)
Stress2 = k x strain
|
|
Gaurav Kumar answered |
The law states that the strain in a solid is proportional to the applied stress within the elastic limit of that solid body i.e. stress = k x strain.
Material is said to be ductile if- a)a large amount of plastic deformation takes place between the elastic limit and the fracture point
- b)fracture occurs soon after the elastic limit is passed
- c)material cross section is not significantly reduced at failure
- d)material breaks suddenly at little elongation
Correct answer is option 'A'. Can you explain this answer?
Material is said to be ductile if
a)
a large amount of plastic deformation takes place between the elastic limit and the fracture point
b)
fracture occurs soon after the elastic limit is passed
c)
material cross section is not significantly reduced at failure
d)
material breaks suddenly at little elongation
|
|
Nandini Iyer answered |
A ductile material is one that can withstand a large amount of plastic deformation between the elastic limit and the fracture point.
A material that breaks suddenly when elongated or fracture occurs in it soon after the elastic limit is crossed is called a brittle material.
A ductile material that exhibits extra elongation or deformation and does not fracture is also referred as superplastic material.
A material that breaks suddenly when elongated or fracture occurs in it soon after the elastic limit is crossed is called a brittle material.
A ductile material that exhibits extra elongation or deformation and does not fracture is also referred as superplastic material.
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?- a)0.065 mm
- b)0.055 mm
- c)0.045 mm
- d)0.075 mm
Correct answer is option 'C'. Can you explain this answer?
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?
a)
0.065 mm
b)
0.055 mm
c)
0.045 mm
d)
0.075 mm
|
|
Pritam Kapoor answered |
Given:
- The flood lamp stretches the wire by 0.18 mm
- The stress is proportional to the strain
To find:
- How much would it have stretched if the wire had the same length but twice the diameter
Let's begin by understanding the given information.
Stress is defined as the force per unit area and is denoted by the symbol σ (sigma). Mathematically, stress is given by:
σ = F / A
where F is the force applied and A is the area over which the force is applied.
Strain is defined as the change in length per unit length and is denoted by the symbol ε (epsilon). Mathematically, strain is given by:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the stress is proportional to the strain. This can be expressed mathematically as:
σ ∝ ε
or
σ = kε
where k is a constant of proportionality.
Now, let's apply this information to the problem at hand.
When the flood lamp is hung from the wire, it exerts a force on the wire which causes it to stretch. Let's assume that the original diameter of the wire is d and the original length is L.
From the given information, we know that the stress is proportional to the strain. Therefore, we can write:
σ = kε
where σ is the stress, k is a constant of proportionality, and ε is the strain.
The stress can be calculated using the formula:
σ = F / A
where F is the force applied and A is the cross-sectional area of the wire.
The force applied is the weight of the flood lamp, which can be calculated using the formula:
F = mg
where m is the mass of the flood lamp and g is the acceleration due to gravity.
The cross-sectional area of the wire can be calculated using the formula:
A = πd^2 / 4
where d is the diameter of the wire.
Therefore, we can write:
σ = (mg) / (πd^2 / 4)
The strain can be calculated using the formula:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the flood lamp stretches the wire by 0.18 mm. Therefore, we can write:
ε = 0.18 / L
Now, let's combine the equations for stress and strain:
σ = kε
σ = (mg) / (πd^2 / 4)
ε = 0.18 / L
Substituting the values of σ and ε, we get:
(mg) / (πd^2 / 4) = k (0.18 / L)
Simplifying, we get:
k = (mgL) / (0.18πd^2)
Now, let's use this value of k to calculate the change in length when the diameter of the wire is doubled.
When the diameter of the wire is doubled, the cross-sectional area of the wire becomes 4 times the original area. Therefore, the new diameter is 2d and the new cross-sectional area is:
A' = π(2d)^2 / 4 = 4πd^2
Using the same formula for stress,
- The flood lamp stretches the wire by 0.18 mm
- The stress is proportional to the strain
To find:
- How much would it have stretched if the wire had the same length but twice the diameter
Let's begin by understanding the given information.
Stress is defined as the force per unit area and is denoted by the symbol σ (sigma). Mathematically, stress is given by:
σ = F / A
where F is the force applied and A is the area over which the force is applied.
Strain is defined as the change in length per unit length and is denoted by the symbol ε (epsilon). Mathematically, strain is given by:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the stress is proportional to the strain. This can be expressed mathematically as:
σ ∝ ε
or
σ = kε
where k is a constant of proportionality.
Now, let's apply this information to the problem at hand.
When the flood lamp is hung from the wire, it exerts a force on the wire which causes it to stretch. Let's assume that the original diameter of the wire is d and the original length is L.
From the given information, we know that the stress is proportional to the strain. Therefore, we can write:
σ = kε
where σ is the stress, k is a constant of proportionality, and ε is the strain.
The stress can be calculated using the formula:
σ = F / A
where F is the force applied and A is the cross-sectional area of the wire.
The force applied is the weight of the flood lamp, which can be calculated using the formula:
F = mg
where m is the mass of the flood lamp and g is the acceleration due to gravity.
The cross-sectional area of the wire can be calculated using the formula:
A = πd^2 / 4
where d is the diameter of the wire.
Therefore, we can write:
σ = (mg) / (πd^2 / 4)
The strain can be calculated using the formula:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the flood lamp stretches the wire by 0.18 mm. Therefore, we can write:
ε = 0.18 / L
Now, let's combine the equations for stress and strain:
σ = kε
σ = (mg) / (πd^2 / 4)
ε = 0.18 / L
Substituting the values of σ and ε, we get:
(mg) / (πd^2 / 4) = k (0.18 / L)
Simplifying, we get:
k = (mgL) / (0.18πd^2)
Now, let's use this value of k to calculate the change in length when the diameter of the wire is doubled.
When the diameter of the wire is doubled, the cross-sectional area of the wire becomes 4 times the original area. Therefore, the new diameter is 2d and the new cross-sectional area is:
A' = π(2d)^2 / 4 = 4πd^2
Using the same formula for stress,
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10−5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10−5 m2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?- a)1.2
- b)1.6
- c)1.8
- d)2.0
Correct answer is option 'C'. Can you explain this answer?
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10−5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10−5 m2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
a)
1.2
b)
1.6
c)
1.8
d)
2.0
|
|
Krishna Iyer answered |
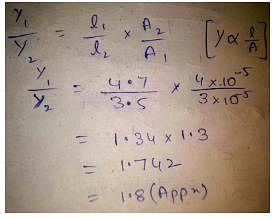
Putty or mud is an example of- a)semi elastic
- b)plastic material
- c)elastomers
- d)elastic material
Correct answer is option 'B'. Can you explain this answer?
Putty or mud is an example of
a)
semi elastic
b)
plastic material
c)
elastomers
d)
elastic material
|
|
Rahul Bansal answered |
Since mud or putty have no gross tendency to regain their previous shape & they get permanently deformed, they are close to ideal plastics.
The S.I unit of stress is- a)Watt
- b)Joule
- c)Pascal
- d)Newton
Correct answer is option 'C'. Can you explain this answer?
The S.I unit of stress is
a)
Watt
b)
Joule
c)
Pascal
d)
Newton
|
|
Krishna Iyer answered |
Stress has its own SI unit called the Pascal. 1 Pascal (Pa) is equal to 1 N/m2. In imperial units stress is measured in pound force per square inch which is often shortened to "psi". The dimension of stress is same as that of pressure.
A solid cylinder can be subjected to- a)tensile stress
- b)compressive stress
- c)shearing stress
- d)all the above
Correct answer is option 'D'. Can you explain this answer?
A solid cylinder can be subjected to
a)
tensile stress
b)
compressive stress
c)
shearing stress
d)
all the above
|
|
Lavanya Menon answered |
To answer this question you should know the definitions of tensile, compressive and shear stress.
Tensile stress causes change (increases the length of cylinder) in the length of the object, compressive strength changes the volume of the object (it can be applied from all sides of the object), shear stress is applied parallel to the surface of an object (in case of the cylinder shear stress will be parallel to circular surface) we can apply all the three stresses in case of cylinder hence option D is correct.
Tensile stress causes change (increases the length of cylinder) in the length of the object, compressive strength changes the volume of the object (it can be applied from all sides of the object), shear stress is applied parallel to the surface of an object (in case of the cylinder shear stress will be parallel to circular surface) we can apply all the three stresses in case of cylinder hence option D is correct.
If proportional limit is not exceeded, energy per unit volume in stretched wire is- a)1/2 x stress x strain
- b)stress x strain
- c)stress x strain 2
- d)1/2 stress x strain 2
Correct answer is 'A'. Can you explain this answer?
If proportional limit is not exceeded, energy per unit volume in stretched wire is
a)
1/2 x stress x strain
b)
stress x strain
c)
stress x strain 2
d)
1/2 stress x strain 2
|
|
Suresh Reddy answered |
strain energy=1/2×stress × strain Work done by a force on a wire
W =2LAy(ΔL)2/2L
=1/2(yALΔ/L)ΔL
=1/2(yΔL/L)(ΔL/L)(AL)
=1/2(Stress)(Strain)(Volume)
(Work)/(volume)=1/2(stress)(strain)
W =2LAy(ΔL)2/2L
=1/2(yALΔ/L)ΔL
=1/2(yΔL/L)(ΔL/L)(AL)
=1/2(Stress)(Strain)(Volume)
(Work)/(volume)=1/2(stress)(strain)
The modulus of elasticity of steel is greater than that of rubber because under the same stress- a)the strain in steel is less than rubber
- b)the strain in steel is more than rubber
- c)elongation in steel is more than in rubber
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The modulus of elasticity of steel is greater than that of rubber because under the same stress
a)
the strain in steel is less than rubber
b)
the strain in steel is more than rubber
c)
elongation in steel is more than in rubber
d)
none of these
|
|
Om Desai answered |
Modulus of elasticity= stress/strain =(F/A)/(ΔL/L) So, for same stress Modulus of elasticity ∝( L/ΔL)and ΔL for rubber is more as compared to steel so Modulus of elasticity for rubber will be less as they are inversely proportional and also ΔL/L is less for steel
Tissue of aorta blood vessel is an example of- a)state of permanant deformation
- b)perfectly plastic body
- c)perfectly elastic body
- d)elastomer
Correct answer is option 'D'. Can you explain this answer?
Tissue of aorta blood vessel is an example of
a)
state of permanant deformation
b)
perfectly plastic body
c)
perfectly elastic body
d)
elastomer
|
|
Gaurav Kumar answered |
Elastomers are popular in vascular engineering applications, as they offer the ability to design implants that match the compliance of native tissue.
Substances like tissue of aorta can be stretched to cause large strain.
Substances like tissue of aorta can be stretched to cause large strain.
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire were twice as long?- a)0.36 mm
- b)0.34 mm
- c)0.38 mm
- d)0.40 mm
Correct answer is option 'A'. Can you explain this answer?
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire were twice as long?
a)
0.36 mm
b)
0.34 mm
c)
0.38 mm
d)
0.40 mm
|
|
Rajesh Gupta answered |
F/A = e/L
F/A = 0.18/l ( let the length be l)
F/A = x/2l
0.18/L = x/2l
0.18×2l = xl
0.36l = xl
x = 0.36
F/A = 0.18/l ( let the length be l)
F/A = x/2l
0.18/L = x/2l
0.18×2l = xl
0.36l = xl
x = 0.36
A 200-kg load is hung on a wire with a length of 4.00 m, a cross-sectional area of 0.200 × 10−4 m2, and a Young’s modulus of 8.00 × 1010N/ m2. What is its increase in length?- a)4.80 mm
- b)4.90 mm
- c)4.80 mm2.4.90 mm
- d)80 mm2.4.90 mm3.
Correct answer is option 'C'. Can you explain this answer?
A 200-kg load is hung on a wire with a length of 4.00 m, a cross-sectional area of 0.200 × 10−4 m2, and a Young’s modulus of 8.00 × 1010N/ m2. What is its increase in length?
a)
4.80 mm
b)
4.90 mm
c)
4.80 mm2.4.90 mm
d)
80 mm2.4.90 mm3.
|
|
Jyoti Sengupta answered |

Yield point may be defined as the point where- a)working stress ends and breaking stress begins
- b)breaking stress ends and working stress begins
- c)elastic behavior ends and plastic behavior begins
- d)plastic behavior ends and elastic behavior begins
Correct answer is option 'C'. Can you explain this answer?
Yield point may be defined as the point where
a)
working stress ends and breaking stress begins
b)
breaking stress ends and working stress begins
c)
elastic behavior ends and plastic behavior begins
d)
plastic behavior ends and elastic behavior begins
|
|
Neha Joshi answered |
At the yield point, stress is not proportional to strain i.e: hooke's law is not obeyed. Hence the elastic behaviour ends and plastic behaviour begins.
When a 13.2 kg mass is placed on top of a vertical spring, the spring compresses by 5.93 cm. Find the force constant of the spring.- a)2281 N/m
- b)3181 N/m
- c)2175 N/m
- d)3085 N/m
Correct answer is option 'C'. Can you explain this answer?
When a 13.2 kg mass is placed on top of a vertical spring, the spring compresses by 5.93 cm. Find the force constant of the spring.
a)
2281 N/m
b)
3181 N/m
c)
2175 N/m
d)
3085 N/m
|
|
Preeti Iyer answered |
From Hooke's Law: F =kx
The force on the spring is the weight of the object , 13.2*9.8 = 129 N
x = 5.93 cm =0.0593 m
129 = (0.0593) x
x = 2175 N/m
What diameter should a 10-m-long steel wire have if we do not want it to stretch more than 0.5 cm under a tension of 940 N? Take Young's modulus of steel as 20 × 1010 Pa- a)3.2 mm
- b)3.0 mm
- c)3.4 mm
- d)3.6 mm
Correct answer is option 'C'. Can you explain this answer?
What diameter should a 10-m-long steel wire have if we do not want it to stretch more than 0.5 cm under a tension of 940 N? Take Young's modulus of steel as 20 × 1010 Pa
a)
3.2 mm
b)
3.0 mm
c)
3.4 mm
d)
3.6 mm
|
|
Rajesh Gupta answered |
Y=F x l/A x Δ l
Δ l=0.5cm=0.5x10-2m, l=10M, F=940N
Y=20x1010pa
20x1010=940x10/πr2x0.5x10-10
πr2=94x100/5x10-3x2x1011=94x102/10x108
r2=94/π x 10-7 =2.99 x 10-6
r2 ≅3x10-6
r=1.13x10-10 m
diameter=2r=3.6mm
Δ l=0.5cm=0.5x10-2m, l=10M, F=940N
Y=20x1010pa
20x1010=940x10/πr2x0.5x10-10
πr2=94x100/5x10-3x2x1011=94x102/10x108
r2=94/π x 10-7 =2.99 x 10-6
r2 ≅3x10-6
r=1.13x10-10 m
diameter=2r=3.6mm
The volume of a spherical body is decreased by 10-3% when it is subjected to pressure of 40 atmospheres. Find the bulk modulus of body.
(1 atm = 1.01 x 105 N/m2).
- a)4.04 x 1011 N/m2
- b)4.04 x 106N/m2
- c)4.04 x 103 N/m2
- d)4.04 x 102 N/m2
Correct answer is option 'A'. Can you explain this answer?
The volume of a spherical body is decreased by 10-3% when it is subjected to pressure of 40 atmospheres. Find the bulk modulus of body.
(1 atm = 1.01 x 105 N/m2).
(1 atm = 1.01 x 105 N/m2).
a)
4.04 x 1011 N/m2
b)
4.04 x 106N/m2
c)
4.04 x 103 N/m2
d)
4.04 x 102 N/m2
|
|
Geetika Shah answered |
We know that magnitude of bulk modulus
K=[P/(dV/V)]
Now, percentage change in volume is. 10-3 %
Therefore, (dV/V)x100=10-3
So, dV/V=10-5
Hence, k is,
K=40atm/10-5=40x1.01x105 /10-5 =4.04x1011 N/m2
K=[P/(dV/V)]
Now, percentage change in volume is. 10-3 %
Therefore, (dV/V)x100=10-3
So, dV/V=10-5
Hence, k is,
K=40atm/10-5=40x1.01x105 /10-5 =4.04x1011 N/m2
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2. It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the elongation. Take Young's modulus of steel as 20 × 1010 Pa- a)2.0 mm
- b)1.6 mm
- c)2.2 mm
- d)1.8 mm
Correct answer is option 'D'. Can you explain this answer?
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2. It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the elongation. Take Young's modulus of steel as 20 × 1010 Pa
a)
2.0 mm
b)
1.6 mm
c)
2.2 mm
d)
1.8 mm
|
|
Gaurav Kumar answered |
σ=Stress and ε=strain
σ=F/A= (550kg) × (9.81m/s2)3×10-5m2/=0.18GPA
ε=Δl/l0=σ/Υ=0.18×109/200×109=9×10-4
Δl=εl0= (9×10-4) (2m) = 0.0018m=1.8mm
σ=F/A= (550kg) × (9.81m/s2)3×10-5m2/=0.18GPA
ε=Δl/l0=σ/Υ=0.18×109/200×109=9×10-4
Δl=εl0= (9×10-4) (2m) = 0.0018m=1.8mm
The area occupied below the stress-strain graph and above strain axis gives the value of
- a)work done in producing extension
- b)energy stored in the material
- c)Restoring force.
- d)energy density of the material
Correct answer is option 'D'. Can you explain this answer?
The area occupied below the stress-strain graph and above strain axis gives the value of
a)
work done in producing extension
b)
energy stored in the material
c)
Restoring force.
d)
energy density of the material
|
|
Jayant Mishra answered |
The area under the stress-strain curve represents the mechanical energy per unit volume consumed by the material. This is true in the elastic range of the graph where the energy is reversibly sorted within the material. Area under the stress strain curve depicts the energy absorbed by the material prior to failure.
A body is said to be perfectly elastic if- a)it can move freely
- b)it is not effected by external force
- c)it recovers its original shape / size when the deforming force is removed
- d)its surface is perfectly smooth
Correct answer is option 'C'. Can you explain this answer?
A body is said to be perfectly elastic if
a)
it can move freely
b)
it is not effected by external force
c)
it recovers its original shape / size when the deforming force is removed
d)
its surface is perfectly smooth
|
|
Hansa Sharma answered |
A body is said to be perfectly elastic when its coefficient of restitution is 1 or we observe total reformation in the body. That means that whatever hits it doesn't lose any of its kinetic energy or once the body gets totally reformed after a collision.
A body is said to be perfectly plastic if- a)it does not recover its original shape / size when the deforming force is removed
- b)it has the property of stretching indefinitely
- c)it expands without breaking, on subjection of large strain
- d)it is not effected by external force
Correct answer is option 'A'. Can you explain this answer?
A body is said to be perfectly plastic if
a)
it does not recover its original shape / size when the deforming force is removed
b)
it has the property of stretching indefinitely
c)
it expands without breaking, on subjection of large strain
d)
it is not effected by external force
|
|
Neha Joshi answered |
A body is said to be plastic when its coefficient of restitution or reformation is zero that means that whatever hits it loses its all kinetic energy once the body gets deformed does not reform.
The stress which is set up in the body due to increase in its dimensions is called- a)volumetric stress
- b)Tangential stress
- c)Normal stress
- d)Tensile stress
Correct answer is option 'D'. Can you explain this answer?
The stress which is set up in the body due to increase in its dimensions is called
a)
volumetric stress
b)
Tangential stress
c)
Normal stress
d)
Tensile stress
|
|
Rahul Bansal answered |
Tensile stress (or tension) is the stress state leading to expansion; that is, the length of a material tends to increase in the tensile direction. The volume of the material stays constant. When equal and opposite forces are applied on a body, then the stress due to this force is called tensile stress.
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm. Bulk modulus of glass 37 GPa.- a)0.0027
- b)0.0030
- c)0.0024
- d)0.0022
Correct answer is option 'A'. Can you explain this answer?
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm. Bulk modulus of glass 37 GPa.
a)
0.0027
b)
0.0030
c)
0.0024
d)
0.0022
|
|
Pranavi Kulkarni answered |
Given data:
Bulk modulus of glass = 37 GPa
Hydraulic pressure = 10 atm
Formula used:
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
Calculation:
Let initial volume of the glass slab be V₀ and let the change in volume be ΔV.
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
⇒ K = (10 atm * V₀)/(ΔV)
⇒ ΔV/V₀ = (10 atm * V₀)/K
⇒ ΔV/V₀ = (10 atm * V₀)/(37 × 10⁹ N/m²)
⇒ ΔV/V₀ = 2.7 × 10⁻⁶
Hence, the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm, is 0.0027. Therefore, option A is the correct answer.
Bulk modulus of glass = 37 GPa
Hydraulic pressure = 10 atm
Formula used:
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
Calculation:
Let initial volume of the glass slab be V₀ and let the change in volume be ΔV.
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
⇒ K = (10 atm * V₀)/(ΔV)
⇒ ΔV/V₀ = (10 atm * V₀)/K
⇒ ΔV/V₀ = (10 atm * V₀)/(37 × 10⁹ N/m²)
⇒ ΔV/V₀ = 2.7 × 10⁻⁶
Hence, the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm, is 0.0027. Therefore, option A is the correct answer.
According to Hooke’s law- a)For small deformations the stress and strain are inversely proportional to each other
- b)For small deformations the stress is proportional to square of strain
- c)For large deformations the stress and strain are proportional to each other
- d)For small deformations the stress and strain are proportional to each other
Correct answer is option 'D'. Can you explain this answer?
According to Hooke’s law
a)
For small deformations the stress and strain are inversely proportional to each other
b)
For small deformations the stress is proportional to square of strain
c)
For large deformations the stress and strain are proportional to each other
d)
For small deformations the stress and strain are proportional to each other
|
|
Krishna Iyer answered |
Hook’s Law states that for small deformations the stress and strain are proportional to each other.
In Hooke’s law, the constant of proportionality signifies- a)modulus of elasticity
- b)modulus of strain
- c)elasticity of wire
- d)modulus of stress
Correct answer is option 'A'. Can you explain this answer?
In Hooke’s law, the constant of proportionality signifies
a)
modulus of elasticity
b)
modulus of strain
c)
elasticity of wire
d)
modulus of stress
|
|
Nayanika Chakraborty answered |
Introduction:
Hooke's Law is a principle in physics that relates the force applied to a spring or elastic material to the resulting deformation or change in length of the material. It states that the force applied to a spring is directly proportional to the displacement or change in length of the spring.
Explanation:
The constant of proportionality in Hooke's Law is known as the modulus of elasticity or Young's modulus. It is represented by the symbol 'E' and is a measure of the stiffness or rigidity of a material. The modulus of elasticity signifies how much a material will deform when a force is applied to it.
Modulus of Elasticity:
The modulus of elasticity is a material property that describes how it responds to stress. It is defined as the ratio of stress to strain within the elastic limit of the material. In other words, it measures how much stress a material can withstand before it starts to deform permanently.
Modulus of Strain:
The modulus of strain is not a property used in Hooke's Law. Strain is the measure of deformation or change in length of a material, and the modulus of strain is not directly related to the constant of proportionality in Hooke's Law.
Elasticity of Wire:
The elasticity of a wire refers to its ability to return to its original shape after being stretched or deformed. It is related to Hooke's Law as the law describes the linear relationship between the force applied to a wire and the resulting deformation or change in length of the wire.
Modulus of Stress:
The modulus of stress is not a term used in Hooke's Law. Stress is defined as the force applied per unit area of a material, and the modulus of stress is not directly related to the constant of proportionality in Hooke's Law.
Conclusion:
In conclusion, the constant of proportionality in Hooke's Law signifies the modulus of elasticity. It is a measure of the stiffness or rigidity of a material and describes how much a material will deform when a force is applied to it. The modulus of elasticity is a fundamental property used to understand the behavior of elastic materials and is essential in various fields such as engineering and materials science.
Hooke's Law is a principle in physics that relates the force applied to a spring or elastic material to the resulting deformation or change in length of the material. It states that the force applied to a spring is directly proportional to the displacement or change in length of the spring.
Explanation:
The constant of proportionality in Hooke's Law is known as the modulus of elasticity or Young's modulus. It is represented by the symbol 'E' and is a measure of the stiffness or rigidity of a material. The modulus of elasticity signifies how much a material will deform when a force is applied to it.
Modulus of Elasticity:
The modulus of elasticity is a material property that describes how it responds to stress. It is defined as the ratio of stress to strain within the elastic limit of the material. In other words, it measures how much stress a material can withstand before it starts to deform permanently.
Modulus of Strain:
The modulus of strain is not a property used in Hooke's Law. Strain is the measure of deformation or change in length of a material, and the modulus of strain is not directly related to the constant of proportionality in Hooke's Law.
Elasticity of Wire:
The elasticity of a wire refers to its ability to return to its original shape after being stretched or deformed. It is related to Hooke's Law as the law describes the linear relationship between the force applied to a wire and the resulting deformation or change in length of the wire.
Modulus of Stress:
The modulus of stress is not a term used in Hooke's Law. Stress is defined as the force applied per unit area of a material, and the modulus of stress is not directly related to the constant of proportionality in Hooke's Law.
Conclusion:
In conclusion, the constant of proportionality in Hooke's Law signifies the modulus of elasticity. It is a measure of the stiffness or rigidity of a material and describes how much a material will deform when a force is applied to it. The modulus of elasticity is a fundamental property used to understand the behavior of elastic materials and is essential in various fields such as engineering and materials science.
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107Pa? Assume that each rivet is to carry one quarter of the load.- a)749 kN
- b)856 kN
- c)652 N
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107Pa? Assume that each rivet is to carry one quarter of the load.
a)
749 kN
b)
856 kN
c)
652 N
d)
None of these
|
|
Sanchita Mukherjee answered |

How does the modulus of elasticity change with temperature?- a)It does not depend on temperature
- b)It decreases with increase in temperature
- c)It increases with increase in temperature
- d)It sometimes increases, sometimes decreases with increase in temperature
Correct answer is option 'B'. Can you explain this answer?
How does the modulus of elasticity change with temperature?
a)
It does not depend on temperature
b)
It decreases with increase in temperature
c)
It increases with increase in temperature
d)
It sometimes increases, sometimes decreases with increase in temperature
|
|
Pooja Shah answered |
As the temperature increases, the inter-atomic distance also increases. So, it results in an increase in the area (stress = force /area). As the area increases stress decreases, this results in a decrease in Young's modulus.
Elasticity is the property of a body, by virtue of which- a)it remains in original size and shape when the force is applied
- b)it changes size and shape when the force is applied and stays in that shape when applied force is removed
- c)it tends to regain its original size and shape when the applied force is removed
- d)it is distorted or stretches without the application of force
Correct answer is option 'C'. Can you explain this answer?
Elasticity is the property of a body, by virtue of which
a)
it remains in original size and shape when the force is applied
b)
it changes size and shape when the force is applied and stays in that shape when applied force is removed
c)
it tends to regain its original size and shape when the applied force is removed
d)
it is distorted or stretches without the application of force
|
|
Lavanya Menon answered |
Explanation:When external force is applied on the solid bodies, the solid bodies get deformed. The atoms or molecules are displaced from their equilibrium positions causing a change in the interatomic ( or intermolicular ) distances. When the deforming foce is removed, the interatomic forces tend to drive them back to their original postions. Thus the body regains its original shape and size.
With reference to figure the elastic zone is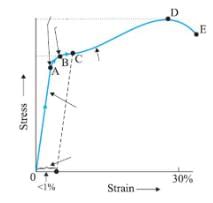
- a)BC
- b)CD
- c)AB
- d)OA
Correct answer is option 'D'. Can you explain this answer?
With reference to figure the elastic zone is

a)
BC
b)
CD
c)
AB
d)
OA
|
|
Hansa Sharma answered |
Hooke’s law: a law stating that the strain in a solid is proportional to the applied stress within the elastic limit of that solid.
In the OA line Hooke’s law is valid because stress is directly proportional to strain.
In the OA line Hooke’s law is valid because stress is directly proportional to strain.
What type of stress is produced in a body when the deforming force produces sheer strain?
- a)shear stress
- b)Longitudinal stress
- c)Normal stress
- d)Tangential stress
Correct answer is option 'A'. Can you explain this answer?
What type of stress is produced in a body when the deforming force produces sheer strain?
a)
shear stress
b)
Longitudinal stress
c)
Normal stress
d)
Tangential stress
|
|
Pooja Shah answered |
Explanation:
When a deforming force is applied to a body in a direction parallel to its surface, it produces a shear strain. Shear strain is the deformation that occurs when one layer of a material slides past another layer. This type of deformation produces shear stress, which is the force that is acting parallel to the surface of the material. Shear stress is calculated as the force per unit area and is expressed in units of pressure, such as pascals (Pa) or pounds per square inch (psi).
Young’s modulus is defined as the ratio of longitudinal stress to longitudinal strain. Which of the following is the unit of Young’s modulus?- a)dyne per square cm.
- b)dyne cm2
- c)dyne/cm
- d)dyne cm
Correct answer is option 'A'. Can you explain this answer?
Young’s modulus is defined as the ratio of longitudinal stress to longitudinal strain. Which of the following is the unit of Young’s modulus?
a)
dyne per square cm.
b)
dyne cm2
c)
dyne/cm
d)
dyne cm
|
|
Riya Banerjee answered |
Stress = Force per area and strain is unit less.
Therefore in CGS units dyne per cm square.
Hence A is correct.
Therefore in CGS units dyne per cm square.
Hence A is correct.
An iron bar of length l cm and cross section A cm2 is pulled by a force F dynes from the ends so as to produce an elongation l cm. Which of the following statements is correct?- a)Elongation is directly proportional to area of cross-section A.
- b)Elongation is inversely proportional to length
- c)Elongation is inversely proportional to area of cross-section A.
- d)Elongation is directly proportional to Young’s modulus.
Correct answer is option 'C'. Can you explain this answer?
An iron bar of length l cm and cross section A cm2 is pulled by a force F dynes from the ends so as to produce an elongation l cm. Which of the following statements is correct?
a)
Elongation is directly proportional to area of cross-section A.
b)
Elongation is inversely proportional to length
c)
Elongation is inversely proportional to area of cross-section A.
d)
Elongation is directly proportional to Young’s modulus.
|
|
Gaurav Kumar answered |
F =AYΔl/L
Δl = FL/AY
Δl = FL/AY
Columns are loaded in- a)shear
- b)hydraulic stress
- c)tension
- d)compression
Correct answer is option 'D'. Can you explain this answer?
Columns are loaded in
a)
shear
b)
hydraulic stress
c)
tension
d)
compression

|
Madhavan Patel answered |
Alternation of generations (also known as metagenesis) is the type of life cycle that occurs in those plants and algae in the Archaeplastida and the Heterokontophyta that have distinct sexual haploid and asexual diploid stages.
Two wires P and Q of same length and material but radii in the ratio 2 : 1 are suspended from a rigid support. Find the ratio of strain produced in the wires when both are under same force.- a)1:2
- b)4:1
- c)1:4
- d)2:1
Correct answer is option 'C'. Can you explain this answer?
Two wires P and Q of same length and material but radii in the ratio 2 : 1 are suspended from a rigid support. Find the ratio of strain produced in the wires when both are under same force.
a)
1:2
b)
4:1
c)
1:4
d)
2:1
|
|
Upasana Bose answered |
Using Hooke ‘s Law we get
Stress directly proportional to stress = Load/Area=F/pie*r*r
And rp:rq=2:1
When both the wires are under the same stress,strain produced will be the same.
When both the wires are under the same stress,strain produced will be the same.
2.when both the wires are loaded by same weight then
Strain p/strain q=(rq)2/(rp)2=¼
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10−2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.- a)1.1 cm
- b)1.0 cm
- c)0.9 cm
- d)1.2 cm
Correct answer is option 'A'. Can you explain this answer?
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10−2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
a)
1.1 cm
b)
1.0 cm
c)
0.9 cm
d)
1.2 cm
|
|
Siddharth Mehra answered |
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched for a copper wire of the original length and diameter?- a)0.39 mm
- b)0.37 mm
- c)0.33 mm
- d)0.18 mm
Correct answer is option 'C'. Can you explain this answer?
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched for a copper wire of the original length and diameter?
a)
0.39 mm
b)
0.37 mm
c)
0.33 mm
d)
0.18 mm
|
|
Darshan Nagesh answered |

Rectangular section is rarely used in beams because- a)stresses are uniform in a rectangular section
- b)more material in kilos is required
- c)stresses are always plastic in rectangular section
- d)less material in kilos is required
Correct answer is option 'B'. Can you explain this answer?
Rectangular section is rarely used in beams because
a)
stresses are uniform in a rectangular section
b)
more material in kilos is required
c)
stresses are always plastic in rectangular section
d)
less material in kilos is required
|
|
Anjali Iyer answered |
I section is generally used as a beam because of its high section modulus as it's most of the area is situated away from it's neutral axis hence it has high moment of inertia i.e high section modulus i.e high moment carrying capacity which is the major requirement for a good beam section.
A lead cube measures 6.00 cm on each side. The bottom face is held in place by very strong glue to a flat horizontal surface, while a horizontal force F is applied to the upper face parallel to one of the edges. How large must F be to cause the cube to deform by 0.250 mm? (Shear modulus of lead = 0.6 × 1010Pa)- a)7.0 * 105 N
- b)6* 105 N
- c)6.6 * 105 N
- d)5.6 * 105 N
Correct answer is option 'C'. Can you explain this answer?
A lead cube measures 6.00 cm on each side. The bottom face is held in place by very strong glue to a flat horizontal surface, while a horizontal force F is applied to the upper face parallel to one of the edges. How large must F be to cause the cube to deform by 0.250 mm? (Shear modulus of lead = 0.6 × 1010Pa)
a)
7.0 * 105 N
b)
6* 105 N
c)
6.6 * 105 N
d)
5.6 * 105 N
|
|
Sanchita Mukherjee answered |

Shear modulus or modulus of rigidity is- a)the ratio of shearing stress to the corresponding lateral strain
- b)the ratio of shearing stress to the corresponding shearing strain
- c)the ratio of longitudinal stress to the corresponding shearing strain
- d)the ratio of shearing strain to the corresponding shearing stress
Correct answer is option 'B'. Can you explain this answer?
Shear modulus or modulus of rigidity is
a)
the ratio of shearing stress to the corresponding lateral strain
b)
the ratio of shearing stress to the corresponding shearing strain
c)
the ratio of longitudinal stress to the corresponding shearing strain
d)
the ratio of shearing strain to the corresponding shearing stress
|
|
Ameya Choudhury answered |
Shear modulus or modulus of rigidity is the ratio of shearing stress to the corresponding shearing strain, by the definition of shear modulus.
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain? Take Young's modulus of copper as 42 × 109Pa
- a)3.65 × 10-8
- b)3.65 × 10-3
- c)3.65 × 10-9
- d)3.65 × 10-2
Correct answer is option 'B'. Can you explain this answer?
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain? Take Young's modulus of copper as 42 × 10
9
Paa)
3.65 × 10-8
b)
3.65 × 10-3
c)
3.65 × 10-9
d)
3.65 × 10-2
|
|
Anjana Sharma answered |
Given Data,
Length of the piece of copper = l = 19.1 mm = 19.1 × 10-3m
Breadth of the piece of copper = b = 15.2 mm = 15.2× 10-3m
Tension force applied on the piece of cooper, F = 44500N
Area of rectangular cross section of copper piece,
Area = l× b
⇒ Area = (19.1 × 10-3m) × (15.2× 10-3m)
⇒ Area = 2.9 × 10-4 m2
Modulus of elasticity of copper from standard list, η = 42× 109 N/m2
By definition, Modulus of elasticity, η = stress/strain
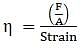
⇒ Strain = F/Aη

⇒ Strain = 3.65 × 10-3
Hence, the resulting strain is 3.65 × 10-3
Length of the piece of copper = l = 19.1 mm = 19.1 × 10-3m
Breadth of the piece of copper = b = 15.2 mm = 15.2× 10-3m
Tension force applied on the piece of cooper, F = 44500N
Area of rectangular cross section of copper piece,
Area = l× b
⇒ Area = (19.1 × 10-3m) × (15.2× 10-3m)
⇒ Area = 2.9 × 10-4 m2
Modulus of elasticity of copper from standard list, η = 42× 109 N/m2
By definition, Modulus of elasticity, η = stress/strain
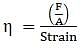
⇒ Strain = F/Aη

⇒ Strain = 3.65 × 10-3
Hence, the resulting strain is 3.65 × 10-3
When a solid is deformed,- a)the atoms or molecules do not move from their equilibrium position
- b)only the atoms or molecules at some points move from their equilibrium position
- c)only the atoms or molecules of the surface move from their equilibrium position
- d)all the atoms or molecules are displaced from their equilibrium positions causing a change in inter atomic (or intermolecular) distances.
Correct answer is option 'D'. Can you explain this answer?
When a solid is deformed,
a)
the atoms or molecules do not move from their equilibrium position
b)
only the atoms or molecules at some points move from their equilibrium position
c)
only the atoms or molecules of the surface move from their equilibrium position
d)
all the atoms or molecules are displaced from their equilibrium positions causing a change in inter atomic (or intermolecular) distances.

|
Sravya Banerjee answered |
Explanation:External force permanently distubed the equilibrium position of the interatomic ( or intermolecular ) forces between the particles of solid bodies.
volume strain is defined- a)as the change in volume ΔV
- b)as the ratio of change in volume (ΔV) to the original volume V
- c)as the ratio of change in volume (ΔV) to thrice the original volume V
- d)as the ratio of change in volume (ΔV) to twice the original volume V
Correct answer is option 'B'. Can you explain this answer?
volume strain is defined
a)
as the change in volume ΔV
b)
as the ratio of change in volume (ΔV) to the original volume V
c)
as the ratio of change in volume (ΔV) to thrice the original volume V
d)
as the ratio of change in volume (ΔV) to twice the original volume V
|
|
Ameya Unni answered |
Understanding Volume Strain
Volume strain is an important concept in mechanics and materials science that describes how a material deforms when subjected to external forces.
Definition of Volume Strain
- Volume strain is defined specifically as the ratio of the change in volume (ΔV) to the original volume (V0) of a material.
- Mathematically, it can be expressed as: Volume Strain = ΔV / V0.
Why Option B is Correct
- Change in Volume (ΔV): This represents the difference between the final volume after deformation and the initial volume before deformation.
- Original Volume (V0): This is the volume of the material before any external forces have been applied.
- Ratio Significance: By taking the ratio of the change in volume to the original volume, we obtain a dimensionless quantity that allows for comparison across different materials and conditions.
Other Options Explained
- Option A (Change in Volume V): This does not provide a comparative metric and lacks the necessary context of the original volume.
- Option C (Thrice the Original Volume): This is an arbitrary scaling that does not conform to the standard definition of volume strain.
- Option D (Twice the Original Volume): Similar to Option C, this does not reflect the true relationship defined in mechanics.
Conclusion
In conclusion, volume strain is fundamentally about understanding how a material's volume changes relative to its original volume, which is effectively captured by Option B. This definition is crucial for engineers and scientists to assess material behavior under stress.
Volume strain is an important concept in mechanics and materials science that describes how a material deforms when subjected to external forces.
Definition of Volume Strain
- Volume strain is defined specifically as the ratio of the change in volume (ΔV) to the original volume (V0) of a material.
- Mathematically, it can be expressed as: Volume Strain = ΔV / V0.
Why Option B is Correct
- Change in Volume (ΔV): This represents the difference between the final volume after deformation and the initial volume before deformation.
- Original Volume (V0): This is the volume of the material before any external forces have been applied.
- Ratio Significance: By taking the ratio of the change in volume to the original volume, we obtain a dimensionless quantity that allows for comparison across different materials and conditions.
Other Options Explained
- Option A (Change in Volume V): This does not provide a comparative metric and lacks the necessary context of the original volume.
- Option C (Thrice the Original Volume): This is an arbitrary scaling that does not conform to the standard definition of volume strain.
- Option D (Twice the Original Volume): Similar to Option C, this does not reflect the true relationship defined in mechanics.
Conclusion
In conclusion, volume strain is fundamentally about understanding how a material's volume changes relative to its original volume, which is effectively captured by Option B. This definition is crucial for engineers and scientists to assess material behavior under stress.
Elastomers are materials- a)which can be stretched without corresponding stress
- b)which cannot be stretched to cause large strains
- c)which cannot be stretched to beyond elastic limit
- d)which can be stretched to cause large strains
Correct answer is option 'D'. Can you explain this answer?
Elastomers are materials
a)
which can be stretched without corresponding stress
b)
which cannot be stretched to cause large strains
c)
which cannot be stretched to beyond elastic limit
d)
which can be stretched to cause large strains
|
|
Rajeev Saxena answered |
An elastomer is a polymer with viscoelasticity (i. e., both viscosity and elasticity) and very weak intermolecular forces, and generally low Young's modulus and high failure strain compared with other materials. Elastomer rubber compounds are made from five to ten ingredients, each ingredient playing a specific role. Polymer is the main component, and determines heat and chemical resistance, as well as low- temperature performance. Reinforcing filler is used, typically carbon black, for strength properties.
After prolonged use, springs deform permanently because of- a)its rigidity
- b)elastic fatigue
- c)elastic after effect
- d)plastic fatigue
Correct answer is option 'B'. Can you explain this answer?
After prolonged use, springs deform permanently because of
a)
its rigidity
b)
elastic fatigue
c)
elastic after effect
d)
plastic fatigue
|
|
Rohan Singh answered |
Springs deform permanently because of elastic fatigueness. The elasticity of the material of spring is lost and it deforms permanently.
Read the assertion and reason carefully to mark the correct option out of the options given below:Assertion: The stretching of a coil is determined by its shear modulus.Reason: Shear modulus change only shape of a body keeping its dimensions unchanged.- a)If both assertion and reason are true and the reason is the correct explanation of the assertion.
- b)If both assertion and reason are true but reason is not the correct explanation of the assertion.
- c)If assertion is true but reason is false.
- d)If the assertion and reason both are false.
Correct answer is option 'A'. Can you explain this answer?
Read the assertion and reason carefully to mark the correct option out of the options given below:
Assertion: The stretching of a coil is determined by its shear modulus.
Reason: Shear modulus change only shape of a body keeping its dimensions unchanged.
a)
If both assertion and reason are true and the reason is the correct explanation of the assertion.
b)
If both assertion and reason are true but reason is not the correct explanation of the assertion.
c)
If assertion is true but reason is false.
d)
If the assertion and reason both are false.

|
Sahana Joshi answered |
Assertion: The stretching of a coil is determined by its shear modulus.
Reason: Shear modulus changes only the shape of a body while keeping its dimensions unchanged.
Explanation:
To understand the given assertion and reason, let's first define the terms involved:
- Stretching: It refers to the extension or elongation of a body when a force is applied to it.
- Coil: It is a helical structure usually made of a flexible material like metal wire, which can be stretched or compressed.
- Shear modulus: It is a measure of the rigidity of a material and represents its resistance to shearing forces. It quantifies the elasticity of a material in response to shear stress.
Now, let's analyze the assertion and reason:
Assertion: The stretching of a coil is determined by its shear modulus.
This means that the shear modulus of a coil material influences how much the coil can be stretched when a force is applied to it. In other words, the shear modulus determines the elasticity and flexibility of the coil material, which directly affects its stretching behavior.
Reason: Shear modulus changes only the shape of a body while keeping its dimensions unchanged.
This reason suggests that when a shear force is applied to a body, it deforms by changing its shape but not its dimensions. In the case of a coil, the shear modulus determines how much the coil can be deformed or stretched while maintaining its original dimensions.
Explanation of Correct Answer:
The correct answer is option 'A': If both the assertion and reason are true and the reason is the correct explanation of the assertion.
The reason provided in the given statement aligns with the assertion. The shear modulus of a coil material indeed determines its stretching behavior, as it reflects the material's elasticity and flexibility. Additionally, the reason explains that the shear modulus only changes the shape of a body while keeping its dimensions constant, which is relevant to the stretching behavior of a coil.
Therefore, the assertion and reason are both true, and the reason correctly explains the assertion.
Reason: Shear modulus changes only the shape of a body while keeping its dimensions unchanged.
Explanation:
To understand the given assertion and reason, let's first define the terms involved:
- Stretching: It refers to the extension or elongation of a body when a force is applied to it.
- Coil: It is a helical structure usually made of a flexible material like metal wire, which can be stretched or compressed.
- Shear modulus: It is a measure of the rigidity of a material and represents its resistance to shearing forces. It quantifies the elasticity of a material in response to shear stress.
Now, let's analyze the assertion and reason:
Assertion: The stretching of a coil is determined by its shear modulus.
This means that the shear modulus of a coil material influences how much the coil can be stretched when a force is applied to it. In other words, the shear modulus determines the elasticity and flexibility of the coil material, which directly affects its stretching behavior.
Reason: Shear modulus changes only the shape of a body while keeping its dimensions unchanged.
This reason suggests that when a shear force is applied to a body, it deforms by changing its shape but not its dimensions. In the case of a coil, the shear modulus determines how much the coil can be deformed or stretched while maintaining its original dimensions.
Explanation of Correct Answer:
The correct answer is option 'A': If both the assertion and reason are true and the reason is the correct explanation of the assertion.
The reason provided in the given statement aligns with the assertion. The shear modulus of a coil material indeed determines its stretching behavior, as it reflects the material's elasticity and flexibility. Additionally, the reason explains that the shear modulus only changes the shape of a body while keeping its dimensions constant, which is relevant to the stretching behavior of a coil.
Therefore, the assertion and reason are both true, and the reason correctly explains the assertion.
The importance of the elastic behavior of materials is- a)that it is useful in making springs
- b)that it enables a safe and sound design of bridges, buildings, machinery parts.
- c)that it is useful in building sling shots
- d)that it gives methods for understanding materials
Correct answer is option 'B'. Can you explain this answer?
The importance of the elastic behavior of materials is
a)
that it is useful in making springs
b)
that it enables a safe and sound design of bridges, buildings, machinery parts.
c)
that it is useful in building sling shots
d)
that it gives methods for understanding materials

|
Puja Das answered |
Explanation:More the elastic a material is , more it has the property to regain its original position which is required in construction works.
Chapter doubts & questions for Solids - Science for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Solids - Science for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Science for ACT
486 videos|517 docs|337 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup












