All Exams >
ACT >
Physics for ACT >
All Questions
All questions of Motion in a plane for ACT Exam
A unit vector has the magnitude of ___- a)5
- b)1
- c)10
- d)0
Correct answer is option 'B'. Can you explain this answer?
A unit vector has the magnitude of ___
a)
5
b)
1
c)
10
d)
0
|
Ajjappa Nidoni answered |
Uint vector is equal to 1 magnitude
A ball is being rotated in a circle of radius 5 m with a constant tangential velocity of 20 m/s. A stone is also being rotated in a circle of radius 4 m with a constant tangential velocity of 16 m/s. Which one of the following choices is true about both the circular motions?- a)Both have same angular velocity
- b)Both have different angular velocity
- c)Angular velocity of ball > angular velocity of stone
- d)Angular velocity of stone > angular velocity of ball
Correct answer is option 'A'. Can you explain this answer?
A ball is being rotated in a circle of radius 5 m with a constant tangential velocity of 20 m/s. A stone is also being rotated in a circle of radius 4 m with a constant tangential velocity of 16 m/s. Which one of the following choices is true about both the circular motions?
a)
Both have same angular velocity
b)
Both have different angular velocity
c)
Angular velocity of ball > angular velocity of stone
d)
Angular velocity of stone > angular velocity of ball
|
Orion Classes answered |
Angular velocity = Tangential velocity/Radius. When we put in the values and calculate the angular velocities for each of the circular motions, we see that both the angular velocities are equal to each other and the value is 4 rad/s.
What happens when a vector is multiplied by a scalar?- a)Its magnitude gets multiplied by that much amount
- b)Its direction rotates in XY plane by that much angle
- c)Its direction rotates in YZ plane by that much angle
- d)Its direction rotates in ZX plane by that much angle
Correct answer is option 'A'. Can you explain this answer?
What happens when a vector is multiplied by a scalar?
a)
Its magnitude gets multiplied by that much amount
b)
Its direction rotates in XY plane by that much angle
c)
Its direction rotates in YZ plane by that much angle
d)
Its direction rotates in ZX plane by that much angle
|
Flembe Academy answered |
Any vector a, can be written as a =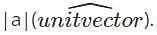 
Hence, when we multiply it by a scalar, the magnitude multiplies by that much amount.
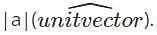Hence, when we multiply it by a scalar, the magnitude multiplies by that much amount.A vector can be resolved along ______- a)Only one direction
- b)Only two directions
- c)Only three directions
- d)Only in independent directions
Correct answer is option 'D'. Can you explain this answer?
A vector can be resolved along ______
a)
Only one direction
b)
Only two directions
c)
Only three directions
d)
Only in independent directions
|
Evan Parker answered |
Understanding Vector Resolution
Vector resolution is a fundamental concept in physics and mathematics that involves breaking down a vector into its components along specified directions.
Independent Directions
Vectors can be resolved along multiple directions, but the key point is that these directions must be independent of each other. Independent directions are those that do not affect each other’s magnitude or direction.
Why Only Independent Directions?
- **Dimensionality**: In a three-dimensional space, any vector can be resolved along three independent axes (x, y, z). However, vectors can also be resolved in two dimensions or even one dimension, depending on the situation.
- **Linear Independence**: Directions like x and y in a 2D plane are independent. Resolving a vector along these axes allows for a complete representation of the vector's effects in that plane.
- **Mathematical Representation**: A vector, represented as **V**, can be expressed as **V = Vx + Vy + Vz**, where Vx, Vy, and Vz are the components along independent axes. This principle applies in any dimensional space.
Applications of Vector Resolution
- **Physics**: Used in analyzing forces, motion, and other physical phenomena.
- **Engineering**: Essential for resolving forces in structures and mechanical systems.
- **Computer Graphics**: Used to render movements and transformations in a 3D space.
In summary, vectors can indeed be resolved along only independent directions, allowing for a complete understanding of their behavior in any given space. This resolution is crucial for accurate analysis in various fields.
Vector resolution is a fundamental concept in physics and mathematics that involves breaking down a vector into its components along specified directions.
Independent Directions
Vectors can be resolved along multiple directions, but the key point is that these directions must be independent of each other. Independent directions are those that do not affect each other’s magnitude or direction.
Why Only Independent Directions?
- **Dimensionality**: In a three-dimensional space, any vector can be resolved along three independent axes (x, y, z). However, vectors can also be resolved in two dimensions or even one dimension, depending on the situation.
- **Linear Independence**: Directions like x and y in a 2D plane are independent. Resolving a vector along these axes allows for a complete representation of the vector's effects in that plane.
- **Mathematical Representation**: A vector, represented as **V**, can be expressed as **V = Vx + Vy + Vz**, where Vx, Vy, and Vz are the components along independent axes. This principle applies in any dimensional space.
Applications of Vector Resolution
- **Physics**: Used in analyzing forces, motion, and other physical phenomena.
- **Engineering**: Essential for resolving forces in structures and mechanical systems.
- **Computer Graphics**: Used to render movements and transformations in a 3D space.
In summary, vectors can indeed be resolved along only independent directions, allowing for a complete understanding of their behavior in any given space. This resolution is crucial for accurate analysis in various fields.
Calculating the relative velocity is an example of ______- a)Vector addition
- b)Vector subtraction
- c)Vector multiplication
- d)Vector division
Correct answer is option 'B'. Can you explain this answer?
Calculating the relative velocity is an example of ______
a)
Vector addition
b)
Vector subtraction
c)
Vector multiplication
d)
Vector division
|
Xavier Hughes answered |
Understanding Relative Velocity
Relative velocity refers to the velocity of one object as observed from another object. To calculate it, we often need to consider the velocities of both objects in a specific frame of reference.
Vector Subtraction in Relative Velocity
- Relative velocity is fundamentally about determining how fast one object is moving compared to another.
- To find the relative velocity of Object A with respect to Object B, you use the formula:
- **VAB = VA - VB**
- Here, **VAB** is the velocity of A relative to B, **VA** is the velocity of A, and **VB** is the velocity of B.
Why is it Vector Subtraction?
- The reason we use subtraction rather than addition is that we are interested in the difference in the velocities.
- For example, if Object A moves north at 10 m/s and Object B moves north at 5 m/s, the relative velocity of A with respect to B is:
- **VAB = 10 m/s (north) - 5 m/s (north) = 5 m/s (north)**
- This subtraction reflects how much faster A is moving compared to B in the same direction.
Conclusion
- Thus, calculating relative velocity is an example of vector subtraction, as it involves determining the difference in motion between two objects in a given frame of reference.
Relative velocity refers to the velocity of one object as observed from another object. To calculate it, we often need to consider the velocities of both objects in a specific frame of reference.
Vector Subtraction in Relative Velocity
- Relative velocity is fundamentally about determining how fast one object is moving compared to another.
- To find the relative velocity of Object A with respect to Object B, you use the formula:
- **VAB = VA - VB**
- Here, **VAB** is the velocity of A relative to B, **VA** is the velocity of A, and **VB** is the velocity of B.
Why is it Vector Subtraction?
- The reason we use subtraction rather than addition is that we are interested in the difference in the velocities.
- For example, if Object A moves north at 10 m/s and Object B moves north at 5 m/s, the relative velocity of A with respect to B is:
- **VAB = 10 m/s (north) - 5 m/s (north) = 5 m/s (north)**
- This subtraction reflects how much faster A is moving compared to B in the same direction.
Conclusion
- Thus, calculating relative velocity is an example of vector subtraction, as it involves determining the difference in motion between two objects in a given frame of reference.
A velocity vector (5m/s) is making and angle of 60 degrees with X axis has a horizonal component of magnitude ___- a)2.5
- b)5.5
- c)5
- d)10/√3
Correct answer is option 'A'. Can you explain this answer?
A velocity vector (5m/s) is making and angle of 60 degrees with X axis has a horizonal component of magnitude ___
a)
2.5
b)
5.5
c)
5
d)
10/√3
|
Max Long answered |
Horizontal Component of Velocity Vector
The horizontal component of a velocity vector is given by the magnitude of the velocity vector multiplied by the cosine of the angle it makes with the x-axis.
Given:
Magnitude of velocity vector = 5 m/s
Angle with x-axis = 60 degrees
Calculating Horizontal Component
Horizontal component = 5 m/s * cos(60)
Horizontal component = 5 m/s * 0.5
Horizontal component = 2.5 m/s
Therefore, the horizontal component of the velocity vector is 2.5 m/s.
This means that the velocity vector has a horizontal component of 2.5 m/s in the positive x-direction.
The horizontal component of a velocity vector is given by the magnitude of the velocity vector multiplied by the cosine of the angle it makes with the x-axis.
Given:
Magnitude of velocity vector = 5 m/s
Angle with x-axis = 60 degrees
Calculating Horizontal Component
Horizontal component = 5 m/s * cos(60)
Horizontal component = 5 m/s * 0.5
Horizontal component = 2.5 m/s
Therefore, the horizontal component of the velocity vector is 2.5 m/s.
This means that the velocity vector has a horizontal component of 2.5 m/s in the positive x-direction.
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string when is horizontal?- a)30 N
- b)50 N
- c)20 N
- d)25 N
Correct answer is option 'B'. Can you explain this answer?
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string when is horizontal?
a)
30 N
b)
50 N
c)
20 N
d)
25 N
|
|
Orion Classes answered |
When the string is horizontal, the tension in the string and the centrifugal force are opposite to each other. Centrifugal force can be calculated as mv2/r = 50 N. Hence the tension = centrifugal force = 50 N.
A car travels 5m in X direction and then 7m in Y direction. What is the final vector position of the car with respect to the origin?- a)5î + 7ĵ
- b)7î + 5ĵ
- c)7î + 7ĵ
- d)5î + 5ĵ
Correct answer is option 'A'. Can you explain this answer?
A car travels 5m in X direction and then 7m in Y direction. What is the final vector position of the car with respect to the origin?
a)
5î + 7ĵ
b)
7î + 5ĵ
c)
7î + 7ĵ
d)
5î + 5ĵ
|
Vanessa Vega answered |
To determine the final vector position of the car with respect to the origin, we need to combine the displacement vectors in the x and y directions.
The displacement in the x direction is 5m and in the y direction is 7m.
Therefore, the final vector position of the car with respect to the origin is (5, 7).
The displacement in the x direction is 5m and in the y direction is 7m.
Therefore, the final vector position of the car with respect to the origin is (5, 7).
Which of the following is not true about projectile motion?- a)It is an example of motion in a plane
- b)It is an example of motion along a curve
- c)It is not an example of motion in space
- d)The acceleration keeps changing in projectile motion
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not true about projectile motion?
a)
It is an example of motion in a plane
b)
It is an example of motion along a curve
c)
It is not an example of motion in space
d)
The acceleration keeps changing in projectile motion
|
|
Victoria Simmons answered |
Projectile Motion
Projectile motion is the motion of an object thrown or projected into the air, subject to only the force of gravity and air resistance (if present).
Not True Statement
a) It is an example of motion in a plane
This statement is not true because projectile motion is actually an example of motion in two dimensions, not just a single plane. In projectile motion, an object moves both horizontally and vertically at the same time. This means that the motion occurs in a plane but not just in one plane.
True Statements
b) It is an example of motion along a curve
Projectile motion follows a curved path known as a parabola. The object's trajectory is curved due to the combined effects of its horizontal and vertical motion.
c) It is not an example of motion in space
Projectile motion does take place in space, as the object is moving through the air in a gravitational field. However, it is important to note that it is not considered motion in outer space.
d) The acceleration keeps changing in projectile motion
In projectile motion, the acceleration due to gravity is constant and acts vertically downward. While the magnitude of the velocity changes, the acceleration remains constant throughout the motion.
Projectile motion is the motion of an object thrown or projected into the air, subject to only the force of gravity and air resistance (if present).
Not True Statement
a) It is an example of motion in a plane
This statement is not true because projectile motion is actually an example of motion in two dimensions, not just a single plane. In projectile motion, an object moves both horizontally and vertically at the same time. This means that the motion occurs in a plane but not just in one plane.
True Statements
b) It is an example of motion along a curve
Projectile motion follows a curved path known as a parabola. The object's trajectory is curved due to the combined effects of its horizontal and vertical motion.
c) It is not an example of motion in space
Projectile motion does take place in space, as the object is moving through the air in a gravitational field. However, it is important to note that it is not considered motion in outer space.
d) The acceleration keeps changing in projectile motion
In projectile motion, the acceleration due to gravity is constant and acts vertically downward. While the magnitude of the velocity changes, the acceleration remains constant throughout the motion.
Adding î + 77ĵ and 7î + ĵ gives ______- a)8î + 78ĵ
- b)0î + 76ĵ
- c)î + 74ĵ
- d)78î + 8ĵ
Correct answer is option 'A'. Can you explain this answer?
Adding î + 77ĵ and 7î + ĵ gives ______
a)
8î + 78ĵ
b)
0î + 76ĵ
c)
î + 74ĵ
d)
78î + 8ĵ
|
|
Emma Carter answered |
Calculation:
- Adding î + 77 gives 78î
- Adding 7î + 7 gives 8î
Answer:
- Therefore, the correct answer is option 'A', which is 8î + 78.
In how many independent directions can a vector in a plane be resolved?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
In how many independent directions can a vector in a plane be resolved?
a)
1
b)
2
c)
3
d)
4
|
|
Orion Classes answered |
A vector in a plane will be defined by the two governing axes, X and Y. Hence, any vector can be resolved in two independent directions. If it is resolved in any other direction, that component of it will be dependent on the existing independent directions.
A body is moving with a constant acceleration of 4î + 3ĵ, starting from the origin. What will be the position of the body after 5s?- a)50î + 37.5ĵ
- b)37.5î + 50ĵ
- c)37.5î – 50ĵ
- d)50î – 37.5ĵ
Correct answer is option 'A'. Can you explain this answer?
A body is moving with a constant acceleration of 4î + 3ĵ, starting from the origin. What will be the position of the body after 5s?
a)
50î + 37.5ĵ
b)
37.5î + 50ĵ
c)
37.5î – 50ĵ
d)
50î – 37.5ĵ
|
Joseph Simmons answered |
Understanding the Problem
The body is moving with a constant acceleration, given as 4i + 3j. We need to find its position after 5 seconds, starting from the origin.
Given Variables
- Initial position (s0) = 0 (origin)
- Initial velocity (u) = 0 (since it starts from rest)
- Acceleration (a) = 4i + 3j
- Time (t) = 5 seconds
Using the Equation of Motion
The position vector (s) after time t under constant acceleration can be calculated using the formula:
s = s0 + ut + (1/2)at²
Since the initial position and velocity are both zero, the equation simplifies to:
s = (1/2)at²
Calculating the Position
- Substitute the acceleration and time into the formula:
s = (1/2)(4i + 3j)(5)²
- Calculate (5)²:
(5)² = 25
- Now, plug this value into the equation:
s = (1/2)(4i + 3j)(25)
s = (1/2)(100i + 75j)
- Simplifying further:
s = 50i + 37.5j
Final Result
After 5 seconds, the position of the body will be:
s = 50i + 37.5j
Thus, the correct answer is option A: 50i + 37.5j.
This detailed calculation confirms that option A is indeed the correct choice.
The body is moving with a constant acceleration, given as 4i + 3j. We need to find its position after 5 seconds, starting from the origin.
Given Variables
- Initial position (s0) = 0 (origin)
- Initial velocity (u) = 0 (since it starts from rest)
- Acceleration (a) = 4i + 3j
- Time (t) = 5 seconds
Using the Equation of Motion
The position vector (s) after time t under constant acceleration can be calculated using the formula:
s = s0 + ut + (1/2)at²
Since the initial position and velocity are both zero, the equation simplifies to:
s = (1/2)at²
Calculating the Position
- Substitute the acceleration and time into the formula:
s = (1/2)(4i + 3j)(5)²
- Calculate (5)²:
(5)² = 25
- Now, plug this value into the equation:
s = (1/2)(4i + 3j)(25)
s = (1/2)(100i + 75j)
- Simplifying further:
s = 50i + 37.5j
Final Result
After 5 seconds, the position of the body will be:
s = 50i + 37.5j
Thus, the correct answer is option A: 50i + 37.5j.
This detailed calculation confirms that option A is indeed the correct choice.
The position of a body, moving in a plane, changes from origin to 14î + 11ĵ in 20s. What is the velocity of the body?- a)0.7î + 0.55ĵ
- b)0.55î + 0.7ĵ
- c)0.3î + 0.7ĵ
- d)0.3î
Correct answer is option 'A'. Can you explain this answer?
The position of a body, moving in a plane, changes from origin to 14î + 11ĵ in 20s. What is the velocity of the body?
a)
0.7î + 0.55ĵ
b)
0.55î + 0.7ĵ
c)
0.3î + 0.7ĵ
d)
0.3î
|
|
Orion Classes answered |
The velocity of a body is the rate at which the displacement changes with time. Here, the change in position is the change in displacement, and is 14î + 11ĵ. The total time taken is 20s. Hence, the acceleration = change in displacement/time = 0.7î + 0.55ĵ.
Vectors lying in the same or parallel to the same plane are called _____- a)Coplanar vectors
- b)Equal vector
- c)Unit Vector
- d)Displacement vector
Correct answer is option 'A'. Can you explain this answer?
Vectors lying in the same or parallel to the same plane are called _____
a)
Coplanar vectors
b)
Equal vector
c)
Unit Vector
d)
Displacement vector
|
Scarlett Reed answered |
Explanation:
Coplanar Vectors:
- Vectors lying in the same plane are called coplanar vectors.
- If two or more vectors lie in the same plane, they are said to be coplanar.
Equal Vector:
- Equal vectors have the same magnitude and direction.
- Two vectors are equal if they have the same length and are parallel.
Unit Vector:
- A unit vector is a vector with a magnitude of 1.
- It is used to indicate direction in a specific coordinate system.
Displacement Vector:
- A displacement vector represents the change in position of an object.
- It is a vector that points from the initial position to the final position of an object.
Therefore, in the context of vectors lying in the same or parallel planes, the correct term to describe them is coplanar vectors. These vectors share the same plane and can be represented as lines within that plane.
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 2 m/s. What is the tension in the string at the lowest point?- a)28 N
- b)20 N
- c)8 N
- d)15 N
Correct answer is option 'A'. Can you explain this answer?
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 2 m/s. What is the tension in the string at the lowest point?
a)
28 N
b)
20 N
c)
8 N
d)
15 N
|
|
Orion Classes answered |
At the lowest point, the body experiences centrifugal force and the weight in the same direction, opposite to the direction of tension in the string. Centrifugal force can be calculated as mv2/r = 8 N. Hence the tension = weight + centrifugal force = 28 N.
A body is moving with a constant acceleration of 11î + 7ĵ, starting from the origin. What will be the position of the body after 10s?- a)550î + 350ĵ
- b)350î + 550ĵ
- c)350î – 550ĵ
- d)550î – 350ĵ
Correct answer is option 'A'. Can you explain this answer?
A body is moving with a constant acceleration of 11î + 7ĵ, starting from the origin. What will be the position of the body after 10s?
a)
550î + 350ĵ
b)
350î + 550ĵ
c)
350î – 550ĵ
d)
550î – 350ĵ
|
|
Orion Classes answered |
The body’s displacement is given by s = (1/2)at2. The body starts from the origin hence, the total displacement is the final position of the body. Therefore, after putting in the values, we get, s = (1/2)(11î + 7ĵ)*102 = 550î + 350ĵ.
A vector, 5 units from the origin, along the X axis, is added to vector 2 units from the origin along the Y axis. What is the resultant vector?- a)3î + 8ĵ
- b)5î + 2ĵ
- c)2î + 5ĵ
- d)2î + 7ĵ
Correct answer is option 'B'. Can you explain this answer?
A vector, 5 units from the origin, along the X axis, is added to vector 2 units from the origin along the Y axis. What is the resultant vector?
a)
3î + 8ĵ
b)
5î + 2ĵ
c)
2î + 5ĵ
d)
2î + 7ĵ
|
|
Madison Butler answered |
To find the resultant vector, we can add the x-components and the y-components separately.
The vector along the X-axis has an x-component of 5 and a y-component of 0.
The vector along the Y-axis has an x-component of 0 and a y-component of 2.
Adding the x-components, we get 5 + 0 = 5.
Adding the y-components, we get 0 + 2 = 2.
So the resultant vector has an x-component of 5 and a y-component of 2.
Thus, the resultant vector is (5, 2).
The vector along the X-axis has an x-component of 5 and a y-component of 0.
The vector along the Y-axis has an x-component of 0 and a y-component of 2.
Adding the x-components, we get 5 + 0 = 5.
Adding the y-components, we get 0 + 2 = 2.
So the resultant vector has an x-component of 5 and a y-component of 2.
Thus, the resultant vector is (5, 2).
A vector, 7 units from the origin, along the X axis, is added to vector 11 units from the origin along the Y axis. What is the resultant vector?- a)3î + 8ĵ
- b)7î + 11ĵ
- c)11î + 7ĵ
- d)2î + 7ĵ
Correct answer is option 'B'. Can you explain this answer?
A vector, 7 units from the origin, along the X axis, is added to vector 11 units from the origin along the Y axis. What is the resultant vector?
a)
3î + 8ĵ
b)
7î + 11ĵ
c)
11î + 7ĵ
d)
2î + 7ĵ
|
Penelope Davis answered |
Given Vectors:
- Vector along X-axis: 7 units (let's call this vector A)
- Vector along Y-axis: 11 units (let's call this vector B)
Finding Resultant Vector:
- To find the resultant vector, we need to add vectors A and B.
- Since vector A is along the X-axis and vector B is along the Y-axis, they are perpendicular to each other.
- Using the Pythagorean theorem, we can calculate the magnitude of the resultant vector:
- Magnitude = sqrt((7)^2 + (11)^2) = sqrt(49 + 121) = sqrt(170) ≈ 13.04 units
- Now, to find the direction of the resultant vector:
- tan(theta) = opposite/adjacent = 11/7
- theta ≈ arctan(11/7) ≈ 56.31 degrees
- Therefore, the resultant vector is 13.04 units at an angle of 56.31 degrees.
- Representing this in component form, we get:
- Resultant Vector = 7î + 11ĵ
Final Answer:
- Therefore, the correct resultant vector is 7î + 11ĵ, which is option B.
- Vector along X-axis: 7 units (let's call this vector A)
- Vector along Y-axis: 11 units (let's call this vector B)
Finding Resultant Vector:
- To find the resultant vector, we need to add vectors A and B.
- Since vector A is along the X-axis and vector B is along the Y-axis, they are perpendicular to each other.
- Using the Pythagorean theorem, we can calculate the magnitude of the resultant vector:
- Magnitude = sqrt((7)^2 + (11)^2) = sqrt(49 + 121) = sqrt(170) ≈ 13.04 units
- Now, to find the direction of the resultant vector:
- tan(theta) = opposite/adjacent = 11/7
- theta ≈ arctan(11/7) ≈ 56.31 degrees
- Therefore, the resultant vector is 13.04 units at an angle of 56.31 degrees.
- Representing this in component form, we get:
- Resultant Vector = 7î + 11ĵ
Final Answer:
- Therefore, the correct resultant vector is 7î + 11ĵ, which is option B.
The angular velocity of a stone being rotated is 11 rad/s. What is the angular displacement covered in 0.5s?- a)5.5 rad
- b)0.55 rad
- c)55 rad
- d)0.5 rad
Correct answer is option 'A'. Can you explain this answer?
The angular velocity of a stone being rotated is 11 rad/s. What is the angular displacement covered in 0.5s?
a)
5.5 rad
b)
0.55 rad
c)
55 rad
d)
0.5 rad
|
Amelia Martin answered |
Angular Displacement Calculation:
Angular displacement is calculated using the formula:
\[ \text{Angular Displacement} = \text{Angular Velocity} \times \text{Time} \]
Given:
- Angular velocity = 11 rad/s
- Time = 0.5s
Calculation:
\[ \text{Angular Displacement} = 11 \text{ rad/s} \times 0.5 \text{ s} \]
\[ \text{Angular Displacement} = 5.5 \text{ rad} \]
Therefore, the angular displacement covered in 0.5s is 5.5 radians, which corresponds to option (a).
Angular displacement is calculated using the formula:
\[ \text{Angular Displacement} = \text{Angular Velocity} \times \text{Time} \]
Given:
- Angular velocity = 11 rad/s
- Time = 0.5s
Calculation:
\[ \text{Angular Displacement} = 11 \text{ rad/s} \times 0.5 \text{ s} \]
\[ \text{Angular Displacement} = 5.5 \text{ rad} \]
Therefore, the angular displacement covered in 0.5s is 5.5 radians, which corresponds to option (a).
Multiplying 2î + 7ĵ by 5 gives ______- a)10î + 35ĵ
- b)2î + 35ĵ
- c)10î + 7ĵ
- d)2î + 7ĵ
Correct answer is option 'A'. Can you explain this answer?
Multiplying 2î + 7ĵ by 5 gives ______
a)
10î + 35ĵ
b)
2î + 35ĵ
c)
10î + 7ĵ
d)
2î + 7ĵ
|
Isabella Iqbal answered |
Understanding the Expression
When we multiply the expression (2i + 7) by 5, we need to apply the distributive property. This means we will multiply each term inside the parentheses by 5.
Step-by-Step Calculation
- Distributing the 5:
- Multiply 5 by 2i:
- 5 * 2i = 10i
- Multiply 5 by 7:
- 5 * 7 = 35
- Combining the Results:
- Now, combine the results of these multiplications:
- 10i + 35
Final Result
The result of multiplying (2i + 7) by 5 is:
- 10i + 35
Conclusion
Thus, the correct answer is option 'A':
- 10i + 35
This shows how the distributive property works in algebra, allowing us to efficiently expand expressions by multiplying each term individually.
When we multiply the expression (2i + 7) by 5, we need to apply the distributive property. This means we will multiply each term inside the parentheses by 5.
Step-by-Step Calculation
- Distributing the 5:
- Multiply 5 by 2i:
- 5 * 2i = 10i
- Multiply 5 by 7:
- 5 * 7 = 35
- Combining the Results:
- Now, combine the results of these multiplications:
- 10i + 35
Final Result
The result of multiplying (2i + 7) by 5 is:
- 10i + 35
Conclusion
Thus, the correct answer is option 'A':
- 10i + 35
This shows how the distributive property works in algebra, allowing us to efficiently expand expressions by multiplying each term individually.
The velocity of a body, moving in a plane, changes from 3î to 3î + 7ĵ in 10s. What is the acceleration of the body?- a)0.7ĵ
- b)0.7î
- c)0.33î + 7ĵ
- d)0.3î + 7ĵ
Correct answer is option 'A'. Can you explain this answer?
The velocity of a body, moving in a plane, changes from 3î to 3î + 7ĵ in 10s. What is the acceleration of the body?
a)
0.7ĵ
b)
0.7î
c)
0.33î + 7ĵ
d)
0.3î + 7ĵ
|
Wyatt Turner answered |
The velocity of a body, moving in a plane, changes from 3 m/s to 5 m/s in a time interval of 2 seconds.
What is the standard form for the resolution of a vector having magnitude ‘a’ and is inclined at an angle θ to the X-axis?- a)a(cos θ î + sin θ ĵ)
- b)a(sin θ î + cos θ ĵ)
- c)a(sin θ î + sin θ ĵ)
- d)a(cos θ î + cos θ ĵ)
Correct answer is option 'A'. Can you explain this answer?
What is the standard form for the resolution of a vector having magnitude ‘a’ and is inclined at an angle θ to the X-axis?
a)
a(cos θ î + sin θ ĵ)
b)
a(sin θ î + cos θ ĵ)
c)
a(sin θ î + sin θ ĵ)
d)
a(cos θ î + cos θ ĵ)
|
|
Orion Classes answered |
The correct answer is a(cos θ î + sin θ ĵ). This is obtained by constructing a right-angled triangle with the distance of the point from the origin with either of the axes and then finding out the corresponding values for X and Y components.
Which of the following affects the angular velocity with its rate of change?- a)Angular acceleration
- b)Angular Distance
- c)Angular Displacement
- d)Torque
Correct answer is option 'C'. Can you explain this answer?
Which of the following affects the angular velocity with its rate of change?
a)
Angular acceleration
b)
Angular Distance
c)
Angular Displacement
d)
Torque
|
Benjamin Sheppard answered |
Understanding Angular Velocity and Its Change
Angular velocity is a measure of how quickly an object rotates around an axis. Its rate of change is influenced by several factors, but let's focus on the correct answer, which is angular displacement.
Why Angular Displacement Affects Angular Velocity
- Definition of Angular Displacement: Angular displacement refers to the angle through which an object has rotated about a specific axis in a given time period.
- Connection to Angular Velocity: Angular velocity (ω) is defined as the rate of change of angular displacement (θ) with respect to time. This relationship can be expressed mathematically as:
ω = dθ/dt
- Rate of Change: When the angular displacement changes, it directly influences the angular velocity. A change in the angle indicates that the object is accelerating or decelerating in its rotation, thus altering its angular velocity.
Distinction from Other Options
- Angular Acceleration: While it represents the rate of change of angular velocity, it does not directly affect angular velocity itself; it describes how velocity changes.
- Angular Distance: This refers to the total angle covered during motion but does not account for direction, thus it doesn't directly influence angular velocity.
- Torque: This is the force causing the rotation but is not a measure of velocity or its change.
Conclusion
In summary, angular displacement is crucial because it directly influences the angular velocity by defining how much rotation has occurred over time. Understanding this relationship is key in rotational motion analysis.
Angular velocity is a measure of how quickly an object rotates around an axis. Its rate of change is influenced by several factors, but let's focus on the correct answer, which is angular displacement.
Why Angular Displacement Affects Angular Velocity
- Definition of Angular Displacement: Angular displacement refers to the angle through which an object has rotated about a specific axis in a given time period.
- Connection to Angular Velocity: Angular velocity (ω) is defined as the rate of change of angular displacement (θ) with respect to time. This relationship can be expressed mathematically as:
ω = dθ/dt
- Rate of Change: When the angular displacement changes, it directly influences the angular velocity. A change in the angle indicates that the object is accelerating or decelerating in its rotation, thus altering its angular velocity.
Distinction from Other Options
- Angular Acceleration: While it represents the rate of change of angular velocity, it does not directly affect angular velocity itself; it describes how velocity changes.
- Angular Distance: This refers to the total angle covered during motion but does not account for direction, thus it doesn't directly influence angular velocity.
- Torque: This is the force causing the rotation but is not a measure of velocity or its change.
Conclusion
In summary, angular displacement is crucial because it directly influences the angular velocity by defining how much rotation has occurred over time. Understanding this relationship is key in rotational motion analysis.
A car moves 25 units in the positive X direction and 75 units in negative Y direction starting from the origin in 25 seconds. What is the velocity vector of the car?- a)î – 3ĵ
- b)3î – ĵ
- c)î + 3ĵ
- d)3î + ĵ
Correct answer is option 'A'. Can you explain this answer?
A car moves 25 units in the positive X direction and 75 units in negative Y direction starting from the origin in 25 seconds. What is the velocity vector of the car?
a)
î – 3ĵ
b)
3î – ĵ
c)
î + 3ĵ
d)
3î + ĵ
|
|
Orion Classes answered |
The initial position of the car is at the origin and the final position is 25î – 75ĵ. Hence the displacement is 25î – 75ĵ. The total time taken is 25 s. Hence, the velocity = change in position/time = î – 3ĵ.
Eleven times unit vector along X added to 7 times unit vector along Y gives ______- a)11î + 7ĵ
- b)7î + 11ĵ
- c)7î + 7ĵ
- d)11î + 11ĵ
Correct answer is option 'A'. Can you explain this answer?
Eleven times unit vector along X added to 7 times unit vector along Y gives ______
a)
11î + 7ĵ
b)
7î + 11ĵ
c)
7î + 7ĵ
d)
11î + 11ĵ
|
|
Jasmine Johnson answered |
Eleven times the unit vector along the X-axis added to 7 times the unit vector along the Y-axis gives us a vector in the XY-plane. The resultant vector can be found by adding the components along the X-axis and Y-axis separately.
The X-component of the resultant vector is 11 times the X-component of the unit vector along the X-axis, which is 11 times 1, giving us 11.
The Y-component of the resultant vector is 7 times the Y-component of the unit vector along the Y-axis, which is 7 times 1, giving us 7.
Therefore, the resultant vector is (11, 7).
So the answer is a) 11.
The X-component of the resultant vector is 11 times the X-component of the unit vector along the X-axis, which is 11 times 1, giving us 11.
The Y-component of the resultant vector is 7 times the Y-component of the unit vector along the Y-axis, which is 7 times 1, giving us 7.
Therefore, the resultant vector is (11, 7).
So the answer is a) 11.
A body moves from point A (3,6) to point B (11,12) to point C (15,15). What is the average speed of the body along the given path if the total time taken is 100s?- a)0.15 units/s
- b)1.5 units/s
- c)15 units/s
- d)0.0015 units/s
Correct answer is option 'A'. Can you explain this answer?
A body moves from point A (3,6) to point B (11,12) to point C (15,15). What is the average speed of the body along the given path if the total time taken is 100s?
a)
0.15 units/s
b)
1.5 units/s
c)
15 units/s
d)
0.0015 units/s
|
|
Orion Classes answered |
The distance between A and B is 10 units. The distance between B and C is 5 units. Hence, the total distance is 15 units. The total time taken is 100 s. Average speed = total distance/total time taken = 15/100 = 0.15 units/s.
Give an example of motion in two dimensions _________- a)Motion along a straight line in any direction
- b)Bird flying
- c)A flying kite
- d)Projectile motion
Correct answer is option 'D'. Can you explain this answer?
Give an example of motion in two dimensions _________
a)
Motion along a straight line in any direction
b)
Bird flying
c)
A flying kite
d)
Projectile motion
|
|
Aubrey Hayes answered |
Projectile Motion:
Projectile motion is a classic example of motion in two dimensions. It involves an object being thrown or projected into the air and moving in both the horizontal and vertical directions simultaneously.
Key Points:
- In projectile motion, an object moves under the influence of gravity only after an initial force has been applied to set it in motion.
- The object follows a curved path known as a projectile trajectory.
- The horizontal component of motion remains constant, while the vertical component is influenced by the force of gravity.
- The object reaches a maximum height at the peak of its trajectory before falling back to the ground.
- Examples of projectile motion include a thrown baseball, a launched rocket, or even a ball kicked into the air.
Importance of Understanding Projectile Motion:
Understanding projectile motion is crucial in various fields such as physics, engineering, sports, and even military applications. By analyzing the motion of projectiles, scientists and engineers can predict their trajectory, range, and impact point with precision. This knowledge is essential for designing efficient systems like artillery, missiles, or sports equipment.
In conclusion, projectile motion serves as a fundamental example of motion in two dimensions, showcasing the interaction between horizontal and vertical motion components. Mastering the principles of projectile motion is essential for various real-world applications and scientific advancements.
A force is inclined at 60° to the horizontal. If its rectangular component in horizontal direction is 50 N. Find the magnitude of the force and its vertical components respectively.- a)100 N, 50 N
- b)50√3 N, 100 N
- c)100 N, 50√3 N
- d)100 N, 100 N
Correct answer is option 'B'. Can you explain this answer?
A force is inclined at 60° to the horizontal. If its rectangular component in horizontal direction is 50 N. Find the magnitude of the force and its vertical components respectively.
a)
100 N, 50 N
b)
50√3 N, 100 N
c)
100 N, 50√3 N
d)
100 N, 100 N
|
|
Orion Classes answered |
Concept:
Resolution of vectors into components: We have a vector (F) where the magnitude of the vector is F and the angle with horizontal is θ.
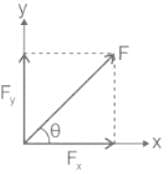
The vector has two components: 1. Vertical component and 2. Horizontal component
Vertical component (Fy) = F Sinθ
Horizontal component (Fx) = F Cosθ
Calculation:
Given that:
Calculation:
Given that:
Fx = 50N , θ = 60°
Fx = Fcosθ
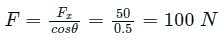
Fy = Fsinθ
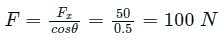
Fy = Fsinθ
What is the dot product of two vectors, vector A and vector B? The angle between both the vector is θ.- a)A B Sinθ
- b)A B Cosθ
- c)A B tanθ
- d)A B Secθ
Correct answer is option 'B'. Can you explain this answer?
What is the dot product of two vectors, vector A and vector B? The angle between both the vector is θ.
a)
A B Sinθ
b)
A B Cosθ
c)
A B tanθ
d)
A B Secθ
|
Charlotte Chen answered |
The dot product of two vectors, vector A and vector B, is a scalar quantity defined as the product of the magnitudes of the vectors and the cosine of the angle between them. Mathematically, it is denoted as A · B.
If the angle between vector A and vector B is θ (theta) in radians, then the dot product can be calculated using the formula:
A · B = |A| |B| cos(θ)
Here, |A| represents the magnitude (or length) of vector A, and |B| represents the magnitude of vector B.
Note that the dot product is commutative, which means A · B = B · A.
If the angle between vector A and vector B is θ (theta) in radians, then the dot product can be calculated using the formula:
A · B = |A| |B| cos(θ)
Here, |A| represents the magnitude (or length) of vector A, and |B| represents the magnitude of vector B.
Note that the dot product is commutative, which means A · B = B · A.
If S = 3t2 - 5t + 7 find initial velocity.- a)2
- b)5
- c)-2
- d)-5
Correct answer is option 'D'. Can you explain this answer?
If S = 3t2 - 5t + 7 find initial velocity.
a)
2
b)
5
c)
-2
d)
-5
|
|
Orion Classes answered |
Formula Used:
Velocity = s/t
Here, S is displacement and t is time
For instantaneous velocity, it expressed as dS/dt
Application:
We have,
S = 3t2 - 5t + 7
Hence,
Instantaneous velocity = dS/dt = (6t - 5)
initial velocity will be found at t = o
Hence,
V|initial = (6 × 0 - 5) = - 5
Velocity = s/t
Here, S is displacement and t is time
For instantaneous velocity, it expressed as dS/dt
Application:
We have,
S = 3t2 - 5t + 7
Hence,
Instantaneous velocity = dS/dt = (6t - 5)
initial velocity will be found at t = o
Hence,
V|initial = (6 × 0 - 5) = - 5
Which one of the following operations is valid?- a)Vector multiplied by scalar
- b)Vector added to scalar
- c)Vector subtracted from scalar
- d)Vector divided by vector
Correct answer is option 'A'. Can you explain this answer?
Which one of the following operations is valid?
a)
Vector multiplied by scalar
b)
Vector added to scalar
c)
Vector subtracted from scalar
d)
Vector divided by vector
|
|
Victoria Walsh answered |
Vector multiplied by scalar
Vectors can be multiplied by scalars, which results in a new vector. This operation involves multiplying each component of the vector by the scalar. The resulting vector has the same direction as the original vector but its magnitude is scaled by the scalar. This operation is commonly used in physics and mathematics to scale vectors by a certain factor.
For example, if we have a vector v = (2, 4, 6) and we multiply it by a scalar k = 3, the resulting vector would be kv = (2*3, 4*3, 6*3) = (6, 12, 18).
This operation is valid and commonly used in various applications such as physics, engineering, and computer graphics. It allows us to scale vectors to represent different quantities or magnitudes.
A child pulls a rope attached to a stone with a force of 60 N. The rope makes an angle of 60 degrees to the ground. What is the effective force along the horizontal direction?- a)45.96 N
- b)40.3 N
- c)28 N
- d)30 N
Correct answer is option 'D'. Can you explain this answer?
A child pulls a rope attached to a stone with a force of 60 N. The rope makes an angle of 60 degrees to the ground. What is the effective force along the horizontal direction?
a)
45.96 N
b)
40.3 N
c)
28 N
d)
30 N
|
|
Sophia Lewis answered |
Analysis:
To find the effective force along the horizontal direction, we need to resolve the force applied by the child into horizontal and vertical components.
Given:
- Force applied by the child (F) = 60 N
- Angle made by the rope with the ground (θ) = 60 degrees
Calculations:
- Horizontal component of the force (F_horizontal) = F * cos(θ)
- F_horizontal = 60 * cos(60)
- F_horizontal = 60 * 0.5
- F_horizontal = 30 N
Therefore, the effective force along the horizontal direction is 30 N. Hence, option 'D' is the correct answer.
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string at the highest point?- a)30 N
- b)50 N
- c)20 N
- d)25 N
Correct answer is option 'A'. Can you explain this answer?
A body of weight 20 N, mass 2 kg is moving in vertical circular motion with the help of a string of radius 1 m and with a velocity of 5 m/s. What is the tension in the string at the highest point?
a)
30 N
b)
50 N
c)
20 N
d)
25 N
|
|
Elizabeth Baker answered |
Given Data:
- Weight of body (W) = 20 N
- Mass of body (m) = 2 kg
- Radius of circular motion (r) = 1 m
- Velocity of body (v) = 5 m/s
Calculating Tension at the Highest Point:
- At the highest point, the tension in the string provides the centripetal force required to keep the body in circular motion.
- The tension in the string can be calculated using the equation: T = (mv^2)/r
- Substituting the given values, T = (2 * 5^2) / 1
- T = 50 N
Conclusion:
The tension in the string at the highest point is 50 N.
- Weight of body (W) = 20 N
- Mass of body (m) = 2 kg
- Radius of circular motion (r) = 1 m
- Velocity of body (v) = 5 m/s
Calculating Tension at the Highest Point:
- At the highest point, the tension in the string provides the centripetal force required to keep the body in circular motion.
- The tension in the string can be calculated using the equation: T = (mv^2)/r
- Substituting the given values, T = (2 * 5^2) / 1
- T = 50 N
Conclusion:
The tension in the string at the highest point is 50 N.
At which position in vertical circular motion is the tension in the string minimum?- a)At the highest position
- b)At the lowest position
- c)When the string is horizontal
- d)At an angle of 35° from the horizontal
Correct answer is option 'A'. Can you explain this answer?
At which position in vertical circular motion is the tension in the string minimum?
a)
At the highest position
b)
At the lowest position
c)
When the string is horizontal
d)
At an angle of 35° from the horizontal
|
|
Mason Hicks answered |
C) When the string is horizontal.
A body is moving in a vertical circular motion. Which one of the following forces does it not experience?- a)Force of gravity
- b)Centripetal force
- c)Normal reaction force
- d)Centrifugal force
Correct answer is option 'C'. Can you explain this answer?
A body is moving in a vertical circular motion. Which one of the following forces does it not experience?
a)
Force of gravity
b)
Centripetal force
c)
Normal reaction force
d)
Centrifugal force
|
|
Scarlett Reed answered |
Explanation:
In a vertical circular motion, a body moves in a circular path in a vertical plane. This motion can be observed in various scenarios such as a roller coaster or a swing. When analyzing the forces acting on the body during this motion, we can identify four main forces: force of gravity, centripetal force, normal reaction force, and centrifugal force.
1. Force of gravity: The force of gravity acts vertically downwards, towards the center of the Earth. It is responsible for pulling the body towards the Earth and giving it weight.
2. Centripetal force: The centripetal force is the force that keeps the body moving in a circular path. It always acts towards the center of the circle and is responsible for changing the direction of the body's velocity. In the case of vertical circular motion, the centripetal force can be provided by tension in a rope or the normal reaction force.
3. Normal reaction force: The normal reaction force is the force exerted by a surface to support the weight of an object resting on it. In the case of vertical circular motion, the normal reaction force acts perpendicular to the surface the body is moving on. It is responsible for preventing the body from falling through the surface.
4. Centrifugal force: The centrifugal force is often referred to as a "fictitious" or "pseudo" force. It is an apparent force that acts in the opposite direction to the centripetal force. In reality, it is not a true force but rather a result of inertia. In vertical circular motion, the centrifugal force would act away from the center of the circle and would be felt by the body as an outward force.
Answer:
The force that the body does not experience in vertical circular motion is the normal reaction force (Option C). This is because the normal reaction force only acts perpendicular to the surface the body is moving on, and in this case, the body is not in contact with any surface. In vertical circular motion, the body is typically suspended or held by a rope, and the centripetal force is provided by tension in the rope. Therefore, the body does not exert any force on a surface, and hence there is no normal reaction force.
It is important to note that the absence of the normal reaction force does not imply that the body is not experiencing any other forces. The force of gravity and the centripetal force are still acting on the body, ensuring its motion in a circular path.
In a vertical circular motion, a body moves in a circular path in a vertical plane. This motion can be observed in various scenarios such as a roller coaster or a swing. When analyzing the forces acting on the body during this motion, we can identify four main forces: force of gravity, centripetal force, normal reaction force, and centrifugal force.
1. Force of gravity: The force of gravity acts vertically downwards, towards the center of the Earth. It is responsible for pulling the body towards the Earth and giving it weight.
2. Centripetal force: The centripetal force is the force that keeps the body moving in a circular path. It always acts towards the center of the circle and is responsible for changing the direction of the body's velocity. In the case of vertical circular motion, the centripetal force can be provided by tension in a rope or the normal reaction force.
3. Normal reaction force: The normal reaction force is the force exerted by a surface to support the weight of an object resting on it. In the case of vertical circular motion, the normal reaction force acts perpendicular to the surface the body is moving on. It is responsible for preventing the body from falling through the surface.
4. Centrifugal force: The centrifugal force is often referred to as a "fictitious" or "pseudo" force. It is an apparent force that acts in the opposite direction to the centripetal force. In reality, it is not a true force but rather a result of inertia. In vertical circular motion, the centrifugal force would act away from the center of the circle and would be felt by the body as an outward force.
Answer:
The force that the body does not experience in vertical circular motion is the normal reaction force (Option C). This is because the normal reaction force only acts perpendicular to the surface the body is moving on, and in this case, the body is not in contact with any surface. In vertical circular motion, the body is typically suspended or held by a rope, and the centripetal force is provided by tension in the rope. Therefore, the body does not exert any force on a surface, and hence there is no normal reaction force.
It is important to note that the absence of the normal reaction force does not imply that the body is not experiencing any other forces. The force of gravity and the centripetal force are still acting on the body, ensuring its motion in a circular path.
An object makes a displacement of 4 m due East from a point P and then makes displacement of 3 m due North. Its resultant displacement from P.- a)7 m
- b)1 m
- c)5 m
- d)1.2 m
Correct answer is option 'C'. Can you explain this answer?
An object makes a displacement of 4 m due East from a point P and then makes displacement of 3 m due North. Its resultant displacement from P.
a)
7 m
b)
1 m
c)
5 m
d)
1.2 m
|
|
Orion Classes answered |
Let the point 4m from east of P be A. So PA is 4m and the point in the north be B such that AB is 3m. Therefore PBA is a right-angled triangle. The resultant displacement is equal to PB
PA2 + AB2 = PB2
42 + 32 = PB2
16 + 9 = 25 = PB2
PB = 5m
PA2 + AB2 = PB2
42 + 32 = PB2
16 + 9 = 25 = PB2
PB = 5m
Velocity of a man is 25 units in the positive X direction and 75 units in negative Y direction starting from the origin. Velocity of a woman is 25 units in the positive Y direction and 75 units in the negative X direction starting from the origin. What is the relative velocity of the man with respect to the woman?- a)100î – 100ĵ
- b)100î + 100ĵ
- c)-100î – 100ĵ
- d)0î + 0ĵ
Correct answer is option 'A'. Can you explain this answer?
Velocity of a man is 25 units in the positive X direction and 75 units in negative Y direction starting from the origin. Velocity of a woman is 25 units in the positive Y direction and 75 units in the negative X direction starting from the origin. What is the relative velocity of the man with respect to the woman?
a)
100î – 100ĵ
b)
100î + 100ĵ
c)
-100î – 100ĵ
d)
0î + 0ĵ
|
|
Orion Classes answered |
The velocity of the man is 25î – 75ĵ and that of the woman is -75î + 25ĵ. Relative velocity = velocity of man – velocity of woman = 100î – 100ĵ.
Which of the following physical quantities can be expressed as the vector product of two vectors?- a)Torque
- b)Angular momentum
- c)Linear velocity
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following physical quantities can be expressed as the vector product of two vectors?
a)
Torque
b)
Angular momentum
c)
Linear velocity
d)
All of the above
|
|
Flembe Academy answered |
Concept:
- Vector Product (cross product): Its magnitude is equal to the products of the magnitude of two vectors and sine of the angle between them and whose direction is perpendicular to the plane of the two vectors
Mathematically it is written as:
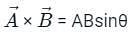
Where θ is the angle between a vector
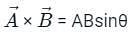
Where θ is the angle between a vector
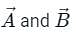
- Torque, Angular momentum, and Instantaneous velocity all can be expressed as the vector products of two vectors.
Explanation:
- Torque (τ): The torque acting on a particle is equal to the vector products of its position vector
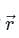and force vector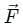 
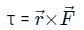
- Angular momentum (L): It is equal to the cross product of its position vector
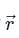and the linear momentum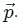 
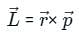
- Linear Velocity (v): It is equal to the cross product of its angular velocity ω and the position vector
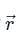
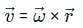
- These physical quantities can be expressed as the vector products of two vectors.
- Hence all of the above options are correct.
The velocity of a car A is to 5î + 11ĵ. The velocity of another car B is 11î + 5ĵ. What is the relative velocity of B with respect to A?- a)6î – 6ĵ
- b)11î + 5ĵ
- c)6î + 6ĵ
- d)5î + 5ĵ
Correct answer is option 'A'. Can you explain this answer?
The velocity of a car A is to 5î + 11ĵ. The velocity of another car B is 11î + 5ĵ. What is the relative velocity of B with respect to A?
a)
6î – 6ĵ
b)
11î + 5ĵ
c)
6î + 6ĵ
d)
5î + 5ĵ
|
|
Orion Classes answered |
The formula for calculating relative velocity of a body with respect to another body is- relative velocity = Velocity vector of A – Velocity vector of B. Hence, here, the relative velocity = velocity of B – velocity of A = 6î – 6ĵ.
At a metro station, a girl walks up a stationary escalator in time t1 . If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be- a)(t1 + t 2)/2
- b)t1t2/(t2 – t1)
- c)t1t2/(t2 + t1)
- d)t1 – t2
Correct answer is option 'C'. Can you explain this answer?
At a metro station, a girl walks up a stationary escalator in time t1 . If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be
a)
(t1 + t 2)/2
b)
t1t2/(t2 – t1)
c)
t1t2/(t2 + t1)
d)
t1 – t2
|
|
Orion Classes answered |
In the situation of a stationary escalator and moving girl velocity,
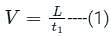
In the situation of stationary girl and moving escalator velocity,
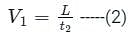
If both escalator and girl keep moving then distance,
L = (V + V1) t3 ----(3)
Where t3 is time to cover that distance when both girl and the escalator keep moving.
Using equations (1), (2), and (3) we get:
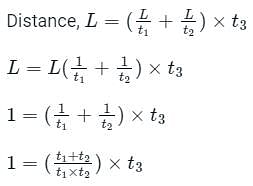
Then, time is taken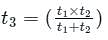
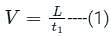
In the situation of stationary girl and moving escalator velocity,
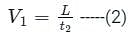
If both escalator and girl keep moving then distance,
L = (V + V1) t3 ----(3)
Where t3 is time to cover that distance when both girl and the escalator keep moving.
Using equations (1), (2), and (3) we get:
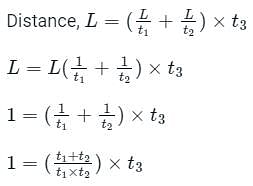
Then, time is taken
The vector obtained by addition of two vectors is termed as ______- a)New vector
- b)Resultant vector
- c)Derived vector
- d)Sum vector
Correct answer is option 'B'. Can you explain this answer?
The vector obtained by addition of two vectors is termed as ______
a)
New vector
b)
Resultant vector
c)
Derived vector
d)
Sum vector
|
|
Orion Classes answered |
The resultant vector is the vector which is obtained by the addition or subtraction of two vectors. The resultant vector can either be calculated by using the graphical method or the analytical method.
The centrifugal force always acts _____- a)Towards the center
- b)Away from the center
- c)In tangential direction
- d)Outside of the plane of motion
Correct answer is option 'B'. Can you explain this answer?
The centrifugal force always acts _____
a)
Towards the center
b)
Away from the center
c)
In tangential direction
d)
Outside of the plane of motion
|
|
Orion Classes answered |
The centrifugal force always acts away from the center of the circle in which the body is moving. In contrast to this, the centripetal force always acts towards the center of the circle, keeping the body moving in the circle.
Subtracting 2î + 7ĵ from î + ĵ gives ______- a)-î – 6ĵ
- b)3î + 8ĵ
- c)î + 6ĵ
- d)7ĵ
Correct answer is option 'A'. Can you explain this answer?
Subtracting 2î + 7ĵ from î + ĵ gives ______
a)
-î – 6ĵ
b)
3î + 8ĵ
c)
î + 6ĵ
d)
7ĵ
|
|
Orion Classes answered |
When 2î + 7ĵ is subtracted from î + ĵ, the corresponding components get subtracted. Hence, the answer is -î – 6ĵ.
Which one of the following devices acts on the principle of circular motion?- a)Centrifuge
- b)Screw Gauge
- c)Ruler
- d)Vernier calipers
Correct answer is option 'A'. Can you explain this answer?
Which one of the following devices acts on the principle of circular motion?
a)
Centrifuge
b)
Screw Gauge
c)
Ruler
d)
Vernier calipers
|
|
Orion Classes answered |
The centrifuge utilizes the centrifugal force produced during circular motion. Centrifuge is commonly used to separate platelets from blood samples. It is an important equipment for studying blood. Other variations of centrifuge include devices like cream separator etc.
What is the resolved form for a vector which is 5 units in long and is inclined at an angle of 45 degrees to the X-axis?- a)
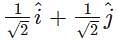
- b)
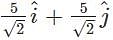
- c)
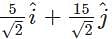
- d)
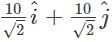
Correct answer is option 'B'. Can you explain this answer?
What is the resolved form for a vector which is 5 units in long and is inclined at an angle of 45 degrees to the X-axis?
a)
b)
c)
d)
|
|
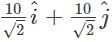
Orion Classes answered |
The standard for is a(cos θ î + sin θ ĵ). Here, a = 5, and θ = 45 degrees. When we substitute this in the equation, we get, the resolved vector as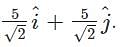 
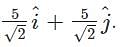
Unit vector which is perpendicular to the vector 4î + 3ĵ is _____- a)ĵ
- b)î
- c)4î + 3ĵ
- d)
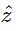
Correct answer is option 'D'. Can you explain this answer?
Unit vector which is perpendicular to the vector 4î + 3ĵ is _____
a)
ĵ
b)
î
c)
4î + 3ĵ
d)
|
|
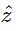
Orion Classes answered |
The dot product of any two vectors which are perpendicular to each other is 0. The dot product of all the vectors in the options with 4î + 3ĵ is non-zero except for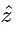 
. Hence 
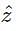is perpendicular to the given vector.
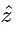. Hence 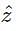is perpendicular to the given vector.The quantity which has the only magnitude is called ________- a)A scalar quantity
- b)A vector quantity
- c)A chemical quantity
- d)A magnitude quantity
Correct answer is option 'A'. Can you explain this answer?
The quantity which has the only magnitude is called ________
a)
A scalar quantity
b)
A vector quantity
c)
A chemical quantity
d)
A magnitude quantity
|
|
Orion Classes answered |
A quantity which has only magnitude and no direction is called scalar quantity. Example: mass
The splitting of a vector into two component vectors is called ______- a)Vector resolution
- b)Vector sum
- c)Vector decomposition
- d)Vector difference
Correct answer is option 'A'. Can you explain this answer?
The splitting of a vector into two component vectors is called ______
a)
Vector resolution
b)
Vector sum
c)
Vector decomposition
d)
Vector difference
|
|
Orion Classes answered |
The splitting of a vector into two component vectors is called vector resolution. The vector can be resolved into as many components as there are independent directions.
Motion in a plane is called ________- a)Motion in one dimension
- b)Motion in two dimensions
- c)Motion in three dimensions
- d)Motion in four dimensions
Correct answer is option 'B'. Can you explain this answer?
Motion in a plane is called ________
a)
Motion in one dimension
b)
Motion in two dimensions
c)
Motion in three dimensions
d)
Motion in four dimensions
|
|
Orion Classes answered |
Motion in a plane is also known as motion in two dimensions.
Which of the following is not an example of motion in a plane?- a)A car moving in a rectangular path
- b)A bicycle moving in a circular path
- c)A rocket moving into space
- d)A truck moving in an infinite spiral
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not an example of motion in a plane?
a)
A car moving in a rectangular path
b)
A bicycle moving in a circular path
c)
A rocket moving into space
d)
A truck moving in an infinite spiral
|
|
Orion Classes answered |
A rocket moving into space is an example of 3-dimensional motion. Hence, it cannot be out in the category of motion in a plane. Rest all examples of motion in a plane. The truck moving in an infinite spiral is also an example of motion in a plane as spiral is a 2-dimensional entity.
Chapter doubts & questions for Motion in a plane - Physics for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Motion in a plane - Physics for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Physics for ACT
169 videos|131 docs|69 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup