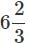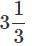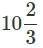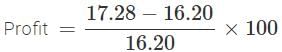All Exams >
JSS 2 >
Mathematics for JSS 2 >
All Questions
All questions of Ratios, Proportions, Percentages and Rates for JSS 2 Exam
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Comparing Quantities, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q. Find the ratio of speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.- a)It is 1:2
- b)It is 1:3
- c)It is 2:1
- d)It is 3:1
Correct answer is option 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Comparing Quantities, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q. Find the ratio of speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
a)
It is 1:2
b)
It is 1:3
c)
It is 2:1
d)
It is 3:1
|
|
Shubham Sharma answered |
Speed of cycle = 15 km per hour
Speed of scooter = 30 km per hour
∴ 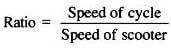
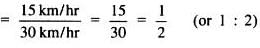
A picnic is being planned in a school for Class VII. Girls are 60% of the total number of students and are 18 in number. Find the ratio of the number of girls to the number of boys in the class.- a)It is 2:1
- b)It is 3:2
- c)It is 2:3
- d)It is 3:1
Correct answer is 'B'. Can you explain this answer?
A picnic is being planned in a school for Class VII. Girls are 60% of the total number of students and are 18 in number. Find the ratio of the number of girls to the number of boys in the class.
a)
It is 2:1
b)
It is 3:2
c)
It is 2:3
d)
It is 3:1
|
|
Prapthi Bhandary answered |
Simple way
Percentage of girls=60
Percentage of boys=100-60
=40
Ratio=60:40
=3:2
Percentage of girls=60
Percentage of boys=100-60
=40
Ratio=60:40
=3:2
A sum of money, at compound interest, yields Rs. 200 and Rs. 220 at the end of first and second years respectively. What is the rate percent?- a)20%
- b)15%
- c)10%
- d)5%
Correct answer is option 'C'. Can you explain this answer?
A sum of money, at compound interest, yields Rs. 200 and Rs. 220 at the end of first and second years respectively. What is the rate percent?
a)
20%
b)
15%
c)
10%
d)
5%
|
|
Geetika Shah answered |
Difference between interests = Rs.220 - Rs. 200 = Rs. 20
⇒ Rs. 20 is the S.I on Rs. 200 for 1 Year.
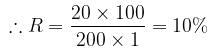
Hence, the rate of interest is 10%.
⇒ Rs. 20 is the S.I on Rs. 200 for 1 Year.
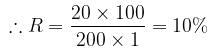
Hence, the rate of interest is 10%.
A shopkeeper purchased 200 bulbs for Rs 10 each. However 5 bulbs were fused and had to be thrown away. The remaining were sold at Rs 12 each. Find the gain or loss %.- a)15%
- b)17%
- c)13%
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A shopkeeper purchased 200 bulbs for Rs 10 each. However 5 bulbs were fused and had to be thrown away. The remaining were sold at Rs 12 each. Find the gain or loss %.
a)
15%
b)
17%
c)
13%
d)
None of these
|
|
Sarita Verma answered |
200 bulbs at rs 10 = 2000
5 bulbs defective
195 bulbs sold at 12
SP= 195*12=2340
profit= 2340-2000=340
profit percent = profit/CP * 100
=340/2000 * 100
=17%
During a sale, a shop offered a discount of 20% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at Rs 1450 and a shirt marked at Rs 850 each?
- a)Rs 1,840
- b)Rs 2,640
- c)Rs 2,740
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
During a sale, a shop offered a discount of 20% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at Rs 1450 and a shirt marked at Rs 850 each?
a)
Rs 1,840
b)
Rs 2,640
c)
Rs 2,740
d)
none of these
|
|
Ananya Das answered |
Discount on Jeans=20% of 1450=290
Price of jeans=1450-290=1160
Discount on shirt=20% of 850=170
Price of shirt=850-170=680
Total price=1160+680= 1840
Price of jeans=1450-290=1160
Discount on shirt=20% of 850=170
Price of shirt=850-170=680
Total price=1160+680= 1840
An item marked at Rs 840 is sold for Rs 714. What is the discount %?
- a)20%
- b)10%
- c)15%
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
An item marked at Rs 840 is sold for Rs 714. What is the discount %?
a)
20%
b)
10%
c)
15%
d)
none of these
|
|
Amita Verma answered |
Given, marked price = 840
selling price = 714
We know that Discount = MP - SP
= 840 - 714
= 126.
Discount% = 126/840 * 100
= 15%.
Find the amount when Rs. 10,800 for 3 years at 12.5% per annum compounded annually.
- a)13,377.34
- b)15377.343
- c)14,377.34
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Find the amount when Rs. 10,800 for 3 years at 12.5% per annum compounded annually.
a)
13,377.34
b)
15377.343
c)
14,377.34
d)
None of these

|
Sounak Sengupta answered |
Given:
Rs. 10,800 for 3 years at 12.5% per annum is compounded annually. We have to find the final amount at the end of three years. This can be easily done as-
Substituting P = 10800, r = 12.5 and t = 3,
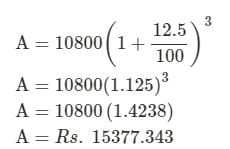
The total amount when Rs. 10,800 for 3 years at 12.5% per annum is compounded annually is Rs. 15377.343. This is the required answer.
Rs. 10,800 for 3 years at 12.5% per annum is compounded annually. We have to find the final amount at the end of three years. This can be easily done as-
Substituting P = 10800, r = 12.5 and t = 3,
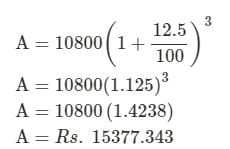
The total amount when Rs. 10,800 for 3 years at 12.5% per annum is compounded annually is Rs. 15377.343. This is the required answer.
The price of a motor bike was Rs 60,000 last year. It has increased by 15% this year. What is the price now?
- a)Rs 69,000
- b)Rs 63,000
- c)Rs 66,000
- d)Rs 30,800
Correct answer is option 'A'. Can you explain this answer?
The price of a motor bike was Rs 60,000 last year. It has increased by 15% this year. What is the price now?
a)
Rs 69,000
b)
Rs 63,000
c)
Rs 66,000
d)
Rs 30,800

|
Shreya Garg answered |
As it was 60,000 initially, but now there is an increase of 15%.
so we calculate 15% of 60,000 that will be ₹9,000.
Then we have to calculate the new price of bike, (i.e. old + increased) = ₹60,000+₹9,000 = ₹69,000
so we calculate 15% of 60,000 that will be ₹9,000.
Then we have to calculate the new price of bike, (i.e. old + increased) = ₹60,000+₹9,000 = ₹69,000
A trader marks his goods 30% above the cost price but makes a reduction of 25/4 on the marked price for ready money. What is his gain percent?
- a)23.75
- b)23.25
- c)21.875
- d)20
Correct answer is option 'C'. Can you explain this answer?
A trader marks his goods 30% above the cost price but makes a reduction of 25/4 on the marked price for ready money. What is his gain percent?
a)
23.75
b)
23.25
c)
21.875
d)
20

|
Learning Education answered |
Gain % = (SP − CP)/CP
Let cost price be Rs. 100.
Let cost price be Rs. 100.
The MP is Rs. 130.
After discount of 6 1/4 %
the SP is Rs. 130(93.75/100)
= Rs. 121.875
Gain% = [(121.875 - 100)/100]*100
= 21.875
After discount of 6 1/4 %
the SP is Rs. 130(93.75/100)
= Rs. 121.875
Gain% = [(121.875 - 100)/100]*100
= 21.875
The C.I. on a certain sum at 5% for 2 years is Rs. 328. Calculate the S.I. for the sum at the same rate and for the same period.
- a)Rs.320
- b)Rs.322
- c)Rs.325
- d)Rs.326
Correct answer is option 'A'. Can you explain this answer?
The C.I. on a certain sum at 5% for 2 years is Rs. 328. Calculate the S.I. for the sum at the same rate and for the same period.
a)
Rs.320
b)
Rs.322
c)
Rs.325
d)
Rs.326
|
|
Kavya Saxena answered |
CI = A-P
CI = P(1+R/100)2-P
328 = P[(1+5/100)2-1]
328 = P*41/400
P = 3200
SI = 3200*2*5/100 = 320
CI = P(1+R/100)2-P
328 = P[(1+5/100)2-1]
328 = P*41/400
P = 3200
SI = 3200*2*5/100 = 320
Rohan bought a second hand refrigerator for Rs 2,500, then spent Rs 500 on its repairs and sold it for Rs 3,300. Find his loss or gain per cent.- a)Loss 15% 2a
- b)Loss 10%
- c)Profit 10%
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Rohan bought a second hand refrigerator for Rs 2,500, then spent Rs 500 on its repairs and sold it for Rs 3,300. Find his loss or gain per cent.
a)
Loss 15% 2a
b)
Loss 10%
c)
Profit 10%
d)
None of these
|
|
Aditi Saxena answered |
Total money spent by sohan (C.P)
= ₹2500 + ₹500
= ₹3000 ( CP )
SP = ₹3300
Hence, a gain as CP < SP
Gain = ₹(3300-3000) = ₹300
Gain% = 300/3000 x 100 = 10 %
What is the C.I. on Rs. 8000 for 1 year at 5% p.a. payable half-yearly?
- a)Rs. 800
- b)Rs. 810
- c)Rs. 400
- d)Rs. 405
Correct answer is option 'D'. Can you explain this answer?
What is the C.I. on Rs. 8000 for 1 year at 5% p.a. payable half-yearly?
a)
Rs. 800
b)
Rs. 810
c)
Rs. 400
d)
Rs. 405
|
|
Kavya Saxena answered |
A = P ( 1 + R/100)t. Since its half yearly,
t = 2
= 8000 (1 + 5/200)2
= 8405
CI = A-P = 8405 - 8000 = 405
t = 2
= 8000 (1 + 5/200)2
= 8405
CI = A-P = 8405 - 8000 = 405
A sum of money doubles itself in 3 years at C.I., when the interest is compounded annually. In how many years will it amount to 16 times of itself?
- a)6 years
- b)8 years
- c)12 years
- d)16 years
Correct answer is option 'C'. Can you explain this answer?
A sum of money doubles itself in 3 years at C.I., when the interest is compounded annually. In how many years will it amount to 16 times of itself?
a)
6 years
b)
8 years
c)
12 years
d)
16 years

|
Trisha Vashisht answered |
⇒ 16 = 2 × 2 × 2 × 2 = 24
⇒ n = 4
⇒ Amount doubles in 3 years
⇒ x = 3
Time = n × x
⇒ Time = 4 × 3 =12 years
∴ The amount will become 16 times in 12 years.
The C.I. on a certain sum for 2 years is Rs. 410 and S.I. is Rs. 400. What is the rate of interest per annum?
- a)10%
- b)8%
- c)5%
- d)4%
Correct answer is option 'C'. Can you explain this answer?
The C.I. on a certain sum for 2 years is Rs. 410 and S.I. is Rs. 400. What is the rate of interest per annum?
a)
10%
b)
8%
c)
5%
d)
4%
|
|
Kavya Saxena answered |
Simple interest for 1 year =400/2=200
CI of 1 year =200
CI for 2nd year=410-200=210
For 2nd year Amount=210 and P=200
A = P (1+R/100)1
210 = 200(1+R/100)
R=5%
CI of 1 year =200
CI for 2nd year=410-200=210
For 2nd year Amount=210 and P=200
A = P (1+R/100)1
210 = 200(1+R/100)
R=5%
A woman bought two packs of toffees, with the same of number of toffees in each pack. She bought the first pack at 25 paise per toffee and the second pack at 3 toffees for 65 paise. She mixed them together and sold at Rs.3.50 a dozen. What is her gain percent?
- a)15
- b)25
- c)
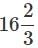
- d)12
Correct answer is option 'B'. Can you explain this answer?
A woman bought two packs of toffees, with the same of number of toffees in each pack. She bought the first pack at 25 paise per toffee and the second pack at 3 toffees for 65 paise. She mixed them together and sold at Rs.3.50 a dozen. What is her gain percent?
a)
15
b)
25
c)
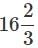
d)
12

|
Aniket Choudhary answered |
A woman bought 3 toffees at 25 paise each. So she spent 75 paise and 3 for 65 paise, then totally for 6 toffees she spent Rs.1.40 or for a dozen she spent
Rs.2.80 and sold the dozen at Rs.3.50.
∴ Gam
The price of a scooter was Rs 34,000 last year. It has increased by 20% this year. What is the price now?- a)Rs 30,800
- b)Rs 30,400
- c)Rs 40,800
- d)Rs 40,400
Correct answer is option 'C'. Can you explain this answer?
The price of a scooter was Rs 34,000 last year. It has increased by 20% this year. What is the price now?
a)
Rs 30,800
b)
Rs 30,400
c)
Rs 40,800
d)
Rs 40,400
|
|
Ujwal Mukherjee answered |
Understanding the Price Increase
To determine the current price of the scooter after a 20% increase, we start with the original price from last year, which was Rs 34,000.
Calculating the Price Increase
- Percentage Increase: The scooter has increased by 20%.
- Calculating 20% of Rs 34,000:
- 20% can be calculated as (20/100) * 34,000.
- This equals Rs 6,800.
Finding the New Price
- Adding the Increase to the Original Price:
- New Price = Original Price + Increase
- New Price = Rs 34,000 + Rs 6,800
- New Price = Rs 40,800
Conclusion
The current price of the scooter after a 20% increase is Rs 40,800. Therefore, the correct answer is option 'C'.
To determine the current price of the scooter after a 20% increase, we start with the original price from last year, which was Rs 34,000.
Calculating the Price Increase
- Percentage Increase: The scooter has increased by 20%.
- Calculating 20% of Rs 34,000:
- 20% can be calculated as (20/100) * 34,000.
- This equals Rs 6,800.
Finding the New Price
- Adding the Increase to the Original Price:
- New Price = Original Price + Increase
- New Price = Rs 34,000 + Rs 6,800
- New Price = Rs 40,800
Conclusion
The current price of the scooter after a 20% increase is Rs 40,800. Therefore, the correct answer is option 'C'.
The population of a city was 40,000 in the year 1999. It increased at the rate of 10% p.a. Find the population at the end of the year 2000.
- a)35000
- b)44000
- c)40000
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The population of a city was 40,000 in the year 1999. It increased at the rate of 10% p.a. Find the population at the end of the year 2000.
a)
35000
b)
44000
c)
40000
d)
None of these
|
|
Amit Kumar answered |
Population of the city in 1999 = 40,000 Percentage increased = 10% Therefore 10% of 40,000 = 10/100 × 40,000 = 4,000 Population of the city in 2000 = 40,000 + 4,000 = 44,000
The price of a car was Rs 3,40,000 last year. It has increased by 20% this year. What is the price now?
- a)Rs 4,00,400
- b)Rs 3,08,000
- c)Rs 4,08,000
- d)Rs 3,04,000
Correct answer is option 'C'. Can you explain this answer?
The price of a car was Rs 3,40,000 last year. It has increased by 20% this year. What is the price now?
a)
Rs 4,00,400
b)
Rs 3,08,000
c)
Rs 4,08,000
d)
Rs 3,04,000
|
|
Kavya Saxena answered |
Original price = 3,40,000
20% increase = 20/100 * 3,40000
= 68000
New price = 3,40,000 + 68000
= 4,08,000
Sohan bought a washing machine for Rs 40,000, then spent Rs 5,000 on its repairs and sold it for Rs 50,000. Find his loss or gain per cent.
- a)Loss 10%
- b)Loss 20%
- c)Profit 11.11%
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Sohan bought a washing machine for Rs 40,000, then spent Rs 5,000 on its repairs and sold it for Rs 50,000. Find his loss or gain per cent.
a)
Loss 10%
b)
Loss 20%
c)
Profit 11.11%
d)
none of these
|
|
Vivek Rana answered |
Cost price of washing machine = 40,000 + 5,000
= 45,000 Rs.
Selling price = Rs. 50,000
Gain = S.P. - C.P. = 50,000 - 45,000
5,000 Rs.
Therefore, Gain percent = (Gain * 100)/ C.P.
= (5,000 * 100)/ 45,000
= 11.11%
A sum of money, at compound interest, yields Rs. 200 and Rs. 220 at the end of first and second years respectively. What is the rate percent?
- a)20%
- b)15%
- c)10%
- d)5%
Correct answer is option 'C'. Can you explain this answer?
A sum of money, at compound interest, yields Rs. 200 and Rs. 220 at the end of first and second years respectively. What is the rate percent?
a)
20%
b)
15%
c)
10%
d)
5%

|
Akshara Iyer answered |
Step-by-step explanation:Step 1: Given DataLet r b... moree rate of interestP is initial sumCompound Interest of first year is Rs 200Second year is Rs.220Step
A shopkeeper purchased 300 bulbs for Rs 10 each. However 10 bulbs were fused and had to be thrown away. The remaining were sold at Rs 12 each. Find the gain or loss %.
- a)15%
- b)13%
- c)16%
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A shopkeeper purchased 300 bulbs for Rs 10 each. However 10 bulbs were fused and had to be thrown away. The remaining were sold at Rs 12 each. Find the gain or loss %.
a)
15%
b)
13%
c)
16%
d)
none of these
|
|
Vivek Rana answered |
Shopkeeper purchased 300 bulbs for ₹3000
If 10 bulbs were fused, the cost of 10 bulbs is ₹100
If he sell 290 bulbs as ₹12 each = 290×12 =3480
when he sell the the cost of each bulb as ₹12 he got ₹480 profit
As a percentage = 480÷3000×100=16
so he got 16% profit
If 10 bulbs were fused, the cost of 10 bulbs is ₹100
If he sell 290 bulbs as ₹12 each = 290×12 =3480
when he sell the the cost of each bulb as ₹12 he got ₹480 profit
As a percentage = 480÷3000×100=16
so he got 16% profit
Rohit bought a machine for Rs 20,000, then spent Rs 500 on its repairs and sold it for Rs 30,000. Find his loss or gain per cent.
- a)Loss 30%
- b)Profit 46.34%
- c)Loss 50%
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Rohit bought a machine for Rs 20,000, then spent Rs 500 on its repairs and sold it for Rs 30,000. Find his loss or gain per cent.
a)
Loss 30%
b)
Profit 46.34%
c)
Loss 50%
d)
none of these
|
|
Rohit Sharma answered |
Cost price of washing machine = 20,000 + 5,00
= 20,500 Rs.
Selling price = Rs. 30,000
Gain = S.P. - C.P. = 30,000 - 20,500
9,500 Rs.
Therefore, Gain percent = (Gain * 100)/ C.P.
= (9,500 * 100)/ 20,500
= 46.34%
The population of a city was 30,000 in the year 2011. It increased at the rate of 5% p.a. Find the population at the end of the year 2013.
- a)33000
- b)24000
- c)25000
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The population of a city was 30,000 in the year 2011. It increased at the rate of 5% p.a. Find the population at the end of the year 2013.
a)
33000
b)
24000
c)
25000
d)
none of these
|
|
Geetika Shah answered |
Population of the city in 2011 = 30,000
Percentage increased = 5%
Therefore 5% of 30,000 = 5/100 × 30,000 = 1,500
Population increased in 2 years = 1,500 × 2 = 3,000
Therefore population in 2013 = 30,000 + 3,000 = 33,000
A picnic is being planned in a school for Class VI. Girls are 40% of the total number of students and are 20 in number. Find the ratio of the number of girls to the number of boys in the class.
- a)It is 2:1
- b)It is 3:2
- c)It is 2:3
- d)It is 3:1
Correct answer is option 'C'. Can you explain this answer?
A picnic is being planned in a school for Class VI. Girls are 40% of the total number of students and are 20 in number. Find the ratio of the number of girls to the number of boys in the class.
a)
It is 2:1
b)
It is 3:2
c)
It is 2:3
d)
It is 3:1
|
|
Rohit Sharma answered |
Let the total no. of students be x.
No. of girls= 20
No. of boys = x-20
A. T. Q. ,
40% of x= 20
=> 40/100 × x = 20
=> x= 20× 100/40
=> x= 50
So, total no. of students = 50
No. of girls= 20
No. of boys = 50-20 = 30
Ratio of girls to boys = 20:30
= 20/30
=2/3
=2:3
No. of girls= 20
No. of boys = x-20
A. T. Q. ,
40% of x= 20
=> 40/100 × x = 20
=> x= 20× 100/40
=> x= 50
So, total no. of students = 50
No. of girls= 20
No. of boys = 50-20 = 30
Ratio of girls to boys = 20:30
= 20/30
=2/3
=2:3
During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at Rs 1450 and two shirts marked at Rs 850 each?- a)Rs 2,835
- b)Rs 2,735
- c)Rs 2,635
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at Rs 1450 and two shirts marked at Rs 850 each?
a)
Rs 2,835
b)
Rs 2,735
c)
Rs 2,635
d)
None of these
|
|
Rohit Sharma answered |
Given: MP (marked price) of 1 pair of jeans=₹1450
MP of 1 shirt= ₹850
Total Marked Price (MP) of a pair of jeans and two shirts
= 1450 + 2 x 850 = 3150
Total MP= ₹3150
Discount = Marked Price (MP) x % Discount
=3150 × (10/100)= ₹315
New Price After Discount = 3150 - 315 =₹ 2835
A customer would have to pay for a pair of jeans and two shirts =₹2835
The cost of a vehicle is Rs.175000. If its value depreciates at the rate of 20% per annum, find the total depreciation after 3 years.
- a)Rs.86400
- b)Rs.82500
- c)Rs.84500
- d)Rs.85400
Correct answer is option 'D'. Can you explain this answer?
The cost of a vehicle is Rs.175000. If its value depreciates at the rate of 20% per annum, find the total depreciation after 3 years.
a)
Rs.86400
b)
Rs.82500
c)
Rs.84500
d)
Rs.85400

|
Aniket Choudhary answered |
Value of the vehicle after 3 years 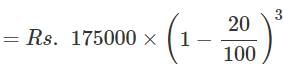
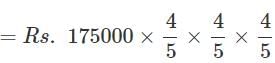
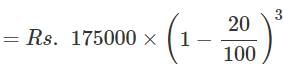
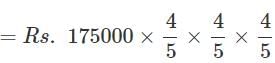
= Rs.89600
∴ Total depreciation
= Rs.(175000−89600)
= Rs.85400
The population of a city was 20,000 in the year 1997. It increased at the rate of 5% p.a. Find the population at the end of the year 2000.
- a)25153
- b)24153
- c)23153
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The population of a city was 20,000 in the year 1997. It increased at the rate of 5% p.a. Find the population at the end of the year 2000.
a)
25153
b)
24153
c)
23153
d)
None of these

|
Malavika Basu answered |
We have,
P = 20,000, R = 5%, T = 3 year
P = 20,000, R = 5%, T = 3 year
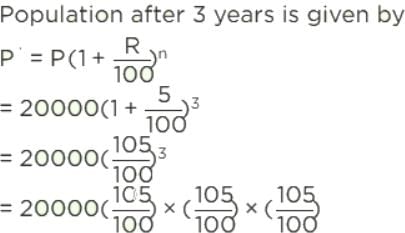
= 23153
The sale price of a shirt is Rs.176. If a discount of 20% is allowed on its marked price, what is the marked price of the shirt?
- a)Rs.160
- b)Rs.180
- c)Rs. 200
- d)Rs. 220
Correct answer is option 'D'. Can you explain this answer?
The sale price of a shirt is Rs.176. If a discount of 20% is allowed on its marked price, what is the marked price of the shirt?
a)
Rs.160
b)
Rs.180
c)
Rs. 200
d)
Rs. 220
|
|
Rohit Sharma answered |
Let x be the marked price
We know
Marked price (Mp)= selling price+discount %of Mp
x=176+20%of x
x=176+0.2x
x-0.2x=176
0.8x=176
x=176÷0.8
x=220
The marked price is Rs 220
Find the ratio of 5 m to 10 km.
- a)It is 1:3
- b)It is 3000:1
- c)It is 2000:1
- d)It is 1:2000
Correct answer is option 'D'. Can you explain this answer?
Find the ratio of 5 m to 10 km.
a)
It is 1:3
b)
It is 3000:1
c)
It is 2000:1
d)
It is 1:2000

|
Sanjana Bose answered |
5:10
covert 10km to meter
1km=1000m
10km= 10000m
so,
5:10000= 5/10000
= 1/2000 =1:2000
The C.I. on a certain sum for 2 years at 10% per annum is Rs. 525. Calculate the S.I. on the same sum for double the time at half the rate percent per annum.
- a)Rs. 400
- b)Rs. 500
- c)Rs. 600
- d)Rs. 800
Correct answer is option 'B'. Can you explain this answer?
The C.I. on a certain sum for 2 years at 10% per annum is Rs. 525. Calculate the S.I. on the same sum for double the time at half the rate percent per annum.
a)
Rs. 400
b)
Rs. 500
c)
Rs. 600
d)
Rs. 800
|
|
Aditya Shah answered |
Let the principal be 100x
First year interest = 10% = 10x
Second year interest =10% = 10/100 *110x =11x
Total interest = 21x
If interest is 21x , principal is 100x
If interest is Rs 525 , principal is = 525 /21x *100x = Rs 2500
Simple interest on Rs 2500 at 5% for 4 years is
2500 x 4 x 5/100= Rs500
The price of a car was Rs 5,00,000 last year. It has increased by 10% this year. What is the price now?- a)Rs 4,40,000
- b)Rs 5,50,000
- c)Rs 3,00,800
- d)Rs 3,00,400
Correct answer is option 'B'. Can you explain this answer?
The price of a car was Rs 5,00,000 last year. It has increased by 10% this year. What is the price now?
a)
Rs 4,40,000
b)
Rs 5,50,000
c)
Rs 3,00,800
d)
Rs 3,00,400
|
|
Aditya Shah answered |
As it was 5,00,000 initially, but now there is an increase of 10%.
so we calculate 10% of 5,00,000 that will be ₹50,000.
Then we have to calculate the new price of bike, (i.e. old + increased) = ₹5,00,000+₹50,000 = ₹5,50,000
so we calculate 10% of 5,00,000 that will be ₹50,000.
Then we have to calculate the new price of bike, (i.e. old + increased) = ₹5,00,000+₹50,000 = ₹5,50,000
The value of an article which was purchased 2 years ago, depreciates at 12% per annum. If its present value is Rs.9680, what is the price at which it was purchased?
- a)Rs.10000
- b)Rs.12500
- c)Rs.14575
- d)Rs.16250
Correct answer is option 'B'. Can you explain this answer?
The value of an article which was purchased 2 years ago, depreciates at 12% per annum. If its present value is Rs.9680, what is the price at which it was purchased?
a)
Rs.10000
b)
Rs.12500
c)
Rs.14575
d)
Rs.16250

|
Aniket Choudhary answered |
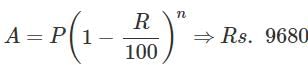
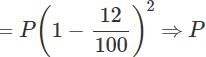
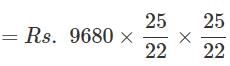
= Rs.12500
During a sale, a shop offered a discount of 10% on the marked price of all the items. What would a customer have to pay for a pair of jeans marked at ₹ 1450 and two shirts marked at ₹ 850 each?
- a)Rs 2,635
- b)Rs 2,835
- c)Rs 2,735
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
During a sale, a shop offered a discount of 10% on the marked price of all the items. What would a customer have to pay for a pair of jeans marked at ₹ 1450 and two shirts marked at ₹ 850 each?
a)
Rs 2,635
b)
Rs 2,835
c)
Rs 2,735
d)
None of these

|
Sanjana Bose answered |
Discount percentage = 10%
The marked price of a pair of jeans = ₹ 1450
Marked Price of a shirt = ₹ 850
(i) M.P. of a pair of jeans = C.P. of two jeans - Discount
(ii) M.P. of a shirt = C.P. of two shirts - Discount
Adding (i) and (ii) will give the amount he has to pay.
M.P of a pair of jeans = 1450
M.P of 2 shirts = 850 × 2 = 1700
Total M.P. = 1450 + 1700 = 3150
Discount on Total M.P =10% of 3150
= (10/100) × 3150
= 315
The amount customer has to pay is = Total M.P - Discount on total M.p
= 3150 - 315 = ₹ 2835
A picnic is being planned in a school. Girls are 60% of the total number of students and are 18 in number. Find the ratio of the number of girls to the number of boys in the class.- a)It is 3:2
- b)It is 3:1
- c)It is 2:3
- d)It is 2:1
Correct answer is option 'A'. Can you explain this answer?
A picnic is being planned in a school. Girls are 60% of the total number of students and are 18 in number. Find the ratio of the number of girls to the number of boys in the class.
a)
It is 3:2
b)
It is 3:1
c)
It is 2:3
d)
It is 2:1
|
|
Simran Bose answered |
Understanding the Problem
To find the ratio of girls to boys in the class, we start by analyzing the information given.
Step 1: Determine Total Students
- The problem states that girls make up 60% of the total number of students.
- We know there are 18 girls.
Step 2: Set Up the Equation
- Let the total number of students be represented as "T".
- According to the information provided, we can express this as:
- 60% of T = 18
- This translates to the equation: 0.6T = 18
Step 3: Solve for Total Students
- To find T, we can rearrange the equation:
- T = 18 / 0.6
- T = 30
Step 4: Calculate Number of Boys
- Now that we know the total number of students (T = 30), we can find the number of boys.
- Since girls are 18, we can calculate boys as follows:
- Number of boys = Total students - Number of girls
- Number of boys = 30 - 18 = 12
Step 5: Find the Ratio
- The ratio of the number of girls to boys is given by:
- Ratio = Number of girls : Number of boys
- Ratio = 18 : 12
Step 6: Simplify the Ratio
- To simplify the ratio, divide both numbers by their greatest common divisor (GCD), which is 6:
- Simplified ratio = (18 ÷ 6) : (12 ÷ 6) = 3 : 2
Conclusion
Thus, the ratio of the number of girls to the number of boys in the class is 3:2. Therefore, the correct answer is option 'A'.
To find the ratio of girls to boys in the class, we start by analyzing the information given.
Step 1: Determine Total Students
- The problem states that girls make up 60% of the total number of students.
- We know there are 18 girls.
Step 2: Set Up the Equation
- Let the total number of students be represented as "T".
- According to the information provided, we can express this as:
- 60% of T = 18
- This translates to the equation: 0.6T = 18
Step 3: Solve for Total Students
- To find T, we can rearrange the equation:
- T = 18 / 0.6
- T = 30
Step 4: Calculate Number of Boys
- Now that we know the total number of students (T = 30), we can find the number of boys.
- Since girls are 18, we can calculate boys as follows:
- Number of boys = Total students - Number of girls
- Number of boys = 30 - 18 = 12
Step 5: Find the Ratio
- The ratio of the number of girls to boys is given by:
- Ratio = Number of girls : Number of boys
- Ratio = 18 : 12
Step 6: Simplify the Ratio
- To simplify the ratio, divide both numbers by their greatest common divisor (GCD), which is 6:
- Simplified ratio = (18 ÷ 6) : (12 ÷ 6) = 3 : 2
Conclusion
Thus, the ratio of the number of girls to the number of boys in the class is 3:2. Therefore, the correct answer is option 'A'.
A shopkeeper purchased 500 pieces for Rs 20 each. However 50 pieces were spoiled in the way and had to be thrown away. The remaining were sold at Rs 25 each. Find the gain or loss %.
- a)18%
- b)15%
- c)12.5%
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A shopkeeper purchased 500 pieces for Rs 20 each. However 50 pieces were spoiled in the way and had to be thrown away. The remaining were sold at Rs 25 each. Find the gain or loss %.
a)
18%
b)
15%
c)
12.5%
d)
none of these
|
|
Sai Chopra answered |
Given:
Number of pieces purchased = 500
Cost price per piece = Rs 20
Number of spoiled pieces = 50
Selling price per piece = Rs 25
To find: Gain or loss %
Solution:
1. Total cost price:
Cost price per piece * Number of pieces purchased = Rs 20 * 500 = Rs 10,000
2. Total selling price:
Number of remaining pieces = Number of pieces purchased - Number of spoiled pieces = 500 - 50 = 450
Selling price per piece * Number of remaining pieces = Rs 25 * 450 = Rs 11,250
3. Profit or loss:
Profit or loss = Total selling price - Total cost price = Rs 11,250 - Rs 10,000 = Rs 1,250
4. Gain or loss %:
Gain or loss % = (Profit or loss / Total cost price) * 100
= (1250 / 10000) * 100
= 12.5%
Therefore, the gain or loss percentage is 12.5%.
Hence, option C is the correct answer.
Number of pieces purchased = 500
Cost price per piece = Rs 20
Number of spoiled pieces = 50
Selling price per piece = Rs 25
To find: Gain or loss %
Solution:
1. Total cost price:
Cost price per piece * Number of pieces purchased = Rs 20 * 500 = Rs 10,000
2. Total selling price:
Number of remaining pieces = Number of pieces purchased - Number of spoiled pieces = 500 - 50 = 450
Selling price per piece * Number of remaining pieces = Rs 25 * 450 = Rs 11,250
3. Profit or loss:
Profit or loss = Total selling price - Total cost price = Rs 11,250 - Rs 10,000 = Rs 1,250
4. Gain or loss %:
Gain or loss % = (Profit or loss / Total cost price) * 100
= (1250 / 10000) * 100
= 12.5%
Therefore, the gain or loss percentage is 12.5%.
Hence, option C is the correct answer.
A man bought 542 kg of sugar for Rs. 7560.90and sold it so as to gain 20%. What is the selling price per kilogram of sugar?
- a)Rs. 16.74
- b)Rs. 22.92
- c)Rs. 31.46
- d)Rs. 12.24
Correct answer is option 'A'. Can you explain this answer?
A man bought 542 kg of sugar for Rs. 7560.90and sold it so as to gain 20%. What is the selling price per kilogram of sugar?
a)
Rs. 16.74
b)
Rs. 22.92
c)
Rs. 31.46
d)
Rs. 12.24

|
Aniket Choudhary answered |
The cost of sugar per kilogram 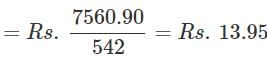
S.P. = C.P.(1 + gain%) S.P. at 20% profit = Rs.13.95 × 1.2 = Rs.16.74
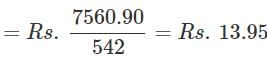
S.P. = C.P.(1 + gain%) S.P. at 20% profit = Rs.13.95 × 1.2 = Rs.16.74
________ means comparing two quantities.- a)Ratio
- b)Proportion
- c)Percent
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
________ means comparing two quantities.
a)
Ratio
b)
Proportion
c)
Percent
d)
None of these

|
Sounak Sengupta answered |
A ratio is a relationship between two numbers indicating how many times the first number contains the second.For example, if a bowl of fruit contains eight oranges and six lemons, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ratio 4:3). Similarly, the ratio of lemons to oranges is 6:8 (or 3:4) and the ratio of oranges to the total amount of fruit is 8:14 (or 4:7).
Find the amount on Rs.12500 for 2 years compounded annually, the rate of interest being 15% for the first year and 16% for the second year.
- a)Rs.16500
- b)Rs.16750
- c)Rs.16675
- d)Rs.16275
Correct answer is option 'C'. Can you explain this answer?
Find the amount on Rs.12500 for 2 years compounded annually, the rate of interest being 15% for the first year and 16% for the second year.
a)
Rs.16500
b)
Rs.16750
c)
Rs.16675
d)
Rs.16275
|
|
Maheshwar Singh answered |
Given:
Principal amount (P) = Rs.12500
Rate of interest for the first year (R1) = 15%
Rate of interest for the second year (R2) = 16%
Time (T) = 2 years
To find:
Amount after 2 years compounded annually
Solution:
To find the amount after 2 years compounded annually, we can use the formula for compound interest:
Amount (A) = P(1 + R/100)^T
Where,
A = Amount after T years
P = Principal amount
R = Rate of interest
T = Time in years
Calculation:
For the first year:
Principal amount (P1) = Rs.12500
Rate of interest (R1) = 15%
Time (T1) = 1 year
Amount after the first year (A1) = P1(1 + R1/100)^T1
= 12500(1 + 15/100)^1
= 12500(1 + 0.15)
= 12500(1.15)
= Rs.14375
Now, for the second year:
Principal amount (P2) = A1 (amount after the first year)
= Rs.14375
Rate of interest (R2) = 16%
Time (T2) = 1 year
Amount after the second year (A2) = P2(1 + R2/100)^T2
= 14375(1 + 16/100)^1
= 14375(1 + 0.16)
= 14375(1.16)
= Rs.16675
Therefore, the amount after 2 years compounded annually is Rs.16675.
Hence, the correct answer is option 'C' Rs.16675.
Principal amount (P) = Rs.12500
Rate of interest for the first year (R1) = 15%
Rate of interest for the second year (R2) = 16%
Time (T) = 2 years
To find:
Amount after 2 years compounded annually
Solution:
To find the amount after 2 years compounded annually, we can use the formula for compound interest:
Amount (A) = P(1 + R/100)^T
Where,
A = Amount after T years
P = Principal amount
R = Rate of interest
T = Time in years
Calculation:
For the first year:
Principal amount (P1) = Rs.12500
Rate of interest (R1) = 15%
Time (T1) = 1 year
Amount after the first year (A1) = P1(1 + R1/100)^T1
= 12500(1 + 15/100)^1
= 12500(1 + 0.15)
= 12500(1.15)
= Rs.14375
Now, for the second year:
Principal amount (P2) = A1 (amount after the first year)
= Rs.14375
Rate of interest (R2) = 16%
Time (T2) = 1 year
Amount after the second year (A2) = P2(1 + R2/100)^T2
= 14375(1 + 16/100)^1
= 14375(1 + 0.16)
= 14375(1.16)
= Rs.16675
Therefore, the amount after 2 years compounded annually is Rs.16675.
Hence, the correct answer is option 'C' Rs.16675.
The difference in S.I. and C.I. on a certain sum of money in 2 years at 15% p.a. is Rs.144. Find the sum.- a)Rs. 6000
- b)Rs. 6200
- c)Rs. 6300
- d)Rs. 6400
Correct answer is option 'D'. Can you explain this answer?
The difference in S.I. and C.I. on a certain sum of money in 2 years at 15% p.a. is Rs.144. Find the sum.
a)
Rs. 6000
b)
Rs. 6200
c)
Rs. 6300
d)
Rs. 6400

|
Trisha Vashisht answered |
The problem involves finding the principal (sum of money) when the difference between Simple Interest (S.I.) and Compound Interest (C.I.) for 2 years at a rate of 15% p.a. is given as Rs. 144.
Formula for the difference between S.I. and C.I. for 2 years:
Formula for the difference between S.I. and C.I. for 2 years:
Difference = P × (R/100)²
Where:
P = Principal (sum of money to find)
R = Rate of interest (15% = 15/100 = 0.15)
Difference = Rs. 144 (given)
Substituting values into the formula:
144 = P × (0.15)²
144 = P × 0.0225
P = 144 / 0.0225
P = 6400
Final Answer:
The principal (sum of money) is Rs. 6400, which matches Option d).
Formula for the difference between S.I. and C.I. for 2 years:
Formula for the difference between S.I. and C.I. for 2 years:
Difference = P × (R/100)²
Where:
P = Principal (sum of money to find)
R = Rate of interest (15% = 15/100 = 0.15)
Difference = Rs. 144 (given)
Substituting values into the formula:
144 = P × (0.15)²
144 = P × 0.0225
P = 144 / 0.0225
P = 6400
Final Answer:
The principal (sum of money) is Rs. 6400, which matches Option d).
The present population of a town is 25000. It grows at 4%, 5% and 8% during first year, second year and third year respectively. Find the population after 3 years.- a)29484
- b)28696
- c)24576
- d)30184
Correct answer is option 'A'. Can you explain this answer?
The present population of a town is 25000. It grows at 4%, 5% and 8% during first year, second year and third year respectively. Find the population after 3 years.
a)
29484
b)
28696
c)
24576
d)
30184

|
EduRev Class 8 answered |
Population after n years is calculated as:
Pn = P0 × (1 + r1) × (1 + r2) × (1 + r3)
Where:
- P0 is the initial population,
- r1, r2, r3 are the growth rates for each year.
Given:
- Initial population P0 = 25000
- Growth rates:
- Year 1: 4% = 0.04
- Year 2: 5% = 0.05
- Year 3: 8% = 0.08
Now, we can calculate the population after each year:
Year 1:
Population after Year 1 = 25000 × (1 + 0.04) = 25000 × 1.04 = 26000
Year 2:
Population after Year 2 = 26000 × (1 + 0.05) = 26000 × 1.05 = 27300
Year 3:
Population after Year 3 = 27300 × (1 + 0.08) = 27300 × 1.08 = 29484
Chapter doubts & questions for Ratios, Proportions, Percentages and Rates - Mathematics for JSS 2 2025 is part of JSS 2 exam preparation. The chapters have been prepared according to the JSS 2 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JSS 2 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Ratios, Proportions, Percentages and Rates - Mathematics for JSS 2 in English & Hindi are available as part of JSS 2 exam.
Download more important topics, notes, lectures and mock test series for JSS 2 Exam by signing up for free.
Mathematics for JSS 2
83 videos|193 docs|36 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

 Thus, the price now is 40,800 Rs.
Thus, the price now is 40,800 Rs.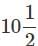

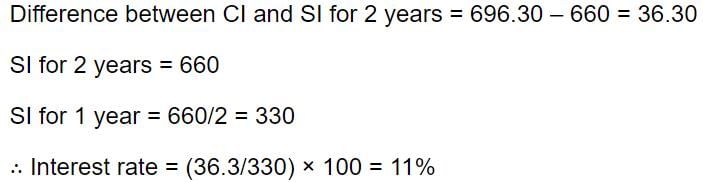
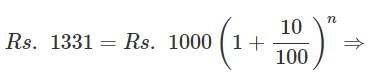
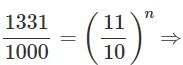
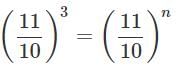
 ?
?