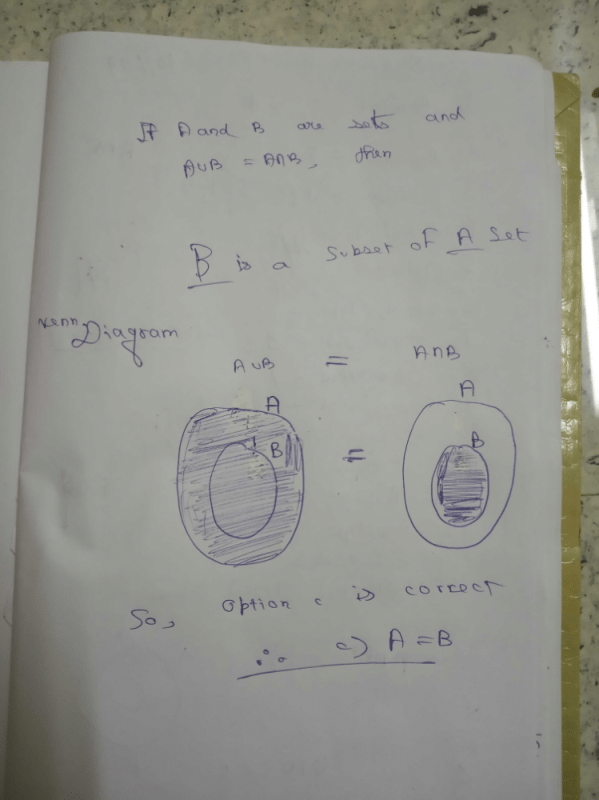Explore Exams
Login Signup
Sign in Open App
All Exams  >   JAMB  >   Mathematics for JAMB  >   All Questions

All questions of Sets for JAMB Exam

Clear all your doubts with EduRev

Let R be a non-empty relation on a collection of sets defined by ARB if and only if A  ∩ B = Ø
Then (pick the TRUE statement) 
  • a)
    R is relexive and transitive
  • b)
    R is symmetric and not transitive
  • c)
    R is an equivalence relation
  • d)
    R is not relexive and not symmetric
Correct answer is option 'B'. Can you explain this answer?

Vivek Patel answered
The correct answer is B 
Let, A={1,2,3}
B={4,5} 
C={1,6,7}

now, A∩B=∅ 
B∩C=∅ but  A∩C≠∅
Relation R is not transitive.
A∩A=A
R is not reflexive.
A∩B=B∩A
R is symmetric
So, 
A is false as R is not reflexive or transitive
B is true.
C is false because R is not transitive or reflexive
D is false because R is symmetric

 If R = ((1, 1), (3, 1), (2, 3), (4, 2)), then which of the following represents R2, where R2 is R composite R?
  • a)
    ((1, 1), (3, 1), (2, 3), (4, 2))
  • b)
    f(1, 1), (9, 1), (4, 9), (16, 4))
  • c)
    1(1, 3), (3, 3), (3, 4), (3, 2))
  • d)
    ((1, 1), (2, 1), (4, 3), (3, 1))
Correct answer is option 'D'. Can you explain this answer?

EduRev CAT answered
The correct answer is D as
 R = ((1, 1), (3, 1), (2, 3), (4, 2))
RoR=R2=((1, 1), (3, 1), (2, 3), (4, 2))((1, 1), (3, 1), (2, 3), (4, 2))
     =((1, 1), (3, 1), (2, 1), (4, 3))
take the first set (1,1) then take the second element of this subset check in the other set R is there any starting with 1 if yes then take its second element and make a subset in R2 similarly check for all.
like (4,2) (2,3)=(4,3)in R2

Let R be a relation "(x -y) is divisible by m", where x, y, m are integers and m > 1, then R is
  • a)
    symmetric but not transitive
  • b)
    partial order
  • c)
    equivalence relation
  • d)
    anti symmetric and not transitive
Correct answer is option 'C'. Can you explain this answer?

Nikita Singh answered
a) Since x - x = 0, m
=> x - x is divisible by m
(x,x) ∈ R
=> R is reflexive
b) Let (x,y) ∈ R
=> x - y = mq for some q ∈ I
=> y - x = m(-q)
y - x is divisible by m
(y,x) ∈ R
=> R is symmetric.
c) Let (x,y) and (y,z) ∈ R
=> x - y is divisible by m and y - z is divisible by m
=> x - y = mq and y - z = mq' for some q, q' ∈ I
=>(x-y)+(y-z) = m(q+q')
=> x - z = m(q + q'), q + q' ∈ I
(x,z) ∈ R
=> R is transitive.
Hence the relation is equivalence relation.

"n/m" means that n is a factor of m, then the relation T is
  • a)
    relexive and symmetric
  • b)
    transitive and symmetric
  • c)
    relexive, transitive and symmetric
  • d)
    relexive, transitive and not symmetric
Correct answer is option 'D'. Can you explain this answer?

Anaya Patel answered
′/′ is reflexive since every natural number is a factor of itself that in n/n for n∈N.
′/′ is transitive if n is a factor of m and m is a factor of P, then n is surely a factor of P.
However, ′/′ is not symmetric.
example, 2 is a factor of 4 but 4 is not a factor of 2. 

In a class of 50 students, 70% students pass in QA and 60% pass in RC. What is the minimum percentage of students who pass in both the papers?
  • a)
    30%
  • b)
    40%
  • c)
    25%
  • d)
    50%
Correct answer is option 'A'. Can you explain this answer?

Gargi Kulkarni answered
We know that n (A∪B ) = n(A ) + n(B) - n(A∩B) 
Assuming that n(Q) = number of students passing QA and n(R) = number of students passing RC.
Hence, n(Q∪R ) = n(Q) + n(R) - n(Q∩R)
Or, n(Q∩R) = n(Q) + n(R) - n(Q∪R) = 70% + 60% - n(Q∪R)
Now the minimum value of n(Q∩R) will occur for the maximum value of n(Q∪R).
The maximum possible value of n(Q∪R) = 100%
So, the minimum value of n(Q∩R) = 30%
 

The number of elements in the power set of the set {{a, b}, c} is
  • a)
    8
  • b)
    4
  • c)
    3
  • d)
    7
Correct answer is option 'B'. Can you explain this answer?

Elite Coaching Classes answered
We can simply solve this problem by using the following mathematical process.
A power set is defined as the set or group of all subsets for any given set, including the empty set.  A set that has 'n' elements has 2n subsets in all.
The power set is denoted by the notation P(S) and the number of elements of the power set is given by 2n.
In the given set, the number of elements is 2
Therefore, in the power set, the number of elements will be
Hence, The number of elements in the power set of the set {{a,b},c} is 4.

Which of the following sets are null sets ?
  • a)
    {0}
  • b)
    ø
  • c)
    { }
  • d)
    Both (b) & (c)
Correct answer is option 'D'. Can you explain this answer?

Aarav Sharma answered
The question seems to be incomplete as option (b) is not provided. Please provide the complete options to answer the question.

The number of elements in the Power set P(S) of the set S = {{1,2}, {2,3}, {2,4}} is given by
  • a)
    2
  • b)
    4
  • c)
    8
  • d)
    none of these
Correct answer is option 'C'. Can you explain this answer?

Rohini S. answered
No of elements in a Power set = 2^N       (where N is the no. of elements in a set)
                                                 = 2^3
                                                  =8

A survey on a sample of 25 new cars being sold at a local auto dealer was conducted to see which of the three popular options—air conditioning, radio and power windows—were already installed. The survey found:
15 had air conditioning
2 had air conditioning and power windows but no radios
12 had radio
6 had air conditioning and radio but no power windows
11 had power windows
4 had radio and power windows
3 had all three options
What is the number of cars that had none of the options?
  • a)
    4
  • b)
    3
  • c)
    1
  • d)
    2
Correct answer is option 'D'. Can you explain this answer?

Aarav Sharma answered
Were most commonly chosen by buyers. The three options being considered were: leather seats, sunroof, and navigation system. The survey asked buyers if they had chosen any of these options when purchasing their new car. The results of the survey are as follows:

- 12 out of 25 buyers chose leather seats
- 9 out of 25 buyers chose a sunroof
- 8 out of 25 buyers chose a navigation system

Based on these results, it can be concluded that leather seats were the most commonly chosen option by buyers, followed by a sunroof and then a navigation system.

Directions for Questions 1 to 3:    
Refer to the data  below and answer  the questions that  follow.
Last year, there were 3 sections in the Catalyst, a mock CAT paper. Out of them 33  students cleared the cut-off in Section 1, 34 students cleared the cut-off in Section 2 and 32 cleared the cut-off in Section 3. 10 students cleared the cut-off in Section 1 and Section 2, 9 cleared the cut-off in Section 2 and Section 3, 8 cleared the cut-off in Section 1 and Section 3. The number of people who cleared each section alone wasequal and was 21 for each section.
How many cleared all the three sections?
  • a)
    3
  • b)
    6
  • c)
    5
  • d)
    7
Correct answer is option 'B'. Can you explain this answer?

Gargi Kulkarni answered
since x = 6 , the figure becomes:
The answer would be :
6. option (B) is correct

How many numbers from 1 to 100 are not divisible by either 2 or 4 or 5?
  • a)
    30
  • b)
    40
  • c)
    25
  • d)
    45
Correct answer is option 'B'. Can you explain this answer?

Rajdeep Ghoshal answered
Let us first understand the meaning of the statement given in the question—
It is given that the numbers are from 1 to 100, so while counting we will include both the limits, i.e., 1 and 100. Had this been “How many numbers in between 1 to 100 are..." then we would not have included either 1 or 100.
Now to solve this question, we will first find out the number of numbers from 1 to 100 which are divisible by either 2 or 5 (since all the numbers which are not divisible by 2 will not be divisible by 4 also, so we do not need to find the numbers divisible by 4). And then we will subtract this from the total number of numbers i.e., 100. It can be seen below:
Total number of numbers = numbers which are divisible + numbers which are not divisible
So, n(2U5) = n(2) + n(5) - n (2∩5)
Now, n(2) = 50 
n(5) = 20 
n(2∩5) = 10
n(2U5) = 50 + 20 - 10 = 60
Numbers which are not divisible = total number of numbers-numbers which are divisible
=100 - 60 = 40

Directions: 
In a locality having 1500  households, 1000 watch Zee TV, 300 watch NDTV and 750 watch Star Plus.
Based on this information answer the questions that follow:
The minimum number of  households watching both Zee TV and NDTV is:
 
  • a)
    250
  • b)
    300
  • c)
    450
  • d)
    0
Correct answer is option 'D'. Can you explain this answer?

Sagar Sharma answered
The minimum number of households watching both Zee TV and NDTV can be found by identifying the overlapping number of households between the two channels.

Given information:
- Total number of households in the locality: 1500
- Number of households watching Zee TV: 1000
- Number of households watching NDTV: 300
- Number of households watching Star Plus: 750

To find the minimum number of households watching both Zee TV and NDTV, we need to find the intersection between these two groups.

Finding the intersection:
- Subtract the number of households watching Star Plus from the total number of households to find the number of households not watching Star Plus: 1500 - 750 = 750
- Subtract the number of households watching NDTV from the number of households not watching Star Plus to find the number of households not watching NDTV: 750 - 300 = 450
- Subtract the number of households not watching NDTV from the number of households not watching Star Plus to find the number of households watching NDTV: 750 - 450 = 300

Therefore, the minimum number of households watching both Zee TV and NDTV is 300.

The correct answer is option 'D'.

Explanation:
- The minimum number of households watching both Zee TV and NDTV can be found by taking the intersection of the two groups.
- By subtracting the number of households watching Star Plus from the total number of households, we find the number of households not watching Star Plus.
- By subtracting the number of households watching NDTV from the number of households not watching Star Plus, we find the number of households not watching NDTV.
- Finally, by subtracting the number of households not watching NDTV from the number of households not watching Star Plus, we find the number of households watching NDTV.
- Therefore, the minimum number of households watching both Zee TV and NDTV is 300.

In a class of 50 students, 70% students pass in QA, 90% pass in EU, 85% pass in DI and 60% pass in RC. What is the minimum percentage of students who pass in all the papers?
  • a)
    3%
  • b)
    4%
  • c)
    5%
  • d)
    8%
Correct answer is option 'C'. Can you explain this answer?

Aarav Sharma answered
Solution:

To find out the minimum percentage of students who pass in all the papers, we need to find out the intersection of all the percentages.

QA = 70%
EU = 90%
DI = 85%
RC = 60%

Step 1: Find out the percentage of students who passed in at least one subject.

Percentage of students who passed in at least one subject = QA + EU + DI + RC - (Sum of any two) - (Sum of three) + (All four)

= 70 + 90 + 85 + 60 - (70 + 90) - (70 + 85 + 90) + (70 + 85 + 90 + 60)

= 305%

Step 2: Find out the percentage of students who passed in all four subjects.

Let the percentage of students who passed in all four subjects be x%.

So, we have

x% + Percentage of students who passed in at least one subject = 100%

Or, x% + 305% = 100%

Or, x% = 100% - 305%

Or, x% = -205%

Since x% cannot be negative, we can conclude that the percentage of students who passed in all four subjects is 0% (or more than 0%, but less than the minimum passing percentage in any of the four subjects).

Step 3: Find out the minimum percentage of students who pass in all the papers.

As we know that the intersection of all the percentages cannot be less than 0%, we can conclude that the minimum percentage of students who pass in all the papers is greater than 0%.

The options are 3%, 4%, 5%, and 8%.

Out of these options, the minimum percentage of students who pass in all the papers is 5%, which is the correct answer.

Therefore, the correct answer is option (c) 5%.

Last year, there were 3 sections in the Catalyst, a mock CAT paper. Out of them 33  students cleared the cut-off in Section 1, 34 students cleared the cut-off in Section 2 and 32 cleared the cut-off in Section 3. 10 students cleared the cut-off in Section 1 and Section 2, 9 cleared the cut-off in Section 2 and Section 3, 8 cleared the cut-off in Section 1 and Section 3. The numberof people who cleared each section alone wasequal and was 21 for each section.
The ratio of  the number of students clearing then cut-off in one or  more of  the sections to     the number of  students clearing the cutoff  in Section 1 alone is?
  • a)
    78/21
  • b)
    3
  • c)
    73/21
  • d)
    none of these
Correct answer is option 'A'. Can you explain this answer?

Madhurima Dey answered
(21+ 21 +21 +6+4+3+2)/21 = 78/21
Option (A) is correct
 

In a group of 120  athletes, the number of athletes who can  play Tennis, Badminton, Squash and Table Tennis is 70, 50, 60 and 30 respectively. What is the maximum number   of athletes who can play none of the games
  • a)
    40
  • b)
    50
  • c)
    60
  • d)
    70
Correct answer is option 'B'. Can you explain this answer?

Aarav Sharma answered
Given Information:
- Total number of athletes = 120
- Number of athletes who can play Tennis = 70
- Number of athletes who can play Badminton = 50
- Number of athletes who can play Squash = 60
- Number of athletes who can play Table Tennis = 30

To find:
The maximum number of athletes who can play none of the games.

Solution:
To find the maximum number of athletes who can play none of the games, we need to determine the number of athletes who can play at least one game and then subtract it from the total number of athletes.

Number of Athletes who can play at least one game:
To find the number of athletes who can play at least one game, we need to find the sum of athletes who can play each game individually and then subtract the athletes who can play multiple games to avoid double counting.

- Number of athletes who can play Tennis = 70
- Number of athletes who can play Badminton = 50
- Number of athletes who can play Squash = 60
- Number of athletes who can play Table Tennis = 30

Number of athletes who can play more than one game:
To find the number of athletes who can play more than one game, we need to find the intersection between different sets of athletes who can play each game.

- Number of athletes who can play Tennis and Badminton = 0 (Given)
- Number of athletes who can play Tennis and Squash = 0 (Given)
- Number of athletes who can play Tennis and Table Tennis = 0 (Given)
- Number of athletes who can play Badminton and Squash = 0 (Given)
- Number of athletes who can play Badminton and Table Tennis = 0 (Given)
- Number of athletes who can play Squash and Table Tennis = 0 (Given)

Calculating the number of athletes who can play at least one game:
We can calculate the number of athletes who can play at least one game by summing up the individual games and subtracting the athletes who can play more than one game.

Total athletes who can play at least one game = (Number of athletes who can play Tennis) + (Number of athletes who can play Badminton) + (Number of athletes who can play Squash) + (Number of athletes who can play Table Tennis) - (Number of athletes who can play more than one game)

Total athletes who can play at least one game = 70 + 50 + 60 + 30 - (0 + 0 + 0 + 0 + 0 + 0)

Total athletes who can play at least one game = 210

Calculating the maximum number of athletes who can play none of the games:
The maximum number of athletes who can play none of the games can be calculated by subtracting the number of athletes who can play at least one game from the total number of athletes.

Maximum number of athletes who can play none of the games = Total number of athletes - Total athletes who can play at least one game

Maximum number of athletes who can play none of the games = 120 - 210

Maximum number of athletes who can play none of the games = -90

Since the number of athletes cannot be negative, the maximum number of athletes who

Directions: 
In a locality having 1500  households, 1000 watch Zee TV, 300 watch NDTV and 750 watch Star Plus.
Based on this information answer the questions that follow:
The maximum number of  households who watch neither of the three channels is:
  • a)
    600
  • b)
    450
  • c)
    500
  • d)
    400
Correct answer is option 'C'. Can you explain this answer?

Shilpa Nambiar answered
For this  to occur  the following situation would give us the required solution:
As you can clearly see from the figure, all the requirements of each category of viewers is fulfilled by the given allocation of 1000 households. In this situation,the maximum number of households who do not watch any of the three channels is visible as 1500 –1000 = 500.

In a class of 50 students, 70% students pass in QA, 90% pass in EU and 60% pass in RC. What is the minimum percentage of students who pass in all the papers?
 
  • a)
    15%
  • b)
    30%
  • c)
    40%
  • d)
    20%
Correct answer is option 'D'. Can you explain this answer?

Madhurima Dey answered
We can do this question by using either the formula for three sets, or we can simply keep on applying the formula for two sets required a number of times.
We know that n(A∪B) = n (A ) + n(B) - n(A∩B)
Assuming that n(Q) = number of students passing QA, n(E) = number of students passing EU and n(R) = number of students passing RC
Hence, n(Q∪R) = n(Q) + n(R) - n(Q∩R).
Or, n(Q∩R) = n(Q) + n(R) - n(QuR) = 70% + 60% - n(Q∪R)
Now the minimum value of n(Q∩R) will occur for the maximum value of n(Q∪R). The maximum possible value of n(Q∪R) =100%
So, the minimum value of n(Q∩R) = 30%
Now, the minimum value of EU, QA and RC will be obtained by finding the minimum of EU and (QA∩RC).
The minimum value of EU and (QA∩RC) = 90% + 30% - 100% = 20%
 

The set of all Equivalence classes of a set A of cardinality C
  • a)
    has the same cardinality as A
  • b)
    forms a partition of A
  • c)
    is of cardinality 2C
  • d)
    is of cardinality C2
Correct answer is option 'B'. Can you explain this answer?

Meera Rana answered
The equivalence classes of any equivalence relation on A partition A. There's no need to talk about cardinalities to know this; that's just the fact that equivalence relations are equivalent to partitions.

If A is the natural numbers, and we take just one equivalence class (all of A), then a), b), d) claim that there are infinitely many equivalence classes. But there's just one.

If  f : X -> Y and a, b  ⊆ X, then f (a  ∩ b) is equal to
  • a)
    f(a) - f(b)
  • b)
    f(a) ∩ f(b)
  • c)
    a proper subset of f(a) ∩ f(b)
  • d)
    f(b) - f(a)
Correct answer is option 'C'. Can you explain this answer?

Arya Roy answered
The only requirement to answer the above question is to know the definition of function- a relation becomes a function if every element in domain is mapped to some element in co-domain and no element is mapped to more than one element.

Now, we have a,b⊆ X. Their intersection can be even empty set. So, lets try out options:

Options a and d don't even need a check.

Lets take a case where a∩b = φ. Now, f(a∩b)=φ, but f(a) ∩ f(b) can be non empty. So, option B can be false.

Option C is always true provided "proper subset" is replaced by "subset". This is because no element in domain of a function can be mapped to more than one element. And the subset needn't be "proper" as for a one-one mapping, we get
f(a∩b) = f(a) ∩ f(b) ,Hence option C

Directions: 
In a locality having 1500  households, 1000 watch Zee TV, 300 watch NDTV and 750 watch Star Plus.
Based on this information answer the questions that follow:
The minimum number of households watching Zee TV and Star Plus is:
  • a)
    300
  • b)
    250
  • c)
    275
  • d)
    350
Correct answer is option 'B'. Can you explain this answer?

Madhurima Dey answered
If we try to consider each of the households watching Zee TV and   StarPlus as independent of  each   other, we would get a total of 1000 + 750 = 1750 households.However, wehave a totalof only1500 householdsi the locality and hence, there has to be a minimum interference of atleast 250 households whowould  be watching both Zee TV and Star Plus. Hence, the answer to this question is 250.

At    the    birthday    party    of    Sherry,    a    baby    boy,    40    persons    chose    to    kiss   him    and    25    chose    to    shake    hands with    him.    10    persons    chose    to    both   kiss    him    and    shake    hands    with    him.    How    many    persons    turned    out    at the    party?
 
  • a)
    35
  • b)
    75
  • c)
    55
  • d)
    25
Correct answer is option 'C'. Can you explain this answer?

Prisha Shah answered
Explanation: 
From the figure, it is clear that the number of  people at  the party were,
30 + 10 + 15 = 55.
We can of course solve this mathematically as below:
Let  n(A) = No. of persons who kissed Sherry = 40
n(B) = No. of persons who shake hands with Sherry = 25
and n(A > B) = No. of   persons who shook  hands with Sherry and kissed him    both =10

Then using  the formula, n(A > B) = n(A) + n(B) -n(A > B)
n(A > B) = 40 + 25 - 10 = 55
Hence, correct answer is 55.
You can know about Important Formulas related to Set Theory through the document:  

Order of the power set of a set of order n is
  • a)
    n
  • b)
    2n
  • c)
    n2
  • d)
    2n
Correct answer is option 'D'. Can you explain this answer?

Rcha answered
It's a standard (proven) equation.You can find explanation in +2 Book.Honestly I don't remember the way.

Chapter doubts & questions for Sets - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Sets - Mathematics for JAMB in English & Hindi are available as part of JAMB exam. Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.

Mathematics for JAMB

134 videos|94 docs|102 tests

Top Courses JAMB

© EduRev
Education Revolution
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily