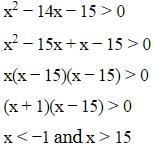All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Inequalities for JAMB Exam
For all integral values of x,|x - 4| x< 5- a)-1 ≤x≤5
- b)1 ≤x≤5
- c)-1 ≤ x ≤ 1
- d)x<5
Correct answer is option 'D'. Can you explain this answer?
For all integral values of x,
|x - 4| x< 5
a)
-1 ≤x≤5
b)
1 ≤x≤5
c)
-1 ≤ x ≤ 1
d)
x<5
|
Preeti Khanna answered |
At x = 0 inequality is satisfied, option (b) is rejected.
At x = 2, inequality is satisfied, option (c) is rejected.
At x = 5, LHS = RHS.
Thus, option (d) is correct.
3x2 - 7x + 6 < 0- a)0.66 <x< 3
- b)-0.66 <x< 3
- c)-1 < x < 3
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
3x2 - 7x + 6 < 0
a)
0.66 <x< 3
b)
-0.66 <x< 3
c)
-1 < x < 3
d)
None of these
|
Avik Choudhury answered |
At x = 0, inequality is not satisfied.
Hence, options (b), (c) and (d) are rejected. At x = 2, inequality is not satisfied. Hence, option (a) is rejected.
Thus, option (d) is correct.
Hence, options (b), (c) and (d) are rejected. At x = 2, inequality is not satisfied. Hence, option (a) is rejected.
Thus, option (d) is correct.
x2 - 7x + 12 < | x - 4 |- a)x < 2
- b)x > 4
- c)2 < x < 4
- d)2 ≤ x ≤ 4
Correct answer is option 'C'. Can you explain this answer?
x2 - 7x + 12 < | x - 4 |
a)
x < 2
b)
x > 4
c)
2 < x < 4
d)
2 ≤ x ≤ 4
|
Harsh Jain answered |
At x = 0, inequality is not satisfied, option (a) is rejected.
At x = 5, inequality is not satisfied, option (b) is rejected.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct.
|x2 – 2x – 3| < 3x – 3- a)2 < x < 5
- b)–2 < x < 5
- c)x > 5
- d)1 < x < 3
Correct answer is option 'A'. Can you explain this answer?
|x2 – 2x – 3| < 3x – 3
a)
2 < x < 5
b)
–2 < x < 5
c)
x > 5
d)
1 < x < 3
|
Yash Patel answered |
x2 - 2x - 3 ≥ 0
(x-3) (x+1) ≥ 0
x belongs to (-∞,-3]∪[3,∞)
Therefore, x belongs to (-1,3)
=> x2 - 2x - 3 > 0
x2 - 2x - 3< 3x - 3
x2 - 5x < 0
x(x-5) < 0
x belongs to (0,5)........(1)
x2 - 2x - 3 < 0
x2 - 2x - 3 < 3x - 3
x2 + x - 6 > 0
(x+3)(x-2) > 0
x belongs to (-∞,-3]∪[2,∞)
x belongs to (2,3)........(2)
Taking intersection of (1) and (2)
we get,
x belongs to (2,5)
(x-3) (x+1) ≥ 0
x belongs to (-∞,-3]∪[3,∞)
Therefore, x belongs to (-1,3)
=> x2 - 2x - 3 > 0
x2 - 2x - 3< 3x - 3
x2 - 5x < 0
x(x-5) < 0
x belongs to (0,5)........(1)
x2 - 2x - 3 < 0
x2 - 2x - 3 < 3x - 3
x2 + x - 6 > 0
(x+3)(x-2) > 0
x belongs to (-∞,-3]∪[2,∞)
x belongs to (2,3)........(2)
Taking intersection of (1) and (2)
we get,
x belongs to (2,5)
If x, y and z are real numbers such that x + y + z = 5 and xy + yz + zx = 3, what is the largest value that x can have?- a)5/3
- b)13/3
- c)√19
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If x, y and z are real numbers such that x + y + z = 5 and xy + yz + zx = 3, what is the largest value that x can have?
a)
5/3
b)
13/3
c)
√19
d)
None of these
|
Upsc Rank Holders answered |
The given equations are x + y + z = 5 — (1) , xy + yz + zx = 3 — (2)
xy + yz + zx = 3
x(y + z) + yz = 3
⇒ x ( 5 - x ) +y ( 5 – x – y) = 3
⇒ -y2 - y(5 - x) - x2 + 5x = 3
⇒ y2 + y(x - 5) + (x2 - 5x + 3) = 0
The above equation should have real roots for y, => Determinant >= 0
⇒ y2 + y(x - 5) + (x2 - 5x + 3) = 0
The above equation should have real roots for y, => Determinant >= 0
⇒ b2 - 4ac0
⇒ (x - 5)2 - 4(x2 - 5x + 3) ≥ 0
⇒ 3x2 - 10x - 13 ≤ 0
⇒ -1 ≤ x ≤ 13/3
Hence maximum value x can take is 13/3, and the corresponding values for y,z are 1/3, 1/3
If a, b, c and d are four positive real numbers such that abcd = 1, what is the minimum value of (1 + a)(1 + b)(1 + c)(1+ d)?- a)16
- b)1
- c)4
- d)18
Correct answer is option 'A'. Can you explain this answer?
If a, b, c and d are four positive real numbers such that abcd = 1, what is the minimum value of (1 + a)(1 + b)(1 + c)(1+ d)?
a)
16
b)
1
c)
4
d)
18
|
|
Upsc Rank Holders answered |
Since the product is constant, (a + b + c + d)/4 > = (abcd)1/4
We know that abcd = 1.
Therefore, a + b + c + d > = 4
(a + 1)(b + 1)(c + 1)(d + 1)
= 1 + a + b + c + d + ab + ac + ad + bc + bd + cd + abc + bed + cda + dab + abcd
We know that abcd = 1
Therefore, a = 1/bcd, b = 1/acd, c = 1/bda and d = 1/abc
Also, cd = 1/ab, bd = 1/ac, bc = 1/ad
The expression can be clubbed together as
1 + abcd + (a+1/a)+(b+1/b)+(c+1/c)+(d+1/d) + (ab+1/ab) + (ac+1/ac) + (ad +1/ad)
For any positive real number x, x + 1/x ≥ 2
Therefore, the least value that (a+1/a), (b+1/b).... (ad + 1/ad) can take is 2.
(a+1)(b+1)(c+1)(d+1) > 1 + 1 + 2 + 2 + 2 + 2 + 2 + 2 + 2
=> (a + 1)(b + 1)(c + 1)(d + 1) ≥ 16
The least value that the given expression can take is 16.
|x2 + x| – 5 < 0
- a)x < 0
- b)x > 0
- c)None of these
- d)All values of x
Correct answer is option 'C'. Can you explain this answer?
|x2 + x| – 5 < 0
a)
x < 0
b)
x > 0
c)
None of these
d)
All values of x
|
Sinjini Gupta answered |
At x = 0 inequality is satisfied.
Thus, options (a), (b), and (d) are rejected.
Option (c) is correct.
Thus, options (a), (b), and (d) are rejected.
Option (c) is correct.
The number of positive integer valued pairs (x, y), satisfying 4x – 17 y = 1 and x < 1000 is:- a)55
- b)57
- c)59
- d)58
Correct answer is option 'C'. Can you explain this answer?
The number of positive integer valued pairs (x, y), satisfying 4x – 17 y = 1 and x < 1000 is:
a)
55
b)
57
c)
59
d)
58
|
EduRev CLAT answered |
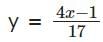
The integral values of x for which y is an integer are 13, 30, 47,……
The values are in the form 17n + 13, where n ≥ 0
17n + 13 < 1000
⇒ 17n < 987
⇒ n < 58.05
⇒ n can take values from 0 to 58
⇒ Number of values = 59
The number of integers n satisfying -n + 2 ≥ 0 and 2n ≥ 4 is- a)1
- b)0
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
The number of integers n satisfying -n + 2 ≥ 0 and 2n ≥ 4 is
a)
1
b)
0
c)
2
d)
3
|
Innovative Classes answered |
First inequality:
-n + 2 ≥ 0
-n ≥ -2
n ≤ 2
Second inequality:
2n ≥ 4
n ≥ 2
Only n = 2 satisfies both inequalities. So, there is only 1 integer that satisfies both the inequalities.
The correct option is A.
|x - 6| > x2 - 5x + 9- a)1 ≤ x < 3
- b)1 < x < 3
- c)2 < x < 5
- d)-3 < x < 1
Correct answer is option 'B'. Can you explain this answer?
|x - 6| > x2 - 5x + 9
a)
1 ≤ x < 3
b)
1 < x < 3
c)
2 < x < 5
d)
-3 < x < 1
|
Shail Jain answered |
At x = 2, inequality is satisfied.
At x = 0, inequality is not satisfied.
At x = 1, inequality is not satisfied but LHS = RHS. At x = 3, inequality is not satisfied but LHS = RHS. Thus, option (b) is correct.
Solve other questions of LOD I and LOD II in the same fashion.
At x = 0, inequality is not satisfied.
At x = 1, inequality is not satisfied but LHS = RHS. At x = 3, inequality is not satisfied but LHS = RHS. Thus, option (b) is correct.
Solve other questions of LOD I and LOD II in the same fashion.
3x2 – 7x – 6 < 0- a)–0.66 < x < 3
- b)x < – 0.66 or x > 3
- c)3 < x < 7
- d)–2 < x < 2
Correct answer is option 'A'. Can you explain this answer?
3x2 – 7x – 6 < 0
a)
–0.66 < x < 3
b)
x < – 0.66 or x > 3
c)
3 < x < 7
d)
–2 < x < 2
|
|
Gargi Kulkarni answered |
At x = 0, inequality is satisfied. Hence, options (b) and (c) are rejected. x = 3 gives LHS = RHS.
and x = – 0.66 also does the same. Hence. roots of the equation are 3 and – 0.66.
Thus, option (a) is correct.
and x = – 0.66 also does the same. Hence. roots of the equation are 3 and – 0.66.
Thus, option (a) is correct.
3x2 - 7x + 4 ≤ 0- a)x > 0
- b)x < 0
- c)All x
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
3x2 - 7x + 4 ≤ 0
a)
x > 0
b)
x < 0
c)
All x
d)
None of these
|
|
Rajdeep Ghoshal answered |
At x = 0, inequality is not satisfied. Thus, option (c) is rejected. Also x = 0 is not a solution of the equation. Since, this is a continuous function, the solution cannot start from 0. Thus options (a) and (b) are not right. Further, we see that the given function is quadratic with real roots. Hence, option (d) is also rejected.
|x2 - 2x| < x- a)l < x < 3
- b)—1 < x < 3
- c)0 < x < 4
- d)x > 3
Correct answer is option 'A'. Can you explain this answer?
|x2 - 2x| < x
a)
l < x < 3
b)
—1 < x < 3
c)
0 < x < 4
d)
x > 3
|
Dishani Banerjee answered |
Method to Solve :
You can factor x^2+2x=0 as:
x(x+2)=0
Now, we can solve each term for 0:
x=0 - no other work needed,
and
x+2=0
x+2−2=0−2
x+0=−2
x=−2
x(x+2)=0
Now, we can solve each term for 0:
x=0 - no other work needed,
and
x+2=0
x+2−2=0−2
x+0=−2
x=−2
x2 – 14x – 15 > 0- a)x < –1
- b)15 < x
- c)Both (a) and (b)
- d)–1 < x < 15
Correct answer is option 'C'. Can you explain this answer?
x2 – 14x – 15 > 0
a)
x < –1
b)
15 < x
c)
Both (a) and (b)
d)
–1 < x < 15
|
|
Aditi Menon answered |
At x = 0 inequality is not satisfied. Thus option (d) is rejected.
x = –1 and x = 15 are the roots of the quadratic equation. Thus, option (c) is correct.
x = –1 and x = 15 are the roots of the quadratic equation. Thus, option (c) is correct.
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is- a)≥ 60 and < 70
- b)≥ 50 and < 60
- c)≥ 40 and < 50
- d)≥ 70 and < 80
Correct answer is option 'A'. Can you explain this answer?
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is
a)
≥ 60 and < 70
b)
≥ 50 and < 60
c)
≥ 40 and < 50
d)
≥ 70 and < 80
|
S.S Career Academy answered |
The product of 2 numbers A and B is maximum when A = B.
If we cannot equate the numbers, then we have to try to minimize the difference between the numbers as much as possible.
pq will be maximum when p=q.
qr will be maximum when q=r.
qr will be maximum when r=p.
Therefore, p, q, and r should be as close to each other as possible.
We know that p,q,and r are integers and p + q + r = 10.
=> p,q, and r should be 3, 3, and 4 in any order.
Substituting the values in the expression, we get,
pq + qr + pr + pqr = 3*3 + 3*4 + 3*4 + 3*3*4
= 9 + 12 + 12 + 36
= 69
For x = 15, y = 10 and z = 9, find the value of le(x, min(y, x-z), le(9, 8, ma(x, y, z)).- a)5
- b)9
- c)12
- d)4
Correct answer is option 'B'. Can you explain this answer?
For x = 15, y = 10 and z = 9, find the value of le(x, min(y, x-z), le(9, 8, ma(x, y, z)).
a)
5
b)
9
c)
12
d)
4
|
|
EduRev CLAT answered |
Given expression can be reduced to
le(15, min(10,15-9) , le(9,8,12))
Or le(15,6,1) = 9
le(15, min(10,15-9) , le(9,8,12))
Or le(15,6,1) = 9
If x > 5 and y < -1, then which of the following statements is true?- a)(x + 4y) > 1
- b)x > -4y
- c)-4x < 5y
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If x > 5 and y < -1, then which of the following statements is true?
a)
(x + 4y) > 1
b)
x > -4y
c)
-4x < 5y
d)
None of these
|
Damini jain answered |
If x = 5, then the equation y = 2x + 3 can be solved as follows:
y = 2(5) + 3
y = 10 + 3
y = 13
y = 2(5) + 3
y = 10 + 3
y = 13
x2 – 7x + 12 < |x – 4|- a)x < 2
- b)x > 4
- c)2 < x < 4
- d)2 £ x £ 4
Correct answer is option 'C'. Can you explain this answer?
x2 – 7x + 12 < |x – 4|
a)
x < 2
b)
x > 4
c)
2 < x < 4
d)
2 £ x £ 4
|
|
Prisha Shah answered |
At x = 0, inequality is not satisfied, option (a) is rejected.
At x = 5, inequality is not satisfied, option (b) is rejected.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct
At x = 5, inequality is not satisfied, option (b) is rejected.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct
x, y and z are three positive integers such that x > y > z. Which of the following is closest to the product xyz?- a)(x - 1)yz
- b)x(y - 1)z
- c)xy(z - 1)
- d)x(y + 1)z
Correct answer is option 'A'. Can you explain this answer?
x, y and z are three positive integers such that x > y > z. Which of the following is closest to the product xyz?
a)
(x - 1)yz
b)
x(y - 1)z
c)
xy(z - 1)
d)
x(y + 1)z
|
|
Innovative Classes answered |
The expressions in the four options can be expanded as
xyz-yz; xyz-xz; xyz-xy and xyz+xz
The closest value to xyz would be xyz-yz, as yz is the least value among yz, xz and xy.
Option a) is the correct answer.
What is the value of ma(10, 4, le((la10, 5, 3), 5, 3))?- a) 7
- b) 6.5
- c) 8
- d) 7.5
Correct answer is option 'B'. Can you explain this answer?
What is the value of ma(10, 4, le((la10, 5, 3), 5, 3))?
a)
7
b)
6.5
c)
8
d)
7.5
|
|
Innovative Classes answered |
Ma(10, 4, le((la10, 5, 3), 5, 3))
Or Ma(10, 4, le(8, 5, 3))
Or Ma(10, 4, 3)
Or 1/2(6 + 7) = 6.5
Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?- a)The minimum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
- b)The maximum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m + 1
- c)The maximum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
- d)The minimum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m +1
Correct answer is option 'D'. Can you explain this answer?
Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?
a)
The minimum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
b)
The maximum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m + 1
c)
The maximum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
d)
The minimum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m +1
|
|
S.S Career Academy answered |
Taking lowest possible positive value of m i.e. 1 .
Such that a + b + c + d = 5, so atleast one of them must be grater than 1, take a = b = c = 1 and d = 2
we get a2 + b2 + c2 + d2 = 7 which is equal to 4m2 + 2m + 1 for other values it is greater
than 4m2 + 2m +1.
than 4m2 + 2m +1.
Chapter doubts & questions for Inequalities - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Inequalities - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily