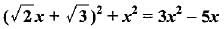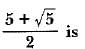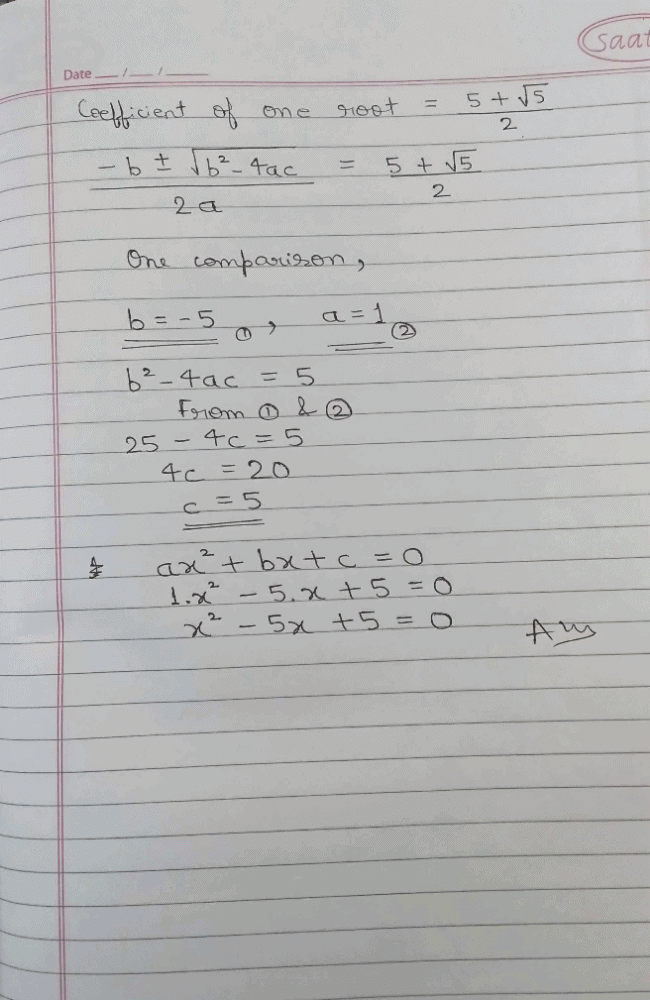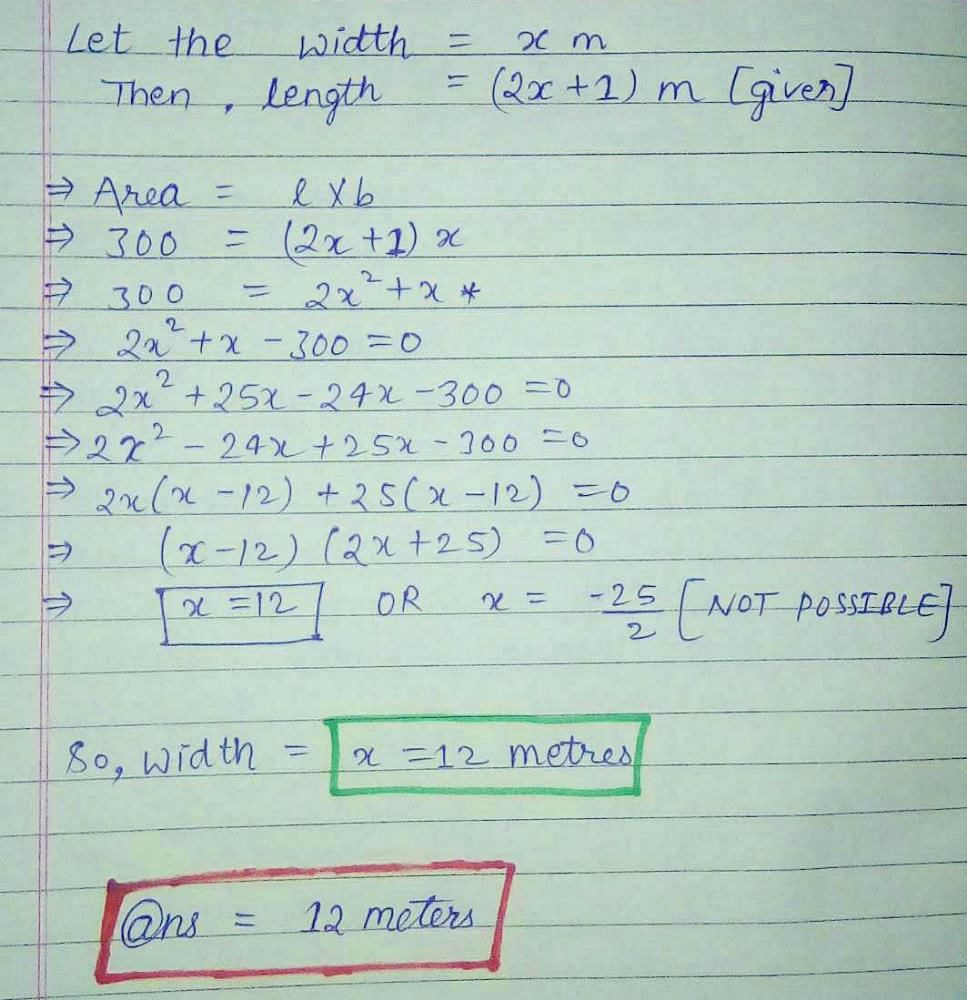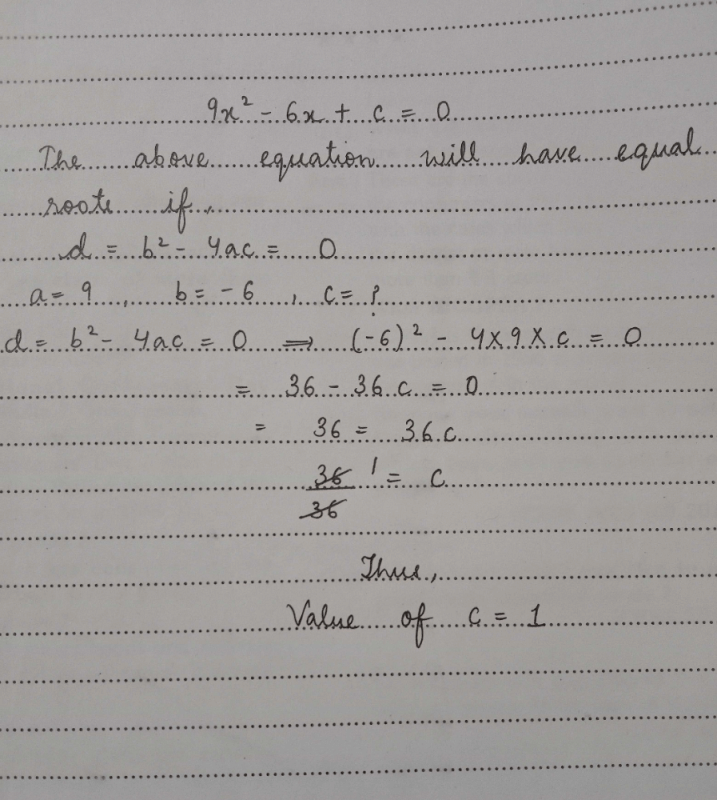All Exams >
Grade 10 >
Mathematics for Grade 10 >
All Questions
All questions of Quadratic Equations for Grade 10 Exam
The two consecutive odd positive integers, sum of whose squares is 290 are- a)13, 15
- b)11, 13
- c)7, 9
- d)5, 7
Correct answer is option 'B'. Can you explain this answer?
The two consecutive odd positive integers, sum of whose squares is 290 are
a)
13, 15
b)
11, 13
c)
7, 9
d)
5, 7
|
|
Drishti Kumari answered |
Let first consecutive odd positive integer be x
Secon = x + 2
(x)^2 + ( x + 2 )^2 = 290
x^2 + x^2 + 4 + 4x = 290
2x^2 + 4x = 290 - 4
2x^2 + 4x = 286
2x^2 + 4x - 286 = 0
x^2 + 2x - 143 = 0
x^2 + 13x - 11x - 143 = 0
x ( x + 13 ) - 11 ( x + 13 ) = 0
( x -11) ( x + 13) = 0
x = 11 Or x = -13
Second = 11 + 2 = 13
Hence option (B) is correct .
The equation 4x2 = 4x has following solution/solutions- a)1
- b)-1, 0
- c)1, -1
- d)0, 1
Correct answer is option 'D'. Can you explain this answer?
The equation 4x2 = 4x has following solution/solutions
a)
1
b)
-1, 0
c)
1, -1
d)
0, 1
|
|
Pooja Shah answered |
We have 4x2=4x
4x2 - 4x=0
4x(x-1)=0
Either 4x=0 = x=0
Or x-1=0 = x=1
4x2 - 4x=0
4x(x-1)=0
Either 4x=0 = x=0
Or x-1=0 = x=1
The difference of a number and its reciprocal is 1.5. Then, the number is/are: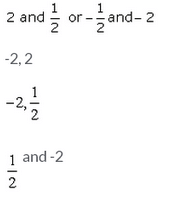
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'A'. Can you explain this answer?
The difference of a number and its reciprocal is 1.5. Then, the number is/are:
a)
A
b)
B
c)
C
d)
D
|
|
Mysterio Man answered |
Let the number=x,
reciprocal of the number=1/x,
given that:->x-1/x=1.5,
x²-1/x=15/10,
(x²-1)10=15x,
10x²-10-15x=0,
5(2x²-2-3x)=0,
2x²-3x-2=0,
by splitting the middle term,
2x²-4x+x-2=0,
2x(x-2)+1(x-2)=0,
(2x+1)=0,or, (x-2)=0,
x=-1/2,or,x=2,
if x=2 then 1/x=1/2 and if x=-1/2 then x=-2
reciprocal of the number=1/x,
given that:->x-1/x=1.5,
x²-1/x=15/10,
(x²-1)10=15x,
10x²-10-15x=0,
5(2x²-2-3x)=0,
2x²-3x-2=0,
by splitting the middle term,
2x²-4x+x-2=0,
2x(x-2)+1(x-2)=0,
(2x+1)=0,or, (x-2)=0,
x=-1/2,or,x=2,
if x=2 then 1/x=1/2 and if x=-1/2 then x=-2
Value(s) of k for which the quadratic equation 2x2 -kx + k = 0 has equal roots is
- a)0
- b)4
- c)8
- d)0 and 8
Correct answer is option 'D'. Can you explain this answer?
Value(s) of k for which the quadratic equation 2x2 -kx + k = 0 has equal roots is
a)
0
b)
4
c)
8
d)
0 and 8
|
|
Kuldeep Kuldeep answered |
Solution:-
Compare given Quadratic equation 2x²-kx+k=0 with ax²+bx+c=0, we get
a = 2,
b = -k ,
c = k,
Discriminant (D) = 0
[ Given roots are equal ]
=> b²-4ac = 0
=> (-k)²-4×2×k=0
=> k²-8k=0
=> k(k-8)=0
=> k = 0 or k=8.
So, option d is correct.
Compare given Quadratic equation 2x²-kx+k=0 with ax²+bx+c=0, we get
a = 2,
b = -k ,
c = k,
Discriminant (D) = 0
[ Given roots are equal ]
=> b²-4ac = 0
=> (-k)²-4×2×k=0
=> k²-8k=0
=> k(k-8)=0
=> k = 0 or k=8.
So, option d is correct.
The roots of quadratic equation are 2x2+3x-9 = 0 are:- a)1.5 and 3
- b)1.5 and -3
- c)-1.5 and -3
- d)-1.5 and 3
Correct answer is option 'B'. Can you explain this answer?
The roots of quadratic equation are 2x2+3x-9 = 0 are:
a)
1.5 and 3
b)
1.5 and -3
c)
-1.5 and -3
d)
-1.5 and 3
|
|
Alisha desai answered |
Explanation:
To find the roots of the quadratic equation 2x^2 + 3x - 9 = 0, we can use the quadratic formula:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
Step 1:
Identify the values of a, b, and c from the given quadratic equation.
a = 2, b = 3, c = -9
Step 2:
Substitute the values of a, b, and c in the quadratic formula.
x = (-3 ± sqrt(3^2 - 4(2)(-9))) / 2(2)
Simplifying the equation, we get:
x = (-3 ± sqrt(105)) / 4
Step 3:
Now we need to simplify the square root of 105.
105 = 3 x 5 x 7
We can simplify the square root of 105 as:
sqrt(105) = sqrt(3 x 5 x 7) = sqrt(3) x sqrt(5) x sqrt(7)
Step 4:
Substitute the simplified value of square root of 105 in the quadratic formula.
x = (-3 ± sqrt(3) x sqrt(5) x sqrt(7)) / 4
Now we can simplify further by dividing the numerator and denominator by 2.
x = (-3/2) ± (sqrt(3) x sqrt(35)) / 4
Step 5:
We can simplify the expression by separating it into two roots.
x = (-3/2) + (sqrt(3) x sqrt(35)) / 4 or x = (-3/2) - (sqrt(3) x sqrt(35)) / 4
Step 6:
We can further simplify the expression by dividing the numerator and denominator of each root by 2.
x = (-3/4) + (sqrt(3) x sqrt(35)) / 8 or x = (-3/4) - (sqrt(3) x sqrt(35)) / 8
Step 7:
Simplify the expression by finding the common denominator.
x = (-6 + sqrt(3 x 35)) / 8 or x = (-6 - sqrt(3 x 35)) / 8
Step 8:
Simplify further by multiplying and dividing the numerator of each root by 2.
x = (-6 + sqrt(105)) / 8 or x = (-6 - sqrt(105)) / 8
Step 9:
Now we can see that the roots are 1.5 and -3.
x = (1.5) or x = (-3)
Therefore, the correct answer is option B, which is 1.5 and -3.
To find the roots of the quadratic equation 2x^2 + 3x - 9 = 0, we can use the quadratic formula:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
Step 1:
Identify the values of a, b, and c from the given quadratic equation.
a = 2, b = 3, c = -9
Step 2:
Substitute the values of a, b, and c in the quadratic formula.
x = (-3 ± sqrt(3^2 - 4(2)(-9))) / 2(2)
Simplifying the equation, we get:
x = (-3 ± sqrt(105)) / 4
Step 3:
Now we need to simplify the square root of 105.
105 = 3 x 5 x 7
We can simplify the square root of 105 as:
sqrt(105) = sqrt(3 x 5 x 7) = sqrt(3) x sqrt(5) x sqrt(7)
Step 4:
Substitute the simplified value of square root of 105 in the quadratic formula.
x = (-3 ± sqrt(3) x sqrt(5) x sqrt(7)) / 4
Now we can simplify further by dividing the numerator and denominator by 2.
x = (-3/2) ± (sqrt(3) x sqrt(35)) / 4
Step 5:
We can simplify the expression by separating it into two roots.
x = (-3/2) + (sqrt(3) x sqrt(35)) / 4 or x = (-3/2) - (sqrt(3) x sqrt(35)) / 4
Step 6:
We can further simplify the expression by dividing the numerator and denominator of each root by 2.
x = (-3/4) + (sqrt(3) x sqrt(35)) / 8 or x = (-3/4) - (sqrt(3) x sqrt(35)) / 8
Step 7:
Simplify the expression by finding the common denominator.
x = (-6 + sqrt(3 x 35)) / 8 or x = (-6 - sqrt(3 x 35)) / 8
Step 8:
Simplify further by multiplying and dividing the numerator of each root by 2.
x = (-6 + sqrt(105)) / 8 or x = (-6 - sqrt(105)) / 8
Step 9:
Now we can see that the roots are 1.5 and -3.
x = (1.5) or x = (-3)
Therefore, the correct answer is option B, which is 1.5 and -3.
If b2 - 4ac = 0 then The roots of the Quadratic equation ax2 + bx + c = 0 are given by :- a)
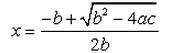
- b)
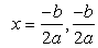
- c)
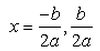
- d)
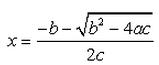
Correct answer is option 'B'. Can you explain this answer?
If b2 - 4ac = 0 then The roots of the Quadratic equation ax2 + bx + c = 0 are given by :
a)
b)
c)
d)

|
Udexy Coaching Center answered |
Formula for finding the roots of a quadratic equation is

So since
b2 - 4ac = 0, putting this value in the equation
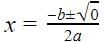
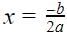 So there are repeated roots
So there are repeated roots
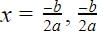

So since
b2 - 4ac = 0, putting this value in the equation
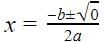
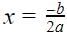 So there are repeated roots
So there are repeated roots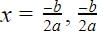
Which of the following is not a quadratic equation ?- a)5x + 3y2 = 0
- b)z2 - 2z = 0
- c)3x + 4 - 7x2 = 0
- d)5x2 - 125 = 0
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a quadratic equation ?
a)
5x + 3y2 = 0
b)
z2 - 2z = 0
c)
3x + 4 - 7x2 = 0
d)
5x2 - 125 = 0
|
|
Priyanshu Intelligent answered |
In equation first there are two variables.
That's why it is not a quadratic equation.
That's why it is not a quadratic equation.
Ruhi’s mother is 26 years older than her. The product of their ages (in years) 3 years from now will be 360. Form a Quadratic equation so as to find Ruhi’s age- a)x 2 + 32 x – 273 = 0
- b)x 2 -32 x – 273=0
- c)x 2 + 32 x + 273 = 0
- d)x 2 – 32 x +273 = 0
Correct answer is option 'A'. Can you explain this answer?
Ruhi’s mother is 26 years older than her. The product of their ages (in years) 3 years from now will be 360. Form a Quadratic equation so as to find Ruhi’s age
a)
x 2 + 32 x – 273 = 0
b)
x 2 -32 x – 273=0
c)
x 2 + 32 x + 273 = 0
d)
x 2 – 32 x +273 = 0
|
|
Amit Sharma answered |
Ruhi’s mother is 26 years older than her
So let Ruhi’s age is x
So mother’s age is x+26
The product of their ages 3 years from now will be 360
So After three years , Ruhi’s age will be x+3
Mother’s age will be x+26+3=x+29
Product of their ages =(x + 3)(x + 29)=360
x2+(3+29)x+87=360
x2+32x-273=0
So let Ruhi’s age is x
So mother’s age is x+26
The product of their ages 3 years from now will be 360
So After three years , Ruhi’s age will be x+3
Mother’s age will be x+26+3=x+29
Product of their ages =(x + 3)(x + 29)=360
x2+(3+29)x+87=360
x2+32x-273=0
If p,q and r are rational numbers and p ≠ q ≠ r, then roots of the equation (p2 - q2)x2 - (q2 - r2)x + (r2 - p2) = 0 are- a)
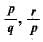
- b)
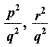
- c)
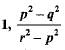
- d)
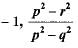
Correct answer is option ''. Can you explain this answer?
If p,q and r are rational numbers and p ≠ q ≠ r, then roots of the equation (p2 - q2)x2 - (q2 - r2)x + (r2 - p2) = 0 are
a)
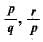
b)
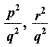
c)
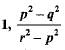
d)
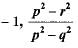

|
Let's Tute answered |
Putting x = - 1, we have
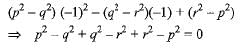 ∴ x = - 1 is one root.
∴ x = - 1 is one root.
Only option (d) has one root - 1.
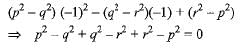 ∴ x = - 1 is one root.
∴ x = - 1 is one root.Only option (d) has one root - 1.
If one root of a Quadratic equation is m + , then the other root is- a)m – √n
- b)m +√n
- c)Can not be determined
- d)√m + n
Correct answer is option 'A'. Can you explain this answer?
If one root of a Quadratic equation is m + , then the other root is
a)
m – √n
b)
m +√n
c)
Can not be determined
d)
√m + n
|
|
Arun Sharma answered |
In a quadratic equation with rational coefficients has an irrational root α + √β, then it has a conjugate root α - √β.
So if the root is m+ √n the other root will be m- √n
So if the root is m+ √n the other root will be m- √n
The roots of x2 – 8x + 12 = 0, are- a)x = 0
- b)no real roots
- c)real and unequal
- d)real and equal
Correct answer is option 'C'. Can you explain this answer?
The roots of x2 – 8x + 12 = 0, are
a)
x = 0
b)
no real roots
c)
real and unequal
d)
real and equal
|
|
Genius answered |
9th standard me kya kr rhe the ?!
If a,b,c are real and b2-4ac >0 then roots of equation are- a)real roots
- b)real and equal
- c)real and unequal
- d)No real roots
Correct answer is option 'C'. Can you explain this answer?
If a,b,c are real and b2-4ac >0 then roots of equation are
a)
real roots
b)
real and equal
c)
real and unequal
d)
No real roots
|
|
Ram trivedi answered |
The expression b^2 - 4ac is the discriminant of a quadratic equation of the form ax^2 + bx + c = 0. It determines the nature of the solutions of the equation.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.- a)14 and 2
- b)11 and 5
- c)12 and 4
- d)10 and 6
Correct answer is option 'D'. Can you explain this answer?
Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.
a)
14 and 2
b)
11 and 5
c)
12 and 4
d)
10 and 6
|
|
Anjana Khatri answered |
Let x and (16 - x) are two parts of 16 where (16 - x) is longer and x is smaller .
A/C to question,
2 * square of longer = square of smaller + 164
⇒ 2 * (16 - x)^2 = x^2 + 164
⇒ 2 * (256 + x^2 - 32x ) = x^2 + 164
⇒ 512 + 2x^2 - 64x = x^2 + 164
⇒ x^2 - 64x + 512 - 164 = 0
⇒ x^2 - 64x + 348 = 0
⇒x^2 - 58x - 6x + 348 = 0
⇒ x(x - 58) - 6(x - 58) = 0
⇒(x - 6)(x - 58) = 0
⇒ x = 6 and 58
But x ≠ 58 because x < 16
so, x = 6 and 16 - x = 10
Hence, answer is 6 and 10
The sum of areas of two squares is 468m2. If the difference of their perimeters is 24m, then the sides of the two squares are:- a)12m and 18m
- b)24m and 28
- c)6m and 12m
- d)18m and 24m
Correct answer is option 'A'. Can you explain this answer?
The sum of areas of two squares is 468m2. If the difference of their perimeters is 24m, then the sides of the two squares are:
a)
12m and 18m
b)
24m and 28
c)
6m and 12m
d)
18m and 24m
|
|
Rahul Kapoor answered |
Let us say that the sides of the two squares are 'a' and 'b'
Sum of their areas = a^2 + b^2 = 468
Difference of their perimeters = 4a - 4b = 24
=> a - b = 6
=> a = b + 6
So, we get the equation
(b + 6)^2 + b^2 = 468
=> 2b^2 + 12b + 36 = 468
=> b^2 + 6b - 216 = 0
=> b = 12
=> a = 18
The sides of the two squares are 12 and 18.
Which of the following are the roots of the quadratic equation, x2 - 9x + 20 = 0 by factorisation?- a)3,4
- b)4, 5
- c)5, 6
- d)6, 7
Correct answer is option 'B'. Can you explain this answer?
Which of the following are the roots of the quadratic equation, x2 - 9x + 20 = 0 by factorisation?
a)
3,4
b)
4, 5
c)
5, 6
d)
6, 7
|
|
Gaurav Kumar answered |
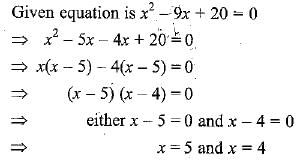
∴ x = 4 and 5 are the roots/solution of the given quadratic equation
If -3 is a root of both the Quadratic equations 2x2 + px – 15 = 0, and p(x2 + x) + q = 0, then the value of q if the equation containing it has equal roots is- a)1/2
- b)1/4
- c)14
- d)2
Correct answer is option 'B'. Can you explain this answer?
If -3 is a root of both the Quadratic equations 2x2 + px – 15 = 0, and p(x2 + x) + q = 0, then the value of q if the equation containing it has equal roots is
a)
1/2
b)
1/4
c)
14
d)
2
|
|
Ananya Das answered |
-3 is root of both
2(9) -3p -15 = 0
p = 1
and
second equation has two equal roots so,
b2-4ac = 0
p2 = 4pq
p = 4q
q = 1/4
The sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, then the sides of the two squares are:- a)18 m and 24 m
- b)6 m and 12 m
- c)12 m and 18 m
- d)24 m and 28 m
Correct answer is option 'C'. Can you explain this answer?
The sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, then the sides of the two squares are:
a)
18 m and 24 m
b)
6 m and 12 m
c)
12 m and 18 m
d)
24 m and 28 m

|
Rishabh Aaruh answered |
Let sides of two squares be s1 nd s2...such that s1>s2.. now.. 4(s1-s2)=24m.. so.. (s1-s2)=6m... (1).. also.. s1^2+s2^2=468m^2... (s1-s2)^2+2s1s2=468... (6)^2+2s1s2=468...(using 1)... 2s1s2=432m^2..(2).. from(1), s1=s2+6.. on putting value of s1 in (2)... 2(s2+6)s2=432.. 2s2^2+12s2-432=0... s2^2+6s2-216=0.. s2^2+18s2-12s2-216=0.. s2(s2+18)-12(s2+18)=0.. (s2+18) (s2-12)=0.. so; s2=12m.. s2 can’t be 18m becoz Distance can't be negative. .. now, s1=(s2+6)=(12+6)m=18m...
A real number is said to be a root of ax2+bx+c = 0- a)
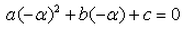
- b)
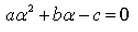
- c)
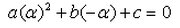
- d)
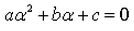
Correct answer is option 'D'. Can you explain this answer?
A real number is said to be a root of ax2+bx+c = 0
a)
b)
c)
d)
|
|
Sameer Diwan answered |
Ni pta re bhai kya likha hai kuch samaj bhi ni aa ra
The roots of the equation x2 – 3x – m (m + 3) = 0, where m is a constant, are- a)–m, m + 3
- b)m, m + 3
- c)–m, – (m + 3)
- d)m, – (m+3)
Correct answer is option 'A'. Can you explain this answer?
The roots of the equation x2 – 3x – m (m + 3) = 0, where m is a constant, are
a)
–m, m + 3
b)
m, m + 3
c)
–m, – (m + 3)
d)
m, – (m+3)
|
|
Aditya Shah answered |
X^2 - 3x - m(m+3) = 0
=> x^2 + mx - (m+3)x- m(m+3) = 0
=> x(x+m) - (m+3)(x+m) = 0
=> (x+m) (x-m-3) = 0
x = - m and m+3
Roots are - m and m+3
The real roots of a quadratic equation 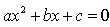 are given by
are given by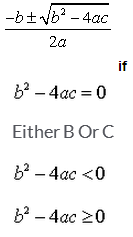
- a)A
- b)B
- c)C
- d)D
Correct answer is 'D'. Can you explain this answer?
The real roots of a quadratic equation 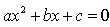 are given by
are given by
a)
A
b)
B
c)
C
d)
D
|
|
Ishan Choudhury answered |
When b2 - 4ac=0 then we have the root as -b/2a.
When b2-4ac < 0,then the root is a complex root ,since we have a negative number ,for which real square root is not possible.
When b2 - 4ac > 0 then we have a square root of it and hence we have real roots. So the correct answer is b2 - 4ac > 0
When b2-4ac < 0,then the root is a complex root ,since we have a negative number ,for which real square root is not possible.
When b2 - 4ac > 0 then we have a square root of it and hence we have real roots. So the correct answer is b2 - 4ac > 0
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48. Find their present ages- a)2 and 18
- b)The situation is not possible
- c)6 and 14
- d)10 and 10
Correct answer is option 'B'. Can you explain this answer?
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48. Find their present ages
a)
2 and 18
b)
The situation is not possible
c)
6 and 14
d)
10 and 10
|
|
Ayush Iyer answered |
Let's assume the present ages of the two friends are x and y.
According to the given information, the sum of their ages is 20 years.
So, we can write the equation: x + y = 20.
Four years ago, the product of their ages was 48.
So, four years ago, their ages would have been x - 4 and y - 4.
The product of their ages four years ago is: (x - 4)(y - 4) = 48.
Now, let's solve these two equations to find the values of x and y.
Solving the first equation, x + y = 20, we can express x in terms of y:
x = 20 - y.
Substituting the value of x in the second equation, we have:
(20 - y - 4)(y - 4) = 48.
Simplifying this equation, we get:
(16 - y)(y - 4) = 48
16y - 4y - 64 = 48
12y = 112
y = 9.33.
Since y is not a whole number, it means there are no two whole numbers that satisfy the given conditions. Therefore, the situation is not possible.
Hence, the correct answer is option B - The situation is not possible.
According to the given information, the sum of their ages is 20 years.
So, we can write the equation: x + y = 20.
Four years ago, the product of their ages was 48.
So, four years ago, their ages would have been x - 4 and y - 4.
The product of their ages four years ago is: (x - 4)(y - 4) = 48.
Now, let's solve these two equations to find the values of x and y.
Solving the first equation, x + y = 20, we can express x in terms of y:
x = 20 - y.
Substituting the value of x in the second equation, we have:
(20 - y - 4)(y - 4) = 48.
Simplifying this equation, we get:
(16 - y)(y - 4) = 48
16y - 4y - 64 = 48
12y = 112
y = 9.33.
Since y is not a whole number, it means there are no two whole numbers that satisfy the given conditions. Therefore, the situation is not possible.
Hence, the correct answer is option B - The situation is not possible.
If the value of the Discriminant function of a quadratic equation is D = 27, then its roots are- a)Distinct, Rational
- b)Same Irrational
- c)Distinct, Irrational
- d) Same, Rational
Correct answer is option 'C'. Can you explain this answer?
If the value of the Discriminant function of a quadratic equation is D = 27, then its roots are
a)
Distinct, Rational
b)
Same Irrational
c)
Distinct, Irrational
d)
Same, Rational
|
|
Roshni chauhan answered |
Quadratic equation is a polynomial equation of degree two, which can be written in the form of ax² + bx + c = 0. The discriminant of a quadratic equation is given by D = b² - 4ac. It is a function of the coefficients of the quadratic equation and is used to determine the nature of the roots of the equation.
Distinct and Irrational Roots
If the value of the discriminant is positive and a perfect square, then the roots of the quadratic equation are distinct and rational. If the value of the discriminant is positive but not a perfect square, then the roots of the quadratic equation are distinct and irrational.
Same and Rational Roots
If the value of the discriminant is zero, then the roots of the quadratic equation are same and rational. If the value of the discriminant is negative, then the roots of the quadratic equation are complex conjugates.
Given, D = 27
From the above discussion, we know that if the value of the discriminant is positive and not a perfect square, then the roots of the quadratic equation are distinct and irrational.
Therefore, the correct answer is option C, which states that the roots of the quadratic equation are distinct and irrational.
Distinct and Irrational Roots
If the value of the discriminant is positive and a perfect square, then the roots of the quadratic equation are distinct and rational. If the value of the discriminant is positive but not a perfect square, then the roots of the quadratic equation are distinct and irrational.
Same and Rational Roots
If the value of the discriminant is zero, then the roots of the quadratic equation are same and rational. If the value of the discriminant is negative, then the roots of the quadratic equation are complex conjugates.
Given, D = 27
From the above discussion, we know that if the value of the discriminant is positive and not a perfect square, then the roots of the quadratic equation are distinct and irrational.
Therefore, the correct answer is option C, which states that the roots of the quadratic equation are distinct and irrational.
Which of the following is a solution of the quadratic equation x2 - b2 = a (2x - a)- a)x = a/b
- b)x = ab
- c)x = a+b
- d)x = b/a
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a solution of the quadratic equation x2 - b2 = a (2x - a)
a)
x = a/b
b)
x = ab
c)
x = a+b
d)
x = b/a
|
|
Ram Mohith answered |
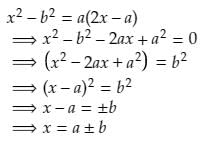
So, x = a + b is one of the solution for the given quadratic equation.
Which of the following is a quadratic equation?- a)x2 + 2x + 1 = (4 - x)2 + 3
- b)
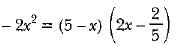
- c)
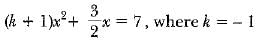
- d) x3 - x2 = ( x -1)3
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a quadratic equation?
a)
x2 + 2x + 1 = (4 - x)2 + 3
b)
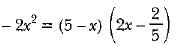
c)
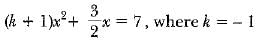
d)
x3 - x2 = ( x -1)3
|
|
Pooja Shah answered |
The correct answer is d
A quadratic equation (from the Latin quadratus for "square") is any equation that can be rearranged in standard form as. where x represents an unknown, and a, b, and c represent known numbers, where a ≠ 0. If a = 0, then the equation is linear, not quadratic, as there is no. term.
Therefore, x3 - x2 = ( x -1)3 is a quadratic equation.
If ax2 + bx + c, a ≠ 0 is factorizable into product of two linear factors, then roots of ax2 + bx + c = 0 can be found by equating each factor to- a)2
- b)-1
- c)0
- d)1
Correct answer is option 'C'. Can you explain this answer?
If ax2 + bx + c, a ≠ 0 is factorizable into product of two linear factors, then roots of ax2 + bx + c = 0 can be found by equating each factor to
a)
2
b)
-1
c)
0
d)
1
|
|
Anjana Khatri answered |
Quadratic equation axx+bx+c=0 has two roots, x1=−b+b2−4ac√2a and x2=−b−b2−4ac√2a. We can investigate their behavior when a→0 by calculating their limits. We assume b>0 (we can always mupltiply the equation by -1):
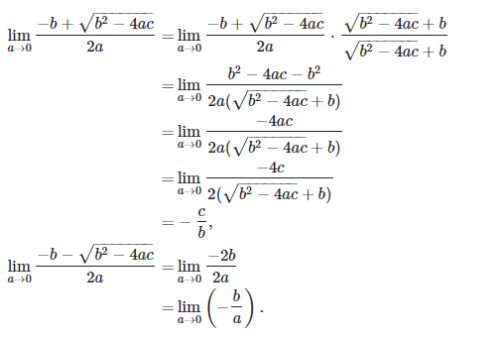
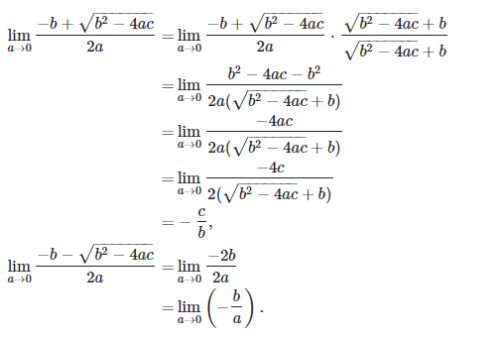
The last expression doesn't only depend on the sign of b but also on the sign of a, i.e. the direction from which we're approaching zero, so the limit does not exist. The one-sided limits are equal to +-∞.
If 1/2 is a root of the equation x2+kx – (5/4) = 0, then the other root of the quadratic equation is- a)-2
- b)1/4
- c)-5/2
- d)1/2
Correct answer is option 'C'. Can you explain this answer?
If 1/2 is a root of the equation x2+kx – (5/4) = 0, then the other root of the quadratic equation is
a)
-2
b)
1/4
c)
-5/2
d)
1/2
|
|
Varsha das answered |
I'm sorry, but the equation you provided is incomplete. Could you please provide the complete equation?
For what value(s) of k will the equation kx2-5x+k = 0 have a repeated root?- a)±5/2
- b)5/2
- c)-5/2
- d)3/2
Correct answer is option 'A'. Can you explain this answer?
For what value(s) of k will the equation kx2-5x+k = 0 have a repeated root?
a)
±5/2
b)
5/2
c)
-5/2
d)
3/2
|
|
Stuti answered |
Kx^2-5x+k=0
a=k, b=-5, c=k
b^2-4ac=0
(-5)^2 - 4×k×k= 0
25 - 4k^2 = 0
25/4 = k^2
+√25/4 = k
-
+-5/2 ANS.
a=k, b=-5, c=k
b^2-4ac=0
(-5)^2 - 4×k×k= 0
25 - 4k^2 = 0
25/4 = k^2
+√25/4 = k
-
+-5/2 ANS.
-3 is a root of the quadratic equation 2x2 +px – 15 = 0. For what value of q , the equation p(x2 + x ) + q= 0 has equal roots?- a)1/4
- b)2
- c)14
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
-3 is a root of the quadratic equation 2x2 +px – 15 = 0. For what value of q , the equation p(x2 + x ) + q= 0 has equal roots?
a)
1/4
b)
2
c)
14
d)
1/2
|
|
Samta menon answered |
**Given Information:**
- The quadratic equation is given as 2x^2 + px + 15 = 0.
- The root of the equation is -3.
- We need to find the value of q for which the equation p(x^2 + x) + q = 0 has equal roots.
**Solution:**
To find the value of q, we need to determine the conditions for the roots of the quadratic equation p(x^2 + x) + q = 0 to be equal.
**Condition for Equal Roots:**
For a quadratic equation ax^2 + bx + c = 0 to have equal roots, the discriminant (b^2 - 4ac) must be equal to zero.
**Finding the Discriminant:**
Let's find the discriminant for the given equation p(x^2 + x) + q = 0.
The given equation can be rewritten as px^2 + px + qx + q = 0.
Comparing it with the standard form ax^2 + bx + c = 0, we can determine the values of a, b, and c as follows:
- a = p
- b = p + q
- c = q
The discriminant is calculated as follows:
D = (b^2 - 4ac)
= [(p + q)^2 - 4pq]
**Condition for Equal Roots:**
To have equal roots, the discriminant D must be equal to zero.
Therefore, we have the equation: (p + q)^2 - 4pq = 0.
**Substituting the Value of p:**
We know that -3 is one of the roots of the quadratic equation 2x^2 + px + 15 = 0.
Substituting x = -3 into the equation, we get:
2(-3)^2 + p(-3) + 15 = 0
18 - 3p + 15 = 0
33 - 3p = 0
3p = 33
p = 11
**Substituting the Value of p in the Equation:**
Now, substitute the value of p = 11 into the equation (p + q)^2 - 4pq = 0.
(11 + q)^2 - 4(11)(q) = 0
121 + 22q + q^2 - 44q = 0
q^2 - 22q + 121 - 44q = 0
q^2 - 66q + 121 = 0
**Finding the Value of q:**
To find the value of q, we need to solve the quadratic equation q^2 - 66q + 121 = 0.
By factoring or using the quadratic formula, we can find that q = 1/4 and q = 121 are the solutions of the equation.
However, we need to select the value of q for which the equation has equal roots.
Since the question asks for the value of q where the equation has equal roots, the correct answer is q = 1/4 (option A).
- The quadratic equation is given as 2x^2 + px + 15 = 0.
- The root of the equation is -3.
- We need to find the value of q for which the equation p(x^2 + x) + q = 0 has equal roots.
**Solution:**
To find the value of q, we need to determine the conditions for the roots of the quadratic equation p(x^2 + x) + q = 0 to be equal.
**Condition for Equal Roots:**
For a quadratic equation ax^2 + bx + c = 0 to have equal roots, the discriminant (b^2 - 4ac) must be equal to zero.
**Finding the Discriminant:**
Let's find the discriminant for the given equation p(x^2 + x) + q = 0.
The given equation can be rewritten as px^2 + px + qx + q = 0.
Comparing it with the standard form ax^2 + bx + c = 0, we can determine the values of a, b, and c as follows:
- a = p
- b = p + q
- c = q
The discriminant is calculated as follows:
D = (b^2 - 4ac)
= [(p + q)^2 - 4pq]
**Condition for Equal Roots:**
To have equal roots, the discriminant D must be equal to zero.
Therefore, we have the equation: (p + q)^2 - 4pq = 0.
**Substituting the Value of p:**
We know that -3 is one of the roots of the quadratic equation 2x^2 + px + 15 = 0.
Substituting x = -3 into the equation, we get:
2(-3)^2 + p(-3) + 15 = 0
18 - 3p + 15 = 0
33 - 3p = 0
3p = 33
p = 11
**Substituting the Value of p in the Equation:**
Now, substitute the value of p = 11 into the equation (p + q)^2 - 4pq = 0.
(11 + q)^2 - 4(11)(q) = 0
121 + 22q + q^2 - 44q = 0
q^2 - 22q + 121 - 44q = 0
q^2 - 66q + 121 = 0
**Finding the Value of q:**
To find the value of q, we need to solve the quadratic equation q^2 - 66q + 121 = 0.
By factoring or using the quadratic formula, we can find that q = 1/4 and q = 121 are the solutions of the equation.
However, we need to select the value of q for which the equation has equal roots.
Since the question asks for the value of q where the equation has equal roots, the correct answer is q = 1/4 (option A).
The length of the plot in meters is 1 more than twice its breadth and the area of a rectangle plot is 528m2. Which of the following quadratic equations represents the given situation:- a)x2+2x- 528 = 0
- b)2x2+x- 528 = 0
- c)2x2+x+ 528 = 0
- d)x2+x- 528 = 0
Correct answer is option 'B'. Can you explain this answer?
The length of the plot in meters is 1 more than twice its breadth and the area of a rectangle plot is 528m2. Which of the following quadratic equations represents the given situation:
a)
x2+2x- 528 = 0
b)
2x2+x- 528 = 0
c)
2x2+x+ 528 = 0
d)
x2+x- 528 = 0
|
|
Navya Shree N answered |
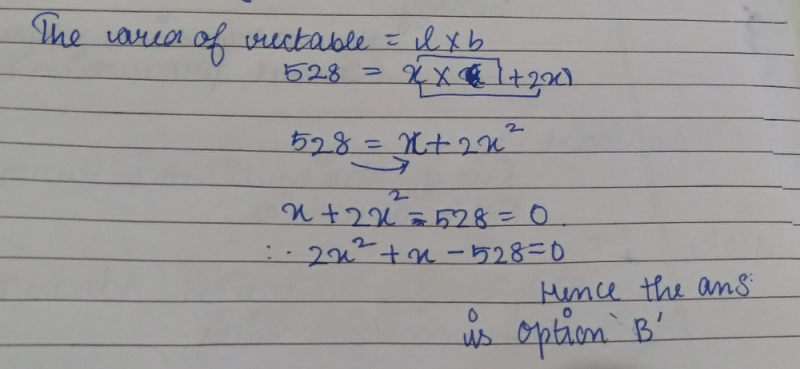
Chapter doubts & questions for Quadratic Equations - Mathematics for Grade 10 2025 is part of Grade 10 exam preparation. The chapters have been prepared according to the Grade 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Quadratic Equations - Mathematics for Grade 10 in English & Hindi are available as part of Grade 10 exam.
Download more important topics, notes, lectures and mock test series for Grade 10 Exam by signing up for free.
Mathematics for Grade 10
138 videos|66 docs|43 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily