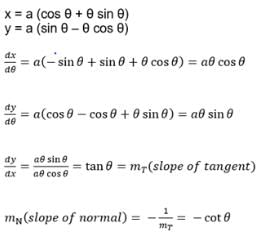All Exams >
Grade 12 >
Mathematics for Grade 12 >
All Questions
All questions of Differentiation for Grade 12 Exam
The function f(x) = ax, 0 < a < 1 is- a)increasing
- b)strictly decreasing on R
- c)neither increasing or decreasing
- d)decreasing
Correct answer is option 'D'. Can you explain this answer?
The function f(x) = ax, 0 < a < 1 is
a)
increasing
b)
strictly decreasing on R
c)
neither increasing or decreasing
d)
decreasing
|
|
Krishna Iyer answered |
f(x) = ax
Taking log bth the sides, log f(x) = xloga
f’(x)/ax = loga
f’(x) = ax loga {ax > 0 for all x implies R,
for loga e<a<1 that implies loga < 0}
Therefore, f’(x) < 0, for all x implies R
f(x) is a decreasing function.
Taking log bth the sides, log f(x) = xloga
f’(x)/ax = loga
f’(x) = ax loga {ax > 0 for all x implies R,
for loga e<a<1 that implies loga < 0}
Therefore, f’(x) < 0, for all x implies R
f(x) is a decreasing function.
Using approximation find the value of 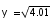
- a)2.025
- b)2.001
- c)2.01
- d)2.0025
Correct answer is option 'D'. Can you explain this answer?
Using approximation find the value of 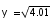
a)
2.025
b)
2.001
c)
2.01
d)
2.0025

|
Gunjan Lakhani answered |
Let x=4, Δx=0.01
y=x^½ = 2
y+Δy = (x+ Δx)^½ = (4.01)^½
Δy = (dy/dx) * Δx
Δy = (x^(-1/2))/2 * Δx
Δy = (½)*(½) * 0.01
Δy = 0.25 * 0.01
Δy = 0.0025
So, (4.01)^½ = 2 + 0.0025 = 2.0025
The maximum value of f (x) = sin x in the interval [π,2π] is
a) 6
b) 0
c) -2
d) -4
Correct answer is option 'B'. Can you explain this answer?
|
|
Kiran Mehta answered |
f(x) = sin x
f’(x) =cosx
f”(x) = -sin x
f”(3pi/2) = -sin(3pi/2)
= -(-1)
=> 1 > 0 (local minima)
f(pi) = sin(pi) = 0
f(2pi) = sin(2pi) = 0
Hence, 0 is the maxima.
f’(x) =cosx
f”(x) = -sin x
f”(3pi/2) = -sin(3pi/2)
= -(-1)
=> 1 > 0 (local minima)
f(pi) = sin(pi) = 0
f(2pi) = sin(2pi) = 0
Hence, 0 is the maxima.
Find the maximum and minimum values of f (x) = 2x3 – 24x + 107 in the interval [1, 3].- a)89, 69
- b)89, 75
- c)59, 56
- d)89, -9
Correct answer is option 'B'. Can you explain this answer?
Find the maximum and minimum values of f (x) = 2x3 – 24x + 107 in the interval [1, 3].
a)
89, 69
b)
89, 75
c)
59, 56
d)
89, -9
|
|
Anjana Sharma answered |
Toolbox:d/dx(x^n) = nx^n−1Maxima & Minima = f′... more(x) = 0Step 1:f(x) = 2x^3−24x+107Differentiating with
Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24 x – 18x2- a)56
- b)49
- c)23
- d)89
Correct answer is option 'B'. Can you explain this answer?
Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24 x – 18x2
a)
56
b)
49
c)
23
d)
89
|
|
Aryan Khanna answered |
p’(x) = -24 - 36x
p”(x) = -36
Now, p’(x) = 0 ⇒ x = (-24)/36
x = -⅔
Also, p”(-⅔) = -36 < 0
By the second derivative test, x = -⅔
Therefore, maximum profit = p(-⅔)
= 41 - 24(-⅔) - 18(-⅔)^2
= 41 +16 - 8
⇒ 49
p”(x) = -36
Now, p’(x) = 0 ⇒ x = (-24)/36
x = -⅔
Also, p”(-⅔) = -36 < 0
By the second derivative test, x = -⅔
Therefore, maximum profit = p(-⅔)
= 41 - 24(-⅔) - 18(-⅔)^2
= 41 +16 - 8
⇒ 49
A stone is dropped into a quiet lake and waves move in circles at a speed of 2cm per second. At the instant, when the radius of the circular wave is 12 cm, how fast is the enclosed area changing ?- a)Decreasing at the rate of 48π cm2 / sec
- b)Increasing at the rate of 24π cm2 / sec
- c)Increasing at the rate of 48π cm2 / sec
- d)Decreasing at the rate of 24π cm2 / sec
Correct answer is option 'C'. Can you explain this answer?
A stone is dropped into a quiet lake and waves move in circles at a speed of 2cm per second. At the instant, when the radius of the circular wave is 12 cm, how fast is the enclosed area changing ?
a)
Decreasing at the rate of 48π cm2 / sec
b)
Increasing at the rate of 24π cm2 / sec
c)
Increasing at the rate of 48π cm2 / sec
d)
Decreasing at the rate of 24π cm2 / sec
|
|
Hansa Sharma answered |
Rate of increase of radius dr/dt = 2 cm/s
Area of circle A = πr2
dA/dt = π*(2r)*(dr/dt)
= π*(24)*2
= 48π cm2/s
Rate of increase of area is 48π cm2/s (increasing as it is positive).
Area of circle A = πr2
dA/dt = π*(2r)*(dr/dt)
= π*(24)*2
= 48π cm2/s
Rate of increase of area is 48π cm2/s (increasing as it is positive).
Find slope of normal to the curve y=5x2-10x + 7 at x=1- a)not defined
- b)-1
- c)1
- d)zero
Correct answer is option 'A'. Can you explain this answer?
Find slope of normal to the curve y=5x2-10x + 7 at x=1
a)
not defined
b)
-1
c)
1
d)
zero
|
|
Neha Sharma answered |
y = 5x2 - 10x + 7
dy/dx = 10x - 10
(At x = 1) 10(1) - 10
m1 = 0
As we know that slope, m1m2 = -1
=> 0(m2) = -1
m2 = -1/0 (which is not defined)
dy/dx = 10x - 10
(At x = 1) 10(1) - 10
m1 = 0
As we know that slope, m1m2 = -1
=> 0(m2) = -1
m2 = -1/0 (which is not defined)
Find the approximate value of f(10.01) where f(x) = 5x2 +6x + 3- a)564.06
- b)564.01
- c)563.00
- d)563.01
Correct answer is option 'A'. Can you explain this answer?
Find the approximate value of f(10.01) where f(x) = 5x2 +6x + 3
a)
564.06
b)
564.01
c)
563.00
d)
563.01
|
|
Naina Sharma answered |
f(x) = 5x2 +6x + 3
f(10.01) = 5*(10.01)2 + 6*(10.01) + 3
To find (10.01)2
Let p=10, Δp=0.01
y=p2 = 100
y+Δy = (p+ Δp)2 = (10.01)2
Δy = (dy/dp) * Δp
Δy = 2*p* Δx
Δy = 2*10* 0.01
Δy = 20 * 0.01
Δy = 0.2
So, (10.01)2 = y + Δy
= 100.2
So,
f(10.01) = 5*(100.2) + 6*(10.01) + 3
= 501 + 60.06 + 3
= 564.06
f(10.01) = 5*(10.01)2 + 6*(10.01) + 3
To find (10.01)2
Let p=10, Δp=0.01
y=p2 = 100
y+Δy = (p+ Δp)2 = (10.01)2
Δy = (dy/dp) * Δp
Δy = 2*p* Δx
Δy = 2*10* 0.01
Δy = 20 * 0.01
Δy = 0.2
So, (10.01)2 = y + Δy
= 100.2
So,
f(10.01) = 5*(100.2) + 6*(10.01) + 3
= 501 + 60.06 + 3
= 564.06
The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 5x2 + 22x + 35. Find the marginal revenue, when x = 7, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant- a)Rs 7
- b)Rs 127
- c)Rs 92
- d)Rs 48
Correct answer is option 'C'. Can you explain this answer?
The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 5x2 + 22x + 35. Find the marginal revenue, when x = 7, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant
a)
Rs 7
b)
Rs 127
c)
Rs 92
d)
Rs 48
|
|
Gaurav Kumar answered |

The equation of the normal to the curve x2 = 4y which passes through the point (1, 2) is.- a)x + y – 3 = 0
- b)4x – y = 2
- c)4x – 2y = 0
- d)4x – 3y + 2= 0
Correct answer is option 'B'. Can you explain this answer?
The equation of the normal to the curve x2 = 4y which passes through the point (1, 2) is.
a)
x + y – 3 = 0
b)
4x – y = 2
c)
4x – 2y = 0
d)
4x – 3y + 2= 0

|
Sushil Kumar answered |
h2 = 4k
slope of normal=−1/(dy/dx) = −2h
equation of normal(y − k)= −2h(x−h)
k = 2 + 2/h(1 − h)
(h2) / 4 = 2 + 2/h (1 − h)
h = 2, k = 1
equation of line (y - 1)= -1(x - 2)
x + y = 3
slope of normal=−1/(dy/dx) = −2h
equation of normal(y − k)= −2h(x−h)
k = 2 + 2/h(1 − h)
(h2) / 4 = 2 + 2/h (1 − h)
h = 2, k = 1
equation of line (y - 1)= -1(x - 2)
x + y = 3
The radius of air bubble is increasing at the rate of 0. 25 cm/s. At what rate the volume of the bubble is increasing when the radius is 1 cm.- a)4π cm3/s
- b)22π cm3/s
- c)2π cm3/s
- d)π cm3/s
Correct answer is option 'D'. Can you explain this answer?
The radius of air bubble is increasing at the rate of 0. 25 cm/s. At what rate the volume of the bubble is increasing when the radius is 1 cm.
a)
4π cm3/s
b)
22π cm3/s
c)
2π cm3/s
d)
π cm3/s
|
|
Rohan Yadav answered |
Given, the rate of increase of radius of the air bubble = 0.25 cm/s
We need to find the rate of increase of volume of the bubble when the radius is 1 cm.
Formula used:
Volume of a sphere = (4/3)πr^3
Differentiating both sides with respect to time t, we get:
dV/dt = 4πr^2(dr/dt)
where dV/dt is the rate of change of volume of the sphere with respect to time t and dr/dt is the rate of change of radius of the sphere with respect to time t.
Substituting the given values, we get:
dV/dt = 4π(1)^2(0.25) = π cm^3/s
Therefore, the rate of increase of volume of the bubble when the radius is 1 cm is π cm^3/s, which is the correct answer.
We need to find the rate of increase of volume of the bubble when the radius is 1 cm.
Formula used:
Volume of a sphere = (4/3)πr^3
Differentiating both sides with respect to time t, we get:
dV/dt = 4πr^2(dr/dt)
where dV/dt is the rate of change of volume of the sphere with respect to time t and dr/dt is the rate of change of radius of the sphere with respect to time t.
Substituting the given values, we get:
dV/dt = 4π(1)^2(0.25) = π cm^3/s
Therefore, the rate of increase of volume of the bubble when the radius is 1 cm is π cm^3/s, which is the correct answer.
The abscissa of the point on the curve ay2 = x3, the normal at which cuts off equal intercepts from the coordinate axes is- a)

- b)
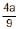
- c) –
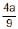
- d)–
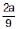
Correct answer is option 'B'. Can you explain this answer?
The abscissa of the point on the curve ay2 = x3, the normal at which cuts off equal intercepts from the coordinate axes is
a)
b)
c)
–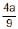
d)
–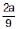
|
|
Kavita Joshi answered |
(That should be "axes" -- plural.)
Find the normal; find the intercepts -- for a point (u, v) say.
To get there, differentiate to find the gradient - of the tangent, hence of the normal.
2 a y dy/dx = 3 x^2
So dy/dx = 3 x^2 / (2 a y) .
At the point (u, v), this is 3 u^2 / (2 a v)
So the gradient of the normal there is (-2 a v) / (3 u^2)
So the equation of the normal is
y - v = (-2 a v) / (3 u^2) * (x - u)
When x = 0,
y = v - 2 a v / (3 u^2) (-u)
= v (1 + 2 a / (3 u) )
When y = 0,
x = u + 3 u^2 / (2 a v) * v
= u (1 + 3 u / (2 a) )
Now, "equal intercepts" could mean just by size, or by size and sign. Take the latter:
Then
v (2a + 3u) / (3u) = u (2a + 3u) / (2a)
So either u = -3 a / 2,
or v / (3u) = u / (2a),
2 a v = 3 u^2 --
each to be taken with a v^2 = u^3
One possibility, which fits all three equations, is (u, v) = (0, 0).; and if either u = 0 or v = 0, the so is the other.
If u ≠ 0, v ≠ 0 then
first case:
u = -3 a / 2
so a v^2 = -27 a^3 / 8
so v^2 = -27 a^2 / 8 -- not possible
second case:
2 a v = 3 u^2
and a v^2 = u^3 divide
So v / 2 = u /3 substitute
so a 4u^2 / 9 = u^3,
(u = 0 or) u = 4 a / 9 substitute, again:
a v^2 = 64 a^3 / 729
v = (-/)+ 8 a / 27
The (only) point that cuts off equal intercepts on the axes is (4a/9, 8a/27).
(if we allow equal distances, we get one other point -- y changes sign.)
Read the following text and answer the following questions, on the basis of the same:An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below: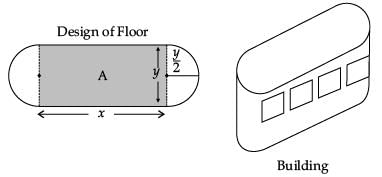 The area of the rectangular region A expressed as a function of x is :
The area of the rectangular region A expressed as a function of x is :- a)
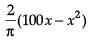
- b)
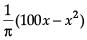
- c)
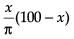
- d)
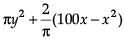
Correct answer is option 'A'. Can you explain this answer?
Read the following text and answer the following questions, on the basis of the same:
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:

The area of the rectangular region A expressed as a function of x is :
a)
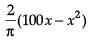
b)
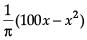
c)
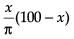
d)
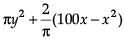

|
Defence Exams answered |
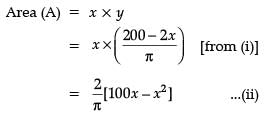
Read the following text and answer the following questions, on the basis of the same:An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below: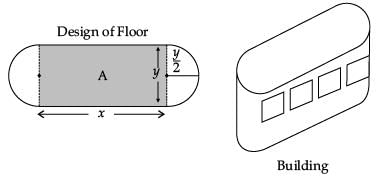 If x and y represents the length and breadth of the rectangular region, then the relation between the variables is :
If x and y represents the length and breadth of the rectangular region, then the relation between the variables is :- a)x + ?y = 100
- b)2x + ?y = 200
- c)?x + y = 50
- d)x + y = 100
Correct answer is option 'B'. Can you explain this answer?
Read the following text and answer the following questions, on the basis of the same:
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:

If x and y represents the length and breadth of the rectangular region, then the relation between the variables is :
a)
x + ?y = 100
b)
2x + ?y = 200
c)
?x + y = 50
d)
x + y = 100
|
|
Anjali Sharma answered |
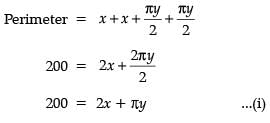
Separate the interval 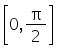 open square brackets 0 comma straight pi over 2 close square brackets into sub-intervals in which f (x) = sin4 x + cos4 x is increasing or decreasing
open square brackets 0 comma straight pi over 2 close square brackets into sub-intervals in which f (x) = sin4 x + cos4 x is increasing or decreasing- a)
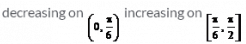
- b)

- c)
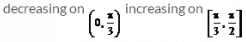
- d)

Correct answer is option 'B'. Can you explain this answer?
Separate the interval 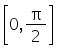 open square brackets 0 comma straight pi over 2 close square brackets into sub-intervals in which f (x) = sin4 x + cos4 x is increasing or decreasing
open square brackets 0 comma straight pi over 2 close square brackets into sub-intervals in which f (x) = sin4 x + cos4 x is increasing or decreasing
a)
b)
c)
d)
|
|
Nandini Iyer answered |
f’(x) = 4sin3x cosx - 4cos3x sinx
= - sin4x
As x is in the interval [0, ∏/2] hence 4x is in the interval [0, 2∏]
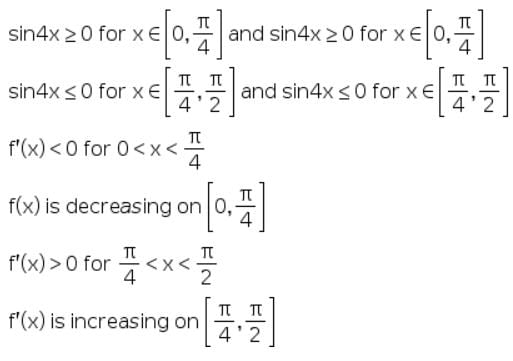
= - sin4x
As x is in the interval [0, ∏/2] hence 4x is in the interval [0, 2∏]
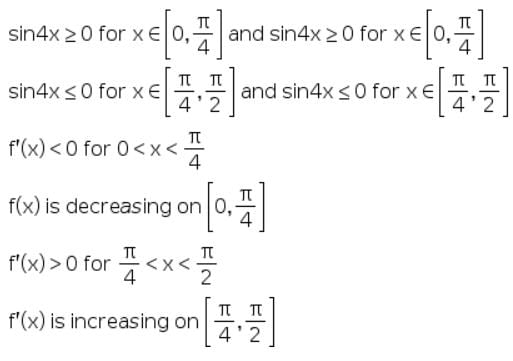
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.The equation of tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x – 5.Assertion (A): The value of a is ±2Reason (R): The value of b is ±7- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'C'. Can you explain this answer?
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
The equation of tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x – 5.
Assertion (A): The value of a is ±2
Reason (R): The value of b is ±7
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Tanuja Kapoor answered |
y2 = ax3 + b
Differentiate with respect to x,
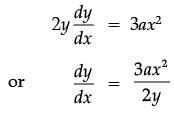
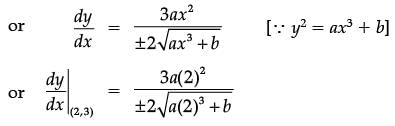
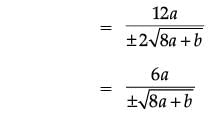
Since (2, 3) lies on the curve
y2 = ax3 + b
Or 9 = 8a + b …. (i)
Also from equation of tangent
y = 4x – 5
slope of the tangent = 4
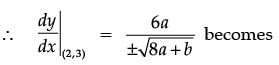
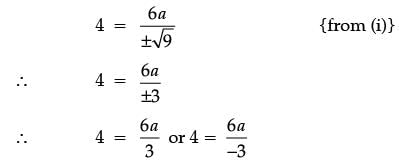
either, a = 2 or a = - 2
For a = 2,
9 = 8(2) + b
or b = - 7
∴ a = 2 and b = - 7 and
for a = - 2,
9 = 8(- 2 )+b or b = 25
or a = - 2 and b = 25
Hence A is true and R is false.
Let f be a real valued function defined on (0, 1) ∪ (2, 4) such that f ‘ (x) = 0 for every x, then- a)f is constant function if f 1/2 = f (3)
- b)f is a constant function
- c)f is a constant function if f 1/2 = 0
- d)f is not a constant function
Correct answer is option 'A'. Can you explain this answer?
Let f be a real valued function defined on (0, 1) ∪ (2, 4) such that f ‘ (x) = 0 for every x, then
a)
f is constant function if f 1/2 = f (3)
b)
f is a constant function
c)
f is a constant function if f 1/2 = 0
d)
f is not a constant function

|
Nandini Choudhury answered |
f ‘ (x) = 0 ⇒ f (x)is constant in (0 , 1)and also in (2, 4). But this does not mean that f (x) has the same value in both the intervals . However , if f (c) = f (d) , where c ∈ (0 , 1) and d ∈ (2, 4) then f (x) assumes the same value at all x ∈ (0 ,1) U (2, 4) and hence f is a constant function.
A real number x when added to its reciprocal give minimum value to the sum when x is- a)1/2
- b)-1
- c)1
- d)2
Correct answer is option 'C'. Can you explain this answer?
A real number x when added to its reciprocal give minimum value to the sum when x is
a)
1/2
b)
-1
c)
1
d)
2
|
|
Krish Das answered |
Finding the Real Number that Gives Minimum Value to the Sum
Solution:
Let x be the real number. Then, its reciprocal is 1/x.
The sum of x and its reciprocal is x + 1/x.
To find the minimum value of this sum, we can use the concept of the arithmetic mean and geometric mean inequality.
We know that for any two positive numbers a and b, the arithmetic mean is (a+b)/2 and the geometric mean is √(ab).
The arithmetic mean is always greater than or equal to the geometric mean, i.e., (a+b)/2 ≥ √(ab).
Let's apply this inequality to x and 1/x.
The arithmetic mean of x and 1/x is (x + 1/x)/2.
The geometric mean of x and 1/x is √(x * 1/x) = √1 = 1.
By the arithmetic mean and geometric mean inequality, we have:
(x + 1/x)/2 ≥ √(x * 1/x) = 1
Multiplying both sides by 2 gives:
x + 1/x ≥ 2
Therefore, the minimum value of x + 1/x is 2, which is attained when x=1.
Hence, the real number x that gives minimum value to the sum x + 1/x is 1.
Solution:
Let x be the real number. Then, its reciprocal is 1/x.
The sum of x and its reciprocal is x + 1/x.
To find the minimum value of this sum, we can use the concept of the arithmetic mean and geometric mean inequality.
We know that for any two positive numbers a and b, the arithmetic mean is (a+b)/2 and the geometric mean is √(ab).
The arithmetic mean is always greater than or equal to the geometric mean, i.e., (a+b)/2 ≥ √(ab).
Let's apply this inequality to x and 1/x.
The arithmetic mean of x and 1/x is (x + 1/x)/2.
The geometric mean of x and 1/x is √(x * 1/x) = √1 = 1.
By the arithmetic mean and geometric mean inequality, we have:
(x + 1/x)/2 ≥ √(x * 1/x) = 1
Multiplying both sides by 2 gives:
x + 1/x ≥ 2
Therefore, the minimum value of x + 1/x is 2, which is attained when x=1.
Hence, the real number x that gives minimum value to the sum x + 1/x is 1.
A point c in the domain of a function f is called a critical point of f if- a)f’ (x) = 0 at x = c
- b)f is not differentiable at x = c
- c)Either f’ (c) = 0 or f is not differentiable
- d)f” (x) = 0, at x = c
Correct answer is option 'B'. Can you explain this answer?
A point c in the domain of a function f is called a critical point of f if
a)
f’ (x) = 0 at x = c
b)
f is not differentiable at x = c
c)
Either f’ (c) = 0 or f is not differentiable
d)
f” (x) = 0, at x = c
|
|
Ishan Choudhury answered |
A point C in the domain of a function f at which either f(c) = 0 or f is not differentiable.
The point f is called the critical point.
c is called the point of local maxima
If f ′(x) changes sign from positive to negative as x increases through c, that is, if f ′(x) > 0 at every point sufficiently close to and to the left of c, and f ′(x) < 0 at every point sufficiently close to and to the right of c.
c is called the point of local minima
If f ′(x) changes sign from negative to positive as x increases through c, that is, if f ′(x) < 0 at every point sufficiently close to and to the left of c, and f ′(x) > 0 at every point sufficiently close to and to the right of c.
c is called the point of inflexion
If f ′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima.
The point f is called the critical point.
c is called the point of local maxima
If f ′(x) changes sign from positive to negative as x increases through c, that is, if f ′(x) > 0 at every point sufficiently close to and to the left of c, and f ′(x) < 0 at every point sufficiently close to and to the right of c.
c is called the point of local minima
If f ′(x) changes sign from negative to positive as x increases through c, that is, if f ′(x) < 0 at every point sufficiently close to and to the left of c, and f ′(x) > 0 at every point sufficiently close to and to the right of c.
c is called the point of inflexion
If f ′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima.
The function 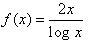 increases in
increases in- a)(0, 1)
- b)(-∞,e)
- c)(e,∞)
- d)(1, e)
Correct answer is option 'C'. Can you explain this answer?
The function 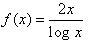 increases in
increases in
a)
(0, 1)
b)
(-∞,e)
c)
(e,∞)
d)
(1, e)
|
|
Vikas Kapoor answered |
f'(x) = [(logx).2−2x.1/x](logx)2
= 2(logx−1)/(logx)^2
∴f'(x)>0
⇔logx−1>0
⇔logx>1
⇔logx>loge
⇔x>e
∴f(x) is increasing in (e,∞)
= 2(logx−1)/(logx)^2
∴f'(x)>0
⇔logx−1>0
⇔logx>1
⇔logx>loge
⇔x>e
∴f(x) is increasing in (e,∞)
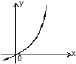
The curve y = f(x) which satisfies the condition f'(x) > 0 and f"(x) < 0 for all real x, is- a)

- b)
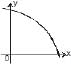
- c)
- d)
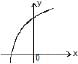
Correct answer is option 'D'. Can you explain this answer?
The curve y = f(x) which satisfies the condition f'(x) > 0 and f"(x) < 0 for all real x, is
a)
b)
c)
d)
|
|
Geetika Shah answered |
f’(x) > 0
=> f(x) is increasing
f’’(x) < 0 => f(x) is convex
=> f(x) is increasing
f’’(x) < 0 => f(x) is convex
The maximum and minimum values of f(x) = 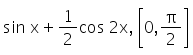 are
are- a)
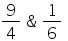
- b)
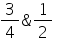
- c)
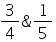
- d)
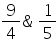
Correct answer is option 'B'. Can you explain this answer?
The maximum and minimum values of f(x) = 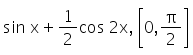 are
are
a)
b)
c)
d)
|
|
Aryan Khanna answered |
f(x) = sinx + 1/2cos2x
⇒ f'(x) = cos x – sin2x
Now, f'(x) = 0 gives cosx – sin2x = 0
⇒ cos x (1 – 2 sinx) = 0
⇒ cos x = 0, (1 – 2 sinx) = 0
⇒ cos x = 0, sinx = 1/2
⇒ x = π/6 , π/2
Now, f(0) = 1/2,
f(π/6) = 1/2 + 1/4 = 3/4,
f(π/2) = 1 – 1/2 = 1/2
Therefore, the absolute max value = 3/4 and absolute min = 1/2
⇒ f'(x) = cos x – sin2x
Now, f'(x) = 0 gives cosx – sin2x = 0
⇒ cos x (1 – 2 sinx) = 0
⇒ cos x = 0, (1 – 2 sinx) = 0
⇒ cos x = 0, sinx = 1/2
⇒ x = π/6 , π/2
Now, f(0) = 1/2,
f(π/6) = 1/2 + 1/4 = 3/4,
f(π/2) = 1 – 1/2 = 1/2
Therefore, the absolute max value = 3/4 and absolute min = 1/2
The function f (x) = -3x + 12 on R.is- a)increasing
- b)strictly decreasing
- c)decreasing
- d)neither increasing or decreasing
Correct answer is option 'B'. Can you explain this answer?
The function f (x) = -3x + 12 on R.is
a)
increasing
b)
strictly decreasing
c)
decreasing
d)
neither increasing or decreasing
|
|
Aryan Khanna answered |
f(x) = -3x + 12
f(0) = -3(0) + 12 = 0 - 12 = 0
f(1) = 9
f(2)= 6
f(3) = 3
f(4) = 0
f(5) = -3
f(0) = -3(0) + 12 = 0 - 12 = 0
f(1) = 9
f(2)= 6
f(3) = 3
f(4) = 0
f(5) = -3
The minimum value of the function defined by f(x) = max (x, x + 1, 2 – x) is- a)0
- b)1/2
- c)1
- d)3/2
Correct answer is option 'D'. Can you explain this answer?
The minimum value of the function defined by f(x) = max (x, x + 1, 2 – x) is
a)
0
b)
1/2
c)
1
d)
3/2
|
|
Leelu Bhai answered |
Bhai dekh iss func ka graph bana ....mtlb ki f(x) = x, f(x) = x+ 1 aur f(x) = 2 - x , ye teeno func ek hi graph pe.now see, jo f(x) = x aur f(x) = x+1 hai woh to kahi bhi intersect nhi krege qki dono ||ᵉˡ line hai..aur jab tu f(x) = 2 - x ka graph banaega to inn dono ko intersect karte hue jyega.ab jo top most intersection point wohi sbse tagda hoga aur wohi f(x) = max. {x, x + 1, 2 - x} ki value hogi...so, f(x) = x + 1 and f(x) = 2 - x ka intersection iss graph ka top point hai ... to isko solve krke x = 1/2 aa rha hai aur iss x ki value ko f(x) me put krde to uski value 3/2 aayegi...and according to ques the value of f(x) = max. {x, x + 1, 2 - x} is the minimum value of function.i hope u will understand....
The radius of a right circular cylinder of greatest curved surface which can be inscribed in a given right circular cone is- a) One third that of the cone
- b)1/
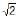 times that of the cone
times that of the cone - c) 2/3 that of the cone
- d)1/2 that of the cone
Correct answer is option 'D'. Can you explain this answer?
The radius of a right circular cylinder of greatest curved surface which can be inscribed in a given right circular cone is
a)
One third that of the cone
b)
1/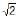 times that of the cone
times that of the cone
c)
2/3 that of the cone
d)
1/2 that of the cone
|
|
Rajat Patel answered |

Find two positive numbers x and y such that x + y = 60 and xy3 is maximum- a)x = 45, y = 15
- b)x = 15, y = 45
- c)x = 10, y = 50
- d)x = 30, y = 30
Correct answer is option 'B'. Can you explain this answer?
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum
a)
x = 45, y = 15
b)
x = 15, y = 45
c)
x = 10, y = 50
d)
x = 30, y = 30
|
|
Gaurav Kumar answered |
two positive numbers x and y are such that x + y = 60.
x + y = 60
⇒ x = 60 – y ...(1)
Let P = xy3
∴ P =(60 – y)y3 = 60y3 – y4
Differentiating both sides with respect to y, we get
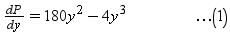
For maximum or minimum dP/dy = 0
⇒ 180y2 - 4y3 = 0
⇒ 4y2 (45 - y) = 0
⇒ y = 0 or 45 - y = 0
⇒ y = 0 or y = 45
⇒ y = 45 (∵ y = 0 is not possible)

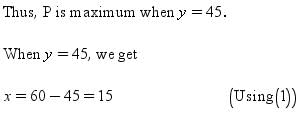
Thus, the two positive numbers are 15 and 45.
x + y = 60
⇒ x = 60 – y ...(1)
Let P = xy3
∴ P =(60 – y)y3 = 60y3 – y4
Differentiating both sides with respect to y, we get
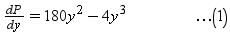
For maximum or minimum dP/dy = 0
⇒ 180y2 - 4y3 = 0
⇒ 4y2 (45 - y) = 0
⇒ y = 0 or 45 - y = 0
⇒ y = 0 or y = 45
⇒ y = 45 (∵ y = 0 is not possible)

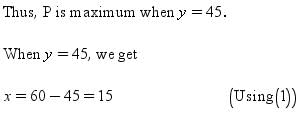
Thus, the two positive numbers are 15 and 45.
The maximum value of 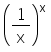 is
is- a)(1/e)1/e
- b)(e)2/e
- c)(e)-1/e
- d)(e)1/e
Correct answer is option 'D'. Can you explain this answer?
The maximum value of 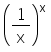 is
is
a)
(1/e)1/e
b)
(e)2/e
c)
(e)-1/e
d)
(e)1/e

|
Shiksha Academy answered |
For every real number (or) valued function f(x), the values of x which satisfies the equation f1(x)=0 are the point of it's local and global maxima or minima.
This occurs due to the fact that, at the point of maxima or minima, the curve of the function has a zero slope.
We have function f(x) = (1/x)x
We will be using the equation, y = (1/x)x
Taking in both sides we get
ln y = −xlnx
Differentiating both sides with respect to x.y.
dy/dx = −lnx−1
dy/dx =−y(lnx+1)
Equating dy/dx to 0, we get
−y(lnx+1)=0
Since y is an exponential function it can never be equal to zero, hence
lnx +1 = 0
lnx = −1
x = e(−1)
So, for the maximum value we put x = e^(−1)in f(x) to get the value of f(x) at the point.
f(e^−1) = e(1/e).
Hence the maximum value of the function is (e)1/e
This occurs due to the fact that, at the point of maxima or minima, the curve of the function has a zero slope.
We have function f(x) = (1/x)x
We will be using the equation, y = (1/x)x
Taking in both sides we get
ln y = −xlnx
Differentiating both sides with respect to x.y.
dy/dx = −lnx−1
dy/dx =−y(lnx+1)
Equating dy/dx to 0, we get
−y(lnx+1)=0
Since y is an exponential function it can never be equal to zero, hence
lnx +1 = 0
lnx = −1
x = e(−1)
So, for the maximum value we put x = e^(−1)in f(x) to get the value of f(x) at the point.
f(e^−1) = e(1/e).
Hence the maximum value of the function is (e)1/e
The equation of the tangent line to the curve y = 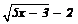 which is parallel to the line 4x -2y + 3 = 0 is
which is parallel to the line 4x -2y + 3 = 0 is
- a)80x +40y – 193 = 0
- b)4x – 2y – 3 = 0
- c)80x – 40y + 193 = 0
- d)80x – 40y – 103 = 0
Correct answer is option 'D'. Can you explain this answer?
The equation of the tangent line to the curve y = 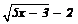 which is parallel to the line 4x -2y + 3 = 0 is
which is parallel to the line 4x -2y + 3 = 0 is
a)
80x +40y – 193 = 0
b)
4x – 2y – 3 = 0
c)
80x – 40y + 193 = 0
d)
80x – 40y – 103 = 0
|
|
Dabhi Bharat answered |
Given curve y=√5x-3 -2
y+2=√5x-3
dy/dx=5/2×√5x-3
m1=5/2(y+2)
given that line 4x-2y+3=0is parallel to tangent of curve
slope of line m2=2
m1=m2
5/2(y+2)=2
5/4=(y+2)
y=-3/4
from y+2=√5x-3
-3/4+2=√5x-3
5/4=√5x-3
5x=25/16+3
X=73/80
points are p(73/80,-3/4)
equ. of tangent :y-y1=m(x-x1)
y+3/4=2(x-73/80)
80x-73=40y+30
80x-40y-103=0
y+2=√5x-3
dy/dx=5/2×√5x-3
m1=5/2(y+2)
given that line 4x-2y+3=0is parallel to tangent of curve
slope of line m2=2
m1=m2
5/2(y+2)=2
5/4=(y+2)
y=-3/4
from y+2=√5x-3
-3/4+2=√5x-3
5/4=√5x-3
5x=25/16+3
X=73/80
points are p(73/80,-3/4)
equ. of tangent :y-y1=m(x-x1)
y+3/4=2(x-73/80)
80x-73=40y+30
80x-40y-103=0
The volume of cube is increasing at the constant rate of 3 cm3/s. Find the rate of change of edge of the cube when its edge is 5 cm.- a)25 cm3/sec
- b)25 cm/s
- c)1/25 cm/s
- d)1/25 cm3/s
Correct answer is option 'C'. Can you explain this answer?
The volume of cube is increasing at the constant rate of 3 cm3/s. Find the rate of change of edge of the cube when its edge is 5 cm.
a)
25 cm3/sec
b)
25 cm/s
c)
1/25 cm/s
d)
1/25 cm3/s
|
|
Aryan Khanna answered |
Let V be the instantaneous volume of the cube.
dV/dt = 3 cm3/s
Let x be the side of the cube.
V = x3
dV/dt = 3x2 * (dx/dt)
3 = 3*(52)*(dx/dt)
So, dx/dt = 1/25 cm/s
dV/dt = 3 cm3/s
Let x be the side of the cube.
V = x3
dV/dt = 3x2 * (dx/dt)
3 = 3*(52)*(dx/dt)
So, dx/dt = 1/25 cm/s
The length of the subtangent to the curve  =3 at the point (4, 1) is
=3 at the point (4, 1) is- a)2
- b)1/2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
The length of the subtangent to the curve  =3 at the point (4, 1) is
=3 at the point (4, 1) is
a)
2
b)
1/2
c)
3
d)
4
|
|
Anjali Sharma answered |
Length of subtangent =y(dx/dy)
Now given √x+√y=3
√y=3−√x
⇒1/2√ydy/dx = −1/(2√x) (On differentiating)
⇒dx/dy=−√x/√y
⇒ydx/dy=−√x/√y
⇒dx/dy/(4,1) = −√1√4
=−2
But the length can never be negative.
So length = 2.
Now given √x+√y=3
√y=3−√x
⇒1/2√ydy/dx = −1/(2√x) (On differentiating)
⇒dx/dy=−√x/√y
⇒ydx/dy=−√x/√y
⇒dx/dy/(4,1) = −√1√4
=−2
But the length can never be negative.
So length = 2.
f(x) = x5 – 5x4 + 5x3 – 1. The local maxima of the function f(x) is at x =- a)1
- b)5
- c)0
- d)3
Correct answer is option 'A'. Can you explain this answer?
f(x) = x5 – 5x4 + 5x3 – 1. The local maxima of the function f(x) is at x =
a)
1
b)
5
c)
0
d)
3
|
|
Rajat Patel answered |
f′(x)=5x4−20x3+15x2
f′(x)=5x2(x2−4x+3)
when f′(x)=0
⇒5x2(x2−4x+3)=0
⇒5x2(x−3)(x−1)=0
⇒x=0,x=3,x=1
Find the equation of tangent to 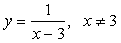 which has slope 2.
which has slope 2.- a)2x – y = 1
- b)No tangent
- c)y – 2x = 0
- d)y – 2x = 3
Correct answer is option 'B'. Can you explain this answer?
Find the equation of tangent to 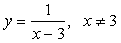 which has slope 2.
which has slope 2.
a)
2x – y = 1
b)
No tangent
c)
y – 2x = 0
d)
y – 2x = 3
|
|
Raghava Rao answered |
Y=1/(x-3)^2
dy/dx=(-1/(x-3)^2)
given slope=2
-1/(x-3)^2 =2
-1/2=(x-3)^2
negative number is not equal to square. so no tangent
dy/dx=(-1/(x-3)^2)
given slope=2
-1/(x-3)^2 =2
-1/2=(x-3)^2
negative number is not equal to square. so no tangent
The function f (x) = x3 has a- a)point of inflexion at = 0
- b)local minima at x = 0
- c)local maxima at x = 0
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The function f (x) = x3 has a
a)
point of inflexion at = 0
b)
local minima at x = 0
c)
local maxima at x = 0
d)
none of these

|
Amrita Sarkar answered |
f ‘(0) = 0 , f ‘’ (0) = 0 and f ‘’’(0) = 6 . So, f has a point of inflexion at 0.
In case of strict decreasing functions, slope of tangent and hence derivative is
- a)Negative
- b)either negative or zero.
- c)Zero
- d)Positive
Correct answer is option 'A'. Can you explain this answer?
In case of strict decreasing functions, slope of tangent and hence derivative is
a)
Negative
b)
either negative or zero.
c)
Zero
d)
Positive

|
Avantika Joshi answered |
In the case of strictly decreasing functions, the slope of the tangent line is always negative. This implies that the derivative of a strictly decreasing function is always negative. The derivative represents the rate of change of the function, and if the function is strictly decreasing, the rate of change is negative.
Read the following text and answer the following questions, on the basis of the same:An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below: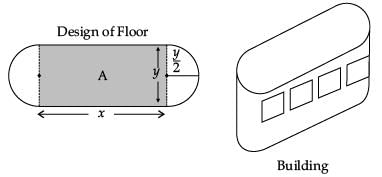 The extra area generated if the area of the whole floor is maximized is :
The extra area generated if the area of the whole floor is maximized is :- a)

- b)
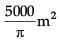
- c)
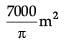
- d)No change. Both areas are equal.
Correct answer is option 'D'. Can you explain this answer?
Read the following text and answer the following questions, on the basis of the same:
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:

The extra area generated if the area of the whole floor is maximized is :
a)

b)
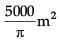
c)
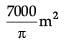
d)
No change. Both areas are equal.

|
Infinity Academy answered |


Let f (x) be differentiable in (0, 4) and f (2) = f (3) and S = {c : 2 < c < 3, f’ (c) = 0} then- a)S has exactly one point
- b)S = { }
- c)S has atleast one point
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Let f (x) be differentiable in (0, 4) and f (2) = f (3) and S = {c : 2 < c < 3, f’ (c) = 0} then
a)
S has exactly one point
b)
S = { }
c)
S has atleast one point
d)
none of these

|
Nandini Choudhury answered |
Conditions of Rolle’s Theorem are satisfied by f(x) in [2,3].Hence there exist atleast one real c in (2, 3) s.t. f ‘(c) = 0 . Therefore , the set S contains atleast one element
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The function y = [x(x – 2)]2 is increasing in (0, 1) ∪ (2, ∞)Reason (R): dy/dx = 0, when x = 0, 1, 2- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The function y = [x(x – 2)]2 is increasing in (0, 1) ∪ (2, ∞)
Reason (R): dy/dx = 0, when x = 0, 1, 2
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Varun Kapoor answered |
y = [x(x-2]2
= [x2 - 2x]2
∴ dy/dx = 2(x2 - 2x) (2x - 2)
or dy/dx = 4x(x-1)(x-2)
On equating dy/dx = 0
4x(x - 1)(x - 2) = 0 ⇒ x = 0, x = 1, x = 2
∴ Intervals are (-∞=, 0), (0,1), (1,2), (2,∞)
Since, dy/dx > 0 in (0,1) or (2, ∞)
∴ f(x) is increasing in (0,1) ∪ (2, ∞)
Both A and R are true. But R is not the correct explanation of A.
Chapter doubts & questions for Differentiation - Mathematics for Grade 12 2025 is part of Grade 12 exam preparation. The chapters have been prepared according to the Grade 12 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 12 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Differentiation - Mathematics for Grade 12 in English & Hindi are available as part of Grade 12 exam.
Download more important topics, notes, lectures and mock test series for Grade 12 Exam by signing up for free.
Mathematics for Grade 12
174 videos|103 docs|119 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

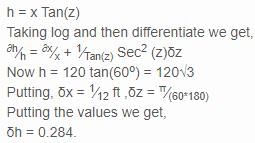

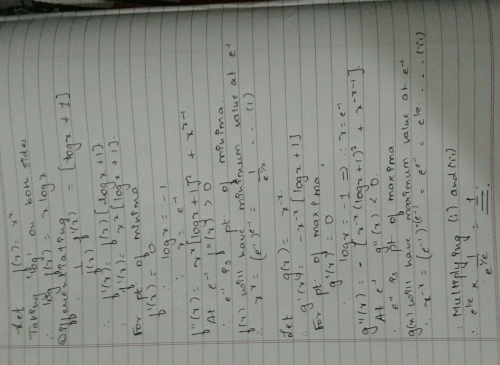


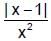 is monotonically decreasing in
is monotonically decreasing in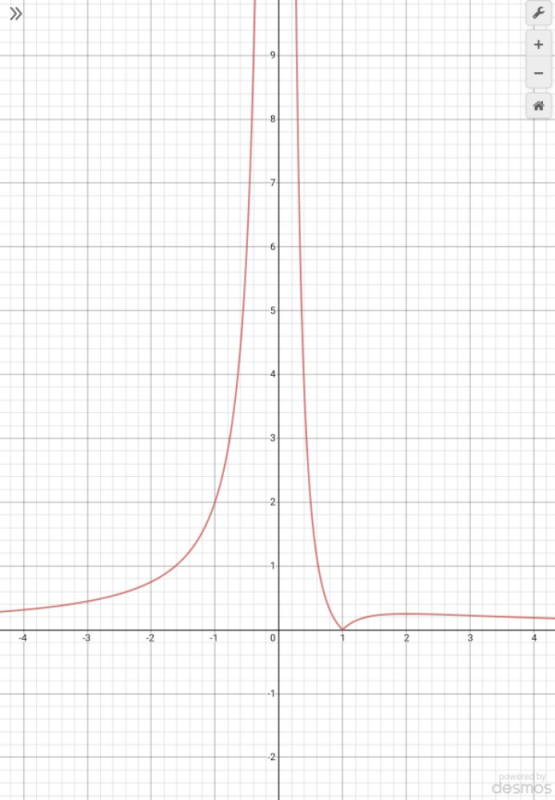
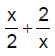 has a local minimum at
has a local minimum at