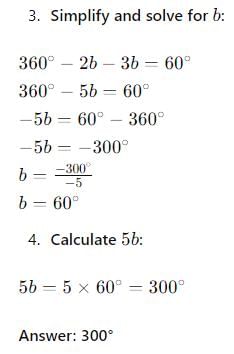All Exams >
EmSAT Achieve >
Mathematics for EmSAT Achieve >
All Questions
All questions of Geometric Theorems for EmSAT Achieve Exam
The degree measure of a semi-circle is- a)0°
- b)90°
- c)360°
- d)180°
Correct answer is option 'D'. Can you explain this answer?
The degree measure of a semi-circle is
a)
0°
b)
90°
c)
360°
d)
180°
|
Vikas Kapoor answered |
One circle measures 360 degrees. The half of the circle is called a semi-circle.
Thus, the measure of semi-circle
= 360/2 = 180 degree.
Thus, the measure of semi-circle
= 360/2 = 180 degree.
In the adjoining figure, AB ║ CD and AB ║ EF. The value of x is :-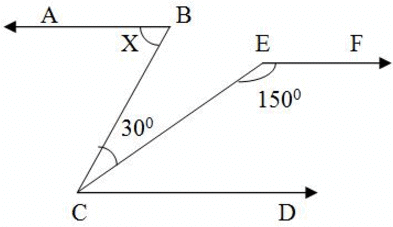
- a)400
- b)600
- c)700
- d)500
Correct answer is option 'B'. Can you explain this answer?
In the adjoining figure, AB ║ CD and AB ║ EF. The value of x is :-
a)
400
b)
600
c)
700
d)
500
|
Skyhigh Academy answered |
Given, AB ║ CD and AB ║ EF
so CD || EF
which means ∠ECD + ∠CEF = 1800 (corresponding angles)
∠ECD = 180 - 150 = 300
since AB || CD so
∠ABC= ∠BCD (alternate interior angles)
∠ABC = 30 + ∠ECD = 30 + 30 = 600
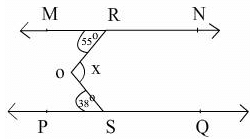
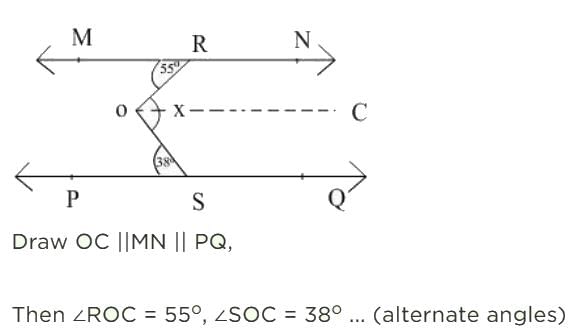
In the figure, PQ || MN, the value of x will be
- a)85°
- b)93°
- c)90°
- d)100°
Correct answer is option 'B'. Can you explain this answer?
In the figure, PQ || MN, the value of x will be
a)
85°
b)
93°
c)
90°
d)
100°
|
Nipun Tuteja answered |
Draw a line AB parallel to MN and PQ
In the figure below, the angle a = 150°. The other angle in the figure which is also 150° is: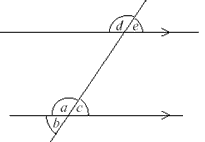
- a)e
- b)b
- c)d
- d)c
Correct answer is option 'C'. Can you explain this answer?
In the figure below, the angle a = 150°. The other angle in the figure which is also 150° is:
a)
e
b)
b
c)
d
d)
c
|
Let's Tute answered |
Correct Answer :- c
Explanation : Angle d is corresponding angle to a
so , if a = 150o
then d is also equal to 150o
Circles having the same centre and different radii are called- a)Equal circles
- b)Concentric circles
- c)Semi-circles
- d)Congruent circles
Correct answer is option 'B'. Can you explain this answer?
Circles having the same centre and different radii are called
a)
Equal circles
b)
Concentric circles
c)
Semi-circles
d)
Congruent circles
|
Hansa Sharma answered |
Concentric circles are circles with a common center. The region between two concentric circles of different radii is called an annulus.
Any two circles can be made concentric by inversion by picking the inversion center as one of the limiting points.
Two supplementary angles are in the ratio 4:5. The angles are :
- a)145°, 35°
- b)45°, 135°
- c)80°, 100°
- d)90°, 90°
Correct answer is 'C'. Can you explain this answer?
Two supplementary angles are in the ratio 4:5. The angles are :
a)
145°, 35°
b)
45°, 135°
c)
80°, 100°
d)
90°, 90°
|
Arun Sharma answered |
Let the angles be x
As they are in ratio of 4:5, so we can write it in the form of 4x ,5x
We know supplementary angle =180°
so,According to the question
4x+5x = 180°
9x = 180°
x = 180° ÷ 9
x = 20°
so, 1 st angle = 4x = 4×20° = 80°
2 nd angle = 5x = 5×20° = 100°
PROOF
4x + 5x = 180°
4×20° +5×20° = 180°
80°+ 100°= 180°
180° = 180°
As they are in ratio of 4:5, so we can write it in the form of 4x ,5x
We know supplementary angle =180°
so,According to the question
4x+5x = 180°
9x = 180°
x = 180° ÷ 9
x = 20°
so, 1 st angle = 4x = 4×20° = 80°
2 nd angle = 5x = 5×20° = 100°
PROOF
4x + 5x = 180°
4×20° +5×20° = 180°
80°+ 100°= 180°
180° = 180°
In the given figure, the value of y is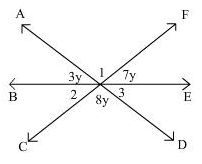
- a)35
- b)37
- c)10
- d)39
Correct answer is option 'C'. Can you explain this answer?
In the given figure, the value of y is
a)
35
b)
37
c)
10
d)
39
|
Nila Warrier answered |
We can write 1=8y(as they are vertically opposite angles)
so, 3y+8y+7y=180
18y=180
y=180/18
y=10
Hence Proved.
so, 3y+8y+7y=180
18y=180
y=180/18
y=10
Hence Proved.
In the figure, if O is the centre of the circle and ∠BOA = 120°, then the value of x is
- a)90°
- b)60°
- c)120°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
In the figure, if O is the centre of the circle and ∠BOA = 120°, then the value of x is
a)
90°
b)
60°
c)
120°
d)
30°
|
Naina Sharma answered |
∠BOA = 120° (Given)
∠AOC = 60° (Linear Pair)
∠AOC = 60° (Linear Pair)
In triangle OAC,
OA = OC (Radii of same circle)
∠OAC = ∠ OCA = x (angle opposite to equal sides are equal)
∵ ∠A + ∠C +∠O = 180°
⇒ x + x + 60 = 180°
⇒ 2x = 120°
⇒ x =60o
OA = OC (Radii of same circle)
∠OAC = ∠ OCA = x (angle opposite to equal sides are equal)
∵ ∠A + ∠C +∠O = 180°
⇒ x + x + 60 = 180°
⇒ 2x = 120°
⇒ x =60o
Given that AB || CD, intersected by a transversal, if the complement of ∠5 equals the supplement of ∠4, then the measures of ∠4 and ∠5 are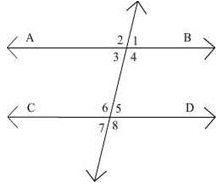
- a)∠4 = 105°, ∠5 = 60°
- b)∠4 = 120°, ∠5 = 80°
- c)∠4 = 45°, ∠5 = 145°
- d)∠4 = 135°, ∠5 = 45°
Correct answer is option 'D'. Can you explain this answer?
Given that AB || CD, intersected by a transversal, if the complement of ∠5 equals the supplement of ∠4, then the measures of ∠4 and ∠5 are
a)
∠4 = 105°, ∠5 = 60°
b)
∠4 = 120°, ∠5 = 80°
c)
∠4 = 45°, ∠5 = 145°
d)
∠4 = 135°, ∠5 = 45°
|
|
Jadhav Gajanan answered |
Because these are corresponding angles and their sum is 180'.
A circle divides the plane in which it lies into- a)4 parts
- b)5 parts
- c)3 parts
- d)2 parts
Correct answer is option 'C'. Can you explain this answer?
A circle divides the plane in which it lies into
a)
4 parts
b)
5 parts
c)
3 parts
d)
2 parts
|
|
Vikram Khanna answered |
A circle divides a plane into three parts: the points INSIDE the circle. the points OUTSIDE the circle. and the points ON the circle.
Can you explain the answer of this question below:Measure of an angle which is supplement of itself is :
- A:
450
- B:
300
- C:
900
- D:
1800
The answer is c.
Measure of an angle which is supplement of itself is :
450
300
900
1800
|
Naina Mukherjee answered |
Let the angle = x
Supplement of angle= 180-x
ATQ
180-x = x
180 = 2x
x = 90°
And its supplement will be 180-90=90°
Supplement of angle= 180-x
ATQ
180-x = x
180 = 2x
x = 90°
And its supplement will be 180-90=90°
If two parallel lines are intersected by a transversal then the bisectors of the interior angles form a :- a)rhombus
- b)parallogram
- c)Square
- d)Rectangle
Correct answer is option 'D'. Can you explain this answer?
If two parallel lines are intersected by a transversal then the bisectors of the interior angles form a :
a)
rhombus
b)
parallogram
c)
Square
d)
Rectangle
|
Arya Roy answered |
if two parallel lines are intersected by a transversal then prove that bisectors of the interior angles form a triangle.if two parallel lines are intersected by a transversal then prove that bisectors of the interior angles form a rectangle.
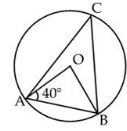
In the given figure, if ∠OAB = 40o then ∠ACB is equal to:
- a)60°
- b)50°
- c)40°
- d)70°
Correct answer is option 'B'. Can you explain this answer?
In the given figure, if ∠OAB = 40o then ∠ACB is equal to:
a)
60°
b)
50°
c)
40°
d)
70°
|
|
Let's Tute answered |
In triangle OAB
OA = OB (radius of a circle)
∠OAB = ∠OBA
∠OBA = 40º (angles opposite to equal sides are equal)
Using the angle sum property
∠AOB + ∠OBA + ∠BAO = 180º
Substituting the values
∠AOB + 40º + 40º = 180º
By further calculation
∠AOB + 80º = 180º
∠AOB = 180º - 80º
∠AOB = 100º
As the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle
∠AOB = 2 ∠ACB
Substituting the values
100º = 2 ∠ACB
Dividing both sides by 2
∠ACB = 50º
Therefore, ∠ACB is equal to 50º.
Two supplementary angles are in the ratio 4:5. The angles are :
- a)145°, 35°
- b)45°, 135°
- c)80°, 100°
- d)90°, 90°
Correct answer is option 'C'. Can you explain this answer?
Two supplementary angles are in the ratio 4:5. The angles are :
a)
145°, 35°
b)
45°, 135°
c)
80°, 100°
d)
90°, 90°
|
Mr.perfect answered |
given supplement angles are in ratio 4:5. let take 1st angle =4x 2nd angle=5x sum of two supplementary angle =180 so, 4x+5x=180 9x=180 x=180/9 x=20. therfore 1st angle =4x=4×20=80. 2nd angle=5x=5×20=100. required angles are 80,100. so correct answer is..(c) ........that's all my friends. .......(*_*)
In the figure, if O is the centre of a circle, then the measure of ∠ACB is: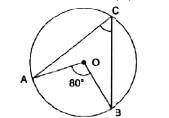
- a)180°
- b)60°
- c)40º
- d)45°
Correct answer is option 'C'. Can you explain this answer?
In the figure, if O is the centre of a circle, then the measure of ∠ACB is:
a)
180°
b)
60°
c)
40º
d)
45°
|
Ishan Choudhury answered |
The angle subtented by the arc at the centre is double the angle subtented by it at any point on the circle.
In the figure, AD is a straight line. OP is perpendicular to AD and O is the centre of both the circles. If AO = 34 cm, OB = 20 cm and OP = 16 cm, then the length of AD is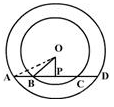
- a)20 cm
- b)50 cm
- c)60 cm
- d)43 cm
Correct answer is option 'C'. Can you explain this answer?
In the figure, AD is a straight line. OP is perpendicular to AD and O is the centre of both the circles. If AO = 34 cm, OB = 20 cm and OP = 16 cm, then the length of AD is
a)
20 cm
b)
50 cm
c)
60 cm
d)
43 cm
|
|
Sarthak Satav answered |
Here OPA is right angle triangle
given OP = 16 cm
AO = 34 cm
AP = ?
using Pythagoras theorem :
AO² = OP² + AP²
34² = 16² + AP²
1156 = 256 + AP²
1156 - 256 = AP²
900 = AP²
*√900 = AP*
30 = AP
Since AD is a straight line and O is at center of both circles
AD = AP + PD
AD = AP + AP
AD = 2AP
AD = 2 x 30
*AD = 60 CM*
In ΔABC fig., ∠x + ∠y + ∠z is equal to: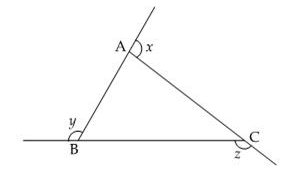
- a)360°
- b)120°
- c)240°
- d)180°
Correct answer is option 'A'. Can you explain this answer?
In ΔABC fig., ∠x + ∠y + ∠z is equal to:
a)
360°
b)
120°
c)
240°
d)
180°
|
|
Himaja Ammu answered |
Sum of exterior angles of a triangle is always 360
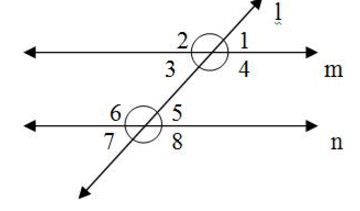
In the adjoining figure, if m ║ n, then ∠4 + ∠7 is equal to –
- a)1800
- b)1200
- c)1500
- d)900
Correct answer is option 'A'. Can you explain this answer?
In the adjoining figure, if m ║ n, then ∠4 + ∠7 is equal to –
a)
1800
b)
1200
c)
1500
d)
900
|
Imk Pathshala answered |
∠4 = ∠8 [ corresponding angles are equal]
∠7 + ∠8 = 180 [replacinig ∠8 by ∠4 ]
∠7 + ∠4 = 180
∠7 + ∠8 = 180 [replacinig ∠8 by ∠4 ]
∠7 + ∠4 = 180
A line that intersects a circle in two distinct points is a- a)Secant
- b)Chord
- c)Radius
- d)Diameter
Correct answer is option 'A'. Can you explain this answer?
A line that intersects a circle in two distinct points is a
a)
Secant
b)
Chord
c)
Radius
d)
Diameter
|
|
Vikram Khanna answered |
SECANT
In geometry, a secant of a curve is a line that intersects the curve in at least two (distinct) points.The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant will intersect the circle in exactly two points and a chord is the line segment determined by these two points, that is the interval on a secant whose endpoints are these points.
In geometry, a secant of a curve is a line that intersects the curve in at least two (distinct) points.The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant will intersect the circle in exactly two points and a chord is the line segment determined by these two points, that is the interval on a secant whose endpoints are these points.
If two angles are complementary of each other, then each angle is :
- a)An Obtuse angle
- b)A Right angle
- c)An Acute angle
- d)A supplementary angle
Correct answer is option 'C'. Can you explain this answer?
If two angles are complementary of each other, then each angle is :
a)
An Obtuse angle
b)
A Right angle
c)
An Acute angle
d)
A supplementary angle
|
Rachit Agrah.ari answered |
C is correct...If angles are complementary or of 90 degrees then each angle is acute angle because acute angles are those angles whose measure is less than 90 degree... ...Each angle will not be obtuse,right and not supplementary...
A pair of angles is called linear pair if sum of two adjacent angles is:- a)360°
- b)270°
- c)180°
- d)90°
Correct answer is option 'C'. Can you explain this answer?
A pair of angles is called linear pair if sum of two adjacent angles is:
a)
360°
b)
270°
c)
180°
d)
90°
|
Janhavi Sen answered |
A linear pair of angles is a pair of adjacent angles formed when two lines intersect. The sum of the measures of the two adjacent angles in a linear pair is always 180 degrees.
Explanation:
- A linear pair is formed when two lines intersect. The point of intersection is called the vertex.
- When two lines intersect, they form four angles. The angles that are adjacent to each other and share a common vertex are called adjacent angles.
- In a linear pair, the non-common sides of the adjacent angles form a straight line.
- The sum of the measures of the two adjacent angles in a linear pair is always 180 degrees. This is because the non-common sides of the adjacent angles form a straight line, which is a 180-degree angle.
- For example, if one angle in a linear pair measures 70 degrees, then the other angle must measure 180 - 70 = 110 degrees to make the sum of the two angles equal to 180 degrees.
Therefore, the correct answer is option C: 180.
Explanation:
- A linear pair is formed when two lines intersect. The point of intersection is called the vertex.
- When two lines intersect, they form four angles. The angles that are adjacent to each other and share a common vertex are called adjacent angles.
- In a linear pair, the non-common sides of the adjacent angles form a straight line.
- The sum of the measures of the two adjacent angles in a linear pair is always 180 degrees. This is because the non-common sides of the adjacent angles form a straight line, which is a 180-degree angle.
- For example, if one angle in a linear pair measures 70 degrees, then the other angle must measure 180 - 70 = 110 degrees to make the sum of the two angles equal to 180 degrees.
Therefore, the correct answer is option C: 180.
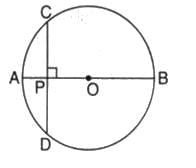
P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is
- a)16 cm
- b)20 cm
- c)10 cm
- d)8 cm
Correct answer is option 'A'. Can you explain this answer?
P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is
a)
16 cm
b)
20 cm
c)
10 cm
d)
8 cm
|
EduRev Class 9 answered |
AP+PB=AB [diameter of circle]
4+16=20[diameter]
so r=AO = CO=10
so clearly PO= OA-AP=10-4=6
PO=6 OC=10 So just apply pythagoreus theorem in triangle PCO
so CP will come 8 So chord CD = 2x8 = 16
4+16=20[diameter]
so r=AO = CO=10
so clearly PO= OA-AP=10-4=6
PO=6 OC=10 So just apply pythagoreus theorem in triangle PCO
so CP will come 8 So chord CD = 2x8 = 16
The region between an arc and the two radii joining the centre of the end points of the arc is called:a) A Segmentb) A Semicirclec) A Minor arcd) A SectorCorrect answer is option 'D'. Can you explain this answer?
|
|
Ananya Das answered |
The sector is the region between an arc and two radii joining the center to the endpoints of the arc.
Example: In the given figure, OAB is the sector of the circle.
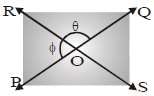
In the given figure, straight lines PQ and RS intersect at O. If the magnitude of θ is 3 times that of ϕ, then (∠ϕ) is equal to :
- a)30°
- b)40°
- c)45°
- d)60°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, straight lines PQ and RS intersect at O. If the magnitude of θ is 3 times that of ϕ, then (∠ϕ) is equal to :
a)
30°
b)
40°
c)
45°
d)
60°
|
Arizona Academy answered |
Correct option is C
In the above figure straight lines PQ and RS intersect at O.
It is given that θ=3ϕ .....(1)
∠POR and ∠QOR form linear pair of angles
Also ∠POR=ϕ and ∠QOR=θ
∠POR+∠QOR=180
ϕ+θ=180
ϕ+3ϕ=180 .....(From 1)
4ϕ=180
ϕ= 180/4 =45
Hence, ∠ϕ=45.
In the above figure straight lines PQ and RS intersect at O.
It is given that θ=3ϕ .....(1)
∠POR and ∠QOR form linear pair of angles
Also ∠POR=ϕ and ∠QOR=θ
∠POR+∠QOR=180
ϕ+θ=180
ϕ+3ϕ=180 .....(From 1)
4ϕ=180
ϕ= 180/4 =45
Hence, ∠ϕ=45.
The measure of angle a in the figure below is :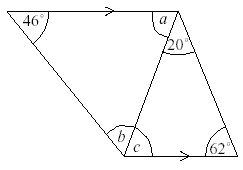
- a)98°
- b)78°
- c)62°
- d)80°
Correct answer is option 'A'. Can you explain this answer?
The measure of angle a in the figure below is :
a)
98°
b)
78°
c)
62°
d)
80°
|
Aarav Love answered |
Ad first u denote the name of figure like A B C then i explain it deplyyyy
If the arms of one angle are respectively parallel to the arms of another angle, then the two angles are :- a)Neither equal nor supplementary
- b)Not equal but supplementary
- c)Equal but not supplementary
- d)Either equal or supplementary
Correct answer is option 'D'. Can you explain this answer?
If the arms of one angle are respectively parallel to the arms of another angle, then the two angles are :
a)
Neither equal nor supplementary
b)
Not equal but supplementary
c)
Equal but not supplementary
d)
Either equal or supplementary
|
|
Imk Pathshala answered |
- Option A: "Neither equal nor supplementary"
This is incorrect because the angles will either be equal or supplementary. - Option B: "Not equal but supplementary"
This is partially correct but does not include the case when the angles are equal. - Option C: "Equal but not supplementary"
This is also partially correct but does not include the case when the angles are supplementary. - Option D: "Either equal or supplementary"
This is correct as it covers both possibilities.
If two angles are said to be supplementary angles and one of the angle is of 122° then the other angle is of
- a)35°
- b)58°
- c)60°
- d)32°
Correct answer is option 'B'. Can you explain this answer?
If two angles are said to be supplementary angles and one of the angle is of 122° then the other angle is of
a)
35°
b)
58°
c)
60°
d)
32°
|
Ravi Verma answered |
Let the angle be = x the supplement = 180o – x
According to the question,
180o – x
180o – 122o
58o
180o – x
180o – 122o
58o
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is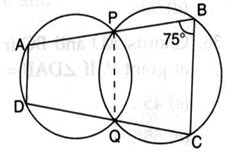
- a)75o
- b)125o
- c)105o
- d)150o
Correct answer is option 'C'. Can you explain this answer?
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is
a)
75o
b)
125o
c)
105o
d)
150o
|
Zachary Foster answered |
In the given figure, the points A, B, C, and D form a cyclic quadrilateral because they lie on the circumferences of the two intersecting circles.
The opposite angles of a cyclic quadrilateral are supplementary, i.e.,
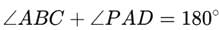
It is given that ∠ABC=75∘
Using the property of cyclic quadrilaterals:
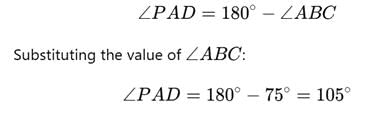
Choose the correct statement- a)If angles forming a linear pair are equal, then each of these angles measures 90°.
- b)Angles forming a linear pair can both be acute angles.
- c)If two adjacent angles are equal, then each angle measures 90°.
- d)Two angles whose sum is 90° are called supplementary angles.
Correct answer is option 'A'. Can you explain this answer?
Choose the correct statement
a)
If angles forming a linear pair are equal, then each of these angles measures 90°.
b)
Angles forming a linear pair can both be acute angles.
c)
If two adjacent angles are equal, then each angle measures 90°.
d)
Two angles whose sum is 90° are called supplementary angles.
|
|
Bhavya Desai answered |
B) If angles forming a linear pair are equal, then each of these angles measures 180.
An exterior angle of triangle is 80° and the interior opposite angles are in the ratio 1:3. Measure of each interior opposite angle is:
- a)30°, 60°
- b)30°, 90°
- c)40°, 120°
- d)20°, 60°
Correct answer is option 'D'. Can you explain this answer?
An exterior angle of triangle is 80° and the interior opposite angles are in the ratio 1:3. Measure of each interior opposite angle is:
a)
30°, 60°
b)
30°, 90°
c)
40°, 120°
d)
20°, 60°
|
|
Ananya shah answered |
so interior angle corresponding to 80° will be 100°
let there ratio be x so angles would be x and 3x
x + 3x + 100° = 180°
4x = 80°
x = 20°
so x and 3x will be 20° and 60° respectively
let there ratio be x so angles would be x and 3x
x + 3x + 100° = 180°
4x = 80°
x = 20°
so x and 3x will be 20° and 60° respectively
The longest chord of the circle is the- a)secant
- b)perpendicular
- c)diameter
- d)radius
Correct answer is option 'C'. Can you explain this answer?
The longest chord of the circle is the
a)
secant
b)
perpendicular
c)
diameter
d)
radius
|
Rachit Agrah.ari answered |
Diameter is the Longest Chord of the Circle...So, 'C' is correct..
Find the measure of the angle which is complement of itself.- a)30°
- b)90°
- c)45°
- d)180°
Correct answer is option 'C'. Can you explain this answer?
Find the measure of the angle which is complement of itself.
a)
30°
b)
90°
c)
45°
d)
180°
|
|
Ravi Verma answered |
Let the angle be x. Its complement will be 90 - x. Therefore,
x = 90 - x
=> 2x = 90
=> x = 45 degree
The answer is 45 degree.
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is- a)45o
- b)30o
- c)60o
- d)90o
Correct answer is option 'B'. Can you explain this answer?
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is
a)
45o
b)
30o
c)
60o
d)
90o
|
|
Zachary Foster answered |
Let AB be the chord of the circle with center O
.
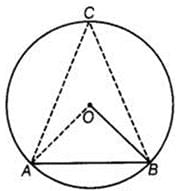
Given that AB = Radius of the circle.
Also, AO = BO = Radius
∴ ΔOAB is an equilateral triangle.
Thus, ∠AOB = ∠OBA = ∠OAB = 60°
Also, angle subtended by an arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = 1/2 (∠AOB)
⇒ ∠ACB = 1/2 (60°) = 30°
The angle whose complement is one-third of its supplement will be- a)135°
- b)90°
- c)180°
- d)45°
Correct answer is option 'D'. Can you explain this answer?
The angle whose complement is one-third of its supplement will be
a)
135°
b)
90°
c)
180°
d)
45°
|
|
Sarita Reddy answered |
Let the angle be 'xdegree'Then complement of that angle -- (90- x)degreeSupplement of that angle -- (180 - x)degreeA/Q ---.>90 - x = 1/3( 180 - x)90 - x = 60 - x/3-x + x/3 = 60 - 90[ - 3x + x] / 3 = - 30-2x/3 = -30x = 30 x 3/2x = 45degreeThe required angle is 45degree.
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions: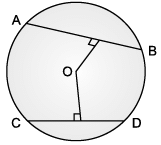
Q. What is the length of AB?- a)12 cm
- b)11 cm
- c)16 cm
- d)8 cm
Correct answer is option 'C'. Can you explain this answer?
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:
Q. What is the length of AB?
a)
12 cm
b)
11 cm
c)
16 cm
d)
8 cm
|
Netbhet Solutions answered |
Length of AB = 16 cm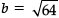
h2 = p2 + b2
102 = 62 + b2
100 = 36 + b2
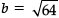
= 8 cm
AB = 8 + 8
= 16 cm
Find the angle which is four times its compliment is 10° less than twice its complement. - a)15°
- b)10°
- c)25°
- d)5°
Correct answer is option 'D'. Can you explain this answer?
Find the angle which is four times its compliment is 10° less than twice its complement.
a)
15°
b)
10°
c)
25°
d)
5°
|
Sounak Sengupta answered |
If we call the angle a, then...
4(90 - a) = 2(180 - a) - 10
360 - 4a = 360 - 2a - 10
2a = 10
a = 5 deg
If two parallel lines are cut by a transversal, then the pairs of ___________ angles are congruent.
- a)Equal
- b)Complementary
- c)Supplementary
- d)corresponding
Correct answer is option 'D'. Can you explain this answer?
If two parallel lines are cut by a transversal, then the pairs of ___________ angles are congruent.
a)
Equal
b)
Complementary
c)
Supplementary
d)
corresponding
|
|
Vivek Rana answered |
If two parallel lines are cut by a transversal, the corresponding angles are congruent. If two lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel.
In the figure if AB ||CD, ∠APQ = 50° and ∠PRD = 127° then y is equal to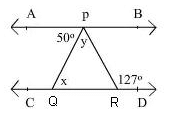
- a)40°
- b)45°
- c)90°
- d)77°
Correct answer is option 'D'. Can you explain this answer?
In the figure if AB ||CD, ∠APQ = 50° and ∠PRD = 127° then y is equal to
a)
40°
b)
45°
c)
90°
d)
77°
|
Papa's Little Princess answered |
X=50,x+y=127(exterior angle theorem)50+y=127y=127-50y=77
Chapter doubts & questions for Geometric Theorems - Mathematics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Geometric Theorems - Mathematics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Mathematics for EmSAT Achieve
146 videos|222 docs|220 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup