All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Rotational Kinematics for EmSAT Achieve Exam
Which of the following relations is wrong?- a)
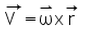
- b)
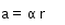
- c)
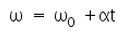
- d)
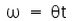
Correct answer is option 'D'. Can you explain this answer?
Which of the following relations is wrong?
a)
b)
c)
d)
|
Gaurav Kumar answered |
Just like the equations of motion in 1D, we get the equations of motion for rotation.
We know that s = d/t, analogous to it is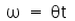
Hence D is the correct answer.
We know that s = d/t, analogous to it is
Hence D is the correct answer.
A right triangular plate ABC of mass m is free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is :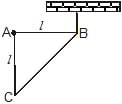 
- a)
- b)
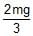
- c)
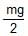
- d)mg
Correct answer is option 'B'. Can you explain this answer?
A right triangular plate ABC of mass m is free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is :
a)
b)
c)
d)
mg
|
Crafty Classes answered |
The distance of Centre Of Mass of the given right angled triangle is 2L/3 along BA and L/3 along AC from the point B.
Force of magnitude mg is acting downwards at its COM.
Moment balance around B gives:
mg(2L/3)−FA(L)=0
(Moment= × =rFsin(θ)=F(rsin(θ))=Fr⊥)
∴FA=2mg/3
Force of magnitude mg is acting downwards at its COM.
Moment balance around B gives:
mg(2L/3)−FA(L)=0
(Moment= × =rFsin(θ)=F(rsin(θ))=Fr⊥)
∴FA=2mg/3
A body is moving with a constant speed v in a circle of radius r. What is the angular acceleration?- a)α = vt/r
- b)α = vr/t
- c)α = v/rt
- d)α = 0
Correct answer is option 'D'. Can you explain this answer?
A body is moving with a constant speed v in a circle of radius r. What is the angular acceleration?
a)
α = vt/r
b)
α = vr/t
c)
α = v/rt
d)
α = 0
|
Abhishek Pandey answered |
When a body performs circular motion it has got two accelerations radial acc. And tangential acc. Radial acc. Is responsible for changing the direction of velocity of body but tangential acc. Is responsible for changing the magnitide of velocity of body. As the body is moving with constant speed so tangential acc. Is zero. As we know that tangential acc. = radius * angular acc. So angular acc.is zero.
A rotating machine is maintained at a uniform angular speed of 150 rad s-1, with a torque of 100 Nm. The power is- a)15 kW
- b)1.5 kW
- c)1500 kW
- d)0.15 kW
Correct answer is option 'A'. Can you explain this answer?
A rotating machine is maintained at a uniform angular speed of 150 rad s-1, with a torque of 100 Nm. The power is
a)
15 kW
b)
1.5 kW
c)
1500 kW
d)
0.15 kW
|
Suresh Reddy answered |
Power = torque × angular velocity
P = 100 × 150
P = 15000 W
P = 15KW
P = 100 × 150
P = 15000 W
P = 15KW
In the pulley system shown, if radii of the bigger and smaller pulley are 2 m and 1 m respectively and the acceleration of block ‘A’ is 5 m/s2 in the downward direction , then the acceleration of block B will be :
- a)0 m / s2
- b)5 m / s2
- c) 10 m / s2
- d) 5 / 2 m / s2
Correct answer is option 'D'. Can you explain this answer?
In the pulley system shown, if radii of the bigger and smaller pulley are 2 m and 1 m respectively and the acceleration of block ‘A’ is 5 m/s2 in the downward direction , then the acceleration of block B will be :
a)
0 m / s2
b)
5 m / s2
c)
10 m / s2
d)
5 / 2 m / s2
|
|
Anjali Sharma answered |
Since both pulley are connected to each other. So, their angular acceleration are equal.
⇒α1=α2⇒a1/ r1=a2/ r2 because α=a/r
⇒a1/1=5/2(Given, a2=5m/s2)
⇒a1=5/2 m/s2
Therefore, D is the correct option.
⇒α1=α2⇒a1/ r1=a2/ r2 because α=a/r
⇒a1/1=5/2(Given, a2=5m/s2)
⇒a1=5/2 m/s2
Therefore, D is the correct option.
A homogeneous cubical brick lies motionless on a rough inclined surface. The half of the brick which applies greater pressure on the plane is :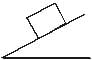 
- a) Left half
- b)Right half
- c)Both applies equal pressure
- d)The answer depend upon coefficient of friction
Correct answer is option 'A'. Can you explain this answer?
A homogeneous cubical brick lies motionless on a rough inclined surface. The half of the brick which applies greater pressure on the plane is :
a)
Left half
b)
Right half
c)
Both applies equal pressure
d)
The answer depend upon coefficient of friction
|
Mohit Rajpoot answered |
As weight of the body (mg) acts along the left side i.e. mg sinx acts along flow of object.
mgcosx acts perpendicular to flow of the object.
The pressure of right half comes on left half hence left half has maximum pressure.
mgcosx acts perpendicular to flow of the object.
The pressure of right half comes on left half hence left half has maximum pressure.
Can you explain the answer of this question below:The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by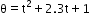 
. The linear velocity of the particle
- A:
1.84 m/s
- B:
1.80 m/s
- C:
1.82 m/s
- D:
1.88 m/s
The answer is a.
The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by 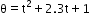. The linear velocity of the particle
1.84 m/s
1.80 m/s
1.82 m/s
1.88 m/s
|
Knowledge Hub answered |
The answer is option A
So, as we know,
After differentiating angular velocity with respect to t,
Linear velocity=2t+2.3=ω
Now,
Velocity=r x ω(where r is 0.8m)
=0.8x2.3
=1.84m/s
So, as we know,
After differentiating angular velocity with respect to t,
Linear velocity=2t+2.3=ω
Now,
Velocity=r x ω(where r is 0.8m)
=0.8x2.3
=1.84m/s
A small cylinder rolling with a velocity v along a horizontal surface encounters a smooth inclined surface. The height ‘h’ up to which the cylinder will ascend is- a)3v2/4g
- b)v2/2g
- c)3v2/2g
- d)v2/4g
Correct answer is option 'B'. Can you explain this answer?
A small cylinder rolling with a velocity v along a horizontal surface encounters a smooth inclined surface. The height ‘h’ up to which the cylinder will ascend is
a)
3v2/4g
b)
v2/2g
c)
3v2/2g
d)
v2/4g
|
|
Shreya Gupta answered |
A body can roll along a surface only if the surface is rough. The body will roll up to the foot of the inclined smooth surface. It will continue to spin with the angular speed it has acquired, and will slide up to a certain height, maintaining its spin motion throughout the smooth surface. Its translational kinetic energy alone is responsible for its upward motion along the smooth incline so that the height up to which it will rise is given by
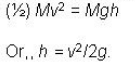
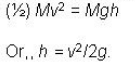
A rigid body is rotating about an axis. Different particles are at different distances from the axis. Which of the following is true?- a)Different particles possess the same angular acceleration
- b)Different particles possess the same angular velocity
- c)Different particles possess the same linear acceleration
- d)Different particles possess the same linear velocity.
Correct answer is option 'B'. Can you explain this answer?
A rigid body is rotating about an axis. Different particles are at different distances from the axis. Which of the following is true?
a)
Different particles possess the same angular acceleration
b)
Different particles possess the same angular velocity
c)
Different particles possess the same linear acceleration
d)
Different particles possess the same linear velocity.
|
|
Suresh Reddy answered |
In the fixed axis rotation we see that every point on the body has two components of velocity, one in the radial direction and one in the tangential direction. The resultant of these velocities is not the same for any two points lying in the plane of the body.
Any two points on the radial line have the radial acceleration directed towards the center of equal magnitude and the tangential acceleration of equal magnitude as well. Thus option B is correct.
All the particles lying on the curved surface of a cylinder whose axis coincides with the axis of rotation have the same speed but different velocities.
Any two points on the radial line have the radial acceleration directed towards the center of equal magnitude and the tangential acceleration of equal magnitude as well. Thus option B is correct.
All the particles lying on the curved surface of a cylinder whose axis coincides with the axis of rotation have the same speed but different velocities.
A solid sphere and a hollow sphere of the same mass have the same moments of inertia about their respective diameters, the ratio of their radii is- a)(5)1/2 : (3)1/2
- b) (3)1/2 : (5)1/2
- c)3 : 2
- d)2 : 3
Correct answer is option 'A'. Can you explain this answer?
A solid sphere and a hollow sphere of the same mass have the same moments of inertia about their respective diameters, the ratio of their radii is
a)
(5)1/2 : (3)1/2
b)
(3)1/2 : (5)1/2
c)
3 : 2
d)
2 : 3
|
|
Gaurav Kumar answered |
We know moment of inertia of solid sphere Is=2/5msRs2 and
moment of inertia of hollow sphere IH=2/3mHRH2 As per question Is=IH
Now,
2/5msRs2=2/3mHRH2
as the masses are equal the ratio of their radii will be
Rs2 /RH2 =2/3/2/5=√5/3=(5)1/2: (3)1/2
moment of inertia of hollow sphere IH=2/3mHRH2 As per question Is=IH
Now,
2/5msRs2=2/3mHRH2
as the masses are equal the ratio of their radii will be
Rs2 /RH2 =2/3/2/5=√5/3=(5)1/2: (3)1/2
A disc of radius b and mass m rolls down an inclined plane of vertical height h. the translational speed when it reaches the bottom of the plane will be - a)
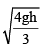
- b)
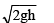
- c)
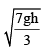
- d)
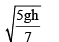
Correct answer is option 'A'. Can you explain this answer?
A disc of radius b and mass m rolls down an inclined plane of vertical height h. the translational speed when it reaches the bottom of the plane will be
a)
b)
c)
d)
|
Preeti Iyer answered |
The difference in the potential of the body when it rolls down through a vertical height h, is mgh.
As the KE at the top point is zero and let say KE at bottom is ½ mv2 + ½ Iw2
Where m is its mass, I is its moment of inertia, I = ½ mr2
Where r is its radius, v is its gained translational speed and w is its gained angular speed.
w = v/r
Hence equating PE and KE gives
mgh = ½ mv2 + ½ Iw2
That is mgh = ½ mv2 + ½ mr2.(v/r)2
We get mgh = ½ mv2 + ¼ mv2
Thus we get v = √gh/3
As the KE at the top point is zero and let say KE at bottom is ½ mv2 + ½ Iw2
Where m is its mass, I is its moment of inertia, I = ½ mr2
Where r is its radius, v is its gained translational speed and w is its gained angular speed.
w = v/r
Hence equating PE and KE gives
mgh = ½ mv2 + ½ Iw2
That is mgh = ½ mv2 + ½ mr2.(v/r)2
We get mgh = ½ mv2 + ¼ mv2
Thus we get v = √gh/3
A uniform rod of length L and mass M is bent to make a reactangle PQRS such that QR/PQ = 1/2 Moment of inertia of the rectangle about the side QR can be expressed as :
- a)
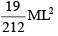
- b)
- c)
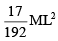
- d)
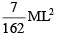
Correct answer is option 'D'. Can you explain this answer?
A uniform rod of length L and mass M is bent to make a reactangle PQRS such that QR/PQ = 1/2 Moment of inertia of the rectangle about the side QR can be expressed as :
a)
b)
c)
d)
|
Sushil Kumar answered |
Firstly, using the relations given in the questions, we will find the length and mass of the parts
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4 kg m2.- a)12 kg m2
- b)3 kg m2
- c)6 kg m2
- d)9 kg m2
Correct answer is option 'C'. Can you explain this answer?
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4 kg m2.
a)
12 kg m2
b)
3 kg m2
c)
6 kg m2
d)
9 kg m2
|
Naina Sharma answered |
At tangent I =MR2/2 + MR2 --- (1)
MR2/2 = 4, MR2 = 8 then substitute in (1) you will get I = 12, this is for tangent perpendicular to plane then divide by 2 you will get tangent along the plane
MR2/2 = 4, MR2 = 8 then substitute in (1) you will get I = 12, this is for tangent perpendicular to plane then divide by 2 you will get tangent along the plane
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is- a)4 unit
- b)6 unit
- c)8 unit
- d)10 unit
Correct answer is option 'D'. Can you explain this answer?
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is
a)
4 unit
b)
6 unit
c)
8 unit
d)
10 unit
|
Krishna Iyer answered |
We know that for a disc of mass m and radius r
MI of a disc about its diameter = mr2/4 = 2
And also MI about a point on its rim = mr2/4 + mr2
= 5mr2/4
= 5 x 2 = 10
MI of a disc about its diameter = mr2/4 = 2
And also MI about a point on its rim = mr2/4 + mr2
= 5mr2/4
= 5 x 2 = 10
A CD accelerates uniformly from rest to 200 spins per minute in 8 seconds. If the rate of change of speed is constant, determine the instantaneous acceleration in rad/s2 .- a)200.2 π rad/s2
- b)25 rad/ s2
- c)20.9 rad/ s2
- d)2.6 rad/ s2
Correct answer is option 'D'. Can you explain this answer?
A CD accelerates uniformly from rest to 200 spins per minute in 8 seconds. If the rate of change of speed is constant, determine the instantaneous acceleration in rad/s2 .
a)
200.2 π rad/s2
b)
25 rad/ s2
c)
20.9 rad/ s2
d)
2.6 rad/ s2
|
Varun Kapoor answered |
The correct option is A
2.6 rad/ s2
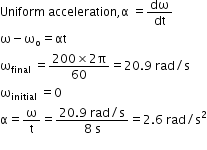
The moment of inertia and rotational kinetic energy of a fly wheel are 20kg-m2 and 1000 joule respectively. Its angular frequency per minute would be -- a)600/π
- b)25/π2
- c)5/π
- d)300/π
Correct answer is option 'D'. Can you explain this answer?
The moment of inertia and rotational kinetic energy of a fly wheel are 20kg-m2 and 1000 joule respectively. Its angular frequency per minute would be -
a)
600/π
b)
25/π2
c)
5/π
d)
300/π
|
Riya Banerjee answered |
Rotational K.E. = ½ × moment of inertia × square of angular velocity = ½Iw2
Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
- a) 3 ml2
- b) ml2
- c) 2 ml2
- d) √3 ml2
Correct answer is option 'A'. Can you explain this answer?
Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
a)
3 ml2b)
ml2c)
2 ml2d)
√3 ml2|
|
Raghav Bansal answered |
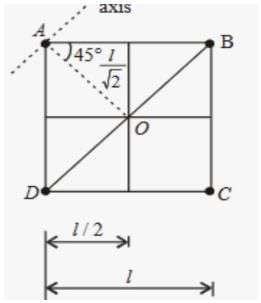
IA=0 (on the Axis .)
IB=ID=mr2
=m(l/√2)2
=ml2/2
IC=m(√2l)2
IC=2ml2
I=IA+IB+IC+ID
I=0+ml2/2+ml2/2+2ml2
I=3ml2
An automobile engine develops 100H.P. when rotating at a speed of 1800 rad/min. The torque it delivers is- a)3.33 W-s
- b)200W-s
- c)248.7 W-s
- d)2487 W-s
Correct answer is option 'D'. Can you explain this answer?
An automobile engine develops 100H.P. when rotating at a speed of 1800 rad/min. The torque it delivers is
a)
3.33 W-s
b)
200W-s
c)
248.7 W-s
d)
2487 W-s
|
Manish Aggarwal answered |
100 HP = 74570 W or 74.57 KW Now, P = 2*π*N*T/60 where, P is the power (in W), N is the operating speed of the engine (in r.p.m.) and T is the Torque (in N.m). Therefore, 74570 = 2*π*1800*T/60 i.e. T = 395.606 N.m
Two rings of radius R and nR made up of same material have the ratio of moment of inertia about an axis passing through centre is 1 : 8. The value of n is- a)2
- b)2√2
- c)4
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Two rings of radius R and nR made up of same material have the ratio of moment of inertia about an axis passing through centre is 1 : 8. The value of n is
a)
2
b)
2√2
c)
4
d)
1/2
|
Naman Flora answered |
Answer should be B as moment of inertia of ring Mr^2 and Mn^2R^2 Mn^2r^2/Mr^2=1/8 ; solving we get n^2=8 and n=2root2
A mixer grinder rotates clockwise, its angular velocity will be :- a)zero
- b)negative
- c)uniform but not zero
- d)positive
Correct answer is option 'B'. Can you explain this answer?
A mixer grinder rotates clockwise, its angular velocity will be :
a)
zero
b)
negative
c)
uniform but not zero
d)
positive
|
Ashish Roy answered |
**Explanation:**
A mixer grinder is a device that is used for grinding and mixing various ingredients. It consists of a motor and a set of blades that rotate at high speeds to perform the grinding and mixing tasks. When the mixer grinder is turned on, the motor starts rotating the blades in a clockwise direction.
**Angular Velocity:**
Angular velocity is a measure of how quickly an object rotates or moves around a central point. It is defined as the rate of change of angular displacement with respect to time. The direction of the angular velocity is determined by the direction of rotation. In the case of a mixer grinder rotating clockwise, the angular velocity will be negative.
**Direction of Angular Velocity:**
The direction of angular velocity is determined by the right-hand rule. According to the right-hand rule, if the fingers of the right hand curl in the direction of rotation, the thumb will point in the direction of the angular velocity vector. In the case of a mixer grinder rotating clockwise, the fingers of the right hand curl in the clockwise direction, and the thumb points in the opposite direction, which is counterclockwise or negative.
**Significance of Negative Angular Velocity:**
A negative angular velocity indicates that the object is rotating in the opposite direction compared to the conventional positive direction. In the case of a mixer grinder, a negative angular velocity means that the blades are rotating counterclockwise when viewed from above. This counterclockwise rotation is necessary for the blades to effectively grind and mix the ingredients.
**Conclusion:**
In conclusion, a mixer grinder rotates clockwise, which means its angular velocity will be negative. The negative angular velocity indicates that the blades are rotating counterclockwise when viewed from above, allowing them to efficiently perform the grinding and mixing tasks.
A mixer grinder is a device that is used for grinding and mixing various ingredients. It consists of a motor and a set of blades that rotate at high speeds to perform the grinding and mixing tasks. When the mixer grinder is turned on, the motor starts rotating the blades in a clockwise direction.
**Angular Velocity:**
Angular velocity is a measure of how quickly an object rotates or moves around a central point. It is defined as the rate of change of angular displacement with respect to time. The direction of the angular velocity is determined by the direction of rotation. In the case of a mixer grinder rotating clockwise, the angular velocity will be negative.
**Direction of Angular Velocity:**
The direction of angular velocity is determined by the right-hand rule. According to the right-hand rule, if the fingers of the right hand curl in the direction of rotation, the thumb will point in the direction of the angular velocity vector. In the case of a mixer grinder rotating clockwise, the fingers of the right hand curl in the clockwise direction, and the thumb points in the opposite direction, which is counterclockwise or negative.
**Significance of Negative Angular Velocity:**
A negative angular velocity indicates that the object is rotating in the opposite direction compared to the conventional positive direction. In the case of a mixer grinder, a negative angular velocity means that the blades are rotating counterclockwise when viewed from above. This counterclockwise rotation is necessary for the blades to effectively grind and mix the ingredients.
**Conclusion:**
In conclusion, a mixer grinder rotates clockwise, which means its angular velocity will be negative. The negative angular velocity indicates that the blades are rotating counterclockwise when viewed from above, allowing them to efficiently perform the grinding and mixing tasks.
A 2 m rod of mass 1 kg rotates at an angular speed of 15 rad/s about its ends. Then K.E. is- a)150 J
- b)1500 J
- c)100 J
- d)1.5 J
Correct answer is option 'A'. Can you explain this answer?
A 2 m rod of mass 1 kg rotates at an angular speed of 15 rad/s about its ends. Then K.E. is
a)
150 J
b)
1500 J
c)
100 J
d)
1.5 J
|
|
Knowledge Hub answered |
Given,
l=2m
m=1kg
ω=15rd//s
K.E.=1/2I ω
=1/2x(ml2/3) ω2
=1/2x(1x4/3)(15)2
=150J
l=2m
m=1kg
ω=15rd//s
K.E.=1/2I ω
=1/2x(ml2/3) ω2
=1/2x(1x4/3)(15)2
=150J
A thin rod of length 4 l , mass 4 m is bent at the points as shown in the fig. What is the moment of inertia of the rod about the axis passing through point O and perpendicular to the plane of the paper :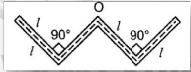 
- a)ml2/3
- b)10ml2/3
- c)ml2/12
- d)ml2/24
Correct answer is option 'B'. Can you explain this answer?
A thin rod of length 4 l , mass 4 m is bent at the points as shown in the fig. What is the moment of inertia of the rod about the axis passing through point O and perpendicular to the plane of the paper :
a)
ml2/3
b)
10ml2/3
c)
ml2/12
d)
ml2/24
|
|
Krishna Iyer answered |
Since the mass of rod is 54m and length is 4l.
so mass C = m
and length of AB = BO=OC= CD = l
WE, know moment of Inertia of a rod about to end = ml2/3
So, moment of Inertia of AB, BO, OC, CD about B, O, O, C respectively = ml2/3
From parallel axis theorem
Moment of Inertia of AB about O.
=ml2/3+ml2=4ml2/3
Similarly od CD about O =4ml2/3
SO moment of Inertia Rod about O
=ml2/3+ml2/3+4ml2/3+4ml2/3
=10ml2/3
so mass C = m
and length of AB = BO=OC= CD = l
WE, know moment of Inertia of a rod about to end = ml2/3
So, moment of Inertia of AB, BO, OC, CD about B, O, O, C respectively = ml2/3
From parallel axis theorem
Moment of Inertia of AB about O.
=ml2/3+ml2=4ml2/3
Similarly od CD about O =4ml2/3
SO moment of Inertia Rod about O
=ml2/3+ml2/3+4ml2/3+4ml2/3
=10ml2/3
Fig shows a flywheel of radius 10 cm. Its moment of inertia about the rotation axis is 0.4 kg m2. A massless string passes over the flywheel and a mass 2 kg is attached at its lower end. Angular acceleration of the mass in rad/s2 is nearly.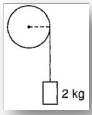 
- a)4.8 rad/s2
- b)6.2 rad/s2
- c) 3.2 rad/s2
- d) 9.6 rad/s2
Correct answer is option 'A'. Can you explain this answer?
Fig shows a flywheel of radius 10 cm. Its moment of inertia about the rotation axis is 0.4 kg m2. A massless string passes over the flywheel and a mass 2 kg is attached at its lower end. Angular acceleration of the mass in rad/s2 is nearly.
a)
4.8 rad/s2
b)
6.2 rad/s2
c)
3.2 rad/s2
d)
9.6 rad/s2
|
|
Mohit Rajpoot answered |
I took g = 10 but if g = 9.8 is taken then we get the exact answer.
An inclined plane makes an angle of 30o with the horizontal. A ring rolling down this inclinedplane from rest without slipping has a linear acceleration equal to :- a)2g/3
- b)g/2
- c)g/3
- d)g/4
Correct answer is option 'D'. Can you explain this answer?
An inclined plane makes an angle of 30o with the horizontal. A ring rolling down this inclinedplane from rest without slipping has a linear acceleration equal to :
a)
2g/3
b)
g/2
c)
g/3
d)
g/4
|
|
Neha Joshi answered |
We know for a rolling body acceleration down an inclined plane, a = g.sinθ / (1 + I/mR2)
Where I is body's moment of inertia. Here, I = mR2
Thus just by putting the values to the formula we get
a = g.sin 30° / 2
= g/4
Where I is body's moment of inertia. Here, I = mR2
Thus just by putting the values to the formula we get
a = g.sin 30° / 2
= g/4
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction m . A horizontal force F is applied on the prism as shown in the fig. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is :
- a)
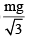
- b)
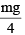
- c)
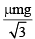
- d)
Correct answer is option 'A'. Can you explain this answer?
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction m . A horizontal force F is applied on the prism as shown in the fig. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is :
a)
b)
c)
d)
|
|
Rajesh Gupta answered |
As the force is applied towards right the prism will topple at O. Now, for the prism to topple the torque due to force "F" must be greater than or equal to the torque due to weight "Mg" about the point O.
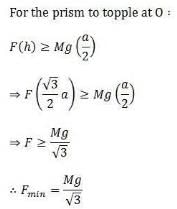
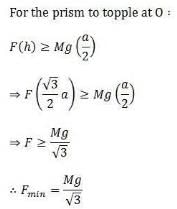
Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be 
- a)
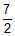PQ2 - b)
PQ2 - c)
PQ2 - d)
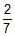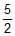PQ2
Correct answer is option 'A'. Can you explain this answer?
Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
a)
PQ2b)
PQ2c)
PQ2d)
PQ2
|
Lohit Matani answered |
For ring 1
(MOI)1 = MOI about diameter + PQ2
MOI about diameter = ½ PQ2
(MOI)1 = 3/2 PQ2
Similarly, (MOI)2 = 3/2 PQ2
(MOI)3 = ½ PQ2
Total MOI = 7/2 PQ2
(MOI)1 = MOI about diameter + PQ2
MOI about diameter = ½ PQ2
(MOI)1 = 3/2 PQ2
Similarly, (MOI)2 = 3/2 PQ2
(MOI)3 = ½ PQ2
Total MOI = 7/2 PQ2
A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total length of the rod AB = 3m. To keep the rod in equilibrium a force of 6N should act in the following manner :- a)Downwards at any point between A and B.
- b) Downwards at mid point of AB.
- c)Downwards at a point C such that AC = 1m.
- d) Downwards at a point D such that BD = 1m.
Correct answer is option 'D'. Can you explain this answer?
A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total length of the rod AB = 3m. To keep the rod in equilibrium a force of 6N should act in the following manner :
a)
Downwards at any point between A and B.
b)
Downwards at mid point of AB.
c)
Downwards at a point C such that AC = 1m.
d)
Downwards at a point D such that BD = 1m.
|
|
Riya Banerjee answered |
The moment of inertia of a body depends upon -- a) mass only
- b) angular velocity only
- c)distribution of particles only
- d)mass and distribution of mass about the axis
Correct answer is option 'D'. Can you explain this answer?
The moment of inertia of a body depends upon -
a)
mass only
b)
angular velocity only
c)
distribution of particles only
d)
mass and distribution of mass about the axis
|
|
Preeti Iyer answered |
I = mr2, therefore it depends on body mass and its mass distribution.
A wheel starting with angular velocity of 10 radian/sec acquires angular velocity of 100 radian/sec in 15 seconds. If moment of inertia is 10kg-m2, then applied torque (in newton-metre) is- a)900
- b)100
- c)90
- d)60
Correct answer is option 'D'. Can you explain this answer?
A wheel starting with angular velocity of 10 radian/sec acquires angular velocity of 100 radian/sec in 15 seconds. If moment of inertia is 10kg-m2, then applied torque (in newton-metre) is
a)
900
b)
100
c)
90
d)
60
|
|
Gaurav Kumar answered |
I(ωf - ωi)/t = τ
Hence, τ = 60
Hence, τ = 60
Consider the following statementsAssertion (A) : The moment of inertia of a rigid body reduces to its minimum value as compared to any other parallel axis when the axis of rotation passes through its centre of mass.Reason (R) : The weight of a rigid body always acts through its centre of mass in uniform gravitational field. Of these statements :- a)both A and R are true and R is the correct explanation of A
- b) both A and R are true but R is not a correct explanation of A
- c)A is true but R is false
- d) A is false but R is true
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements
Assertion (A) : The moment of inertia of a rigid body reduces to its minimum value as compared to any other parallel axis when the axis of rotation passes through its centre of mass.
Reason (R) : The weight of a rigid body always acts through its centre of mass in uniform gravitational field. Of these statements :
a)
both A and R are true and R is the correct explanation of A
b)
both A and R are true but R is not a correct explanation of A
c)
A is true but R is false
d)
A is false but R is true
|
|
Neha Joshi answered |
Moment of inertia about its centroidal axis has a minimum value as the centroidal axis has mass evenly distributed around it thereby providing minimum resistance to rotation as compared to any other axis. Also the statement-2 is correct but is not the correct explanation for statement-1.
Vectorially, angular velocity of a rotating body is represented :- a)along the radius towards the centre
- b)along the radius away from the centre
- c)along the axis of rotation
- d)none of thses
Correct answer is 'C'. Can you explain this answer?
Vectorially, angular velocity of a rotating body is represented :
a)
along the radius towards the centre
b)
along the radius away from the centre
c)
along the axis of rotation
d)
none of thses
|
Lavanya Menon answered |
Angular velocity is a pseudovector , with its magnitude measuring the rate of rotation and its direction pointing along the axis of rotation ( perpendicular to radius and velocity vectors ) .
On applying a constant torque on a body- a) Linear velocity may be increases
- b)Angular velocity may be increases
- c)It will rotate with constant angular velocity
- d)It will move with constant velocity
Correct answer is option 'A'. Can you explain this answer?
On applying a constant torque on a body
a)
Linear velocity may be increases
b)
Angular velocity may be increases
c)
It will rotate with constant angular velocity
d)
It will move with constant velocity
|
|
Geetika Shah answered |
If a constant torque is applied it is possible that a positive angular acceleration gets generated which can generate a positive acceleration and hence increasing both velocity and angular velocity.
Kinetic Energy of a rotating body i.e. Rotational Kinetic Energy can be converted to various forms of energy they are- a)Heat, Potential Energy
- b)Linear Kinetic Energy, Potential Energy
- c)Heat, Linear Kinetic Energy, Potential Energy
- d)Heat, Linear Kinetic Energy
Correct answer is option 'C'. Can you explain this answer?
Kinetic Energy of a rotating body i.e. Rotational Kinetic Energy can be converted to various forms of energy they are
a)
Heat, Potential Energy
b)
Linear Kinetic Energy, Potential Energy
c)
Heat, Linear Kinetic Energy, Potential Energy
d)
Heat, Linear Kinetic Energy
|
|
Lavanya Menon answered |
Take an example where the system is attached with spring and the spring is attached to a wall, if you rotate the system that system has KE and spring will also rotate with that system and thus spring will start to compress which will create PE in it and heat will obviously be generated.
A man standing on a table rotating about the central axis pulls his hands holding the dumb bells towards chest. How the angular velocity will change?- a)increase
- b)remains same
- c)increase or decrease depending on the magnitude of angular velocity of the wheel
- d)decrease
Correct answer is option 'A'. Can you explain this answer?
A man standing on a table rotating about the central axis pulls his hands holding the dumb bells towards chest. How the angular velocity will change?
a)
increase
b)
remains same
c)
increase or decrease depending on the magnitude of angular velocity of the wheel
d)
decrease
|
|
Preeti Iyer answered |
When the man pulls his hands towards chest, the moment of inertia will decrease and due to conservation of angular momentum, angular velocity will increase.
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωA and ωB respectively. Then- a)ωB = ω
- b)ωA< ωB
- c)ωA = ω
- d)ωA = ωB
Correct answer is option 'C'. Can you explain this answer?
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωA and ωB respectively. Then
a)
ωB = ω
b)
ωA< ωB
c)
ωA = ω
d)
ωA = ωB
|
|
Geetika Shah answered |
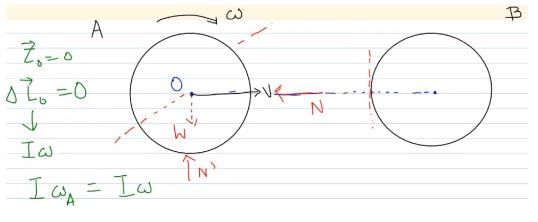
So, “I” gets cancelled.
The angular momentum of a body is 31.4 Js and its rate of revolution is 10 cycle per second. The momentum of inertia of the body about the axis of rotation is- a)0.5 kgm2
- b)0.15 kgm2
- c)1.5 kgm2
- d)2.5 kgm2
Correct answer is option 'A'. Can you explain this answer?
The angular momentum of a body is 31.4 Js and its rate of revolution is 10 cycle per second. The momentum of inertia of the body about the axis of rotation is
a)
0.5 kgm2
b)
0.15 kgm2
c)
1.5 kgm2
d)
2.5 kgm2
|
|
Raghav Bansal answered |
F = w/2π
w = 2πf
w = 2π × 10
w = 62.8
L = Iw
I = L/w
I = 31.4/62.8
I = 0.5 kgm2
Hence A
w = 2πf
w = 2π × 10
w = 62.8
L = Iw
I = L/w
I = 31.4/62.8
I = 0.5 kgm2
Hence A
A boy is playing with a tire of radius 0.5m. He accelerates it from 5rpm to 25 rpm in 15 seconds. The linear acceleration of tire is- a)70 m/s2
- b)7 m/s2
- c)10 m/s2
- d)0.07 m/s2
Correct answer is option 'D'. Can you explain this answer?
A boy is playing with a tire of radius 0.5m. He accelerates it from 5rpm to 25 rpm in 15 seconds. The linear acceleration of tire is
a)
70 m/s2
b)
7 m/s2
c)
10 m/s2
d)
0.07 m/s2
|
|
Naina Sharma answered |
r=0.5m, t=15s
n1=5rpm=5/60 rps
n2=25rpm=25/60rps
… ω1=2π(5) rad/s
… ω2=2π(25) rad/s
As,
a=r∝ [∝=ω2- ω1/t]
so, a=0.5[2π(n2-n1)/t]
a=0.5x6.28x20/60x15
a=6.28x2/60x3
a=6.28/90
a=0.697 m/s2
a≈0.7 m/s2
n1=5rpm=5/60 rps
n2=25rpm=25/60rps
… ω1=2π(5) rad/s
… ω2=2π(25) rad/s
As,
a=r∝ [∝=ω2- ω1/t]
so, a=0.5[2π(n2-n1)/t]
a=0.5x6.28x20/60x15
a=6.28x2/60x3
a=6.28/90
a=0.697 m/s2
a≈0.7 m/s2
A merry- go- round ( diameter 4.0 m ) starts from rest and uniformly accelerates until it rotates at 0.8 rev/min. This occurs in 11s. Once it has reached this rate , it rotates at 0.8 rev/min uniformly . Determine the angular acceleration- a)7.55 x 10-3 rad/s2
- b)6.7 x 10-3 rad/s2
- c)0.083 rad/s2
- d)0.083 rad/s
Correct answer is option 'A'. Can you explain this answer?
A merry- go- round ( diameter 4.0 m ) starts from rest and uniformly accelerates until it rotates at 0.8 rev/min. This occurs in 11s. Once it has reached this rate , it rotates at 0.8 rev/min uniformly . Determine the angular acceleration
a)
7.55 x 10-3 rad/s2
b)
6.7 x 10-3 rad/s2
c)
0.083 rad/s2
d)
0.083 rad/s
|
|
Lavanya Menon answered |
First we have to find ‘v’ by using the relation v = rw
Now, v = 0.167m/s
Then we find ‘a’ by using the relation a = v/t
So, a = 0.0152m/s2.
Now, we can find angular acceleration by using the formula α = a/r
Finally, α = 0.0076 rad/sec2
Now, v = 0.167m/s
Then we find ‘a’ by using the relation a = v/t
So, a = 0.0152m/s2.
Now, we can find angular acceleration by using the formula α = a/r
Finally, α = 0.0076 rad/sec2
To maximize torque on a lever, which of the following will not help?- a)Apply the force in a direction perpendicular to the lever
- b)Increasing the magnitude of the force, F that we apply
- c)Increasing the distance, r, from the axis of rotation of the point to which you apply the force
- d)Increasing the density of material.
Correct answer is option 'D'. Can you explain this answer?
To maximize torque on a lever, which of the following will not help?
a)
Apply the force in a direction perpendicular to the lever
b)
Increasing the magnitude of the force, F that we apply
c)
Increasing the distance, r, from the axis of rotation of the point to which you apply the force
d)
Increasing the density of material.
|
|
Rohan Singh answered |
In order to maximize torque, you need to:
Maximize the magnitude of the force, F, that you apply to the lever.
Maximize the distance, r, from the axis of rotation of the point on the lever to which you apply the force.
Apply the force in a direction perpendicular to the lever.
One end of a uniform rod of mass m and length I is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity w. The force exerted by the clamp on the rod has a horizontal component- a)mw2l
- b)zero
- c) mg
- d)
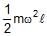
Correct answer is option 'D'. Can you explain this answer?
One end of a uniform rod of mass m and length I is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity w. The force exerted by the clamp on the rod has a horizontal component
a)
mw2l
b)
zero
c)
mg
d)
|
|
Raghav Bansal answered |
Consider a rod of length l and mass m rotating with an angular velocity of w
dF = dm l w2
dF = (m/l) dμ l w2
Integrating
F = ½mlw2
dF = dm l w2
dF = (m/l) dμ l w2
Integrating
F = ½mlw2
In case of couples, which statement is not true?- a)Couple can be balanced by a single force.
- b)The sum of moment of all forces about any point is same.
- c)Couple is always balanced by a couple.
- d)Couple cannot be balanced by a single force.
Correct answer is option 'A'. Can you explain this answer?
In case of couples, which statement is not true?
a)
Couple can be balanced by a single force.
b)
The sum of moment of all forces about any point is same.
c)
Couple is always balanced by a couple.
d)
Couple cannot be balanced by a single force.
|
|
Naina Sharma answered |
When two forces of equal magnitude opposite in direction and acting along parallel straight lines, then they are said to form a couple. The perpendicular distance between the two force forming a couple is called the arm of the couple.
‘Couple’ are the types of forces acting clockwise or anti-clockwise. We can only balance them by two forces minimum.
Chapter doubts & questions for Rotational Kinematics - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Rotational Kinematics - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup