Class 11 Exam > Class 11 Questions > A smooth sphere A is moving on a frictionless...
Start Learning for Free
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωA and ωB respectively. Then
- a)ωB = ω
- b)ωA< ωB
- c)ωA = ω
- d)ωA = ωB
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A smooth sphere A is moving on a frictionless horizontal plane with an...
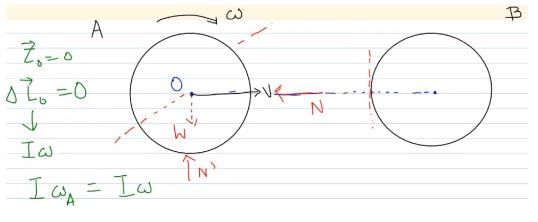
So, “I” gets cancelled.
Most Upvoted Answer
A smooth sphere A is moving on a frictionless horizontal plane with an...
ΩA. Another sphere B of the same radius and mass is at rest on the same plane. Sphere A collides elastically with sphere B. After the collision, sphere A moves off at an angle of 60 degrees to its original direction of motion. What is the final angular speed of sphere A?
Let us consider the motion of the center of mass of the system before and after the collision. Since sphere B is at rest, the center of mass of the system is at a point equidistant from spheres A and B, and initially moves in the direction of sphere A's velocity vector. After the collision, the center of mass continues to move in the same direction, but at a lower speed since some of the kinetic energy has been transferred to sphere B.
Let vA and vB be the velocities of spheres A and B, respectively, after the collision. The velocity of the center of mass of the system is then:
vcm = (mA*vA + mB*vB)/(mA + mB)
where mA and mB are the masses of spheres A and B, respectively. Since the center of mass moves at a constant velocity, the direction of vA must be 60 degrees to the left of the initial velocity vector of sphere A.
Using conservation of kinetic energy and momentum, we can relate vA and vB:
(mA/2)*ωA^2 = (mA/2)*vA^2 + (mB/2)*vB^2
mA*ωA = mA*vA + mB*vB
Solving these equations for vA and vB, we get:
vA = (2/3)*ωA
vB = (1/3)*ωA
The final angular speed of sphere A is given by:
ωf = vA/r
where r is the radius of the spheres. Substituting the value of vA, we get:
ωf = (2/3)*ωA/r
Therefore, the final angular speed of sphere A is (2/3) times its initial angular speed.
Let us consider the motion of the center of mass of the system before and after the collision. Since sphere B is at rest, the center of mass of the system is at a point equidistant from spheres A and B, and initially moves in the direction of sphere A's velocity vector. After the collision, the center of mass continues to move in the same direction, but at a lower speed since some of the kinetic energy has been transferred to sphere B.
Let vA and vB be the velocities of spheres A and B, respectively, after the collision. The velocity of the center of mass of the system is then:
vcm = (mA*vA + mB*vB)/(mA + mB)
where mA and mB are the masses of spheres A and B, respectively. Since the center of mass moves at a constant velocity, the direction of vA must be 60 degrees to the left of the initial velocity vector of sphere A.
Using conservation of kinetic energy and momentum, we can relate vA and vB:
(mA/2)*ωA^2 = (mA/2)*vA^2 + (mB/2)*vB^2
mA*ωA = mA*vA + mB*vB
Solving these equations for vA and vB, we get:
vA = (2/3)*ωA
vB = (1/3)*ωA
The final angular speed of sphere A is given by:
ωf = vA/r
where r is the radius of the spheres. Substituting the value of vA, we get:
ωf = (2/3)*ωA/r
Therefore, the final angular speed of sphere A is (2/3) times its initial angular speed.
Free Test
FREE
| Start Free Test |
Community Answer
A smooth sphere A is moving on a frictionless horizontal plane with an...
It's not an answer...I want to clear my doubt
e=v2-v1/u1-u2
and e=1
so angular speed should be half of the initial of both the spheres as they are identical and B is initial at rest.
e=v2-v1/u1-u2
and e=1
so angular speed should be half of the initial of both the spheres as they are identical and B is initial at rest.
|
Explore Courses for Class 11 exam
|
|
Similar Class 11 Doubts
Top Courses for Class 11View all
Question Description
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer?.
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A smooth sphere A is moving on a frictionless horizontal plane with angular speed ωand center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAand ωBrespectively. Thena)ωB= ωb)ωA< ωBc)ωA= ωd)ωA= ωBCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 11 tests.
|
|
Explore Courses for Class 11 exam
|
|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily