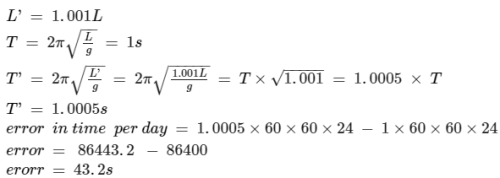All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Driven (Forced) Oscillations and Resonance for EmSAT Achieve Exam
If the length of a simple pendulum is increases by 1percent, then the new time-period
a) Decreases by 0.5 percent
b) Increases by 0.5 percent
c) Increases by 1 percent
d) Increases by 2.0 percent
Correct answer is option 'B'. Can you explain this answer?
|
|
Krishna Iyer answered |
Time period, T=2π√l/g
=>T∝√l
=>ΔT/T=1/2 Δl/l
Δl/l=1%
Therefore, ΔT/T=1/2x1%=0.5%
=>T∝√l
=>ΔT/T=1/2 Δl/l
Δl/l=1%
Therefore, ΔT/T=1/2x1%=0.5%
What determines the natural frequency of a body?- a)Position of the body with respect to force applied
- b)Mass and speed of the body
- c)Oscillations in the body
- d)Elastic properties and dimensions of the body
Correct answer is option 'D'. Can you explain this answer?
What determines the natural frequency of a body?
a)
Position of the body with respect to force applied
b)
Mass and speed of the body
c)
Oscillations in the body
d)
Elastic properties and dimensions of the body
|
|
Lavanya Menon answered |
Natural frequency is the frequency at which a body tends to oscillate in the absence of any driving or damping force.
Free vibrations of any elastic body are called natural vibration and happen at a frequency called natural frequency. Natural vibrations are different from forced vibration which happen at frequency of applied force .
Free vibrations of any elastic body are called natural vibration and happen at a frequency called natural frequency. Natural vibrations are different from forced vibration which happen at frequency of applied force .
If the period of oscillation of mass M suspended from a spring is one second, then the period of mass 4 M will be- a)1/ 4s
- b)4s
- c)1/ 2s
- d)2s
Correct answer is option 'D'. Can you explain this answer?
If the period of oscillation of mass M suspended from a spring is one second, then the period of mass 4 M will be
a)
1/ 4s
b)
4s
c)
1/ 2s
d)
2s
|
|
Geetika Shah answered |
T=2*3.14*√m/√k=1 s (given)
T’=2*3.14*√4m/√k=2*3.14*2√m/√k=2*1s
Therefore T’=2s
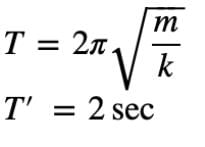
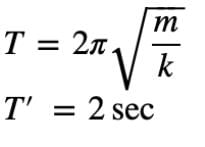
If  is the natural frequency of the system and
is the natural frequency of the system and  is the frequency of the external force that acts on an oscillating system then at resonance
is the frequency of the external force that acts on an oscillating system then at resonance- a)ωd ≥ ω
- b)ωd = ω
- c)ωd ≤ ω
- d)ωd ≠ ω
Correct answer is option 'B'. Can you explain this answer?
If  is the natural frequency of the system and
is the natural frequency of the system and  is the frequency of the external force that acts on an oscillating system then at resonance
is the frequency of the external force that acts on an oscillating system then at resonance
 is the natural frequency of the system and
is the natural frequency of the system and  is the frequency of the external force that acts on an oscillating system then at resonance
is the frequency of the external force that acts on an oscillating system then at resonancea)
ωd ≥ ω
b)
ωd = ω
c)
ωd ≤ ω
d)
ωd ≠ ω
|
|
Om Desai answered |
When the natural frequency and external frequency of an object are equal the phenomenon is called resonance.
The restoring force in a simple harmonic motion is _________ in magnitude when the particle is instantaneously at rest.- a)zero
- b)maximum
- c)minimum
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The restoring force in a simple harmonic motion is _________ in magnitude when the particle is instantaneously at rest.
a)
zero
b)
maximum
c)
minimum
d)
none of these

|
Knowledge Hub answered |
The restoring force in a simple harmonic motion is maximum in magnitude when the particle is instantaneously at rest because in SHM object’s tendency is to return to mean position and here particle is instantaneously at rest after that instant restoring force will be max to bring particle to mean position.
If an external force with angular frequency ωd acts on an oscillating system with natural angular frequency ω, the system oscillates with angular frequency ωd. The amplitude of oscillations is the greatest when:- a)ωd > ω
- b)ωd < ω
- c)ωd ≥ ω
- d)ωd = ω
Correct answer is option 'D'. Can you explain this answer?
If an external force with angular frequency ωd acts on an oscillating system with natural angular frequency ω, the system oscillates with angular frequency ωd. The amplitude of oscillations is the greatest when:
a)
ωd > ω
b)
ωd < ω
c)
ωd ≥ ω
d)
ωd = ω
|
|
Jyoti Aiims Aspirant answered |
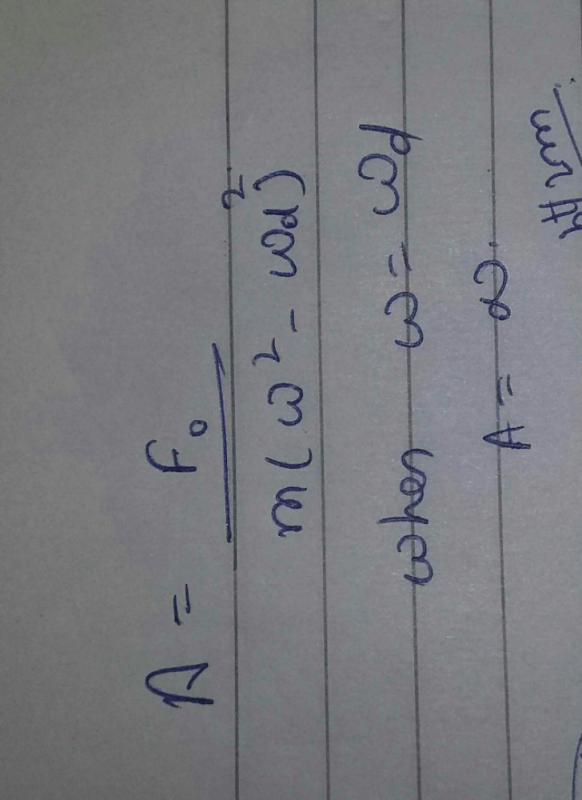
Under what condition angular frequency ω of the damped oscillator would be equivalent to angular velocity Ω of the undamped oscillator.- a)Velocity of oscillator is small
- b)Damping constant, b is small
- c)Damping constant ,b is large
- d)Force applied is small
Correct answer is option 'B'. Can you explain this answer?
Under what condition angular frequency ω of the damped oscillator would be equivalent to angular velocity Ω of the undamped oscillator.
a)
Velocity of oscillator is small
b)
Damping constant, b is small
c)
Damping constant ,b is large
d)
Force applied is small
|
|
Priya Patel answered |
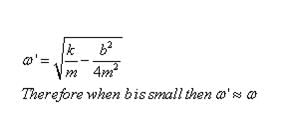
Whose motion is an ideal case of SHM?- a)An electric dipole placed stably in a uniform electric field and then given a very small regular displacement
- b)A simple pendulum with very small angle of swing
- c)Shadow of a point mass having uniform circular motion, on the vertical diameter
- d)none
Correct answer is option 'A'. Can you explain this answer?
Whose motion is an ideal case of SHM?
a)
An electric dipole placed stably in a uniform electric field and then given a very small regular displacement
b)
A simple pendulum with very small angle of swing
c)
Shadow of a point mass having uniform circular motion, on the vertical diameter
d)
none
|
|
Raghav Bansal answered |
Simple pendulum is not a case of ideal SHM as it is mention in NCERT.
Shadow of a point mass having uniform circular motion on the horizontal diameter is a case of SHM but not on the vertical diameter.
Shadow of a point mass having uniform circular motion on the horizontal diameter is a case of SHM but not on the vertical diameter.
A rubber ball with water, having a small hole in its bottom is used as the bob of a simple pendulum. The time-period of such a pendulum:- a)Increases with time
- b)First increases and then decreases finally having same value as at the beginning
- c)Decreases with time
- d)Is a constant
Correct answer is option 'B'. Can you explain this answer?
A rubber ball with water, having a small hole in its bottom is used as the bob of a simple pendulum. The time-period of such a pendulum:
a)
Increases with time
b)
First increases and then decreases finally having same value as at the beginning
c)
Decreases with time
d)
Is a constant
|
|
Rajesh Gupta answered |
When rubber ball completely filled with water its centre of gravity will be at its centre, as water will fall through hole its COG will shift towards lower side leading to increase in length of pendulum and thus T, when very small amount of water will be left in rubber ball its COG will again shifts upward causing decrease in length and thus T, and finally when rubber ball becomes empty its COG will be at its centre and T will remains same as earlier.
Damping is due to- a)electrostatic forces
- b)resistive forces like air drag, friction etc.
- c)reaction forces
- d)conservative forces like gravity
Correct answer is option 'B'. Can you explain this answer?
Damping is due to
a)
electrostatic forces
b)
resistive forces like air drag, friction etc.
c)
reaction forces
d)
conservative forces like gravity
|
|
Om Desai answered |
Damping is due to resistive forces like air drag, friction etc.
The ratio of maximum acceleration to maximum velocity of a particle performing S.H.M is equal to- a)Square of amplitude
- b)Square of angular velocity
- c)Amplitude
- d)Angular velocity
Correct answer is option 'D'. Can you explain this answer?
The ratio of maximum acceleration to maximum velocity of a particle performing S.H.M is equal to
a)
Square of amplitude
b)
Square of angular velocity
c)
Amplitude
d)
Angular velocity
|
|
Om Desai answered |
Maximum acceleration = w2A
Maximum velocity = wA
Ratio = w2A/wA = w
w = angular velocity
A = amplitude
Maximum velocity = wA
Ratio = w2A/wA = w
w = angular velocity
A = amplitude
Damped natural frequency is- a)same as natural frequency
- b)lower than natural frequency
- c)higher than natural frequency
- d)none of the above
Correct answer is option 'B'. Can you explain this answer?
Damped natural frequency is
a)
same as natural frequency
b)
lower than natural frequency
c)
higher than natural frequency
d)
none of the above
|
|
Geetika Shah answered |
If a resonant mechanical structure is set in motion and left to its own devices, it will continue to oscillate at a particular frequency known as its natural frequency, or "damped natural frequency". This will be a little lower in frequency than the resonant frequency, which is the frequency it would assume if there were no damping. The resonant frequency is also called the "undamped natural frequency”
In a simple pendulum the restoring force is due to- a) The tangential component of the gravitational force
- b)The radial component of the gravitational force
- c)The tangential component of the tension in string
- d)The radial component of the tension in string
Correct answer is option 'A'. Can you explain this answer?
In a simple pendulum the restoring force is due to
a)
The tangential component of the gravitational force
b)
The radial component of the gravitational force
c)
The tangential component of the tension in string
d)
The radial component of the tension in string
|
|
Pooja Shah answered |
In a simple pendulum the restoring force is due to the tangential component of the gravitational force because on applying torque equation on the radial forces the effect is nullified due to it passing from centre & only tangential component remains.
The kinetic energy of a body executing S.H.M. is 1/3 of the potential energy. Then, the displacement of the body is x percent of the amplitude, where x is- a)33
- b)50
- c)67
- d)87
Correct answer is option 'A'. Can you explain this answer?
The kinetic energy of a body executing S.H.M. is 1/3 of the potential energy. Then, the displacement of the body is x percent of the amplitude, where x is
a)
33
b)
50
c)
67
d)
87
|
|
Pooja Shah answered |
We know that PE + KE = TE = constant
Hence at the extremis TE = PE = ½ kz2
Where z is amplitude and k is shm constant.
Thus when KE = ⅓ PE
We get PE = ¾ TE = ½ kz2
Hence we get ½ kx2 = ¾ ½ kz2
We get x/z = √3/4
= 1.73 / 2
= .87
Thus we get x is 87 percent of the amplitude.
Hence at the extremis TE = PE = ½ kz2
Where z is amplitude and k is shm constant.
Thus when KE = ⅓ PE
We get PE = ¾ TE = ½ kz2
Hence we get ½ kx2 = ¾ ½ kz2
We get x/z = √3/4
= 1.73 / 2
= .87
Thus we get x is 87 percent of the amplitude.
Any periodic function can be expressed as a.- a)superposition of sine and cosine functions of different time periods with suitable coefficients
- b)superposition of exponential functions of real time periods with suitable coefficients
- c)superposition of polynomial functions of different time periods with suitable coefficients
- d)superposition of sine and cosine functions of same time period with suitable coefficients
Correct answer is option 'A'. Can you explain this answer?
Any periodic function can be expressed as a.
a)
superposition of sine and cosine functions of different time periods with suitable coefficients
b)
superposition of exponential functions of real time periods with suitable coefficients
c)
superposition of polynomial functions of different time periods with suitable coefficients
d)
superposition of sine and cosine functions of same time period with suitable coefficients

|
Sushil Kumar answered |
All periodic functions can, in principle, be represented as a sum of sine and cosine functions, since they form what's known as a complete set.
The amplitude of S.H.M at resonance is _______ in the ideal case of zero damping.- a)Maximum
- b)Minimum
- c)Zero
- d)Infinite
Correct answer is option 'D'. Can you explain this answer?
The amplitude of S.H.M at resonance is _______ in the ideal case of zero damping.
a)
Maximum
b)
Minimum
c)
Zero
d)
Infinite
|
|
Neha Joshi answered |
In an ideal environment where there is no resistance to oscillation motion i.e. damping is zero, when we oscillate a system at its resonant frequency since there is no opposition to oscillation, the amplitude will go on increasing and reach infinity.
In the ideal case of zero damping, the amplitude of simple harmonic motion at resonance is:- a)zero
- b)infinite
- c)cannot be said
- d)varies from zero to infinite
Correct answer is option 'B'. Can you explain this answer?
In the ideal case of zero damping, the amplitude of simple harmonic motion at resonance is:
a)
zero
b)
infinite
c)
cannot be said
d)
varies from zero to infinite
|
|
Priya Patel answered |
In an ideal environment where there is no resistance to oscillatory motion, that is, damping is zero, when we oscillate a system at its resonant frequency, since there is no opposition to oscillation, a very large value of amplitude will be recorded. Forced oscillation is when you apply an external oscillating force.
The length of the second’s pendulum on the surface of earth is 1m. The length of second’s pendulum on the surface of moon, where g is 1/6th the value on earth is- a)6m
- b)1/ 36m
- c)36m
- d)1/ 6m
Correct answer is option 'D'. Can you explain this answer?
The length of the second’s pendulum on the surface of earth is 1m. The length of second’s pendulum on the surface of moon, where g is 1/6th the value on earth is
a)
6m
b)
1/ 36m
c)
36m
d)
1/ 6m
|
|
Pooja Shah answered |
Time period remains same since
T = 2π √(L/g)
So, from proportionality we can solve
T = 2π √(L/g)
So, from proportionality we can solve
The pendulum of a wall clock executes- a)a translatory motion
- b)a rotary motion
- c)a random motion
- d)an oscillatory motion
Correct answer is option 'D'. Can you explain this answer?
The pendulum of a wall clock executes
a)
a translatory motion
b)
a rotary motion
c)
a random motion
d)
an oscillatory motion
|
|
Chirag Mehta answered |
The bob of a pendulum moves in such a way that it repeats its positions several time but alternately the time gap between these positions is always equal which proves that the motion of a pendulum is oscillatory.
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes simple harmonic oscillations with a time period T. If the mass is increased by m, the time period becomes 5T/3. then the ratio of m/M is- a)9/ 16
- b)25/ 16
- c)3/9
- d)25/22
Correct answer is option 'D'. Can you explain this answer?
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes simple harmonic oscillations with a time period T. If the mass is increased by m, the time period becomes 5T/3. then the ratio of m/M is
a)
9/ 16
b)
25/ 16
c)
3/9
d)
25/22
|
|
Alok Mehta answered |

A particle executes SHM of time period T, the time period with which the total energy changes is- a)2T
- b)T
- c)T/2
- d)Infinite
Correct answer is option 'D'. Can you explain this answer?
A particle executes SHM of time period T, the time period with which the total energy changes is
a)
2T
b)
T
c)
T/2
d)
Infinite
|
|
Kavita Joshi answered |
Potential energy is a function of height. Now the motion of a simple pendulum can be expressed in terms of the angle at which the string makes with the normal (the angle it would hang at if it didn't swing.)Now Because the bob of the pendulum is always in motion except at the two turning points where the angle is at a maximum (and even at these points the bob is only motionless at one instant in time but for no inteval) the hight is always changing for every inteval of time and thus the potential energy is always changing.Also the potential energy is the same for all values of the angle that have the same magnatude (independent of the sign.)
A body is executing S.H.M When its displacement from the mean position is 4 cm and 5 cm, the corresponding velocities of the body are 10 cm per sec and 8 cm per sec. Then the time period of the body is- a)2 π/2 sec
- b)π sec
- c)3 π/2 sec
- d)2 π sec
Correct answer is option 'B'. Can you explain this answer?
A body is executing S.H.M When its displacement from the mean position is 4 cm and 5 cm, the corresponding velocities of the body are 10 cm per sec and 8 cm per sec. Then the time period of the body is
a)
2 π/2 sec
b)
π sec
c)
3 π/2 sec
d)
2 π sec
|
|
Pranavi Chopra answered |
v=ω√A2−x2
⇒8=ω √A2−25
&10=ω√A2−16
⇒(8/10)2= A2−25/ A2−16
⇒16/25= A2−25/ A2−16
⇒16A2−256=25A2−625
⇒9A2=369
A2=41
⇒8=ω41−25
⇒8=4ω
∴ω=2=T2π
T=π sec
⇒8=ω √A2−25
&10=ω√A2−16
⇒(8/10)2= A2−25/ A2−16
⇒16/25= A2−25/ A2−16
⇒16A2−256=25A2−625
⇒9A2=369
A2=41
⇒8=ω41−25
⇒8=4ω
∴ω=2=T2π
T=π sec
If the maximum velocity and acceleration of a particle executing S.H.M are equal in magnitude, the time period will be- a)6.28 s
- b)1.57 s
- c)3.14 s
- d)12.56 s
Correct answer is option 'A'. Can you explain this answer?
If the maximum velocity and acceleration of a particle executing S.H.M are equal in magnitude, the time period will be
a)
6.28 s
b)
1.57 s
c)
3.14 s
d)
12.56 s
|
|
Jyoti Dey answered |
**Explanation:**
When a particle is executing Simple Harmonic Motion (SHM), its displacement from the mean position follows a sinusoidal function. The maximum displacement of the particle is called the amplitude (A) of the motion. The particle oscillates back and forth between two extreme positions, which are equal in magnitude but opposite in direction.
The time taken for one complete oscillation of the particle is called the time period (T) of the motion. It is the time taken for the particle to go from one extreme position to the other and back again.
The maximum velocity (vmax) of the particle occurs when the particle passes through the mean position (equilibrium position). At this point, the velocity is at a maximum and is in the same direction as the acceleration. The maximum acceleration (amax) of the particle occurs when the particle is at its extreme positions. At these points, the acceleration is at a maximum and is in the opposite direction to the displacement.
If the maximum velocity and acceleration of the particle are equal in magnitude, it means that the amplitude of the motion is equal to the acceleration. Mathematically, this can be represented as:
amax = vmax
Using the equations of SHM, we can relate the amplitude, time period, maximum velocity, and maximum acceleration as follows:
amax = ω^2 A
vmax = ω A
where ω is the angular frequency of the motion.
Since amax = vmax, we can equate the above two equations:
ω^2 A = ω A
Simplifying the equation:
ω^2 = ω
ω = 1
The angular frequency ω is related to the time period T by ω = 2π/T. Substituting this value into the equation:
(2π/T)^2 = 2π/T
Simplifying the equation:
4π^2/T^2 = 2π/T
2π/T = 4π^2/T^2
T = 2
Therefore, the time period of the motion is T = 2 seconds, which is equivalent to 6.28 seconds (approximately). Hence, the correct answer is option A: 6.28 s.
When a particle is executing Simple Harmonic Motion (SHM), its displacement from the mean position follows a sinusoidal function. The maximum displacement of the particle is called the amplitude (A) of the motion. The particle oscillates back and forth between two extreme positions, which are equal in magnitude but opposite in direction.
The time taken for one complete oscillation of the particle is called the time period (T) of the motion. It is the time taken for the particle to go from one extreme position to the other and back again.
The maximum velocity (vmax) of the particle occurs when the particle passes through the mean position (equilibrium position). At this point, the velocity is at a maximum and is in the same direction as the acceleration. The maximum acceleration (amax) of the particle occurs when the particle is at its extreme positions. At these points, the acceleration is at a maximum and is in the opposite direction to the displacement.
If the maximum velocity and acceleration of the particle are equal in magnitude, it means that the amplitude of the motion is equal to the acceleration. Mathematically, this can be represented as:
amax = vmax
Using the equations of SHM, we can relate the amplitude, time period, maximum velocity, and maximum acceleration as follows:
amax = ω^2 A
vmax = ω A
where ω is the angular frequency of the motion.
Since amax = vmax, we can equate the above two equations:
ω^2 A = ω A
Simplifying the equation:
ω^2 = ω
ω = 1
The angular frequency ω is related to the time period T by ω = 2π/T. Substituting this value into the equation:
(2π/T)^2 = 2π/T
Simplifying the equation:
4π^2/T^2 = 2π/T
2π/T = 4π^2/T^2
T = 2
Therefore, the time period of the motion is T = 2 seconds, which is equivalent to 6.28 seconds (approximately). Hence, the correct answer is option A: 6.28 s.
The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is known as- a)Accelerated Amplitude
- b)Epoch
- c)Resonance
- d)Dampening
Correct answer is option 'C'. Can you explain this answer?
The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is known as
a)
Accelerated Amplitude
b)
Epoch
c)
Resonance
d)
Dampening
|
|
Lavanya Menon answered |
The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is known as resonance. By the definition of resonance.
A particle is executing S.H.M with an amplitude of 4 cm and time period 12 sec. The time taken by the particle in going from its mean position to a position of displacement equal to 2 cm is T1..The time taken from this displaced position of 2 cm to reach the extreme position is T2. Therefore, T1/ T2 will be- a)1/ 3
- b)1/2
- c)41276.0
- d)1
Correct answer is option 'B'. Can you explain this answer?
A particle is executing S.H.M with an amplitude of 4 cm and time period 12 sec. The time taken by the particle in going from its mean position to a position of displacement equal to 2 cm is T1..The time taken from this displaced position of 2 cm to reach the extreme position is T2. Therefore, T1/ T2 will be
a)
1/ 3
b)
1/2
c)
41276.0
d)
1
|
|
Raza Great answered |

For all practical purposes, the motion of a simple pendulum is SHM,- a)None of these
- b)Only if the length of its string is at least one meter
- c)Only if the maximum angle which its string makes with the vertical is less than 342.
- d)Only if the maximum angle which the string makes with the vertical is less than I
Correct answer is option 'A'. Can you explain this answer?
For all practical purposes, the motion of a simple pendulum is SHM,
a)
None of these
b)
Only if the length of its string is at least one meter
c)
Only if the maximum angle which its string makes with the vertical is less than 342.
d)
Only if the maximum angle which the string makes with the vertical is less than I

|
Nitin Nair answered |
The motion of Simple Pendulum as Simple Harmonic Motion. When we pull a simple pendulum from its equilibrium position and then release it, it swings in a vertical plane under the influence of gravity. It begins to oscillate about its mean position. Therefore, the motion is periodic and oscillatory.
SO OPTION A IS CORRECT.
Oscillatory motion is- a)combination of translation and rotation
- b)periodic to and fro motion
- c)rotation about a point
- d)none
Correct answer is option 'B'. Can you explain this answer?
Oscillatory motion is
a)
combination of translation and rotation
b)
periodic to and fro motion
c)
rotation about a point
d)
none
|
|
Ananya Datta answered |
Oscillatory motion is periodic to and fro motion. By definition
Under forced oscillation, the phase of the harmonic motion of the particle and phase of driving force- a)Are same
- b)Are different
- c)Both are zero
- d)Not present
Correct answer is option 'B'. Can you explain this answer?
Under forced oscillation, the phase of the harmonic motion of the particle and phase of driving force
a)
Are same
b)
Are different
c)
Both are zero
d)
Not present
|
|
Pratibha Sharma answered |
Harmonic motion is the natural motion of a body(we consider no air friction) under no force where as damped oscillation are under force hence the iscilation are different
Two pendulums of length 1 m and 16 m start vibrating one behind the other from the same stand. At some instant, the two are in the mean position in the same phase. The time period of shorter pendulum is T. The minimum time after which the two threads of the pendulum will be one behind the other is- a)2T/5
- b)T/3
- c)T/4
- d)4T/3
Correct answer is option 'D'. Can you explain this answer?
Two pendulums of length 1 m and 16 m start vibrating one behind the other from the same stand. At some instant, the two are in the mean position in the same phase. The time period of shorter pendulum is T. The minimum time after which the two threads of the pendulum will be one behind the other is
a)
2T/5
b)
T/3
c)
T/4
d)
4T/3
|
|
Anushka Banerjee answered |
T1=2π√1/g=T, T2=2π√16/g=4T
(ω1−ω2)t=2π
(2π/T−2π/4T)t=2π
t=4T/3
(ω1−ω2)t=2π
(2π/T−2π/4T)t=2π
t=4T/3
Period of a periodic motion is the ________ interval of time after which the motion is __________.- a)smallest, repeated
- b)mean, not repeated
- c)largest, repeated
- d)average, repeated
Correct answer is option 'A'. Can you explain this answer?
Period of a periodic motion is the ________ interval of time after which the motion is __________.
a)
smallest, repeated
b)
mean, not repeated
c)
largest, repeated
d)
average, repeated

|
Puja Das answered |
Explanation:Time period of an oscillatory motion is the smallest interval of time for one complete oscillation.As when we apply the force on the bob,bob moves from mean position to extreme position then form extreme position to mean position and then again from mean to extreme in opposite direction and at last come to mean position.The time taken by bob in this whole process is called period of oscillation.
Energy is supplied to the damped oscillatory system at the same rate at which it is dissipating energy, then the amplitude of such oscillations would become constant. Such oscillations are called- a)Damped oscillations
- b)Undamped oscillations
- c)Coupled oscillations
- d)Maintained oscillations
Correct answer is option 'D'. Can you explain this answer?
Energy is supplied to the damped oscillatory system at the same rate at which it is dissipating energy, then the amplitude of such oscillations would become constant. Such oscillations are called
a)
Damped oscillations
b)
Undamped oscillations
c)
Coupled oscillations
d)
Maintained oscillations
|
|
Anoushka Basu answered |
Energy is supplied to the damped oscillatory system at the same rate at which it is dissipating energy, and then the amplitude of such oscillations would become constant. Such oscillations are called maintained oscillations. By the definition of maintained oscillations.
In simple models damping force is- a)directly proportional to velocity
- b)inversely proportional to acceleration
- c)inversely proportional to velocity
- d)directly proportional to acceleration
Correct answer is option 'A'. Can you explain this answer?
In simple models damping force is
a)
directly proportional to velocity
b)
inversely proportional to acceleration
c)
inversely proportional to velocity
d)
directly proportional to acceleration
|
|
Kritika Khanna answered |
Damping force is a resistance force that opposes the motion of an object in a medium, such as air or water. It is responsible for reducing the amplitude of oscillations or the speed of a moving object. In simple models, the damping force is directly proportional to velocity.
Explanation:
The damping force is caused by the interaction between the object and the medium it is moving through. As the object moves, it displaces the medium particles, causing them to collide and exert a resistance force on the object. This resistance force is proportional to the velocity of the object.
Mathematical Representation:
The mathematical representation of damping force can be given by the equation:
F_damping = -bv
Where F_damping is the damping force, b is the damping coefficient, and v is the velocity of the object.
Directly Proportional to Velocity:
According to the equation, the damping force is directly proportional to the velocity of the object. This means that as the velocity increases, the damping force also increases, resulting in a greater resistance to the object's motion. Conversely, if the velocity decreases, the damping force decreases as well.
Relationship with Acceleration:
Although the damping force is not directly proportional to acceleration, it does have an indirect relationship with it. Since acceleration is the rate of change of velocity, an increase in acceleration results in a greater change in velocity over time. Therefore, a larger acceleration would lead to a larger damping force, and vice versa.
Conclusion:
In simple models, the damping force is directly proportional to velocity. This relationship is important in understanding the behavior of objects in the presence of damping forces, as it helps explain the gradual decrease in amplitude or speed of oscillations or motion.
Explanation:
The damping force is caused by the interaction between the object and the medium it is moving through. As the object moves, it displaces the medium particles, causing them to collide and exert a resistance force on the object. This resistance force is proportional to the velocity of the object.
Mathematical Representation:
The mathematical representation of damping force can be given by the equation:
F_damping = -bv
Where F_damping is the damping force, b is the damping coefficient, and v is the velocity of the object.
Directly Proportional to Velocity:
According to the equation, the damping force is directly proportional to the velocity of the object. This means that as the velocity increases, the damping force also increases, resulting in a greater resistance to the object's motion. Conversely, if the velocity decreases, the damping force decreases as well.
Relationship with Acceleration:
Although the damping force is not directly proportional to acceleration, it does have an indirect relationship with it. Since acceleration is the rate of change of velocity, an increase in acceleration results in a greater change in velocity over time. Therefore, a larger acceleration would lead to a larger damping force, and vice versa.
Conclusion:
In simple models, the damping force is directly proportional to velocity. This relationship is important in understanding the behavior of objects in the presence of damping forces, as it helps explain the gradual decrease in amplitude or speed of oscillations or motion.
The period of a simple pendulum is doubled when- a)The mass of the bob and the length of the pendulum are doubled
- b)The mass of the bob is doubled
- c)Its length is increased four times
- d)Its length is doubled
Correct answer is option 'C'. Can you explain this answer?
The period of a simple pendulum is doubled when
a)
The mass of the bob and the length of the pendulum are doubled
b)
The mass of the bob is doubled
c)
Its length is increased four times
d)
Its length is doubled
|
|
Muskaan Chakraborty answered |
The Period of a Simple Pendulum
The period of a simple pendulum is determined by the formula:
T = 2π√(L/g)
where:
- T is the period
- L is the length of the pendulum
- g is the acceleration due to gravity
Understanding the Influence of Length on Period
- The period T is directly proportional to the square root of the length L.
- This means if you increase the length L, the period T increases.
Explaining the Correct Answer (Option C)
- If the length of the pendulum is increased four times (L becomes 4L), the new period T' can be calculated as follows:
T' = 2π√(4L/g) = 2π√(4)√(L/g) = 2 * 2π√(L/g) = 2T
- This shows that the period T' is now doubled.
Analysis of Other Options
- Option A: Doubling mass and length does not double the period. The mass does not impact the period; it only affects the amplitude.
- Option B: Doubling the mass of the bob does not change the period at all; it remains T.
- Option D: Doubling the length (L becomes 2L) results in:
T' = 2π√(2L/g) = √2 * T (not doubled).
Conclusion
Thus, the only scenario where the period of a simple pendulum is doubled is when its length is increased four times, making Option C the correct answer.
The period of a simple pendulum is determined by the formula:
T = 2π√(L/g)
where:
- T is the period
- L is the length of the pendulum
- g is the acceleration due to gravity
Understanding the Influence of Length on Period
- The period T is directly proportional to the square root of the length L.
- This means if you increase the length L, the period T increases.
Explaining the Correct Answer (Option C)
- If the length of the pendulum is increased four times (L becomes 4L), the new period T' can be calculated as follows:
T' = 2π√(4L/g) = 2π√(4)√(L/g) = 2 * 2π√(L/g) = 2T
- This shows that the period T' is now doubled.
Analysis of Other Options
- Option A: Doubling mass and length does not double the period. The mass does not impact the period; it only affects the amplitude.
- Option B: Doubling the mass of the bob does not change the period at all; it remains T.
- Option D: Doubling the length (L becomes 2L) results in:
T' = 2π√(2L/g) = √2 * T (not doubled).
Conclusion
Thus, the only scenario where the period of a simple pendulum is doubled is when its length is increased four times, making Option C the correct answer.
Periodic motion is- a)motion that involves coming to a mean position at random intervals of time
- b)motion that repeats itself at regular intervals of time
- c)motion that does not repeat itself at regular intervals of time
- d)motion that repeats itself at irregular intervals of time
Correct answer is option 'B'. Can you explain this answer?
Periodic motion is
a)
motion that involves coming to a mean position at random intervals of time
b)
motion that repeats itself at regular intervals of time
c)
motion that does not repeat itself at regular intervals of time
d)
motion that repeats itself at irregular intervals of time
|
|
Rajdeep Singh answered |
Periodic motion is a type of motion that repeats itself at regular intervals of time. It is characterized by the recurring pattern of the motion, where the object or system returns to its initial state after a certain period of time. This motion can be observed in various natural and man-made phenomena, such as the swinging of a pendulum, the rotation of the Earth around its axis, the vibration of a guitar string, or the oscillation of a spring.
Characteristics of periodic motion:
- Repetition: Periodic motion involves the repetition of a certain pattern or motion over time. The object or system returns to its initial position, velocity, and other properties after completing one cycle of motion.
- Regular intervals: The time taken to complete one cycle of motion is constant and is known as the period. This means that the motion occurs at regular intervals of time. For example, the period of a pendulum is the time taken to swing from one extreme position to the other and back again.
- Consistent amplitude: In periodic motion, the amplitude remains constant throughout the motion. The amplitude represents the maximum displacement or distance from the mean position.
- Harmonic motion: Many periodic motions, such as the swinging of a pendulum or the vibration of a guitar string, can be described by simple harmonic motion. Simple harmonic motion is a type of periodic motion where the restoring force is directly proportional to the displacement from the mean position and acts in the opposite direction.
- Periodic function: The mathematical representation of periodic motion is often described by a periodic function, such as a sine or cosine function. These functions repeat themselves after a certain interval, corresponding to one cycle of the motion.
- Examples of periodic motion: Some common examples of periodic motion include the swinging of a pendulum, the rotation of the Earth around its axis, the vibration of a guitar string, the oscillation of a spring, the motion of a bouncing ball, and the orbit of planets around the sun.
In conclusion, periodic motion is a type of motion that repeats itself at regular intervals of time. It is characterized by the recurring pattern of the motion, where the object or system returns to its initial state after completing one cycle of motion.
Characteristics of periodic motion:
- Repetition: Periodic motion involves the repetition of a certain pattern or motion over time. The object or system returns to its initial position, velocity, and other properties after completing one cycle of motion.
- Regular intervals: The time taken to complete one cycle of motion is constant and is known as the period. This means that the motion occurs at regular intervals of time. For example, the period of a pendulum is the time taken to swing from one extreme position to the other and back again.
- Consistent amplitude: In periodic motion, the amplitude remains constant throughout the motion. The amplitude represents the maximum displacement or distance from the mean position.
- Harmonic motion: Many periodic motions, such as the swinging of a pendulum or the vibration of a guitar string, can be described by simple harmonic motion. Simple harmonic motion is a type of periodic motion where the restoring force is directly proportional to the displacement from the mean position and acts in the opposite direction.
- Periodic function: The mathematical representation of periodic motion is often described by a periodic function, such as a sine or cosine function. These functions repeat themselves after a certain interval, corresponding to one cycle of the motion.
- Examples of periodic motion: Some common examples of periodic motion include the swinging of a pendulum, the rotation of the Earth around its axis, the vibration of a guitar string, the oscillation of a spring, the motion of a bouncing ball, and the orbit of planets around the sun.
In conclusion, periodic motion is a type of motion that repeats itself at regular intervals of time. It is characterized by the recurring pattern of the motion, where the object or system returns to its initial state after completing one cycle of motion.
Chapter doubts & questions for Driven (Forced) Oscillations and Resonance - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Driven (Forced) Oscillations and Resonance - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup