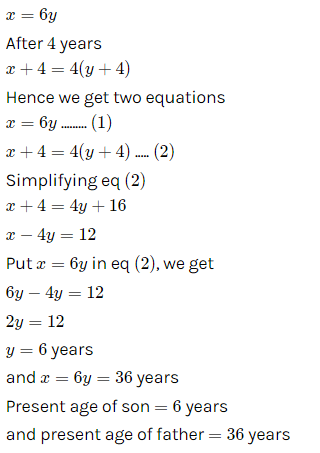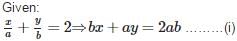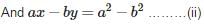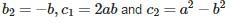All Exams >
Year 10 >
Mathematics for Year 10 >
All Questions
All questions of Simultaneous Equations for Year 10 Exam
Can you explain the answer of this question below:The area of the triangle formed by the lines 2x + y = 6, 2x – y + 2 = 0 and the x – axis is
- A:
15sq. units
- B:
8sq. units
- C:
10sq. units
- D:
12sq. units
The answer is b.
The area of the triangle formed by the lines 2x + y = 6, 2x – y + 2 = 0 and the x – axis is
15sq. units
8sq. units
10sq. units
12sq. units
|
|
Arun Sharma answered |
Here are the two solutions of each of the given equations. 2x+y = 6
2x+y=0
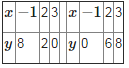
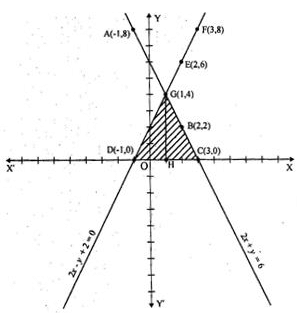
The area bounded by the given lines and x−axis has been shaded in the graph.
∴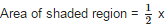
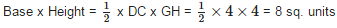
2x+y=0
The area bounded by the given lines and x−axis has been shaded in the graph.
∴
The pair of linear equations 2kx + 5y = 7, 6x – 5y = 11 has a unique solution if –
- a)k ≠ -3
- b)k = 3
- c)k = 5
- d)k = -5
Correct answer is option 'A'. Can you explain this answer?
The pair of linear equations 2kx + 5y = 7, 6x – 5y = 11 has a unique solution if –
a)
k ≠ -3
b)
k = 3
c)
k = 5
d)
k = -5
|
|
Rohit Sharma answered |
Given :
2 k x + 5 y – 7 = 0 ...( i )
6 x – 5 y – 1 = 0 ... ( ii )
Pair of linear equations has a unique solution.
We know for unique solution.
6 x – 5 y – 1 = 0 ... ( ii )
Pair of linear equations has a unique solution.
We know for unique solution.
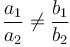
Comparing from ( i ) and ( ii ) we have

Put these values in formula.
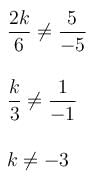
Thus we get answer many values of k but leaving k ≠ -3.
The pair of linear equations 2x + 5y = k, kx + 15y = 18 has infinitely many solutions if –- a)k = 3
- b)k = 6
- c)k = 9
- d)k = 18
Correct answer is option 'B'. Can you explain this answer?
The pair of linear equations 2x + 5y = k, kx + 15y = 18 has infinitely many solutions if –
a)
k = 3
b)
k = 6
c)
k = 9
d)
k = 18
|
|
Vivek Rana answered |
An equation has infinitely many solutions when the lines are coincident.
The lines are coincident when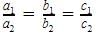
So 2x + 5y = k, kx + 15y = 18 are coincident when

The lines are coincident when
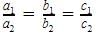
So 2x + 5y = k, kx + 15y = 18 are coincident when

The value of x in mx + ny = c; nx – ny = c + 1 is
- a)x = (m + n) / (c + 1)
- b)x = (2c + 1) / (m + n)
- c)x = m + n
- d)x = 2c + 1
Correct answer is option 'B'. Can you explain this answer?
The value of x in mx + ny = c; nx – ny = c + 1 is
a)
x = (m + n) / (c + 1)
b)
x = (2c + 1) / (m + n)
c)
x = m + n
d)
x = 2c + 1
|
|
Mansi desai answered |
To find the value of x in the equation mx + ny = c, we need more information or another equation. The equation nx = 0 does not provide enough information to solve for x.
For what value of ‘K’ will the system of equations: 3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1 have no solution- a)3
- b)2
- c)1
- d)-2
Correct answer is option 'B'. Can you explain this answer?
For what value of ‘K’ will the system of equations: 3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1 have no solution
a)
3
b)
2
c)
1
d)
-2
|
|
Krishna Iyer answered |
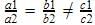 is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent
is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1
b1=1,b2=k-1,c1=-1,c2=-2k-1
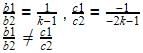
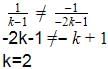
Can you explain the answer of this question below:The pair of equations y = 0 and y = -7 has :
- A:
no solution
- B:
infinitely many solutions
- C:
one solution
- D:
two solutions
The answer is a.
The pair of equations y = 0 and y = -7 has :
no solution
infinitely many solutions
one solution
two solutions
|
|
Raghav Bansal answered |
y=0 is x-axis… since every point has y=0. y=-7 is a line parallel to x-axis passing through x=0,y=-7. So the two lines are parallel to each other and are inconsistent which means that it has no solutions because it will never meet.
Which of following is not a solution of 3a + b = 12 ?
- a)(3, 3)
- b)(5, -3)
- c)(4, 0)
- d)(2, 4)
Correct answer is option 'D'. Can you explain this answer?
Which of following is not a solution of 3a + b = 12 ?
a)
(3, 3)
b)
(5, -3)
c)
(4, 0)
d)
(2, 4)

|
Prashant Gujjar Pgv answered |
D correct h 3(2)+4=10this is not a solution
In elimination method _____________ is an important condition.- a)Equating either of the coefficients
- b)Equating only the y coefficient.
- c)Equating only the x co-efficient.
- d)Equating both the coefficients.
Correct answer is option 'A'. Can you explain this answer?
In elimination method _____________ is an important condition.
a)
Equating either of the coefficients
b)
Equating only the y coefficient.
c)
Equating only the x co-efficient.
d)
Equating both the coefficients.
|
|
Rajiv Gupta answered |
Elimination Method (by Equating Coefficients)
There is another method of eliminating a variable, than often used method i. e --------Suppose you are to solve
23x - 17y + 11=0 ------(1)
and 31x + 13y - 57 = 0 -------(2)
Now expressing x in terms of y would involve division by 23 or 31. Express y in terms of x, it would involve division by 17 or 13. You know that multiplication is more convenient than division, better to convert the division process into a multiplication process.
Multiplying the first equation by 13 viz., coefficient of y in (2), and second by 17 viz., coefficient of y in (1), you will get an equivalent system of equations. The new system has the advantage that y has the same numerical coefficient 17x13 in both the equations. When you add these new equations, the terms containing y would cancel out as these have opposite signs and the same numerical coefficient. Thus, y has been eliminated. Now proceed as before, and solve the system. This method of elimination is also called elimination by equating coefficients for obvious reasons.
Example: Solve the following system of equations using the elimination method by equating coefficients:
11x - 5y + 61 = 0 (1)
3x - 20y - 2 = 0 (2)
Solution: Let us multiply equation (1) by 3 and equation (2) by 11. This gives
33x - 15y + 183 = 0 (3)
and 33x - 220y - 22 = 0 (4)
Subtracting (4) from (3), you will get 205y + 205 = 0
, or y = - 1
Substituting this value of y in equation (2), you will get
3x - 20 * (- 1) - 2 = 0
or 3x = -18
or x = - 6
Thus, the required solution is
x = - 6 and y = -1.
Now you should verify; substitute x = - 6 and y = -1 in the given equations, you will notice both the equations are satisfied. Hence, the solution is correct
A train overtakes two persons who are walking at the rate of 8 kmph and 12 kmph in the same direction in which the train is going, and passes them completely in 9 and 10 seconds respectively. What is the length of the train?- a)200 m
- b) 500 m
- c) 100 m
- d)300 m
Correct answer is option 'C'. Can you explain this answer?
A train overtakes two persons who are walking at the rate of 8 kmph and 12 kmph in the same direction in which the train is going, and passes them completely in 9 and 10 seconds respectively. What is the length of the train?
a)
200 m
b)
500 m
c)
100 m
d)
300 m
|
|
Rajiv Gupta answered |
8 kmph = (8 x 5/18) = 20/9 m/sec
4 kmph = (12 x 5/18 = 10/3 m/sec
18 9
Let the length of the train be x metres and its speed by y m/sec.
Then, [x/(y - 20/9)] = 9 and [x/(y - 10/3)] = 10
Therefore 9y - 20 = x and 10y - 100/3 = x
=> 9y - 20 = 10y - 100/3
solving: y = 40/3
putting value of y in (1):
9 . (40/3) - 20 = x
so, x = 100 m
On solving, we get: x = 100.
Therefore Length of the train is 100 m.
The Index of Coincidence for English language is approximately- a)0.068
- b)0.038
- c)0.065
- d)0.048
Correct answer is option 'C'. Can you explain this answer?
The Index of Coincidence for English language is approximately
a)
0.068
b)
0.038
c)
0.065
d)
0.048

|
Hariteja Patnala answered |
Yes actually you said option C is correct it is actually correct but the actual answer is different
actual answer for index of coincide of English language is 0.0 667
index of coincide is a technique to find the probability of the repeating letters in an encrypted text
the index of coincide value is calculated on the basis of the probability of occurrence of a specified letter and the probability of comparing it to the same letter from the second text
so this is my answer for index of coincide of English language is 0.0667 but you have given that C is correct option
actual answer for index of coincide of English language is 0.0 667
index of coincide is a technique to find the probability of the repeating letters in an encrypted text
the index of coincide value is calculated on the basis of the probability of occurrence of a specified letter and the probability of comparing it to the same letter from the second text
so this is my answer for index of coincide of English language is 0.0667 but you have given that C is correct option
Can you explain the answer of this question below:The sum of the numerator and denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to 1/3. The fraction is
- A:
7/11
- B:
-5/13
- C:
-7/11
- D:
5/13
The answer is d.
The sum of the numerator and denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to 1/3. The fraction is
7/11
-5/13
-7/11
5/13
|
|
Rahul Kapoor answered |
Let the numer be x & denom be y..
x+y= 18....(1)
x/y+2 =1/3
3x=y+2
x=(y+2)/3
put this value in eq 1
x+y=18
(y+2)/3+y=18
(y+2+3y= 18x3
4y+2 =54
4y=54-2
4y= 52
y= 52/4
y= 13
put the value of y in eq 1
x+y=18
x+ 13=18
x= 18- 13
x= 5
Hence req. fraction = x/ y = 5/13
A lending library has a fixed charge for the first two days and an additional charge for each day thereafter. Sunil paid Rs 28 for a book kept for seven days, while Sohail paid Rs 32 for the book he kept for nine days. Find the charge for each extra day.- a)Rs 3
- b)Rs 20
- c)Rs 2
- d)Rs 18
Correct answer is option 'C'. Can you explain this answer?
A lending library has a fixed charge for the first two days and an additional charge for each day thereafter. Sunil paid Rs 28 for a book kept for seven days, while Sohail paid Rs 32 for the book he kept for nine days. Find the charge for each extra day.
a)
Rs 3
b)
Rs 20
c)
Rs 2
d)
Rs 18
|
|
Abhishek Bhai answered |

Which of the following pair of linear equations is inconsistent?- a)5x – 3y = 11; 7x + 2y =13
- b)x – 2y = 6; 2x + 3y = 4
- c)9x – 8y = 17; 18x -16y = 34
- d)2x + 3y = 7; 4x + 6y = 5
Correct answer is option 'D'. Can you explain this answer?
Which of the following pair of linear equations is inconsistent?
a)
5x – 3y = 11; 7x + 2y =13
b)
x – 2y = 6; 2x + 3y = 4
c)
9x – 8y = 17; 18x -16y = 34
d)
2x + 3y = 7; 4x + 6y = 5
|
|
Krishna Iyer answered |
Pair of linear equations are inconsistent when they are parallel. When the two equations are parallel ,we have  .
.
 .
.In D, we have 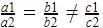 which is
which is 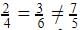 , so it is inconsistent.
, so it is inconsistent.
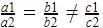 which is
which is 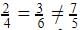 , so it is inconsistent.
, so it is inconsistent.Find the solution to the following system of linear equations: 2x-y+6=0 4x+5y-16=0- a)(2,-3)
- b)(-1,4)
- c)(2,3)
- d)(1,4)
Correct answer is option 'B'. Can you explain this answer?
Find the solution to the following system of linear equations: 2x-y+6=0 4x+5y-16=0
a)
(2,-3)
b)
(-1,4)
c)
(2,3)
d)
(1,4)
|
|
Pooja Shah answered |
2x-y+6=0
y=2x+6 ….(1)
4x+5y-16=0
Substituting the values
4x+5(2x+6)-16=0
14x+14=0
x=-1
y=4
y=2x+6 ….(1)
4x+5y-16=0
Substituting the values
4x+5(2x+6)-16=0
14x+14=0
x=-1
y=4
The values of x and y which satisfy the equations: 47x + 31y = 63 and 31x + 47y=15 are ____________- a)-2 and -1
- b)2 and -1
- c)2 and 1
- d)-2 and 1
Correct answer is 'B'. Can you explain this answer?
The values of x and y which satisfy the equations: 47x + 31y = 63 and 31x + 47y=15 are ____________
a)
-2 and -1
b)
2 and -1
c)
2 and 1
d)
-2 and 1
|
|
Rohan Kapoor answered |
Given pair of linear equations:
47x+31y =63 ---(1)
31x+47y =15 ---(2)
multiply equation (1) by 31 and equation (2) by 47
substract (2) from (1) we get
(961 - 2209)y = 63x31 - 15x47
-1248 y = 1953 - 705
-1248 y = 1248
Therefore, y = -1.
Substitute y = -1 in equation (1) we get
47x = 94
So, x = 2.
Hence, The values of x and y are 2, -1.
The pair of linear equations kx + 4y = 5, 3x + 2y = 5 is consistent only when –- a)k≌6
- b)k = 6
- c)k≌3
- d)k = 3
Correct answer is option 'A'. Can you explain this answer?
The pair of linear equations kx + 4y = 5, 3x + 2y = 5 is consistent only when –
a)
k≌6
b)
k = 6
c)
k≌3
d)
k = 3
|
|
Aditya Shah answered |
kx + 4y = 5, 3x + 2y = 5
Here, a1=k,b1=4,c1=−5
and a2=3,b2=2,c2=-5
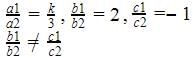
So , The equation is consistent when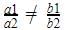
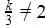
k ≠ 6
Here, a1=k,b1=4,c1=−5
and a2=3,b2=2,c2=-5
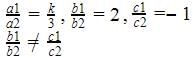
So , The equation is consistent when
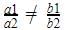
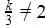
k ≠ 6
The number of solutions of the pair of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 are:- a)None
- b)Infinitely many
- c)0
- d)1
Correct answer is option 'B'. Can you explain this answer?
The number of solutions of the pair of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 are:
a)
None
b)
Infinitely many
c)
0
d)
1
|
|
Pooja Shah answered |
We have the equations x + 2y – 8 = 0 and 2x + 4y = 16 Where 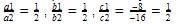
Here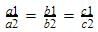 which is the case of coincident lines . So there are infinitely many solutions.
which is the case of coincident lines . So there are infinitely many solutions.
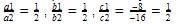
Here
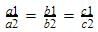 which is the case of coincident lines . So there are infinitely many solutions.
which is the case of coincident lines . So there are infinitely many solutions. If x + 2y = 5 & x – 2y = 7, then the value of x & y is: -- a)x = 6 & y = 3
- b)x = 12 & y = -1/2
- c)x = 6 & y = -1/2
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
If x + 2y = 5 & x – 2y = 7, then the value of x & y is: -
a)
x = 6 & y = 3
b)
x = 12 & y = -1/2
c)
x = 6 & y = -1/2
d)
None of the above
|
|
Roshni jain answered |
Solution:
Given, x + 2y = 5 ...(1)
and x + 2y = 7 ...(2)
Subtracting Equation (1) from Equation (2), we get
( x + 2y ) - ( x + 2y ) = 7 - 5
⇒ 0 = 2
The above equation is not satisfied for any value of x and y. Therefore, such values of x and y do not exist.
Hence, the correct option is (d) None of the above.
Given, x + 2y = 5 ...(1)
and x + 2y = 7 ...(2)
Subtracting Equation (1) from Equation (2), we get
( x + 2y ) - ( x + 2y ) = 7 - 5
⇒ 0 = 2
The above equation is not satisfied for any value of x and y. Therefore, such values of x and y do not exist.
Hence, the correct option is (d) None of the above.
At a closing down sale, a book store was selling 3 books and 5 notebooks for Rs 309 or 6 books and 2 notebooks for Rs 282. How much would one book and 1 notebook cost?- a)75
- b)33
- c)57
- d)42
Correct answer is option 'A'. Can you explain this answer?
At a closing down sale, a book store was selling 3 books and 5 notebooks for Rs 309 or 6 books and 2 notebooks for Rs 282. How much would one book and 1 notebook cost?
a)
75
b)
33
c)
57
d)
42
|
|
Mahaveer bhattacharya answered |
Given:
3 books + 5 notebooks = Rs 309
6 books + 2 notebooks = Rs 282
To find:
Cost of one book and one notebook
Let the cost of one book be x and the cost of one notebook be y.
Using the given information, we can form the following equations:
3x + 5y = 309 ...(1)
6x + 2y = 282 ...(2)
We can solve these equations using the elimination method.
Multiplying equation (1) by 2, we get:
6x + 10y = 618
Subtracting equation (2) from this, we get:
8y = 336
Dividing both sides by 8, we get:
y = 42
Substituting this value of y in equation (1), we get:
3x + 5(42) = 309
3x + 210 = 309
3x = 99
x = 33
Therefore, the cost of one book is Rs 33 and the cost of one notebook is Rs 42.
Hence, the cost of one book and one notebook together is Rs 75.
Answer: Option (a) 75.
3 books + 5 notebooks = Rs 309
6 books + 2 notebooks = Rs 282
To find:
Cost of one book and one notebook
Let the cost of one book be x and the cost of one notebook be y.
Using the given information, we can form the following equations:
3x + 5y = 309 ...(1)
6x + 2y = 282 ...(2)
We can solve these equations using the elimination method.
Multiplying equation (1) by 2, we get:
6x + 10y = 618
Subtracting equation (2) from this, we get:
8y = 336
Dividing both sides by 8, we get:
y = 42
Substituting this value of y in equation (1), we get:
3x + 5(42) = 309
3x + 210 = 309
3x = 99
x = 33
Therefore, the cost of one book is Rs 33 and the cost of one notebook is Rs 42.
Hence, the cost of one book and one notebook together is Rs 75.
Answer: Option (a) 75.
A system of simultaneous linear equations has infinitely many solutions if two lines:- a)are coincident
- b)intersect at two points
- c)are parallel
- d)intersect at one point
Correct answer is option 'A'. Can you explain this answer?
A system of simultaneous linear equations has infinitely many solutions if two lines:
a)
are coincident
b)
intersect at two points
c)
are parallel
d)
intersect at one point
|
|
Damini kumar answered |
Explanation:
Simultaneous linear equations are equations with two or more variables that are to be solved at the same time. These equations can be represented by lines, and the solutions represent the points where these lines intersect.
When two lines intersect at one point, there is only one solution to the system of equations. When two lines are parallel, there is no solution to the system of equations. However, when two lines are coincident, they overlap each other and have infinite solutions.
Example:
Consider the system of equations:
2x + 3y = 6
4x + 6y = 12
We can solve this system of equations by using elimination or substitution method.
Using the elimination method, we can multiply the first equation by 2 and subtract the second equation from it to eliminate x, which gives:
4x + 6y = 12
- (4x + 6y = 12)
-----------------
0x + 0y = 0
This equation is always true, which means that the two equations are equivalent. Therefore, they represent the same line, and there are infinitely many solutions to this system of equations.
Using the substitution method, we can solve for y in the first equation and substitute it into the second equation, which gives:
y = (6 - 2x)/3
4x + 6((6 - 2x)/3) = 12
Simplifying the second equation, we get:
4x + 4x = 12
Which gives:
x = 3/2
Substituting this value of x into the first equation, we get:
2(3/2) + 3y = 6
Simplifying, we get:
3y = 3
Which gives:
y = 1
Therefore, the solution to this system of equations is (3/2, 1). However, this is just one solution, and there are infinitely many solutions to this system of equations since the two lines are coincident.
Simultaneous linear equations are equations with two or more variables that are to be solved at the same time. These equations can be represented by lines, and the solutions represent the points where these lines intersect.
When two lines intersect at one point, there is only one solution to the system of equations. When two lines are parallel, there is no solution to the system of equations. However, when two lines are coincident, they overlap each other and have infinite solutions.
Example:
Consider the system of equations:
2x + 3y = 6
4x + 6y = 12
We can solve this system of equations by using elimination or substitution method.
Using the elimination method, we can multiply the first equation by 2 and subtract the second equation from it to eliminate x, which gives:
4x + 6y = 12
- (4x + 6y = 12)
-----------------
0x + 0y = 0
This equation is always true, which means that the two equations are equivalent. Therefore, they represent the same line, and there are infinitely many solutions to this system of equations.
Using the substitution method, we can solve for y in the first equation and substitute it into the second equation, which gives:
y = (6 - 2x)/3
4x + 6((6 - 2x)/3) = 12
Simplifying the second equation, we get:
4x + 4x = 12
Which gives:
x = 3/2
Substituting this value of x into the first equation, we get:
2(3/2) + 3y = 6
Simplifying, we get:
3y = 3
Which gives:
y = 1
Therefore, the solution to this system of equations is (3/2, 1). However, this is just one solution, and there are infinitely many solutions to this system of equations since the two lines are coincident.
Which of the following pairs of equations represent inconsistent system?- a)3x – y = -8 3x – y = 24
- b)5x – y = 10 10x – 2y = 20
- c)3x – 2y = 8 2x + 3y = 1
- d)lx – y = m x + my = l
Correct answer is option 'A'. Can you explain this answer?
Which of the following pairs of equations represent inconsistent system?
a)
3x – y = -8 3x – y = 24
b)
5x – y = 10 10x – 2y = 20
c)
3x – 2y = 8 2x + 3y = 1
d)
lx – y = m x + my = l
|
|
Amit Sharma answered |
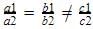 is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent.
is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent.3x – y = -8 ,3x – y = 24
3x – y +8=0 ,3x – y -24=0
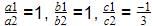
So,
 Therefore the equations are inconsistent.
Therefore the equations are inconsistent.Chapter doubts & questions for Simultaneous Equations - Mathematics for Year 10 2025 is part of Year 10 exam preparation. The chapters have been prepared according to the Year 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Year 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Simultaneous Equations - Mathematics for Year 10 in English & Hindi are available as part of Year 10 exam.
Download more important topics, notes, lectures and mock test series for Year 10 Exam by signing up for free.
Mathematics for Year 10
125 videos|468 docs|168 tests
|




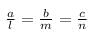

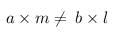
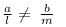



 So,
So,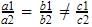 a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.
a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.

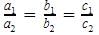
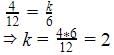

 which is satisfied by 10x – 14y = -4 only.
which is satisfied by 10x – 14y = -4 only.