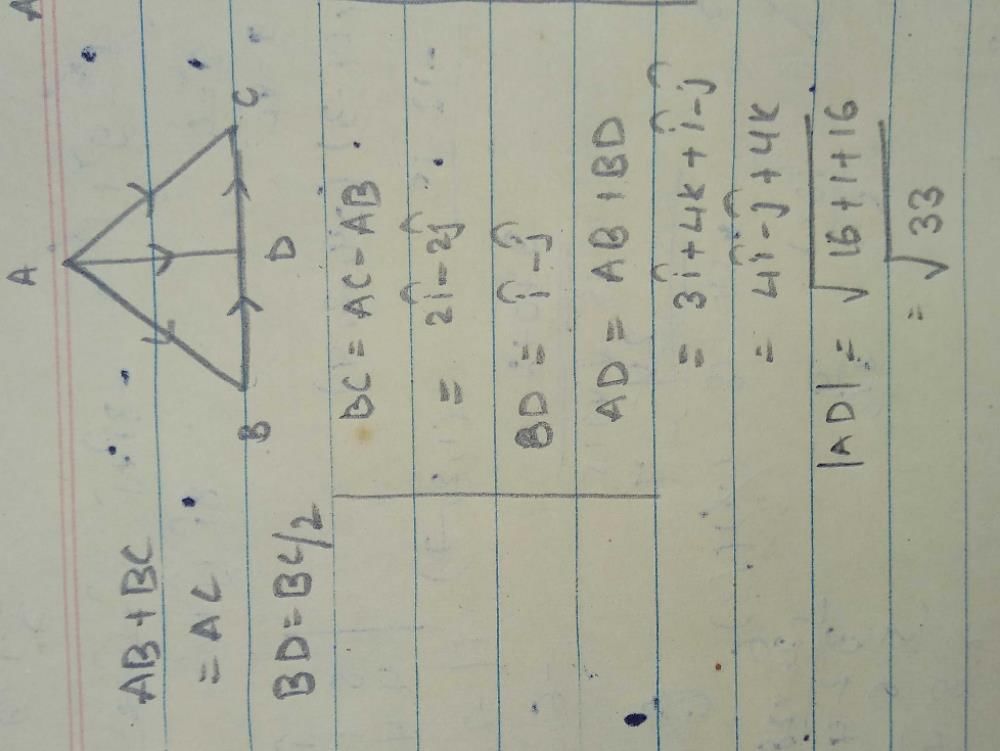All Exams >
Grade 12 >
Mathematics for Grade 12 >
All Questions
All questions of Vectors for Grade 12 Exam
The area of triangle whose adjacent sides are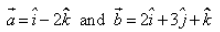 is :
is :- a)√70/2 sq. units
- b)9√2 /2 sq. units
- c)3√3 /2 sq. units
- d)2√3 /2 sq. units
Correct answer is option 'A'. Can you explain this answer?
The area of triangle whose adjacent sides are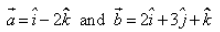 is :
is :
a)
√70/2 sq. units
b)
9√2 /2 sq. units
c)
3√3 /2 sq. units
d)
2√3 /2 sq. units
|
|
Suresh Iyer answered |
Area of triangle = ½(a * b)
a = (1, 0, -2) b = (2, 3, 1)
= i(0 + 6) + j(-4 - 1) + k(3 - 0)
= 6i - 5j + 3k
|a * b| = (36 + 25 + 9)½
|a * b| = (70)½
Area of triangle = ½(a * b)
= [(70)½]/2
a = (1, 0, -2) b = (2, 3, 1)
= i(0 + 6) + j(-4 - 1) + k(3 - 0)
= 6i - 5j + 3k
|a * b| = (36 + 25 + 9)½
|a * b| = (70)½
Area of triangle = ½(a * b)
= [(70)½]/2
A vector of magnitude 14 units, which is parallel to the vector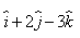
- a)
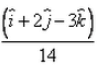
- b)
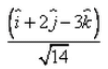
- c)
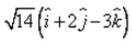
- d)

Correct answer is option 'C'. Can you explain this answer?
A vector of magnitude 14 units, which is parallel to the vector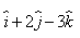
a)
b)
c)
d)
|
|
Preeti Iyer answered |
Given vector = i + 2j - 3k
Magnitude = √12 + 22 + (-3)2 = √14
Unit vector in direction of resultant = (i + 2j - 3k) / √14
Vector of magnitude 14 unit in direction of resultant,
⇒ 14[ (i + 2j - 3k) / √14 ]
⇒ √14(i + 2j - 3k)
Magnitude = √12 + 22 + (-3)2 = √14
Unit vector in direction of resultant = (i + 2j - 3k) / √14
Vector of magnitude 14 unit in direction of resultant,
⇒ 14[ (i + 2j - 3k) / √14 ]
⇒ √14(i + 2j - 3k)
If a, b, c and d are the position vectors of the points A, B, C and D such that a + c = b + d, then ABCD is a- a)Trapezium
- b)Rectangle
- c)Square
- d)Parallelogram
Correct answer is option 'D'. Can you explain this answer?
If a, b, c and d are the position vectors of the points A, B, C and D such that a + c = b + d, then ABCD is a
a)
Trapezium
b)
Rectangle
c)
Square
d)
Parallelogram
|
|
Tejas Verma answered |
Given:
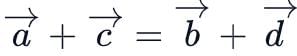
If we divide both sides with 2 we get,

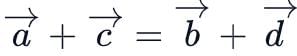
If we divide both sides with 2 we get,

⇒ Mid pt. of AC = Mid. pt. of BD
∴ ABCD is a parallelogram.
∴ ABCD is a parallelogram.
The position vector of mid-point of joining the points (2, – 1, 3) and (4, 3, –5) is :- a)
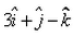
- b)
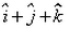
- c)
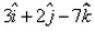
- d)
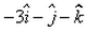
Correct answer is option 'A'. Can you explain this answer?
The position vector of mid-point of joining the points (2, – 1, 3) and (4, 3, –5) is :
a)
b)
c)
d)
|
|
Neha Sharma answered |
The position vector of point P = 2i - j + 3k
Position Vector of point Q = 4i + 3j - 5k
The position vector of R which divides PQ in half is given by:
r = (2i - j + 3k + 4i + 3j - 5k)/2
r = (6i + 2j - 2k)/2
r = 3i + j - k
Position Vector of point Q = 4i + 3j - 5k
The position vector of R which divides PQ in half is given by:
r = (2i - j + 3k + 4i + 3j - 5k)/2
r = (6i + 2j - 2k)/2
r = 3i + j - k
The area of parallelogram whose sides are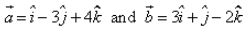 is:
is:- a)14 sq. units
- b)10√3 sq. units
- c)5√3 units
- d)7 sq. units
Correct answer is option 'B'. Can you explain this answer?
The area of parallelogram whose sides are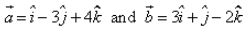 is:
is:
a)
14 sq. units
b)
10√3 sq. units
c)
5√3 units
d)
7 sq. units

|
Shivani answered |
Area of parallegram=|a×b|..calculate u will get the ans...HOPE U GOT IT..
The value of 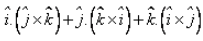 is:
is:- a)0
- b)3
- c)1/3
- d)1
Correct answer is option 'B'. Can you explain this answer?
The value of 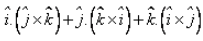 is:
is:
a)
0
b)
3
c)
1/3
d)
1

|
Sahil Soni answered |
Cross multiply in maths take place in cycle like i》j》k i×j=k j×k=i k×i=j but j×i=-k k×j=-i i×k=-j and dotmultiply takes place as i.i=1j.j=1K.K=1BUTI.J=0J.K=0k.i=0so the correct answer is b
The points with position vectors 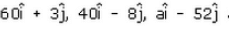 are collinear vectors, Value of a =
are collinear vectors, Value of a =- a)-20
- b)20
- c)-40
- d)40
Correct answer is option 'C'. Can you explain this answer?
The points with position vectors 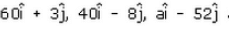 are collinear vectors, Value of a =
are collinear vectors, Value of a =
a)
-20
b)
20
c)
-40
d)
40
|
|
Om Desai answered |
Position vector A = 60i+3j
Position vector B = 40i-8j
Position vector C = aj-52j
Now, find vector AB and BC
AB = -20i-11j
BC= (a-40)i-44j
To be collinear, angle between the vector AB and BC made by the given position vectors should be 0 or 180 degree.
That’s why the cross product of the vectors should be zero
ABXBC=(-20i-11j)X(a-40)i-44j
0i+0j+(880+11(a-40))=0
a-40= -80
a=-40
Therefore, a should be -40 to be the given positions vectors collinear.
Position vector B = 40i-8j
Position vector C = aj-52j
Now, find vector AB and BC
AB = -20i-11j
BC= (a-40)i-44j
To be collinear, angle between the vector AB and BC made by the given position vectors should be 0 or 180 degree.
That’s why the cross product of the vectors should be zero
ABXBC=(-20i-11j)X(a-40)i-44j
0i+0j+(880+11(a-40))=0
a-40= -80
a=-40
Therefore, a should be -40 to be the given positions vectors collinear.
Unit vectors along the axes OX, OY and OZ are denoted by - a)

- b)
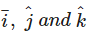
- c)

- d)
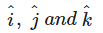
Correct answer is option 'D'. Can you explain this answer?
Unit vectors along the axes OX, OY and OZ are denoted by
a)
b)
c)
d)
|
|
Krishna Iyer answered |
If a and b are the position vectors of two points A and B and C is a point on AB produced such that AC = 3AB, then position vector of C will be- a)3b – 2a
- b)3a – b
- c)3a – 2b
- d)3b – a
Correct answer is option 'A'. Can you explain this answer?
If a and b are the position vectors of two points A and B and C is a point on AB produced such that AC = 3AB, then position vector of C will be
a)
3b – 2a
b)
3a – b
c)
3a – 2b
d)
3b – a
|
|
Anuj Datta answered |
Given information:
- Position vector of point A: a
- Position vector of point B: b
- Point C is on line AB produced such that AC = 3AB
To find:
- Position vector of point C
Solution:
Step 1: Find the vector AB
The vector AB is given by:
AB = b - a
Step 2: Find the vector AC
Since AC = 3AB, we can write:
AC = 3(b - a)
Step 3: Find the position vector of C
The position vector of C can be obtained by adding the vector AC to the position vector of A:
C = A + AC
Substituting the values of A and AC, we get:
C = a + 3(b - a)
Simplifying, we get:
C = 3b - 2a
Therefore, the position vector of point C is 3b - 2a.
Answer: Option A (3b - 2a)
- Position vector of point A: a
- Position vector of point B: b
- Point C is on line AB produced such that AC = 3AB
To find:
- Position vector of point C
Solution:
Step 1: Find the vector AB
The vector AB is given by:
AB = b - a
Step 2: Find the vector AC
Since AC = 3AB, we can write:
AC = 3(b - a)
Step 3: Find the position vector of C
The position vector of C can be obtained by adding the vector AC to the position vector of A:
C = A + AC
Substituting the values of A and AC, we get:
C = a + 3(b - a)
Simplifying, we get:
C = 3b - 2a
Therefore, the position vector of point C is 3b - 2a.
Answer: Option A (3b - 2a)
In the triangle ABC, which statement is not true?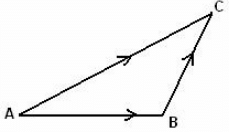
- a)

- b)
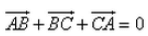
- c)
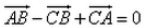
- d)
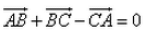
Correct answer is option 'D'. Can you explain this answer?
In the triangle ABC, which statement is not true?
a)
b)
c)
d)

|
sanju sura answered |
Ab + bc > ac ...it is property of a triangle .... that sum of two sides is greater than the third side ... so I think it is no possible that ab +bc -ca =0...but I'm not understanding the logic behind the question.......😊
The value of  is equal to the box product
is equal to the box product - a)
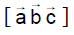
- b)
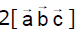
- c)
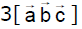
- d)
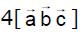
Correct answer is option 'C'. Can you explain this answer?
The value of  is equal to the box product
is equal to the box product
 is equal to the box product
is equal to the box product a)
b)
c)
d)
|
|
Geetika Shah answered |
Matrix {(1,2,-1) (1,-1,0) (1,-1,-1)} [a b c]
= {1(1) -2(-1) -1(0)} [a b c]
= 3[a b c]
= {1(1) -2(-1) -1(0)} [a b c]
= 3[a b c]
If the magnitude of the position vector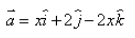 is 7, the value of x is:
is 7, the value of x is:- a)±1
- b)±5
- c)±3
- d)±2
Correct answer is option 'C'. Can you explain this answer?
If the magnitude of the position vector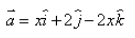 is 7, the value of x is:
is 7, the value of x is:
a)
±1
b)
±5
c)
±3
d)
±2
|
|
Aryan Khanna answered |
|a| = (x2 + 22 + (2x)2)1/2
7 = (x2 + 22 + (2x)2)1/2
⇒ 49 = x2 + 22 + 4x2
⇒ 49 = 4 + 5x2
⇒ 5x2 = 45
⇒ x2 = 9
x = ±3
If 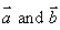 are two vectors, such that
are two vectors, such that 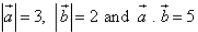 , then
, then 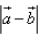 = ……
= ……- a)3
- b)√7
- c)√5
- d)√3
Correct answer is option 'D'. Can you explain this answer?
If  are two vectors, such that
are two vectors, such that 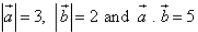 , then
, then 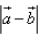 = ……
= ……
a)
3
b)
√7
c)
√5
d)
√3
|
|
Neha Sharma answered |
|a - b|2 = |a|2 + |b|2 - 2|a||b|
|a - b|2 = (3)2 + (2)2 - 2(5)
|a - b|2 = 9 + 4 - 10
|a - b|2 = 3
|a - b| = (3)½.
|a - b|2 = (3)2 + (2)2 - 2(5)
|a - b|2 = 9 + 4 - 10
|a - b|2 = 3
|a - b| = (3)½.
The angles α, β, γ made by the vector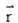 with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector
with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector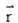 are:
are: - a)cos α, cos β, cos γ
- b)sin α, sin β, sin γ
- c)180° - α, 180° - β, 180° γ
- d)tan α, tan β, tan γ
Correct answer is option 'A'. Can you explain this answer?
The angles α, β, γ made by the vector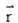 with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector
with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector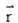 are:
are:
a)
cos α, cos β, cos γ
b)
sin α, sin β, sin γ
c)
180° - α, 180° - β, 180° γ
d)
tan α, tan β, tan γ
|
|
Sarita Yadav answered |
Direction Cosines for angle α, β, γ are:
cos α, cos β, cos γ

cos α, cos β, cos γ

What is the additive identity of a vector?- a)zero vector
- b)Negative of the vector
- c)unit vector
- d)The vector itself
Correct answer is option 'A'. Can you explain this answer?
What is the additive identity of a vector?
a)
zero vector
b)
Negative of the vector
c)
unit vector
d)
The vector itself
|
|
Nandini Iyer answered |
In the Additive Identity of vectors, the additive identity is zero vector 0.
For any vector V additive identity is defined as,
0 + V = V and V + 0 = V
For any vector V additive identity is defined as,
0 + V = V and V + 0 = V
ABCD is a parallelogram. If coordinates of A,B,C are (2,3), (1,4) and (0, -2). Coordinates of D =- a)(-1,3)
- b)(1,-3)
- c)(1,3)
- d)(-1,-3)
Correct answer is option 'B'. Can you explain this answer?
ABCD is a parallelogram. If coordinates of A,B,C are (2,3), (1,4) and (0, -2). Coordinates of D =
a)
(-1,3)
b)
(1,-3)
c)
(1,3)
d)
(-1,-3)
|
|
Naina Bansal answered |
Here's a generic way to solve problems like this.
For any two vectors a and b, we always have
- a)|a – b| ≥ |a| – |b|
- b)|a + b| ≤ |a| + |b|
- c)|a + b| ≤ |a| – |b|
- d)|a – b| = |a + b|
Correct answer is option 'B'. Can you explain this answer?
For any two vectors a and b, we always have
a)
|a – b| ≥ |a| – |b|
b)
|a + b| ≤ |a| + |b|
c)
|a + b| ≤ |a| – |b|
d)
|a – b| = |a + b|
|
|
Nandini Iyer answered |
|a + b|2 = |a|2 + |b|2 + 2|a||b|.cosθ
|a|2 + |b|2 = |a|2 + |b|2 + 2|a| + |b| ∵ −1 ⩽ cosθ ⩽ 1
⇒ 2|a||b|.cosθ ⩽ 2|a||b|
So, |a + b|2 ⩽ (|a| + |b|
⇒ |a + b| ≤ |a| + |b|
This is also known as Triangle Inequality of vectors.
|a|2 + |b|2 = |a|2 + |b|2 + 2|a| + |b| ∵ −1 ⩽ cosθ ⩽ 1
⇒ 2|a||b|.cosθ ⩽ 2|a||b|
So, |a + b|2 ⩽ (|a| + |b|
)2
⇒ |a + b| ≤ |a| + |b|
This is also known as Triangle Inequality of vectors.

If a unit vector 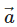 makes angles
makes angles 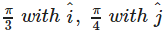 and an acute angle θ with
and an acute angle θ with  , then the components of
, then the components of  are
are- a)
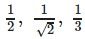
- b)
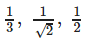
- c)
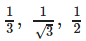
- d)
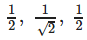
Correct answer is option 'D'. Can you explain this answer?
If a unit vector 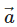 makes angles
makes angles 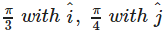 and an acute angle θ with
and an acute angle θ with  , then the components of
, then the components of 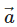 are
are
a)
b)
c)
d)

|
Siddhi Bhardwaj answered |
L²+m²+n²=1 1/2+1/4+n²=1 (((cosπ/3=m and cosπ/4=l))) n²=1/4 n=+-1/2 n=1/2 here n is k
4-points whose position vector 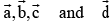 are coplanar and
are coplanar and 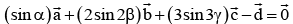 then the least value of
then the least value of 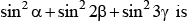
- a)1
- b)1/14
- c)2
- d)1/10
Correct answer is option 'B'. Can you explain this answer?
4-points whose position vector 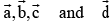 are coplanar and
are coplanar and 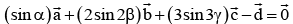 then the least value of
then the least value of 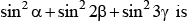
a)
1
b)
1/14
c)
2
d)
1/10
|
|
Ishan Choudhury answered |
As the vectors are complainer sum of coefficient =0
sinα + 2sinβ + 3sinγ = 1
this can be also LHS can also be called to be dot product of two vectors (1,2,3) and (sinα,sinβ,sinγ)
dot product of these two vectors is
sinα + 2sinβ + 3sinγ
aˉ.bˉ=|a||b|cosθ
(sinα+2sinβ+3sinγ)/1 = (sin2α+sin2β+sin2γ)×14cosθ
1/14cosθ = sin^2α+sin^2β+sin^2γ
∴ Minimum value is 1/14
sinα + 2sinβ + 3sinγ = 1
this can be also LHS can also be called to be dot product of two vectors (1,2,3) and (sinα,sinβ,sinγ)
dot product of these two vectors is
sinα + 2sinβ + 3sinγ
aˉ.bˉ=|a||b|cosθ
(sinα+2sinβ+3sinγ)/1 = (sin2α+sin2β+sin2γ)×14cosθ
1/14cosθ = sin^2α+sin^2β+sin^2γ
∴ Minimum value is 1/14
Coinitial Vectors are- a)Two or more vectors having the same final point
- b)Two or more pseudo vectors having the same initial point
- c)Two or more force vectors having the same initial point
- d)Two or more vectors having the same initial point
Correct answer is option 'D'. Can you explain this answer?
Coinitial Vectors are
a)
Two or more vectors having the same final point
b)
Two or more pseudo vectors having the same initial point
c)
Two or more force vectors having the same initial point
d)
Two or more vectors having the same initial point

|
Bhavana Dey answered |
Two vectors whose initial point is same are called co- initial vectors
The position vectors of the end points of diameter of a circle are 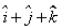 and
and 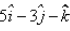 , then the position vector of the centre of the circle is:
, then the position vector of the centre of the circle is:- a)
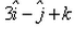
- b)
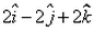
- c)
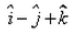
- d)
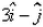
Correct answer is option 'D'. Can you explain this answer?
The position vectors of the end points of diameter of a circle are 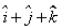 and
and 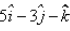 , then the position vector of the centre of the circle is:
, then the position vector of the centre of the circle is:
a)
b)
c)
d)
|
|
Om Desai answered |
{(1+5)î +(1-3)j + (1-1)k} / 2
= {6i - 2j + 0k}/2
= 3i - j
= {6i - 2j + 0k}/2
= 3i - j
Let 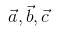 be vectors of length 3,4,5 respectively. Let
be vectors of length 3,4,5 respectively. Let 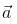 be perpendicular to
be perpendicular to 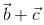 ,
,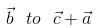 and
and 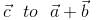 . then
. then 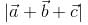
- a)
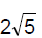
- b)
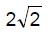
- c)
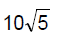
- d)
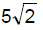
Correct answer is option 'D'. Can you explain this answer?
Let 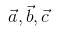 be vectors of length 3,4,5 respectively. Let
be vectors of length 3,4,5 respectively. Let 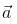 be perpendicular to
be perpendicular to 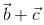 ,
,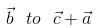 and
and 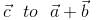 . then
. then 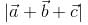
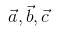 be vectors of length 3,4,5 respectively. Let
be vectors of length 3,4,5 respectively. Let 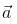 be perpendicular to
be perpendicular to 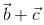 ,
,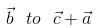 and
and 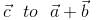 . then
. then 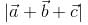
a)
b)
c)
d)
|
|
Vivek Patel answered |
|A| = 3, |B| = 4, |C| = 5
Since A.(B + C) = B.(C+A) = C(A+B) = 0...........(1)
|A+B+C|2 = |A| + |B|2 + |C|2 + 2(A.B + B+C + C.A)
= 9+16+25+0
from eq(1) {A.B + B+C + C.A = 0}
therefore, |A+B+C|2 = 50
=> |A+B+C| = 5(2)1/2
Since A.(B + C) = B.(C+A) = C(A+B) = 0...........(1)
|A+B+C|2 = |A| + |B|2 + |C|2 + 2(A.B + B+C + C.A)
= 9+16+25+0
from eq(1) {A.B + B+C + C.A = 0}
therefore, |A+B+C|2 = 50
=> |A+B+C| = 5(2)1/2
If 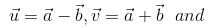
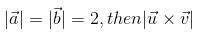 is equal to
is equal to - a)
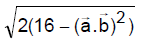
- b)
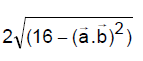
- c)

- d)

Correct answer is option 'B'. Can you explain this answer?
If 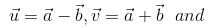
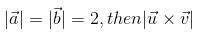 is equal to
is equal to
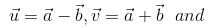
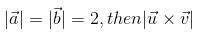 is equal to
is equal to a)
b)
c)
d)

|
Md Jisan answered |
(u × v) = a square - b square , now mod of (u × v) = √( a to the power 4 + b to the power 4 + 2 (ab) square cosx ) . So ab cosx will give (a.b); now the determination of the value is much easy
If the distance of the point P (1, –2, 1) from the plane x + 2y – 2z = α , where α > 0, is 5, then the foot of the perpendicular from P to the plane is- a)
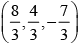
- b)
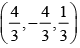
- c)
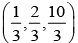
- d)
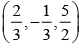
Correct answer is option 'A'. Can you explain this answer?
If the distance of the point P (1, –2, 1) from the plane x + 2y – 2z = α , where α > 0, is 5, then the foot of the perpendicular from P to the plane is
a)
b)
c)
d)
|
|
Tejas Verma answered |
As perpendicular distance of x + 2y – 2z = α from the point (1, –2, 1) is 5

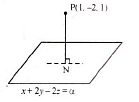
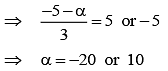
∴ Plane becomes x + 2y – 2z – 10 = 0
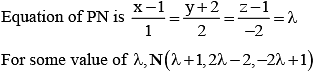
It lies on x + 2y – 2z – 10 = 0
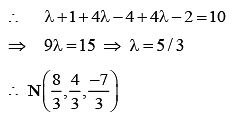
∴ Plane becomes x + 2y – 2z – 10 = 0
It lies on x + 2y – 2z – 10 = 0
A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of each of the points of intersection are given by- a)(2a, 3a, 3a), (2a, a, a)
- b)(3a, 2a, 3a), (a, a, a)
- c)(3a, 2a, 3a), (a, a, 2a)
- d)(3a, 3a, 3a), (a, a, a)
Correct answer is option 'B'. Can you explain this answer?
A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of each of the points of intersection are given by
a)
(2a, 3a, 3a), (2a, a, a)
b)
(3a, 2a, 3a), (a, a, a)
c)
(3a, 2a, 3a), (a, a, 2a)
d)
(3a, 3a, 3a), (a, a, a)
|
|
Vivek answered |
IT'S SIMPLE!!!!
The direction cosines are proportional to 2,1,2.
The difference of the points of intersection will give the direction ratios. So, subtract the the points of intersection given in the options. In option B , the direction ratios obtained are (2a,a,2a). Here it's easy to see from the direction ratios obtained that the direction cosines of this line will be proportional to 2,1,2.
Hence B is the correct answer.
I hope you have got it. If not then u can discuss it with me.
The distance between the point (2, 3, 1) and (–1, 2, – 3) is:
- a)√26 units
- b)5 units
- c)√20 units
- d)4 units
Correct answer is option 'A'. Can you explain this answer?
The distance between the point (2, 3, 1) and (–1, 2, – 3) is:
a)
√26 units
b)
5 units
c)
√20 units
d)
4 units
|
|
Giriraj Gupta answered |
Use the distance formula
distance=root of [ (x1-x2)^2+(y1-y2)^2+(z1-z2)^2]
distance=root of [ (x1-x2)^2+(y1-y2)^2+(z1-z2)^2]
The vector joining the points A(2, – 3, 1) and B(1, – 2, – 5) directed from B to A is:- a)
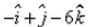
- b)

- c)
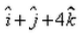
- d)
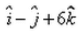
Correct answer is option 'D'. Can you explain this answer?
The vector joining the points A(2, – 3, 1) and B(1, – 2, – 5) directed from B to A is:
a)
b)
c)
d)

|
Siddhant Kumar answered |
The vector goes from B to A means that its initial coordinates is at B and final at A.
so the vector BA will be [ (2-1)i + (-3+2) j + (1+5)k ] = i-j+6k.
so the vector BA will be [ (2-1)i + (-3+2) j + (1+5)k ] = i-j+6k.
A vector whose initial and terminal points coincide, is called- a)zero vector
- b)unit vector
- c)equal vectors
- d)coterminus vectors
Correct answer is option 'A'. Can you explain this answer?
A vector whose initial and terminal points coincide, is called
a)
zero vector
b)
unit vector
c)
equal vectors
d)
coterminus vectors
|
|
Nandini Patel answered |
Zero Vector Or Null Vector – A vector whose initia... morel and terminal points coincide is known as zero vector.Unit Vector
If 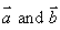 are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors
are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors 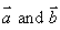 are collinear.
are collinear. - a)1
- b)2
- c)-1
- d)-2
Correct answer is option 'B'. Can you explain this answer?
If 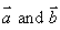 are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors
are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors 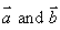 are collinear.
are collinear.
a)
1
b)
2
c)
-1
d)
-2
|
|
Neha Sharma answered |
Given a = (-1,1) and b = (m,-2)
Given that above two vectors are collinear, so they are parallel
⇒ -1/m = 1/-2
⇒ m = 2
Given that above two vectors are collinear, so they are parallel
⇒ -1/m = 1/-2
⇒ m = 2
If u and v are unit vectors and θ is the acute angle between them, then 2u × 3v is a unit vector for- a)Exactly two values of θ
- b)More than two values of θ
- c)No value of θ
- d)Exactly one value of θ
Correct answer is option 'D'. Can you explain this answer?
If u and v are unit vectors and θ is the acute angle between them, then 2u × 3v is a unit vector for
a)
Exactly two values of θ
b)
More than two values of θ
c)
No value of θ
d)
Exactly one value of θ
|
|
Bhargavi Sen answered |
If u and v are unit vectors, it means that their magnitudes are equal to 1. Thus, ||u|| = ||v|| = 1.
Given that ||u + v|| = 2, we want to prove that ||u - v|| = 2.
Using the triangle inequality, we have:
||u + v|| ≤ ||u|| + ||v||
Since ||u|| = ||v|| = 1, the inequality becomes:
||u + v|| ≤ 1 + 1
||u + v|| ≤ 2
Since we are given that ||u + v|| = 2, the inequality becomes:
2 ≤ 2
This inequality is true, so the triangle inequality holds.
Now, let's consider ||u - v||:
||u - v|| = ||u + (-v)||
Since -v is the additive inverse of v, its magnitude is the same as v's magnitude, so ||-v|| = ||v|| = 1.
Using the triangle inequality again, we have:
||u + (-v)|| ≤ ||u|| + ||-v||
Since ||u|| = 1 and ||-v|| = 1, the inequality becomes:
||u + (-v)|| ≤ 1 + 1
||u + (-v)|| ≤ 2
However, since we are given that ||u + v|| = 2, we can replace u + (-v) with u + v in the inequality:
||u + v|| ≤ 2
Therefore, ||u - v|| ≤ 2.
But we also know that ||u - v|| ≥ 0, since magnitudes are always non-negative.
Since ||u - v|| ≤ 2 and ||u - v|| ≥ 0, the only possible value for ||u - v|| is 2.
Therefore, ||u - v|| = 2.
In conclusion, if u and v are unit vectors and ||u + v|| = 2, then ||u - v|| = 2.
Given that ||u + v|| = 2, we want to prove that ||u - v|| = 2.
Using the triangle inequality, we have:
||u + v|| ≤ ||u|| + ||v||
Since ||u|| = ||v|| = 1, the inequality becomes:
||u + v|| ≤ 1 + 1
||u + v|| ≤ 2
Since we are given that ||u + v|| = 2, the inequality becomes:
2 ≤ 2
This inequality is true, so the triangle inequality holds.
Now, let's consider ||u - v||:
||u - v|| = ||u + (-v)||
Since -v is the additive inverse of v, its magnitude is the same as v's magnitude, so ||-v|| = ||v|| = 1.
Using the triangle inequality again, we have:
||u + (-v)|| ≤ ||u|| + ||-v||
Since ||u|| = 1 and ||-v|| = 1, the inequality becomes:
||u + (-v)|| ≤ 1 + 1
||u + (-v)|| ≤ 2
However, since we are given that ||u + v|| = 2, we can replace u + (-v) with u + v in the inequality:
||u + v|| ≤ 2
Therefore, ||u - v|| ≤ 2.
But we also know that ||u - v|| ≥ 0, since magnitudes are always non-negative.
Since ||u - v|| ≤ 2 and ||u - v|| ≥ 0, the only possible value for ||u - v|| is 2.
Therefore, ||u - v|| = 2.
In conclusion, if u and v are unit vectors and ||u + v|| = 2, then ||u - v|| = 2.
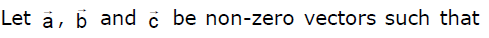

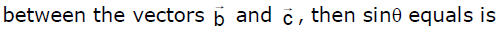
- a)
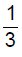
- b)
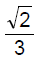
- c)
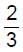
- d)
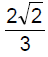
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
|
Swati Verma answered |
(a→*b→)*c→ = (1/3)|b→||c→||a→|
⇒ − c→*(a→*b→) = (1/3)|b→||c→||a→|
⇒(c→.a→)b→ −(c→.b→)a→ =(1/3)|b→||c→|a→|
Now, as all of them are non-collinear, (c→⋅a→) can be 0 that means,
(c→.b→) = (−1/3)|b→||c→|
⇒|b→|.|c→|cosθ = (−1/3)|b→||c→|
⇒ cosθ = −1/3
sinθ = √1−(1/3)^2
= √8/9
= (2√2)/√3
⇒ − c→*(a→*b→) = (1/3)|b→||c→||a→|
⇒(c→.a→)b→ −(c→.b→)a→ =(1/3)|b→||c→|a→|
Now, as all of them are non-collinear, (c→⋅a→) can be 0 that means,
(c→.b→) = (−1/3)|b→||c→|
⇒|b→|.|c→|cosθ = (−1/3)|b→||c→|
⇒ cosθ = −1/3
sinθ = √1−(1/3)^2
= √8/9
= (2√2)/√3
For what values of x and y, the vectors are equal?
are equal?- a)
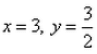
- b)x = 3, y = 6
- c)
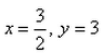
- d)x = 6, y = 3
Correct answer is option 'C'. Can you explain this answer?
For what values of x and y, the vectors are equal?
are equal?
a)
b)
x = 3, y = 6
c)
d)
x = 6, y = 3

|
Satyam Sriraj answered |
For equal vector
2x=3
and 2x=y
now
solve it.
2x=3
and 2x=y
now
solve it.
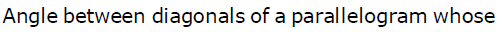
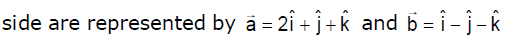
- a)
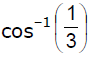
- b)
- c)
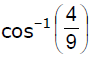
- d)
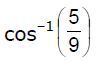
Correct answer is option 'A'. Can you explain this answer?
a)
b)
c)
d)
|
|
Lavanya Menon answered |
D1 = a+b
D2 = a-b
D1 = 3i + 0j + 0k
D2 = i + 2j + 2k
|D1| = 3
D1.D2 = |D1| . |D2| . cos θ
3 + 0 + 0 = (3) . (3) cos θ
3 = 9 cosθ
cos-1 = (⅓)
D2 = a-b
D1 = 3i + 0j + 0k
D2 = i + 2j + 2k
|D1| = 3
D1.D2 = |D1| . |D2| . cos θ
3 + 0 + 0 = (3) . (3) cos θ
3 = 9 cosθ
cos-1 = (⅓)
Chapter doubts & questions for Vectors - Mathematics for Grade 12 2025 is part of Grade 12 exam preparation. The chapters have been prepared according to the Grade 12 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 12 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Vectors - Mathematics for Grade 12 in English & Hindi are available as part of Grade 12 exam.
Download more important topics, notes, lectures and mock test series for Grade 12 Exam by signing up for free.
Mathematics for Grade 12
99 videos|124 docs|82 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup




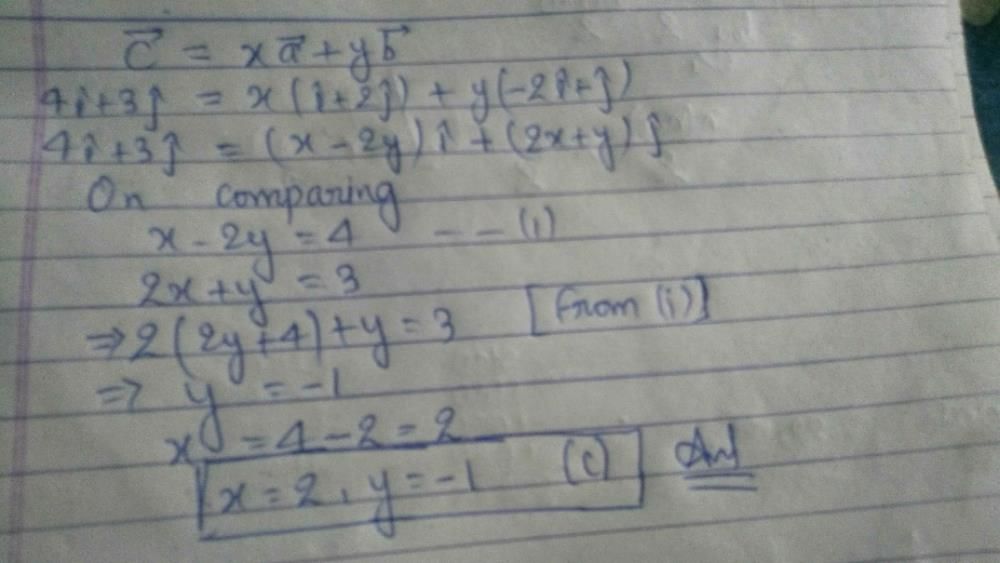
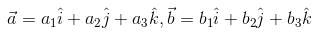 and
and 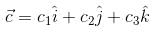 be three non-zero vectors such that
be three non-zero vectors such that  is a unit vector perpendicular to both
is a unit vector perpendicular to both  . if the angle between
. if the angle between 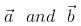 is π/6, then
is π/6, then  is equal to
is equal to 


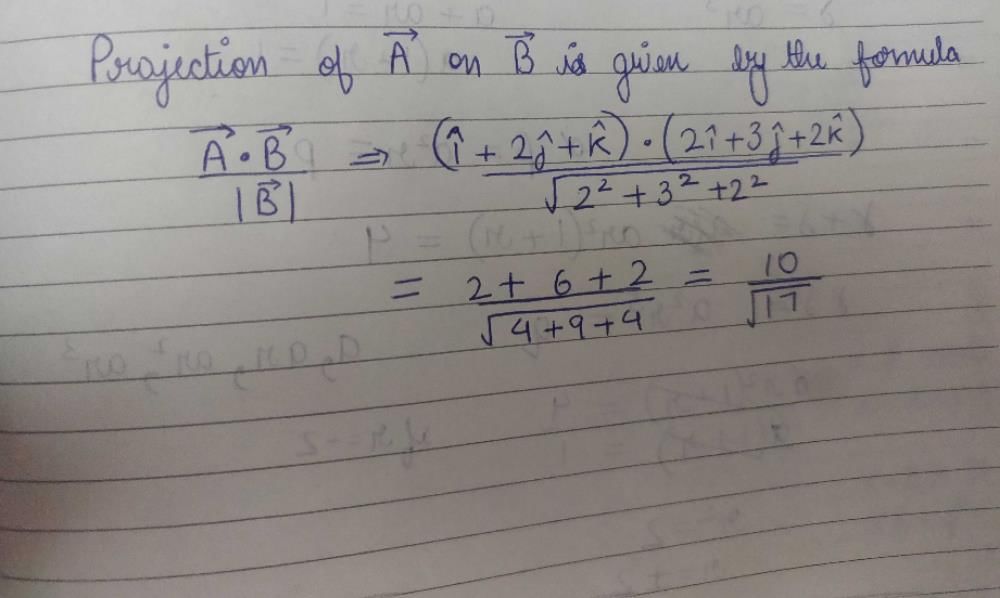





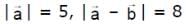 and
and 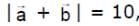 then
then  is equal to
is equal to 
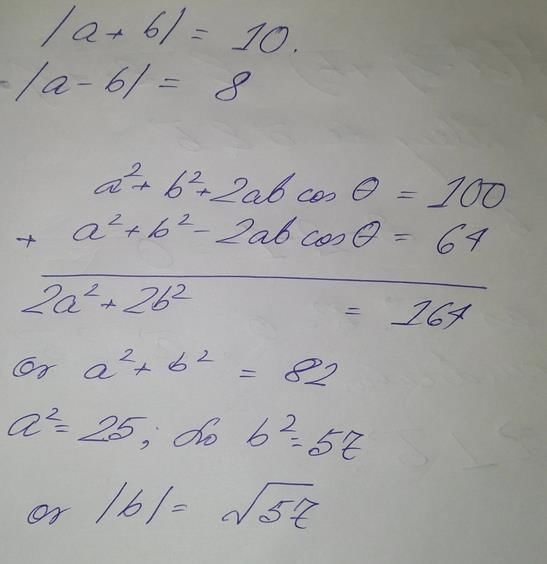





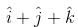 and lies in the plane of
and lies in the plane of 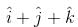 and
and 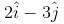
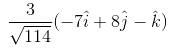
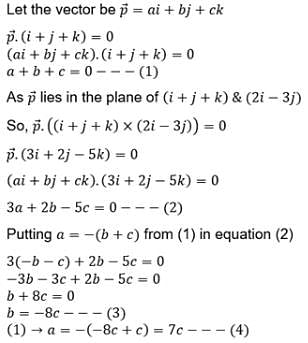
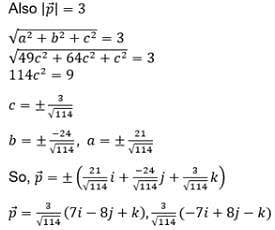


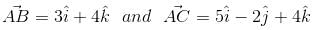 are the sides of a triangle ABC. The length of the median through A is
are the sides of a triangle ABC. The length of the median through A is