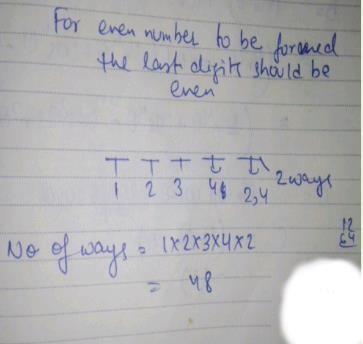All Exams >
Grade 12 >
Mathematics for Grade 12 >
All Questions
All questions of Permutations and Counting for Grade 12 Exam
The number of ways in which the 6 faces of a cube can be painted with 6 different colours is- a)6
- b)12
- c)6!
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The number of ways in which the 6 faces of a cube can be painted with 6 different colours is
a)
6
b)
12
c)
6!
d)
none of these
|
|
Preeti Iyer answered |
Consider the face that has red color. There are fi... moreve face
Four alphabets A, M, P, O are purchased from a warehouse. How many ordered pairs of initials can be formed using these?- a)10
- b)16
- c)18
- d)12
Correct answer is option 'D'. Can you explain this answer?
Four alphabets A, M, P, O are purchased from a warehouse. How many ordered pairs of initials can be formed using these?
a)
10
b)
16
c)
18
d)
12
|
|
Riya Banerjee answered |
Total number of letters = 4
Number of ordered pairs of letters that can be formed like (A, M) or (P, O) etc = 4P2 = 4!/2!
= 24/2
= 12
Number of ordered pairs of letters that can be formed like (A, M) or (P, O) etc = 4P2 = 4!/2!
= 24/2
= 12
In how many ways can a cricket team of 11 players be chosen out from a squad of 14 players, if 5 particular players are always chosen?- a)84
- b)144
- c)1001
- d)1365
Correct answer is option 'A'. Can you explain this answer?
In how many ways can a cricket team of 11 players be chosen out from a squad of 14 players, if 5 particular players are always chosen?
a)
84
b)
144
c)
1001
d)
1365
|
|
Aryan Khanna answered |
Total no of players = 14 out of which 5 are fixed.
So, 11-5 = 6
Remaining players = 14 - 6
= 9 players
9C6 = 9!/(3!*6!)
= 84
So, 11-5 = 6
Remaining players = 14 - 6
= 9 players
9C6 = 9!/(3!*6!)
= 84
In how many ways can 3 letters be posted in 4 letter boxes?- a)27
- b)4!
- c)64
- d)3!
Correct answer is option 'C'. Can you explain this answer?
In how many ways can 3 letters be posted in 4 letter boxes?
a)
27
b)
4!
c)
64
d)
3!
|
|
Preeti Iyer answered |
The first letter can be posted in 4 ways. So, total outcomes about the first letter = 4.
For every outcome about the first letter, the second letter can be posted in 4 ways. So, total outcomes about the first and the second letters= (4*4) = 16.
Therefore, following the same route, we can say, total possible outcomes about the first and the second letters = (4*4*4) = 64.
In how many ways 2 directors and 3 executives can be arranged for a meeting? If there are 6 chairs available two on one side and remaining four on the other side of the table and the two directors has to be together on one side and the executives on the other side.- a)24
- b)48
- c)720
- d)120
Correct answer is option 'B'. Can you explain this answer?
In how many ways 2 directors and 3 executives can be arranged for a meeting? If there are 6 chairs available two on one side and remaining four on the other side of the table and the two directors has to be together on one side and the executives on the other side.
a)
24
b)
48
c)
720
d)
120
|
|
Hansa Sharma answered |
3 executives in 4 chairs = 4P3 ways
Total no. of ways = 2! * 4P3
=> 2*1*(4!/1!)
= 2*24
= 48
Total no. of ways = 2! * 4P3
=> 2*1*(4!/1!)
= 2*24
= 48
A room has 8 doors. In how many ways, a man can enter in the room through one door and exit through a different door?- a)5040
- b)40320
- c)56
- d)8
Correct answer is option 'C'. Can you explain this answer?
A room has 8 doors. In how many ways, a man can enter in the room through one door and exit through a different door?
a)
5040
b)
40320
c)
56
d)
8
|
|
Naina Sharma answered |
The person has 8 options to enter the hall. For each of these 8 options, he has 7 options to exit the hall. Thus, he has 8 × 7 = 56 ways to enter and exit from different doors.
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is- a)164
- b)140
- c)112
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is
a)
164
b)
140
c)
112
d)
none of these
|
|
Neha Joshi answered |
Let us say that the two particular friends are A and B.
If A is invited among six guests and B is not, then: number of combinations to select 5 more guests from the remaining 8 friends:
C(8, 5) = 8 ! / (5! 3!) = 56
If B is invited among the six guests and A is not , then the number of ways of selecting the remaining 5 guests = C(8, 5) = 56
Suppose both A and B are not included in the six guests list : then the number of such combinations = C(8, 6) = 7 * 8 /2 = 28
So the total number of sets of guests that can be selected = 140.
If A is invited among six guests and B is not, then: number of combinations to select 5 more guests from the remaining 8 friends:
C(8, 5) = 8 ! / (5! 3!) = 56
If B is invited among the six guests and A is not , then the number of ways of selecting the remaining 5 guests = C(8, 5) = 56
Suppose both A and B are not included in the six guests list : then the number of such combinations = C(8, 6) = 7 * 8 /2 = 28
So the total number of sets of guests that can be selected = 140.
The number of ways in which 6 “ + “ and 4 “ – “ signs can be arranged in a line such that no two “ – “ signs occur together is- a)P(10,4)
- b)C(7,4)
- c)C(10,4)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of ways in which 6 “ + “ and 4 “ – “ signs can be arranged in a line such that no two “ – “ signs occur together is
a)
P(10,4)
b)
C(7,4)
c)
C(10,4)
d)
none of these

|
Sushil Kumar answered |
′+′ signs can be put in a row in one way creating seven gaps shown as arrows:
Now 4′−′ signs must be kept in these gaps. So, no tow ′−′ signs should be together.
Out of these 7 gaps 4 can be chosen in 7C4 ways.
Now 4′−′ signs must be kept in these gaps. So, no tow ′−′ signs should be together.
Out of these 7 gaps 4 can be chosen in 7C4 ways.
Number of signals that can be made using given 4 flags of which 3 are blue and 1 is red?- a)3i
- b)12
- c)4i
- d)4
Correct answer is option 'D'. Can you explain this answer?
Number of signals that can be made using given 4 flags of which 3 are blue and 1 is red?
a)
3i
b)
12
c)
4i
d)
4

|
Shiksha Academy answered |
Total flags = 4
Blue = 3
red = 1
Total no. of signals = (4!*3!)/3!
= 4
Blue = 3
red = 1
Total no. of signals = (4!*3!)/3!
= 4
The total number of ways of answering 5 objective questions, each question having four choices are- a)2880
- b)120
- c)1024
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
The total number of ways of answering 5 objective questions, each question having four choices are
a)
2880
b)
120
c)
1024
d)
None of the above
|
|
Preeti Iyer answered |
The total ways of answering would be. 4x4x4x4x4=4^5 that will be 1024.
In how many ways can 4 red, 3 yellow and 2 green chairs be arranged in a row if the chairs of the same colour are indistinguishable?- a)15120
- b)1260
- c)362880
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
In how many ways can 4 red, 3 yellow and 2 green chairs be arranged in a row if the chairs of the same colour are indistinguishable?
a)
15120
b)
1260
c)
362880
d)
None of the above
|
|
Hansa Sharma answered |
Total no of balls = 9
red balls = 4
yellow balls = 3
green balls = 2
Total no. of arrangements = 9!/(4!*3!*2!)
= 1260
red balls = 4
yellow balls = 3
green balls = 2
Total no. of arrangements = 9!/(4!*3!*2!)
= 1260
Among 7 flags 4 are of red colour and the rest are all different colours.How mant different signals can be generated using these flags?- a)240
- b)210
- c)180
- d)120
Correct answer is option 'B'. Can you explain this answer?
Among 7 flags 4 are of red colour and the rest are all different colours.How mant different signals can be generated using these flags?
a)
240
b)
210
c)
180
d)
120
|
|
Poonam Reddy answered |
Total flags = 4
Different colour = 3
red = 4
Total no. of signals = 7P3
= 7!/(4!)
= 210
Different colour = 3
red = 4
Total no. of signals = 7P3
= 7!/(4!)
= 210
A coin is tossed 6 times, in how many throws can 4 heads and 2 tails be obtained?- a)24
- b)18
- c)15
- d)10
Correct answer is option 'C'. Can you explain this answer?
A coin is tossed 6 times, in how many throws can 4 heads and 2 tails be obtained?
a)
24
b)
18
c)
15
d)
10
|
|
Naina Bansal answered |
Whether we toss a coin 6 times or six coins one time the number of arrangement will remain same .
As to find number of ways we get 4 heads and 2 tails out of 6 times
In how many ways, a party of 5 men and 5 women be seated at a circular table, so that no two women are adjacent?- a)720
- b)14400
- c)2880
- d)1440
Correct answer is option 'C'. Can you explain this answer?
In how many ways, a party of 5 men and 5 women be seated at a circular table, so that no two women are adjacent?
a)
720
b)
14400
c)
2880
d)
1440

|
Ayush Joshi answered |
Lets first place the men (M). '*' here indicates the linker of round table
* M -M - M - M - M *
which is in (5-1)! ways
So we have to place the women in between the men which is on the 5 empty seats ( 4 -'s and 1 linker i.e * )
SO 5 women can sit on 5 seats in (5)! ways or
1st seat in 5 ways
2nd seat 4
3rd seat 3
4th seat 2
5th seat 1
i.e 5*4*3*2*1 ways
So the answer is 5! * 4! = 2880
Sonia has 10 balloons out of which 5 are red, 2 white, 2 blue and 1pink, which she wants to use for the decoration. Her favourite pink colour balloon should be filled with toffees and should be put at the centre of the room above the cake table and remaining 9 at the wall behind the cake table. How many ways she can arrange the balloons?- a)956
- b)756
- c)9!
- d)7560
Correct answer is option 'B'. Can you explain this answer?
Sonia has 10 balloons out of which 5 are red, 2 white, 2 blue and 1pink, which she wants to use for the decoration. Her favourite pink colour balloon should be filled with toffees and should be put at the centre of the room above the cake table and remaining 9 at the wall behind the cake table. How many ways she can arrange the balloons?
a)
956
b)
756
c)
9!
d)
7560
|
|
Pooja Shah answered |
1 balloon is fixed that is to be placed above the cake
Now she have to arrange 9 balloons = 9!/(5!*2!*2!)
(9*8*7*6*5!)/((5!*2*2)
= (9*8*7*6)/(2*2)
= 756
Now she have to arrange 9 balloons = 9!/(5!*2!*2!)
(9*8*7*6*5!)/((5!*2*2)
= (9*8*7*6)/(2*2)
= 756
The number of ways in which three different rings can be worn in four fingers with at most one in each finger, are- a)12
- b)64
- c)24
- d)6
Correct answer is 'C'. Can you explain this answer?
The number of ways in which three different rings can be worn in four fingers with at most one in each finger, are
a)
12
b)
64
c)
24
d)
6
|
|
Gaurav Kumar answered |
The total number of ways is same as the number of arrangements of 4 fingers, taken 3 at a time.
So, required number of ways = 4P3
= 4!/(4-3)!
= 4!/1!
= 4! => 24
So, required number of ways = 4P3
= 4!/(4-3)!
= 4!/1!
= 4! => 24
A coin is tossed n times, the number of all the possible outcomes is- a)C(n , 2)
- b)P(n , 2)
- c)2n
- d)2n
Correct answer is option 'D'. Can you explain this answer?
A coin is tossed n times, the number of all the possible outcomes is
a)
C(n , 2)
b)
P(n , 2)
c)
2n
d)
2n
|
|
Krishna Iyer answered |
If coin is tossed n times then possible number of outcomes = 2n
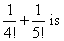
- a)4/5!
- b)5/5!
- c)6/5!
- d)1/5!
Correct answer is option 'C'. Can you explain this answer?
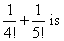
a)
4/5!
b)
5/5!
c)
6/5!
d)
1/5!
|
|
Pooja Shah answered |
1/4! + 1/5!
= 1/4![1 + 1/5]
1/4![6/5]
=> 6/5!
= 1/4![1 + 1/5]
1/4![6/5]
=> 6/5!
The number of different ways in which a man can invite one or more of his 6 friends to dinner is- a)63
- b)15
- c)30
- d)120
Correct answer is option 'A'. Can you explain this answer?
The number of different ways in which a man can invite one or more of his 6 friends to dinner is
a)
63
b)
15
c)
30
d)
120
|
|
Om Desai answered |
He can invite one or more friends by inviting 1 friend, or 2 friends or 3 friends, or all the 6 friends.
1 friend can be selected out of 6 in 6C1 = 6 ways
2 friends can be selected out of 6 in 6C2 = 15 ways
3 friends can be selected out of 6 in 6C3 = 20 ways
4 friends can be selected out of 6 in 6C4 = 15 ways
5 friends can be selected out of 6 in 6C5 = 6 ways
6 friends can be selected out of 6 in 6C6 = 1 ways
Therefore the required number of ways (combinations) = 6 + 15 + 20 + 15 + 6 + 1 = 63
1 friend can be selected out of 6 in 6C1 = 6 ways
2 friends can be selected out of 6 in 6C2 = 15 ways
3 friends can be selected out of 6 in 6C3 = 20 ways
4 friends can be selected out of 6 in 6C4 = 15 ways
5 friends can be selected out of 6 in 6C5 = 6 ways
6 friends can be selected out of 6 in 6C6 = 1 ways
Therefore the required number of ways (combinations) = 6 + 15 + 20 + 15 + 6 + 1 = 63
The number of all numbers that can be formed by using some or all of the digits 1, 3, 5, 7, 9 (without repetitions) is- a)325
- b)120
- c)32
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of all numbers that can be formed by using some or all of the digits 1, 3, 5, 7, 9 (without repetitions) is
a)
325
b)
120
c)
32
d)
none of these
|
|
Pooja Shah answered |
Out of 1, 3, 5, 7, 9
No. of 1-digit numbers = 5
No. of 2-digit numbers = 5*4 = 20
No. of 3-digit numbers = 5*4*3 = 60
No. of 4-digit numbers = 5*4*3*2 = 120
No. of 5-digit numbers = 5*4*3*2*1 = 120
Total no. of numbers = 5 + 20 + 60 + 120 + 120 = 325
No. of 1-digit numbers = 5
No. of 2-digit numbers = 5*4 = 20
No. of 3-digit numbers = 5*4*3 = 60
No. of 4-digit numbers = 5*4*3*2 = 120
No. of 5-digit numbers = 5*4*3*2*1 = 120
Total no. of numbers = 5 + 20 + 60 + 120 + 120 = 325
If (n + 1)! = 20(n – 1)!, then n is equal to- a)20
- b)5
- c)-5
- d)4
Correct answer is option 'D'. Can you explain this answer?
If (n + 1)! = 20(n – 1)!, then n is equal to
a)
20
b)
5
c)
-5
d)
4
|
|
Vikas Kapoor answered |
(n + 1)! = 20 (n – 1)!
n (n + 1) = 20
(n – 4) (n + 5) = 0
Since, (n – 1)! exists, n ≥ 1
So, n = 4
n (n + 1) = 20
(n – 4) (n + 5) = 0
Since, (n – 1)! exists, n ≥ 1
So, n = 4
The number of three digit numbers having atleast one digit as 5 is- a)225
- b)246
- c)648
- d)252
Correct answer is option 'D'. Can you explain this answer?
The number of three digit numbers having atleast one digit as 5 is
a)
225
b)
246
c)
648
d)
252
|
|
Ravi Sharma answered |
These digit number without digit 5 →100....999
→ these are 900 three-digit number
→ from 100 to 199 → 19 number with 5.
200−299→19
300−399→19
400−499→19
600−699→19
700−799→19
800−899→19
900−999→19
500−599→100
total number with 5=19×8+100 for (500-599)
=152+100
=252
→ these are 900 three-digit number
→ from 100 to 199 → 19 number with 5.
200−299→19
300−399→19
400−499→19
600−699→19
700−799→19
800−899→19
900−999→19
500−599→100
total number with 5=19×8+100 for (500-599)
=152+100
=252
On a railway track, there are 20 stations. The number of tickets required in order that it may be possible to book a passenger from every station to every other is- a)C(20,2)
- b)P(20,2)
- c)400
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
On a railway track, there are 20 stations. The number of tickets required in order that it may be possible to book a passenger from every station to every other is
a)
C(20,2)
b)
P(20,2)
c)
400
d)
none of these
|
|
Chirag Verma answered |
Number of tickets selected from first station =20
from second =19
.... for last station =0
We have to select 2 consecutive stations
so total number of possible tickets = P(20,2)
from second =19
.... for last station =0
We have to select 2 consecutive stations
so total number of possible tickets = P(20,2)
The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is- a)98
- b)72
- c)90
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is
a)
98
b)
72
c)
90
d)
none of these
|
|
Riya Banerjee answered |
There are in total 6 numbers, 4,5,6,7,8.
Now consider the number 56000
Consider the numbers of the form
56−−−.
Considering no repetitions we get
3×2×1 = 6 numbers.
Similarly for 57−−− and 58−−−.
Hence 3×6 = 18 numbers.
Now consider the numbers starting with 6.
6−−−−
We get 4×3×2×1 = 24.
Similarly for the numbers starting with 7 and 8 we get in total 24 numbers each.
Hence total number of numbers greater than 56000 will be
= (24×3)+18
= 72+18 = 90
Now consider the number 56000
Consider the numbers of the form
56−−−.
Considering no repetitions we get
3×2×1 = 6 numbers.
Similarly for 57−−− and 58−−−.
Hence 3×6 = 18 numbers.
Now consider the numbers starting with 6.
6−−−−
We get 4×3×2×1 = 24.
Similarly for the numbers starting with 7 and 8 we get in total 24 numbers each.
Hence total number of numbers greater than 56000 will be
= (24×3)+18
= 72+18 = 90
Find the number of words with or without meaning which can be made using all the letters of the word SWEET.- a)120
- b)24
- c)48
- d)60
Correct answer is option 'D'. Can you explain this answer?
Find the number of words with or without meaning which can be made using all the letters of the word SWEET.
a)
120
b)
24
c)
48
d)
60

|
Md Jisan answered |
Sweet has 5 letters, so it gives 5! but there are two letters which are same , so number of words will be = (5! ÷ 2!) = 60
How many three letter codes can be formed by only vowels of English alphabets, given that repetition of letters is allowed?- a)125
- b)5
- c)25
- d)5!
Correct answer is option 'A'. Can you explain this answer?
How many three letter codes can be formed by only vowels of English alphabets, given that repetition of letters is allowed?
a)
125
b)
5
c)
25
d)
5!
|
|
Ishan Choudhury answered |
We have 5 choices (a, e, i, o, u)
3 letter codes = 5 * 5 * 5
= 125
3 letter codes = 5 * 5 * 5
= 125
A team of 7 players is to be formed out of 5 under 19 players and 6 senior players. In how many ways, the team can be chosen when at least 4 senior players are included?- a)185
- b)215
- c)115
- d)125
Correct answer is option 'B'. Can you explain this answer?
A team of 7 players is to be formed out of 5 under 19 players and 6 senior players. In how many ways, the team can be chosen when at least 4 senior players are included?
a)
185
b)
215
c)
115
d)
125
|
|
Om Desai answered |
No. of ways to select 4 senior and 3 U-19 players = 6C4 * 5C3 = 150
No. of ways to select 5 senior and 2 U-19 players = 6C5 * 5C2 = 60
No. of ways to select 6 senior and 1 U-19 players = 6C6 * 5C1 = 5
Total no. of ways to select the team = 150 + 60 + 5 = 215
No. of ways to select 5 senior and 2 U-19 players = 6C5 * 5C2 = 60
No. of ways to select 6 senior and 1 U-19 players = 6C6 * 5C1 = 5
Total no. of ways to select the team = 150 + 60 + 5 = 215
The number of all three digit even numbers such that if 5 is one of the digits then next digit is 7 is- a)360
- b)370
- c)365
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of all three digit even numbers such that if 5 is one of the digits then next digit is 7 is
a)
360
b)
370
c)
365
d)
none of these
|
|
Raghav Bansal answered |
Correct Answer :- c
Explanation : As given condition is , 5 must be followed by 7. So only possible way is 57X where X denotes 0,2,4,6 and 8.
So,total no. of ways=1×1×5=5
Hence, total ways in which we can make a 3-digit even no. without violating given condition are:
360+5=365
How many different words can be formed using the letters of the word BHARAT, which begin with B and end with T?- a)36
- b)16
- c)24
- d)12
Correct answer is option 'D'. Can you explain this answer?
How many different words can be formed using the letters of the word BHARAT, which begin with B and end with T?
a)
36
b)
16
c)
24
d)
12
|
|
Sarita Yadav answered |
If the first & last letter is fixed, then we find out, the number of permutations of the remaining letters, i.e. 4
= 4!/2!
= 4*3*2!/2!
= 12
= 4!/2!
= 4*3*2!/2!
= 12
In how many ways can a mixed doubles tennis game be arranged from a group of 10 players consisting of 6 men and 4 women- a)180
- b)90
- c)120
- d)48
Correct answer is option 'A'. Can you explain this answer?
In how many ways can a mixed doubles tennis game be arranged from a group of 10 players consisting of 6 men and 4 women
a)
180
b)
90
c)
120
d)
48

|
Anireddy Charan answered |
The number of ways a doubles tennis game be arranged = 45 ways (i.e.^10C2)
But in a mixed doubles tennis game, you will get 4 ways
i.e. two women vs two men, one woman and a man vs two men, one woman and a man vs two women, one woman and a man vs one woman and a man.
So, the total number of ways = 45 x 4 ways = 180
In how many ways 4 boys and 3 girls can be seated in a row so that they are alternate.
- a)144
- b)288
- c)12
- d)256
Correct answer is option 'A'. Can you explain this answer?
In how many ways 4 boys and 3 girls can be seated in a row so that they are alternate.
a)
144
b)
288
c)
12
d)
256
|
|
Jaideep Mukherjee answered |
Problem:
In how many ways 4 boys and 3 girls can be seated in a row so that they are alternate.
Solution:
To solve the problem, we need to arrange the boys and girls in alternate positions. Let's first arrange the boys and girls separately in the row.
- Arranging the boys: There are 4 boys, and they can be arranged in 4! ways.
- Arranging the girls: There are 3 girls, and they can be arranged in 3! ways.
Now, we need to arrange the boys and girls in alternate positions. There are 2 cases to consider:
Case 1: The first person in the row is a boy.
In this case, we have the following arrangement:
B G B G B G B
- The first boy can be any of the 4 boys.
- The second boy can be any of the 3 remaining boys.
- The third boy can be any of the 2 remaining boys.
- The fourth boy can be the only remaining boy.
- The first girl can be any of the 3 girls.
- The second girl can be any of the 2 remaining girls.
- The third girl can be the only remaining girl.
Therefore, the total number of arrangements in this case is 4! x 3! = 144.
Case 2: The first person in the row is a girl.
In this case, we have the following arrangement:
G B G B G B B
- The first girl can be any of the 3 girls.
- The second girl can be any of the 2 remaining girls.
- The third girl can be the only remaining girl.
- The first boy can be any of the 4 boys.
- The second boy can be any of the 3 remaining boys.
- The third boy can be any of the 2 remaining boys.
- The fourth boy can be the only remaining boy.
Therefore, the total number of arrangements in this case is 3! x 4! = 144.
Hence, the total number of arrangements in which the boys and girls are seated in alternate positions is 144 + 144 = 288.
Answer: (a) 144.
In how many ways 4 boys and 3 girls can be seated in a row so that they are alternate.
Solution:
To solve the problem, we need to arrange the boys and girls in alternate positions. Let's first arrange the boys and girls separately in the row.
- Arranging the boys: There are 4 boys, and they can be arranged in 4! ways.
- Arranging the girls: There are 3 girls, and they can be arranged in 3! ways.
Now, we need to arrange the boys and girls in alternate positions. There are 2 cases to consider:
Case 1: The first person in the row is a boy.
In this case, we have the following arrangement:
B G B G B G B
- The first boy can be any of the 4 boys.
- The second boy can be any of the 3 remaining boys.
- The third boy can be any of the 2 remaining boys.
- The fourth boy can be the only remaining boy.
- The first girl can be any of the 3 girls.
- The second girl can be any of the 2 remaining girls.
- The third girl can be the only remaining girl.
Therefore, the total number of arrangements in this case is 4! x 3! = 144.
Case 2: The first person in the row is a girl.
In this case, we have the following arrangement:
G B G B G B B
- The first girl can be any of the 3 girls.
- The second girl can be any of the 2 remaining girls.
- The third girl can be the only remaining girl.
- The first boy can be any of the 4 boys.
- The second boy can be any of the 3 remaining boys.
- The third boy can be any of the 2 remaining boys.
- The fourth boy can be the only remaining boy.
Therefore, the total number of arrangements in this case is 3! x 4! = 144.
Hence, the total number of arrangements in which the boys and girls are seated in alternate positions is 144 + 144 = 288.
Answer: (a) 144.
The number of all possible positive integral solutions of the equation xyz = 30 is- a)25
- b)26
- c)27
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of all possible positive integral solutions of the equation xyz = 30 is
a)
25
b)
26
c)
27
d)
none of these
|
|
Paridhi Nagori answered |
27 possible solutions
X-Y-Z
1-1-30 3 sets
1-2-15 6 sets
1-3-10 6 sets
1-5-6 6 sets
2-3-5 6 sets
In a class 6 students have to be arranged for a photograph. If the prefect and the vice must occupy the positions at either ends, how many ways the students can be arranged?- a)58
- b)48
- c)64
- d)32
Correct answer is option 'B'. Can you explain this answer?
In a class 6 students have to be arranged for a photograph. If the prefect and the vice must occupy the positions at either ends, how many ways the students can be arranged?
a)
58
b)
48
c)
64
d)
32
|
|
Om Desai answered |
In a class of 6 students. Two students at both ends. Remaining four students have to be arranged
= 2 * 4!
= 2 * 24
= 48
= 2 * 4!
= 2 * 24
= 48
In a room there are 2 green chairs, 3 yellow chairs and 4 blue chairs. In how many ways can Raj choose 3 chairs so that at least one yellow chair is included? - a)3
- b)30
- c)64
- d)84
Correct answer is option 'C'. Can you explain this answer?
In a room there are 2 green chairs, 3 yellow chairs and 4 blue chairs. In how many ways can Raj choose 3 chairs so that at least one yellow chair is included?
a)
3
b)
30
c)
64
d)
84
|
|
Geetika Shah answered |
At least one yellow chair means “total way no yellow chair
Total ways to select 3 chairs form the total (2+3+4) chairs 9C3
9C3 = 9!/3!*6! = 84ways
Now, we dont want even one yellow chair
So, we should select 3 chairs from 6 chairs (2green & 4blue) = 6C3
6C3 = 6!/3!3! = 20 ways
hence , ways to select at least one yellow chair = 84-20 = 64 ways.
Total ways to select 3 chairs form the total (2+3+4) chairs 9C3
9C3 = 9!/3!*6! = 84ways
Now, we dont want even one yellow chair
So, we should select 3 chairs from 6 chairs (2green & 4blue) = 6C3
6C3 = 6!/3!3! = 20 ways
hence , ways to select at least one yellow chair = 84-20 = 64 ways.
Number of ways in which 10 different things can be divided into two groups containing 6 and 4 things respectively is- a)P(10,2)
- b)P(10,4)
- c)C(10,4)
- d)P(10,6)
Correct answer is option 'C'. Can you explain this answer?
Number of ways in which 10 different things can be divided into two groups containing 6 and 4 things respectively is
a)
P(10,2)
b)
P(10,4)
c)
C(10,4)
d)
P(10,6)
|
|
Ananya Das answered |
Forming the first group by choosing 4 things out of 10 things,the total number of ways will be =10C4
Now,forming these group by choosing 6 things,the total number of ways =
6C6
Therefore,the total number of ways = 10C4∗6C6
= C(10,4)
Now,forming these group by choosing 6 things,the total number of ways =
6C6
Therefore,the total number of ways = 10C4∗6C6
= C(10,4)
5 boys and 5 girls are to be seated around a table such that boys and girls sit alternately. The number of ways of seating them is- a)5! × 4!
- b)4! × 4!
- c)5! × 5!
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
5 boys and 5 girls are to be seated around a table such that boys and girls sit alternately. The number of ways of seating them is
a)
5! × 4!
b)
4! × 4!
c)
5! × 5!
d)
none of these
|
|
Lavanya Menon answered |
First we fix the alternate position of the girls. Five girls can be seated around the circle in (5−1)!=4! , 5 boys can be seated in five -vacant place by 5!
∴ Required number of ways =4!×5!
∴ Required number of ways =4!×5!
How many ways can three white and three red balloons be arranged in a row?- a)6!
- b)10
- c)20
- d)3!.3!
Correct answer is option 'C'. Can you explain this answer?
How many ways can three white and three red balloons be arranged in a row?
a)
6!
b)
10
c)
20
d)
3!.3!
|
|
Sai Iyer answered |
Arranging Three White and Three Red Balloons in a Row
To determine the number of ways in which three white and three red balloons can be arranged in a row, we can use the formula for permutations of objects with repetition.
Formula: n! / (n1!n2!...nk!), where n is the total number of objects, and n1, n2,...nk are the number of objects of each type.
Using this formula, we can calculate the number of arrangements as follows:
n = 6 (total number of balloons)
n1 = 3 (number of white balloons)
n2 = 3 (number of red balloons)
Number of arrangements = 6! / (3! 3!) = 20
Therefore, there are 20 ways in which three white and three red balloons can be arranged in a row.
Explanation:
- The formula for permutations with repetition is n! / (n1!n2!...nk!), where n is the total number of objects, and n1, n2,...nk are the number of objects of each type.
- In this case, we have a total of six balloons, with three white and three red balloons.
- Using the formula, we can calculate the number of arrangements as 6! / (3! 3!) = 20.
- This means that there are 20 ways in which we can arrange the three white and three red balloons in a row.
- Therefore, the correct answer is option C.
To determine the number of ways in which three white and three red balloons can be arranged in a row, we can use the formula for permutations of objects with repetition.
Formula: n! / (n1!n2!...nk!), where n is the total number of objects, and n1, n2,...nk are the number of objects of each type.
Using this formula, we can calculate the number of arrangements as follows:
n = 6 (total number of balloons)
n1 = 3 (number of white balloons)
n2 = 3 (number of red balloons)
Number of arrangements = 6! / (3! 3!) = 20
Therefore, there are 20 ways in which three white and three red balloons can be arranged in a row.
Explanation:
- The formula for permutations with repetition is n! / (n1!n2!...nk!), where n is the total number of objects, and n1, n2,...nk are the number of objects of each type.
- In this case, we have a total of six balloons, with three white and three red balloons.
- Using the formula, we can calculate the number of arrangements as 6! / (3! 3!) = 20.
- This means that there are 20 ways in which we can arrange the three white and three red balloons in a row.
- Therefore, the correct answer is option C.
An online examination have 12 question out of which we havethe alternative to select the answer. Choose how many ways can be there in which one can answer the question
- a)312+1
- b)212
- c)312−1
- d)312
Correct answer is option 'C'. Can you explain this answer?
An online examination have 12 question out of which we havethe alternative to select the answer. Choose how many ways can be there in which one can answer the question
a)
312+1
b)
212
c)
312−1
d)
312
|
|
Lavanya Menon answered |
No.of choices for each question = 3
There are six questions so total = (3)12
So no.of ways = (3)12 - 1
There are six questions so total = (3)12
So no.of ways = (3)12 - 1
Numbers greater than 1000 but not greater than 4000 are to be formed with the digits 0, 1, 2, 3, 4, allowing repetitions, the number of possible numbers is- a)370
- b)376
- c)365
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
Numbers greater than 1000 but not greater than 4000 are to be formed with the digits 0, 1, 2, 3, 4, allowing repetitions, the number of possible numbers is
a)
370
b)
376
c)
365
d)
none of these.
|
|
Niks Niks answered |
By reapeating digit 0,1,3,4 there are 376 numbers are formed between 1000- 4000
In a multiple choice question, there are 4 alternatives, of which one or more are correct. The number of ways in which a candidate can attempt this question is
- a)4
- b)25
- c)16
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
In a multiple choice question, there are 4 alternatives, of which one or more are correct. The number of ways in which a candidate can attempt this question is
a)
4
b)
25
c)
16
d)
none of these
|
|
Geetika Shah answered |
To solve this problem, we need to calculate the total number of ways a candidate can attempt the multiple-choice question where there are 4 alternatives, and one or more can be correct.
Step 1: Consider each alternative
Each of the 4 alternatives can either be:
- Selected (included in the answer)
- Not selected (excluded from the answer)
So, for each alternative, there are 2 choices (select or not select).
Step 2: Calculate the total number of combinations
If there were no restrictions (i.e., selecting none is allowed), the total number of combinations would be 24=16
Step 3: Subtract the invalid case
Since at least one alternative must be selected (one or more are correct), we subtract the one case where none of the alternatives are selected:
24−1=16−1=15
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is- a)164
- b)140
- c)112
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is
a)
164
b)
140
c)
112
d)
none of these
|
|
Alok Mehta answered |
Case I : Both of them don't attend the party.then, no of ways = 8C6 = 28Case
II : Either of them is selected for party.then, no of ways = 2C1 * 8C5 = 112
Total no of ways = 112+28 = 140
The number of triangles that can be formed with 6 points on a circle is- a)15
- b)6
- c)20
- d)12
Correct answer is option 'C'. Can you explain this answer?
The number of triangles that can be formed with 6 points on a circle is
a)
15
b)
6
c)
20
d)
12
|
|
Lakshmi Sharma answered |
Understanding the Problem
To determine how many triangles can be formed from 6 points on a circle, we need to consider the properties of combinations.
Combination Concept
- A triangle is formed by selecting 3 points.
- The formula to calculate combinations is given by C(n, r) = n! / (r! * (n - r)!), where n is the total number of points, and r is the number of points to choose.
Calculating Combinations
- Here, n = 6 (the points on the circle) and r = 3 (points needed to form a triangle).
- We apply the combination formula:
C(6, 3) = 6! / (3! * (6 - 3)!)
= 6! / (3! * 3!)
= (6 × 5 × 4) / (3 × 2 × 1)
= 20.
Conclusion
- Therefore, the number of triangles that can be formed with 6 points on a circle is 20.
- The correct answer is option 'C'.
This approach highlights that any three points chosen from the six points on the circle will always form a triangle, as no three points are collinear on a circle.
To determine how many triangles can be formed from 6 points on a circle, we need to consider the properties of combinations.
Combination Concept
- A triangle is formed by selecting 3 points.
- The formula to calculate combinations is given by C(n, r) = n! / (r! * (n - r)!), where n is the total number of points, and r is the number of points to choose.
Calculating Combinations
- Here, n = 6 (the points on the circle) and r = 3 (points needed to form a triangle).
- We apply the combination formula:
C(6, 3) = 6! / (3! * (6 - 3)!)
= 6! / (3! * 3!)
= (6 × 5 × 4) / (3 × 2 × 1)
= 20.
Conclusion
- Therefore, the number of triangles that can be formed with 6 points on a circle is 20.
- The correct answer is option 'C'.
This approach highlights that any three points chosen from the six points on the circle will always form a triangle, as no three points are collinear on a circle.
The number of all odd divisors of 3600 is- a)9
- b)18
- c)45
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of all odd divisors of 3600 is
a)
9
b)
18
c)
45
d)
none of these
|
|
Sreemoyee Kumar answered |
Number 1 is odd. As any number is divisible by 1: 1
Do prime factorisation of 3600: 2*2*2*2*3*3*5*5
Select all odd numbers from above: 3,3,5,5
Try every possible products of these:
Single number: 3, 5
Two numbers: 3*3, 3*5, 5*5: 9,15,25
Three numbers: 3*3*5, 3*5*5: 45, 75
All four: 3*3*5*5: 225
The odd divisors are: 1,3,5,9,15,25,45,75,225
There are 9 odd divisors of 3600.
Do prime factorisation of 3600: 2*2*2*2*3*3*5*5
Select all odd numbers from above: 3,3,5,5
Try every possible products of these:
Single number: 3, 5
Two numbers: 3*3, 3*5, 5*5: 9,15,25
Three numbers: 3*3*5, 3*5*5: 45, 75
All four: 3*3*5*5: 225
The odd divisors are: 1,3,5,9,15,25,45,75,225
There are 9 odd divisors of 3600.
The sum of all the numbers which can be formed by using the digits 1,3,5,7 all at a time and which have no digit repeated, is
- a)16×1111×4!
- b)16×1111×3!
- c)16×4!
- d)1111×3!
Correct answer is option 'B'. Can you explain this answer?
The sum of all the numbers which can be formed by using the digits 1,3,5,7 all at a time and which have no digit repeated, is
a)
16×1111×4!
b)
16×1111×3!
c)
16×4!
d)
1111×3!

|
Nipun Tuteja answered |
Sum of the numbers (S) formed by taking all the given n digits is-
S=(sum of all digits)×(n−1)!×(111....n times)
Now according to the question, the digits are 1,3,5,7
∴n = 4
Sum of digits = 1+3+5+7 = 16
∴S = 16×3!×1111
Hence the correct answer is (C) 16×3!×1111.
There are 3 white, 4 red and 1 blue marbles in a bag. They are drawn one by one and arranged in a row. Assuming that all 8 marbles are drawn, determine the number of different arrangements if marbles of same colour are indistinguishable.- a)56
- b)296
- c)280
- d)240
Correct answer is option 'C'. Can you explain this answer?
There are 3 white, 4 red and 1 blue marbles in a bag. They are drawn one by one and arranged in a row. Assuming that all 8 marbles are drawn, determine the number of different arrangements if marbles of same colour are indistinguishable.
a)
56
b)
296
c)
280
d)
240
|
|
Bhavya Kulkarni answered |
To solve this problem, we can use the concept of permutations. A permutation is an arrangement of objects in a specific order.
**Step 1: Count the number of marbles**
We have 3 white marbles, 4 red marbles, and 1 blue marble in total. So, we have 8 marbles in the bag.
**Step 2: Calculate the total number of arrangements without any restrictions**
If all the marbles were distinguishable, the total number of arrangements would be 8! (8 factorial), which is equal to 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40,320.
**Step 3: Consider the indistinguishable marbles**
Since the marbles of the same color are indistinguishable, we need to adjust the total number of arrangements to account for this.
- For the 3 white marbles, there are 3! (3 factorial) ways to arrange them amongst themselves. This is because all the white marbles are identical, so their order doesn't matter.
- Similarly, for the 4 red marbles, there are 4! ways to arrange them amongst themselves.
- The blue marble is unique and does not have any duplicates, so it does not need to be adjusted.
**Step 4: Calculate the final number of arrangements**
To calculate the final number of arrangements, we divide the total number of arrangements without restrictions (40,320) by the adjustments made for the indistinguishable marbles.
Number of arrangements = 8! / (3! x 4!) = (8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) / (3 x 2 x 1) x (4 x 3 x 2 x 1) = 56.
Therefore, the correct answer is option C: 280.
This approach considers the indistinguishability of marbles of the same color and accounts for it in the final calculation.
**Step 1: Count the number of marbles**
We have 3 white marbles, 4 red marbles, and 1 blue marble in total. So, we have 8 marbles in the bag.
**Step 2: Calculate the total number of arrangements without any restrictions**
If all the marbles were distinguishable, the total number of arrangements would be 8! (8 factorial), which is equal to 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40,320.
**Step 3: Consider the indistinguishable marbles**
Since the marbles of the same color are indistinguishable, we need to adjust the total number of arrangements to account for this.
- For the 3 white marbles, there are 3! (3 factorial) ways to arrange them amongst themselves. This is because all the white marbles are identical, so their order doesn't matter.
- Similarly, for the 4 red marbles, there are 4! ways to arrange them amongst themselves.
- The blue marble is unique and does not have any duplicates, so it does not need to be adjusted.
**Step 4: Calculate the final number of arrangements**
To calculate the final number of arrangements, we divide the total number of arrangements without restrictions (40,320) by the adjustments made for the indistinguishable marbles.
Number of arrangements = 8! / (3! x 4!) = (8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) / (3 x 2 x 1) x (4 x 3 x 2 x 1) = 56.
Therefore, the correct answer is option C: 280.
This approach considers the indistinguishability of marbles of the same color and accounts for it in the final calculation.
The number of arrangements of n different things taken r at a time which include a particular thing is- a)P(n-1, r-1)
- b)nP(n-1,r)
- c)rP(n-1,r-1)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of arrangements of n different things taken r at a time which include a particular thing is
a)
P(n-1, r-1)
b)
nP(n-1,r)
c)
rP(n-1,r-1)
d)
none of these
|
|
Geetika Shah answered |
Total Permutations of n different things taken r at a time when a particular item is always included in the arrangement is : r * (n-1 p r-1).
Chapter doubts & questions for Permutations and Counting - Mathematics for Grade 12 2025 is part of Grade 12 exam preparation. The chapters have been prepared according to the Grade 12 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 12 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Permutations and Counting - Mathematics for Grade 12 in English & Hindi are available as part of Grade 12 exam.
Download more important topics, notes, lectures and mock test series for Grade 12 Exam by signing up for free.
Mathematics for Grade 12
99 videos|133 docs|90 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

 ?
?