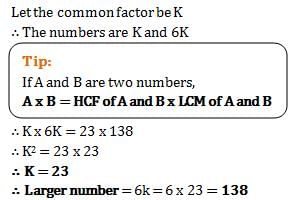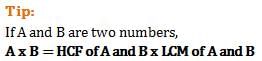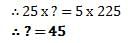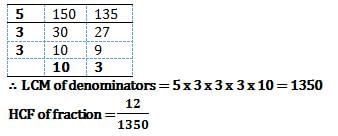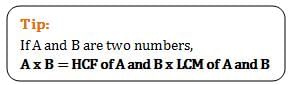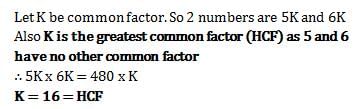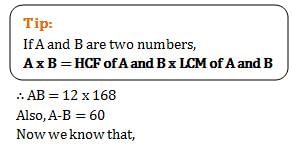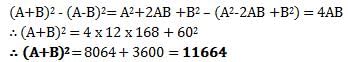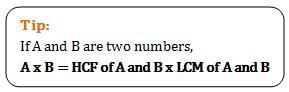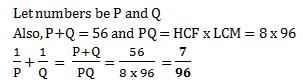All Exams >
GMAT >
Quantitative for GMAT >
All Questions
All questions of Highest Common Factor & Least Common Multiple for GMAT Exam
When a number is divided by 893 the remainder is 193. What will be the remainder when it is divided by 47?- a)19
- b)5
- c)33
- d)23
- e)44
Correct answer is option 'B'. Can you explain this answer?
When a number is divided by 893 the remainder is 193. What will be the remainder when it is divided by 47?
a)
19
b)
5
c)
33
d)
23
e)
44

|
Prisha Mukherjee answered |
In such cases and sums, simply follow these easy steps
Number is divided by 893. Remainder =193.
Also, we observe that 893 is exactly divisible by 47.
So now simply divide the remainder by 47.

Number is divided by 893. Remainder =193.
Also, we observe that 893 is exactly divisible by 47.
So now simply divide the remainder by 47.

What is the least number which when divided by the numbers 3, 5, 6, 8, 10 and 12 leaves in each case a remainder 2 but which when divided by 13 leaves no remainder?- a)312
- b)962
- c)1586
- d)1562
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the least number which when divided by the numbers 3, 5, 6, 8, 10 and 12 leaves in each case a remainder 2 but which when divided by 13 leaves no remainder?
a)
312
b)
962
c)
1586
d)
1562
e)
None of these

|
Sharmila Singh answered |
To find the least number that satisfies the conditions given in the question, we need to find the least common multiple (LCM) of the numbers 3, 5, 6, 8, 10, and 12.
Step 1: Prime Factorization
We start by finding the prime factorization of each number:
3 = 3
5 = 5
6 = 2 * 3
8 = 2^3
10 = 2 * 5
12 = 2^2 * 3
Step 2: Identify Common Factors
Next, we identify the common factors among the prime factorizations:
2 * 3 * 2^2 * 5 = 2^3 * 3 * 5
Step 3: Find the LCM
Finally, we take the product of the common factors to find the LCM:
LCM = 2^3 * 3 * 5 = 120
The LCM of the numbers 3, 5, 6, 8, 10, and 12 is 120.
Step 4: Adding the Remainder Condition
We need to find a number that leaves a remainder of 2 when divided by each of the numbers 3, 5, 6, 8, 10, and 12, but leaves no remainder when divided by 13.
To satisfy the remainder condition, we add 2 to the LCM:
120 + 2 = 122
However, 122 is not divisible by 13, so we continue adding the LCM until we find a number that satisfies the condition:
122 + 120 = 242
242 + 120 = 362
362 + 120 = 482
482 + 120 = 602
602 + 120 = 722
722 + 120 = 842
842 + 120 = 962
Therefore, the least number that satisfies the given conditions is 962.
Hence, the correct answer is option C: 1586.
Step 1: Prime Factorization
We start by finding the prime factorization of each number:
3 = 3
5 = 5
6 = 2 * 3
8 = 2^3
10 = 2 * 5
12 = 2^2 * 3
Step 2: Identify Common Factors
Next, we identify the common factors among the prime factorizations:
2 * 3 * 2^2 * 5 = 2^3 * 3 * 5
Step 3: Find the LCM
Finally, we take the product of the common factors to find the LCM:
LCM = 2^3 * 3 * 5 = 120
The LCM of the numbers 3, 5, 6, 8, 10, and 12 is 120.
Step 4: Adding the Remainder Condition
We need to find a number that leaves a remainder of 2 when divided by each of the numbers 3, 5, 6, 8, 10, and 12, but leaves no remainder when divided by 13.
To satisfy the remainder condition, we add 2 to the LCM:
120 + 2 = 122
However, 122 is not divisible by 13, so we continue adding the LCM until we find a number that satisfies the condition:
122 + 120 = 242
242 + 120 = 362
362 + 120 = 482
482 + 120 = 602
602 + 120 = 722
722 + 120 = 842
842 + 120 = 962
Therefore, the least number that satisfies the given conditions is 962.
Hence, the correct answer is option C: 1586.
What least number when divided by 36, 24 and 16 leaves 11 as remainder in each case? - a)36
- b)133
- c)144
- d)155
- e)166
Correct answer is option 'D'. Can you explain this answer?
What least number when divided by 36, 24 and 16 leaves 11 as remainder in each case?
a)
36
b)
133
c)
144
d)
155
e)
166

|
Arnab Kumar answered |
Here least number is needed that means we need the LCM
We must first find LCM of 36, 24 and 16

We must first find LCM of 36, 24 and 16

The ratio of two numbers is 4 : 5 and their H.C.F is 4. Find their L.C.M. - a)96
- b)80
- c)73
- d)48
- e)64
Correct answer is option 'B'. Can you explain this answer?
The ratio of two numbers is 4 : 5 and their H.C.F is 4. Find their L.C.M.
a)
96
b)
80
c)
73
d)
48
e)
64

|
Sravya Joshi answered |
Let the numbers be 4x and 5x.
H.C.F = x. So, x=4.
So, the numbers are 16 and 20
L.C.M of 16 and 20 = 80.
So, the numbers are 16 and 20
L.C.M of 16 and 20 = 80.
LCM of two numbers is 495. HCF of these numbers is 5. If the sum of the numbers is 100, find out the difference between the two numbers.- a)15
- b)12
- c)10
- d)20
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
LCM of two numbers is 495. HCF of these numbers is 5. If the sum of the numbers is 100, find out the difference between the two numbers.
a)
15
b)
12
c)
10
d)
20
e)
None of these

|
Mihir Ghoshal answered |
It is given that sum of two numbers is 100. Let the two numbers be x and 100 – x and HCF is 5 and LCM is 495
=> We need to apply the formula: HCF x LCM = Product of two numbers
Which gives x(100 – x) = 495 x 5
Solving the equation we get a quadratic which looks like this:
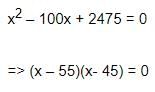
Therefore, Two numbers are 55 and 45
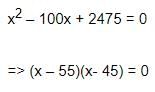
Therefore, Two numbers are 55 and 45
A man decides to pave with square tiles his hall which is 4.8 metres long and 5.38 metres wide. Find the largest size of the tile that he could use.- a)21 cm
- b)2 cm
- c)269 cm
- d)38 cm
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A man decides to pave with square tiles his hall which is 4.8 metres long and 5.38 metres wide. Find the largest size of the tile that he could use.
a)
21 cm
b)
2 cm
c)
269 cm
d)
38 cm
e)
None of these

|
Isha Sen answered |
The largest size of the tile is H.C.F. of 480 cm and 538 cm is 2 cm.
What will be least number of marbles with Rohit if he can arrange them in rows of 18, 10 and 15 marbles each as well as make a perfect solid square out of all the marbles?- a)133
- b)43
- c)90
- d)900
- e)75
Correct answer is option 'D'. Can you explain this answer?
What will be least number of marbles with Rohit if he can arrange them in rows of 18, 10 and 15 marbles each as well as make a perfect solid square out of all the marbles?
a)
133
b)
43
c)
90
d)
900
e)
75

|
Sreemoyee Nambiar answered |
Given information:
Rohit needs to arrange marbles in rows of 18, 10, and 15 marbles each. Additionally, he wants to make a perfect solid square out of all the marbles.
Approach:
To find the least number of marbles with Rohit, we need to find the least common multiple (LCM) of 18, 10, and 15. The LCM will give us the minimum number of marbles required to satisfy all the given conditions.
Calculating the LCM:
To calculate the LCM, we can use the prime factorization method.
1. Prime factorization of 18: 18 = 2 * 3^2
2. Prime factorization of 10: 10 = 2 * 5
3. Prime factorization of 15: 15 = 3 * 5
Now, we take the highest power of each prime factor:
- 2^1
- 3^2
- 5^1
The LCM is the product of these prime factors with their highest powers:
LCM = 2^1 * 3^2 * 5^1 = 2 * 9 * 5 = 90
Therefore, the least number of marbles Rohit needs is 90.
Final Answer:
The correct answer is option C) 90.
Rohit needs to arrange marbles in rows of 18, 10, and 15 marbles each. Additionally, he wants to make a perfect solid square out of all the marbles.
Approach:
To find the least number of marbles with Rohit, we need to find the least common multiple (LCM) of 18, 10, and 15. The LCM will give us the minimum number of marbles required to satisfy all the given conditions.
Calculating the LCM:
To calculate the LCM, we can use the prime factorization method.
1. Prime factorization of 18: 18 = 2 * 3^2
2. Prime factorization of 10: 10 = 2 * 5
3. Prime factorization of 15: 15 = 3 * 5
Now, we take the highest power of each prime factor:
- 2^1
- 3^2
- 5^1
The LCM is the product of these prime factors with their highest powers:
LCM = 2^1 * 3^2 * 5^1 = 2 * 9 * 5 = 90
Therefore, the least number of marbles Rohit needs is 90.
Final Answer:
The correct answer is option C) 90.
3 birds fly along the circumference of a jungle. They complete one round in 27 minutes, 45 minutes and 63 minutes respectively. Since they start together, when will they meet again at the starting position? - a)945 minutes
- b)126 minutes
- c)135 minutes
- d)9 hours
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
3 birds fly along the circumference of a jungle. They complete one round in 27 minutes, 45 minutes and 63 minutes respectively. Since they start together, when will they meet again at the starting position?
a)
945 minutes
b)
126 minutes
c)
135 minutes
d)
9 hours
e)
None of these

|
Maya Khanna answered |

∴ LCM = 9x3x5x7 = 945 = They meet after 945 minutes.
Sum of two numbers x, y = 1050. What is the maximum value of the HCF between x and y?- a)350
- b)700
- c)1050
- d)525
- e)900
Correct answer is option 'D'. Can you explain this answer?
Sum of two numbers x, y = 1050. What is the maximum value of the HCF between x and y?
a)
350
b)
700
c)
1050
d)
525
e)
900

|
Saumya Shah answered |
x = 525 and y = 525 works best.
If the question states x, y have to be distinct, then the best solution would be x = 350, y = 700, HCF = 350.
So the HCF is 525.
The question is "What is the maximum value of the HCF between x and y?"
Hence the answer is "525"
If the question states x, y have to be distinct, then the best solution would be x = 350, y = 700, HCF = 350.
So the HCF is 525.
The question is "What is the maximum value of the HCF between x and y?"
Hence the answer is "525"
Find the smallest number that leaves a remainder of 4 on division by 5, 5 on division by 6, 6 on division by 7, 7 on division by 8 and 8 on division by 9?- a)2519
- b)5039
- c)1079
- d)979
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the smallest number that leaves a remainder of 4 on division by 5, 5 on division by 6, 6 on division by 7, 7 on division by 8 and 8 on division by 9?
a)
2519
b)
5039
c)
1079
d)
979
e)
None of these

|
Mehul Nair answered |
Note: When a number is divided by 8, a remainder of 7 can be thought of as a remainder of -1.
This idea is very useful in a bunch of questions. So, N = 5a - 1 or N + 1 = 5a
This idea is very useful in a bunch of questions. So, N = 5a - 1 or N + 1 = 5a
N = 6b - 1 or N + 1 = 6b
N = 7c - 1 or N + 1 = 7c
N = 8d - 1 or N + 1 = 8d
N = 9e - 1 or N + 1 = 9e
N + 1 can be expressed as a multiple of (5, 6, 7, 8, 9)
N = 7c - 1 or N + 1 = 7c
N = 8d - 1 or N + 1 = 8d
N = 9e - 1 or N + 1 = 9e
N + 1 can be expressed as a multiple of (5, 6, 7, 8, 9)
N + 1 = 5a*6b*7c*8d*9e
Or N = (5a*6b*7c*8d*9e) - 1
Or N = (5a*6b*7c*8d*9e) - 1
Smallest value of N will be when we find the smallest common multiple of (5, 6, 7, 8, 9) or LCM of (5, 6, 7, 8, 9)
N = LCM (5, 6, 7, 8, 9) - 1 = 2520 - 1 = 2519.
The question is "Find the smallest number that leaves a remainder of 4 on division by 5, 5 on division by 6, 6 on division by 7, 7 on division by 8 and 8 on division by 9?"
N = LCM (5, 6, 7, 8, 9) - 1 = 2520 - 1 = 2519.
The question is "Find the smallest number that leaves a remainder of 4 on division by 5, 5 on division by 6, 6 on division by 7, 7 on division by 8 and 8 on division by 9?"
Hence the answer is "2519"
The sum of two non co–prime numbers added to their HCF gives us 91. How many such pairs are possible?- a)2
- b)4
- c)3
- d)6
- e)8
Correct answer is option 'C'. Can you explain this answer?
The sum of two non co–prime numbers added to their HCF gives us 91. How many such pairs are possible?
a)
2
b)
4
c)
3
d)
6
e)
8

|
Nitya Kumar answered |
Let HCF of the numbers be h. The numbers can be taken as ha + hb, where a, b are coprime.
h + ha + hb = 91
h(1 + a + b) = 91
h ≠ 1
h = 7
=> 1 + a + b = 13 a + b = 12
h + ha + hb = 91
h(1 + a + b) = 91
h ≠ 1
h = 7
=> 1 + a + b = 13 a + b = 12
h = 13
=> 1 + a + b = 7
=> a + b = 6
=> 1 + a + b = 7
=> a + b = 6
Case 1: h = 7, a + b = 12
(1, 11), (5, 7) => Only 2 pairs are possible as a, b have to be coprime.
(1, 11), (5, 7) => Only 2 pairs are possible as a, b have to be coprime.
Case 2: h = 13, a + b = 6
(1, 5) only one pair is possible as a, b have to be coprime.
(1, 5) only one pair is possible as a, b have to be coprime.
Overall, 3 pairs of numbers are possible – (7, 77) (35, 49) and (13, 65)
The question is "How many such pairs are possible?"
Hence the answer is "3 Pairs"
The sum of two numbers is 156 and their HCF is 13. The numbers of such number pairs is- a)2
- b)5
- c)4
- d)3
- e)6
Correct answer is option 'A'. Can you explain this answer?
The sum of two numbers is 156 and their HCF is 13. The numbers of such number pairs is
a)
2
b)
5
c)
4
d)
3
e)
6

|
Mihir Nambiar answered |
Highest Common Factor (HCF) is 13, that means
the numbers are multiples of 13.
We need sum of numbers to be 156.
In such sums, first write multiples of 13 till 156
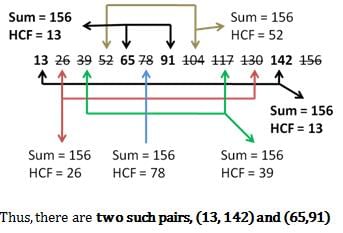
the numbers are multiples of 13.
We need sum of numbers to be 156.
In such sums, first write multiples of 13 till 156

How many pairs of positive integers x, y exist such that HCF (x, y) + LCM (x, y) = 91?- a)10
- b)8
- c)6
- d)7
- e)9
Correct answer is option 'B'. Can you explain this answer?
How many pairs of positive integers x, y exist such that HCF (x, y) + LCM (x, y) = 91?
a)
10
b)
8
c)
6
d)
7
e)
9

|
Ananya Iyer answered |
Let us x = h * a; y = h * b
a and b are co-prime. So, LCM of (x, y) = h * a * b
a and b are co-prime. So, LCM of (x, y) = h * a * b
So, in essence h + h * a * b = 91. Or h(ab + 1) = 91
Now, 91 can be written as 1 * 91 or 7 * 13
Or, we can have HCF as 1, LCM as 90 -
There are 4 pairs of numbers like this (2, 45), (9, 10), (1, 90) and (5, 18)
Now, 91 can be written as 1 * 91 or 7 * 13
Or, we can have HCF as 1, LCM as 90 -
There are 4 pairs of numbers like this (2, 45), (9, 10), (1, 90) and (5, 18)
We can have HCF as 7, ab + 1 = 13 => ab = 12 => 1 * 12 or 4 * 3
Or, the pairs of numbers are (7, 84) or (21, 28)
The third option is when HCF = 13, ab + 1 = 7 => ab = 6
Or (a, b) can be either (1, 6) or (2, 3)
The pairs possible are (13, 78) and (26, 39)
There are totally 8 options possible - (2, 45), (9, 10), (1, 90), (5, 18), (7, 84), (21, 28), (13, 78) and (26, 39).
8 Pairs.
Or (a, b) can be either (1, 6) or (2, 3)
The pairs possible are (13, 78) and (26, 39)
There are totally 8 options possible - (2, 45), (9, 10), (1, 90), (5, 18), (7, 84), (21, 28), (13, 78) and (26, 39).
8 Pairs.
The question is "How many pairs of positive integers x, y exist such that HCF (x, y) + LCM (x, y) = 91?"
Hence the answer is "8 pairs"
In a large school auditorium, the students are made to sit to watch the programmes. If the teachers make a row of students of 16 each, there will be 12 students left. If they make rows of 24 each, then there will be 20 students left, if they make rows of 25 each, there will be 21 students left and if they make rows of 30 each, there will be 26 students left. What is the minimum number of students present in the school?- a)1216
- b)1784
- c)1196
- d)2396
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In a large school auditorium, the students are made to sit to watch the programmes. If the teachers make a row of students of 16 each, there will be 12 students left. If they make rows of 24 each, then there will be 20 students left, if they make rows of 25 each, there will be 21 students left and if they make rows of 30 each, there will be 26 students left. What is the minimum number of students present in the school?
a)
1216
b)
1784
c)
1196
d)
2396
e)
None of these

|
Pranav Kulkarni answered |
16 in a row --> 12 left
24 in a row --> 20 left
25 in a row --> 21 left
30 in a row --> 26 left
24 in a row --> 20 left
25 in a row --> 21 left
30 in a row --> 26 left
In all the 4 cases above, the remainder is 4.
(16 – 12) = (24 – 20) = (25 – 21) = (30 – 26)
(16 – 12) = (24 – 20) = (25 – 21) = (30 – 26)
Hence the required students = LCM (16, 24, 25, 30 ) – 4
= 1200 – 4
= 1196
= 1200 – 4
= 1196
The question is "What is the minimum number of students present in the school?"
Hence the answer is "1196 students minimum"
The length and breadth of a rectangular floor are 16.25 metre and 12.75 metre respectively. Find how many minimum number of square tiles would be required to cover it completely? - a)375
- b)2570
- c)2800
- d)3315
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The length and breadth of a rectangular floor are 16.25 metre and 12.75 metre respectively. Find how many minimum number of square tiles would be required to cover it completely?
a)
375
b)
2570
c)
2800
d)
3315
e)
None of these

|
Bhavya Khanna answered |
Since we require minimum number of square tiles, the size of the tile is given as the H.C.F. of two sides of the room. The H.C.F. Of 1625 cm & 1275 cm. is 25 cms. Hence, we get,
Required Number = (1625 * 1275) / (25 * 25) = 3315
Required Number = (1625 * 1275) / (25 * 25) = 3315
What least number when divided by 20, 48 and 36 leaves the remainders 13, 41 and 29, respectively? - a)720
- b)713
- c)727
- d)187
- e)735
Correct answer is option 'B'. Can you explain this answer?
What least number when divided by 20, 48 and 36 leaves the remainders 13, 41 and 29, respectively?
a)
720
b)
713
c)
727
d)
187
e)
735

|
Ruchi Pillai answered |
Here least number is needed that means we need
the Least Common Multiple i.e. LCM
We must now first find LCM of 20, 36 and 48
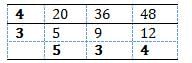
:.LCM=4x3 x5 x 3 x 4 = 720
But this is not the mnverbecause there are remainders as per the given condition.
If we observe dosely, the difference between the given numbers and remainders is same
20-13 = 7; 48-1 = 7; 36-29 = 7
Difference is same = 7
So simply subtract this difference from LCM.
Number = 720 - 7 = 713
the Least Common Multiple i.e. LCM
We must now first find LCM of 20, 36 and 48

:.LCM=4x3 x5 x 3 x 4 = 720
But this is not the mnverbecause there are remainders as per the given condition.
If we observe dosely, the difference between the given numbers and remainders is same
20-13 = 7; 48-1 = 7; 36-29 = 7
Difference is same = 7
So simply subtract this difference from LCM.
Number = 720 - 7 = 713
The least number which is a multiple of 11 and when divided by 3, 5 and 9 leaves 2 as remainder:- a)297
- b)319
- c)407
- d)512
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The least number which is a multiple of 11 and when divided by 3, 5 and 9 leaves 2 as remainder:
a)
297
b)
319
c)
407
d)
512
e)
None of these

|
Abhishek Choudhury answered |
The L.C.M. of 3, 5 and 9 is 45.
Hence, the number is of the form (45a + 2).
The least value of ‘a’ for which (45a + 2) is multiple of 11 is 9.
Therefore, the number is 407.
Hence, the number is of the form (45a + 2).
The least value of ‘a’ for which (45a + 2) is multiple of 11 is 9.
Therefore, the number is 407.
If (x - 4) is the HCF of x2 - 8x + 15 and x2 - kx +1 , then what is k?- a)8/15
- b)4
- c)5
- d)15/8
- e)5/4
Correct answer is option 'B'. Can you explain this answer?
If (x - 4) is the HCF of x2 - 8x + 15 and x2 - kx +1 , then what is k?
a)
8/15
b)
4
c)
5
d)
15/8
e)
5/4

|
Abhishek Kapoor answered |
(x-4) is HCF i.e. a factor of both equations
∴ The equations must get satisfied for x=4
Also, when x=4, both equations are equal in value.
Putting x=4 in both equations
42 - 8(4) + 15 = 42- k(4) +1
∴ The equations must get satisfied for x=4
Also, when x=4, both equations are equal in value.
Putting x=4 in both equations
42 - 8(4) + 15 = 42- k(4) +1
∴ 31-32 = 17- 4k
∴ k=4
∴ k=4
Find the least number which should be added to 2430 so that the sum is exactly divisible by 5, 4 and 2 - a)3
- b)10
- c)13
- d)33
- e)23
Correct answer is option 'B'. Can you explain this answer?
Find the least number which should be added to 2430 so that the sum is exactly divisible by 5, 4 and 2
a)
3
b)
10
c)
13
d)
33
e)
23

|
Niharika Sen answered |
L.C.M of 5, 4, and 2 = 20. On dividing 2430 by 20, the remainder is 10.
Therefore, number to be added = (20 - 10) = 10
Therefore, number to be added = (20 - 10) = 10
What is LCM of 36/225, 48/150 , 72/65 ? - a)36/65
- b)144/5
- c)72/225
- d)288/5
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
What is LCM of 36/225, 48/150 , 72/65 ?
a)
36/65
b)
144/5
c)
72/225
d)
288/5
e)
None of these

|
Mihir Ghoshal answered |

Numerators = 36, 48 and 72.
72 is largest number among them. 72 is not divisible by 36 or 48
Start with table of 72.
72 x 2 = 144 = divisible by 72, 36 and 48
∴ LCM of numerators =144
Denominators= 225, 150 and 65.
We can see that they can be divided by 5.
On dividing by 5 Imeget 45, 30 and 13
We cannot divide further. So, HCF = GCD =5

How many pairs of positive integers x, y exist such that HCF of x, y = 35 and sum of x and y = 1085?- a)12
- b)8
- c)15
- d)30
- e)16
Correct answer is option 'C'. Can you explain this answer?
How many pairs of positive integers x, y exist such that HCF of x, y = 35 and sum of x and y = 1085?
a)
12
b)
8
c)
15
d)
30
e)
16

|
Bhavana Kulkarni answered |
Let HCF of (x, y) be h. Then we can write x = h * a and y = h * b.
Furthermore, note that HCF (a, b) = 1. This is a very important property. One that seems obvious when it is mentioned but a property a number of people overlook.
Furthermore, note that HCF (a, b) = 1. This is a very important property. One that seems obvious when it is mentioned but a property a number of people overlook.
So, we can write x = 35a; y = 35b
x + y = 1085 => 35(a + b) = 1085. => (a + b) = 31. We need to find pairs of co-prime integers that add up to 31. (Another way of looking at it is to find out integers less than 31 those are co-prime with it or phi(31) as had mentioned. More on this wonderful function in another post).
Since 31 is prime. All pairs of integers that add up to 31 will be co-prime to each other. Or, there are totally 15 pairs that satisfy this condition.
The question is "How many pairs of positive integers x, y exist such that HCF of x, y = 35 and sum of x and y = 1085?"
Hence the answer is "15"
6 different sweet varieties of count 32, 216, 136, 88, 184, 120 were ordered for a particular occasion. They need to be packed in such a way that each box has the same variety of sweet and the number of sweets in each box is also the same. What is the minimum number of boxes required to pack?- a)129
- b)64
- c)48
- d)97
- e)88
Correct answer is option 'D'. Can you explain this answer?
6 different sweet varieties of count 32, 216, 136, 88, 184, 120 were ordered for a particular occasion. They need to be packed in such a way that each box has the same variety of sweet and the number of sweets in each box is also the same. What is the minimum number of boxes required to pack?
a)
129
b)
64
c)
48
d)
97
e)
88

|
Rajdeep Nair answered |
All sweets need to packed and each box has the same variety.
This implies the number of sweets in each box should be HCF of different count of sweets
HCF of 32, 216, 136, 88, 184, 120 = 23 = 8
Minimum number of boxes = (32 + 216 + 136 + 88 + 184 + 120) / 8 = 97
This implies the number of sweets in each box should be HCF of different count of sweets
HCF of 32, 216, 136, 88, 184, 120 = 23 = 8
Minimum number of boxes = (32 + 216 + 136 + 88 + 184 + 120) / 8 = 97
The question is "What is the minimum number of boxes required to pack?"
Hence the answer is "97 boxes"
If the product of two positive integers is 144, which of the following could be the LCM and HCF of the two numbers?
I. LCM : 24; HCF : 6
II. LCM : 18; HCF : 8
III. LCM : 16; HCF : 9
- a)I and II only
- b)II and III only
- c)I only
- d)I and III only
- e)I, II and III
Correct answer is option 'C'. Can you explain this answer?
If the product of two positive integers is 144, which of the following could be the LCM and HCF of the two numbers?
I. LCM : 24; HCF : 6
II. LCM : 18; HCF : 8
III. LCM : 16; HCF : 9
I. LCM : 24; HCF : 6
II. LCM : 18; HCF : 8
III. LCM : 16; HCF : 9
a)
I and II only
b)
II and III only
c)
I only
d)
I and III only
e)
I, II and III

|
Maya Khanna answered |
Result 1:
The product of two positive integers ‘a’ and ‘b’ is equal to the product of the LCM (a, b) and HCF (a, b).
i.e., a * b = LCM (a, b) * HCF (a, b)
The product of two positive integers ‘a’ and ‘b’ is equal to the product of the LCM (a, b) and HCF (a, b).
i.e., a * b = LCM (a, b) * HCF (a, b)
Result 2:
HCF is a factor of both the positive integers.
LCM is a multiple of both the positive integers.
So, it is evident that the LCM of the two positive integers has to be a multiple of the HCF of the two numbers.
HCF is a factor of both the positive integers.
LCM is a multiple of both the positive integers.
So, it is evident that the LCM of the two positive integers has to be a multiple of the HCF of the two numbers.
Combining these two results, we have to find out which among the pairs has a product of 144 such that the LCM is a multiple of the HCF.
I. LCM : 24 and HCF : 6. Product of the LCM and HCF = 24 * 6 = 144. The LCM 24 is a multiple of the HCF 6. Hence, this is a possible pair.
II. LCM : 18 and HCF : 8. Product of the LCM and HCF = 18 * 8 = 144. However, the LCM 18 is NOT a multiple of the HCF 8. Hence, this one is not a possible pair.
III. LCM : 16 and HCF : 9. Product of the LCM and HCF = 16 * 9 = 144. However, the LCM 16 is NOT a multiple of the HCF 9. Hence, this one is also not a possible pair.
LCM of 2 natural numbers p and q where p > q is 935. What is the maximum possible sum of the digits of q?
- a)1
- b)13
- c)8
- d)2
- e)5
Correct answer is option 'B'. Can you explain this answer?
LCM of 2 natural numbers p and q where p > q is 935. What is the maximum possible sum of the digits of q?
a)
1
b)
13
c)
8
d)
2
e)
5

|
Athira Choudhury answered |
We know, 935 = 5*11*17
Let p = hx
q = hy
Where h is the hcf of p and q.
Therefore, lcm of p and q= hxy
q = hy
Where h is the hcf of p and q.
Therefore, lcm of p and q= hxy
We have lcm = 935.
hxy = 935
hxy = 935
If h = 1,
Then p = 935
q = 1
Sum of digits of q = 1
Then p = 935
q = 1
Sum of digits of q = 1
If h = 5,
p = 5*17 = 85
q = 5*11 = 55
Sum of digits of q = 10
p = 5*17 = 85
q = 5*11 = 55
Sum of digits of q = 10
If h = 11,
p = 11*17 = 187
q = 11*5 = 55
Sum of digits of q = 10
p = 11*17 = 187
q = 11*5 = 55
Sum of digits of q = 10
If h = 17,
p = 17*11 = 187
q = 17*5 = 85
Sum of digits of q = 13
p = 17*11 = 187
q = 17*5 = 85
Sum of digits of q = 13
Maximum possible sum of digits of q = 13.
The question is "What is the maximum possible sum of the digits of q?"
The question is "What is the maximum possible sum of the digits of q?"
Hence the answer is "13"
There are 2 numbers such that a > b, HCF (a, b) = h and LCM (a, b) = l. What is the LCM of a – b and b?- a)l
- b)(a - b) b
- c)(a - b) b / h
- d)h (a - b)
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
There are 2 numbers such that a > b, HCF (a, b) = h and LCM (a, b) = l. What is the LCM of a – b and b?
a)
l
b)
(a - b) b
c)
(a - b) b / h
d)
h (a - b)
e)
None of these

|
Pranav Das answered |
Can you please provide additional information or context so I can assist you better?
The L.C.M. Of 2, 2.7 and 0.09 is: - a)5.4
- b)0.54
- c)0.054
- d)0.0054
- e)54
Correct answer is option 'E'. Can you explain this answer?
The L.C.M. Of 2, 2.7 and 0.09 is:
a)
5.4
b)
0.54
c)
0.054
d)
0.0054
e)
54

|
Tanishq Yadav answered |
Given numbers are 2.00, 2.70 and 0.09.
L.C.M. of 200, 270 and 9 is 5400.
L.C.M. Of given numbers = 54.00 = 54
L.C.M. of 200, 270 and 9 is 5400.
L.C.M. Of given numbers = 54.00 = 54
What least possible 4-digit number, when divided by 12, 16, 18 and 20 leaves 21 as remainder?- a)36
- b)133
- c)144
- d)1461
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
What least possible 4-digit number, when divided by 12, 16, 18 and 20 leaves 21 as remainder?
a)
36
b)
133
c)
144
d)
1461
e)
None of these

|
Amrutha Jain answered |
Here least possible 4 digit number is needed that means we need the LCM We must first find LCM of 12, 16, 18 and 20 .

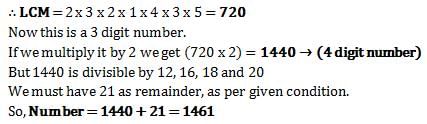

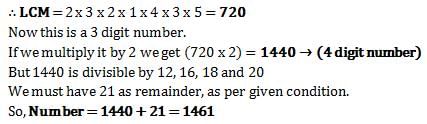
5 clocks ring automatically at intervals of 12 minutes, 8 minutes, 3 minutes, 4 minutes and 10 minutes, respectively. In 8 hours from the moment they start, how many times will they ring together?- a)12 times
- b)5 times
- c)3 times
- d)4 times
- e)8 times
Correct answer is option 'D'. Can you explain this answer?
5 clocks ring automatically at intervals of 12 minutes, 8 minutes, 3 minutes, 4 minutes and 10 minutes, respectively. In 8 hours from the moment they start, how many times will they ring together?
a)
12 times
b)
5 times
c)
3 times
d)
4 times
e)
8 times

|
Prisha Mukherjee answered |
We need the next instances when the alarm rings.
That means the Least Common Multiple (LCM) of 3, 4, 8, 10, 12 3, 4 divide 12 so neglect them.
LCM of 8, 10 and 12

∴ LCM = 4x2x5x3= 120 = They ring after 2 hours
After starting, they ring together ist time in 2 hours.
Then 2nd time in 2+2 = 4 hours.
Then 3rd time in 6 hours.
And 4th time in 8 hours.
That means the Least Common Multiple (LCM) of 3, 4, 8, 10, 12 3, 4 divide 12 so neglect them.
LCM of 8, 10 and 12

∴ LCM = 4x2x5x3= 120 = They ring after 2 hours
After starting, they ring together ist time in 2 hours.
Then 2nd time in 2+2 = 4 hours.
Then 3rd time in 6 hours.
And 4th time in 8 hours.
Rajesh had to arrange his books in uniform groups. He makes groups of 4 books each. But 3 books are left. He tries it with groups of 5 books each. But still 3 books are left. 3 books are still left when he tried with groups of 9 or 10 books each. How many books does he have?- a)90
- b)180
- c)900
- d)183
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Rajesh had to arrange his books in uniform groups. He makes groups of 4 books each. But 3 books are left. He tries it with groups of 5 books each. But still 3 books are left. 3 books are still left when he tried with groups of 9 or 10 books each. How many books does he have?
a)
90
b)
180
c)
900
d)
183
e)
None of these

|
Tanishq Yadav answered |
Since we need total number of books, we must find LCM of 4,5,9,10
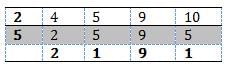

If the LCM of two numbers a and b is 1104 and their HCF is 4, which of the following MUST be true?
I. a * b = 4416
II. a and b are both divisible by 8
III. a : b = 48 : 23 or a : b = 23 : 48
- a)I and III only
- b)II only
- c)I only
- d)II and III only
- e)I, II, and III
Correct answer is option 'C'. Can you explain this answer?
If the LCM of two numbers a and b is 1104 and their HCF is 4, which of the following MUST be true?
I. a * b = 4416
II. a and b are both divisible by 8
III. a : b = 48 : 23 or a : b = 23 : 48
I. a * b = 4416
II. a and b are both divisible by 8
III. a : b = 48 : 23 or a : b = 23 : 48
a)
I and III only
b)
II only
c)
I only
d)
II and III only
e)
I, II, and III

|
Saumya Shah answered |
Before we start solving the question in hand, here are a couple of important concepts that we need to know.
Concept 1:
Product of two numbers is the same as the product of the LCM and HCF of those two numbers.
i.e., If the numbers are a and b, a * b = LCM (a, b) * HCF (a, b)
Note: a * b * c NEED NOT be equal to LCM(a, b, c) * HCF(a, b, c).
This rule works for 2 numbers, irrespective of whether the numbers are both integers, both fractions, one fraction and the other an integer.
Concept 2:
Let ‘h’ be the HCF of a and b and ‘L’ be the LCM of a and b.
a can be expressed as m*h and b can be expressed as n*h because h is a factor common to both the numbers.
a = mh and b = nh.
a can be expressed as m*h and b can be expressed as n*h because h is a factor common to both the numbers.
a = mh and b = nh.
Note, m and n are co-prime (have no factor in common) because ‘h’ is the HCF of the two numbers. HCF of two numbers holds all factors common to both the numbers.Hence, we can deduce that the LCM (a, b), L = m*n*hi.e., the HCF of two numbers will be a factor of the LCM of the two numbers.
Data given in the question stem:
LCM of a and b is 1104 and their HCF is 4.
Statement I: a * b = 4416
Result 1 states that a * b = LCM (a, b) * HCF (a, b).
So, a * b = 1104 * 4 = 4416.
Statement I is true.
Statement II: a and b are both divisible by 8
The HCF of a and b is 4. So, the largest number that could divide both a and b is 4.
If 8 could divide both a and b, the largest number that could divide both would have been 8.
Consequently, the HCF of the two numbers would have been 8 and not 4.
So, statement II is NOT true.
Statement III: a : b = 48 : 23 or a : b = 23 : 48
Result 2 comes in handy to evaluate statement III.
If L is the LCM(a, b) and h is the HCF(a, b), L = m * n * h.
Where a = mh and b = nh and m and n are co-prime.
We have to determine whether a : b = 48 : 23 or 23 : 48.
i.e., we have to determine whether m : n = 48 : 23 or 23 : 48.
Because L = m * n * h, 1104 = m * n * 4
Or m * n = 1104/4 = 276
Note: m and n are co-prime.
If m and n are 48 and 23 or vice versa, m * n = 1104 and not 276.
Statement III is NOT true.
The greatest number of four digits which is divisible by 15, 25, 40, 75 is - a)600
- b)9000
- c)9600
- d)9400
- e)9200
Correct answer is option 'C'. Can you explain this answer?
The greatest number of four digits which is divisible by 15, 25, 40, 75 is
a)
600
b)
9000
c)
9600
d)
9400
e)
9200

|
Ameya Yadav answered |
To find the greatest number of four digits that is divisible by 15, 25, 40, and 75, we need to find the least common multiple (LCM) of these numbers.
Finding the LCM:
1. Prime factorize each number:
- 15 = 3 * 5
- 25 = 5 * 5
- 40 = 2 * 2 * 2 * 5
- 75 = 3 * 5 * 5
2. Take the highest power of each prime factor:
- 2^3 * 3^1 * 5^2
3. Multiply the highest powers of all prime factors:
- LCM = 2^3 * 3^1 * 5^2 = 8 * 3 * 25 = 600
Finding the greatest four-digit number divisible by 600:
To find the greatest four-digit number divisible by 600, we need to find the largest multiple of 600 that is less than 10,000.
Dividing 10,000 by 600 gives us a quotient of 16 and a remainder of 400.
Therefore, the greatest four-digit number divisible by 600 is:
- 600 * 16 = 9,600
Hence, the correct answer is option C) 9600.
Finding the LCM:
1. Prime factorize each number:
- 15 = 3 * 5
- 25 = 5 * 5
- 40 = 2 * 2 * 2 * 5
- 75 = 3 * 5 * 5
2. Take the highest power of each prime factor:
- 2^3 * 3^1 * 5^2
3. Multiply the highest powers of all prime factors:
- LCM = 2^3 * 3^1 * 5^2 = 8 * 3 * 25 = 600
Finding the greatest four-digit number divisible by 600:
To find the greatest four-digit number divisible by 600, we need to find the largest multiple of 600 that is less than 10,000.
Dividing 10,000 by 600 gives us a quotient of 16 and a remainder of 400.
Therefore, the greatest four-digit number divisible by 600 is:
- 600 * 16 = 9,600
Hence, the correct answer is option C) 9600.
What greatest number divides 17, 42 and 93 and leaves remainders 4, 3 and 15, respectively?- a)89
- b)78
- c)13
- d)17
- e)None of the above
Correct answer is option 'C'. Can you explain this answer?
What greatest number divides 17, 42 and 93 and leaves remainders 4, 3 and 15, respectively?
a)
89
b)
78
c)
13
d)
17
e)
None of the above

|
Palak Yadav answered |
Here greatest number that can divide means the HCF
Remainders are different so simply subtract remainders from numbers
17-4 = 13; 42-3 = 39; 93-15 = 78
Now let's find HCF of 13, 39 and 78
By direct observation we can see that all numbers are divisible by 13.
∴ HCF =13 = required greatest number
Remainders are different so simply subtract remainders from numbers
17-4 = 13; 42-3 = 39; 93-15 = 78
Now let's find HCF of 13, 39 and 78
By direct observation we can see that all numbers are divisible by 13.
∴ HCF =13 = required greatest number
The greatest length of the scale that can measure exactly 30 cm, 90 cm, 1 m 20 cm and 1 m 35 cm lengths is- a)5 cm
- b)10 cm
- c)15 cm
- d)30 cm
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The greatest length of the scale that can measure exactly 30 cm, 90 cm, 1 m 20 cm and 1 m 35 cm lengths is
a)
5 cm
b)
10 cm
c)
15 cm
d)
30 cm
e)
None of these

|
Ruchi Pillai answered |
Here we need to exactly measure these lengths.
Also, lm = 100 cm; ... 1m 35cm = 135cm and 1m 20cm = 120cm
Option 1- 5 cm can measure 30cm, 90cm, 1m 20cm and 1m 35 cm
Option 2 - 10 cm cannot measure 1m 35cm i.e. 135cm
Option 3 -15 cm can measure30cm, 90cm, 1m 20cm and 1m 35 cm
Option 4 -30 cm cannot measure 1m 35cm
Since we want greatest length 15 > 5
∴ Answer = 15cm
Also, lm = 100 cm; ... 1m 35cm = 135cm and 1m 20cm = 120cm
Option 1- 5 cm can measure 30cm, 90cm, 1m 20cm and 1m 35 cm
Option 2 - 10 cm cannot measure 1m 35cm i.e. 135cm
Option 3 -15 cm can measure30cm, 90cm, 1m 20cm and 1m 35 cm
Option 4 -30 cm cannot measure 1m 35cm
Since we want greatest length 15 > 5
∴ Answer = 15cm
The L.C.M. of two number is 60. The numbers are in the ratio 4 : 5. Find the sum of numbers. - a)27
- b)33
- c)38
- d)45
- e)60
Correct answer is option 'A'. Can you explain this answer?
The L.C.M. of two number is 60. The numbers are in the ratio 4 : 5. Find the sum of numbers.
a)
27
b)
33
c)
38
d)
45
e)
60

|
Sinjini Mukherjee answered |
Let the numbers be 4x and 5x.
Then, their L.C.M. = 20x.
20x = 60 or x = 3.
The numbers are 12 and 15.
Hence, required sum = (12 + 15) = 27.
Then, their L.C.M. = 20x.
20x = 60 or x = 3.
The numbers are 12 and 15.
Hence, required sum = (12 + 15) = 27.
3 bells beep at an interval of 12, 20, and 35 minutes. If they beep together at 10 a.m., then they will again beep together at:- a)12 p.m.
- b)1 p.m.
- c)4 p.m.
- d)5 p.m.
- e)3 p.m.
Correct answer is option 'D'. Can you explain this answer?
3 bells beep at an interval of 12, 20, and 35 minutes. If they beep together at 10 a.m., then they will again beep together at:
a)
12 p.m.
b)
1 p.m.
c)
4 p.m.
d)
5 p.m.
e)
3 p.m.

|
Shivam Ghoshal answered |
The L.C.M. of 12, 20 and 35 is 420. Hence, all 3 bells beep together after 420 minutes = 7 hours
Hence, the 3 bells will beep together 7 hours after 10 a.m. i.e. at 5 p.m.
Hence, the 3 bells will beep together 7 hours after 10 a.m. i.e. at 5 p.m.
Manoj wants to paste wallpaper on wall of his room. The wall is 4 meters and 50 cm in length and 3 meters and 50 cm in height. But the wall should be covered completely only by square pieces of wallpaper having same size. What is the number of maximum sized wallpaper squares needed to cover the walls completely?- a)8
- b)15.75
- c)63
- d)12
- e)24
Correct answer is option 'C'. Can you explain this answer?
Manoj wants to paste wallpaper on wall of his room. The wall is 4 meters and 50 cm in length and 3 meters and 50 cm in height. But the wall should be covered completely only by square pieces of wallpaper having same size. What is the number of maximum sized wallpaper squares needed to cover the walls completely?
a)
8
b)
15.75
c)
63
d)
12
e)
24

|
Isha Sen answered |
Wall can be covered only by using square sized wallpaper pieces.
Different sized squares are not allowed.
Length = 4 m 50 cm = 450 cm ; Height = 3 m 50 cm = 350 cm
Maximum square size of possible means HCF of 350 and 450
We can see that 350 and 450 can be divided by 50.
On dividing by 50, we get 7 and 9.
Since we cannot divide further, HCF = 50 = size of side of square
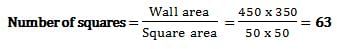
Different sized squares are not allowed.
Length = 4 m 50 cm = 450 cm ; Height = 3 m 50 cm = 350 cm
Maximum square size of possible means HCF of 350 and 450
We can see that 350 and 450 can be divided by 50.
On dividing by 50, we get 7 and 9.
Since we cannot divide further, HCF = 50 = size of side of square
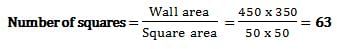
What largest number will divide 47, 35 and 27 leaving same remainder in each case? What will be the common remainder?- a)9,1
- b)1,9
- c)4,3
- d)3,4
- e)4,9
Correct answer is option 'C'. Can you explain this answer?
What largest number will divide 47, 35 and 27 leaving same remainder in each case? What will be the common remainder?
a)
9,1
b)
1,9
c)
4,3
d)
3,4
e)
4,9

|
Chirag Roy answered |
What to do when we don't lcnow the remainder and the largest number which divides?
In such cases subtract the 3 numbers from each other
47-35 = 12
35-27 = 8
27-47 = -20 (Ignore minus sign)
Largest number is needed that means we need HCF of 12, 8 and 20


In such cases subtract the 3 numbers from each other
47-35 = 12
35-27 = 8
27-47 = -20 (Ignore minus sign)
Largest number is needed that means we need HCF of 12, 8 and 20


Chapter doubts & questions for Highest Common Factor & Least Common Multiple - Quantitative for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Highest Common Factor & Least Common Multiple - Quantitative for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Quantitative for GMAT
127 videos|154 docs|111 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup