All Exams >
MCAT >
Physics for MCAT >
All Questions
All questions of Vectors and Scalars for MCAT Exam
The portion of the Mississippi River has a velocity of 1.0 meters per second. In still water, the ferry travels with a velocity of 1.4 meters per second. The ferry must transport the residents directly across the 1600 meter river span. Which of the following correctly describes the motion of the ferry?- a)The ferry can launch at 90° from the shore if it travels at its maximum velocity.
- b)The ferry must launch upstream at an angle of 45° from the shore with a velocity of 1.4 meters per second.
- c)The ferry will take about half an hour to cross the river at a relative velocity of 10 meters per second.
- d)The ferry will take about an hour to cross the river at its current velocity of 1.4 meters per second.
Correct answer is option 'B'. Can you explain this answer?
The portion of the Mississippi River has a velocity of 1.0 meters per second. In still water, the ferry travels with a velocity of 1.4 meters per second. The ferry must transport the residents directly across the 1600 meter river span. Which of the following correctly describes the motion of the ferry?
a)
The ferry can launch at 90° from the shore if it travels at its maximum velocity.
b)
The ferry must launch upstream at an angle of 45° from the shore with a velocity of 1.4 meters per second.
c)
The ferry will take about half an hour to cross the river at a relative velocity of 10 meters per second.
d)
The ferry will take about an hour to cross the river at its current velocity of 1.4 meters per second.
|
|
Lily King answered |
A) The ferry can launch at 90
Which of the following is NOT considered a vector quantity?- a)force
- b)electric potential difference
- c)electric field
- d)momentum
Correct answer is option 'B'. Can you explain this answer?
Which of the following is NOT considered a vector quantity?
a)
force
b)
electric potential difference
c)
electric field
d)
momentum

|
Orion Classes answered |
In identifying a vector quantity, look for a quantity that has both direction and magnitude, but a more surefire method is to find a quantity that consists of a vector multiplied by a scalar. The vector quantities are the wrong answers.
Force is mass multiplied by acceleration, which is a scalar multiplied by a vector. Hence, it is a vector:
F = ma
F = ma
Momentum is mass multiplied by velocity, which is a scalar multiplied by a vector. Hence, it is a vector:
p = mv
p = mv
Electric field is force divided by charge, which is a vector divided by a scalar. Hence, it is a vector:
E = F/q
E = F/q
Electric potential is electric potential energy divided by charge, which is a scalar divided by a scalar. Hence, it is a scalar, and electric potential is the correct answer.
V = U/q
V = U/q
Which of the following statements correctly identifies an example of the respective scalar or vector product processes?
I. Vector and scalar : torque
II. Vector and vector : magnetic force
III. Scalar and scalar : power- a)I and II
- b)III only
- c)II and III
- d)I only
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements correctly identifies an example of the respective scalar or vector product processes?
I. Vector and scalar : torque
II. Vector and vector : magnetic force
III. Scalar and scalar : power
I. Vector and scalar : torque
II. Vector and vector : magnetic force
III. Scalar and scalar : power
a)
I and II
b)
III only
c)
II and III
d)
I only
|
|
Charlotte Martinez answered |
Understanding Scalar and Vector Products
To clarify why option 'C' is correct, let's analyze the statements related to scalar and vector products.
Statement I: Vector and Scalar - Torque
- Torque is defined as the cross product of a vector (lever arm) and a force vector.
- It results in a vector quantity, not a scalar.
- Therefore, this statement is incorrect for identifying scalar or vector processes.
Statement II: Vector and Vector - Magnetic Force
- Magnetic force on a charged particle moving in a magnetic field is indeed a vector quantity.
- It is derived from the cross product of the velocity vector and the magnetic field vector.
- Hence, this statement correctly identifies a vector and vector process.
Statement III: Scalar and Scalar - Power
- Power is defined as the rate at which work is done or energy is transferred.
- It can be computed as the dot product of force (vector) and velocity (vector), resulting in a scalar quantity.
- Hence, this statement accurately identifies a scalar product.
Conclusion
Based on the analysis:
- I is incorrect.
- II is correct (Vector and Vector: Magnetic Force).
- III is also correct (Scalar and Scalar: Power).
Thus, the correct answer is option 'C' (II and III).
To clarify why option 'C' is correct, let's analyze the statements related to scalar and vector products.
Statement I: Vector and Scalar - Torque
- Torque is defined as the cross product of a vector (lever arm) and a force vector.
- It results in a vector quantity, not a scalar.
- Therefore, this statement is incorrect for identifying scalar or vector processes.
Statement II: Vector and Vector - Magnetic Force
- Magnetic force on a charged particle moving in a magnetic field is indeed a vector quantity.
- It is derived from the cross product of the velocity vector and the magnetic field vector.
- Hence, this statement correctly identifies a vector and vector process.
Statement III: Scalar and Scalar - Power
- Power is defined as the rate at which work is done or energy is transferred.
- It can be computed as the dot product of force (vector) and velocity (vector), resulting in a scalar quantity.
- Hence, this statement accurately identifies a scalar product.
Conclusion
Based on the analysis:
- I is incorrect.
- II is correct (Vector and Vector: Magnetic Force).
- III is also correct (Scalar and Scalar: Power).
Thus, the correct answer is option 'C' (II and III).
Which of the following vector combinations will result in the least amount of displacement? (Note: Vectors 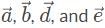 have magnitudes double that of vectors
have magnitudes double that of vectors 
- a)
- b)
- c)
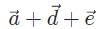
- d)
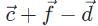
Correct answer is option 'B'. Can you explain this answer?
Which of the following vector combinations will result in the least amount of displacement? (Note: Vectors 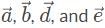 have magnitudes double that of vectors
have magnitudes double that of vectors 

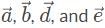 have magnitudes double that of vectors
have magnitudes double that of vectors 

a)
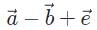
b)
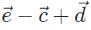
c)
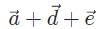
d)
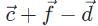

|
Orion Classes answered |
Let’s consider each case graphically to narrow down our choices. Recall that vectors  are half the magnitude of vector
are half the magnitude of vector 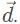 By drawing out
By drawing out 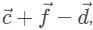 we can see that the displacement is somewhat large:
we can see that the displacement is somewhat large:
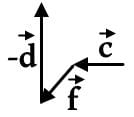
 are half the magnitude of vector
are half the magnitude of vector 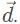 By drawing out
By drawing out 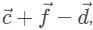 we can see that the displacement is somewhat large:
we can see that the displacement is somewhat large:
All three vectors have the same magnitude here. By drawing out 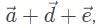 , we can see that displacement is not large, but could be closer to zero:
, we can see that displacement is not large, but could be closer to zero:
Between the remaining two, it becomes hard to discern visually which has the least displacement:

In analyzing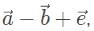 let’s pick 10 for the magnitude of each vector, and resolve all the vectors into the x and y direction. In a 45 − 45 − 90 triangle, remember that the sides are in a proportion of 1 : 1 : √2 so with the hypotenuse as 10 units, the x and y components are 5√2, units. In the x-direction, the x component vectors
let’s pick 10 for the magnitude of each vector, and resolve all the vectors into the x and y direction. In a 45 − 45 − 90 triangle, remember that the sides are in a proportion of 1 : 1 : √2 so with the hypotenuse as 10 units, the x and y components are 5√2, units. In the x-direction, the x component vectors  overlap and add up to 10 √2, which is opposed by vector
overlap and add up to 10 √2, which is opposed by vector 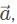 , with, vector, on top, with a magnitude of 10.
, with, vector, on top, with a magnitude of 10.
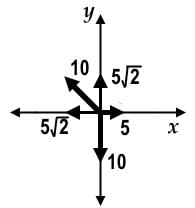
In the y-direction, the y-component of vectors cancel each other out. The resultant vector points in the negative y-direction with an approximate magnitude of 4 since √2, is approximately equal to 1.4.
cancel each other out. The resultant vector points in the negative y-direction with an approximate magnitude of 4 since √2, is approximately equal to 1.4.
In analyzing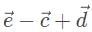 let’s pick 10 for the magnitude of vectors
let’s pick 10 for the magnitude of vectors  and 5 for the magnitude of vector
and 5 for the magnitude of vector  resolve all the vectors into the x and y components. Vector
resolve all the vectors into the x and y components. Vector  resolves into an x and y components with magnitudes of 5√2 units:
resolves into an x and y components with magnitudes of 5√2 units:
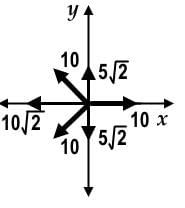
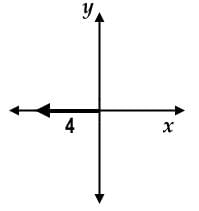
The resultant x-component is 2 in the negative-x direction, and the resultant y-component is 3 in the negative-y direction. To find our displacement, use the Pythagorean theorem to obtain √13 which is less than 4.
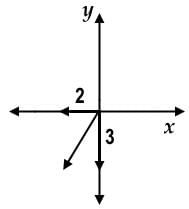
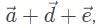 , we can see that displacement is not large, but could be closer to zero:
, we can see that displacement is not large, but could be closer to zero:
Between the remaining two, it becomes hard to discern visually which has the least displacement:


In analyzing
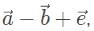 let’s pick 10 for the magnitude of each vector, and resolve all the vectors into the x and y direction. In a 45 − 45 − 90 triangle, remember that the sides are in a proportion of 1 : 1 : √2 so with the hypotenuse as 10 units, the x and y components are 5√2, units. In the x-direction, the x component vectors
let’s pick 10 for the magnitude of each vector, and resolve all the vectors into the x and y direction. In a 45 − 45 − 90 triangle, remember that the sides are in a proportion of 1 : 1 : √2 so with the hypotenuse as 10 units, the x and y components are 5√2, units. In the x-direction, the x component vectors  overlap and add up to 10 √2, which is opposed by vector
overlap and add up to 10 √2, which is opposed by vector 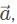 , with, vector, on top, with a magnitude of 10.
, with, vector, on top, with a magnitude of 10.
In the y-direction, the y-component of vectors
 cancel each other out. The resultant vector points in the negative y-direction with an approximate magnitude of 4 since √2, is approximately equal to 1.4.
cancel each other out. The resultant vector points in the negative y-direction with an approximate magnitude of 4 since √2, is approximately equal to 1.4.
In analyzing
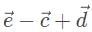 let’s pick 10 for the magnitude of vectors
let’s pick 10 for the magnitude of vectors  and 5 for the magnitude of vector
and 5 for the magnitude of vector 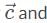 resolve all the vectors into the x and y components. Vector
resolve all the vectors into the x and y components. Vector 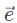 resolves into an x and y components with magnitudes of 5√2 units:
resolves into an x and y components with magnitudes of 5√2 units:
The resultant x-component is 2 in the negative-x direction, and the resultant y-component is 3 in the negative-y direction. To find our displacement, use the Pythagorean theorem to obtain √13 which is less than 4.

Aisha, Saul, and Lorenzo are playing a tug-of-war. Saul and Lorenzo are pulling at 90° to each other, while Aisha is pulling with 20 N on her rope at an angle (90 + θ)° from Lorenzo. Given that θ = arctan(1.33), what are the magnitudes of force with which Saul and Lorenzo must pull in order to keep this system in equilibrium? (Figure may not be drawn to scale.)
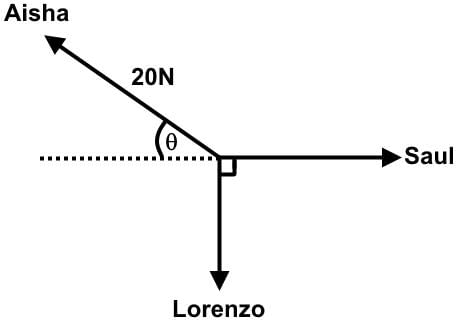
- a)10√2 N for Saul, 10√2 N for Lorenzo
- b)10 N for Lorenzo, 20 N for Saul
- c)16 N for Lorenzo, 12 N for Saul
- d)Not enough information has been given.
Correct answer is option 'C'. Can you explain this answer?
Aisha, Saul, and Lorenzo are playing a tug-of-war. Saul and Lorenzo are pulling at 90° to each other, while Aisha is pulling with 20 N on her rope at an angle (90 + θ)° from Lorenzo. Given that θ = arctan(1.33), what are the magnitudes of force with which Saul and Lorenzo must pull in order to keep this system in equilibrium? (Figure may not be drawn to scale.)


a)
10√2 N for Saul, 10√2 N for Lorenzo
b)
10 N for Lorenzo, 20 N for Saul
c)
16 N for Lorenzo, 12 N for Saul
d)
Not enough information has been given.

|
Orion Classes answered |
Aisha is pulling with 20 N, so in order for this system to be in equilibrium, Saul and Lorenzo together must be pulling with the same force in the opposite direction. That vector would represent the hypotenuse of the right triangle where Saul’s force is the adjacent side and Lorenzo’s opposite.
One big clue to solving this problem is that the angle is equal to arctan (1.33). 1.33 is the value of the opposite side divided by the adjacent side.
Let’s represent the decimal by a fraction, which would be 4/3. So the ratio of the opposite side to the adjacent side is 4 : 3.
Either by Pythagorean theorem or by past memorization, the hypotenuse will have the value of 5, and we have our 3 - 4 - 5 triangle.
As we said, Aisha represents the hypotenuse, which has a value of 20 N. Divide that by the calculated value for the hypotenuse to obtain the factor to multiply the other sides. That factor is 4.
The other sides of the triangle are 12 N and 16 N. Match it to the right person. The correct answer is 16 N for Lorenzo and 12 N for Saul.
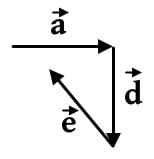
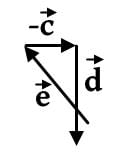
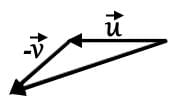
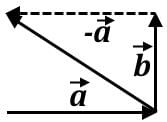
Which of the following most accurately represents the resultant vector 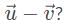
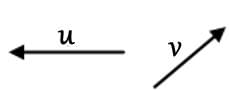
- a)
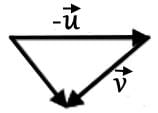
- b)
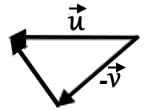
- c)
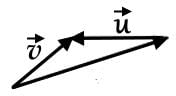
- d)
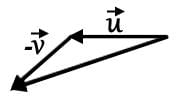
Correct answer is option 'D'. Can you explain this answer?
Which of the following most accurately represents the resultant vector 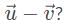
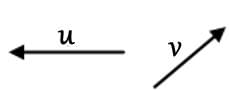
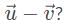
a)

b)

c)

d)


|
Orion Classes answered |
For two vectors  the vector sum
the vector sum  is obtained by placing them head to tail and drawing the vector from the free tail to the free head. A vector difference is equivalent to a vector sum with the orientation of the second vector reversed.
is obtained by placing them head to tail and drawing the vector from the free tail to the free head. A vector difference is equivalent to a vector sum with the orientation of the second vector reversed.
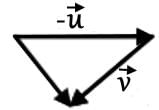
This vector combination below best represents the resultant vector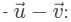
This vector combination was probably intended to represent but it doesn't follow the head-to-tail rule.
but it doesn't follow the head-to-tail rule.
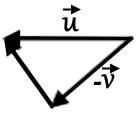
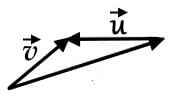
This vector combination was probably intended to represent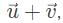 but it doesn't follow the head-to-tail rule.
but it doesn't follow the head-to-tail rule.
This vector combination below can be represented by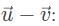
 the vector sum
the vector sum  is obtained by placing them head to tail and drawing the vector from the free tail to the free head. A vector difference is equivalent to a vector sum with the orientation of the second vector reversed.
is obtained by placing them head to tail and drawing the vector from the free tail to the free head. A vector difference is equivalent to a vector sum with the orientation of the second vector reversed.This vector combination below best represents the resultant vector
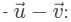

This vector combination was probably intended to represent
 but it doesn't follow the head-to-tail rule.
but it doesn't follow the head-to-tail rule.
This vector combination was probably intended to represent
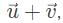 but it doesn't follow the head-to-tail rule.
but it doesn't follow the head-to-tail rule.
This vector combination below can be represented by
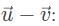

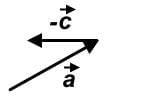
Which of the following vector combinations will result in the greatest displacement?
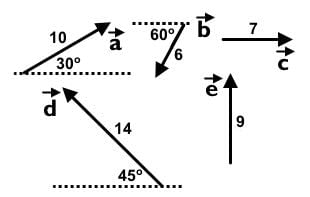
- a)
- b)
- c)
- d)
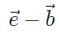
Correct answer is option 'B'. Can you explain this answer?
Which of the following vector combinations will result in the greatest displacement?


a)
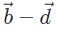
b)
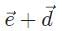
c)
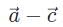
d)
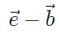

|
Orion Classes answered |
This question can be solved visually and without any math. Let’s go through drawing each vector combination.
The vector combination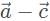 can be drawn like the following:
can be drawn like the following:
The vector combination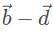 can be drawn like the following:
can be drawn like the following:
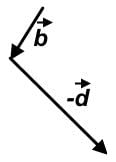
The vector combination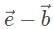 can be drawn like the following:
can be drawn like the following:
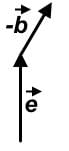
The vector combination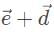 can be drawn like the following:
can be drawn like the following:
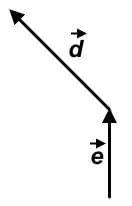
Visually, we can eliminate down to and since
and since 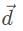 is much longer than
is much longer than  the vector combination
the vector combination 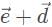 will have the greatest displacement.
will have the greatest displacement.
The vector combination
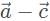 can be drawn like the following:
can be drawn like the following:
The vector combination
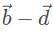 can be drawn like the following:
can be drawn like the following:
The vector combination
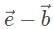 can be drawn like the following:
can be drawn like the following:
The vector combination
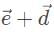 can be drawn like the following:
can be drawn like the following:
Visually, we can eliminate down to
 and since
and since 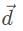 is much longer than
is much longer than  the vector combination
the vector combination 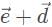 will have the greatest displacement.
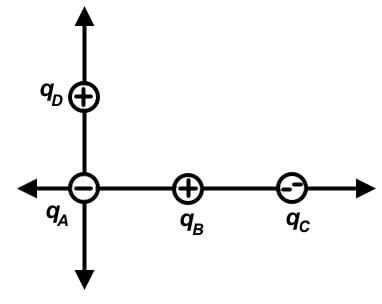
will have the greatest displacement.Which of the following best represents the resultant electrostatic force on qA due to the other charges? (The formula for electrostatic force is 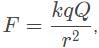 where q is a test charge, Q is the source charge, and r is the distance between their center of masses.)
where q is a test charge, Q is the source charge, and r is the distance between their center of masses.)
- a)
- b)

- c)

- d)

Correct answer is option 'B'. Can you explain this answer?
Which of the following best represents the resultant electrostatic force on qA due to the other charges? (The formula for electrostatic force is 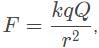 where q is a test charge, Q is the source charge, and r is the distance between their center of masses.)
where q is a test charge, Q is the source charge, and r is the distance between their center of masses.)

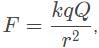 where q is a test charge, Q is the source charge, and r is the distance between their center of masses.)
where q is a test charge, Q is the source charge, and r is the distance between their center of masses.)
a)
b)

c)

d)


|
Orion Classes answered |
Given this formula, we have to extrapolate that charge q is directly proportional to F, while r has an inverse-square relationship to F.
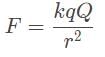
Each charge will exert a force on charge A, and their force vectors are in the diagram below:
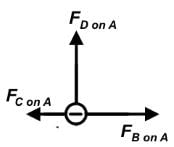
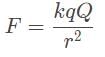
Each charge will exert a force on charge A, and their force vectors are in the diagram below:

If the force of charges B and D on charge A are each 1 unit, then the force of charge C will be 1/2 unit. The doubling of the charge on C is balanced by the doubling of the distance, but distance is squared, so the ratio becomes
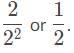
The resultant vector would be the following:

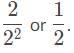
The resultant vector would be the following:

Which of the following is NOT considered a scalar quantity?- a)power
- b)density
- c)capacitance
- d)torque
Correct answer is option 'D'. Can you explain this answer?
Which of the following is NOT considered a scalar quantity?
a)
power
b)
density
c)
capacitance
d)
torque

|
Orion Classes answered |
In identifying a scalar quantity, look for a quantity that only has magnitude, but a more surefire method is to find a quantity that consists of a scalar multiplied by a scalar. These, of course, would be the wrong answers.
Power is energy divided by time, which is a scalar divided by a scalar. Hence, it is a scalar:
P = E/t
P = E/t
Density is mass divided by volume, which also is a scalar divided by a scalar. Hence, it is a scalar:
ρ = m/V
ρ = m/V
Capacitance is charge divided by voltage, which also is a scalar divided by a scalar. Hence, it is a scalar:
C = Q/V
Torque does have a direction, either counterclockwise or clockwise, and is level arm multiplied by force, which is a scalar multiplied by a vector. Hence, it is a vector, and torque is the correct answer.
τ = rF sinθ
τ = rF sinθ
Which of the following combinations for the vector 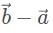 will result in the greatest magnitude? (
will result in the greatest magnitude? ( is 10 units long and
is 10 units long and 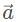 is 15 units long)
is 15 units long)- a)
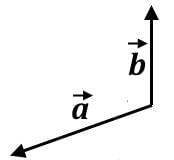
- b)
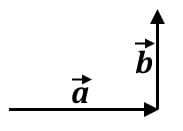
- c)
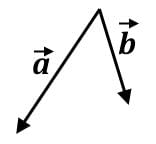
- d)
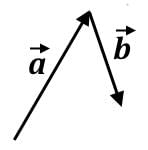
Correct answer is option 'D'. Can you explain this answer?
Which of the following combinations for the vector 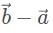 will result in the greatest magnitude? (
will result in the greatest magnitude? ( is 10 units long and
is 10 units long and  is 15 units long)
is 15 units long)
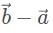 will result in the greatest magnitude? (
will result in the greatest magnitude? ( is 10 units long and
is 10 units long and 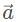 is 15 units long)
is 15 units long)a)

b)

c)

d)


|
Orion Classes answered |
In each of these combinations, vector 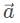 must be flipped for the subtractive process. Each one must be drawn out to decide what one has the greatest magnitude.
must be flipped for the subtractive process. Each one must be drawn out to decide what one has the greatest magnitude.
Once vector A is inverted, the tail of vector should be placed at the head of vector
should be placed at the head of vector 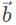 to obtain the resultant vector. The vector combination only shows the greatest displacement in the x-direction, which is 15 units:
to obtain the resultant vector. The vector combination only shows the greatest displacement in the x-direction, which is 15 units:
 must be flipped for the subtractive process. Each one must be drawn out to decide what one has the greatest magnitude.
must be flipped for the subtractive process. Each one must be drawn out to decide what one has the greatest magnitude.Once vector A is inverted, the tail of vector
 should be placed at the head of vector
should be placed at the head of vector  to obtain the resultant vector. The vector combination only shows the greatest displacement in the x-direction, which is 15 units:
to obtain the resultant vector. The vector combination only shows the greatest displacement in the x-direction, which is 15 units:
This vector combination shows the greatest displacement in the y-axis, but in either axes, there is loss of displacement, so in either direction it would not surpass 15 units from the previous hint:
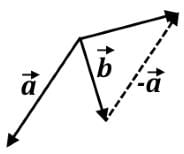

This vector combination shows comparable displacement in the x- and y-axes. In the horizontal, it will be some value less than 15 units, and in the vertical, it will be some value greater than 10 units:
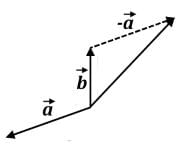

This vector combination shows the greatest displacement in y-axis. The y-component of each will definitely add to some value greater than 15 units:
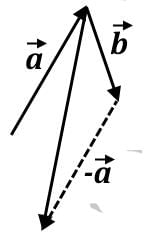
The last vector combination will show the greatest displacement in the y-axis.

The last vector combination will show the greatest displacement in the y-axis.
Chapter doubts & questions for Vectors and Scalars - Physics for MCAT 2025 is part of MCAT exam preparation. The chapters have been prepared according to the MCAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for MCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Vectors and Scalars - Physics for MCAT in English & Hindi are available as part of MCAT exam.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
Physics for MCAT
158 videos|21 docs|21 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









