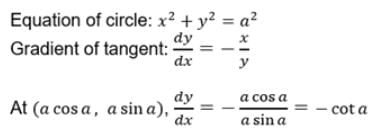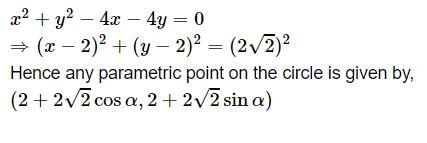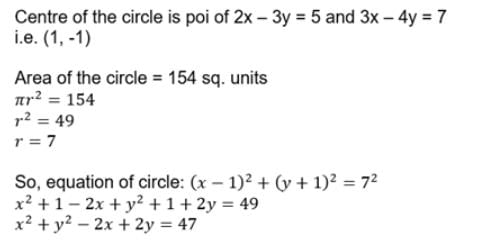All Exams >
JEE >
Chapter-wise Tests for JEE Main & Advanced >
All Questions
All questions of Circle for JEE Exam
The angle between the two tangents from the origin to the circle (x – 7)2 + (y + 1)2 = 25 equals- a)π/2
- b)π/3
- c)π/4
- d)None
Correct answer is option 'A'. Can you explain this answer?
The angle between the two tangents from the origin to the circle (x – 7)2 + (y + 1)2 = 25 equals
a)
π/2
b)
π/3
c)
π/4
d)
None
|
Krishna Iyer answered |
Let tangent from origin be y = mx
Using the condition of tangency, we get
The angle between tangents = π/2
Using the condition of tangency, we get
The angle between tangents = π/2
The equation of circle of radius 5 units touches the coordinates axes in the second quadrant is:- a)x2 + y2 + 10x – 10y + 25 = 0
- b)x2 + y2 – 10x – 10y + 25 = 0
- c)x2 + y2 + 10x + 10y + 25 = 0
- d)x2 + y2 – 10x – 10y – 25 = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of circle of radius 5 units touches the coordinates axes in the second quadrant is:
a)
x2 + y2 + 10x – 10y + 25 = 0
b)
x2 + y2 – 10x – 10y + 25 = 0
c)
x2 + y2 + 10x + 10y + 25 = 0
d)
x2 + y2 – 10x – 10y – 25 = 0
|
Suresh Reddy answered |
If the circle lies in second quadrant
The equation of a circle touches both the coordinate axes and has radius a is
x2 + y2 + 2ax - 2ay + a2 = 0
Radius of circle, a = 5
x2 + y2 + 10x - 10y + 25 = 0
The equation of a circle touches both the coordinate axes and has radius a is
x2 + y2 + 2ax - 2ay + a2 = 0
Radius of circle, a = 5
x2 + y2 + 10x - 10y + 25 = 0
The equation of circle whose centre is (2, 1) and which passes through the point (3, – 5) is:- a)
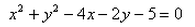
- b)
- c)
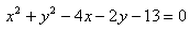
- d)
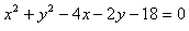
Correct answer is option 'B'. Can you explain this answer?
The equation of circle whose centre is (2, 1) and which passes through the point (3, – 5) is:
a)
b)
c)
d)
|
Poonam Reddy answered |
Radius of circle is given by -
r = √[(h-x1)² + (k-y1)²]
r = √[(2-3)² + (1+5)²]
r = √(-1² + 6²)
r = √(1 + 36)
r = √37
if centre (2,-]1) and radius=√26 are given,
(x-h)2+(y-k)2=r2
equation is (x-2)2 + (y-1)2 = (√37)2
x2 + 4 - 4x + y2 + 1 - 2y = 37
x2 + y2 - 4x - 2y - 32 = 0
r = √[(h-x1)² + (k-y1)²]
r = √[(2-3)² + (1+5)²]
r = √(-1² + 6²)
r = √(1 + 36)
r = √37
if centre (2,-]1) and radius=√26 are given,
(x-h)2+(y-k)2=r2
equation is (x-2)2 + (y-1)2 = (√37)2
x2 + 4 - 4x + y2 + 1 - 2y = 37
x2 + y2 - 4x - 2y - 32 = 0
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:- a)
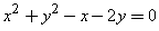
- b)
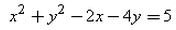
- c)
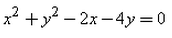
- d)
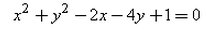
Correct answer is option 'C'. Can you explain this answer?
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:
a)
b)
c)
d)
|
Geetika Shah answered |
The circle intercept the co-ordinate axes at a and b. it means x - intercept at ( a, 0) and y-intercept at (0, b) .
Now, we observed that circle passes through points (0, 0) , (a, 0) and (0, b) .
we also know, General equation of circle is
x² + y² + 2gx + 2fy + C = 0
when point (0,0)
(0)² + (0)² + 2g(0) + 2f(0) + C = 0
0 + 0 + 0 + 0 + C = 0
C = 0 -------(1)
when point (a,0)
(a)² + (0)² + 2g(a) + 2f(0) + C = 0
a² + 2ag + C = 0
from equation (1)
a² + 2ag = 0
a(a + 2g) = 0
g = -a/2
when point ( 0, b)
(0)² + (b)² + 2g(0) + 2f(b) + C = 0
b² + 2fb + C = 0
f = -b/2
Now, equation of circle is
x² + y² + 2x(-a/2) + 2y(-b/2) + 0 = 0 { after putting values of g, f and C }
x² + y² - ax - by = 0
As we know that, a=2, b=4
x^2 + y^2 - 2x - 4y = 0
Now, we observed that circle passes through points (0, 0) , (a, 0) and (0, b) .
we also know, General equation of circle is
x² + y² + 2gx + 2fy + C = 0
when point (0,0)
(0)² + (0)² + 2g(0) + 2f(0) + C = 0
0 + 0 + 0 + 0 + C = 0
C = 0 -------(1)
when point (a,0)
(a)² + (0)² + 2g(a) + 2f(0) + C = 0
a² + 2ag + C = 0
from equation (1)
a² + 2ag = 0
a(a + 2g) = 0
g = -a/2
when point ( 0, b)
(0)² + (b)² + 2g(0) + 2f(b) + C = 0
b² + 2fb + C = 0
f = -b/2
Now, equation of circle is
x² + y² + 2x(-a/2) + 2y(-b/2) + 0 = 0 { after putting values of g, f and C }
x² + y² - ax - by = 0
As we know that, a=2, b=4
x^2 + y^2 - 2x - 4y = 0
The centre and radius of the circle x2 + y2 + 4x – 6y = 5 is:- a)(2, – 3), 2√2
- b)(– 2, 3), 3√2
- c)(– 2, 3), 2√2
- d)(2, – 3), 3√2
Correct answer is option 'B'. Can you explain this answer?
The centre and radius of the circle x2 + y2 + 4x – 6y = 5 is:
a)
(2, – 3), 2√2
b)
(– 2, 3), 3√2
c)
(– 2, 3), 2√2
d)
(2, – 3), 3√2
|
Riya Banerjee answered |
x2+y2+4x-6y=5
Circle Equation
(x-a)2+(y-b)2=r2 is the circle equation with a radius r, centered at (a,b)
Rewrite x2+y24x-6y=5 in the form of circle standard circle equation
(x-(-2))
Therefore the circle properties are:
(a,b) = (-2,3), r = 3√2
Circle Equation
(x-a)2+(y-b)2=r2 is the circle equation with a radius r, centered at (a,b)
Rewrite x2+y24x-6y=5 in the form of circle standard circle equation
(x-(-2))
2
+(y-3)2=(3
√2)2Therefore the circle properties are:
(a,b) = (-2,3), r = 3√2
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
- a)x2 + y2 + 4x + 6y + 13 = 0
- b)x2 + y2 - 4x - 6y + 13 = 0
- c)x2 + y2 - 4x - 6y + 9 = 0
- d)x2 + y2 - 4x - 6y + 4 = 0
Correct answer is option 'C'. Can you explain this answer?
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
a)
x2 + y2 + 4x + 6y + 13 = 0
b)
x2 + y2 - 4x - 6y + 13 = 0
c)
x2 + y2 - 4x - 6y + 9 = 0
d)
x2 + y2 - 4x - 6y + 4 = 0
|
Aryan Khanna answered |
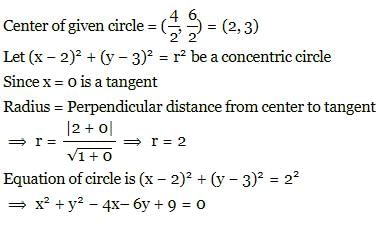
Point (-2, – 5) lies on the circle x2 + y2 = 25.- a)On the axis outside the circle
- b)Outside
- c)Inside
- d)On the circle
Correct answer is option 'B'. Can you explain this answer?
Point (-2, – 5) lies on the circle x2 + y2 = 25.
a)
On the axis outside the circle
b)
Outside
c)
Inside
d)
On the circle
|
Hansa Sharma answered |
X2 +Y2 =25 Points =(-2,-5)
Put the points in the variables
(-2)2 + (-5)2 = 29
As 29 > 25 (lies outside).
Put the points in the variables
(-2)2 + (-5)2 = 29
As 29 > 25 (lies outside).
The point diametrically opposite to the point P(1, 0) on the circle x2 + y2 + 2x + 4y – 3 = 0 is [2008]- a)(3, – 4)
- b)(–3, 4)
- c)(–3, –4)
- d)(3, 4)
Correct answer is option 'C'. Can you explain this answer?
The point diametrically opposite to the point P(1, 0) on the circle x2 + y2 + 2x + 4y – 3 = 0 is [2008]
a)
(3, – 4)
b)
(–3, 4)
c)
(–3, –4)
d)
(3, 4)
|
|
Srestha Iyer answered |
The given circle is x2 + y2 + 2x + 4y –3 = 0
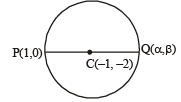
Centre (–1, –2)
Let Q (α, β) be the point diametrically opposite to the point P(1, 0),
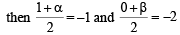
⇒ α = –3, β = – 4, So, Q is (–3, –4)
A parabola has the origin as its focus and the line x = 2 as the directrix. Then the vertex of the parabola is at [2008]- a)(0, 2)
- b)(1, 0)
- c)(0, 1)
- d)(2, 0)
Correct answer is option 'B'. Can you explain this answer?
A parabola has the origin as its focus and the line x = 2 as the directrix. Then the vertex of the parabola is at [2008]
a)
(0, 2)
b)
(1, 0)
c)
(0, 1)
d)
(2, 0)
|
|
Geetika Shah answered |
Vertex of a parabola is the mid point of focus and the point
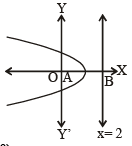
where directrix meets the axis of the parabola.
Here focus is O(0, 0) and directxix meets the axis at B(2, 0)
∴ Vertex of the parabola is (1, 0)
Here focus is O(0, 0) and directxix meets the axis at B(2, 0)
∴ Vertex of the parabola is (1, 0)
If a circle of radius 3 units is touching the lines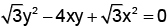
in the first quadrant then length of chord of contact to this circle is- a)
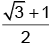
- b)
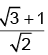
- c)
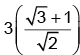
- d)
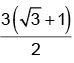
Correct answer is option 'C'. Can you explain this answer?
If a circle of radius 3 units is touching the lines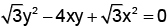 in the first quadrant then length of chord of contact to this circle is
in the first quadrant then length of chord of contact to this circle isa)
b)
c)
d)
|
Lalit Yadav answered |
Given equation of lines
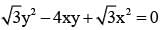
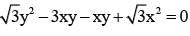
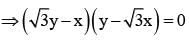
∠APO = 75°
Length of chord of contact AB
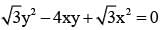
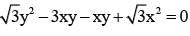
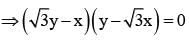
∠APO = 75°
Length of chord of contact AB
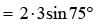
= 6(sin45°cos30° + sin30°cos45°)
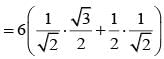
If y=c is a tangent to the circle x2+y2–2x+2y–2 =0 at (1, 1), then the value of c is- a)1
- b)2
- c)–1
- d)–2
Correct answer is option 'A'. Can you explain this answer?
If y=c is a tangent to the circle x2+y2–2x+2y–2 =0 at (1, 1), then the value of c is
a)
1
b)
2
c)
–1
d)
–2
|
|
Raghav Bansal answered |
For line y=c to be tangent to the given circle at point (1,1)
It has to pass through (1,1)
⇒ c = 1
It has to pass through (1,1)
⇒ c = 1
The equation of the circle having the lines y2 – 2y + 4x – 2xy = 0 as its normals & passing through the point (2, 1) is- a)x2 + y2 – 2x – 4y + 3 = 0
- b)x2 + y2 – 2x + 4y – 5 = 0
- c)x2 + y2 + 2x + 4y – 13 = 0
- d)None
Correct answer is option 'A'. Can you explain this answer?
The equation of the circle having the lines y2 – 2y + 4x – 2xy = 0 as its normals & passing through the point (2, 1) is
a)
x2 + y2 – 2x – 4y + 3 = 0
b)
x2 + y2 – 2x + 4y – 5 = 0
c)
x2 + y2 + 2x + 4y – 13 = 0
d)
None
|
|
Geetika Shah answered |
The normal line to circle is →y² - 2 y + 4 x -2 xy=0
→ y(y-2) - 2x(y-2)=0
→ (y-2)(y-2x)=0
the two lines are , y=2 and 2 x -y =0
The point of intersection of normals are centre of circle.
→ Put , y=2 in 2 x -y=0, we get
→2 x -2=0
→2 x=2
→ x=1
So, the point of intersection of normals is (1,2) which is the center of circle.
Also, the circle passes through (2,1).
Radius of circle is given by distance formula = [(1-2)² + (2-1)²]½
=(1+1)½ =(2)½
The equation of circle having center (1,2) and radius √2 is
= (x-1)²+(y-2)²=[√2]²
→ (x-1)²+(y-2)²= 2
x²+y² -2x-4y+3 = 0
→ y(y-2) - 2x(y-2)=0
→ (y-2)(y-2x)=0
the two lines are , y=2 and 2 x -y =0
The point of intersection of normals are centre of circle.
→ Put , y=2 in 2 x -y=0, we get
→2 x -2=0
→2 x=2
→ x=1
So, the point of intersection of normals is (1,2) which is the center of circle.
Also, the circle passes through (2,1).
Radius of circle is given by distance formula = [(1-2)² + (2-1)²]½
=(1+1)½ =(2)½
The equation of circle having center (1,2) and radius √2 is
= (x-1)²+(y-2)²=[√2]²
→ (x-1)²+(y-2)²= 2
x²+y² -2x-4y+3 = 0
is
The equations of the tangents drawn from the point (0, 1) to the circle x2 + y2 - 2x + 4y = 0 are- a)2x - y + 1 = 0, x + 2y - 2 = 0
- b)2x - y - 1 = 0, x + 2y - 2 = 0
- c)2x - y + 1 = 0, x + 2y + 2 = 0
- d)2x - y - 1 = 0, x + 2y + 2 = 0
Correct answer is option 'A'. Can you explain this answer?
The equations of the tangents drawn from the point (0, 1) to the circle x2 + y2 - 2x + 4y = 0 are
a)
2x - y + 1 = 0, x + 2y - 2 = 0
b)
2x - y - 1 = 0, x + 2y - 2 = 0
c)
2x - y + 1 = 0, x + 2y + 2 = 0
d)
2x - y - 1 = 0, x + 2y + 2 = 0
|
|
Geetika Shah answered |
Let equation of tangent with slope =m and point (0,1)
(y−1)=m(x−0)⇒y=mx+1
Intersection point
x2+(mx+1)2−2x+4(mx+1)=0
(1+m2)x2+(−2+6m)x+5=0
For y=mx+1 to be tangent, discriminant =0
(6m−2)2−4×5(1+m2)=0
36m2+4−24m−20m2+20=0
16m2−20m+24=0
⇒ 2m2−3m−2=0
(2m+1)(m−2)=0
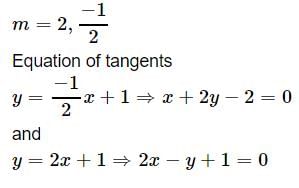
(y−1)=m(x−0)⇒y=mx+1
Intersection point
x2+(mx+1)2−2x+4(mx+1)=0
(1+m2)x2+(−2+6m)x+5=0
For y=mx+1 to be tangent, discriminant =0
(6m−2)2−4×5(1+m2)=0
36m2+4−24m−20m2+20=0
16m2−20m+24=0
⇒ 2m2−3m−2=0
(2m+1)(m−2)=0
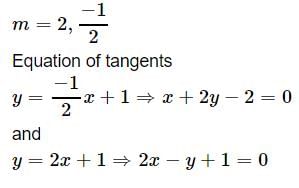
The locus of the mid-points of the chords of the circle x2 + y2 – 2x – 4y – 11 = 0 which subtend 60º at the centre is- a)x2 + y2 – 4x – 2y – 7 = 0
- b)x2 + y2 + 4x + 2y – 7 = 0
- c)x2 + y2 – 2x – 4y – 7 = 0
- d)x2 + y2 + 2x + 4y + 7 = 0
Correct answer is option 'C'. Can you explain this answer?
The locus of the mid-points of the chords of the circle x2 + y2 – 2x – 4y – 11 = 0 which subtend 60º at the centre is
a)
x2 + y2 – 4x – 2y – 7 = 0
b)
x2 + y2 + 4x + 2y – 7 = 0
c)
x2 + y2 – 2x – 4y – 7 = 0
d)
x2 + y2 + 2x + 4y + 7 = 0
|
|
Preeti Iyer answered |
Let AB be the chord of the circle and P be the midpoint of AB.
It is known that perpendicular from the center bisects a chord.
Thus △ACP is a right-angled triangle.
Now AC=BC= radius.
The equation of the give circle can be written as
(x−1)2+(y−2)2=16
Hence, centre C=(1,2) and radius =r=4 units.
PC=ACsin60degree
= rsin60degree
= 4([2(3)½]/2
= 2(3)1/2 units
Therefore, PC=2(3)1/2
⇒ PC2=12
⇒ (x−1)2+(y−2)2=12
⇒ x2+y2−2x−4y+5=12
⇒ x2+y2−2x−4y−7=0
It is known that perpendicular from the center bisects a chord.
Thus △ACP is a right-angled triangle.
Now AC=BC= radius.
The equation of the give circle can be written as
(x−1)2+(y−2)2=16
Hence, centre C=(1,2) and radius =r=4 units.
PC=ACsin60degree
= rsin60degree
= 4([2(3)½]/2
= 2(3)1/2 units
Therefore, PC=2(3)1/2
⇒ PC2=12
⇒ (x−1)2+(y−2)2=12
⇒ x2+y2−2x−4y+5=12
⇒ x2+y2−2x−4y−7=0
The number of common tangents of the circles x2 + y2 – 2x – 1 = 0 and x2 + y2 – 2y – 7 = 0- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
The number of common tangents of the circles x2 + y2 – 2x – 1 = 0 and x2 + y2 – 2y – 7 = 0
a)
1
b)
2
c)
3
d)
4
|
Neha Joshi answered |
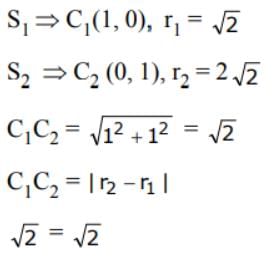
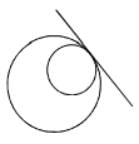
Internally touch ∴ common tangent is one.
y = √3x + c1 & y = √3x + c2 are two parallel tangents of a circle of radius 2 units, then |c1 – c2| is equal to
- a)8
- b)4
- c)2
- d)1
Correct answer is option 'A'. Can you explain this answer?
y = √3x + c1 & y = √3x + c2 are two parallel tangents of a circle of radius 2 units, then |c1 – c2| is equal to
a)
8
b)
4
c)
2
d)
1
|
|
Anmol Chauhan answered |
For both lines to be parallel tangent the distance between both lines
should be equal to the diameter of the circle
⇒ 4 = |c1−c2|/(1+3)1/2
⇒∣c1−c2∣ = 8
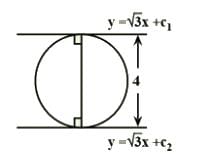
should be equal to the diameter of the circle
⇒ 4 = |c1−c2|/(1+3)1/2
⇒∣c1−c2∣ = 8
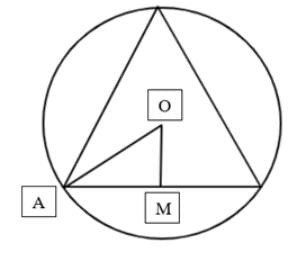
The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have coordinates (3, 4) and (–4, 3) respectively, then ∠QPR may be equal to- a)π/2
- b)π/3
- c)π/4
- d)π/6
Correct answer is option 'C'. Can you explain this answer?
The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have coordinates (3, 4) and (–4, 3) respectively, then ∠QPR may be equal to
a)
π/2
b)
π/3
c)
π/4
d)
π/6
|
|
Rohit Jain answered |
(i.e. angle subtended at the centre of a circle is double the angle subtended in the alternate segment).Hence (c) is the correct answer.
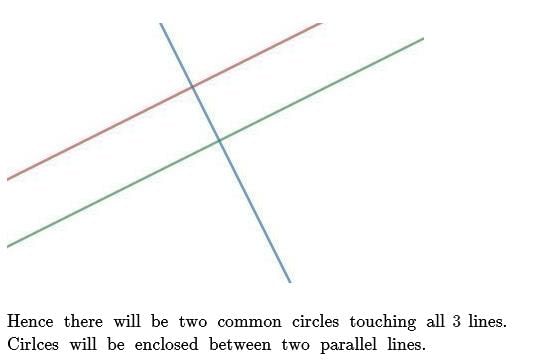
Number of different circles that can be drawn touching 3 lines, no two of which are parallel and they are neither coincident nor concurrent, are- a)1
- b)2
- c)3
- d)4
Correct answer is option 'D'. Can you explain this answer?
Number of different circles that can be drawn touching 3 lines, no two of which are parallel and they are neither coincident nor concurrent, are
a)
1
b)
2
c)
3
d)
4
|
|
Raghav Bansal answered |
If three lines are given such that no two of them are parallel and they are not concurrent then a definite triangle is formed by them. There are four circles which touch sides of a triangle (3-excircles and 1-incircle).
If a circle of constant radius 3k passes through the origin `O' and meets co-ordinate axes at A and B then the locus of the centroid of the triangle OAB is- a)x2 + y2 = (2k)2
- b)x2 + y2 = (3k)2
- c)x2 + y2 = (4k)2
- d)x2 + y2 = (6k)2
Correct answer is option 'A'. Can you explain this answer?
If a circle of constant radius 3k passes through the origin `O' and meets co-ordinate axes at A and B then the locus of the centroid of the triangle OAB is
a)
x2 + y2 = (2k)2
b)
x2 + y2 = (3k)2
c)
x2 + y2 = (4k)2
d)
x2 + y2 = (6k)2
|
|
Geetika Shah answered |
let centroid of circle is (l,m)
then point A and B will be as shown in figure
and center of circle will be (3l/2 ,3m/2)
so (3k)2 =(3l/2)2 +(3m/2)2
(2k)2 =(l)2 +(m)2
so locus
x2 +y2 = (4k)2
x2 + y2 = (2k)2
then point A and B will be as shown in figure
and center of circle will be (3l/2 ,3m/2)
so (3k)2 =(3l/2)2 +(3m/2)2
(2k)2 =(l)2 +(m)2
so locus
x2 +y2 = (4k)2
x2 + y2 = (2k)2
The ellipse x2 + 4y2 = 4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is : [2009]- a)x2 + 12y2= 16
- b)4 x2 + 48y2= 48
- c)4 x2 + 64y2 = 48
- d)x2 + 16y2= 16
Correct answer is option 'A'. Can you explain this answer?
The ellipse x2 + 4y2 = 4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is : [2009]
a)
x2 + 12y2= 16
b)
4 x2 + 48y2= 48
c)
4 x2 + 64y2 = 48
d)
x2 + 16y2= 16
|
Anushka Ahuja answered |
Solution:
Given that the ellipse x^2/4 + y^2 = 1 is inscribed in a rectangle aligned with the coordinate axes and this rectangle is inscribed in another ellipse that passes through the point (4, 0).
Let's find the equation of the outer ellipse.
Step 1: Find the coordinates of the four corners of the rectangle.
The corners of the rectangle can be obtained by solving the equation of the ellipse with x = ±2 and y = ±1.
For x = 2, we have 4/4 + y^2 = 1, which gives y = ±√3.
So, the coordinates are (2, √3) and (2, -√3).
Similarly, for x = -2, we have 4/4 + y^2 = 1, which gives y = ±√3.
So, the coordinates are (-2, √3) and (-2, -√3).
Step 2: Find the equation of the ellipse passing through the points (2, √3), (2, -√3), (-2, √3), and (-2, -√3).
Using the standard form of an ellipse, the equation is:
(x - h)^2/a^2 + (y - k)^2/b^2 = 1, where (h, k) is the center of the ellipse, and a and b are the semi-major and semi-minor axes, respectively.
Step 3: Find the center of the ellipse.
The center of the ellipse is the midpoint of the diagonals of the rectangle.
The midpoint of the diagonals is ((2 + (-2))/2, (√3 + (-√3))/2) = (0, 0).
Step 4: Find the semi-major and semi-minor axes.
The semi-major axis is the distance from the center to one of the corners of the rectangle, which is 2.
The semi-minor axis is the distance from the center to one of the sides of the rectangle, which is 1.
Therefore, the equation of the outer ellipse is:
(x - 0)^2/2^2 + (y - 0)^2/1^2 = 1
Simplifying, we get x^2/4 + y^2 = 1.
Hence, the correct answer is option A) x^2 - 12y^2 = 16.
Given that the ellipse x^2/4 + y^2 = 1 is inscribed in a rectangle aligned with the coordinate axes and this rectangle is inscribed in another ellipse that passes through the point (4, 0).
Let's find the equation of the outer ellipse.
Step 1: Find the coordinates of the four corners of the rectangle.
The corners of the rectangle can be obtained by solving the equation of the ellipse with x = ±2 and y = ±1.
For x = 2, we have 4/4 + y^2 = 1, which gives y = ±√3.
So, the coordinates are (2, √3) and (2, -√3).
Similarly, for x = -2, we have 4/4 + y^2 = 1, which gives y = ±√3.
So, the coordinates are (-2, √3) and (-2, -√3).
Step 2: Find the equation of the ellipse passing through the points (2, √3), (2, -√3), (-2, √3), and (-2, -√3).
Using the standard form of an ellipse, the equation is:
(x - h)^2/a^2 + (y - k)^2/b^2 = 1, where (h, k) is the center of the ellipse, and a and b are the semi-major and semi-minor axes, respectively.
Step 3: Find the center of the ellipse.
The center of the ellipse is the midpoint of the diagonals of the rectangle.
The midpoint of the diagonals is ((2 + (-2))/2, (√3 + (-√3))/2) = (0, 0).
Step 4: Find the semi-major and semi-minor axes.
The semi-major axis is the distance from the center to one of the corners of the rectangle, which is 2.
The semi-minor axis is the distance from the center to one of the sides of the rectangle, which is 1.
Therefore, the equation of the outer ellipse is:
(x - 0)^2/2^2 + (y - 0)^2/1^2 = 1
Simplifying, we get x^2/4 + y^2 = 1.
Hence, the correct answer is option A) x^2 - 12y^2 = 16.
Pair of tangents are drawn from every point on the line 3x + 4y = 12 on the circle x2+ y2 = 4. Their variable chord of contact always passes through a fixed point whose co-ordinates are- a)
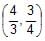
- b)
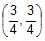
- c)(1, 1)
- d)
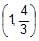
Correct answer is option 'D'. Can you explain this answer?
Pair of tangents are drawn from every point on the line 3x + 4y = 12 on the circle x2+ y2 = 4. Their variable chord of contact always passes through a fixed point whose co-ordinates are
a)
b)
c)
(1, 1)
d)
|
|
Geetika Shah answered |
Let P(x1,y1) be a point on the line 3x + 4y = 12
Equation of variable chord of contact of P(x1,y1) w.r.t circle x2 + y2 = 4
xx1 + yy1 − 4 = 0 ...(1)
Also 3x1 + 4y1 − 12 = 0
⇒ x1 + 4/3y1 − 4 = 0 ...(2)
Comparing (1) and (2), we get
x = 1; y = 4/3
∴ Variable chord of contact always passes through (1, 4/3)
Equation of variable chord of contact of P(x1,y1) w.r.t circle x2 + y2 = 4
xx1 + yy1 − 4 = 0 ...(1)
Also 3x1 + 4y1 − 12 = 0
⇒ x1 + 4/3y1 − 4 = 0 ...(2)
Comparing (1) and (2), we get
x = 1; y = 4/3
∴ Variable chord of contact always passes through (1, 4/3)
The equation of the chord of x2 + y2 - 4x + 6y + 3 = 0 whose mid point is (1, -2) is
- a)x + y + 1 = 0
- b)2x + 3y + 4 = 0
- c)x - y - 3 = 0
- d)Not existing
Correct answer is option 'C'. Can you explain this answer?
The equation of the chord of x2 + y2 - 4x + 6y + 3 = 0 whose mid point is (1, -2) is
a)
x + y + 1 = 0
b)
2x + 3y + 4 = 0
c)
x - y - 3 = 0
d)
Not existing
|
Shounak Datta answered |
Solution:
Given equation is x^2 + y^2 - 4x - 6y + 3 = 0
We need to find the equation of the chord whose midpoint is (1,-2).
Midpoint of the chord = (1,-2)
Let the co-ordinates of the end points of the chord be (x1, y1) and (x2, y2)
Therefore, the midpoint of the chord is ((x1+x2)/2, (y1+y2)/2)
Given that midpoint of the chord is (1,-2)
=> (x1+x2)/2 = 1 and (y1+y2)/2 = -2
=> x1+x2 = 2 and y1+y2 = -4
Let the equation of the chord be y = mx + c
By substituting y = mx + c in the given equation, we get
x^2 + (mx + c)^2 - 4x - 6(mx + c) + 3 = 0
=> (m^2 + 1)x^2 + (2mc - 4m - 6)x + c^2 - 6c + 3 = 0
Since the given line is a chord of the circle, it should intersect the circle at two points.
Therefore, the discriminant of the above quadratic equation should be greater than or equal to 0.
=> (2mc - 4m - 6)^2 - 4(m^2 + 1)(c^2 - 6c + 3) >= 0
Simplifying the above inequality, we get
=> (m^2 + 1)c^2 - 2m(3 + 2x) c + (x^2 - 4x + 3m^2 - 6m + 3) >= 0
Since the given line passes through (1,-2), we can substitute x=1 and y=-2 in the equation of the line.
=> -2 = m + c
=> c = -2 - m
Substituting this value of c in the above inequality, we get
=> (m^2 + 1)(m^2 - 4m + 6) >= 0
The above inequality is satisfied for all values of m.
Therefore, the equation of the chord is of the form x - y - 3 = 0.
Hence, option (C) is the correct answer.
Given equation is x^2 + y^2 - 4x - 6y + 3 = 0
We need to find the equation of the chord whose midpoint is (1,-2).
Midpoint of the chord = (1,-2)
Let the co-ordinates of the end points of the chord be (x1, y1) and (x2, y2)
Therefore, the midpoint of the chord is ((x1+x2)/2, (y1+y2)/2)
Given that midpoint of the chord is (1,-2)
=> (x1+x2)/2 = 1 and (y1+y2)/2 = -2
=> x1+x2 = 2 and y1+y2 = -4
Let the equation of the chord be y = mx + c
By substituting y = mx + c in the given equation, we get
x^2 + (mx + c)^2 - 4x - 6(mx + c) + 3 = 0
=> (m^2 + 1)x^2 + (2mc - 4m - 6)x + c^2 - 6c + 3 = 0
Since the given line is a chord of the circle, it should intersect the circle at two points.
Therefore, the discriminant of the above quadratic equation should be greater than or equal to 0.
=> (2mc - 4m - 6)^2 - 4(m^2 + 1)(c^2 - 6c + 3) >= 0
Simplifying the above inequality, we get
=> (m^2 + 1)c^2 - 2m(3 + 2x) c + (x^2 - 4x + 3m^2 - 6m + 3) >= 0
Since the given line passes through (1,-2), we can substitute x=1 and y=-2 in the equation of the line.
=> -2 = m + c
=> c = -2 - m
Substituting this value of c in the above inequality, we get
=> (m^2 + 1)(m^2 - 4m + 6) >= 0
The above inequality is satisfied for all values of m.
Therefore, the equation of the chord is of the form x - y - 3 = 0.
Hence, option (C) is the correct answer.
A circle is drawn touching the x-axis and centre at the point which is the reflection of (a, b) in the line y – x = 0. The equation of the circle is- a)x2 + y2 – 2bx – 2ay + a2 = 0
- b)x2 + y2 – 2bx – 2ay + b2 = 0
- c)x2 + y2 – 2ax – 2by + b2 = 0
- d)x2 + y2 – 2ax – 2by + a2 = 0
Correct answer is option 'B'. Can you explain this answer?
A circle is drawn touching the x-axis and centre at the point which is the reflection of (a, b) in the line y – x = 0. The equation of the circle is
a)
x2 + y2 – 2bx – 2ay + a2 = 0
b)
x2 + y2 – 2bx – 2ay + b2 = 0
c)
x2 + y2 – 2ax – 2by + b2 = 0
d)
x2 + y2 – 2ax – 2by + a2 = 0
|
|
Geetika Shah answered |
Radius of the circle = a
and centre ≡ (b,a)
And circle is touching the x-axis.
The equation of the circle :
x2+y2−2bx−2ay+b2 = 0
and centre ≡ (b,a)
And circle is touching the x-axis.
The equation of the circle :
x2+y2−2bx−2ay+b2 = 0
Equation of circles touching x-axis at the origin and the line 4x – 3y + 24 = 0 are- a)x2 + y2 -6y = 0,x2 + y2 + 24y = 0
- b)x2 + y2 + 2y = 0,x2 + y2 -18y = 0
- c)x2 + y2 +18x = 0, x2 + y2 - 8x = 0
- d)x2 + y2 + 4x = 0, x2 + y2 -16x = 0
Correct answer is option 'A'. Can you explain this answer?
Equation of circles touching x-axis at the origin and the line 4x – 3y + 24 = 0 are
a)
x2 + y2 -6y = 0,x2 + y2 + 24y = 0
b)
x2 + y2 + 2y = 0,x2 + y2 -18y = 0
c)
x2 + y2 +18x = 0, x2 + y2 - 8x = 0
d)
x2 + y2 + 4x = 0, x2 + y2 -16x = 0
|
|
Anjali Sharma answered |
Number of points (x, y) having integral coordinates satisfying the condition x2 + y2 < 25 is- a)69
- b)80
- c)81
- d)77
Correct answer is option 'A'. Can you explain this answer?
Number of points (x, y) having integral coordinates satisfying the condition x2 + y2 < 25 is
a)
69
b)
80
c)
81
d)
77
|
|
Hansa Sharma answered |
Since x2+y2<25 and a and y are integers, the possible values of x and y∈(0,±1,±2,±3,±4,).
Thus,x and y can be chosen in 9 ways each and (x,y) can be chosen in 9×9=81 ways.
However, we have to exclude cases (±3,±4),(±4,±3)
and (±4,±4)i.e.,3×4=12
Hence, the number of permissible values = 81−12=69
Thus,x and y can be chosen in 9 ways each and (x,y) can be chosen in 9×9=81 ways.
However, we have to exclude cases (±3,±4),(±4,±3)
and (±4,±4)i.e.,3×4=12
Hence, the number of permissible values = 81−12=69
If P(2, 8) is an interior point of a circle x2 + y2 –2x + 4y – p = 0 which neither touches nor intersects the axes, then set for p is- a)p < -1
- b)p < -4
- c)p > 96
- d)φ
Correct answer is option 'D'. Can you explain this answer?
If P(2, 8) is an interior point of a circle x2 + y2 –2x + 4y – p = 0 which neither touches nor intersects the axes, then set for p is
a)
p < -1
b)
p < -4
c)
p > 96
d)
φ
|
|
Lavanya Menon answered |
For internal point p(2, 8), 4 + 64 – 4 + 32 – p < 0 ⇒ p > 96
and x intercept =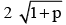
therefore 1 + p < 0
⇒ p < -1 and y intercept =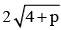
⇒ p < -4
Hence (D) is the correct answer.
and x intercept =
therefore 1 + p < 0⇒ p < -1 and y intercept =
⇒ p < -4Hence (D) is the correct answer.
If P an d Q are the points of intersection of the circles x2 + y2 + 3x + 7y+ 2p- 5 =0 and x2 + y2 + 2x + 2y – p2 = 0 then there is a circle passing through P, Q and (1, 1) for: [2009]- a)all except one value of p
- b)all except two values of p
- c)exactly one value of p
- d)all values of p
Correct answer is option 'A'. Can you explain this answer?
If P an d Q are the points of intersection of the circles x2 + y2 + 3x + 7y+ 2p- 5 =0 and x2 + y2 + 2x + 2y – p2 = 0 then there is a circle passing through P, Q and (1, 1) for: [2009]
a)
all except one value of p
b)
all except two values of p
c)
exactly one value of p
d)
all values of p
|
|
Asif Ali answered |
A circle touches a straight line lx + my + n = 0 and cuts the circle x2 + y2 = 9 orthogonally, The locus of centres of such circles is- a)(lx + my + n)2 = (l2 + m2) (x2 + y2 – 9)
- b)(lx + my – n)2 = (l2 + m2) (x2 + y2– 9)
- c)(lx + my + n)2 = (l2 + m2) (x2+ y2 + 9)
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A circle touches a straight line lx + my + n = 0 and cuts the circle x2 + y2 = 9 orthogonally, The locus of centres of such circles is
a)
(lx + my + n)2 = (l2 + m2) (x2 + y2 – 9)
b)
(lx + my – n)2 = (l2 + m2) (x2 + y2– 9)
c)
(lx + my + n)2 = (l2 + m2) (x2+ y2 + 9)
d)
None of these
|
|
Neha Joshi answered |
Let the equation of the circle is-
x2+y2+2gx+2fy+c = 0
Given, this circle is orthogonal to x2 +y2 −9=0
Condition of orthogonality
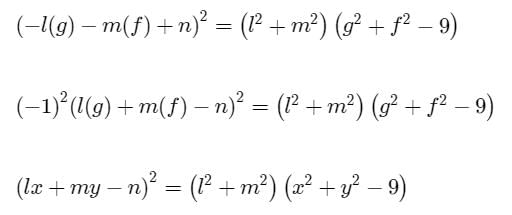
x2+y2+2gx+2fy+c = 0
Given, this circle is orthogonal to x2 +y2 −9=0
Condition of orthogonality
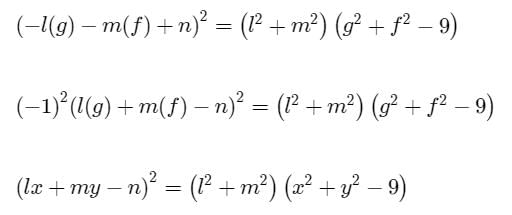
If a be the radius of a circle which touches x-axis at the origin, then its equation is- a)x2 + y2 + ax = 0
- b)x2 + y2 ± 2ya = 0
- c)x2 + y2 ± 2xa = 0
- d)x2 + y2 + ya = 0
Correct answer is option 'B'. Can you explain this answer?
If a be the radius of a circle which touches x-axis at the origin, then its equation is
a)
x2 + y2 + ax = 0
b)
x2 + y2 ± 2ya = 0
c)
x2 + y2 ± 2xa = 0
d)
x2 + y2 + ya = 0
|
|
Sushant Ghosh answered |
The equation of the circle with centre at (h,k) and radius equal to a is (x−h)2 +(y−k)2 = a2
When the circle passes through the origin and centre lies on x− axis
⇒h = a and k = 0
Then the equation (x−h)2+(y−k)2=a2 becomes (x−a)2+y2=a2
If a circle passes through the origin and centre lies on x−axis then the abscissa will be equal to the radius of the circle and the y−co-ordinate of the centre will be zero Hence, the equation of the circle will be of the form
(x±a)2+y2=a2⇒x2+a2 ±2ax+y2=a2
=x2 +y2 ±2ax=0 is the required equation of the circle.
When the circle passes through the origin and centre lies on x− axis
⇒h = a and k = 0
Then the equation (x−h)2+(y−k)2=a2 becomes (x−a)2+y2=a2
If a circle passes through the origin and centre lies on x−axis then the abscissa will be equal to the radius of the circle and the y−co-ordinate of the centre will be zero Hence, the equation of the circle will be of the form
(x±a)2+y2=a2⇒x2+a2 ±2ax+y2=a2
=x2 +y2 ±2ax=0 is the required equation of the circle.
The locus of the centre of a circle which touches externally the circle, x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis is given by the equation- a)x2 – 6x – 10y + 14 = 0
- b)x2 – 10x – 6y + 14 = 0
- c)y2 – 6x – 10y + 14 = 0
- d)y2 – 10x – 6y+14 = 0
Correct answer is option 'D'. Can you explain this answer?
The locus of the centre of a circle which touches externally the circle, x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis is given by the equation
a)
x2 – 6x – 10y + 14 = 0
b)
x2 – 10x – 6y + 14 = 0
c)
y2 – 6x – 10y + 14 = 0
d)
y2 – 10x – 6y+14 = 0
|
|
Hansa Sharma answered |
let the center of the circle be (h,k) and since it touches the y-axis
Therefore, its radius will be h it touches the circle x2+y2−6x−6y+14=0 externally
Therefore, C1C2 = r1 + r2
⇒ [(h-3)2 + (k-3)2]½ = h+2
⇒ k2−10h−6k+14=0
⇒ y2−10x−6y+14=0
Therefore, its radius will be h it touches the circle x2+y2−6x−6y+14=0 externally
Therefore, C1C2 = r1 + r2
⇒ [(h-3)2 + (k-3)2]½ = h+2
⇒ k2−10h−6k+14=0
⇒ y2−10x−6y+14=0
What is the length of shortest path by which one can go from (–2, 0) to (2, 0) without entering the interior of circle, x2 + y2 = 1- a)2√3
- b)√3 + 2π/3
- c) 2√3 + π/3
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the length of shortest path by which one can go from (–2, 0) to (2, 0) without entering the interior of circle, x2 + y2 = 1
a)
2√3
b)
√3 + 2π/3
c)
2√3 + π/3
d)
None of these
|
|
Neha Joshi answered |
Center of circle = C(0,0), radius, r=1.
Tangents from Point A(−2,0) and B(2,0) meets circle at points P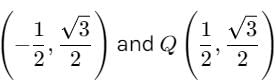
respectively.
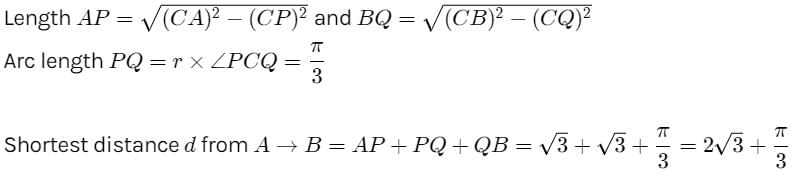
Tangents from Point A(−2,0) and B(2,0) meets circle at points P
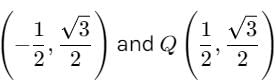
respectively.
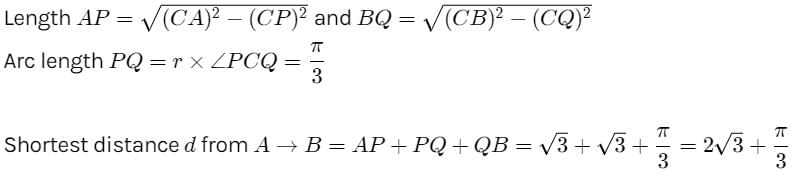
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =- a)6
- b)9
- c)3
- d)12
Correct answer is option 'B'. Can you explain this answer?
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =
a)
6
b)
9
c)
3
d)
12
|
|
Rajesh Gupta answered |
x2 + y2 + 6x − 6y + 5 = 0
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
The locus of the vertices of the family of parabol as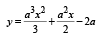 
[2006]- a)
- b)
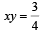
- c)
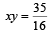
- d)
Correct answer is option 'A'. Can you explain this answer?
The locus of the vertices of the family of parabol as 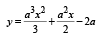[2006]
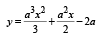[2006]a)
b)
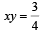
c)
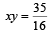
d)
|
|
Rohit Jain answered |
Given parabola is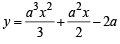 
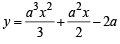
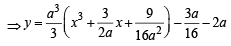
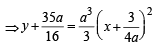
∴ Vertex of parabola is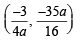 
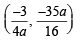
To find locus of this vertex,
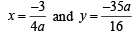
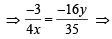64xy = 105
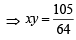which is the required locus.Find the equation of the circle passing through (–2, 14) and concentric with the circle x2 + y2 - 6x - 4y -12 = 0 .- a)x2 + y2 - 6x - 4y -156 = 0
- b)x2 + y2 - 6x + 4y -156 = 0
- c)x2 + y2 - 6x + 4y + 156 = 0
- d)x2 + y2 + 6x + 4y + 156 = 0
Correct answer is option 'A'. Can you explain this answer?
Find the equation of the circle passing through (–2, 14) and concentric with the circle x2 + y2 - 6x - 4y -12 = 0 .
a)
x2 + y2 - 6x - 4y -156 = 0
b)
x2 + y2 - 6x + 4y -156 = 0
c)
x2 + y2 - 6x + 4y + 156 = 0
d)
x2 + y2 + 6x + 4y + 156 = 0
|
|
Abhay Mehta answered |
To find the equation of the circle passing through the point (2, 14) and concentric with the given circle, we need to determine the center and the radius of the circle.
Here are the steps to find the equation of the circle:
1. Find the center of the given circle:
To find the center of the given circle, we need to rewrite the equation of the circle in the standard form, which is (x - h)^2 + (y - k)^2 = r^2, where (h, k) represents the center of the circle.
Given equation: x^2 + y^2 - 6x - 4y - 12 = 0
Rearrange the equation: x^2 - 6x + y^2 - 4y = 12
Complete the square for x terms:
(x^2 - 6x + 9) + y^2 - 4y = 12 + 9
Complete the square for y terms:
(x^2 - 6x + 9) + (y^2 - 4y + 4) = 12 + 9 + 4
Simplify:
(x - 3)^2 + (y - 2)^2 = 25
The center of the given circle is (3, 2).
2. Find the radius of the given circle:
The radius of the given circle is the square root of the constant term in the standard form equation. In this case, the radius is √25 = 5.
3. Find the equation of the circle concentric with the given circle and passing through the point (2, 14):
Since the new circle is concentric with the given circle, the center will be the same at (3, 2). The radius of the new circle will also be 5.
Using the standard form of the circle, the equation of the new circle is:
(x - 3)^2 + (y - 2)^2 = 5^2
Simplifying:
(x - 3)^2 + (y - 2)^2 = 25
Therefore, the equation of the circle passing through (2, 14) and concentric with the given circle is:
x^2 + y^2 - 6x - 4y - 156 = 0
Hence, the correct answer is option 'A'.
Here are the steps to find the equation of the circle:
1. Find the center of the given circle:
To find the center of the given circle, we need to rewrite the equation of the circle in the standard form, which is (x - h)^2 + (y - k)^2 = r^2, where (h, k) represents the center of the circle.
Given equation: x^2 + y^2 - 6x - 4y - 12 = 0
Rearrange the equation: x^2 - 6x + y^2 - 4y = 12
Complete the square for x terms:
(x^2 - 6x + 9) + y^2 - 4y = 12 + 9
Complete the square for y terms:
(x^2 - 6x + 9) + (y^2 - 4y + 4) = 12 + 9 + 4
Simplify:
(x - 3)^2 + (y - 2)^2 = 25
The center of the given circle is (3, 2).
2. Find the radius of the given circle:
The radius of the given circle is the square root of the constant term in the standard form equation. In this case, the radius is √25 = 5.
3. Find the equation of the circle concentric with the given circle and passing through the point (2, 14):
Since the new circle is concentric with the given circle, the center will be the same at (3, 2). The radius of the new circle will also be 5.
Using the standard form of the circle, the equation of the new circle is:
(x - 3)^2 + (y - 2)^2 = 5^2
Simplifying:
(x - 3)^2 + (y - 2)^2 = 25
Therefore, the equation of the circle passing through (2, 14) and concentric with the given circle is:
x^2 + y^2 - 6x - 4y - 156 = 0
Hence, the correct answer is option 'A'.
The equation of a circle which passes through the three points (3, 0) (1, –6), (4, –1) is- a)2x2 + 2y2 + 5x – 11y + 3 = 0
- b)x2 + y2 – 5x + 11y – 3 = 0
- c)x2 + y2 + 5x – 11y + 3 = 0
- d)2x2 + 2y2 – 5x + 11y – 3 = 0
Correct answer is option 'D'. Can you explain this answer?
The equation of a circle which passes through the three points (3, 0) (1, –6), (4, –1) is
a)
2x2 + 2y2 + 5x – 11y + 3 = 0
b)
x2 + y2 – 5x + 11y – 3 = 0
c)
x2 + y2 + 5x – 11y + 3 = 0
d)
2x2 + 2y2 – 5x + 11y – 3 = 0
|
|
Pooja Shah answered |
Gen equation of a circle is (x−h)2+(y−k)2=r2 (3,0),(1,−6),(4,−1) circle passes through these points
∴ These three points should satisfy the equation
of circle.
(3−h)2+k2=r2 ___ (I)
(1−h)2 +(−6−k)2 = r2(1−h)2+(6+k)2=r2 ___ (II)
From (I) & (II)
(3−h)2+k2 =(1−h)2+(6+k)2
9+h2−6h+k2 =1+h2 2h+36+k2+12k
9−6h=1−2h+36+12k
9−37=4h+12k
−28=4h+12k
h+3k=−7
h=−7−3k ___ (III)
(4−h)2+(−1−k)2=r2 ___ (IV)
From (I) & (IV)
(3−h)2+k2 = (4−h)2 +(1+k)2
9+h2 −6h+k2
=16+h2 −8h+1+k2+2k
9−6h=17−8h+2k
9−17=−2h+2k
−8=−2h+2k
−h+k=−4
k=−4+h ___ (V)
Put (V) in (III)
h=−7−3(−4+h)
h=−7+12−3h
h=5/4,k=−11/4,r=170/16
Eq of circle: (x−5/4)2 +(y+11/4)2 =170/16
x2+25/16−10x/4+y2 +121/16+22y/4=170/16
Simplifying, we get 2x2+xy2−5x+11y−3=0
∴ These three points should satisfy the equation
of circle.
(3−h)2+k2=r2 ___ (I)
(1−h)2 +(−6−k)2 = r2(1−h)2+(6+k)2=r2 ___ (II)
From (I) & (II)
(3−h)2+k2 =(1−h)2+(6+k)2
9+h2−6h+k2 =1+h2 2h+36+k2+12k
9−6h=1−2h+36+12k
9−37=4h+12k
−28=4h+12k
h+3k=−7
h=−7−3k ___ (III)
(4−h)2+(−1−k)2=r2 ___ (IV)
From (I) & (IV)
(3−h)2+k2 = (4−h)2 +(1+k)2
9+h2 −6h+k2
=16+h2 −8h+1+k2+2k
9−6h=17−8h+2k
9−17=−2h+2k
−8=−2h+2k
−h+k=−4
k=−4+h ___ (V)
Put (V) in (III)
h=−7−3(−4+h)
h=−7+12−3h
h=5/4,k=−11/4,r=170/16
Eq of circle: (x−5/4)2 +(y+11/4)2 =170/16
x2+25/16−10x/4+y2 +121/16+22y/4=170/16
Simplifying, we get 2x2+xy2−5x+11y−3=0
The lines 2 x - 3y=5 and 3x - 4 y = 7 are diameters of a circle having area as 154 sq.units.Then the equation of the circle is[2003]- a) x2 + y2 - 2x + 2y = 62
- b) x2 + y2 + 2x - 2y = 62
- c) x2 + y2 +2x-2y = 47
- d) x2 + y2 -2x+2y = 47
Correct answer is option 'D'. Can you explain this answer?
The lines 2 x - 3y=5 and 3x - 4 y = 7 are diameters of a circle having area as 154 sq.units.Then the equation of the circle is[2003]
a)
x2 + y2 - 2x + 2y = 62
b)
x2 + y2 + 2x - 2y = 62
c)
x2 + y2 +2x-2y = 47
d)
x2 + y2 -2x+2y = 47
|
|
Nerella Dange Naveen answered |
Chapter doubts & questions for Circle - Chapter-wise Tests for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circle - Chapter-wise Tests for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Chapter-wise Tests for JEE Main & Advanced
446 docs|929 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup