All Exams >
JEE >
Mock Tests for JEE Main and Advanced 2026 >
All Questions
All questions of JEE Main & Advanced Mock Test Series 2026 for JEE Exam
Consider the following cell reaction:2Fe(s) + O2(g) + 4H+(aq) 2Fe2+(aq) + 2H2O(l); E° = 1.67 VAt [Fe2+] = 10-3 M, P(O2) = 0.1 atom and pH = 3, the cell potential (in V) at 25°C is
Correct answer is '1.57'. Can you explain this answer?
Consider the following cell reaction:
2Fe(s) + O2(g) + 4H+(aq) 2Fe2+(aq) + 2H2O(l); E° = 1.67 V
At [Fe2+] = 10-3 M, P(O2) = 0.1 atom and pH = 3, the cell potential (in V) at 25°C is
|
|
Lakshmi Roy answered |
The given cell reaction is as follows:
2Fe(s) + O2(g) + 4H+(aq) -> 2Fe2+(aq) + 2H2O(l)
To determine the cell potential, we need to use the Nernst equation, which is given by:
E = E° - (0.0592/n) log(Q)
where E is the cell potential, E° is the standard cell potential, n is the number of moles of electrons transferred in the balanced equation, and Q is the reaction quotient.
Given:
E° = 1.67 V
[Fe2+] = 10^-3 M
P(O2) = 0.1 atm
pH = 3
First, let's calculate the reaction quotient Q:
Q = [Fe2+]^2[H2O]/[O2][H+]^4
Since the coefficients in the balanced equation are all 1, we can simplify the expression to:
Q = [Fe2+]^2[H2O]/[O2][H+]^4
Substituting the given values:
Q = (10^-3)^2/(0.1)(10^-3)^4
Q = 10^-6/(10^-1)(10^-12)
Q = 10^-6/(10^-13)
Q = 10^7
Now we can plug the values into the Nernst equation to find the cell potential:
E = 1.67 V - (0.0592/2) log(10^7)
E = 1.67 V - (0.0296) log(10^7)
E = 1.67 V - (0.0296)(7)
E = 1.67 V - 0.2072
E = 1.4628 V
Therefore, the cell potential at 25°C is approximately 1.46 V.
2Fe(s) + O2(g) + 4H+(aq) -> 2Fe2+(aq) + 2H2O(l)
To determine the cell potential, we need to use the Nernst equation, which is given by:
E = E° - (0.0592/n) log(Q)
where E is the cell potential, E° is the standard cell potential, n is the number of moles of electrons transferred in the balanced equation, and Q is the reaction quotient.
Given:
E° = 1.67 V
[Fe2+] = 10^-3 M
P(O2) = 0.1 atm
pH = 3
First, let's calculate the reaction quotient Q:
Q = [Fe2+]^2[H2O]/[O2][H+]^4
Since the coefficients in the balanced equation are all 1, we can simplify the expression to:
Q = [Fe2+]^2[H2O]/[O2][H+]^4
Substituting the given values:
Q = (10^-3)^2/(0.1)(10^-3)^4
Q = 10^-6/(10^-1)(10^-12)
Q = 10^-6/(10^-13)
Q = 10^7
Now we can plug the values into the Nernst equation to find the cell potential:
E = 1.67 V - (0.0592/2) log(10^7)
E = 1.67 V - (0.0296) log(10^7)
E = 1.67 V - (0.0296)(7)
E = 1.67 V - 0.2072
E = 1.4628 V
Therefore, the cell potential at 25°C is approximately 1.46 V.
A rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency ' f '. Its magnetic moment. - a)
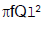
- b)
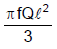
- c)
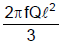
- d)
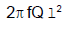
Correct answer is option 'B'. Can you explain this answer?
A rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency ' f '. Its magnetic moment.
a)
b)
c)
d)
|
|
Vijay Kumar answered |

Charge on the differential element dx,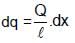
equivalent current di = f dq
∴ magnetic moment of this element
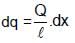
equivalent current di = f dq
∴ magnetic moment of this element
dμ = (di) NA (N = 1)
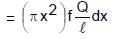
⇒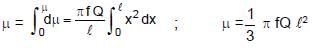
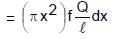
⇒
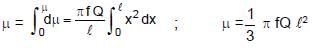
Amphoteric oxides, such as aluminium oxide, are soluble both in strongly acidic and in strongly basic
solutions :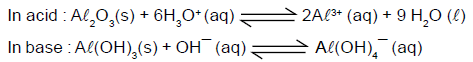 Dissolution of Al(OH)3 in excess base is just a special case of the effect of complex-ion formation on solubility. Al(OH)3 dissolves because excess OH¯ ions convert it to the soluble complex ion Al(OH)4¯ (aluminate ion).The effect of pH on the solubility of Al(OH)3 is shown in figure.
Dissolution of Al(OH)3 in excess base is just a special case of the effect of complex-ion formation on solubility. Al(OH)3 dissolves because excess OH¯ ions convert it to the soluble complex ion Al(OH)4¯ (aluminate ion).The effect of pH on the solubility of Al(OH)3 is shown in figure. 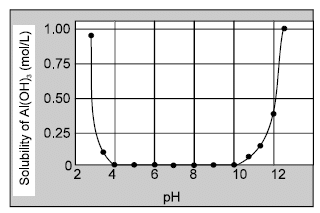 Other examples of amphoteric hydroxides include Zn(OH)2, Cr(OH)3, Sn(OH)2 and Pb(OH)2, which react with
Other examples of amphoteric hydroxides include Zn(OH)2, Cr(OH)3, Sn(OH)2 and Pb(OH)2, which react with
excess OH- ions to form the soluble complex ions Zn(OH)42- (zincate ion),Cr(OH)4- (chromite ion),Sn(OH)3¯(stannite ion), and Pb(OH)3¯ (plumbite ion), respectively. By contrast, basic hydroxides, such as Mn(OH)2, Fe(OH)2,and Fe(OH)3, dissolve in strong acid but not in strong base.Zn(OH)2 is a amphoteric hydroxide and is involved in the following two equilibria in aqueous solutions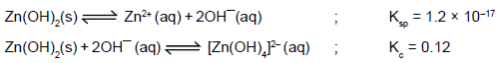 At what pH the solubility of Zn(OH)2 be minimum ?
At what pH the solubility of Zn(OH)2 be minimum ?- a)4
- b)10
- c)6
- d)8
Correct answer is option 'B'. Can you explain this answer?
Amphoteric oxides, such as aluminium oxide, are soluble both in strongly acidic and in strongly basic
solutions :
solutions :
Dissolution of Al(OH)3 in excess base is just a special case of the effect of complex-ion formation on solubility. Al(OH)3 dissolves because excess OH¯ ions convert it to the soluble complex ion Al(OH)4¯ (aluminate ion).The effect of pH on the solubility of Al(OH)3 is shown in figure.
Other examples of amphoteric hydroxides include Zn(OH)2, Cr(OH)3, Sn(OH)2 and Pb(OH)2, which react with
excess OH- ions to form the soluble complex ions Zn(OH)42- (zincate ion),Cr(OH)4- (chromite ion),Sn(OH)3¯(stannite ion), and Pb(OH)3¯ (plumbite ion), respectively. By contrast, basic hydroxides, such as Mn(OH)2, Fe(OH)2,and Fe(OH)3, dissolve in strong acid but not in strong base.
excess OH- ions to form the soluble complex ions Zn(OH)42- (zincate ion),Cr(OH)4- (chromite ion),Sn(OH)3¯(stannite ion), and Pb(OH)3¯ (plumbite ion), respectively. By contrast, basic hydroxides, such as Mn(OH)2, Fe(OH)2,and Fe(OH)3, dissolve in strong acid but not in strong base.
Zn(OH)2 is a amphoteric hydroxide and is involved in the following two equilibria in aqueous solutions
At what pH the solubility of Zn(OH)2 be minimum ?
a)
4
b)
10
c)
6
d)
8
|
|
Krishna Iyer answered |
Let solubility of Zn(OH)2 = s, some of will go in Zn2+ form and some in complex |Zn(OH)4|2-, of  = 10-x M,
= 10-x M,
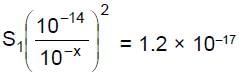 ........(1)
........(1)
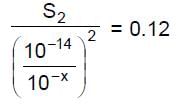 [S1 + S2 total solubility]
[S1 + S2 total solubility]
So, S1 S2 = 1.2 x 1.2 10-18
Now, we want S = S1 + S2 to be minimum we will have S1 = S2
So, = S1 = S2 = 1.2 x 10-9 M
Hence from 1" equation we get
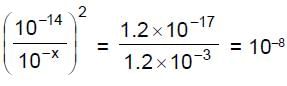
So,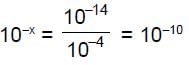
Hence x = 10
 = 10-x M,
= 10-x M, 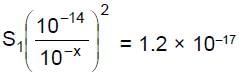 ........(1)
........(1)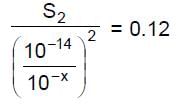 [S1 + S2 total solubility]
[S1 + S2 total solubility]So, S1 S2 = 1.2 x 1.2 10-18
Now, we want S = S1 + S2 to be minimum we will have S1 = S2
So, = S1 = S2 = 1.2 x 10-9 M
Hence from 1" equation we get
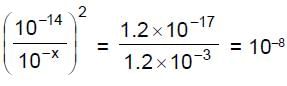
So,
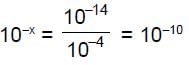
Hence x = 10
In the figure shown a parallel plate capacitor has a dielectric of width d/2 and dielectric constant K = 2. The other dimensions of the dielectric are same as that of the plates. The plates P1 and P2 of the capacitor have area 'A' each. The energy of the capacitor is : 
- a)

- b)
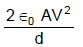
- c)
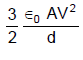
- d)
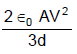
Correct answer is option 'D'. Can you explain this answer?
In the figure shown a parallel plate capacitor has a dielectric of width d/2 and dielectric constant K = 2. The other dimensions of the dielectric are same as that of the plates. The plates P1 and P2 of the capacitor have area 'A' each. The energy of the capacitor is :

a)
b)
c)
d)
|
|
Lalit Yadav answered |
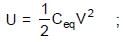
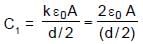

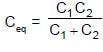

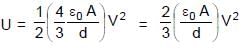
A water tank stands on the roof of a building as shown. Then the value of 'h' for which the distance covered by the water 'x' is greatest is - 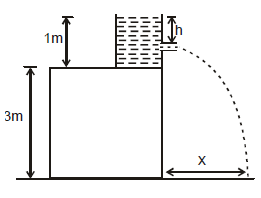
- a)0.5 m
- b)0.67 m
- c)1 m
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A water tank stands on the roof of a building as shown. Then the value of 'h' for which the distance covered by the water 'x' is greatest is -
a)
0.5 m
b)
0.67 m
c)
1 m
d)
none of these
|
|
Rohit Jain answered |
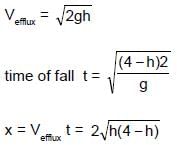
the roots of x are (0,4) and the maximum of x is at h = 2.
The permitted value of h is 0 to 1 clearly h = 1 will give the maximum value of x is this interval.
Aliter : If the column of water itself were from ground upto a height of 4m, h = 2m would give the maximum range x. Farther the hole is from this midpoint ,lower the range.Here the nearest point possible to this midpoint is the base of the container. Hence h = 1m.
Which of the following statement(s) is/are incorrect regarding chloride of iron?- a)Iron chloride is back at anhydrous condition.
- b)It sublimes at 300°C and forms a dimer.
- c)It is an oxidising agent.
- d)It is ether soluble but water insoluble.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statement(s) is/are incorrect regarding chloride of iron?
a)
Iron chloride is back at anhydrous condition.
b)
It sublimes at 300°C and forms a dimer.
c)
It is an oxidising agent.
d)
It is ether soluble but water insoluble.
|
|
Ajay Yadav answered |
This problem is based on various properties of iron chlorides. To solve this problem, students must have the knowledge of solubility of iron chloride in aqueous solution, the existence of iron chloride in ether solution, oxidising properties of iron chloride.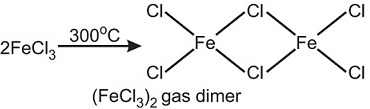
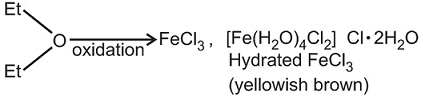
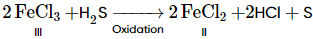
Properties of iron chloride
(i) FeCl3 (Iron chloride) is back coloured in anhydrous conditions. But its hydrated form is yellowish-brown.
(ii) FeCl3 sublimes at 300°C3 to give a dimer.

(iii) FeCl3 is water-soluble as well as ether soluble due to solvation.
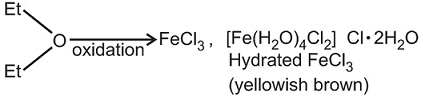
(iv) It is an oxidising agent, during oxidation. The yellow colour of aqueous Fe (III) changes to light green aqueous Fe (II).
The curve of pressure volume (PV) against pressure (P) of the gas at a particular temperature is as shown, according to the graph which of the following is / are incorrect (in the low pressure region):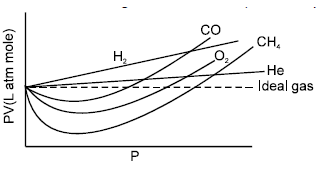
- a)H2 and He show positive deviation from ideal gas equation.
- b)CO, CH4 and O2 show negative deviation from ideal gas equation.
- c)H2 and He show negative deviation while CO2, CH4 and O2 show positive deviation.
- d)H2 and He are less compressible than that of an ideal gas while CO2, CH4 and O2 more compressible than that of ideal gas.
Correct answer is option 'C'. Can you explain this answer?
The curve of pressure volume (PV) against pressure (P) of the gas at a particular temperature is as shown, according to the graph which of the following is / are incorrect (in the low pressure region):
a)
H2 and He show positive deviation from ideal gas equation.
b)
CO, CH4 and O2 show negative deviation from ideal gas equation.
c)
H2 and He show negative deviation while CO2, CH4 and O2 show positive deviation.
d)
H2 and He are less compressible than that of an ideal gas while CO2, CH4 and O2 more compressible than that of ideal gas.
|
|
Yash Patel answered |
If Z > 1 positive deviation
Z < 1 negative deviation
Z < 1 negative deviation
A bell rings at an interval of every 2 minutes, second bell rings at every 5 minutes, 3rd bell rings at every 6 minutes and 4th ring in every 8 minutes. In a span of 8 hours, how many times all 4 bells be ringing simultaneously- a)60
- b)32
- c)16
- d)4
Correct answer is option 'D'. Can you explain this answer?
A bell rings at an interval of every 2 minutes, second bell rings at every 5 minutes, 3rd bell rings at every 6 minutes and 4th ring in every 8 minutes. In a span of 8 hours, how many times all 4 bells be ringing simultaneously
a)
60
b)
32
c)
16
d)
4
|
|
Anaya Patel answered |
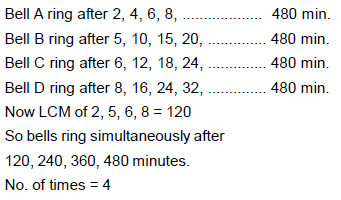
The string of a step rolling wheel is pulled by applying force F with different lines of action in two situations as shown. The wheel starts rolling without slipping due to application of the force : 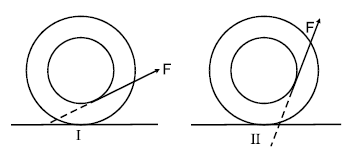
- a)The wheel rolls to the right in situation I and to the left in situation II.
- b)The wheel rolls to the left in situation I and to the right in situation II
- c)The wheel rolls to the right in both situations.
- d)The wheel rolls to the left in both situations.
Correct answer is option 'A'. Can you explain this answer?
The string of a step rolling wheel is pulled by applying force F with different lines of action in two situations as shown. The wheel starts rolling without slipping due to application of the force :
a)
The wheel rolls to the right in situation I and to the left in situation II.
b)
The wheel rolls to the left in situation I and to the right in situation II
c)
The wheel rolls to the right in both situations.
d)
The wheel rolls to the left in both situations.
|
|
Krishna Iyer answered |
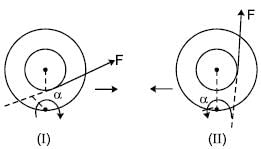
(Pure rotation about instantaneous point of contact)
Note : If line action passes through point of contact, it only spins.
In a sample of H-atom electrons make transition from 5th excited state to ground state, producing all possible types of photons, then number of lines in infrared region are - a)4
- b)5
- c)6
- d)3
Correct answer is option 'C'. Can you explain this answer?
In a sample of H-atom electrons make transition from 5th excited state to ground state, producing all possible types of photons, then number of lines in infrared region are
a)
4
b)
5
c)
6
d)
3
|
|
Krishna Iyer answered |
5 lines belong to ultra violet region and 4 lines are in visible region and rest are in infrared region.
An object approaches a fixed diverging lens with a constant velocity from infinity along the principal axis. The relative velocity between object and its image will be :- a)increasing
- b)decreasing
- c)first increases then decreases
- d)first decreases and then increases
Correct answer is option 'B'. Can you explain this answer?
An object approaches a fixed diverging lens with a constant velocity from infinity along the principal axis. The relative velocity between object and its image will be :
a)
increasing
b)
decreasing
c)
first increases then decreases
d)
first decreases and then increases

|
Praveen Kumar answered |

Let A and B be two fixed points and P, another point in the plane, move such that k1PA + k2PB = k3 where k1, k2 & k3 being real constants. The locus of P is- a)A circle if k1 = 0 and k2, k3 > 0
- b)A circle if k1 > 0, k2 < 0="" and="" />3 = 0
- c)An ellipse if k1 = k2 > 0 and k3 > 0
- d)A hyperbola if k2 = −1 and k1, k3 > 0
Correct answer is option 'A,B,C'. Can you explain this answer?
Let A and B be two fixed points and P, another point in the plane, move such that k1PA + k2PB = k3 where k1, k2 & k3 being real constants. The locus of P is
a)
A circle if k1 = 0 and k2, k3 > 0
b)
A circle if k1 > 0, k2 < 0="" and="" />3 = 0
c)
An ellipse if k1 = k2 > 0 and k3 > 0
d)
A hyperbola if k2 = −1 and k1, k3 > 0
|
|
Sameer Saha answered |
, and k3 are constants.
Let's consider the triangle formed by points A, B, and P. The ratio k1PA/k2PB represents the ratio of the distances from P to A and P to B. This ratio is constant for all positions of P.
Now, let's consider a point Q that is also in the plane. The ratio k1QA/k2QB should also be equal to k3, according to the given condition.
So, we can say that for any two points P and Q in the plane, the ratio of their distances to A and B respectively will always be the same, equal to k3.
Therefore, the locus of points P that satisfy the given condition is a circle. The center of the circle is the midpoint of line segment AB, and the radius of the circle is given by k3 times the distance between A and B.
Let's consider the triangle formed by points A, B, and P. The ratio k1PA/k2PB represents the ratio of the distances from P to A and P to B. This ratio is constant for all positions of P.
Now, let's consider a point Q that is also in the plane. The ratio k1QA/k2QB should also be equal to k3, according to the given condition.
So, we can say that for any two points P and Q in the plane, the ratio of their distances to A and B respectively will always be the same, equal to k3.
Therefore, the locus of points P that satisfy the given condition is a circle. The center of the circle is the midpoint of line segment AB, and the radius of the circle is given by k3 times the distance between A and B.
Figure shows a uniformly charged hemispherical shell. The direction of electric field at point p, that is off-centre (but in the plane of the largest circle of the hemisphere), will be along 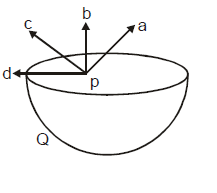
- a)pa
- b)pb
- c)pc
- d)pd
Correct answer is option 'B'. Can you explain this answer?
Figure shows a uniformly charged hemispherical shell. The direction of electric field at point p, that is off-centre (but in the plane of the largest circle of the hemisphere), will be along

a)
pa
b)
pb
c)
pc
d)
pd

|
Pioneer Academy answered |
Let electric field at point. 'p' has both x and y component.
So similar electric field will be, for other hemisphere (upper half).
Now lets overlap both.
So similar electric field will be, for other hemisphere (upper half).
Now lets overlap both.
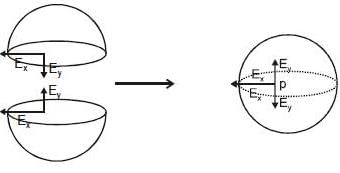
(Enet)p = 2 Ex and it should be zero (as E inside a full shell = 0).
So Ex = 0, So electric field at 'p' is purely in y direction.
A painter is applying force himself to raise him and the box with an cceleration of 5 m/s2 by a massless rope and pulley arrangement as shown in figure. Mass of painter is 100 kg and that of box is 50 kg. If g = 10 m/s2, then : 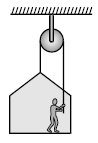
- a)tension in the rope is 1125 N
- b)tension in the rope is 2250 N
- c)force of contact between the painter and the floor is 375 N
- d)none of these
Correct answer is option 'A,C'. Can you explain this answer?
A painter is applying force himself to raise him and the box with an cceleration of 5 m/s2 by a massless rope and pulley arrangement as shown in figure. Mass of painter is 100 kg and that of box is 50 kg. If g = 10 m/s2, then :
a)
tension in the rope is 1125 N
b)
tension in the rope is 2250 N
c)
force of contact between the painter and the floor is 375 N
d)
none of these

|
Cstoppers Instructors answered |
For the whole system, 2T – 1500 = 150 x 5 ⇒ T = 1125 N
For the person, T – 1000 + N = 100 x 5 N = 1500 – 1125 = 375 N
For the person, T – 1000 + N = 100 x 5 N = 1500 – 1125 = 375 N
Which of the following statements is/are correct ? - a)Out of trimethylamine and trimethylphosphine, trimethylamine has higher dipole moment ?
- b)Out of (SiH3)2O and (CH3)2O, (SiH3)2O is more basic.
- c)C–C bond length (in pm) in C2 molecule is greater than O–O bond length in O2 molecule.
- d)N(SiMe3)3 and BF3 molecules are isostructural.
Correct answer is option 'A,C,D'. Can you explain this answer?
Which of the following statements is/are correct ?
a)
Out of trimethylamine and trimethylphosphine, trimethylamine has higher dipole moment ?
b)
Out of (SiH3)2O and (CH3)2O, (SiH3)2O is more basic.
c)
C–C bond length (in pm) in C2 molecule is greater than O–O bond length in O2 molecule.
d)
N(SiMe3)3 and BF3 molecules are isostructural.
|
|
Lavanya Menon answered |
(A) Nitrogen is more electronegative than phosphorus.
So, dipole moment of trimethylamine is greater than trimethy phosphine.
In trisilyl ether the lone pair of electron on oxygen atom is less easily available for donation because of pπ-dπ
delocalisation due to presence of the vacant d-orbital with Si. This however is not possible with carbon in CH3–O–CH3 due to the absence of d-orbital making it more basic.
(C) Bond order of C2
and O2 are same i.e., 2. In C2 molecules both bonds are π-bonds whereas, there is one σ and one π-bond in O2 molecule
C2 = 131 pm ; O2 = 121 pm.
delocalisation due to presence of the vacant d-orbital with Si. This however is not possible with carbon in CH3–O–CH3 due to the absence of d-orbital making it more basic.
(C) Bond order of C2
and O2 are same i.e., 2. In C2 molecules both bonds are π-bonds whereas, there is one σ and one π-bond in O2 molecule
C2 = 131 pm ; O2 = 121 pm.
Let ‘P’ be a point which does not lie outside the triangle ABC, A = (3, 2), B = (0, 0), C = (0, 4) which satisfy d (P, A) < maximum {d (P, B), d (P, C)} then maximum distance of P from side BC, where d (P, A) gives the distance between P & A, is - a)3/4
- b)4/3
- c)3
- d)0
Correct answer is option 'C'. Can you explain this answer?
Let ‘P’ be a point which does not lie outside the triangle ABC, A = (3, 2), B = (0, 0), C = (0, 4) which satisfy d (P, A) < maximum {d (P, B), d (P, C)} then maximum distance of P from side BC, where d (P, A) gives the distance between P & A, is
a)
3/4
b)
4/3
c)
3
d)
0
|
|
Sarita Yadav answered |
A is a thin walled sphere at rest made up of glass. The radius of the sphere is 1m and it is filled with a
transparent liquid of refractive index m. S is the luminous source moving directly towards a plane
vertical mirror M. A fish in the liquid is moving towards S. The eye of the fish and S are collinear &
perpendicular to mirror M. At the moment S is 3m away from the centre of the sphere, fish observes
that image of S due to reflection is moving with speed of 13m/s. If speed of the fish relative to the
sphere is 10m/s and m = 1.5 then find the speed of the source at that instant. The system is placed
in air.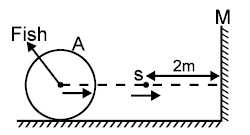
Correct answer is '8'. Can you explain this answer?
A is a thin walled sphere at rest made up of glass. The radius of the sphere is 1m and it is filled with a
transparent liquid of refractive index m. S is the luminous source moving directly towards a plane
vertical mirror M. A fish in the liquid is moving towards S. The eye of the fish and S are collinear &
perpendicular to mirror M. At the moment S is 3m away from the centre of the sphere, fish observes
that image of S due to reflection is moving with speed of 13m/s. If speed of the fish relative to the
sphere is 10m/s and m = 1.5 then find the speed of the source at that instant. The system is placed
in air.
transparent liquid of refractive index m. S is the luminous source moving directly towards a plane
vertical mirror M. A fish in the liquid is moving towards S. The eye of the fish and S are collinear &
perpendicular to mirror M. At the moment S is 3m away from the centre of the sphere, fish observes
that image of S due to reflection is moving with speed of 13m/s. If speed of the fish relative to the
sphere is 10m/s and m = 1.5 then find the speed of the source at that instant. The system is placed
in air.
|
|
Hansa Sharma answered |
Two roads OA and OB intersect at an angle of 60º. A car driver approaches O from A where OA = 800m at a uniform speed of 20m/s. Simultaneously another car moves from O towards B at a uniform speed of 25m/s. If t is time when two cars are closest, find t.- a)1
- b)2
- c)1040/61
- d)3/2
Correct answer is option 'C'. Can you explain this answer?
Two roads OA and OB intersect at an angle of 60º. A car driver approaches O from A where OA = 800m at a uniform speed of 20m/s. Simultaneously another car moves from O towards B at a uniform speed of 25m/s. If t is time when two cars are closest, find t.
a)
1
b)
2
c)
1040/61
d)
3/2
|
|
Vijay Kumar answered |
Let the distance between two cars after t seconds be s. Distance covered by first car in t second is 20t meter, so its distance from O will be (800 – 20t) meter and distance covered by second car will be 25t meter.
Product of 22 integers is equal to 1, then their sum cannot be- a)0
- b)1
- c)2
- d)4
Correct answer is option 'A,B,D'. Can you explain this answer?
Product of 22 integers is equal to 1, then their sum cannot be
a)
0
b)
1
c)
2
d)
4

|
Shraddha Sharma answered |
Only integers which can satisfy this condition are -1 & +1. taking 10 times -1 and 12times +1 we will get the product 1. and sum will result in 2. check other cases similarly.
A single circular loop of wire with radius 0.02 m carries a current of 8.0 A. It is placed at the centre of a solenoid that has length 0.65 m, radius 0.080 m and 1300 turns. 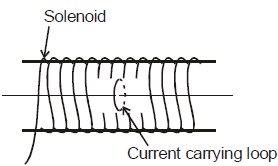
- a)The value of the current in the solenoid so that the magnetic field at the centre of the loop becomes zero, is equal to 44 mA.
- b)The value of the current in the solenoid so that the magnetic field at the centre of the loop becomes zero, is equal to 100 mA.
- c)The magnitude of the total magnetic field at the centre of the loop (due to both the loop and the solenoid) if the current in the loop is reversed in direction from that needed to make the total field equal to zero tesla, is 8p x 10–5 T.
- d)The magnitude of the total magnetic field at the centre of the loop (due to both the loop and the solenoid) if the current in the loop is reversed in direction from that needed to make the total field equal to zero tesla, is 16p x 10–5 T.
Correct answer is option 'B,D'. Can you explain this answer?
A single circular loop of wire with radius 0.02 m carries a current of 8.0 A. It is placed at the centre of a solenoid that has length 0.65 m, radius 0.080 m and 1300 turns.

a)
The value of the current in the solenoid so that the magnetic field at the centre of the loop becomes zero, is equal to 44 mA.
b)
The value of the current in the solenoid so that the magnetic field at the centre of the loop becomes zero, is equal to 100 mA.
c)
The magnitude of the total magnetic field at the centre of the loop (due to both the loop and the solenoid) if the current in the loop is reversed in direction from that needed to make the total field equal to zero tesla, is 8p x 10–5 T.
d)
The magnitude of the total magnetic field at the centre of the loop (due to both the loop and the solenoid) if the current in the loop is reversed in direction from that needed to make the total field equal to zero tesla, is 16p x 10–5 T.
|
|
Neha Joshi answered |

A straight line source of sound of length L = 10m, emitts a pulse of sound that travels radially outward from the source. What sound energy (in mW) is intercepted by an acoustic cylindrical detector of surface area 2.4cm2, located at a perpendicular distance 7m from the source. The waves reach perpendicularly at the surface of the detector. The total power emitted by the source in the form of sound is 2.2 × 104 W.
(Use π = 22/7)
Correct answer is '12'. Can you explain this answer?
A straight line source of sound of length L = 10m, emitts a pulse of sound that travels radially outward from the source. What sound energy (in mW) is intercepted by an acoustic cylindrical detector of surface area 2.4cm2, located at a perpendicular distance 7m from the source. The waves reach perpendicularly at the surface of the detector. The total power emitted by the source in the form of sound is 2.2 × 104 W.
(Use π = 22/7)
(Use π = 22/7)
|
|
Lavanya Menon answered |
Imagine a cylinder of radius 7m and length 10m. Intensity of sound at the surface of cylinder is same everywhere.
An X-ray tube is working at potential of 20 kV. The potential difference is decreased to 10 kV. It is found that
the difference of the wavelength of Kα X-ray and the most energetic continuous X-ray becomes 4 times the
difference before the change of voltage. Find the atomic number of the target element. Take b = 1 and 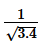 =0.54.
=0.54.
Correct answer is '55'. Can you explain this answer?
An X-ray tube is working at potential of 20 kV. The potential difference is decreased to 10 kV. It is found that
the difference of the wavelength of Kα X-ray and the most energetic continuous X-ray becomes 4 times the
difference before the change of voltage. Find the atomic number of the target element. Take b = 1 and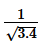 =0.54.
=0.54.
the difference of the wavelength of Kα X-ray and the most energetic continuous X-ray becomes 4 times the
difference before the change of voltage. Find the atomic number of the target element. Take b = 1 and
|
|
Anaya Patel answered |

Statement-1 Alkylation of benzene by Friedel -Crafts reaction gives polyalkylated benzene.Statement-2 The ring gets activated for further substitution after the introduction of one alkyl group.- a)Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1.
- b)Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
- c)Statement-1 is True, Statement-2 is False
- d)Statement-1 is False, Statement-2 is True
Correct answer is option 'A'. Can you explain this answer?
Statement-1 Alkylation of benzene by Friedel -Crafts reaction gives polyalkylated benzene.
Statement-2 The ring gets activated for further substitution after the introduction of one alkyl group.
a)
Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1.
b)
Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
c)
Statement-1 is True, Statement-2 is False
d)
Statement-1 is False, Statement-2 is True
|
|
Yash Patel answered |
An electron donor group increases the reactivity towards alkylation so further alkylation occurs.
The molar conductance of NaCl varies with the concentration as shown in the following table and all values follows the equation 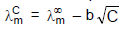

 When a certain conductivity cell (C) was filled with 25 x 10–4 (M) NaCl solution. The resistance of the cell was found to be 1000 ohm. At Infinite dilution, conductance of Cl– and SO4–2 are 80 ohm–1 cm2 mole–1 and 160 ohm–1 cm2 mole–1 respectively.Q. What is the molar conductance of NaCl at infinite dilution ?
When a certain conductivity cell (C) was filled with 25 x 10–4 (M) NaCl solution. The resistance of the cell was found to be 1000 ohm. At Infinite dilution, conductance of Cl– and SO4–2 are 80 ohm–1 cm2 mole–1 and 160 ohm–1 cm2 mole–1 respectively.Q. What is the molar conductance of NaCl at infinite dilution ?- a)147 ohm–1 cm2 mole–1
- b)107 ohm–1 cm2 mole–1
- c)127 ohm–1 cm2 mole–1
- d)157 ohm–1 cm2 mole–1
Correct answer is option 'C'. Can you explain this answer?
The molar conductance of NaCl varies with the concentration as shown in the following table and all values follows the equation
When a certain conductivity cell (C) was filled with 25 x 10–4 (M) NaCl solution. The resistance of the cell was found to be 1000 ohm. At Infinite dilution, conductance of Cl– and SO4–2 are 80 ohm–1 cm2 mole–1 and 160 ohm–1 cm2 mole–1 respectively.
Q. What is the molar conductance of NaCl at infinite dilution ?
a)
147 ohm–1 cm2 mole–1
b)
107 ohm–1 cm2 mole–1
c)
127 ohm–1 cm2 mole–1
d)
157 ohm–1 cm2 mole–1
|
|
Anaya Patel answered |

From a point P(1, 2) pair of tangent’s are drawn to a hyperbola ‘H’ in which one tangent to each arm of hyperbola. Equation of asymptotes of hyperbola H are √3x – y + 5 = 0 & √3x + y – 1 = 0 then eccentricity of ‘H’ is - a)2
- b)
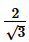
- c)
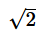
- d)
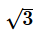
Correct answer is option 'B'. Can you explain this answer?
From a point P(1, 2) pair of tangent’s are drawn to a hyperbola ‘H’ in which one tangent to each arm of hyperbola. Equation of asymptotes of hyperbola H are √3x – y + 5 = 0 & √3x + y – 1 = 0 then eccentricity of ‘H’ is
a)
2
b)
c)
d)
|
|
Vivek Patel answered |
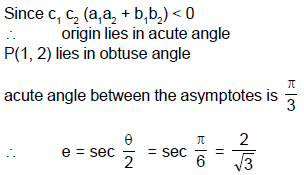
An ellipse has semi-major axes of lengths 2 and semi-minor axis of length 1. It is slipping between the coordinate axes in the first quadrant while maintaining contact with both x-axis and y-axis.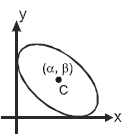 Q. The locus of foci of the ellipse is
Q. The locus of foci of the ellipse is - a)
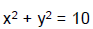
- b)
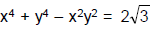
- c)x2+y2
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
An ellipse has semi-major axes of lengths 2 and semi-minor axis of length 1. It is slipping between the coordinate axes in the first quadrant while maintaining contact with both x-axis and y-axis.
Q. The locus of foci of the ellipse is
a)
b)
c)
x2+y2
d)
None of these
|
|
Anaya Patel answered |

In the figure shown strings AB and BC have masses m and 2m respectively. Both are of same length l. Mass of each string is uniformly distributed on its length. The string is suspended vertically from the ceiling of a room. A small jerk wave pulse is given at the end 'C'. It goes up to upper end 'A' in time 't'. If m = 2 kg, l = 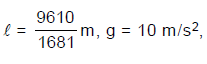
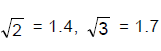 , Then find the value of 't' in seconds
, Then find the value of 't' in seconds
Correct answer is '2'. Can you explain this answer?
In the figure shown strings AB and BC have masses m and 2m respectively. Both are of same length l. Mass of each string is uniformly distributed on its length. The string is suspended vertically from the ceiling of a room. A small jerk wave pulse is given at the end 'C'. It goes up to upper end 'A' in time 't'. If m = 2 kg, l = 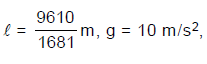
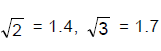 , Then find the value of 't' in seconds
, Then find the value of 't' in seconds

|
Telecom Tuners answered |
What happens when a mixture of NaCl and K2Cr2O7 is gently warmed with conc. H2SO4?- a)A deep red vapour is evolved.
- b)The vapour when passed into NaOH solution gives a yellow solution of Na2CrO4.
- c)Chlorine gas is evolved.
- d)Chromyl chloride is formed.
Correct answer is option 'A,B,D'. Can you explain this answer?
What happens when a mixture of NaCl and K2Cr2O7 is gently warmed with conc. H2SO4?
a)
A deep red vapour is evolved.
b)
The vapour when passed into NaOH solution gives a yellow solution of Na2CrO4.
c)
Chlorine gas is evolved.
d)
Chromyl chloride is formed.
|
|
Vijay Kumar answered |
During this process, chromyl chloride is formed which is deep red coloured fuming liquid.
4NaCl + K2Cr2O7 + H2SO4  + 4NaHSO4 + 2KHSO4 + 3H2O
+ 4NaHSO4 + 2KHSO4 + 3H2O
 + 4NaHSO4 + 2KHSO4 + 3H2O
+ 4NaHSO4 + 2KHSO4 + 3H2OThe vapour of CrO2Cl2 when passed into NaOH solution gives a yellow solution of Na2CrO4.

Directions: The following question has four choices, out of which ONE or MORE are correct.Cv and Cp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then,- a)Cp + Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
- b)Cp / Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
- c)Cp . Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
- d)Cp - Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
Correct answer is option 'A,C'. Can you explain this answer?
Directions: The following question has four choices, out of which ONE or MORE are correct.
Cv and Cp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then,
a)
Cp + Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
b)
Cp / Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
c)
Cp . Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
d)
Cp - Cv is larger for a diatomic ideal gas than for a monatomic ideal gas
|
|
Lekshmi Joshi answered |
Answer:
Introduction:
The molar specific heat capacities of a gas at constant volume (Cv) and constant pressure (Cp) are important thermodynamic properties that describe how the gas responds to changes in temperature. In this question, we are comparing the values of Cp and Cv for diatomic and monatomic ideal gases.
Cv and Cp for an ideal gas:
For an ideal gas, the molar specific heat capacity at constant volume (Cv) is the amount of heat required to raise the temperature of one mole of the gas by one degree Celsius while keeping the volume constant. On the other hand, the molar specific heat capacity at constant pressure (Cp) is the amount of heat required to raise the temperature of one mole of the gas by one degree Celsius while allowing the pressure to remain constant.
Comparison between diatomic and monatomic ideal gases:
To compare the values of Cp and Cv for diatomic and monatomic ideal gases, we need to consider the degrees of freedom of the gas molecules. The degrees of freedom represent the number of independent ways in which the gas molecules can store energy.
Monatomic ideal gas:
A monatomic ideal gas consists of single atoms, such as helium or argon. Since these atoms can only move in three dimensions (x, y, and z), they have three degrees of freedom. For a monatomic ideal gas, the molar specific heat capacities at constant volume (Cv) and constant pressure (Cp) are related by the equation Cp/Cv = γ, where γ is the adiabatic index. For a monatomic ideal gas, γ is equal to 5/3 or approximately 1.67.
Diatomic ideal gas:
A diatomic ideal gas consists of molecules with two atoms, such as oxygen or nitrogen. In addition to the three translational degrees of freedom, diatomic molecules can also rotate about their center of mass. Since a diatomic molecule can rotate about two independent axes, it has a total of five degrees of freedom. For a diatomic ideal gas, the molar specific heat capacities at constant volume (Cv) and constant pressure (Cp) are related by the equation Cp/Cv = γ, where γ is equal to 7/5 or approximately 1.4.
Comparison of Cp and Cv:
From the above information, we can conclude that Cp/Cv is larger for a diatomic ideal gas than for a monatomic ideal gas. This means that the molar specific heat capacity at constant pressure (Cp) is larger than the molar specific heat capacity at constant volume (Cv) for a diatomic ideal gas. Therefore, option B is incorrect.
Furthermore, the product Cp.Cv is larger for a diatomic ideal gas than for a monatomic ideal gas. This can be seen from the equation Cp/Cv = γ, where γ is greater for a monatomic ideal gas (5/3) compared to a diatomic ideal gas (7/5). Therefore, option C is correct.
In addition, Cp - Cv is also larger for a diatomic ideal gas than for a monatomic ideal gas. This can be seen from the difference in values of γ for the two types of gases. Therefore, option D is correct.
Summary:
In summary, for a diatomic ideal
Introduction:
The molar specific heat capacities of a gas at constant volume (Cv) and constant pressure (Cp) are important thermodynamic properties that describe how the gas responds to changes in temperature. In this question, we are comparing the values of Cp and Cv for diatomic and monatomic ideal gases.
Cv and Cp for an ideal gas:
For an ideal gas, the molar specific heat capacity at constant volume (Cv) is the amount of heat required to raise the temperature of one mole of the gas by one degree Celsius while keeping the volume constant. On the other hand, the molar specific heat capacity at constant pressure (Cp) is the amount of heat required to raise the temperature of one mole of the gas by one degree Celsius while allowing the pressure to remain constant.
Comparison between diatomic and monatomic ideal gases:
To compare the values of Cp and Cv for diatomic and monatomic ideal gases, we need to consider the degrees of freedom of the gas molecules. The degrees of freedom represent the number of independent ways in which the gas molecules can store energy.
Monatomic ideal gas:
A monatomic ideal gas consists of single atoms, such as helium or argon. Since these atoms can only move in three dimensions (x, y, and z), they have three degrees of freedom. For a monatomic ideal gas, the molar specific heat capacities at constant volume (Cv) and constant pressure (Cp) are related by the equation Cp/Cv = γ, where γ is the adiabatic index. For a monatomic ideal gas, γ is equal to 5/3 or approximately 1.67.
Diatomic ideal gas:
A diatomic ideal gas consists of molecules with two atoms, such as oxygen or nitrogen. In addition to the three translational degrees of freedom, diatomic molecules can also rotate about their center of mass. Since a diatomic molecule can rotate about two independent axes, it has a total of five degrees of freedom. For a diatomic ideal gas, the molar specific heat capacities at constant volume (Cv) and constant pressure (Cp) are related by the equation Cp/Cv = γ, where γ is equal to 7/5 or approximately 1.4.
Comparison of Cp and Cv:
From the above information, we can conclude that Cp/Cv is larger for a diatomic ideal gas than for a monatomic ideal gas. This means that the molar specific heat capacity at constant pressure (Cp) is larger than the molar specific heat capacity at constant volume (Cv) for a diatomic ideal gas. Therefore, option B is incorrect.
Furthermore, the product Cp.Cv is larger for a diatomic ideal gas than for a monatomic ideal gas. This can be seen from the equation Cp/Cv = γ, where γ is greater for a monatomic ideal gas (5/3) compared to a diatomic ideal gas (7/5). Therefore, option C is correct.
In addition, Cp - Cv is also larger for a diatomic ideal gas than for a monatomic ideal gas. This can be seen from the difference in values of γ for the two types of gases. Therefore, option D is correct.
Summary:
In summary, for a diatomic ideal
Statement-1 : A point object moves near the principal axis of a fixed spherical mirror along a straight line. Then the image formed by the spherical mirror also moves along a straight line.Statement-2 : For an incident ray on a fixed spherical mirror there is a fixed reflected ray. If a point object moves along this incident ray, its image will always lie on the given reflected ray. Further an incident ray may be drawn from the moving point object in its direction of velocity towards the mirror.- a)Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1.
- b)Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
- c)Statement-1 is True, Statement-2 is False
- d)Statement-1 is False, Statement-2 is True
Correct answer is option 'A'. Can you explain this answer?
Statement-1 : A point object moves near the principal axis of a fixed spherical mirror along a straight line. Then the image formed by the spherical mirror also moves along a straight line.
Statement-2 : For an incident ray on a fixed spherical mirror there is a fixed reflected ray. If a point object moves along this incident ray, its image will always lie on the given reflected ray. Further an incident ray may be drawn from the moving point object in its direction of velocity towards the mirror.
a)
Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1.
b)
Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
c)
Statement-1 is True, Statement-2 is False
d)
Statement-1 is False, Statement-2 is True
|
|
Geetika Shah answered |
Draw an incident ray on the mirror and trace the corresponding reflected ray. If a point object moves along this ray,its image will always lies on the traced reflected ray. Hence when a point object moves near the principal axisof a fixed spherical mirror along a straight line, then its image formed by the spherical mirror also moves along
a straight line.Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1.
a straight line.Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1.
If range of the function f(x) = sin-1 x + 2 tan-1 x + x2 + 4x + 1 is [a, b], then the value of a + b is
Correct answer is '4'. Can you explain this answer?
If range of the function f(x) = sin-1 x + 2 tan-1 x + x2 + 4x + 1 is [a, b], then the value of a + b is
|
|
Avik Nambiar answered |
To find the range of the function f(x) = sin^{-1}x * 2tan^{-1}x * x^2 * 4x * 1, we need to consider the range of each individual term and then find the combined range.
1. Range of sin^{-1}x:
The range of the arcsine function is [-pi/2, pi/2]. This means that the function sin^{-1}x will give values between -pi/2 and pi/2 for all values of x.
2. Range of 2tan^{-1}x:
The range of the arctangent function is (-pi/2, pi/2). When multiplied by 2, the range becomes (-pi, pi). This means that the function 2tan^{-1}x will give values between -pi and pi for all values of x.
3. Range of x^2:
The range of x^2 is [0, infinity). This means that the function x^2 will give values greater than or equal to 0 for all values of x.
4. Range of 4x:
The range of 4x is (-infinity, infinity). This means that the function 4x will give all real values for all values of x.
5. Range of 1:
The range of a constant function is the single value that it represents. In this case, the function 1 will always give the value 1.
Now, to find the combined range, we need to consider the intersection of the ranges of the individual terms.
- The intersection of the ranges of sin^{-1}x and 2tan^{-1}x is (-pi/2, pi/2).
- The intersection of this range and the range of x^2 is [0, pi/2].
- The intersection of this range and the range of 4x is [0, pi/2].
- The intersection of this range and the range of 1 is [0, pi/2].
Therefore, the range of the function f(x) is [0, pi/2].
However, the question asks for the value of a + b. Since the range is [0, pi/2], a = 0 and b = pi/2. Therefore, a + b = 0 + pi/2 = pi/2.
Hence, the correct answer is 4.
1. Range of sin^{-1}x:
The range of the arcsine function is [-pi/2, pi/2]. This means that the function sin^{-1}x will give values between -pi/2 and pi/2 for all values of x.
2. Range of 2tan^{-1}x:
The range of the arctangent function is (-pi/2, pi/2). When multiplied by 2, the range becomes (-pi, pi). This means that the function 2tan^{-1}x will give values between -pi and pi for all values of x.
3. Range of x^2:
The range of x^2 is [0, infinity). This means that the function x^2 will give values greater than or equal to 0 for all values of x.
4. Range of 4x:
The range of 4x is (-infinity, infinity). This means that the function 4x will give all real values for all values of x.
5. Range of 1:
The range of a constant function is the single value that it represents. In this case, the function 1 will always give the value 1.
Now, to find the combined range, we need to consider the intersection of the ranges of the individual terms.
- The intersection of the ranges of sin^{-1}x and 2tan^{-1}x is (-pi/2, pi/2).
- The intersection of this range and the range of x^2 is [0, pi/2].
- The intersection of this range and the range of 4x is [0, pi/2].
- The intersection of this range and the range of 1 is [0, pi/2].
Therefore, the range of the function f(x) is [0, pi/2].
However, the question asks for the value of a + b. Since the range is [0, pi/2], a = 0 and b = pi/2. Therefore, a + b = 0 + pi/2 = pi/2.
Hence, the correct answer is 4.
At a certain temperature in a 5 L vessel, 2 moles of carbon monoxide and 3 moles of chlorine were allowed to reach equilibrium, according to the following reaction:
CO + Cl2 ⇌ COCl2
At equilibrium, if 1 mole of CO is present, then equilibrium constant (KC) for the reaction is:(Nearest integer)Correct answer is '3'. Can you explain this answer?
At a certain temperature in a 5 L vessel, 2 moles of carbon monoxide and 3 moles of chlorine were allowed to reach equilibrium, according to the following reaction:
CO + Cl2 ⇌ COCl2
At equilibrium, if 1 mole of CO is present, then equilibrium constant (KC) for the reaction is:(Nearest integer)
CO + Cl2 ⇌ COCl2
At equilibrium, if 1 mole of CO is present, then equilibrium constant (KC) for the reaction is:(Nearest integer)
|
|
Pallavi Ahuja answered |
Understanding the Reaction
The reaction given is:
- CO + Cl2 ⇌ COCl2
Initially, there are 2 moles of CO and 3 moles of Cl2 in a 5 L vessel.
Initial Moles
- CO: 2 moles
- Cl2: 3 moles
- COCl2: 0 moles
Change in Moles
At equilibrium, 1 mole of CO is present. Therefore, the change in moles for CO is:
- CO: 2 moles - 1 mole = 1 mole reacted
From the stoichiometry of the reaction, 1 mole of CO reacts with 1 mole of Cl2 to produce 1 mole of COCl2.
Calculating Change for Cl2 and COCl2
- Cl2: 3 moles - 1 mole = 2 moles reacted
- COCl2: 0 moles + 1 mole = 1 mole formed
Equilibrium Moles
At equilibrium, we have:
- CO: 1 mole
- Cl2: 2 moles
- COCl2: 1 mole
Calculating Concentrations
To find the equilibrium concentrations, divide the moles by the volume (5 L):
- [CO] = 1/5 = 0.2 M
- [Cl2] = 2/5 = 0.4 M
- [COCl2] = 1/5 = 0.2 M
Equilibrium Constant (Kc)
The equilibrium constant expression for the reaction is:
Kc = [COCl2] / ([CO][Cl2])
Substituting the equilibrium concentrations:
Kc = (0.2) / (0.2 * 0.4) = 0.2 / 0.08 = 2.5
Rounding to the nearest integer gives Kc as 3.
Conclusion
The equilibrium constant Kc for the reaction is 3.
The reaction given is:
- CO + Cl2 ⇌ COCl2
Initially, there are 2 moles of CO and 3 moles of Cl2 in a 5 L vessel.
Initial Moles
- CO: 2 moles
- Cl2: 3 moles
- COCl2: 0 moles
Change in Moles
At equilibrium, 1 mole of CO is present. Therefore, the change in moles for CO is:
- CO: 2 moles - 1 mole = 1 mole reacted
From the stoichiometry of the reaction, 1 mole of CO reacts with 1 mole of Cl2 to produce 1 mole of COCl2.
Calculating Change for Cl2 and COCl2
- Cl2: 3 moles - 1 mole = 2 moles reacted
- COCl2: 0 moles + 1 mole = 1 mole formed
Equilibrium Moles
At equilibrium, we have:
- CO: 1 mole
- Cl2: 2 moles
- COCl2: 1 mole
Calculating Concentrations
To find the equilibrium concentrations, divide the moles by the volume (5 L):
- [CO] = 1/5 = 0.2 M
- [Cl2] = 2/5 = 0.4 M
- [COCl2] = 1/5 = 0.2 M
Equilibrium Constant (Kc)
The equilibrium constant expression for the reaction is:
Kc = [COCl2] / ([CO][Cl2])
Substituting the equilibrium concentrations:
Kc = (0.2) / (0.2 * 0.4) = 0.2 / 0.08 = 2.5
Rounding to the nearest integer gives Kc as 3.
Conclusion
The equilibrium constant Kc for the reaction is 3.
Which of the following expression (s) represent the voltage of cell at 298 K:Ag+ | AgI (saturated solution)|Ag2C2O4(saturated solution)| Ag+- a)
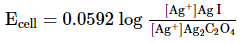
- b)
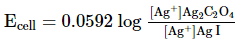
- c)
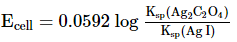
- d)
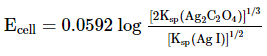
Correct answer is option 'B,D'. Can you explain this answer?
Which of the following expression (s) represent the voltage of cell at 298 K:
Ag+ | AgI (saturated solution)|Ag2C2O4(saturated solution)| Ag+
a)
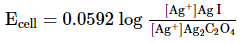
b)
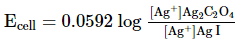
c)
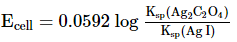
d)
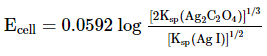
|
|
Neha Sharma answered |
The given cell is concentration cell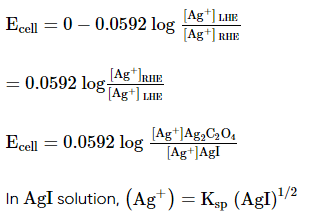
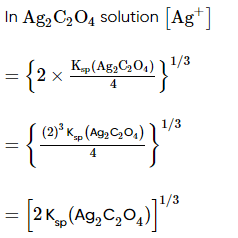
Ag ⟶(Ag+) LHE + e−
(Ag+)RHE+ e− ⟶ Ag
Net reaction:(Ag+)RHE ⟶ (Ag+)LHE
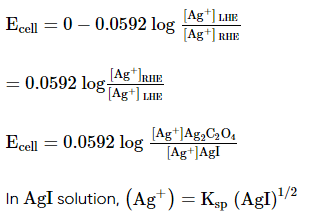
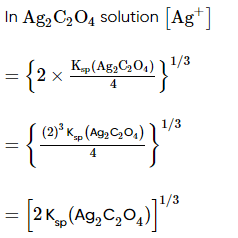
In the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'l' (in medium n1) is incident at an angle 'q' as shown. Distance S1O = S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is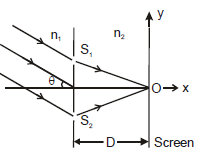 D. Using D = 1m, d = 1mm, q = 30°, l = 0.3mm, n1 = 4/3, n2 = , 10/9answer the following :Q. The y-coordinate of the point where the total phase difference between the interefering waves is zero, is
D. Using D = 1m, d = 1mm, q = 30°, l = 0.3mm, n1 = 4/3, n2 = , 10/9answer the following :Q. The y-coordinate of the point where the total phase difference between the interefering waves is zero, is - a)y = 0
- b)
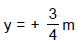
- c)
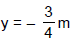
- d)
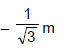
Correct answer is option 'C'. Can you explain this answer?
In the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'l' (in medium n1) is incident at an angle 'q' as shown. Distance S1O = S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is

D. Using D = 1m, d = 1mm, q = 30°, l = 0.3mm, n1 = 4/3, n2 = , 10/9
answer the following :
Q. The y-coordinate of the point where the total phase difference between the interefering waves is zero, is
a)
y = 0
b)
c)
d)

|
Praveen Kumar answered |
It is negative because upper path in medium n2 is longer than lower path in the same medium.
An isosceles ΔABC is inscribed in the circle x2 + y2 = 16. From points A, B and C three ordinates are drawn
which cut the ellipse 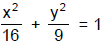 at the points P, Q and R respectively such that A and P are on the
at the points P, Q and R respectively such that A and P are on the
opposite sides, Q and B are on the same side and C and R are on the same side of the major axis. If ΔPQR
is right angled at P and θ is the smallest angle of the ΔABC, then find the value of 16tan2θ + 8 tan θ + 9.
Correct answer is '24'. Can you explain this answer?
An isosceles ΔABC is inscribed in the circle x2 + y2 = 16. From points A, B and C three ordinates are drawn
which cut the ellipse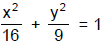 at the points P, Q and R respectively such that A and P are on the
at the points P, Q and R respectively such that A and P are on the
opposite sides, Q and B are on the same side and C and R are on the same side of the major axis. If ΔPQR
is right angled at P and θ is the smallest angle of the ΔABC, then find the value of 16tan2θ + 8 tan θ + 9.
which cut the ellipse
opposite sides, Q and B are on the same side and C and R are on the same side of the major axis. If ΔPQR
is right angled at P and θ is the smallest angle of the ΔABC, then find the value of 16tan2θ + 8 tan θ + 9.
|
|
Anaya Patel answered |
Match the statements in column-I with the statements in column-II.
Column-I Column-II
(A) A tight string is fixed at both ends and (p) At the middle, antinode is formed
sustaining standing wave in odd harmonic
(B) A tight string is fixed at one end and (q) At the middle, node is formed
free at the other end in even harmonic
(C) Standing wave is formed in an open organ (r) At the middle, neither node nor
pipe. End correction is not negligible. antinode is formed
(D) Standing wave is formed in a closed (s) Phase difference between SHMs of any
organ pipe. End correction is not negligible. two particles will be either p or zero. (t) The displacement of the particle in the middle is always non zero.- a)(A) p,q,s (B) r,s (C) s (D) r,s
- b)(A) r,q (B) s (C) p,q,r (D) p
- c)(A) r (B) p,q (C) r,p (D) p,q
- d)(A) r (B) q (C) p,q (D) r
Correct answer is option 'A'. Can you explain this answer?
Match the statements in column-I with the statements in column-II.
Column-I Column-II
(A) A tight string is fixed at both ends and (p) At the middle, antinode is formed
sustaining standing wave in odd harmonic
(B) A tight string is fixed at one end and (q) At the middle, node is formed
free at the other end in even harmonic
(C) Standing wave is formed in an open organ (r) At the middle, neither node nor
pipe. End correction is not negligible. antinode is formed
(D) Standing wave is formed in a closed (s) Phase difference between SHMs of any
organ pipe. End correction is not negligible. two particles will be either p or zero.
Column-I Column-II
(A) A tight string is fixed at both ends and (p) At the middle, antinode is formed
sustaining standing wave in odd harmonic
(B) A tight string is fixed at one end and (q) At the middle, node is formed
free at the other end in even harmonic
(C) Standing wave is formed in an open organ (r) At the middle, neither node nor
pipe. End correction is not negligible. antinode is formed
(D) Standing wave is formed in a closed (s) Phase difference between SHMs of any
organ pipe. End correction is not negligible. two particles will be either p or zero.
(t) The displacement of the particle in the middle is always non zero.
a)
(A) p,q,s (B) r,s (C) s (D) r,s
b)
(A) r,q (B) s (C) p,q,r (D) p
c)
(A) r (B) p,q (C) r,p (D) p,q
d)
(A) r (B) q (C) p,q (D) r

|
Aadhar Academy answered |
(A) Number of loops (of length λ/2) will be even or odd and node or antinode will respectively be formed at the
middle.
Phase of difference between two particle in same loop will be zero and that between two particles in adjacent
loops will be π.
(B) and (D) Number of loops will not be integral. Hence neither a node nor an antinode will be formed in in the
middle.
Phase of difference between two particle in same loop will be zero and that between two particles in adjacent
loops will be π.
(C) Number of loops (of length λ/2) will be even or odd and antinode or node will respectively be formed at the
middle.
Phase of difference between two particle in same loop will be zero and that between two particles in adjacent loops will be π ..
middle.
Phase of difference between two particle in same loop will be zero and that between two particles in adjacent
loops will be π.
(B) and (D) Number of loops will not be integral. Hence neither a node nor an antinode will be formed in in the
middle.
Phase of difference between two particle in same loop will be zero and that between two particles in adjacent
loops will be π.
(C) Number of loops (of length λ/2) will be even or odd and antinode or node will respectively be formed at the
middle.
Phase of difference between two particle in same loop will be zero and that between two particles in adjacent loops will be π ..
A current of 2.68 A is passed for one hour through an aqueous solution of CuSO4 using copper electrodes . Select the correct statement(s) from the following :- a)increase in mass of cathode = 3.174 g
- b)decrease in mass of anode = 3.174 g
- c)no change in masses of electrodes
- d)the ratio between the change of masses of cathode and anode is 1 : 2 .
Correct answer is option 'A,B'. Can you explain this answer?
A current of 2.68 A is passed for one hour through an aqueous solution of CuSO4 using copper electrodes . Select the correct statement(s) from the following :
a)
increase in mass of cathode = 3.174 g
b)
decrease in mass of anode = 3.174 g
c)
no change in masses of electrodes
d)
the ratio between the change of masses of cathode and anode is 1 : 2 .
|
|
Anaya Patel answered |
Increase in mass of cathode = decrease in mass of Anode =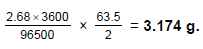
For Cyclooctatetraene which is/are correct :- a)There are two types of C–C bond.
- b)Structure is non planar and resonance is not observed in molecule.
- c)Extensive resonance is found within the molecule and all bonds are of same type.
- d)It is non aromatic tub-shape molecule.
Correct answer is option 'A,B,D'. Can you explain this answer?
For Cyclooctatetraene which is/are correct :
a)
There are two types of C–C bond.
b)
Structure is non planar and resonance is not observed in molecule.
c)
Extensive resonance is found within the molecule and all bonds are of same type.
d)
It is non aromatic tub-shape molecule.
|
|
Anaya Patel answered |

Hailstones falling vertically with a speed of 10 m/s, hit the wind screen (wind screen makes an angle 30° with the horizontal) of a moving car and rebound elastically. The velocity of the car if the driver finds the hailstones rebound vertically after striking is :- a)10√3 m/s
- b)20√3 m/s
- c)10 m/s
- d)10/√3m/s
Correct answer is option 'A'. Can you explain this answer?
Hailstones falling vertically with a speed of 10 m/s, hit the wind screen (wind screen makes an angle 30° with the horizontal) of a moving car and rebound elastically. The velocity of the car if the driver finds the hailstones rebound vertically after striking is :
a)
10√3 m/s
b)
20√3 m/s
c)
10 m/s
d)
10/√3m/s
|
|
Preeti Iyer answered |
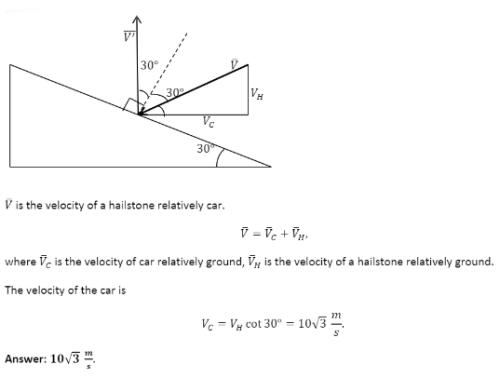
Figure shows block A of mass 0.2 kg sliding to the right over a frictionless elevated surface at a speed of 10 m/s. The block undergoes a collision with stationary block B, which is connected to a nondeformed spring of spring constant 1000 Nm–1. The coefficient of restitution between the blocks is 0.5. After the collision, block B oscillates in SHM with a period of 0.2 s, and block A slides off the left end of the elevated surface, landing a distance 'd' from the base of that surface after falling height 5m. (use π2 = 10; g = 10 m/s2) Assume that the spring does not affect the collision. 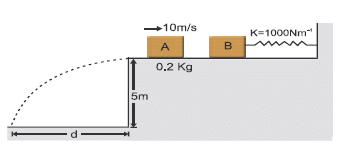 Amplitude of the SHM as being executed by block B-spring system, is -
Amplitude of the SHM as being executed by block B-spring system, is -- a)2.5√10 cm
- b)10 cm
- c)3√10cm
- d)5√10cm
Correct answer is option 'A'. Can you explain this answer?
Figure shows block A of mass 0.2 kg sliding to the right over a frictionless elevated surface at a speed of 10 m/s. The block undergoes a collision with stationary block B, which is connected to a nondeformed spring of spring constant 1000 Nm–1. The coefficient of restitution between the blocks is 0.5. After the collision, block B oscillates in SHM with a period of 0.2 s, and block A slides off the left end of the elevated surface, landing a distance 'd' from the base of that surface after falling height 5m. (use π2 = 10; g = 10 m/s2) Assume that the spring does not affect the collision.
Amplitude of the SHM as being executed by block B-spring system, is -
a)
2.5√10 cm
b)
10 cm
c)
3√10cm
d)
5√10cm

|
Veda Institute answered |
Immediately after the collision, suppose velocities of the blocks are V1 and V1 as shown 1/2 vel. of approach = velocity of separation.
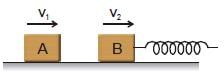
⇒ 5 = V2 - V1 .... (1)
Using principle of conservation of momentum for the collision
2 = 0.2 V1 + V2
or 10 = V1 + 5V2 .....(2)
On solving V2 = 2.5 m/s; V1 = - 2.5 m/s
Hence block A moves leftward after the collision with speed 2.5 m/s. And the block B moves towards right with speed 2.5 m/s.
The maximum velocity of B = 2.5 = ωA
⇒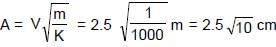

⇒ 5 = V2 - V1 .... (1)
Using principle of conservation of momentum for the collision
2 = 0.2 V1 + V2
or 10 = V1 + 5V2 .....(2)
On solving V2 = 2.5 m/s; V1 = - 2.5 m/s
Hence block A moves leftward after the collision with speed 2.5 m/s. And the block B moves towards right with speed 2.5 m/s.
The maximum velocity of B = 2.5 = ωA
⇒
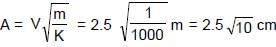
In the figure shown a small block ‘B’ of mass ‘m’ is released from the top of a smooth movable wedge ‘A’ of the same mass ‘m’. ‘B’ ascends another movable smooth wedge ‘C’ of the same mass. Neglecting friction any where the maximum height attained by ‘B’ on ‘C’ is h/2x Find the value of x .
Correct answer is '2'. Can you explain this answer?
In the figure shown a small block ‘B’ of mass ‘m’ is released from the top of a smooth movable wedge ‘A’ of the same mass ‘m’. ‘B’ ascends another movable smooth wedge ‘C’ of the same mass. Neglecting friction any where the maximum height attained by ‘B’ on ‘C’ is h/2x Find the value of x .
|
|
Dev Kumar answered |
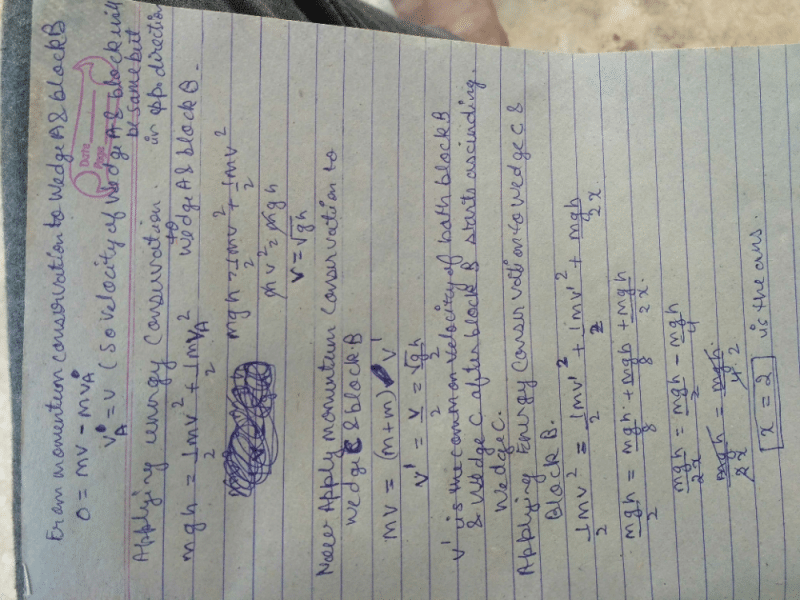
In a head-on elastic collision of two bodies of equal masses- a)the velocities are interchanged
- b)the speeds are interchanged
- c)the momenta are interchanged
- d)the faster body slows down and the slower body speeds up
Correct answer is option 'A,B,C,D'. Can you explain this answer?
In a head-on elastic collision of two bodies of equal masses
a)
the velocities are interchanged
b)
the speeds are interchanged
c)
the momenta are interchanged
d)
the faster body slows down and the slower body speeds up
|
|
Hiral Rane answered |
Understanding Head-On Elastic Collisions
In a head-on elastic collision involving two bodies of equal masses, several important principles apply. Here’s a breakdown of the outcomes:
1. Velocities are Interchanged
- In an elastic collision, the law of conservation of momentum and kinetic energy applies.
- When two bodies of equal mass collide, their velocities effectively swap.
- If Body A moves towards Body B with velocity V1 and Body B moves towards Body A with velocity V2, after the collision, Body A will take on the velocity of Body B and vice versa.
2. Speeds are Interchanged
- Since the masses are equal, the speeds (magnitude of velocity) are also exchanged.
- This means if Body A was faster, it slows down while Body B speeds up to match the speed of Body A prior to the collision.
3. Momenta are Interchanged
- The momentum of a body is the product of its mass and velocity.
- In this case, because the masses are equal and velocities are interchanged, the momenta are also effectively swapped between the two bodies.
4. The Faster Body Slows Down and the Slower Body Speeds Up
- The kinetic energy, which is proportional to the square of the speed, is conserved in elastic collisions.
- As a result, the faster body loses some speed while the slower body gains speed, leading to an overall exchange of kinetic energy.
In summary, for two equal-mass bodies in a head-on elastic collision, the outcomes are interconnected: velocities, speeds, and momenta are interchanged, and each body adjusts its speed accordingly based on its initial conditions.
In a head-on elastic collision involving two bodies of equal masses, several important principles apply. Here’s a breakdown of the outcomes:
1. Velocities are Interchanged
- In an elastic collision, the law of conservation of momentum and kinetic energy applies.
- When two bodies of equal mass collide, their velocities effectively swap.
- If Body A moves towards Body B with velocity V1 and Body B moves towards Body A with velocity V2, after the collision, Body A will take on the velocity of Body B and vice versa.
2. Speeds are Interchanged
- Since the masses are equal, the speeds (magnitude of velocity) are also exchanged.
- This means if Body A was faster, it slows down while Body B speeds up to match the speed of Body A prior to the collision.
3. Momenta are Interchanged
- The momentum of a body is the product of its mass and velocity.
- In this case, because the masses are equal and velocities are interchanged, the momenta are also effectively swapped between the two bodies.
4. The Faster Body Slows Down and the Slower Body Speeds Up
- The kinetic energy, which is proportional to the square of the speed, is conserved in elastic collisions.
- As a result, the faster body loses some speed while the slower body gains speed, leading to an overall exchange of kinetic energy.
In summary, for two equal-mass bodies in a head-on elastic collision, the outcomes are interconnected: velocities, speeds, and momenta are interchanged, and each body adjusts its speed accordingly based on its initial conditions.
Light of wavelength 4000 Å is incident at small angle on a prism of apex angle 4º. The prism has nv = 1.5 & nr = 1.48. The angle of dispersion produced by the prism in this light is : - a)0.2º
- b)0.08º
- c)0.192º
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
Light of wavelength 4000 Å is incident at small angle on a prism of apex angle 4º. The prism has nv = 1.5 & nr = 1.48. The angle of dispersion produced by the prism in this light is :
a)
0.2º
b)
0.08º
c)
0.192º
d)
none of these
|
|
Rishika Bose answered |

In the shown circuit involving a resistor of resistance R W, capacitor of capacitance C farad and an ideal cell of emf E volts, the capacitor is initially uncharged and the key is in position 1. At t = 0 second the key is pushed to position 2 for t0 = RC seconds and then key is pushed back to position 1 for t0 = RC seconds. This process is repeated again and again. Assume the time taken to push key from position 1 to 2 and vice versa to be negligible.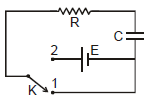 Q. The charge on capacitor at t = 2RC second is
Q. The charge on capacitor at t = 2RC second is - a)CE
- b)
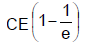
- c)
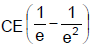
- d)
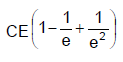
Correct answer is option 'C'. Can you explain this answer?
In the shown circuit involving a resistor of resistance R W, capacitor of capacitance C farad and an ideal cell of emf E volts, the capacitor is initially uncharged and the key is in position 1. At t = 0 second the key is pushed to position 2 for t0 = RC seconds and then key is pushed back to position 1 for t0 = RC seconds. This process is repeated again and again. Assume the time taken to push key from position 1 to 2 and vice versa to be negligible.

Q. The charge on capacitor at t = 2RC second is
a)
CE
b)
c)
d)

|
Kamna Science Academy answered |
For t = 0 to t0 = RC seconds, the circuit is of charging type. The charging equation for this time is
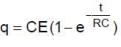
Therefore the charge on capacitor at time t0 = RC is q0
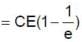
For t = RC to t = 2RC seconds, the circuit is of discharging type. The charge and current equation for this time are
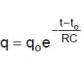 and
and 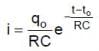
Hence charge at t = 2 RC and current at t = 1.5 RC are
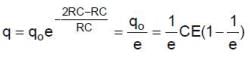
and
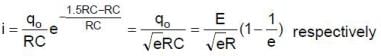
Since the capacitor gets more charged up from t = 2RC to t = 3RC than in the interval t = 0 to t = RC, the graph representing the charge variation is as shown in figure
The minimum value of 3x + 4y, subject to the condition x2y3 = 6 and x > 0, y > 0, is
Correct answer is '10'. Can you explain this answer?
The minimum value of 3x + 4y, subject to the condition x2y3 = 6 and x > 0, y > 0, is
|
|
Ajay Yadav answered |
Break 3x as 3x/2 and 3x/2 and 4y as 4y/3, 4y/3 and 4y/3.
Now, we know that AM ≥ GM.
So, applying on numbers 3x/2, 3x/2 and 4y/3, 4y/3 and 4y/3,
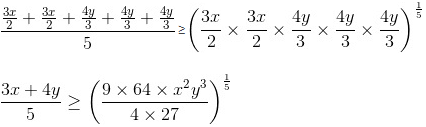
Putting the value of x2y3 = 6, we get
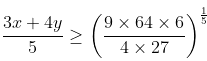
3x + 4y ≥ 10
Minimum value of 3x + 4y = 10
Chapter doubts & questions for JEE Main & Advanced Mock Test Series 2026 - Mock Tests for JEE Main and Advanced 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of JEE Main & Advanced Mock Test Series 2026 - Mock Tests for JEE Main and Advanced 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily