All Exams >
Commerce >
Applied Mathematics for Class 12 >
All Questions
All questions of Boats and Streams for Commerce Exam
A boat can travel with a speed of 22 km/hr in still water. If the speed of the stream is 5 km/hr, find the time taken by the boat to go 54 km downstream.
- a)5 hours
- b)4 hours
- c)3 hours
- d)2 hours
Correct answer is option 'D'. Can you explain this answer?
a)
5 hours
b)
4 hours
c)
3 hours
d)
2 hours
|
Naroj Boda answered |
Speed downstream = (22 + 5) km/hr = 27 km/hr.
Time taken to travel 54 km downstream = (54/27) hours
= 2 hours
A man can row at 5 kmph in still water. If the velocity of current is 1 kmph and it takes him 1 hour to row to a place and come back, how far is the place?
- a)3.2 km
- b)3 km
- c)2.4 km
- d)3.6 km
Correct answer is option 'C'. Can you explain this answer?
a)
3.2 km
b)
3 km
c)
2.4 km
d)
3.6 km
|
EduRev SSC CGL answered |
Let the distance is x km
Rate downstream = 5 + 1 = 6 kmph
Rate upstream = 5 - 1 = 4 kmph
then
x/6 + x/4 = 1 [because distance/speed = time]
⇒ 2x + 3x = 12
⇒ x = 12/5
= 2.4 km
Rate downstream = 5 + 1 = 6 kmph
Rate upstream = 5 - 1 = 4 kmph
then
x/6 + x/4 = 1 [because distance/speed = time]
⇒ 2x + 3x = 12
⇒ x = 12/5
= 2.4 km
So option C is correct
Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
- a)700 hours
- b)350 hours
- c)1400 hours
- d)1010 hours
Correct answer is option 'A'. Can you explain this answer?
a)
700 hours
b)
350 hours
c)
1400 hours
d)
1010 hours
|
Aditya Kumar answered |
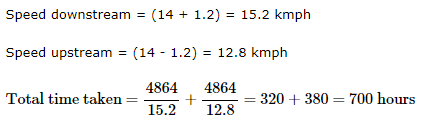
A boat running downstream covers a distance of 22 km in 4 hours while for covering the same distance upstream, it takes 5 hours. What is the speed of the boat in still water?
- a)5 kmph
- b)4.95 kmph
- c)4.75 kmph
- d)4.65 kmph
Correct answer is option 'B'. Can you explain this answer?
a)
5 kmph
b)
4.95 kmph
c)
4.75 kmph
d)
4.65 kmph
|
Palak Sharma answered |
Let's assume that the speed of the boat in still water is x km/h, and the speed of the current is y km/h.
When the boat is traveling downstream, it gets a boost from the current, so its effective speed is increased by the speed of the current. Therefore, the speed of the boat downstream is (x + y) km/h.
Similarly, when the boat is traveling upstream, it has to work against the current, so its effective speed is decreased by the speed of the current. Therefore, the speed of the boat upstream is (x - y) km/h.
We are given that the boat covers a distance of 22 km downstream in 4 hours. Using the formula speed = distance/time, we can write the equation:
(x + y) = 22/4
Simplifying this equation, we get:
x + y = 5.5
We are also given that the boat covers the same distance of 22 km upstream in 5 hours. Using the same formula, we can write the equation:
(x - y) = 22/5
Simplifying this equation, we get:
x - y = 4.4
Now we have a system of equations with two variables (x and y). We can solve this system of equations to find the values of x and y.
Adding the two equations together, we get:
(x + y) + (x - y) = 5.5 + 4.4
Simplifying, we get:
2x = 9.9
Dividing both sides by 2, we get:
x = 4.95
Therefore, the speed of the boat in still water is 4.95 km/h, which corresponds to option B.
When the boat is traveling downstream, it gets a boost from the current, so its effective speed is increased by the speed of the current. Therefore, the speed of the boat downstream is (x + y) km/h.
Similarly, when the boat is traveling upstream, it has to work against the current, so its effective speed is decreased by the speed of the current. Therefore, the speed of the boat upstream is (x - y) km/h.
We are given that the boat covers a distance of 22 km downstream in 4 hours. Using the formula speed = distance/time, we can write the equation:
(x + y) = 22/4
Simplifying this equation, we get:
x + y = 5.5
We are also given that the boat covers the same distance of 22 km upstream in 5 hours. Using the same formula, we can write the equation:
(x - y) = 22/5
Simplifying this equation, we get:
x - y = 4.4
Now we have a system of equations with two variables (x and y). We can solve this system of equations to find the values of x and y.
Adding the two equations together, we get:
(x + y) + (x - y) = 5.5 + 4.4
Simplifying, we get:
2x = 9.9
Dividing both sides by 2, we get:
x = 4.95
Therefore, the speed of the boat in still water is 4.95 km/h, which corresponds to option B.
Two pipes A and B can fill a tank in 10 hrs and 40 hrs respectively. If both the pipes are opened simultaneously, how much time will be taken to fill the tank?
- a)8 hours
- b)6 hours
- c)4 hours
- d)2 hours
Correct answer is option 'A'. Can you explain this answer?
a)
8 hours
b)
6 hours
c)
4 hours
d)
2 hours
|
Kabir Verma answered |
Pipe A can fill 1/10 of the tank in 1 hr
Pipe B can fill 1/40 of the tank in 1 hr
Pipe A and B together can fill 1/10 + 1/40 = 1/8 of the tank in 1 hr
i.e., Pipe A and B together can fill the tank in 8 hours
Pipe B can fill 1/40 of the tank in 1 hr
Pipe A and B together can fill 1/10 + 1/40 = 1/8 of the tank in 1 hr
i.e., Pipe A and B together can fill the tank in 8 hours
A boat covers a certain distance downstream in 4 hours but takes 6 hours to return upstream to the starting point. If the speed of the stream be 3 km/hr, find the speed of the boat in still water
- a)15 km/hr
- b)12 km/hr
- c)13 km/hr
- d)14 km/hr
Correct answer is option 'A'. Can you explain this answer?
a)
15 km/hr
b)
12 km/hr
c)
13 km/hr
d)
14 km/hr
|
|
Kiran Reddy answered |
Let the speed of the water in still water = x
Given that speed of the stream = 3 kmph
Speed downstream = (x+3) kmph
Speed upstream = (x-3) kmph
He travels a certain distance downstream in 4 hour and come back in 6 hour.
ie, distance travelled downstream in 4 hour = distance travelled upstream in 6 hour
since distance = speed × time, we have
(x+3)4=(x−3)6
⇒ (x + 3)2 = (x - 3)3
⇒ 2x + 6 = 3x - 9
⇒ x = 6+9 = 15 kmph
Given that speed of the stream = 3 kmph
Speed downstream = (x+3) kmph
Speed upstream = (x-3) kmph
He travels a certain distance downstream in 4 hour and come back in 6 hour.
ie, distance travelled downstream in 4 hour = distance travelled upstream in 6 hour
since distance = speed × time, we have
(x+3)4=(x−3)6
⇒ (x + 3)2 = (x - 3)3
⇒ 2x + 6 = 3x - 9
⇒ x = 6+9 = 15 kmph
A boatman goes 2 km against the current of the stream in 1 hour and goes 1 km along the current in 10 minutes. How long will it take to go 5 km in stationary water?- a)1 hr 15 min
- b)2 hr
- c)4 hr
- d)2 hr 30 min
Correct answer is option 'A'. Can you explain this answer?
A boatman goes 2 km against the current of the stream in 1 hour and goes 1 km along the current in 10 minutes. How long will it take to go 5 km in stationary water?
a)
1 hr 15 min
b)
2 hr
c)
4 hr
d)
2 hr 30 min
|
Rishabh Rane answered |
Rate downstream =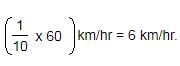 
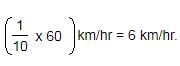
Rate upstream = 2 km/hr.
Speed in still water =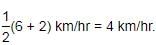 
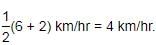
Required time = 
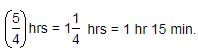
A Cistern is filled by pipe A in 8 hrs and the full Cistern can be leaked out by an exhaust pipe B in 12 hrs. If both the pipes are opened in what time the Cistern is full?
- a)12 hrs
- b)24 hrs
- c)16 hrs
- d)32 hrs
Correct answer is option 'B'. Can you explain this answer?
a)
12 hrs
b)
24 hrs
c)
16 hrs
d)
32 hrs
|
|
Bhavya Chopra answered |
Given Data:
- Pipe A fills the cistern in 8 hours.
- Pipe B can empty the cistern in 12 hours.
Approach:
- First, find the rate of filling of pipe A and rate of emptying of pipe B.
- Then, calculate the net rate of both pipes working together.
- Use the net rate to find the time taken to fill the cistern.
Calculation:
- Rate of filling by pipe A = 1/8 cistern/hour
- Rate of emptying by pipe B = 1/12 cistern/hour
- Net rate of filling when both pipes are open = (1/8) - (1/12) = 1/24 cistern/hour
- Time taken to fill the cistern when both pipes are open = 1 / (1/24) = 24 hours
Therefore, the cistern will be filled in 24 hours when both pipes A and B are open simultaneously. Hence, the correct answer is option 'B' (24 hrs).
- Pipe A fills the cistern in 8 hours.
- Pipe B can empty the cistern in 12 hours.
Approach:
- First, find the rate of filling of pipe A and rate of emptying of pipe B.
- Then, calculate the net rate of both pipes working together.
- Use the net rate to find the time taken to fill the cistern.
Calculation:
- Rate of filling by pipe A = 1/8 cistern/hour
- Rate of emptying by pipe B = 1/12 cistern/hour
- Net rate of filling when both pipes are open = (1/8) - (1/12) = 1/24 cistern/hour
- Time taken to fill the cistern when both pipes are open = 1 / (1/24) = 24 hours
Therefore, the cistern will be filled in 24 hours when both pipes A and B are open simultaneously. Hence, the correct answer is option 'B' (24 hrs).
A man rows to a place 48 km distant and come back in 14 hours. He finds that he can row 4 km with the stream in the same time as 3 km against the stream. The rate of the stream is:
- a) 1 km/hr
- b) 2 km/hr.
- c) 1.5 km/hr.
- d) 2.5 km/hr.
Correct answer is option `A`. Can you explain this answer?
a) 1 km/hr
b) 2 km/hr.
c) 1.5 km/hr.
d) 2.5 km/hr.
|
Rohan Chauhan answered |
A man can row 18 km upstream and 42 km downstream in 6 hours. Also he can row 30 km upstream and 28 km downstream in 7 hours. Find the speed of the man in still water.- a)8 km/h
- b)10 km/h
- c)4 km/h
- d)12 km/h
Correct answer is option 'B'. Can you explain this answer?
A man can row 18 km upstream and 42 km downstream in 6 hours. Also he can row 30 km upstream and 28 km downstream in 7 hours. Find the speed of the man in still water.
a)
8 km/h
b)
10 km/h
c)
4 km/h
d)
12 km/h
|
Learning Education answered |
Let the speed of boat and speed of stream be x km/hr and y km/hr respectively
So, D = 1/(x + y) km/hr
U = 1/(x – y) km/hr
According to the question,
[18U)] + [42D] = 6 ----(i)
[30U] + [28D] = 7 ----(ii)
Now, multiplying equation (i) by 5 and equation (ii) by 3 and then subtracting
210D - 84D = 9 ----(iii)
126D = 9
x + y = 14
18U = 3
x - y = 6
x = (14 + 6)/2 = 10 km/hr.
The answer is 10km/hr
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Boats and Streams" under Logical Reasoning. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. A man's speed with the current is 15 km/hr and the speed of the current is 2.5 km/hr. The man's speed against the current is:- a)8.5 km/hr
- b)10 km/hr.
- c)12.5 km/hr
- d)9 km/hr
Correct answer is option 'B'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Boats and Streams" under Logical Reasoning. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. A man's speed with the current is 15 km/hr and the speed of the current is 2.5 km/hr. The man's speed against the current is:
a)
8.5 km/hr
b)
10 km/hr.
c)
12.5 km/hr
d)
9 km/hr
|
Tanvi Dey answered |
Man's speed with the current = 15 km/hr
=> speed of the man + speed of the current = 15 km/hr
speed of the current is 2.5 km/hr
Hence, speed of the man = 15 - 2.5 = 12.5 km/hr
man's speed against the current = speed of the man - speed of the current
= 12.5 - 2.5 = 10 km/hr
A boat running upstream takes 8 hours 48 minutes to cover a certain distance, while it takes 4 hours to cover the same distance running downstream. What is the ratio between the speed of the boat and speed of the water current respectively?
- a)5 : 6
- b)6 : 5
- c)8 : 3
- d)3 : 8
Correct answer is option 'C'. Can you explain this answer?
a)
5 : 6
b)
6 : 5
c)
8 : 3
d)
3 : 8
|
|
Rohan Chauhan answered |
Let the man's rate upstream be x kmph and that downstream be y kmph.
Then, distance covered upstream in 8 hrs 48 min = Distance covered downstream in 4 hrs.
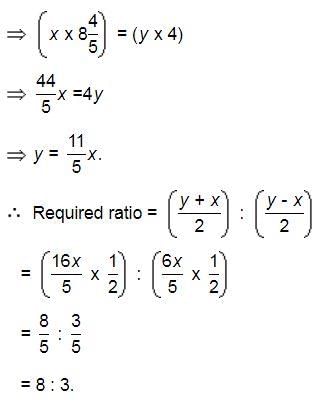
In a river flowing at 2 km/hr, a boat travels 32 km upstream and then returns downstream to the starting point. If its speed in still water be 6 km/hr, find the total journey time.
- a)10 hours
- b)12 hours
- c)14 hours
- d)16 hours
Correct answer is option 'B'. Can you explain this answer?
a)
10 hours
b)
12 hours
c)
14 hours
d)
16 hours
|
|
Anushka Choudhury answered |
speed of the boat = 6 km/hr
Speed downstream = (6+2) = 8 km/hr
Speed upstream = (6-2) = 4 km/hr
Distance travelled downstream = Distance travelled upstream = 32 km
Total time taken = Time taken downstream + Time taken upstream
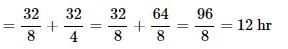
Chapter doubts & questions for Boats and Streams - Applied Mathematics for Class 12 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Boats and Streams - Applied Mathematics for Class 12 in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Applied Mathematics for Class 12
64 videos|110 docs|63 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup