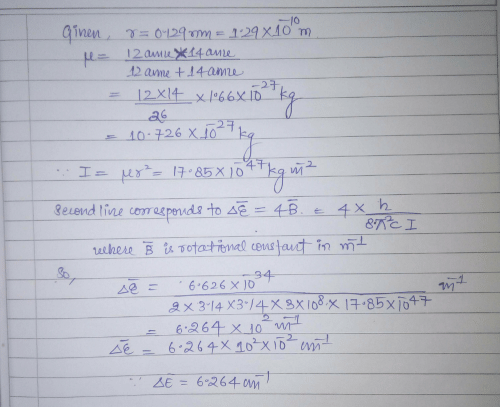All Exams >
Chemistry >
Topicwise Question Bank for IIT JAM/CSIR/GATE Chemistry >
All Questions
All questions of Physical Spectroscopy for Chemistry Exam
The increase in rotational energy shows absorption spectrum in.- a)IR region
- b)UV region
- c)Visible region
- d)Microwave region
Correct answer is option 'D'. Can you explain this answer?
The increase in rotational energy shows absorption spectrum in.
a)
IR region
b)
UV region
c)
Visible region
d)
Microwave region

|
Palak Singh answered |
Increase in Rotational Energy and Absorption Spectrum in Microwave Region
Rotational energy is the energy associated with the rotation of a molecule around its axis. When a molecule absorbs electromagnetic radiation, its rotational energy increases. This increase in rotational energy can be observed in the absorption spectrum in the microwave region.
Microwave region
The microwave region is a part of the electromagnetic spectrum that has wavelengths ranging from 1 millimeter to 1 meter and frequencies ranging from 300 MHz to 300 GHz. This region is commonly used for communication, cooking, and spectroscopy.
Absorption spectrum
An absorption spectrum is a graph that shows the wavelengths of electromagnetic radiation absorbed by a substance. It is obtained by passing a beam of electromagnetic radiation through a sample of the substance and measuring the intensity of the transmitted radiation at different wavelengths.
Increase in rotational energy and absorption spectrum in microwave region
When a molecule absorbs electromagnetic radiation in the microwave region, its rotational energy increases. This increase in rotational energy can be observed in the absorption spectrum as a series of sharp peaks or lines. These peaks or lines are known as rotational transitions.
The frequency of the absorbed radiation is directly proportional to the difference in energy between the initial and final rotational states of the molecule. This relationship is described by the equation:
ΔE = hν
where ΔE is the difference in energy, h is Planck's constant, and ν is the frequency of the absorbed radiation.
In conclusion, the increase in rotational energy of a molecule due to absorption of electromagnetic radiation can be observed in the absorption spectrum in the microwave region. This region is commonly used for spectroscopy because many molecules have rotational transitions in this region, making it useful for identifying and studying different types of molecules.
Rotational energy is the energy associated with the rotation of a molecule around its axis. When a molecule absorbs electromagnetic radiation, its rotational energy increases. This increase in rotational energy can be observed in the absorption spectrum in the microwave region.
Microwave region
The microwave region is a part of the electromagnetic spectrum that has wavelengths ranging from 1 millimeter to 1 meter and frequencies ranging from 300 MHz to 300 GHz. This region is commonly used for communication, cooking, and spectroscopy.
Absorption spectrum
An absorption spectrum is a graph that shows the wavelengths of electromagnetic radiation absorbed by a substance. It is obtained by passing a beam of electromagnetic radiation through a sample of the substance and measuring the intensity of the transmitted radiation at different wavelengths.
Increase in rotational energy and absorption spectrum in microwave region
When a molecule absorbs electromagnetic radiation in the microwave region, its rotational energy increases. This increase in rotational energy can be observed in the absorption spectrum as a series of sharp peaks or lines. These peaks or lines are known as rotational transitions.
The frequency of the absorbed radiation is directly proportional to the difference in energy between the initial and final rotational states of the molecule. This relationship is described by the equation:
ΔE = hν
where ΔE is the difference in energy, h is Planck's constant, and ν is the frequency of the absorbed radiation.
In conclusion, the increase in rotational energy of a molecule due to absorption of electromagnetic radiation can be observed in the absorption spectrum in the microwave region. This region is commonly used for spectroscopy because many molecules have rotational transitions in this region, making it useful for identifying and studying different types of molecules.
The molecule which is IR-inactive but Raman–active is:- a)N2
- b)HCl
- c)SO2
- d)Protein
Correct answer is 'A'. Can you explain this answer?
The molecule which is IR-inactive but Raman–active is:
a)
N2
b)
HCl
c)
SO2
d)
Protein

|
Bijoy Kapoor answered |
Homonuclear diatomic molecules such as H2, N2, and O2 have no dipole moment and are IR inactive (but Raman active) while heteronuclear diatomic molecules such as HCl, NO, and CO do have dipole moments and have IR active vibrations.
The rotational spectrum of HI is found to contain a series of lines with a separation of 12.8 cm–1 . Moment of for the molecule is:- a)4.36 x 10-40 g cm2
- b)1.13 x 10-39 g cm2
- c)2.23 x 10-40 g cm2
- d)8.72 x 10-40 g cm2
Correct answer is option 'A'. Can you explain this answer?
The rotational spectrum of HI is found to contain a series of lines with a separation of 12.8 cm–1 . Moment of for the molecule is:
a)
4.36 x 10-40 g cm2
b)
1.13 x 10-39 g cm2
c)
2.23 x 10-40 g cm2
d)
8.72 x 10-40 g cm2
|
|
Nirbhay Kumar answered |
Spacing between rotation spectrum is 2B. ie 2B=12.8 and B=h/8πsqIc where I is moment of inertia and c is speed of light
The Jmax for a rigid diatomic molecule for which at 300K, the rotational constant is 1.566 cm–1, is:- a)4
- b)6
- c)8
- d)10
Correct answer is option 'C'. Can you explain this answer?
The Jmax for a rigid diatomic molecule for which at 300K, the rotational constant is 1.566 cm–1, is:
a)
4
b)
6
c)
8
d)
10

|
Sinjini Nair answered |
Given information:
- Rotational constant of a rigid diatomic molecule = 1.566 cm^-1 at 300K
To find:
- Jmax value for the given molecule
Explanation:
- For a rigid diatomic molecule, the rotational energy levels are given by the expression: EJ = J(J+1)h^2/8π^2I
- Where EJ is the energy of the Jth rotational level, J is the rotational quantum number, h is Planck's constant, and I is the moment of inertia of the molecule.
- The moment of inertia of a rigid diatomic molecule is given by the expression: I = μr^2, where μ is the reduced mass of the molecule and r is the bond length.
- At a given temperature, the population of different rotational levels is given by the Boltzmann distribution: N(J) = N0 exp(-EJ/kT)
- Where N(J) is the number of molecules in the Jth rotational level, N0 is the total number of molecules, k is the Boltzmann constant, and T is the temperature in Kelvin.
- The maximum value of J, i.e., Jmax, is the value of J for which the population in the (J+1)th level is negligible compared to that in the Jth level.
- Mathematically, this can be expressed as: N(J+1)/N(J) ≈ exp(-EJ+1/kT) < />
- Taking the natural logarithm of both sides and simplifying, we get: Jmax ≈ 2.303kT/hB
- Where B is the rotational constant of the molecule.
Calculation:
- Substituting the given values, we get: Jmax ≈ 2.303(1.38×10^-23)(300)/(6.626×10^-34)(1.566×10^3)
- Solving this expression, we get: Jmax ≈ 8
Therefore, the Jmax value for the given rigid diatomic molecule is 8 (option C).
- Rotational constant of a rigid diatomic molecule = 1.566 cm^-1 at 300K
To find:
- Jmax value for the given molecule
Explanation:
- For a rigid diatomic molecule, the rotational energy levels are given by the expression: EJ = J(J+1)h^2/8π^2I
- Where EJ is the energy of the Jth rotational level, J is the rotational quantum number, h is Planck's constant, and I is the moment of inertia of the molecule.
- The moment of inertia of a rigid diatomic molecule is given by the expression: I = μr^2, where μ is the reduced mass of the molecule and r is the bond length.
- At a given temperature, the population of different rotational levels is given by the Boltzmann distribution: N(J) = N0 exp(-EJ/kT)
- Where N(J) is the number of molecules in the Jth rotational level, N0 is the total number of molecules, k is the Boltzmann constant, and T is the temperature in Kelvin.
- The maximum value of J, i.e., Jmax, is the value of J for which the population in the (J+1)th level is negligible compared to that in the Jth level.
- Mathematically, this can be expressed as: N(J+1)/N(J) ≈ exp(-EJ+1/kT) < />
- Taking the natural logarithm of both sides and simplifying, we get: Jmax ≈ 2.303kT/hB
- Where B is the rotational constant of the molecule.
Calculation:
- Substituting the given values, we get: Jmax ≈ 2.303(1.38×10^-23)(300)/(6.626×10^-34)(1.566×10^3)
- Solving this expression, we get: Jmax ≈ 8
Therefore, the Jmax value for the given rigid diatomic molecule is 8 (option C).
The normal modes of vibrations of N2O is:- a)1
- b)3
- c)4
- d)7
Correct answer is option 'C'. Can you explain this answer?
The normal modes of vibrations of N2O is:
a)
1
b)
3
c)
4
d)
7

|
Bijoy Kapoor answered |
N2O is a linear triatomic molecule and has four normal modes of vibration (and only two of rotation). Associated with each normal mode is a vibrational frequency and a normal coordinate.
Amo ng the singlet (S), doublet (D) and triplet (T). electronic states, phosphorescence involves transition between:- a)S → S
- b)D → D
- c)T → S
- d)S → T
Correct answer is option 'C'. Can you explain this answer?
Amo ng the singlet (S), doublet (D) and triplet (T). electronic states, phosphorescence involves transition between:
a)
S → S
b)
D → D
c)
T → S
d)
S → T

|
Nandini Das answered |
Phosphorescence involves transition between T and S electronic states. This can be explained as follows:
T and S states:
- T state refers to the triplet electronic state which has two unpaired electrons with opposite spins.
- S state refers to the singlet electronic state which has all electrons paired with opposite spins.
Phosphorescence:
- Phosphorescence involves the emission of light from a molecule after it has been excited to higher energy levels by absorption of light.
- In this process, electrons are excited from the ground state (S0) to the excited singlet state (S1) via absorption of a photon.
- From the excited singlet state (S1), the molecule can undergo two possible routes for de-excitation:
- It can either return to the ground state (S0) by emitting a photon, which is called fluorescence.
- Or it can undergo intersystem crossing to the triplet state (T1) and then relax to the ground state (S0) by emitting a photon, which is called phosphorescence.
Transition between T and S states:
- Intersystem crossing is a process that occurs between electronic states of different multiplicities, i.e., singlet to triplet or triplet to singlet.
- In the case of phosphorescence, the molecule undergoes intersystem crossing from the excited singlet state (S1) to the triplet state (T1).
- The transition from S to T state involves a change in electron spin, which is a quantum mechanical property.
- Therefore, the transition from S to T state is a spin-forbidden process, which means it occurs with a low probability and is relatively slow.
- However, once the molecule reaches the triplet state (T1), it can undergo radiative or non-radiative decay to the ground state (S0) with a high probability.
Conclusion:
- Thus, phosphorescence involves the transition between T and S electronic states, where the molecule undergoes intersystem crossing from S1 to T1 and then relaxes to S0 by emitting a photon.
T and S states:
- T state refers to the triplet electronic state which has two unpaired electrons with opposite spins.
- S state refers to the singlet electronic state which has all electrons paired with opposite spins.
Phosphorescence:
- Phosphorescence involves the emission of light from a molecule after it has been excited to higher energy levels by absorption of light.
- In this process, electrons are excited from the ground state (S0) to the excited singlet state (S1) via absorption of a photon.
- From the excited singlet state (S1), the molecule can undergo two possible routes for de-excitation:
- It can either return to the ground state (S0) by emitting a photon, which is called fluorescence.
- Or it can undergo intersystem crossing to the triplet state (T1) and then relax to the ground state (S0) by emitting a photon, which is called phosphorescence.
Transition between T and S states:
- Intersystem crossing is a process that occurs between electronic states of different multiplicities, i.e., singlet to triplet or triplet to singlet.
- In the case of phosphorescence, the molecule undergoes intersystem crossing from the excited singlet state (S1) to the triplet state (T1).
- The transition from S to T state involves a change in electron spin, which is a quantum mechanical property.
- Therefore, the transition from S to T state is a spin-forbidden process, which means it occurs with a low probability and is relatively slow.
- However, once the molecule reaches the triplet state (T1), it can undergo radiative or non-radiative decay to the ground state (S0) with a high probability.
Conclusion:
- Thus, phosphorescence involves the transition between T and S electronic states, where the molecule undergoes intersystem crossing from S1 to T1 and then relaxes to S0 by emitting a photon.
Which of the following diatomic molecule will not give a rotation in spectrum:- a)N2
- b)CO
- c)NO
- d)HF
Correct answer is option 'A'. Can you explain this answer?
Which of the following diatomic molecule will not give a rotation in spectrum:
a)
N2
b)
CO
c)
NO
d)
HF

|
Srishti Kulkarni answered |
Explanation:
When a diatomic molecule is irradiated with electromagnetic radiation, it absorbs energy and undergoes a rotational transition from one energy level to another. This results in the appearance of rotational lines in its spectrum. However, for a molecule to show rotational spectra, it must satisfy certain conditions. Let's see what these conditions are and then apply them to the given options.
Conditions for a molecule to show rotational spectra:
1. The molecule must be diatomic: This is because only diatomic molecules have a non-zero dipole moment and can interact with electromagnetic radiation.
2. The molecule must have a permanent dipole moment: This is necessary for the molecule to have a rotational energy level structure.
3. The molecule must not be in a vibrationally excited state: This is because a molecule in a vibrationally excited state will have a different rotational energy level structure.
Now, let's apply these conditions to the given options:
a) N2: Nitrogen is a diatomic molecule, but it has a zero dipole moment. Therefore, it cannot interact with electromagnetic radiation and will not show rotational spectra.
b) CO: Carbon monoxide is a diatomic molecule with a non-zero dipole moment. It will show rotational spectra.
c) NO: Nitric oxide is a diatomic molecule with a non-zero dipole moment. It will show rotational spectra.
d) HF: Hydrogen fluoride is a diatomic molecule with a non-zero dipole moment. It will show rotational spectra.
Therefore, the correct answer is option 'A' - N2, as it does not have a permanent dipole moment and cannot interact with electromagnetic radiation to show rotational spectra.
When a diatomic molecule is irradiated with electromagnetic radiation, it absorbs energy and undergoes a rotational transition from one energy level to another. This results in the appearance of rotational lines in its spectrum. However, for a molecule to show rotational spectra, it must satisfy certain conditions. Let's see what these conditions are and then apply them to the given options.
Conditions for a molecule to show rotational spectra:
1. The molecule must be diatomic: This is because only diatomic molecules have a non-zero dipole moment and can interact with electromagnetic radiation.
2. The molecule must have a permanent dipole moment: This is necessary for the molecule to have a rotational energy level structure.
3. The molecule must not be in a vibrationally excited state: This is because a molecule in a vibrationally excited state will have a different rotational energy level structure.
Now, let's apply these conditions to the given options:
a) N2: Nitrogen is a diatomic molecule, but it has a zero dipole moment. Therefore, it cannot interact with electromagnetic radiation and will not show rotational spectra.
b) CO: Carbon monoxide is a diatomic molecule with a non-zero dipole moment. It will show rotational spectra.
c) NO: Nitric oxide is a diatomic molecule with a non-zero dipole moment. It will show rotational spectra.
d) HF: Hydrogen fluoride is a diatomic molecule with a non-zero dipole moment. It will show rotational spectra.
Therefore, the correct answer is option 'A' - N2, as it does not have a permanent dipole moment and cannot interact with electromagnetic radiation to show rotational spectra.
Which of the following spectroscopic techniques provides the most information about an organic molecule's framework/structure?- a)UV visible spectroscopy
- b)Melting point
- c)NMR spectroscopy
- d)Mass spectrometry
Correct answer is option 'C'. Can you explain this answer?
Which of the following spectroscopic techniques provides the most information about an organic molecule's framework/structure?
a)
UV visible spectroscopy
b)
Melting point
c)
NMR spectroscopy
d)
Mass spectrometry

|
Asf Institute answered |
- NMR spectroscopy is most useful for determining the type of nuclei (most commonly studied nuclei are 1H and 13C) present and their relative locations within a molecule. H-NMR is most commonly used because it is practically present in all organic compounds.
- This technique is useful for a complete determination of the structure of organic compounds. IR spectroscopy is best for determining the functional groups of a molecule, however, it does not give information of the electric environment like NMR.
- Mass spectrometry is a technique used to determine the amount and mass of substances present in a sample. UV-visible spectroscopy is used to determine the amount of analyte present in a given sample - this method is best for transition metals and/or highly conjugated compounds.
- Melting point analysis gives information about the purity of a sample, pure substances tend to have higher melting points and more narrow ranges than impure samples.
Calculate the frequency at which the transition between the two spin states of a free electron may be observed at a field strength of 0.3000 T:- a)8.4 x 109 s-1
- b)5.39 x 108 s-1
- c)4.82 x 106 s-1
- d)1.93 x 1010 s-1
Correct answer is option 'A'. Can you explain this answer?
Calculate the frequency at which the transition between the two spin states of a free electron may be observed at a field strength of 0.3000 T:
a)
8.4 x 109 s-1
b)
5.39 x 108 s-1
c)
4.82 x 106 s-1
d)
1.93 x 1010 s-1
|
|
Vikram Kapoor answered |
Correct Answer :- a
Explanation : g = 2.0025
uN = 9.2741 * 10-24J
B = 0.300 T
v = (uN * (g) * B)/h
v = [(9.2741 * 10-24) (2.0025) * (0.300)]/(6.626 * 10-34)
= 8.408 * 109 s-1
The vibrational frequency of a homonuclear diatomic molecule is v. The temperature at which the population of the first excited state will be half that of the ground state is given by.
- a)hv . ln2 / kB
- b)hv /(ln2 . kB)
- c)ln2 /( hv . kB)
- d)hv . log 2 / kB
Correct answer is option 'B'. Can you explain this answer?
The vibrational frequency of a homonuclear diatomic molecule is v. The temperature at which the population of the first excited state will be half that of the ground state is given by.
a)
hv . ln2 / kB
b)
hv /(ln2 . kB)
c)
ln2 /( hv . kB)
d)
hv . log 2 / kB

|
Asf Institute answered |




The pure rotational (microwave) spectrum of the gaseous molecule CN consists of a series of equally spaced line separated by 3.7978 cm–1. The inter nuclear distance of the molecule is [Molar masses are 12C=12.011 and 14N=14.007 g mol–1]:- a)130 pm
- b)117 pm
- c)150 pm
- d)93 pm
Correct answer is option 'B'. Can you explain this answer?
The pure rotational (microwave) spectrum of the gaseous molecule CN consists of a series of equally spaced line separated by 3.7978 cm–1. The inter nuclear distance of the molecule is [Molar masses are 12C=12.011 and 14N=14.007 g mol–1]:
a)
130 pm
b)
117 pm
c)
150 pm
d)
93 pm

|
Saikat Ghoshal answered |
Given:
- Equally spaced lines in pure rotational (microwave) spectrum of CN
- Separation between the lines = 3.7978 cm^-1
- Molar masses of C and N = 12.011 g/mol and 14.007 g/mol, respectively
To find:
- Inter-nuclear distance of CN molecule
Formula used:
- The separation between the rotational energy levels (ΔE) of a diatomic molecule is given by:
ΔE = hB,
where h is Planck's constant and B is the rotational constant.
- The rotational constant of a diatomic molecule is given by:
B = h / (8π^2μr_e^2),
where μ is the reduced mass of the molecule, and r_e is the equilibrium bond length.
- The reduced mass (μ) of a diatomic molecule is given by:
μ = m_1m_2 / (m_1 + m_2),
where m_1 and m_2 are the masses of the two atoms in the molecule.
- The equilibrium bond length of a diatomic molecule can be estimated using the formula:
r_e = (r_1 + r_2) / 2,
where r_1 and r_2 are the covalent radii of the two atoms in the molecule.
Solution:
1. Calculate the rotational constant (B) of CN molecule using the given separation between the lines:
ΔE = hB
⇒ B = ΔE / h
⇒ B = 3.7978 cm^-1 / (6.626 x 10^-34 J s)
⇒ B = 5.72 x 10^-4 cm^-1
2. Calculate the reduced mass (μ) of CN molecule:
μ = m_1m_2 / (m_1 + m_2)
⇒ μ = 12.011 x 14.007 / (12.011 + 14.007) g/mol
⇒ μ = 6.68 g/mol
3. Estimate the equilibrium bond length (r_e) of CN molecule using the covalent radii of carbon and nitrogen:
r_e = (r_1 + r_2) / 2
⇒ r_e = (0.77 Å + 0.75 Å) / 2
⇒ r_e = 0.76 Å = 0.76 x 10^-10 m
4. Calculate the inter-nuclear distance (r) of CN molecule using the rotational constant (B) and reduced mass (μ):
B = h / (8π^2μr_e^2)
⇒ r = √(h / (8π^2μB))
⇒ r = √((6.626 x 10^-34 J s) / (8π^2 x 6.68 x 10^-3 kg/mol x 5.72 x 10^-4 cm^-1))
⇒ r = 117 pm
Therefore, the inter-nuclear distance of CN molecule is 117 pm.
- Equally spaced lines in pure rotational (microwave) spectrum of CN
- Separation between the lines = 3.7978 cm^-1
- Molar masses of C and N = 12.011 g/mol and 14.007 g/mol, respectively
To find:
- Inter-nuclear distance of CN molecule
Formula used:
- The separation between the rotational energy levels (ΔE) of a diatomic molecule is given by:
ΔE = hB,
where h is Planck's constant and B is the rotational constant.
- The rotational constant of a diatomic molecule is given by:
B = h / (8π^2μr_e^2),
where μ is the reduced mass of the molecule, and r_e is the equilibrium bond length.
- The reduced mass (μ) of a diatomic molecule is given by:
μ = m_1m_2 / (m_1 + m_2),
where m_1 and m_2 are the masses of the two atoms in the molecule.
- The equilibrium bond length of a diatomic molecule can be estimated using the formula:
r_e = (r_1 + r_2) / 2,
where r_1 and r_2 are the covalent radii of the two atoms in the molecule.
Solution:
1. Calculate the rotational constant (B) of CN molecule using the given separation between the lines:
ΔE = hB
⇒ B = ΔE / h
⇒ B = 3.7978 cm^-1 / (6.626 x 10^-34 J s)
⇒ B = 5.72 x 10^-4 cm^-1
2. Calculate the reduced mass (μ) of CN molecule:
μ = m_1m_2 / (m_1 + m_2)
⇒ μ = 12.011 x 14.007 / (12.011 + 14.007) g/mol
⇒ μ = 6.68 g/mol
3. Estimate the equilibrium bond length (r_e) of CN molecule using the covalent radii of carbon and nitrogen:
r_e = (r_1 + r_2) / 2
⇒ r_e = (0.77 Å + 0.75 Å) / 2
⇒ r_e = 0.76 Å = 0.76 x 10^-10 m
4. Calculate the inter-nuclear distance (r) of CN molecule using the rotational constant (B) and reduced mass (μ):
B = h / (8π^2μr_e^2)
⇒ r = √(h / (8π^2μB))
⇒ r = √((6.626 x 10^-34 J s) / (8π^2 x 6.68 x 10^-3 kg/mol x 5.72 x 10^-4 cm^-1))
⇒ r = 117 pm
Therefore, the inter-nuclear distance of CN molecule is 117 pm.
Upon application of a weak magnetic field, a line in the microwave absorption spectrum of rigid rotor splits into 3 lines. The quantum number (J) of the rotational energy level from which the transition originates is:
- a)1
- b)0
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
Upon application of a weak magnetic field, a line in the microwave absorption spectrum of rigid rotor splits into 3 lines. The quantum number (J) of the rotational energy level from which the transition originates is:
a)
1
b)
0
c)
2
d)
3

|
Edurev.iitjam answered |

J=1
Which of the following statements regarding electron-impact mass spectrometry is true?- a)Samples need isotopic labels.
- b)The base peak is formed by loss of one electron from each vaporised molecule by an electron beam.
- c)Compounds must have a functional group to show a mass spectrum.
- d)A meaningful mass spectrum can sometimes be obtained on a very small sample of an impure compound.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements regarding electron-impact mass spectrometry is true?
a)
Samples need isotopic labels.
b)
The base peak is formed by loss of one electron from each vaporised molecule by an electron beam.
c)
Compounds must have a functional group to show a mass spectrum.
d)
A meaningful mass spectrum can sometimes be obtained on a very small sample of an impure compound.

|
Edurev.iitjam answered |
For the electron-impact mass spectrometric method. A mass spectrum records relative abundances of the molecular cation and its fragment cations by their mass-to-charge ratios, m/z. The base peak corresponds to the most abundant cation which is not usually the molecular cation. Mass spectrometric signals of impurities do not normally obscure the significant peaks of the main compound; in fact, mass spectrometry is a useful technique for identifying impurities.
The Q band in the vibrational spectrum of acetylene is observed in the:- a)C–C stretching mode
- b)C–H symmetric mode
- c)Bending mode
- d)C–H antisymmetric stretching mode.
Correct answer is option 'A'. Can you explain this answer?
The Q band in the vibrational spectrum of acetylene is observed in the:
a)
C–C stretching mode
b)
C–H symmetric mode
c)
Bending mode
d)
C–H antisymmetric stretching mode.

|
Chirag Nambiar answered |
Understanding the Q Band in Acetylene
The vibrational spectrum of acetylene (C2H2) showcases distinct bands corresponding to different molecular vibrations. The Q band specifically relates to the vibrational transitions occurring due to the C–C bond.
Why the Q Band is Observed in C–C Stretching Mode
- C–C Stretching Mode:
- Acetylene features a triple bond between the two carbon atoms, which allows for a significant amount of energy to be absorbed during vibrations.
- The Q band corresponds to transitions where the molecule transitions between vibrational states associated with this bond.
- Vibrational Modes of Acetylene:
- Acetylene has several vibrational modes, including:
- C–H symmetric stretching
- C–H antisymmetric stretching
- Bending modes
- However, the Q band is specifically linked to the energy changes in the C–C stretching mode.
Importance of C–C Stretching in Spectroscopy
- Energy Levels:
- The stretching of the C–C bond involves significant changes in the dipole moment, making it more detectable in infrared spectroscopy.
- Spectral Significance:
- The Q band provides valuable insights into the molecular structure and bonding, specifically demonstrating the strength and character of the C–C bond in acetylene.
Conclusion
In summary, the Q band in the vibrational spectrum of acetylene is observed in the C–C stretching mode due to its significant energy absorption characteristics and its role in defining the molecular structure. Understanding this helps in analyzing molecular vibrations and their implications in spectroscopy effectively.
The vibrational spectrum of acetylene (C2H2) showcases distinct bands corresponding to different molecular vibrations. The Q band specifically relates to the vibrational transitions occurring due to the C–C bond.
Why the Q Band is Observed in C–C Stretching Mode
- C–C Stretching Mode:
- Acetylene features a triple bond between the two carbon atoms, which allows for a significant amount of energy to be absorbed during vibrations.
- The Q band corresponds to transitions where the molecule transitions between vibrational states associated with this bond.
- Vibrational Modes of Acetylene:
- Acetylene has several vibrational modes, including:
- C–H symmetric stretching
- C–H antisymmetric stretching
- Bending modes
- However, the Q band is specifically linked to the energy changes in the C–C stretching mode.
Importance of C–C Stretching in Spectroscopy
- Energy Levels:
- The stretching of the C–C bond involves significant changes in the dipole moment, making it more detectable in infrared spectroscopy.
- Spectral Significance:
- The Q band provides valuable insights into the molecular structure and bonding, specifically demonstrating the strength and character of the C–C bond in acetylene.
Conclusion
In summary, the Q band in the vibrational spectrum of acetylene is observed in the C–C stretching mode due to its significant energy absorption characteristics and its role in defining the molecular structure. Understanding this helps in analyzing molecular vibrations and their implications in spectroscopy effectively.
The rotational (microwave) spectrum of a rigid diatomic rotor consists of equally spaced lines with spacing equal to:- a)B
- b)B/2
- c)3B/2
- d)2B
Correct answer is option 'D'. Can you explain this answer?
The rotational (microwave) spectrum of a rigid diatomic rotor consists of equally spaced lines with spacing equal to:
a)
B
b)
B/2
c)
3B/2
d)
2B

|
Mrinalini Sen answered |
For a rigid rotor diatomic molecule, the selection rules for rotational transitions are ΔJ = +/-1, ΔMJ = 0 . The rotational spectrum of a diatomic molecule consists of a series of equally spaced absorption lines, typically in the microwave region of the electromagnetic spectrum.
Which of the following statements regarding mass spectrometry is wrong?- a)In a normal mass spectrometer, electron impact causes a molecule to lose an electron and become a molecular radical cation which decomposes into fragment cations and radicals.
- b)Only cations can be detected by a normal mass spectrometer.
- c)A compound whose molecules contain just one bromine atom shows two molecular ion peaks of similar intensity, one at +1 and one at -1 of the average m/z value.
- d)Molecular ion peaks always have even-numbered values of m/z.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements regarding mass spectrometry is wrong?
a)
In a normal mass spectrometer, electron impact causes a molecule to lose an electron and become a molecular radical cation which decomposes into fragment cations and radicals.
b)
Only cations can be detected by a normal mass spectrometer.
c)
A compound whose molecules contain just one bromine atom shows two molecular ion peaks of similar intensity, one at +1 and one at -1 of the average m/z value.
d)
Molecular ion peaks always have even-numbered values of m/z.

|
Asf Institute answered |
The molecular mass of a molecule containing one nitrogen atom, for example, is an odd number of atomic mass units, so its molecular ion peak has an odd numbered m/z ratio; statement (d) is wrong.
The fundamental vibration frequency and rotational constant of carbon monoxide molecule are 6.5 x 1013 s-1 and 1.743 x 1011 s-1 respectively. The rotational will have the same energy as ir would have in its first vibrational states with no rotational energy is:- a)10
- b)9
- c)19
- d)25
Correct answer is option 'C'. Can you explain this answer?
The fundamental vibration frequency and rotational constant of carbon monoxide molecule are 6.5 x 1013 s-1 and 1.743 x 1011 s-1 respectively. The rotational will have the same energy as ir would have in its first vibrational states with no rotational energy is:
a)
10
b)
9
c)
19
d)
25

|
Swara Reddy answered |
Given:
Fundamental vibration frequency (v1) = 6.5 x 10^13 s^-1
Rotational constant (B) = 1.743 x 10^11 s^-1
To find: Energy of the rotational state when there is no rotational energy in the first vibrational state.
Solution:
The energy of a vibrational state is given by the formula:
Ev = (v + 1/2)hν1
where v is the vibrational quantum number, h is Planck's constant, and ν1 is the fundamental vibration frequency.
The energy of a rotational state is given by the formula:
Er = J(J+1)hB
where J is the rotational quantum number and B is the rotational constant.
When there is no rotational energy in the first vibrational state, the quantum number J for the first vibrational state is zero. Therefore, the energy of the first vibrational state with no rotational energy is:
E1 = (0+1/2)hν1 = 1/2hν1
To find the energy of the rotational state that has the same energy as the first vibrational state with no rotational energy, we need to find the value of J that satisfies the following equation:
Er = E1
J(J+1)hB = 1/2hν1
J(J+1) = 1/2ν1/B
J(J+1) = 3.7278 x 10^3
J = 61
Therefore, the rotational state that has the same energy as the first vibrational state with no rotational energy is the state with J = 61. The energy of this state is:
Er = J(J+1)hB = 62 x 63 x 1.743 x 10^11 x 6.626 x 10^-34
Er = 1.879 x 10^-20 J
Er = 1.879 x 10^-20 x 61
Er = 1.147 x 10^-18 J
Finally, we need to convert the energy from joules to wavenumbers:
1 J = 1.196 x 10^-5 cm^-1
Er = 1.147 x 10^-18 x 1.196 x 10^-5
Er = 1.373 cm^-1
Therefore, the answer is option (c) 19.
Fundamental vibration frequency (v1) = 6.5 x 10^13 s^-1
Rotational constant (B) = 1.743 x 10^11 s^-1
To find: Energy of the rotational state when there is no rotational energy in the first vibrational state.
Solution:
The energy of a vibrational state is given by the formula:
Ev = (v + 1/2)hν1
where v is the vibrational quantum number, h is Planck's constant, and ν1 is the fundamental vibration frequency.
The energy of a rotational state is given by the formula:
Er = J(J+1)hB
where J is the rotational quantum number and B is the rotational constant.
When there is no rotational energy in the first vibrational state, the quantum number J for the first vibrational state is zero. Therefore, the energy of the first vibrational state with no rotational energy is:
E1 = (0+1/2)hν1 = 1/2hν1
To find the energy of the rotational state that has the same energy as the first vibrational state with no rotational energy, we need to find the value of J that satisfies the following equation:
Er = E1
J(J+1)hB = 1/2hν1
J(J+1) = 1/2ν1/B
J(J+1) = 3.7278 x 10^3
J = 61
Therefore, the rotational state that has the same energy as the first vibrational state with no rotational energy is the state with J = 61. The energy of this state is:
Er = J(J+1)hB = 62 x 63 x 1.743 x 10^11 x 6.626 x 10^-34
Er = 1.879 x 10^-20 J
Er = 1.879 x 10^-20 x 61
Er = 1.147 x 10^-18 J
Finally, we need to convert the energy from joules to wavenumbers:
1 J = 1.196 x 10^-5 cm^-1
Er = 1.147 x 10^-18 x 1.196 x 10^-5
Er = 1.373 cm^-1
Therefore, the answer is option (c) 19.
State which of the following molecules can show a pure rotational microwave spectrum:- a)N2
- b)CO2
- c)OCS
- d)HCl
Correct answer is option 'D'. Can you explain this answer?
State which of the following molecules can show a pure rotational microwave spectrum:
a)
N2
b)
CO2
c)
OCS
d)
HCl

|
Soumya Sengupta answered |
Explanation:
Pure rotational microwave spectrum refers to the rotational transitions of a molecule in the microwave region of the electromagnetic spectrum. For a molecule to show a pure rotational microwave spectrum, it must meet certain criteria:
1. The molecule must have a permanent dipole moment.
2. The molecule must be a linear molecule or have a symmetric top structure.
Based on these criteria, the molecule that can show a pure rotational microwave spectrum is HCl.
Explanation for each option:
a) N2: Nitrogen is a diatomic molecule with a linear structure. However, it has no permanent dipole moment, so it cannot show a pure rotational microwave spectrum.
b) CO2: Carbon dioxide is a linear molecule with a permanent dipole moment. However, it has a symmetric top structure, so it cannot show a pure rotational microwave spectrum.
c) OCS: Carbonyl sulfide has a linear structure, but it has no permanent dipole moment. Thus, it cannot show a pure rotational microwave spectrum.
d) HCl: Hydrogen chloride has a linear structure and a permanent dipole moment. Therefore, it meets both criteria for showing a pure rotational microwave spectrum.
Conclusion:
In conclusion, out of the given options, HCl is the only molecule that can show a pure rotational microwave spectrum due to its linear structure and permanent dipole moment.
Pure rotational microwave spectrum refers to the rotational transitions of a molecule in the microwave region of the electromagnetic spectrum. For a molecule to show a pure rotational microwave spectrum, it must meet certain criteria:
1. The molecule must have a permanent dipole moment.
2. The molecule must be a linear molecule or have a symmetric top structure.
Based on these criteria, the molecule that can show a pure rotational microwave spectrum is HCl.
Explanation for each option:
a) N2: Nitrogen is a diatomic molecule with a linear structure. However, it has no permanent dipole moment, so it cannot show a pure rotational microwave spectrum.
b) CO2: Carbon dioxide is a linear molecule with a permanent dipole moment. However, it has a symmetric top structure, so it cannot show a pure rotational microwave spectrum.
c) OCS: Carbonyl sulfide has a linear structure, but it has no permanent dipole moment. Thus, it cannot show a pure rotational microwave spectrum.
d) HCl: Hydrogen chloride has a linear structure and a permanent dipole moment. Therefore, it meets both criteria for showing a pure rotational microwave spectrum.
Conclusion:
In conclusion, out of the given options, HCl is the only molecule that can show a pure rotational microwave spectrum due to its linear structure and permanent dipole moment.
What is the absorbance of an IR peak with a 36% transmittance?- a)0.53
- b)0.85
- c)0.44
- d)0.12
Correct answer is option 'C'. Can you explain this answer?
What is the absorbance of an IR peak with a 36% transmittance?
a)
0.53
b)
0.85
c)
0.44
d)
0.12

|
Sahil Kapoor answered |
Absorbance Calculation:
Absorbance (A) is defined as -log(T), where T is the transmittance of light through a sample. In this case, the transmittance is given as 36%.
Calculation:
- Transmittance (T) = 36%
- Absorbance (A) = -log(36%)
Using Logarithmic Properties:
- A = -log(0.36)
- A ≈ 0.44
Therefore, the absorbance of an IR peak with a transmittance of 36% is approximately 0.44.
Therefore, the correct answer is option 'c) 0.44'.
Absorbance (A) is defined as -log(T), where T is the transmittance of light through a sample. In this case, the transmittance is given as 36%.
Calculation:
- Transmittance (T) = 36%
- Absorbance (A) = -log(36%)
Using Logarithmic Properties:
- A = -log(0.36)
- A ≈ 0.44
Therefore, the absorbance of an IR peak with a transmittance of 36% is approximately 0.44.
Therefore, the correct answer is option 'c) 0.44'.
Which hydrogen of 1-chloropent-2-ene shows the largest chemical (downfield) shift in its NMR spectrum?- a) the H on C1
- b) the H on either C2 or C3
- c) the H on C4
- d) the H on C5
Correct answer is option 'B'. Can you explain this answer?
Which hydrogen of 1-chloropent-2-ene shows the largest chemical (downfield) shift in its NMR spectrum?
a)
the H on C1
b)
the H on either C2 or C3
c)
the H on C4
d)
the H on C5

|
Asf Institute answered |
Hydrogens on unsaturated carbons generally have larger chemical shifts than those on saturated carbons.
For pure vibrational spectra, the selection rule is:- a)0
- b)±1
- c)0, ±1
- d)±1 ,2
Correct answer is option 'B'. Can you explain this answer?
For pure vibrational spectra, the selection rule is:
a)
0
b)
±1
c)
0, ±1
d)
±1 ,2

|
Anagha Chauhan answered |
Vibrational Spectra and Selection Rules
Vibrational spectroscopy is a technique used to study the vibrational motion of molecules. It provides valuable information about the chemical structure and bonding of molecules. In the context of vibrational spectroscopy, selection rules determine which transitions are allowed and which are forbidden.
Selection Rules
Selection rules are a set of criteria that determine whether a transition between two vibrational energy levels is allowed or forbidden. These rules are based on the conservation of energy, momentum, and symmetry.
The Selection Rule for Pure Vibrational Spectra
The selection rule for pure vibrational spectra is that only transitions with a change in vibrational quantum number (∆v) of ±1 are allowed. This means that the molecule can only transition from one vibrational energy level to an adjacent one, either higher or lower in energy.
Explanation
The vibrational energy levels of a molecule are quantized, meaning they can only have certain discrete values. Each vibrational energy level is characterized by a vibrational quantum number (v), which represents the number of vibrational quanta or energy units associated with that level. The ground state of a molecule has a vibrational quantum number of v=0.
When a molecule undergoes a transition from one vibrational energy level to another, it absorbs or emits energy in the form of a photon. The energy of the photon is directly related to the difference in energy between the initial and final vibrational states.
According to the selection rule, for a pure vibrational transition to be allowed, the change in vibrational quantum number (∆v) must be ±1. This means that the molecule can only absorb or emit a photon and undergo a transition to an adjacent vibrational energy level. Transitions with ∆v = 0 or ∆v > 1 are forbidden in pure vibrational spectra.
For example, if a molecule is initially in the v=0 ground state, it can transition to the v=+1 or v=-1 energy level. Transitions to higher energy levels (v>1) or lower energy levels (v<-1) are="" not="" allowed="" in="" pure="" vibrational="">
Summary
In summary, the selection rule for pure vibrational spectra states that only transitions with a change in vibrational quantum number (∆v) of ±1 are allowed. This rule is based on the conservation of energy, momentum, and symmetry. Transitions with ∆v = 0 or ∆v > 1 are forbidden in pure vibrational spectra. Understanding selection rules is essential for interpreting vibrational spectra and extracting information about the molecular structure and bonding.
Vibrational spectroscopy is a technique used to study the vibrational motion of molecules. It provides valuable information about the chemical structure and bonding of molecules. In the context of vibrational spectroscopy, selection rules determine which transitions are allowed and which are forbidden.
Selection Rules
Selection rules are a set of criteria that determine whether a transition between two vibrational energy levels is allowed or forbidden. These rules are based on the conservation of energy, momentum, and symmetry.
The Selection Rule for Pure Vibrational Spectra
The selection rule for pure vibrational spectra is that only transitions with a change in vibrational quantum number (∆v) of ±1 are allowed. This means that the molecule can only transition from one vibrational energy level to an adjacent one, either higher or lower in energy.
Explanation
The vibrational energy levels of a molecule are quantized, meaning they can only have certain discrete values. Each vibrational energy level is characterized by a vibrational quantum number (v), which represents the number of vibrational quanta or energy units associated with that level. The ground state of a molecule has a vibrational quantum number of v=0.
When a molecule undergoes a transition from one vibrational energy level to another, it absorbs or emits energy in the form of a photon. The energy of the photon is directly related to the difference in energy between the initial and final vibrational states.
According to the selection rule, for a pure vibrational transition to be allowed, the change in vibrational quantum number (∆v) must be ±1. This means that the molecule can only absorb or emit a photon and undergo a transition to an adjacent vibrational energy level. Transitions with ∆v = 0 or ∆v > 1 are forbidden in pure vibrational spectra.
For example, if a molecule is initially in the v=0 ground state, it can transition to the v=+1 or v=-1 energy level. Transitions to higher energy levels (v>1) or lower energy levels (v<-1) are="" not="" allowed="" in="" pure="" vibrational="">
Summary
In summary, the selection rule for pure vibrational spectra states that only transitions with a change in vibrational quantum number (∆v) of ±1 are allowed. This rule is based on the conservation of energy, momentum, and symmetry. Transitions with ∆v = 0 or ∆v > 1 are forbidden in pure vibrational spectra. Understanding selection rules is essential for interpreting vibrational spectra and extracting information about the molecular structure and bonding.
Which carbon of (a)-(d) of hex-3-en-2-one shows the largest (most downfield) chemical shift in the NMR spectrum?- a) C1
- b) C2
- c) C4
- d) C6
Correct answer is option 'B'. Can you explain this answer?
Which carbon of (a)-(d) of hex-3-en-2-one shows the largest (most downfield) chemical shift in the NMR spectrum?
a)
C1
b)
C2
c)
C4
d)
C6

|
Mihir Singh answered |
Chemical Shift in NMR Spectrum of Hex-3-en-2-one
Hex-3-en-2-one is a compound with a carbon-carbon double bond and a carbonyl group. The chemical shift in the NMR spectrum of this compound can be analyzed to determine which carbon atom experiences the largest (most downfield) shift.
Explanation:
- C1: Carbon 1 is directly attached to the carbonyl group, which causes it to experience a deshielding effect, leading to a downfield shift in the NMR spectrum.
- C2: Carbon 2 is part of the carbon-carbon double bond, which also experiences deshielding due to the presence of pi electrons. This results in a significant downfield shift in the NMR spectrum.
- C4: Carbon 4 is further away from the functional groups and is not as affected by deshielding effects, resulting in a smaller chemical shift compared to C1 and C2.
- C6: Carbon 6 is also not directly involved in any functional groups and experiences the least deshielding effect, leading to the smallest chemical shift in the NMR spectrum.
Therefore, in the NMR spectrum of hex-3-en-2-one, carbon 2 (C2) shows the largest (most downfield) chemical shift due to its proximity to the carbon-carbon double bond, which causes significant deshielding effects.
Hex-3-en-2-one is a compound with a carbon-carbon double bond and a carbonyl group. The chemical shift in the NMR spectrum of this compound can be analyzed to determine which carbon atom experiences the largest (most downfield) shift.
Explanation:
- C1: Carbon 1 is directly attached to the carbonyl group, which causes it to experience a deshielding effect, leading to a downfield shift in the NMR spectrum.
- C2: Carbon 2 is part of the carbon-carbon double bond, which also experiences deshielding due to the presence of pi electrons. This results in a significant downfield shift in the NMR spectrum.
- C4: Carbon 4 is further away from the functional groups and is not as affected by deshielding effects, resulting in a smaller chemical shift compared to C1 and C2.
- C6: Carbon 6 is also not directly involved in any functional groups and experiences the least deshielding effect, leading to the smallest chemical shift in the NMR spectrum.
Therefore, in the NMR spectrum of hex-3-en-2-one, carbon 2 (C2) shows the largest (most downfield) chemical shift due to its proximity to the carbon-carbon double bond, which causes significant deshielding effects.
Which of the following statements is wrong?- a) UV absorption is attributable to electronic transitions.
- b) UV spectra provide information about valence electrons.
- c)IR absorption is attributable to transitions between rotational energy levels of whole molecules.
- d) NMR spectrometers use radiofrequency electromagnetic radiation.
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is wrong?
a)
UV absorption is attributable to electronic transitions.
b)
UV spectra provide information about valence electrons.
c)
IR absorption is attributable to transitions between rotational energy levels of whole molecules.
d)
NMR spectrometers use radiofrequency electromagnetic radiation.

|
Asf Institute answered |
For a general discussion on electromagnetic radiation and spectroscopy. Transitions between molecular rotational energy levels are induced not by IR radiation, but by microwave radiation.
The increase in vibrational energy leads to absorption spectrum in:
a)IR regionb)Visible regionc)Microwave regiond)UV regionCorrect answer is option 'A'. Can you explain this answer?
a)IR region
b)Visible region
c)Microwave region
d)UV region
Correct answer is option 'A'. Can you explain this answer?

|
Shivam Sharma answered |
This leads to an increased vibrational energy level. The third route involves electrons of molecules being raised to a higher electron energy, which is the electronic transition. It's important to state that the energy is quantized and absorption of radiation causes a molecule to move to a higher internal energy level.
The frequency of UV radiation is greater than:- a)Microwaves
- b)IR radiation
- c)Both (a) and (b)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The frequency of UV radiation is greater than:
a)
Microwaves
b)
IR radiation
c)
Both (a) and (b)
d)
None of these

|
Bijoy Patel answered |
Frequency of UV radiation compared to microwaves and IR radiation
UV radiation has a higher frequency than microwaves and IR radiation. This can be explained by looking at the electromagnetic spectrum, which shows the range of wavelengths and frequencies of different types of radiation.
Electromagnetic spectrum
The electromagnetic spectrum is the range of all types of electromagnetic radiation. It includes radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays.
Frequency and wavelength
Frequency refers to the number of waves that pass a point in a given amount of time. It is measured in hertz (Hz). Wavelength refers to the distance between two consecutive peaks or troughs of a wave. It is measured in meters (m).
Relationship between frequency and wavelength
There is an inverse relationship between frequency and wavelength. This means that as the frequency of a wave increases, its wavelength decreases, and vice versa.
UV radiation
UV radiation has a higher frequency than visible light, which is why it is not visible to the human eye. It is divided into three categories based on wavelength: UVA (320-400 nm), UVB (280-320 nm), and UVC (100-280 nm).
Microwaves
Microwaves have a lower frequency than UV radiation. They are commonly used for communication and heating in microwave ovens. The frequency of microwaves is typically in the range of 300 MHz to 300 GHz.
IR radiation
IR radiation has a lower frequency than UV radiation and a higher frequency than microwaves. It is commonly used for heating and sensing. The frequency of IR radiation is typically in the range of 300 GHz to 400 THz.
Conclusion
In conclusion, UV radiation has a higher frequency than both microwaves and IR radiation. This is because it has a shorter wavelength and more waves pass a point in a given amount of time.
UV radiation has a higher frequency than microwaves and IR radiation. This can be explained by looking at the electromagnetic spectrum, which shows the range of wavelengths and frequencies of different types of radiation.
Electromagnetic spectrum
The electromagnetic spectrum is the range of all types of electromagnetic radiation. It includes radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays.
Frequency and wavelength
Frequency refers to the number of waves that pass a point in a given amount of time. It is measured in hertz (Hz). Wavelength refers to the distance between two consecutive peaks or troughs of a wave. It is measured in meters (m).
Relationship between frequency and wavelength
There is an inverse relationship between frequency and wavelength. This means that as the frequency of a wave increases, its wavelength decreases, and vice versa.
UV radiation
UV radiation has a higher frequency than visible light, which is why it is not visible to the human eye. It is divided into three categories based on wavelength: UVA (320-400 nm), UVB (280-320 nm), and UVC (100-280 nm).
Microwaves
Microwaves have a lower frequency than UV radiation. They are commonly used for communication and heating in microwave ovens. The frequency of microwaves is typically in the range of 300 MHz to 300 GHz.
IR radiation
IR radiation has a lower frequency than UV radiation and a higher frequency than microwaves. It is commonly used for heating and sensing. The frequency of IR radiation is typically in the range of 300 GHz to 400 THz.
Conclusion
In conclusion, UV radiation has a higher frequency than both microwaves and IR radiation. This is because it has a shorter wavelength and more waves pass a point in a given amount of time.
Which of (a)-(d) indicates the multiplicities for hydrogens on C1, C3, and C4 of butanone attributable to spin-spin coupling in its 1H NMR spectrum.- a)Hs on C1, singlet; Hs on C3, doublet; Hs on C4, triplet.
- b)Hs on C1, singlet; Hs on C3, triplet; Hs on C4, quartet.
- c)Hs on C1, singlet; Hs on C3, quartet; Hs on C4, triplet.
- d)Hs on C1, triplet; Hs on C3, doublet; Hs on C4, triplet.
Correct answer is option 'C'. Can you explain this answer?
Which of (a)-(d) indicates the multiplicities for hydrogens on C1, C3, and C4 of butanone attributable to spin-spin coupling in its 1H NMR spectrum.
a)
Hs on C1, singlet; Hs on C3, doublet; Hs on C4, triplet.
b)
Hs on C1, singlet; Hs on C3, triplet; Hs on C4, quartet.
c)
Hs on C1, singlet; Hs on C3, quartet; Hs on C4, triplet.
d)
Hs on C1, triplet; Hs on C3, doublet; Hs on C4, triplet.

|
Asf Institute answered |
The proton signal splits into n + 1 peaks when the adjacent carbon has n equivalent hydrogens. C1 is the isolated methyl, and C3 is the methylene linked to C4 (methyl) in butanone; Hs on C1, C3, and C4 are a singlet, a quartet, and a triplet, respectively.
All of the following molecules would exhibit two distinct singlets in a 1H-NMR spectrum except __________.- a)2,4-hexadiyne
- b)1,4-dimethylbenzene
- c)methyl-tert-butyl ether
- d)1,2,4,5-tetramethylbenzene
Correct answer is option 'A'. Can you explain this answer?
All of the following molecules would exhibit two distinct singlets in a 1H-NMR spectrum except __________.
a)
2,4-hexadiyne
b)
1,4-dimethylbenzene
c)
methyl-tert-butyl ether
d)
1,2,4,5-tetramethylbenzene

|
Isha Bose answered |
Understanding 1H-NMR Spectra
1H-NMR (Proton Nuclear Magnetic Resonance) spectroscopy is a powerful technique used to analyze the hydrogen environment in organic molecules. The number of distinct signals (singlets, doublets, etc.) in a spectrum indicates the number of different hydrogen environments.
Analyzing the Molecules
- **2,4-hexadiyne**:
- Structure: H-C≡C-C≡C-H
- This molecule has two terminal alkynes, leading to a symmetrical structure.
- Result: Exhibits **one distinct environment** for terminal protons and two different environments for the internal protons, leading to **two distinct singlets**.
- **1,4-dimethylbenzene (p-xylene)**:
- Structure: A benzene ring with two methyl groups in the para position.
- Result: The protons on the methyl groups are equivalent, leading to **two distinct singlets**.
- **Methyl-tert-butyl ether**:
- Structure: CH3-O-C(CH3)3
- The molecule has two types of environments: one for the methyl group and one for the tert-butyl protons.
- Result: Exhibits **two distinct singlets**.
- **1,2,4,5-tetramethylbenzene**:
- Structure: A benzene ring with four methyl groups positioned symmetrically.
- Result: The protons on the methyl groups are equivalent, leading to **one distinct signal**.
Conclusion
The correct answer is option **A (2,4-hexadiyne)**, which exhibits **two distinct singlets** due to its unique hydrogen environments arising from the alkyne structure. All other options result in two singlets due to the symmetry and positioning of the methyl groups in their respective structures.
1H-NMR (Proton Nuclear Magnetic Resonance) spectroscopy is a powerful technique used to analyze the hydrogen environment in organic molecules. The number of distinct signals (singlets, doublets, etc.) in a spectrum indicates the number of different hydrogen environments.
Analyzing the Molecules
- **2,4-hexadiyne**:
- Structure: H-C≡C-C≡C-H
- This molecule has two terminal alkynes, leading to a symmetrical structure.
- Result: Exhibits **one distinct environment** for terminal protons and two different environments for the internal protons, leading to **two distinct singlets**.
- **1,4-dimethylbenzene (p-xylene)**:
- Structure: A benzene ring with two methyl groups in the para position.
- Result: The protons on the methyl groups are equivalent, leading to **two distinct singlets**.
- **Methyl-tert-butyl ether**:
- Structure: CH3-O-C(CH3)3
- The molecule has two types of environments: one for the methyl group and one for the tert-butyl protons.
- Result: Exhibits **two distinct singlets**.
- **1,2,4,5-tetramethylbenzene**:
- Structure: A benzene ring with four methyl groups positioned symmetrically.
- Result: The protons on the methyl groups are equivalent, leading to **one distinct signal**.
Conclusion
The correct answer is option **A (2,4-hexadiyne)**, which exhibits **two distinct singlets** due to its unique hydrogen environments arising from the alkyne structure. All other options result in two singlets due to the symmetry and positioning of the methyl groups in their respective structures.
Which is the correct order of increasing wave number of the stretching vibrations of (1) C-H (alkane), (2) O-H (alcohol), (3) C=O (ketone), and (4) C≡C (alkyne)?- a)(4) < (3) < (2) < (1)
- b)(3) < (4) < (2) < (1)
- c)(3) < (4) < (1) < (2)
- d)(4) < (3) < (1) < (2)
Correct answer is option 'C'. Can you explain this answer?
Which is the correct order of increasing wave number of the stretching vibrations of (1) C-H (alkane), (2) O-H (alcohol), (3) C=O (ketone), and (4) C≡C (alkyne)?
a)
(4) < (3) < (2) < (1)
b)
(3) < (4) < (2) < (1)
c)
(3) < (4) < (1) < (2)
d)
(4) < (3) < (1) < (2)

|
Edurev.iitjam answered |
The stretching vibrations for C-H and O-H bonds are in the ranges 2850-2960 cm-1 and 3200-3600 cm-1, respectively, while those for C=O and C≡C are about 1700 and 2200 cm-1, as summarized.
Which carbon of (a)-(d) of hex-3-en-2-one has the smallest (most upfield) chemical shift in the NMR spectrum?- a) C1
- b) C2
- c) C4
- d) C6
Correct answer is option 'D'. Can you explain this answer?
Which carbon of (a)-(d) of hex-3-en-2-one has the smallest (most upfield) chemical shift in the NMR spectrum?
a)
C1
b)
C2
c)
C4
d)
C6

|
Edurev.iitjam answered |
C1 and C6 are methyl carbons (both sp3 hybridized) while C2 is a carbonyl and C4 is vinylic (both sp2). Of the two methyl carbons, C1 is more strongly affected (more downfield) by the carbonyl group, so the signal for C6 will be most upfield (smallest chemical shift) of the four.
The different types of energies associated with a molecule are __________.- a)Electronic energy
- b)Vibrational energy
- c)Rotational energy
- d)All of the mentioned
Correct answer is option 'D'. Can you explain this answer?
The different types of energies associated with a molecule are __________.
a)
Electronic energy
b)
Vibrational energy
c)
Rotational energy
d)
All of the mentioned
|
|
Pooja Choudhury answered |
The different types of energies associated with a molecule are electronic energy, vibrational energy, rotational energy and translational energy.
Which of the following spectroscopic techniques will be useful to dist inguish between M–SCN and M–NCS binding modes:- a)NMR
- b)IR
- c)EPR
- d)Mass
Correct answer is option 'B'. Can you explain this answer?
Which of the following spectroscopic techniques will be useful to dist inguish between M–SCN and M–NCS binding modes:
a)
NMR
b)
IR
c)
EPR
d)
Mass

|
Rahul Chatterjee answered |
In addition to identifying the type of functional groups present, IR can also be used to distinguish between different types of bonding, such as complexes containing SCN- or NO2- ligands.
SCN- can bind to the metal via either the S or N atoms, and the different coordination modes give rise to different characteristic IR frequencies.

Vibrational transitions are always accompanied by ………… transitions.- a)Vibrational
- b)Rotational
- c)Electronic
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Vibrational transitions are always accompanied by ………… transitions.
a)
Vibrational
b)
Rotational
c)
Electronic
d)
None of these

|
Shubham Rane answered |
Understanding Vibrational Transitions
Vibrational transitions in molecules occur due to changes in the vibrational energy levels of the molecules. These transitions often involve the movement of atoms within a molecule, which can affect its rotational states.
Key Points on Vibrational Transitions
- Coupling of Vibrational and Rotational Motion
When a molecule undergoes a vibrational transition, it is not isolated; it also experiences rotational changes. This is because the vibrational state of a molecule is inherently linked to its rotational state. As the atoms vibrate, they also rotate around their center of mass.
- Energy Levels
In a diatomic molecule, for example, the energy levels are quantized for both vibrational and rotational motions. When a molecule absorbs or emits energy (such as in infrared spectroscopy), it can transition to a higher vibrational state, leading to a change in its rotational state as well.
- Rotational Transitions Accompany Vibrational Changes
During a vibrational transition, the rotational quantum number can change. Therefore, when a molecule vibrates, it can simultaneously transition to a different rotational level. This is a crucial aspect in spectroscopy, where both vibrational and rotational spectra are observed.
Conclusion
In summary, vibrational transitions are always accompanied by rotational transitions due to the interconnectedness of vibrational and rotational energy levels in molecular dynamics. Thus, the correct answer to the question is option 'B' - Rotational transitions.
Vibrational transitions in molecules occur due to changes in the vibrational energy levels of the molecules. These transitions often involve the movement of atoms within a molecule, which can affect its rotational states.
Key Points on Vibrational Transitions
- Coupling of Vibrational and Rotational Motion
When a molecule undergoes a vibrational transition, it is not isolated; it also experiences rotational changes. This is because the vibrational state of a molecule is inherently linked to its rotational state. As the atoms vibrate, they also rotate around their center of mass.
- Energy Levels
In a diatomic molecule, for example, the energy levels are quantized for both vibrational and rotational motions. When a molecule absorbs or emits energy (such as in infrared spectroscopy), it can transition to a higher vibrational state, leading to a change in its rotational state as well.
- Rotational Transitions Accompany Vibrational Changes
During a vibrational transition, the rotational quantum number can change. Therefore, when a molecule vibrates, it can simultaneously transition to a different rotational level. This is a crucial aspect in spectroscopy, where both vibrational and rotational spectra are observed.
Conclusion
In summary, vibrational transitions are always accompanied by rotational transitions due to the interconnectedness of vibrational and rotational energy levels in molecular dynamics. Thus, the correct answer to the question is option 'B' - Rotational transitions.
In a rotational spectrum, transitions are only observed between rotational levels of ΔJ =- a) ±1
- b)±2
- c)+1
- d)+3
Correct answer is option 'A'. Can you explain this answer?
In a rotational spectrum, transitions are only observed between rotational levels of ΔJ =
a)
±1
b)
±2
c)
+1
d)
+3

|
Swara Dasgupta answered |
Molecular rotations require little energy to excite them. Pure rotation spectra occur in the microwave region of the spectrum (~1 - 200 cm-1). It is important to note that a molecule cannot rotate about some arbitrary axis - the principle of conservation of angular momentum dictates that only a few rotations are possible. In general, rotation must be about the centre of mass of a molecule, and the axis must allow for conservation of angular momentum. In simple cases, this can often be recognised intuitively through symmetry - such as with the water molecule.
A pure rotation spectrum can only arise when the molecule possesses a permanent electric dipole moment. Like with vibrational spectroscopy, the physical effect that couples to photons is a changing dipole moment. Since molecular bond lengths remain constant in pure rotation, the magnitude of a molecule's dipole cannot change. However, since electric dipole is a vector quantity (it has both size and direction) rotation can cause a permanent dipole to change direction, and hence we observe its spectra. Since homonuclear molecules such as dinitrogen (N2) have no dipole moment they have no rotation spectrum. Highly symmetric polyatomic molecules, such as carbon dioxide, also have no net dipole moment - the dipoles along the C-O bonds are always equal and opposite and cancel each other out. It is important to recognise also that if a molecule has a permanent dipole, but this dipole lies along the main rotation axis, then the molecule will not have a rotational spectrum - such as for a water molecule.
In pure rotational spectroscopy for a simple diatomic molecule, the energy levels - as displayed below - are given by EJ = BJ(J+1), where J is the rotational quantum number, B is the rotational constant for the particular molecule given by B = h2 / 8π2I with the unit of Joules, where I is the moment of inertia, given by I = μr2 - where r is the bond length of this particular diatomic molecule and μ is the reduced mass, given by μ = m1m2 / m1 + m2.
Most energy level transitions in spectroscopy come with selection rules. These rules restrict certain transitions from occuring - though often they can be broken. In pure rotational spectroscopy, the selection rule is ΔJ = +_1.
Which of the following statements regarding mass spectrometry is false?- a)The base peak of a simple ketone is usually attributable to an acylium ion.
- b)The molecular ion of carbonyl compounds with a -C-H readily undergoes elimination of an alkene to give a relatively stable enol radical cation.
- c)The molecular ion peak of some alcohols is very weak because it readily loses an alkyl radical to give a relatively stable oxonium (hydroxycarbenium) ion.
- d)Structurally isomeric alkanes cannot be distinguished by low resolution mass spectrometry.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements regarding mass spectrometry is false?
a)
The base peak of a simple ketone is usually attributable to an acylium ion.
b)
The molecular ion of carbonyl compounds with a -C-H readily undergoes elimination of an alkene to give a relatively stable enol radical cation.
c)
The molecular ion peak of some alcohols is very weak because it readily loses an alkyl radical to give a relatively stable oxonium (hydroxycarbenium) ion.
d)
Structurally isomeric alkanes cannot be distinguished by low resolution mass spectrometry.

|
Ameya Reddy answered |
Understanding Mass Spectrometry and Structural Isomerism
In mass spectrometry, the ability to distinguish between isomeric compounds is crucial for accurate analysis. Let's break down why option 'D' is the correct answer.
Isomeric Alkanes and Mass Spectrometry
- Structural Isomers: Alkanes can exist as structural isomers, which have the same molecular formula but different arrangements of atoms.
- Low Resolution Mass Spectrometry: Low resolution mass spectrometry typically measures mass-to-charge ratios (m/z) without providing detailed structural information. As a result, it cannot differentiate between isomers that have the same m/z value.
Why Option D is True
- Identical Molar Mass: Structurally isomeric alkanes (e.g., pentane, 2-methylbutane) possess the same molecular formula (C5H12) and hence the same molecular ion peak in low resolution mass spectrometry.
- Insufficient Resolution: Low resolution instruments lack the capability to resolve small differences in mass that would distinguish isomers, making it impossible to identify them based solely on their mass spectra.
Conclusion
- While other options (a, b, c) accurately describe specific behaviors of different functional groups in mass spectrometry, option 'D' correctly highlights a limitation of low resolution mass spectrometry in distinguishing structurally isomeric alkanes.
This understanding is critical in organic chemistry and analytical applications, where precise identification of compounds is essential.
In mass spectrometry, the ability to distinguish between isomeric compounds is crucial for accurate analysis. Let's break down why option 'D' is the correct answer.
Isomeric Alkanes and Mass Spectrometry
- Structural Isomers: Alkanes can exist as structural isomers, which have the same molecular formula but different arrangements of atoms.
- Low Resolution Mass Spectrometry: Low resolution mass spectrometry typically measures mass-to-charge ratios (m/z) without providing detailed structural information. As a result, it cannot differentiate between isomers that have the same m/z value.
Why Option D is True
- Identical Molar Mass: Structurally isomeric alkanes (e.g., pentane, 2-methylbutane) possess the same molecular formula (C5H12) and hence the same molecular ion peak in low resolution mass spectrometry.
- Insufficient Resolution: Low resolution instruments lack the capability to resolve small differences in mass that would distinguish isomers, making it impossible to identify them based solely on their mass spectra.
Conclusion
- While other options (a, b, c) accurately describe specific behaviors of different functional groups in mass spectrometry, option 'D' correctly highlights a limitation of low resolution mass spectrometry in distinguishing structurally isomeric alkanes.
This understanding is critical in organic chemistry and analytical applications, where precise identification of compounds is essential.
Which is the correct order of increasing wave number of the stretching vibrations of (1) C-H (alkane), (2) C-H (alkene), (3) C-H (alkyne), and (4) C-H (arene)?- a)(1) < (2) ≈ (3) < (4)
- b)(4) < (3) ≈ (2) < (1)
- c)(3) < (4) ≈ (2) < (1)
- d)(1) < (4) ≈ (2) < (3)
Correct answer is option 'D'. Can you explain this answer?
Which is the correct order of increasing wave number of the stretching vibrations of (1) C-H (alkane), (2) C-H (alkene), (3) C-H (alkyne), and (4) C-H (arene)?
a)
(1) < (2) ≈ (3) < (4)
b)
(4) < (3) ≈ (2) < (1)
c)
(3) < (4) ≈ (2) < (1)
d)
(1) < (4) ≈ (2) < (3)

|
Sahana Sharma answered |
Increasing wave number of the stretching vibrations of C-H bonds:
Alkane (C-H):
- Alkanes have the simplest C-H bonds.
- They have the lowest wave number among the given options.
Alkene (C-H):
- Alkenes have more double bonds compared to alkanes.
- The wave number of C-H stretching vibrations in alkenes is higher than in alkanes.
Alkyne (C-H):
- Alkynes have triple bonds, which are stronger than double bonds.
- The wave number of C-H stretching vibrations in alkynes is higher than in alkenes.
Arene (C-H):
- Arene refers to aromatic compounds like benzene.
- The C-H bonds in arenes are unique due to the resonance in the aromatic ring.
- The wave number of C-H stretching vibrations in arenes is the highest among the given options.
Therefore, the correct order of increasing wave number of the stretching vibrations is:
(1) < (4)="" ≈="" (2)="" />< (3)="" />
Alkane (C-H):
- Alkanes have the simplest C-H bonds.
- They have the lowest wave number among the given options.
Alkene (C-H):
- Alkenes have more double bonds compared to alkanes.
- The wave number of C-H stretching vibrations in alkenes is higher than in alkanes.
Alkyne (C-H):
- Alkynes have triple bonds, which are stronger than double bonds.
- The wave number of C-H stretching vibrations in alkynes is higher than in alkenes.
Arene (C-H):
- Arene refers to aromatic compounds like benzene.
- The C-H bonds in arenes are unique due to the resonance in the aromatic ring.
- The wave number of C-H stretching vibrations in arenes is the highest among the given options.
Therefore, the correct order of increasing wave number of the stretching vibrations is:
(1) < (4)="" ≈="" (2)="" />< (3)="" />
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?
- a)0 lines
- b)9 lines (multiplet)
- c)3 lines (triplet)
- d)10 lines (multiplet)
Correct answer is option 'D'. Can you explain this answer?
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?


a)
0 lines
b)
9 lines (multiplet)
c)
3 lines (triplet)
d)
10 lines (multiplet)

|
Edurev.iitjam answered |
(9+1)=10 lines
- Within 1H NMR spectroscopy there are a couple important factors to understand, including the ppm shift (Delta) and the splitting pattern. Here we are focusing on the splitting pattern for individual hydrogens. This is important for it lays the groundwork for understanding the patterns of peaks seen on large compound NMR’s.
- When determining the splitting of any hydrogen you must use the n+1 rule. Before going into that rule we must understand two things, 1. only nonequivalent hydrogens (protons) couple and 2. usually they only couple to other hydrogens (protons) attached to adjacent carbons. Nonequivalent means the protons occupy their own unique spatial environment with different atoms surrounding them.
- Typically two hydrogens attached to the same carbon are equivalent (though this isn’t always the case and you must think about where the hydrogens are located in space and see whether they are adjacent to different or similar chemical groups).
- The n+1 rule is performed as follows. N stands for the number of equivalent protons that are not equivalent to the proton of interest (the one we are trying to determine the splitting for). We multiply together each group of protons that are nonequivalent to the proton of interest. For example, lets say there are two groups of protons that are nonequivalent to the proton of interest, in group A there are 2 protons, and in group B there are 3 protons.
- We would use the n+1 rule for group A and get (2+1) = 3 and for group B get (3+1) = 4. We would then multiply these two numbers together to get the splitting for the proton of interest, thus 3 x 4 = 12 lines that the proton of interest would be split into. Proper use of this rule should allow you to get all NMR splitting questions correct (and elevate your understanding of why a certain NMR printout looks the way it does).
Which of the following statements regarding NMR spectroscopy is wrong?- a)NMR signals towards the left of the spectral chart correspond to larger chemical shifts.
- b)Chemical shifts are larger when the frequencies of the radiation which induces the nuclear transitions are higher.
- c)Chemical shifts are larger when shielding effects are greater.
- d)A hydrogen signal splits into n+1 peaks by spin-spin coupling when the number of equivalent hydrogen atoms on adjacent atom(s) is n, and no other neighbouring atoms are involved.
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements regarding NMR spectroscopy is wrong?
a)
NMR signals towards the left of the spectral chart correspond to larger chemical shifts.
b)
Chemical shifts are larger when the frequencies of the radiation which induces the nuclear transitions are higher.
c)
Chemical shifts are larger when shielding effects are greater.
d)
A hydrogen signal splits into n+1 peaks by spin-spin coupling when the number of equivalent hydrogen atoms on adjacent atom(s) is n, and no other neighbouring atoms are involved.

|
Shruti Datta answered |
Understanding NMR Spectroscopy and Chemical Shifts
Nuclear Magnetic Resonance (NMR) spectroscopy is an essential technique in chemistry, used for analyzing molecular structure. The statements provided highlight some key concepts, and option 'C' is indeed the incorrect one. Let’s explore why.
Chemical Shifts and Shielding Effects
- Chemical shifts are a measure of how far a resonance frequency of a nucleus differs from a standard reference frequency.
- Shielding refers to the effect where surrounding electrons reduce the magnetic field experienced by a nucleus, typically resulting in a lower frequency signal (downfield shift).
Why Option 'C' is Incorrect
- The statement "Chemical shifts are larger when shielding effects are greater" is misleading.
- **Greater shielding** actually leads to **smaller chemical shifts**. When a nucleus is well-shielded, it resonates at a lower frequency because the surrounding electron cloud opposes the external magnetic field.
- Conversely, **decreased shielding** (or increased deshielding) results in **larger chemical shifts** as the nucleus experiences a stronger effective magnetic field.
Clarifying Other Options
- **Option 'A'**: Correct. Signals on the left (downfield) correspond to larger chemical shifts.
- **Option 'B'**: Correct. Higher frequencies of radiation correspond to larger chemical shifts.
- **Option 'D'**: Correct. Spin-spin coupling splits a hydrogen signal into \( n+1 \) peaks, where \( n \) is the number of adjacent equivalent hydrogens.
Conclusion
Thus, in NMR spectroscopy, shielding effects, rather than enhancing chemical shifts, actually reduce them, making option 'C' the inaccurate statement. Understanding these principles is crucial for interpreting NMR spectra effectively.
Nuclear Magnetic Resonance (NMR) spectroscopy is an essential technique in chemistry, used for analyzing molecular structure. The statements provided highlight some key concepts, and option 'C' is indeed the incorrect one. Let’s explore why.
Chemical Shifts and Shielding Effects
- Chemical shifts are a measure of how far a resonance frequency of a nucleus differs from a standard reference frequency.
- Shielding refers to the effect where surrounding electrons reduce the magnetic field experienced by a nucleus, typically resulting in a lower frequency signal (downfield shift).
Why Option 'C' is Incorrect
- The statement "Chemical shifts are larger when shielding effects are greater" is misleading.
- **Greater shielding** actually leads to **smaller chemical shifts**. When a nucleus is well-shielded, it resonates at a lower frequency because the surrounding electron cloud opposes the external magnetic field.
- Conversely, **decreased shielding** (or increased deshielding) results in **larger chemical shifts** as the nucleus experiences a stronger effective magnetic field.
Clarifying Other Options
- **Option 'A'**: Correct. Signals on the left (downfield) correspond to larger chemical shifts.
- **Option 'B'**: Correct. Higher frequencies of radiation correspond to larger chemical shifts.
- **Option 'D'**: Correct. Spin-spin coupling splits a hydrogen signal into \( n+1 \) peaks, where \( n \) is the number of adjacent equivalent hydrogens.
Conclusion
Thus, in NMR spectroscopy, shielding effects, rather than enhancing chemical shifts, actually reduce them, making option 'C' the inaccurate statement. Understanding these principles is crucial for interpreting NMR spectra effectively.
Absorption of radiation in the UV range attributable to n→π* electronic transitions is characteristic of which of the following types of compounds?- a) Aromatic hydrocarbons.
- b) Unsaturated carbonyl compounds.
- c) Non-conjugated polyenes.
- d) Conjugated polyenes.
Correct answer is option 'B'. Can you explain this answer?
Absorption of radiation in the UV range attributable to n→π* electronic transitions is characteristic of which of the following types of compounds?
a)
Aromatic hydrocarbons.
b)
Unsaturated carbonyl compounds.
c)
Non-conjugated polyenes.
d)
Conjugated polyenes.

|
Asf Institute answered |
An n→π* electronic transition is the promotion of an electron from a nonbonding into a π* antibonding orbital, so is possible only for compounds with nonbonding electrons (lone pairs) as well as a π-electron system.
How many signals does the unsaturated ketone
(CH3)2CHCH2C(O)CH=CH2 have in 1H NMR and 13C NMR spectra?- a)five 1H signals and six 13C signals
- b)six 1H signals and six 13C signals
- c)six 1H signals and seven 13C signals
- d)five 1H signals and seven 13C signals
Correct answer is option 'B'. Can you explain this answer?
How many signals does the unsaturated ketone
(CH3)2CHCH2C(O)CH=CH2 have in 1H NMR and 13C NMR spectra?
(CH3)2CHCH2C(O)CH=CH2 have in 1H NMR and 13C NMR spectra?
a)
five 1H signals and six 13C signals
b)
six 1H signals and six 13C signals
c)
six 1H signals and seven 13C signals
d)
five 1H signals and seven 13C signals

|
Anshul Mehra answered |
Understanding the Structure
The compound in question, (CH3)2CHCH2C(O)CH=CH2, is an unsaturated ketone. To determine the number of signals for both 1H and 13C NMR spectra, we need to analyze its structure and identify the unique environments for hydrogen and carbon atoms.
1H NMR Signals
- The hydrogen atoms can be grouped based on their unique environments:
- **CH3 groups (2)**: The two methyl (CH3) groups attached to the isopropyl carbon contribute **2 signals**.
- **CH2 group (1)**: The methylene (CH2) group adjacent to the carbonyl contributes **1 signal**.
- **H on carbon adjacent to carbonyl (1)**: The hydrogen on the carbon adjacent to the carbonyl (C=O) contributes **1 signal**.
- **Alkenic hydrogens (2)**: The two hydrogens on the alkene (CH=CH2) contribute **2 signals**.
Thus, the total number of unique 1H signals is **6**.
13C NMR Signals
- Now, let’s analyze the carbon atoms:
- **Two CH3 groups**: Each CH3 contributes **1 signal** (total **2 signals**).
- **One CH (connected to the carbonyl)**: This carbon contributes **1 signal**.
- **One CH2 (next to the CH)**: This carbon contributes **1 signal**.
- **One carbonyl carbon (C=O)**: This contributes **1 signal**.
- **Two carbons from the alkene (C=C)**: Each contributes **1 signal** (total **2 signals**).
Thus, the total number of unique 13C signals is **6**.
Conclusion
In summary, the unsaturated ketone (CH3)2CHCH2C(O)CH=CH2 has **6 unique 1H NMR signals** and **6 unique 13C NMR signals**. Therefore, the correct answer is option **B**: six 1H signals and six 13C signals.
The compound in question, (CH3)2CHCH2C(O)CH=CH2, is an unsaturated ketone. To determine the number of signals for both 1H and 13C NMR spectra, we need to analyze its structure and identify the unique environments for hydrogen and carbon atoms.
1H NMR Signals
- The hydrogen atoms can be grouped based on their unique environments:
- **CH3 groups (2)**: The two methyl (CH3) groups attached to the isopropyl carbon contribute **2 signals**.
- **CH2 group (1)**: The methylene (CH2) group adjacent to the carbonyl contributes **1 signal**.
- **H on carbon adjacent to carbonyl (1)**: The hydrogen on the carbon adjacent to the carbonyl (C=O) contributes **1 signal**.
- **Alkenic hydrogens (2)**: The two hydrogens on the alkene (CH=CH2) contribute **2 signals**.
Thus, the total number of unique 1H signals is **6**.
13C NMR Signals
- Now, let’s analyze the carbon atoms:
- **Two CH3 groups**: Each CH3 contributes **1 signal** (total **2 signals**).
- **One CH (connected to the carbonyl)**: This carbon contributes **1 signal**.
- **One CH2 (next to the CH)**: This carbon contributes **1 signal**.
- **One carbonyl carbon (C=O)**: This contributes **1 signal**.
- **Two carbons from the alkene (C=C)**: Each contributes **1 signal** (total **2 signals**).
Thus, the total number of unique 13C signals is **6**.
Conclusion
In summary, the unsaturated ketone (CH3)2CHCH2C(O)CH=CH2 has **6 unique 1H NMR signals** and **6 unique 13C NMR signals**. Therefore, the correct answer is option **B**: six 1H signals and six 13C signals.
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?
- a)1 line (singlet)
- b)2 lines (doublet)
- c)6 lines (doublet of triplets)
- d)7 lines (septet)
Correct answer is option 'D'. Can you explain this answer?
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?


a)
1 line (singlet)
b)
2 lines (doublet)
c)
6 lines (doublet of triplets)
d)
7 lines (septet)

|
Asf Institute answered |
(6+1)=7 lines
- Within 1H NMR spectroscopy there are a couple important factors to understand, including the ppm shift (delta) and the splitting pattern. Here we are focusing on the splitting pattern for individual hydrogens. This is important for it lays the groundwork for understanding the patterns of peaks seen on large compound NMR’s.
- When determining the splitting of any hydrogen you must use the n+1 rule. Before going into that rule we must understand two things, 1. only nonequivalent hydrogens (protons) couple and 2. usually they only couple to other hydrogens (protons) attached to adjacent carbons.
- Nonequivalent means the protons occupy their own unique spatial environment with different atoms surrounding them. Typically two hydrogens attached to the same carbon are equivalent (though this isn’t always the case and you must think about where the hydrogens are located in space and see whether they are adjacent to different or similar chemical groups).
- The n+1 rule is performed as follows. N stands for the number of equivalent protons that are not equivalent to the proton of interest (the one we are trying to determine the splitting for). We multiply together each group of protons that are nonequivalent to the proton of interest.
- For example, lets say there are two groups of protons that are nonequivalent to the proton of interest, in group A there are 2 protons, and in group B there are 3 protons. We would use the n+1 rule for group A and get (2+1) = 3 and for group B get (3+1) = 4. We would then multiply these two numbers together to get the splitting for the proton of interest, thus 3 x 4 = 12 lines that the proton of interest would be split into.
- Proper use of this rule should allow you to get all NMR splitting questions correct (and elevate your understanding of why a certain NMR printout looks the way it does).
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?
- a)3 lines (triplet)
- b)8 lines (multiplet)
- c)2 lines (doublet)
- d)0 lines
Correct answer is option 'B'. Can you explain this answer?
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?


a)
3 lines (triplet)
b)
8 lines (multiplet)
c)
2 lines (doublet)
d)
0 lines

|
Asf Institute answered |
(3+1)∗(1+1)=8 lines
- Within 1H NMR spectroscopy there are a couple important factors to understand, including the ppm shift (delta) and the splitting pattern. Here we are focusing on the splitting pattern for individual hydrogens. This is important for it lays the groundwork for understanding the patterns of peaks seen on large compound NMR’s.
- When determining the splitting of any hydrogen you must use the n+1 rule. Before going into that rule we must understand two things, 1. Only nonequivalent hydrogens (protons) couple and 2. Usually they only couple to other hydrogens (protons) attached to adjacent carbons.
- Nonequivalent means the protons occupy their own unique spatial environment with different atoms surrounding them. Typically two hydrogens attached to the same carbon are equivalent (though this isn’t always the case and you must think about where the hydrogens are located in space and see whether they are adjacent to different or similar chemical groups).
- The n+1 rule is performed as follows. n stands for the number of equivalent protons that are not equivalent to the proton of interest (the one we are trying to determine the splitting for). We multiply together each group of protons that are nonequivalent to the proton of interest. For example, lets say there are two groups of protons that are nonequivalent to the proton of interest, in group A there are 2 protons, and in group B there are 3 protons.
- We would use the n+1 rule for group A and get (2+1) = 3 and for group B get (3+1) = 4. We would then multiply these two numbers together to get the splitting for the proton of interest, thus there are 12 lines that the proton of interest would be split into. Proper use of this rule should allow you to get all NMR splitting questions correct (and elevate your understanding of why a certain NMR printout looks the way it does).
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?
- a)21 lines (multiplet)
- b)7 lines (septet)
- c)1 line (singlet)
- d)2 lines (doublet)
Correct answer is option 'D'. Can you explain this answer?
Observe the underlined/bold hydrogen. In HNMR, how many spectral lines will that bolded hydrogen be split into?


a)
21 lines (multiplet)
b)
7 lines (septet)
c)
1 line (singlet)
d)
2 lines (doublet)

|
Edurev.iitjam answered |
(1+1)=2 lines
- Within 1H NMR spectroscopy there are a couple important factors to understand, including the ppm shift (delta) and the splitting pattern. Here we are focusing on the splitting pattern for individual hydrogens. This is important for it lays the groundwork for understanding the patterns of peaks seen on large compound NMR’s.
- When determining the splitting of any hydrogen you must use the n+1 rule. Before going into that rule we must understand two things, 1. only nonequivalent hydrogens (protons) couple and 2. usually they only couple to other hydrogens (protons) attached to adjacent carbons. Nonequivalent means the protons occupy their own unique spatial environment with different atoms surrounding them. Typically two hydrogens attached to the same carbon are equivalent (though this isn’t always the case and you must think about where the hydrogens are located in space and see whether they are adjacent to different or similar chemical groups).
- The n+1 rule is performed as follows. N stands for the number of equivalent protons that are not equivalent to the proton of interest (the one we are trying to determine the splitting for). We multiply together each group of protons that are nonequivalent to the proton of interest. For example, lets say there are two groups of protons that are nonequivalent to the proton of interest, in group A there are 2 protons, and in group B there are 3 protons. We would use the n+1 rule for group A and get (2+1) = 3 and for group B get (3+1) = 4. We would then multiply these two numbers together to get the splitting for the proton of interest, thus 3 x 4 = 12 lines that the proton of interest would be split into. Proper use of this rule should allow you to get all NMR splitting questions correct (and elevate your understanding of why a certain NMR printout looks the way it does).
The selection rule of the translation energy levels in the Raman spectrum is:- a)ΔJ = ±1
- b)±2
- c)+1
- d)+2
Correct answer is option 'B'. Can you explain this answer?
The selection rule of the translation energy levels in the Raman spectrum is:
a)
ΔJ = ±1
b)
±2
c)
+1
d)
+2

|
Sahana Roy answered |
Selection Rule for Translation Energy Levels in Raman Spectrum
The Raman effect is a phenomenon in which a molecule scatters incident light, leading to a change in the energy of the scattered photons. This effect can be used to obtain information about the vibrational and rotational energy levels of a molecule. However, it can also provide information on the translation energy levels of a molecule.
The selection rule for translation energy levels in the Raman spectrum is as follows:
- ΔJ = ±2
Here, J represents the rotational quantum number. This selection rule means that the Raman spectrum will only show transitions between translation energy levels that differ by a change in rotational quantum number of ±2.
Explanation of the Selection Rule
The selection rule for translation energy levels in the Raman spectrum is based on the fact that the Raman effect is a second-order scattering process. This means that the change in energy of the scattered photons is proportional to the square of the interaction between the incident light and the molecule.
In the case of translation energy levels, the interaction between the incident light and the molecule is due to the change in the polarizability of the molecule as it moves through the electric field of the incident light. This change in polarizability is related to the molecular geometry and the electronic structure of the molecule.
When a molecule undergoes a transition between translation energy levels, its geometry and electronic structure change, leading to a change in its polarizability. This change in polarizability leads to a change in the scattered light, which can be detected in the Raman spectrum.
However, for the Raman effect to be observable, the change in polarizability must be accompanied by a change in the rotational quantum number of the molecule. This is because the rotational quantum number is related to the orientation of the molecule in space, and a change in orientation leads to a change in the polarizability.
Therefore, the selection rule for translation energy levels in the Raman spectrum is ΔJ = ±2. This means that the Raman spectrum will only show transitions between translation energy levels that differ by a change in rotational quantum number of ±2.
Conclusion
In conclusion, the selection rule for translation energy levels in the Raman spectrum is ΔJ = ±2. This selection rule is based on the second-order scattering process of the Raman effect, which requires a change in the polarizability of the molecule accompanied by a change in the rotational quantum number. Understanding this selection rule is important for interpreting Raman spectra and obtaining information on the translation energy levels of a molecule.
The Raman effect is a phenomenon in which a molecule scatters incident light, leading to a change in the energy of the scattered photons. This effect can be used to obtain information about the vibrational and rotational energy levels of a molecule. However, it can also provide information on the translation energy levels of a molecule.
The selection rule for translation energy levels in the Raman spectrum is as follows:
- ΔJ = ±2
Here, J represents the rotational quantum number. This selection rule means that the Raman spectrum will only show transitions between translation energy levels that differ by a change in rotational quantum number of ±2.
Explanation of the Selection Rule
The selection rule for translation energy levels in the Raman spectrum is based on the fact that the Raman effect is a second-order scattering process. This means that the change in energy of the scattered photons is proportional to the square of the interaction between the incident light and the molecule.
In the case of translation energy levels, the interaction between the incident light and the molecule is due to the change in the polarizability of the molecule as it moves through the electric field of the incident light. This change in polarizability is related to the molecular geometry and the electronic structure of the molecule.
When a molecule undergoes a transition between translation energy levels, its geometry and electronic structure change, leading to a change in its polarizability. This change in polarizability leads to a change in the scattered light, which can be detected in the Raman spectrum.
However, for the Raman effect to be observable, the change in polarizability must be accompanied by a change in the rotational quantum number of the molecule. This is because the rotational quantum number is related to the orientation of the molecule in space, and a change in orientation leads to a change in the polarizability.
Therefore, the selection rule for translation energy levels in the Raman spectrum is ΔJ = ±2. This means that the Raman spectrum will only show transitions between translation energy levels that differ by a change in rotational quantum number of ±2.
Conclusion
In conclusion, the selection rule for translation energy levels in the Raman spectrum is ΔJ = ±2. This selection rule is based on the second-order scattering process of the Raman effect, which requires a change in the polarizability of the molecule accompanied by a change in the rotational quantum number. Understanding this selection rule is important for interpreting Raman spectra and obtaining information on the translation energy levels of a molecule.
Which of (a)-(d) indicates the correct order of carbon chemical shifts of the four carbons of the following compound.
- a)CMe < C2 < C3 < C1
- b)CMe < C3 < C2 < C1
- c)CMe < C2 < C1 < C3
- d)CMe < C1 < C2 < C3
Correct answer is option 'A'. Can you explain this answer?
Which of (a)-(d) indicates the correct order of carbon chemical shifts of the four carbons of the following compound.


a)
CMe < C2 < C3 < C1
b)
CMe < C3 < C2 < C1
c)
CMe < C2 < C1 < C3
d)
CMe < C1 < C2 < C3

|
Edurev.iitjam answered |
The chemical shift of the carbonyl carbon (C1) is the largest (most downfield), and those of the alkene carbons are the next largest Of C2 and C3, the β carbon (C3) is the more strongly influenced by the electron-withdrawing effect of the carbonyl.
Which of hydrogens a-d in the following molecule gives a triplet signal in a normal 1H NMR spectrum?
- a) hydrogen a
- b) hydrogen b
- c) hydrogen c
- d) hydrogen d
Correct answer is option 'C'. Can you explain this answer?
Which of hydrogens a-d in the following molecule gives a triplet signal in a normal 1H NMR spectrum?


a)
hydrogen a
b)
hydrogen b
c)
hydrogen c
d)
hydrogen d

|
Asf Institute answered |
A triplet signal results from the spin-spin coupling with two equivalent adjacent hydrogen atoms. For spin-spin splitting (coupling).
Which of the following statements in the context of 1H NMR spectroscopy is true?- a)Arene C-H chemical shift (δ) values are greater than simple alkenes C-H chemical shift values because of the aromatic ring current.
- b)Arene C-H chemical shift (δ) values are smaller than simple alkenes C-H chemical shift values because of the aromatic ring current.
- c)Arene C-H signals are always multiplets.
- d)Arene C-H signals are always singlets.
Correct answer is option 'A'. Can you explain this answer?
Which of the following statements in the context of 1H NMR spectroscopy is true?
a)
Arene C-H chemical shift (δ) values are greater than simple alkenes C-H chemical shift values because of the aromatic ring current.
b)
Arene C-H chemical shift (δ) values are smaller than simple alkenes C-H chemical shift values because of the aromatic ring current.
c)
Arene C-H signals are always multiplets.
d)
Arene C-H signals are always singlets.

|
Saikat Ghoshal answered |
Understanding Arene C-H Chemical Shifts in 1H NMR Spectroscopy
In the context of 1H NMR spectroscopy, the chemical shifts of hydrogen atoms in aromatic compounds (arenes) differ significantly from those in simple alkenes due to the unique electronic environment created by the aromatic ring.
1. Chemical Shift Values
- Arene C-H chemical shift values (δ) are typically higher than those for simple alkenes.
- This increase is attributed to the **aromatic ring current**, which is a result of the delocalized π-electrons in the aromatic system.
- The ring current generates an induced magnetic field that enhances the applied magnetic field at the position of the aromatic protons, leading to an upfield (higher δ) shift.
2. Implications of the Aromatic Ring Current
- The presence of the aromatic ring current affects how the protons resonate in the magnetic field.
- As a result, the protons in arenes generally resonate at a higher frequency compared to those in alkenes, which lack such a stabilizing electronic effect.
3. Multiplet vs. Singlet Signals
- While the chemical shift is higher, it is also important to note that the splitting patterns of arene C-H signals can vary.
- Typically, arene C-H signals can appear as multiplets due to the presence of neighboring hydrogen atoms (J-coupling).
- Therefore, stating that they are always multiplets or always singlets is not accurate.
Conclusion
The correct answer is option 'A' because the aromatic ring current causes arene C-H chemical shifts to be greater than those of simple alkenes, reflecting the unique electronic environment of aromatic compounds in NMR spectroscopy.
In the context of 1H NMR spectroscopy, the chemical shifts of hydrogen atoms in aromatic compounds (arenes) differ significantly from those in simple alkenes due to the unique electronic environment created by the aromatic ring.
1. Chemical Shift Values
- Arene C-H chemical shift values (δ) are typically higher than those for simple alkenes.
- This increase is attributed to the **aromatic ring current**, which is a result of the delocalized π-electrons in the aromatic system.
- The ring current generates an induced magnetic field that enhances the applied magnetic field at the position of the aromatic protons, leading to an upfield (higher δ) shift.
2. Implications of the Aromatic Ring Current
- The presence of the aromatic ring current affects how the protons resonate in the magnetic field.
- As a result, the protons in arenes generally resonate at a higher frequency compared to those in alkenes, which lack such a stabilizing electronic effect.
3. Multiplet vs. Singlet Signals
- While the chemical shift is higher, it is also important to note that the splitting patterns of arene C-H signals can vary.
- Typically, arene C-H signals can appear as multiplets due to the presence of neighboring hydrogen atoms (J-coupling).
- Therefore, stating that they are always multiplets or always singlets is not accurate.
Conclusion
The correct answer is option 'A' because the aromatic ring current causes arene C-H chemical shifts to be greater than those of simple alkenes, reflecting the unique electronic environment of aromatic compounds in NMR spectroscopy.
Chapter doubts & questions for Physical Spectroscopy - Topicwise Question Bank for IIT JAM/CSIR/GATE Chemistry 2025 is part of Chemistry exam preparation. The chapters have been prepared according to the Chemistry exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Chemistry 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Physical Spectroscopy - Topicwise Question Bank for IIT JAM/CSIR/GATE Chemistry in English & Hindi are available as part of Chemistry exam.
Download more important topics, notes, lectures and mock test series for Chemistry Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily