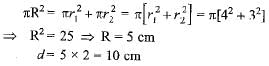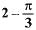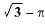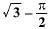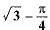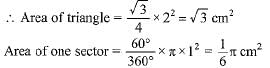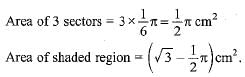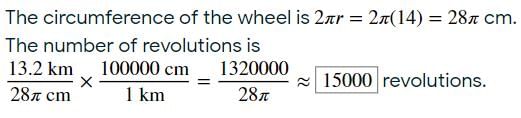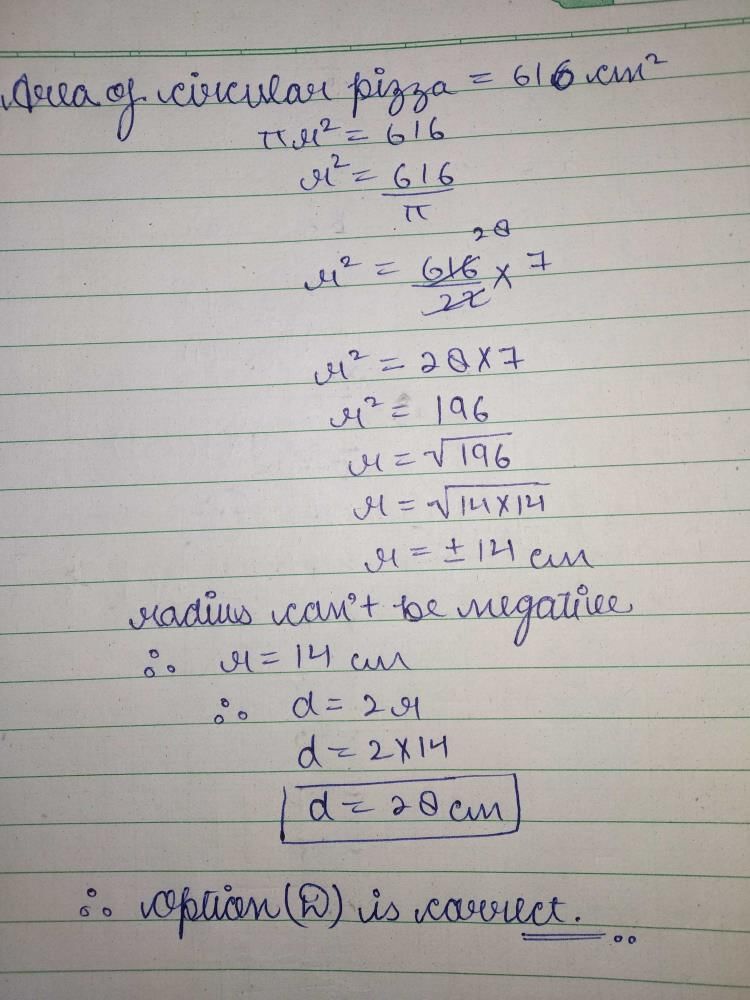All Exams >
Class 10 >
Mathematics (Maths) Class 10 >
All Questions
All questions of Areas Related to Circles for Class 10 Exam
The shaded part of the circle in the given figure represents a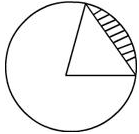
- a)semi-circle
- b)Chord
- c)Sector
- d)Segment
Correct answer is option 'D'. Can you explain this answer?
The shaded part of the circle in the given figure represents a
a)
semi-circle
b)
Chord
c)
Sector
d)
Segment

|
Neer Shreyansh answered |
¶¶ According to the arithmetic definition of segment.
•• segment is a area which is form when a chord joins two point of arc of a circle....
→→And here the shaded portion verif all the possible conditions of segment so we say that the shaded area is a segment.
§ That's all §
•• segment is a area which is form when a chord joins two point of arc of a circle....
→→And here the shaded portion verif all the possible conditions of segment so we say that the shaded area is a segment.
§ That's all §
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then- a)R1 + R2 = R
- b)R1 + R2 > R
- c)R1 + R2 < R
- d)nothing definite can be said about the relation among R1, R2 and R
Correct answer is option 'A'. Can you explain this answer?
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then
a)
R1 + R2 = R
b)
R1 + R2 > R
c)
R1 + R2 < R
d)
nothing definite can be said about the relation among R1, R2 and R
|
|
Pooja Shah answered |
2π R1 + 2πR2 = 2πR
⇒ R1 + R2 = R.
⇒ R1 + R2 = R.
If the area of a circle is 154 cm2, then its perimeter is- a)11cm
- b)22 cm
- c)44 cm
- d)55 cm
Correct answer is option 'C'. Can you explain this answer?
If the area of a circle is 154 cm2, then its perimeter is
a)
11cm
b)
22 cm
c)
44 cm
d)
55 cm
|
|
Vivek Rana answered |
Given area of circle=154
⇒area of circle=πr²
=22/7 ×7×7.
=154
so radius of the circle=7cm
perimeter of circle=2πr
=2 ×22/7×7
=44cm
⇒perimeter of the circle=44 cm.
⇒area of circle=πr²
=22/7 ×7×7.
=154
so radius of the circle=7cm
perimeter of circle=2πr
=2 ×22/7×7
=44cm
⇒perimeter of the circle=44 cm.
If the circumference of a circle and the perimeter of a square are equal, the- a)Area of the circle = Area of the square
- b)Area of the circle > Area of the square
- c)Area of the circle < Area of the square
- d)Nothing definite can be said about the relation between the areas of the circle and square
Correct answer is option 'B'. Can you explain this answer?
If the circumference of a circle and the perimeter of a square are equal, the
a)
Area of the circle = Area of the square
b)
Area of the circle > Area of the square
c)
Area of the circle < Area of the square
d)
Nothing definite can be said about the relation between the areas of the circle and square

|
Tanishka Gupta answered |

The ratio of radii of two circles is in the ratio of 1:5. Calculate the ratio of their perimeters.
- a)1:2
- b)1:5
- c)1:6
- d)1:8
Correct answer is option 'B'. Can you explain this answer?
The ratio of radii of two circles is in the ratio of 1:5. Calculate the ratio of their perimeters.
a)
1:2
b)
1:5
c)
1:6
d)
1:8

|
Abhishek Anand answered |
Let the radii of circles be R1 and R2
according to question,
R1/R2 = 1/5
therefore, R1 = R2/5
Also,
2πR1/2πR2
By Putting the value of R1 here we can write this like,
2πR2/5/ 2πR2
now 2π and 2π will be cancelled, and this will be left ->
R2/5 × 5/R2
After cancelling R2 and R2, 1/5 will be left
= 1:5
So, the ratio of 2πR1 / 2πR2 = 1:5
according to question,
R1/R2 = 1/5
therefore, R1 = R2/5
Also,
2πR1/2πR2
By Putting the value of R1 here we can write this like,
2πR2/5/ 2πR2
now 2π and 2π will be cancelled, and this will be left ->
R2/5 × 5/R2
After cancelling R2 and R2, 1/5 will be left
= 1:5
So, the ratio of 2πR1 / 2πR2 = 1:5
The perimeter of a protractor is- a)π + 2r
- b)πr
- c)πr + 2r
- d)π + r
Correct answer is option 'C'. Can you explain this answer?
The perimeter of a protractor is
a)
π + 2r
b)
πr
c)
πr + 2r
d)
π + r

|
Bhavya Banerjee answered |
Let radius of the protractor be r
∴ Perimeter of protractor = Perimeter of semicircle + Diameter of semicircle ⇒ Perimeter of protractor = πr+2r
∴ Perimeter of protractor = Perimeter of semicircle + Diameter of semicircle ⇒ Perimeter of protractor = πr+2r
The radius of a circle whose circumference is equal to the sum of the circumferences of the two circles of diameters 36 cm and 20 cm is- a)56 cm
- b)42 cm
- c)28 cm
- d)16 cm
Correct answer is option 'C'. Can you explain this answer?
The radius of a circle whose circumference is equal to the sum of the circumferences of the two circles of diameters 36 cm and 20 cm is
a)
56 cm
b)
42 cm
c)
28 cm
d)
16 cm
|
|
Amit Sharma answered |
Diameter of first circle = d1 = 36 cm
Diameter of second circle = d2 = 20 cm
∴ Circumference of first circle = πd1 = 36π cm
Circumference of second circle = πd2 = 20π cm
Now, we are given that,
Circumference of circle = Circumference of first circle + Circumference of second circle
πD = πd1 + πd2
⇒ πD = 36π + 20π
⇒ πD = 56π ⇒ D = 56
⇒ Radius = 56/2 = 28 cm
Diameter of second circle = d2 = 20 cm
∴ Circumference of first circle = πd1 = 36π cm
Circumference of second circle = πd2 = 20π cm
Now, we are given that,
Circumference of circle = Circumference of first circle + Circumference of second circle
πD = πd1 + πd2
⇒ πD = 36π + 20π
⇒ πD = 56π ⇒ D = 56
⇒ Radius = 56/2 = 28 cm
The diameter of a wheel is 1.26 m. The distance travelled in 500 revolutions is- a)2670 m
- b)2880 m
- c)1980 m
- d)1596 m
Correct answer is option 'C'. Can you explain this answer?
The diameter of a wheel is 1.26 m. The distance travelled in 500 revolutions is
a)
2670 m
b)
2880 m
c)
1980 m
d)
1596 m

|
Akshay Nair answered |
Diameter of circle =1.26m
travel distance=circumference of circle �500 revolution
circumference of circle = one relvolution
now,
according to questions (A.T.Q),
finding distance,
circumference of circle = 2πr
=2x22/7x(1.26/2)
=3.96
distance in 500 revolution = 3.96x500
=1980.00
The area of a circle is 38.5 sq. cm. Its circumference is
- a)22 cm
- b)33 cm
- c)11 cm
- d)44 cm
Correct answer is option 'A'. Can you explain this answer?
The area of a circle is 38.5 sq. cm. Its circumference is
a)
22 cm
b)
33 cm
c)
11 cm
d)
44 cm
|
|
Rohan Kapoor answered |


Therefore, the correct answer is Option 1: 22 cm.
The circumference of a circle whose diameter is 4.2cm is- a)11 cm
- b)22 cm
- c)4.2 cm
- d)13.2cm
Correct answer is option 'D'. Can you explain this answer?
The circumference of a circle whose diameter is 4.2cm is
a)
11 cm
b)
22 cm
c)
4.2 cm
d)
13.2cm

|
Bhavya Banerjee answered |
Given : Diameter (d) = 4.2 cm
∴ Circumference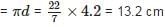
∴ Circumference
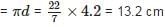
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is- a)8 a
- b)4 a
- c)2 a
- d)16
Correct answer is option 'A'. Can you explain this answer?
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
a)
8 a
b)
4 a
c)
2 a
d)
16

|
Naina Chopra answered |
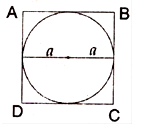
Given: Radius of the circle = r = a cm
To find the perimeter of the square.
Since the diameter of the circle is equal to the side of the square, therefore, side of the square = 2r = 2a cm a
Now, the perimeter of the square = 4 � (Side)
Thus, the perimeter of the square = 4(2a) cm
= 8a cm
If the radius of a circle is increased by 100%, then its area is increased by- a)100%
- b)300%
- c)200%
- d)400%
Correct answer is option 'B'. Can you explain this answer?
If the radius of a circle is increased by 100%, then its area is increased by
a)
100%
b)
300%
c)
200%
d)
400%

|
Harshitha Das answered |
Area of the circle with radius r =πr2
Now, New Radius = r + 100% of r = r + r = 2r
∴ New Area = π(2r)2 - 4πr2
∴ Increased Area = 4πr2 - πr2 = 3πr2
And Area increased in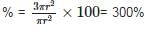
Now, New Radius = r + 100% of r = r + r = 2r
∴ New Area = π(2r)2 - 4πr2
∴ Increased Area = 4πr2 - πr2 = 3πr2
And Area increased in
Find the circumference of the circle, whose area is 144 cm2- a)24 πcm
- b)46 πcm
- c)72 πcm
- d)12 πcm
Correct answer is option 'A'. Can you explain this answer?
Find the circumference of the circle, whose area is 144 cm2
a)
24 πcm
b)
46 πcm
c)
72 πcm
d)
12 πcm
|
|
Anjana Khatri answered |
area = pi times the square of the radius
so the radius is the square root of 144, or 12cm
circumference is pi times twice the radius, so it would be 24 pi cm
The area of a circular plot is 9856 sq. m. The cost of fencing the plot at the rate of Rs. 6 per meter will be- a)Rs. 2112
- b)Rs. 3456
- c)Rs. 2000
- d)Rs. 2211
Correct answer is option 'A'. Can you explain this answer?
The area of a circular plot is 9856 sq. m. The cost of fencing the plot at the rate of Rs. 6 per meter will be
a)
Rs. 2112
b)
Rs. 3456
c)
Rs. 2000
d)
Rs. 2211

|
Pardeep Singh answered |
Area of circle=πr²
9856=πr²
9856*7/22=r²
√3136=r
56=r
circumference=2*22/7*56
=352m
cost of fencing 352m=352*6
=rs2112
9856=πr²
9856*7/22=r²
√3136=r
56=r
circumference=2*22/7*56
=352m
cost of fencing 352m=352*6
=rs2112
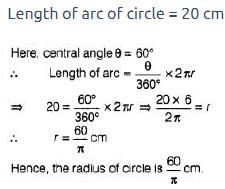
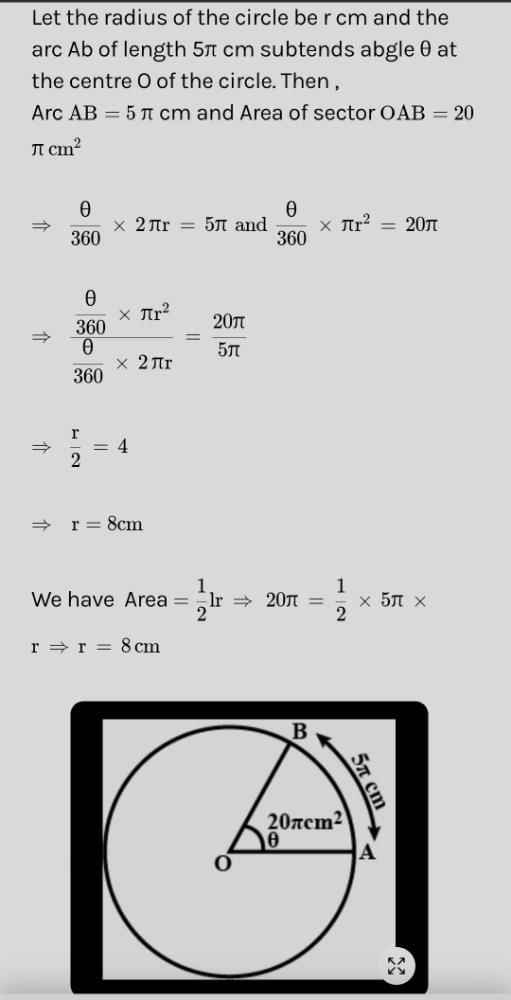
If the perimeter of a sector of a circle of radius 5.2 cm. is 16.4 cm. What multiple of the radius is the area of the sector?- a)5th
- b)3rd
- c)4th
- d)2nd
Correct answer is option 'B'. Can you explain this answer?
If the perimeter of a sector of a circle of radius 5.2 cm. is 16.4 cm. What multiple of the radius is the area of the sector?
a)
5th
b)
3rd
c)
4th
d)
2nd
|
|
Nisha Choudhury answered |
Let AOB be the given sector.
Given,
Radius of circle r = 5.2 cm
Perimeter of sector AOB = 16.4 cm
So, OA + OB + Arc AB = 16.4 cm
5.2 + 5.2 + Arc AB = 16.4 cm
Arc AB = 6 cm
l = Arc length AB
= 6 cm
Area of sector AOB = 1/2 * r * l
= 1 / 2 * 5.2 x 6
= 15.6 cm^2 Ans.
The diameter of a wheel is 1 m. The number of revolutions it will make to travel a distance of 22 km will be- a)2,800
- b)4,000
- c)5,500
- d)7,000
Correct answer is option 'D'. Can you explain this answer?
The diameter of a wheel is 1 m. The number of revolutions it will make to travel a distance of 22 km will be
a)
2,800
b)
4,000
c)
5,500
d)
7,000
|
|
Khushi Pandey answered |
Here is the solution to your question:
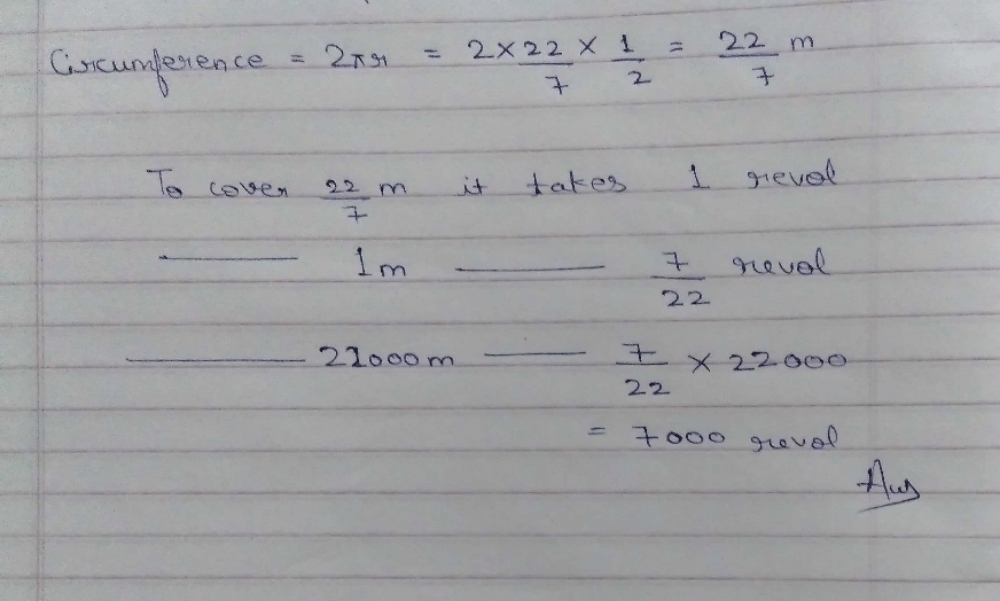
So, the Correct Answer is Option D
P.S. Cover everything related to the chapter Circles of Class 10 Mathematics by going through the link:
If the difference between the circumference and the radius of a circle is 37 cm, then using π = 22/7, the circumference (in cm) of the circle is:- a)44
- b)7
- c)14
- d)154
Correct answer is option 'A'. Can you explain this answer?
If the difference between the circumference and the radius of a circle is 37 cm, then using π = 22/7, the circumference (in cm) of the circle is:
a)
44
b)
7
c)
14
d)
154

|
Adidev Nair answered |
Let r be the radius of circle.
Difference between circumference and radius of circle = 37 cm
Circumference of circle = 2
r
= 2 x 22/7 x r = 44/7 x r
Now,
Difference between circumference and radius of circle = 2
r - r
37 = 44/7 x r - r
37 = r(44/7-1)
37 = r(44 - 7)/7
37 = 37 / 7 x r
37 x 7/37 = r
r = 7 cm
Now , Circumference of circle = 44/7 x r
= 44/7 x 7
= 44 cm .
∴ Circumference of circle = 44 cm
If the diameter of semicircular protractor is 14 cm, then its perimeter is:- a)30 cm
- b)36 cm
- c)44 cm
- d)40 cm
Correct answer is option 'B'. Can you explain this answer?
If the diameter of semicircular protractor is 14 cm, then its perimeter is:
a)
30 cm
b)
36 cm
c)
44 cm
d)
40 cm
|
|
Gaurav Kumar answered |
Diameter=14, Radius=d/2=14/2=7cm
Perimeter of the semi- circle= Boundary of the semi-circle =Circumference of the semi-circle +Diameter= πr+D=
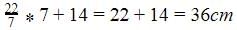
Perimeter of the semi- circle= Boundary of the semi-circle =Circumference of the semi-circle +Diameter= πr+D=
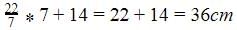
The area of a circle with diameter 6 m exceeds the combined areas of circles with diameters 4m and 2 m by- a)5π m2
- b)0 m2
- c)π m2
- d)4π m2
Correct answer is option 'D'. Can you explain this answer?
The area of a circle with diameter 6 m exceeds the combined areas of circles with diameters 4m and 2 m by
a)
5π m2
b)
0 m2
c)
π m2
d)
4π m2

|
Pardeep Singh answered |
R=d/2=6/2=3cm
area of circle1=πr²
=9πcm² ......(1)
R=d/2=4/2=2cm
area of circle2=πr²
=4πcm²
R=d/2=2/2=1cm
area of circle=πr²
=πcm²
now add area of circle 2and3
=4π+π
=5π........(2)
now sub 2 from 1
=9π-5π
=4πcm²
If C is the circumference of a circle of radius r, then perimeter of one of the quadrants will be- a)C/2
- b)C/4+r
- c)C/4
- d)C/4+2r
Correct answer is option 'D'. Can you explain this answer?
If C is the circumference of a circle of radius r, then perimeter of one of the quadrants will be
a)
C/2
b)
C/4+r
c)
C/4
d)
C/4+2r

|
Adithya Shasan answered |
Circumference = 2Πr
radius = r
Perimeter of quadrant = 2r + 2Πr/4
= 2r + C/4
= C/4 + 2r
Therefore, Correct answer is option 'D'.
radius = r
Perimeter of quadrant = 2r + 2Πr/4
= 2r + C/4
= C/4 + 2r
Therefore, Correct answer is option 'D'.
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is- a)8 a
- b)2 a
- c)16 a
- d)4 a
Correct answer is option 'A'. Can you explain this answer?
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
a)
8 a
b)
2 a
c)
16 a
d)
4 a

|
Learning Education answered |
Let ABCD is a square circumscribing a circle of radius a cm.
The side of square ABCD = Diameter of circle
⇒AB=2a
Therefore, perimeter of square AB=4×AB=4×2a=8 cm
The side of square ABCD = Diameter of circle
⇒AB=2a
Therefore, perimeter of square AB=4×AB=4×2a=8 cm
The area of the square that can be inscribed in a circle of radius 12 cm is- a)288 sq. cm
- b)576 sq. cm
- c)144 sq.cm
- d)500 sq. cm
Correct answer is option 'A'. Can you explain this answer?
The area of the square that can be inscribed in a circle of radius 12 cm is
a)
288 sq. cm
b)
576 sq. cm
c)
144 sq.cm
d)
500 sq. cm

|
Ayush Saha answered |
According to question, Diameter (BD) = 2 x radius = 2 x 12 = 24 cm
∴ Area of square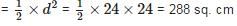
∴ Area of square
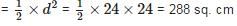
A garden roller has a circumference of 4 m. The number of revolutions it makes in moving 40 metres are:- a)12
- b)16
- c)8
- d)10
Correct answer is option 'D'. Can you explain this answer?
A garden roller has a circumference of 4 m. The number of revolutions it makes in moving 40 metres are:
a)
12
b)
16
c)
8
d)
10
|
|
Avinash Patel answered |
We have circumference which is equal to the boundary of the circle. So we have one revolution equal to circumference of the circle which is equal to 4
Distance covered by the roller=circumference of the roller*number of revolutions
⇒ number of revolutions = distance covered by the roller/circumference of the roller
= 40/4 = 10
Distance covered by the roller=circumference of the roller*number of revolutions
⇒ number of revolutions = distance covered by the roller/circumference of the roller
= 40/4 = 10
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then- a)
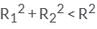
- b)
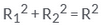
- c)
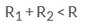
- d)
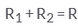
Correct answer is option 'B'. Can you explain this answer?
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
a)
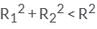
b)
c)
d)
|
|
Ananya Das answered |
Area of circle with radius R1 = πR12
Area of circle with radius R2 = πR22
Area of circle with radius R = πR2
Area of circle with radius R1+Area of circle with radius R2 =Area of circle with radius R
πR12 + πR22=πR2
R12+R22=R2
Area of circle with radius R2 = πR22
Area of circle with radius R = πR2
Area of circle with radius R1+Area of circle with radius R2 =Area of circle with radius R
πR12 + πR22=πR2
R12+R22=R2
The length of the wire is 66m. The number of circles of circumference 13.2cm can be made from the wire is- a)50
- b)5000
- c)500
- d)1
Correct answer is option 'C'. Can you explain this answer?
The length of the wire is 66m. The number of circles of circumference 13.2cm can be made from the wire is
a)
50
b)
5000
c)
500
d)
1

|
Sonal Joshi answered |
Given: Length of wire = 66 m = 6600 cm and Circumference = 13.2 cm
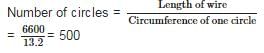
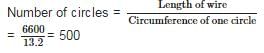
A wire is bent in the form of a circle of radius 28 cm. It is bent to form a square. The length of the side of the square will be- a)44 cm
- b)40 cm
- c)88 cm
- d)30 cm
Correct answer is option 'A'. Can you explain this answer?
A wire is bent in the form of a circle of radius 28 cm. It is bent to form a square. The length of the side of the square will be
a)
44 cm
b)
40 cm
c)
88 cm
d)
30 cm
|
|
Gaurav Kumar answered |
Circumference of a circle = 2πr
= 2*22/7*28
= 2*22*4
= 176
now, perimeter of square = circumference of a circle = 176
Therefore, side of square = perimeter/4
= 176/4
= 44 answer.
= 2*22/7*28
= 2*22*4
= 176
now, perimeter of square = circumference of a circle = 176
Therefore, side of square = perimeter/4
= 176/4
= 44 answer.
If the area of a circle is ‘A’, radius of the circle is ‘r’ and its circumference is ‘C’, then- a)
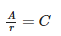
- b)
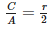
- c)
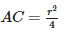
- d)rC = 2A
Correct answer is option 'D'. Can you explain this answer?
If the area of a circle is ‘A’, radius of the circle is ‘r’ and its circumference is ‘C’, then
a)
b)
c)
d)
rC = 2A

|
Anagha Yadav answered |
Here, Area of circle (A) = πr2 and Circumference of circle (C) = 2πr
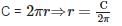
Putting value of C in A = πr2, we get
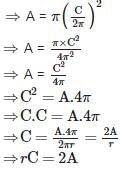
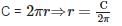
Putting value of C in A = πr2, we get
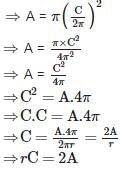
The length of the line that marks out a circle and its region is the- a)Diameter
- b)Circumference
- c)Radius
- d)Chord
Correct answer is option 'B'. Can you explain this answer?
The length of the line that marks out a circle and its region is the
a)
Diameter
b)
Circumference
c)
Radius
d)
Chord
|
|
Papa answered |
Because line become it boundary which is circumference of circle
If the area and circumference of a circle are numerically equal, then its radius is- a)4 units
- b)π units
- c)2π units
- d)2 units
Correct answer is option 'D'. Can you explain this answer?
If the area and circumference of a circle are numerically equal, then its radius is
a)
4 units
b)
π units
c)
2π units
d)
2 units

|
Srishti Mishra answered |
Let radius of the circle berunits.
∴ Area of the circle = Circumference of the circle
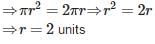
∴ Area of the circle = Circumference of the circle
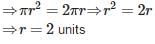
If the circumference of a circle and the perimeter of a square are equal, then- a)area of the circle < area of the square
- b)area of the circle = area of the square
- c)area of the circle > area of the square
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the circumference of a circle and the perimeter of a square are equal, then
a)
area of the circle < area of the square
b)
area of the circle = area of the square
c)
area of the circle > area of the square
d)
none of these

|
Anoushka Nambiar answered |
Let the radius of the circle be r and side of the square be a.
Then, according to question,
2πr = 4a
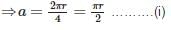
Now, ratio of their areas,
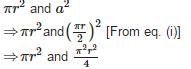
Therefore, Area of the circle > Area of the square
Then, according to question,
2πr = 4a
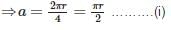
Now, ratio of their areas,
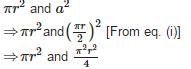
Therefore, Area of the circle > Area of the square
The radius of a circle if its perimeter and area are numerically equal is- a)8 units
- b)5 units
- c)2 units
- d)4 units
Correct answer is option 'C'. Can you explain this answer?
The radius of a circle if its perimeter and area are numerically equal is
a)
8 units
b)
5 units
c)
2 units
d)
4 units
|
|
Ananya Das answered |
The perimeter of a circle is 2πr where r is the radius of the circle.
And it's area is πr^2
If area = perimeter
Then,
2πr = πr^2
2 = πr^2 / πr = r
Therefore, if r is 2units then the area and perimeter of the circle would be numerically equal.
If the area of a circle is equal to the area of a square, then the ratio of their perimeters is- a)π : 2
- b)1 : 2
- c)2 : π
- d)√π : 2
Correct answer is option 'D'. Can you explain this answer?
If the area of a circle is equal to the area of a square, then the ratio of their perimeters is
a)
π : 2
b)
1 : 2
c)
2 : π
d)
√π : 2
|
|
Leelu Bhai answered |
Acc. to ques,...
⇒ πr² = a²
⇒ r/a = 1/√π
now, ratio of perimeter = 2πr/4a
⇒ ratio = 2π/4√π = √π/2 or √π : 2
hence, D option is correct.
⇒ πr² = a²
⇒ r/a = 1/√π
now, ratio of perimeter = 2πr/4a
⇒ ratio = 2π/4√π = √π/2 or √π : 2
hence, D option is correct.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is- a)50 cm
- b)31 cm
- c)62 cm
- d)25 cm
Correct answer is option 'A'. Can you explain this answer?
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is
a)
50 cm
b)
31 cm
c)
62 cm
d)
25 cm
|
|
Mohini iyer answered |
Given:
Radius of first circle = 24 cm
Radius of second circle = 7 cm
We need to find the diameter of a circle whose area is equal to the sum of the areas of the two circles.
Formula for the area of a circle:
Area = πr^2
Let's calculate the areas of the two circles first.
Area of the first circle = π(24)^2
= 576π cm^2
Area of the second circle = π(7)^2
= 49π cm^2
Now, we need to find the diameter of a circle whose area is equal to the sum of the areas of the two circles.
Sum of the areas of the two circles = 576π + 49π
= 625π cm^2
To find the diameter, we can use the formula for the area of a circle:
Area = πr^2
Let's substitute the given area into the formula:
625π = πr^2
Dividing both sides by π:
625 = r^2
Taking the square root of both sides:
r = √625
r = 25 cm
Since the radius is 25 cm, the diameter will be twice the radius:
Diameter = 2r
= 2(25)
= 50 cm
Therefore, the diameter of the circle whose area is equal to the sum of the areas of the two circles is 50 cm, which corresponds to option A.
Radius of first circle = 24 cm
Radius of second circle = 7 cm
We need to find the diameter of a circle whose area is equal to the sum of the areas of the two circles.
Formula for the area of a circle:
Area = πr^2
Let's calculate the areas of the two circles first.
Area of the first circle = π(24)^2
= 576π cm^2
Area of the second circle = π(7)^2
= 49π cm^2
Now, we need to find the diameter of a circle whose area is equal to the sum of the areas of the two circles.
Sum of the areas of the two circles = 576π + 49π
= 625π cm^2
To find the diameter, we can use the formula for the area of a circle:
Area = πr^2
Let's substitute the given area into the formula:
625π = πr^2
Dividing both sides by π:
625 = r^2
Taking the square root of both sides:
r = √625
r = 25 cm
Since the radius is 25 cm, the diameter will be twice the radius:
Diameter = 2r
= 2(25)
= 50 cm
Therefore, the diameter of the circle whose area is equal to the sum of the areas of the two circles is 50 cm, which corresponds to option A.
Chapter doubts & questions for Areas Related to Circles - Mathematics (Maths) Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Areas Related to Circles - Mathematics (Maths) Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup