Explore Exams
Login Signup
Sign in Open App

All questions of Theory of Machines (TOM) for Mechanical Engineering Exam

Clear all your doubts with EduRev

In a gear drive, module is equal to
  • a)
    1/diameter pitch
  • b)
    1/ circular pitch
  • c)
    circular pitch / p
  • d)
    diameteral pitch/π
  • e)
    π/ diameteral pitch
Correct answer is option 'A'. Can you explain this answer?

Zoya Sharma answered
Correct Answer :- a
Explanation : It is the reciprocal of dia. pitch. diametral pitch is, by definition, the number of teeth divided by the pitch diameter.
Therefore, module = 1/diameter pitch

If two moving elements have surface contact in motion, such pair is known as
  • a)
    sliding pair
  • b)
    rolling pair
  • c)
    surface pair
  • d)
    lower pair
  • e)
    higher pair
Correct answer is option 'E'. Can you explain this answer?

Rajeev Sharma answered
Answer is d) Lower pair
When two elements of a pair have a surface contact when relative motion takes place and the surface of one element slides over the surface of the other, the pair formed is known as lower pair.

When a ship travels in a sea, which of the effect is more dangerous
a) steering
b) pitching
c) rolling
d) all of the above
e)none of the above
Correct answer is option 'B'. Can you explain this answer?

Mrinalini Sen answered
Heavy rolling has the danger of flipping the ship over or having someone or something fall overboard. That would make it very dangerous specially to top heavy ships.

Heavy pitching could break the ships hull or breach it if the pitch is too violent. either case it would quickly sink.

However heavy pitching is only caused by the most extreme storms. While as rolling can be caused by less powerful ones or even an inbalance loading.

So rolling is more dangerous, that's why ships steer the nose into oncomming high waves to avoid hitting it with the side and rolling.

Which of the following is a lower pair?
  • a)
    ball and socket
  • b)
    piston and cylinder
  • c)
    cam and follower
  • d)
    (a) and (b) above
  • e)
    belt drive
Correct answer is option 'D'. Can you explain this answer?

Soumya Basak answered
Lower Pair in Mechanical Engineering

In mechanical engineering, a pair refers to the connection between two rigid bodies that allows them to move relative to each other in a specific way. Based on the types of motion allowed, pairs can be categorized into two types: higher pairs and lower pairs.

Higher pair: It refers to a pair of links that have point or line contact between them. For example, a gear pair or a roller bearing.

Lower pair: It refers to a pair of links that have surface contact between them, such as a sliding pair or a revolute pair.

Answer Explanation

In the given options, the following pairs are mentioned:
a) Ball and socket - It is a type of spherical joint, which is an example of a higher pair.
b) Piston and cylinder - It is an example of a sliding pair, which is a lower pair.
c) Cam and follower - It is an example of a higher pair.
d) (a) and (b) above - Ball and socket is a higher pair, and piston and cylinder is a lower pair. Hence, option D is correct.
e) Belt drive - It is not an example of a pair.

Hence, the correct answer is option D, as it contains a lower pair (piston and cylinder) along with a higher pair (ball and socket).

The circle passing through the bottom of the teeth of gear is known as
  • a)
    inner circle
  • b)
    prime circle
  • c)
    base circle
  • d)
    addendum circle
  • e)
    dedendum circle
Correct answer is option 'E'. Can you explain this answer?

Rajeev Sharma answered
Dedendum circle is the circle drawn through the bottom of the teeth. It is also called root circle. Pitch circle is an imaginary circle which by pure rolling action, would give the same motion as the actual gear. Explanation: Pitch circle diameter is the diameter of the pitch circle

In the scotch yoke mechanism, Corioli's component is
  • a) 
    involved
  • b) 
    not involved
  • c) 
    possible in some position
  • d) 
    a rate possibility
  • e) 
    unpredictable
Correct answer is option 'A'. Can you explain this answer?

Aditya Deshmukh answered
The Scotch yoke (also known as slotted link mechanism) is a reciprocating motion mechanism, converting the linear motion of a slider into rotational motion, or vice versa. The piston or other reciprocating part is directly coupled to a sliding yoke with a slot that engages a pin on the rotating part In the scotch yoke mechanism Corioli's component is involved.

A universal joint is an example of
  • a)
    higher pair
  • b)
    lower pair
  • c)
    rolling pair
  • d)
    sliding pair
  • e)
    Turning pair
Correct answer is option 'B'. Can you explain this answer?

Anirban Khanna answered
A lower pair is one in which there occurs a surface or area contact between two members, e.g. nut and screw, universal joint used to connect two propeller shafts.A screw pair requires cut threads in two links, so that there is a turning as well as sliding motion between them. This joint has one degree of freedom.

The quality of a governor can be judged by its
  • a)
    stability
  • b)
    sensitivity
  • c)
    effort and power
  • d)
    all of the above
  • e)
    none of the above
Correct answer is option 'E'. Can you explain this answer?

Anu Deshpande answered
Explanation:

The question asks about the quality of a governor, and the options provided are stability, sensitivity, and effort and power. However, the correct answer is none of the above, which means that these qualities are not sufficient or relevant to judge a governor's effectiveness.

Here are some reasons why the options are not accurate or complete:

Stability: While stability can be a desirable trait for a governor, it is not a guarantee of good governance. A stable governor may still be corrupt, incompetent, or unresponsive to the needs of the people. Moreover, stability can also be a form of stagnation if the governor resists change or innovation that could benefit the state.

Sensitivity: Similarly, sensitivity to the needs and concerns of the citizens is important for a governor, but it is not the only factor that determines their effectiveness. A governor may be empathetic and compassionate, but if they lack the skills or resources to address the root causes of the problems, their sensitivity may not lead to any tangible results.

Effort and power: The amount of effort or power a governor exerts is also not a reliable indicator of their quality. A governor may work hard and use their authority to implement policies, but if those policies are misguided, harmful, or ineffective, their efforts may be counterproductive. Moreover, a governor may also abuse their power or neglect their duties, which would undermine their legitimacy and trustworthiness.

So, what are some other factors that can help assess the quality of a governor? Here are some possibilities:

1. Vision and goals: A good governor should have a clear vision of what they want to achieve for the state and its people, and set realistic and measurable goals to track their progress. This requires a deep understanding of the state's strengths and weaknesses, as well as the challenges and opportunities that lie ahead.

2. Leadership and communication: A good governor should also be an effective leader who can inspire and motivate their team, build consensus and partnerships with stakeholders, and communicate their plans and achievements to the public. This requires strong communication skills, both verbal and written, as well as the ability to listen and learn from feedback.

3. Integrity and accountability: A good governor should uphold high standards of ethics and integrity, and be accountable to the people for their actions and decisions. This requires transparency, honesty, and a willingness to admit mistakes and learn from them. It also requires a commitment to fairness, justice, and the rule of law.

4. Results and impact: Ultimately, a good governor should be judged by the results they achieve and the impact they have on the state and its people. This means measuring their success in terms of concrete outcomes such as economic growth, job creation, poverty reduction, health and education outcomes, environmental sustainability, and social cohesion. It also means being responsive to the evolving needs and aspirations of the citizens, and adapting to changing circumstances and trends.

In higher pair, the relative motion is
  • a)
    purely turning
  • b)
    purely sliding
  • c)
    purely rotary
  • d)
    purely surface contact
  • e)
    Combination of sliding and turning
Correct answer is option 'E'. Can you explain this answer?

Sagarika Patel answered
When the two elements of a pair have a line or point contact when relative motion takes place and the motion between the two elements is partly turning and partly sliding, then the pair is known as higher pair. A pair of friction discs, toothed gearing, belt and rope drives, ball and roller bearings and cam and follower are the examples of higher pairs.

If the opposite links of a four bar linkage are equal, the links will always form a
  • a)
    triangle
  • b)
    rectangle
  • c)
    parallelogram
  • d)
    pentagon
  • e)
    trapezoid
Correct answer is option 'C'. Can you explain this answer?

Siddharth Datta answered
Four Bar Linkage with Equal Opposite Links

A four bar linkage is a mechanism consisting of four links that are connected by four joints. The links can be of different lengths and can be arranged in a variety of configurations. One important configuration is when the opposite links of the four bar linkage are equal. In this case, the links will always form a parallelogram.

Parallelogram Configuration

A parallelogram is a four-sided shape in which opposite sides are parallel and equal in length. When the opposite links of a four bar linkage are equal, the mechanism will always form a parallelogram. This is because the two parallel links will always remain parallel, while the other two links will move in a way that preserves the parallelism of the opposite links.

Mechanism Applications

The parallelogram configuration of the four bar linkage is useful for a variety of mechanical applications. For example, it is often used in suspension systems for vehicles. The suspension system connects the wheels to the frame of the vehicle and allows the wheels to move up and down over bumps and uneven surfaces. The parallelogram configuration of the four bar linkage helps to keep the wheels aligned with the frame of the vehicle, which improves handling and stability.

Conclusion

In conclusion, when the opposite links of a four bar linkage are equal, the mechanism will always form a parallelogram. This configuration is useful for a variety of mechanical applications, such as suspension systems for vehicles.

Elements of pairs held together mechanically is known as
  • a)
    closed pair
  • b)
    open pair
  • c)
    mechanical pair
  • d)
    rolling pair
  • e)
    none of the above
Correct answer is option 'A'. Can you explain this answer?

Rajeev Menon answered
When the two elements of a pair have a line or point contact when relative motion takes place and the motion between the two elements is partly turning and partly sliding, then the pair is known as higher pair. In a force-closed pair, the two elements of a pair are not held together mechanically.

Typewriter constitutes
  • a)
    machine
  • b)
    structure
  • c)
    mechanism
  • d)
    inversion
  • e)
    none of the above
Correct answer is option 'C'. Can you explain this answer?

Kritika Joshi answered
The Typewriter as a Mechanism

Introduction:
The typewriter is a mechanical device that was used for writing before the invention of computers. It consists of a keyboard that is used to type letters, numbers, and symbols onto a piece of paper that is inserted into the machine. The machine is then activated by pressing a key, which causes a metal type bar to strike the paper and leave an impression of the typed character.

Definition of Mechanism:
A mechanism is a system of moving parts that work together to accomplish a task. In the case of a typewriter, the mechanism is the set of levers, gears, and linkages that work together to move the type bars and create the printed characters.

Working of Typewriter Mechanism:
The typewriter mechanism is activated when the user presses a key on the keyboard. This causes a lever to move, which in turn activates a series of linkages and gears that move the selected type bar into position. The type bar is then struck by a hammer, which presses the inked ribbon against the paper, leaving an impression of the typed character.

Components of Typewriter Mechanism:
The typewriter mechanism consists of several components, including:

1. Keyboard: The keyboard is the input device that is used to select the characters to be typed.

2. Type Bars: The type bars are metal bars that have a raised character on the end. When a key is pressed, the corresponding type bar is moved into position.

3. Ribbon: The ribbon is an inked fabric that is used to transfer ink onto the paper.

4. Hammer: The hammer is the mechanism that strikes the type bar and presses the inked ribbon onto the paper.

5. Linkages and Gears: These are the mechanisms that connect the keyboard to the type bars, and the type bars to the hammer.

Conclusion:
In conclusion, the typewriter is a mechanical device that uses a system of linkages, gears, and levers to create printed characters on paper. It is an excellent example of a mechanism in action and demonstrates how mechanical devices can be used to accomplish complex tasks.

Whit Worth quick return mechanism is contained by inversion of
  • a)
    slider crank mechanism
  • b)
    kinematic chain
  • c)
    five link mechanism
  • d)
    roller cam mechanism
  • e)
    none of the above
Correct answer is option 'A'. Can you explain this answer?

Raj Kumar answered
The correct answer is option 'A': the Whitworth quick return mechanism is contained by the inversion of a slider-crank mechanism.

Explanation:
The Whitworth quick return mechanism is a well-known mechanism used in machines such as shapers and slotting machines. It is used to convert the rotary motion of a crank into a reciprocating motion of a slider.

The mechanism consists of four main links: the crank, the connecting rod, the slider, and the fixed frame. The crank is connected to the connecting rod, which in turn is connected to the slider. The fixed frame provides a reference point for the other links.

The key feature of the Whitworth quick return mechanism is that the slider's motion is not symmetrical with respect to the rotation of the crank. During one half of the crank's rotation, the slider moves slowly in one direction, while during the other half of the rotation, the slider moves quickly in the opposite direction. This non-uniform motion is useful for certain machining operations.

In order to achieve this motion, the slider-crank mechanism needs to be inverted. In the standard slider-crank mechanism, the crank is driven by a motor, and the slider provides the output motion. However, in the Whitworth quick return mechanism, the slider is driven by an external force, such as a cutting tool. This external force causes the slider to move in a non-uniform manner, as desired.

By inverting the slider-crank mechanism, the Whitworth quick return mechanism is created. This inversion allows for the desired non-uniform motion of the slider, making it suitable for applications where a quick return stroke is required.

In conclusion, the Whitworth quick return mechanism is contained by the inversion of a slider-crank mechanism. This inversion allows for the non-uniform motion of the slider, which is a key feature of the Whitworth mechanism.

Any point on a link connecting double slider crank chain will trace a
  • a)
    straight line
  • b)
    circle
  • c)
    ellipse
  • d)
    parabola
  • e)
    hyperbola
Correct answer is option 'C'. Can you explain this answer?

Subhankar Khanna answered
Explanation:

Double slider crank chain is a mechanism that is used in many engineering applications. It consists of two sliding pairs and two turning pairs. The motion of the mechanism is governed by the geometry of the links that connect the pairs. Any point on a link connecting double slider crank chain will trace an ellipse. This can be explained by understanding the kinematics of the mechanism.

Kinematics of Double Slider Crank Chain:

The kinematics of the double slider crank chain can be explained by considering the motion of the links that connect the pairs. The links are connected in such a way that they form a closed loop. This loop is known as the kinematic chain. The motion of the links is governed by the geometry of the mechanism.

The motion of the mechanism can be described using the following parameters:

1. Crank length: The length of the link that is connected to the crank.

2. Connecting rod length: The length of the link that connects the crank to the slider.

3. Slider length: The length of the link that is connected to the slider.

4. Crank angle: The angle between the crank and the horizontal.

5. Slider position: The position of the slider along the slider link.

The motion of the mechanism can be described using the above parameters. The motion of the slider is governed by the motion of the crank. The motion of the crank is a circular motion. The motion of the slider is a combination of linear and circular motion.

Ellipse as the trajectory of a point on the link:

Any point on a link connecting double slider crank chain will trace an ellipse. This can be explained by understanding the motion of the mechanism. The motion of the slider is a combination of linear and circular motion. The motion of the crank is a circular motion. The combination of these motions results in an elliptical motion of any point on the link.

Conclusion:

Double slider crank chain is a mechanism that is used in many engineering applications. Any point on a link connecting double slider crank chain will trace an ellipse. This can be explained by understanding the kinematics of the mechanism. The motion of the mechanism is governed by the geometry of the links that connect the pairs. The elliptical motion of any point on the link is a combination of linear and circular motion.

Davis steering gear consists of
  • a)
    sliding pairs
  • b)
    turning pairs
  • c)
    rolling pairs
  • d)
    higher pairs
  • e)
    lower pairs
Correct answer is option 'A'. Can you explain this answer?

Avinash Mehta answered
The Davis gear mechanism consists of a cross-link sliding parallel to another link is connected to the stub axles of the two front wheels by means of two similar bell crank levers pivoted. The crosslink slides in slides in the bearing and carries pins at its end. 
A Davis steering gear has sliding pairs which means more friction and easy wearing. The gear fulfills the fundamental equation of gearing in all the positions. 

The motion transmitted between the teeth of gears in mesh is
  • a)
    sliding
  • b)
    rolling
  • c)
    rotary
  • d)
    could be either sliding or rolling depending upon shape of teeth
  • e)
    Partly sliding and partly rolling
Correct answer is option 'E'. Can you explain this answer?

Bijoy Kapoor answered
When the two elements of a pair have a line or point contact when relative motion takes place and the motion between the two elements is partly turning and partly sliding, and in mesh the gears have a point contact.

A foot step bearing and rotor of a vertical turbine form examples of
  • a)
    incompletely constrained motion
  • b)
    partially constrained motion
  • c)
    completely constrained motion
  • d)
    successfully constrained motion
  • e)
    none of the above
Correct answer is option 'B'. Can you explain this answer?

Sagarika Patel answered
A kinematic pair is said to be partially or successfully constrained if the relative motion between its links occurs in a definite direction, not by itself, but by some other means. A good example of successfully constrained motion is piston reciprocating inside a cylinder in an internal combustion engine.

The example of higher pair is
  • a)
    belt, rope and chain drives
  • b)
    gears, cams
  • c)
    ball and roller bearings
  • d)
    all of the above
Correct answer is option 'D'. Can you explain this answer?

Anmol Saini answered
Higher Pair in Mechanical Engineering

Higher pair refers to the type of contact between two surfaces that has both rotary and translatory motion. There are several examples of higher pairs in mechanical engineering, including belt, rope and chain drives, gears, cams, ball and roller bearings, and more. In this answer, we will discuss these examples in detail.

Belt, Rope and Chain Drives

Belt, rope and chain drives are systems that transmit motion and power from one shaft to another. They are commonly used in machines like automobiles, conveyor belts, and bicycles. In these systems, the higher pair occurs between the belt, rope or chain and the pulley or sprocket. The contact between the two surfaces involves both rotary and translatory motion, making this an example of higher pair.

Gears

Gears are another common example of higher pair in mechanical engineering. They are used to transmit motion and power between two shafts that are not in the same plane. The higher pair occurs between the teeth of the gears, which have both rotary and translatory motion during operation.

Cams

Cams are mechanical devices that convert rotary motion into linear motion. They are commonly used in machines like engines, pumps and compressors. In these systems, the higher pair occurs between the cam and the follower, which is the part of the machine that is moved by the cam. The contact between the two surfaces involves both rotary and translatory motion, making this an example of higher pair.

Ball and Roller Bearings

Ball and roller bearings are used to reduce friction and support loads in machines like automobiles, airplanes, and industrial equipment. In these systems, the higher pair occurs between the balls or rollers and the raceway. The contact between the two surfaces involves both rotary and translatory motion, making this an example of higher pair.

Conclusion

In conclusion, higher pair refers to the type of contact between two surfaces that has both rotary and translatory motion. There are several examples of higher pairs in mechanical engineering, including belt, rope and chain drives, gears, cams, ball and roller bearings, and more. These systems are commonly used in machines and equipment to transmit motion and power, reduce friction, and support loads.

A simple mechanism has
  • a)
    1 link
  • b)
    2 links
  • c)
    3 link
  • d)
    4 links
  • e)
    5 links
Correct answer is option 'D'. Can you explain this answer?

Sagarika Dey answered
Mechanical Engineering - Simple Mechanism

A mechanism is a combination of various machine elements that are arranged to transmit motion or force in a predetermined way. A simple mechanism is a machine that consists of a minimum number of parts and provides a simple, useful function.

A simple mechanism has four links that are connected to each other in a specific way. A link is a rigid bar or a rod that has a fixed length and can rotate about a fixed axis.

The four links in a simple mechanism are:

1. Input link: It is the link that receives the input motion or force. It is also known as the driver link or the prime mover.

2. Output link: It is the link that delivers the output motion or force. It is also known as the driven link or the follower.

3. Connecting link: It is the link that connects the input and output links. It is also known as the coupler or the connecting rod.

4. Fixed link: It is the link that provides a fixed point of attachment for the other links. It is also known as the frame or the ground.

Therefore, the correct answer to the question is option 'D' which states that a simple mechanism has four links.

Oldham's coupling is the
  • a)
    second inversion of double slider crank chain
  • b)
    Third inversion of double slider crank chain
  • c)
    second inversion of single slider crank chain
  • d)
    third inversion of slider crank chain
  • e)
    Fourth inversion of double slider crank chain
Correct answer is option 'B'. Can you explain this answer?

Baishali Bajaj answered
A four bar chain having two turning and two sliding pairs such that two pairs of the same kind are adjacent is known as double slider crank chain. Inversions of Double slider Crank chain: They are three important inversions of double slider crank chain. 1) Elliptical trammel. 2) Scotch yoke mechanism.

A quarternary joint is equivalent to
  • a)
    one binary joint
  • b)
    two binary joints
  • c)
    three binary joints
  • d)
    four binary joints
  • e)
    none of the above
Correct answer is option 'C'. Can you explain this answer?

Yash Das answered
**Quaternary Joint in Mechanical Engineering**

A quaternary joint in mechanical engineering refers to a type of joint that allows movement in four different directions. It is a complex joint that consists of multiple binary joints combined together. To understand why a quaternary joint is equivalent to three binary joints, let's explore the concept of binary joints first.

**Binary Joints**

A binary joint is a type of joint that allows movement in two different directions or axes. It is the most basic type of joint commonly used in mechanical systems. For example, a hinge joint allows rotational movement around one axis, while a sliding joint allows linear movement along one axis.

**Quaternary Joint**

A quaternary joint, on the other hand, is a more complex joint that enables movement in four different directions or axes. It is achieved by combining multiple binary joints. By using a combination of binary joints, a quaternary joint can provide a wide range of motion and flexibility in mechanical systems.

**Equivalent to Three Binary Joints**

The statement that a quaternary joint is equivalent to three binary joints means that the movement provided by a quaternary joint can be achieved by using three separate binary joints. This concept can be better understood by considering the degrees of freedom.

**Degrees of Freedom**

Degrees of freedom refer to the number of independent directions or axes in which a body or system can move. In mechanical systems, degrees of freedom are determined by the number and types of joints present.

**Quaternary Joint and Degrees of Freedom**

A quaternary joint provides four degrees of freedom, meaning it allows movement in four independent directions or axes. To achieve this, it combines multiple binary joints, each providing two degrees of freedom. Therefore, by combining three binary joints, each with two degrees of freedom, we can achieve the same movement provided by a quaternary joint.

**Conclusion**

In conclusion, a quaternary joint in mechanical engineering is a complex joint that allows movement in four different directions. It is equivalent to three binary joints, meaning that the movement provided by a quaternary joint can be achieved by using three separate binary joints. This concept is based on the degrees of freedom, where a quaternary joint provides four degrees of freedom and each binary joint provides two degrees of freedom.

The tendency of a body to resist change from rest or motion is known as
  • a)
    mass
  • b)
    friction
  • c)
    inertia
  • d)
    resisting force
  • e)
    resisting torque
Correct answer is option 'C'. Can you explain this answer?

Arnab Saini answered
Tendency to Resist Change
The concept of inertia is fundamental in physics and engineering, particularly in mechanical engineering. It describes a body's resistance to any change in its state of rest or uniform motion.
What is Inertia?
- Inertia is a property of matter that quantifies how much an object resists changes to its motion.
- The greater the mass of an object, the greater its inertia. Therefore, massive objects require more force to change their state of motion compared to lighter objects.
Examples of Inertia
- Stationary Objects: A heavy box sitting on the floor will not move unless a sufficient force is applied to overcome its inertia.
- Moving Objects: A car cruising at a steady speed will continue to do so until forces such as friction or braking are applied to alter its motion.
Inertia in Everyday Life
- Inertia is why passengers lurch forward in a car when it suddenly stops. Their bodies tend to continue moving due to inertia until acted upon by another force (like a seatbelt).
Importance in Mechanical Engineering
- Understanding inertia is crucial for designing safe and efficient machines. Engineers account for inertia in calculations to ensure that systems operate smoothly and safely under various loads and speeds.
In summary, inertia is the key property that explains why objects resist changes to their motion, and this understanding is vital in various applications in mechanical engineering.

The magnitude of the Corioli's component of acceleration of a slider moving at velocity V on a link rotating at angular speedw is
  • a)
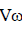
  • b)
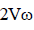
  • c)
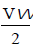
  • d)
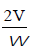
  • e)
    none of the above
Correct answer is option 'B'. Can you explain this answer?

Sarita Yadav answered
The magnitude of tangential acceleration is equal to velocity2/ crank radius.
The magnitude of the Corioli’s component of acceleration of a slider moving at velocity V on a link rotating at angular speed ω is 2Vω.

The direction of Corioli's component of acceleration is the direction
  • a)
    of relative velocity vector for the two coincident points rotated by 90º in the direction of the angular velocity of the rotation of the link.
  • b)
    along the centripetal acceleration
  • c)
    along tangential acceleration
  • d)
    along perpendicular to angular velocity
  • e)
    none of the above
Correct answer is option 'A'. Can you explain this answer?

Dipika Kulkarni answered
The Coriolis component of acceleration is a result of the Coriolis effect, which is caused by the rotation of the Earth. It is a fictitious force that appears to act on objects moving in a rotating reference frame. This effect is most commonly observed in the rotation of large-scale weather systems and ocean currents.

The direction of the Coriolis component of acceleration can be determined by considering the relative velocity vector for two coincident points. The relative velocity vector is the vector difference between the velocity vectors of the two points. The direction of this vector is then rotated by 90 degrees in the direction of the angular velocity of the rotation of the reference frame.

Let's break down the options given:

a) The direction of the Coriolis component of acceleration is the direction of the relative velocity vector for the two coincident points rotated by 90 degrees in the direction of the angular velocity of the rotation of the link. This is the correct answer because it describes the correct relationship between the relative velocity vector and the Coriolis component of acceleration.

b) The direction of the Coriolis component of acceleration is not along the centripetal acceleration. Centripetal acceleration is the acceleration directed towards the center of a circular path and is not related to the Coriolis effect.

c) The direction of the Coriolis component of acceleration is not along the tangential acceleration. Tangential acceleration is the acceleration directed tangent to the path of an object moving in a circular path and is not related to the Coriolis effect.

d) The direction of the Coriolis component of acceleration is not along the perpendicular to the angular velocity. This option is close to the correct answer, but it does not include the 90-degree rotation of the relative velocity vector.

e) None of the above. This option is incorrect as option A is the correct answer.

In conclusion, the direction of the Coriolis component of acceleration is the direction of the relative velocity vector for two coincident points rotated by 90 degrees in the direction of the angular velocity of the rotation of the link.

Cam size depends upon
  • a)
    pitch circle
  • b)
    base circle
  • c)
    prime circle
  • d)
    outer circle
  • e)
    none of the above
Correct answer is option 'B'. Can you explain this answer?

Akash Mukherjee answered
Introduction:
In mechanical engineering, the design and analysis of cams are crucial for various applications such as engines, machines, and mechanisms. The cam size plays a significant role in determining the performance and functionality of a cam system. The size of the cam is primarily dependent on the base circle.

Explanation:
The base circle is an essential element in the design of a cam. It is the theoretical circle from which the cam profile is developed. The cam profile determines the motion and displacement of the follower that is in contact with the cam. The size of the cam is determined by the dimensions of the base circle.

Effects of Base Circle Size:
The size of the base circle has a direct impact on the cam's performance. Here are a few key points to consider:

1. Cam Lift: The base circle diameter determines the maximum lift or displacement of the follower. A larger base circle will result in a higher lift, while a smaller base circle will result in a lower lift.

2. Cam Profile: The shape of the cam profile is determined by the base circle. The base circle acts as a reference point for developing the cam profile. The profile is designed to achieve the desired motion of the follower, and it is directly influenced by the size of the base circle.

3. Contact Stresses: The size of the base circle affects the contact stresses between the cam and the follower. A larger base circle distributes the contact forces over a larger area, reducing the stress concentration. Conversely, a smaller base circle concentrates the contact forces, leading to higher stresses.

4. Dynamic Loads: The size of the base circle also affects the dynamic loads on the cam system. The base circle diameter influences the inertia forces and accelerations experienced by the cam and follower during operation.

5. Manufacturing Considerations: The size of the base circle can also impact the manufacturing process. The machining or forming operations required to create the cam profile may vary depending on the size of the base circle.

Conclusion:
In conclusion, the size of the cam is primarily determined by the base circle. The base circle diameter influences various aspects of the cam's performance, including lift, profile, contact stresses, dynamic loads, and manufacturing considerations. A proper understanding of the base circle size is essential for designing efficient and reliable cam systems.

The c.g. of a link in any mechanism would experience
  • a)
    no acceleration
  • b)
    linear acceleration
  • c)
    angular acceleration
  • d)
    both angular and linear accelerations
  • e)
    none of the above
Correct answer is option 'D'. Can you explain this answer?

Devansh Nambiar answered
The correct answer is option 'D' - both angular and linear accelerations. Let's understand why this is the case:

Explanation:
1. Motion of a Link: In a mechanism, a link is a rigid body that connects two or more elements. The motion of a link can be both translational (linear) and rotational (angular) depending on the type of mechanism and the motion it is designed to produce.

2. Center of Gravity (c.g.): The center of gravity of a link is the point through which the entire weight of the link appears to act. It is the point where all the gravitational forces acting on the individual particles of the link can be considered to be concentrated.

3. Acceleration: Acceleration is the rate of change of velocity. In the case of a link in a mechanism, the velocity of the link can change in both linear and angular directions. Therefore, the acceleration of the center of gravity of the link can be both linear and angular.

4. Linear Acceleration: Linear acceleration refers to the change in linear velocity of an object. If a link is moving in a straight line, its center of gravity will experience linear acceleration. This can occur when the link is part of a mechanism that produces translational motion, such as a slider-crank mechanism.

5. Angular Acceleration: Angular acceleration refers to the change in angular velocity of an object. If a link is rotating about an axis, its center of gravity will experience angular acceleration. This can occur when the link is part of a mechanism that produces rotational motion, such as a crankshaft in an engine.

6. Combined Accelerations: In many mechanisms, the motion of a link may involve both linear and angular components simultaneously. For example, in a four-bar linkage, the motion of the link will have both linear and angular components. In such cases, the center of gravity of the link will experience both linear and angular accelerations.

Hence, the correct answer is option 'D' - both angular and linear accelerations, as the center of gravity of a link in any mechanism can experience both types of accelerations depending on the nature of the motion.

Rectangular bar in a rectangular hole is the following type of pair
  • a)
    completely constrained motion
  • b)
    partially constrained motion
  • c)
    incompletely constrained motion
  • d)
    freely constrained motion
  • e)
    none of the above
Correct answer is option 'A'. Can you explain this answer?

Abhay Kapoor answered
Rectangular bar in a rectangular hole is an example of completely constrained motion.

Explanation:
Completely constrained motion refers to a situation where the motion of a body or object is completely restricted or controlled by its surroundings. In other words, the object can only move in a specific manner or along a specific path without any freedom of movement.

In the case of a rectangular bar in a rectangular hole, the bar is designed to fit perfectly within the hole. This means that the dimensions of the bar are such that it fits snugly and does not have any space for movement in any direction. The sides of the bar are in contact with the sides of the hole, ensuring that the bar cannot move or rotate within the hole.

This type of arrangement provides complete constraint to the motion of the bar. It restricts the bar from moving in any direction and limits its motion to the confines of the hole. The bar is completely constrained within the hole, and its motion is determined by the shape and dimensions of the hole.

By contrast, partially constrained motion refers to a situation where the motion of a body or object is restricted in some directions or degrees of freedom but still has some freedom of movement. Incompletely constrained motion refers to a situation where the object has some restrictions on its motion but is not completely restricted. Freely constrained motion refers to a situation where the object has no restrictions on its motion and can move freely in any direction.

In conclusion, a rectangular bar in a rectangular hole is an example of completely constrained motion because the motion of the bar is completely restricted by the dimensions and shape of the hole. The bar cannot move or rotate within the hole and is constrained to the confines of the hole.

The centrifugal tension in belts
  • a)
    does not affect power transmission
  • b)
    increases power transmission
  • c)
    reduces power transmission 
  • d)
    increases power transmission upto certain speed and then decreases
  • e)
    none of the above
Correct answer is option 'A'. Can you explain this answer?

Rounak Choudhary answered
**Centrifugal Tension in Belts**

Centrifugal tension is a phenomenon that occurs in belt drives when the belt is rotating at high speeds. It refers to the outward force exerted on the belt due to its rotation, which causes the belt to stretch and tighten. This tension is caused by the centrifugal force acting on the mass of the belt.

**Impact on Power Transmission**

The centrifugal tension in belts does not directly affect power transmission. Power transmission in belt drives is primarily dependent on the tension in the belt, which is determined by the force applied to the belt by the pulleys. The tension in the belt is responsible for transmitting the torque from the driving pulley to the driven pulley.

**Explanation**

1. **Centrifugal Tension and Power Transmission:** The centrifugal tension in belts does not increase or decrease the power transmission capability of the belt drive system. It is a result of the belt's rotation but does not contribute to the torque or power transferred between the pulleys. Therefore, option A is the correct answer.

2. **Tension in Belt Drives:** The tension in belt drives is crucial for proper power transmission. The tension in the belt is carefully adjusted to ensure adequate grip between the belt and the pulleys. It is the tension that allows the belt to transmit the torque and power effectively.

3. **Factors Affecting Power Transmission:** The power transmission capability of a belt drive system depends on several factors, including the coefficient of friction between the belt and the pulleys, the tension in the belt, and the angle of wrap around the pulleys. These factors determine the maximum torque and power that can be transmitted without slipping.

4. **Slippage and Power Loss:** If the tension in the belt is too low or the coefficient of friction is inadequate, slippage can occur between the belt and the pulleys. This results in a loss of power transmission efficiency and can lead to decreased performance of the driven system.

5. **Centrifugal Tension and Belt Design:** Centrifugal tension is taken into account during the design of belts to ensure that the belt does not exceed its maximum allowable tension limit at high speeds. This is important to prevent belt failure and ensure safe operation of the belt drive system.

In conclusion, while centrifugal tension is a phenomenon that occurs in belt drives at high speeds, it does not directly affect power transmission. The tension in the belt, determined by the force applied by the pulleys, is the primary factor influencing power transmission capability.

Bevel gears are used to transmit rotary motion between two shafts whose axes are
  • a)
    parallel
  • b)
    non-intersecting
  • c)
    non-coplanar
  • d)
    any of the above
  • e)
    none of the above
Correct answer is option `E`. Can you explain this answer?

Kritika Joshi answered
Explanation:

Bevel gears are used to transmit rotary motion between two shafts. The axes of these two shafts can be parallel, non-intersecting, or non-coplanar. Therefore, the correct answer to this question is option `E`, which is "none of the above".

Parallel Axes:
If the axes of two shafts are parallel, then the bevel gears used to transmit rotary motion between them are called straight bevel gears.

Non-Intersecting Axes:
If the axes of two shafts are non-intersecting, then the bevel gears used to transmit rotary motion between them are called spiral bevel gears.

Non-Coplanar Axes:
If the axes of two shafts are non-coplanar, then the bevel gears used to transmit rotary motion between them are called hypoid bevel gears.

Conclusion:
Therefore, bevel gears can be used to transmit rotary motion between two shafts, regardless of whether their axes are parallel, non-intersecting, or non-coplanar.

The function of governor is to
  • a)
    store energy and give up whenever required
  • b)
    regulate the speed during one cycle of a prime mover
  • c)
    decrease variation of speed
  • d)
    increase variation of speed
  • e)
    adjust variation of speed by varying the input to the engine
Correct answer is option 'E'. Can you explain this answer?

Devansh Nambiar answered
Explanation:

A governor is a device that is used to regulate the speed of a machine such as an engine or a turbine. It is commonly used in steam engines, gas engines, and hydroelectric generators.

The function of a governor is to adjust the input to the engine or prime mover in order to regulate its speed. This is achieved by sensing the speed of the machine and adjusting the input accordingly. The governor works on the principle of centrifugal force, which is created by the rotation of the machine.

The governor consists of a set of weights that are attached to the machine. The weights are connected to a spindle that rotates with the machine. As the machine speeds up, the weights move outwards due to centrifugal force. This movement of the weights is used to adjust the input to the machine.

The governor has several functions, including:

1. Regulating speed: The primary function of a governor is to regulate the speed of the machine. It does this by adjusting the input to the machine in response to changes in its speed.

2. Decreasing variation of speed: A governor also helps to decrease the variation of speed in a machine. By regulating the input to the machine, it ensures that the speed remains constant within a certain range.

3. Increasing variation of speed: In some cases, a governor may be used to increase the variation of speed in a machine. This is done by adjusting the input to the machine in a way that causes it to speed up and slow down in a controlled manner.

4. Storing energy: Some governors are designed to store energy and release it when required. This is done by using a flywheel or other mechanism to store the energy generated by the machine. The energy can then be released when needed to maintain the speed of the machine.

Overall, the function of a governor is to regulate the speed of a machine and ensure that it operates within a safe and efficient range. By adjusting the input to the machine in response to changes in speed, it helps to maintain a stable and consistent level of performance.

The brake commonly used on train boggies is
  • a)
    internal expanding
  • b)
    band brake
  • c)
    band and block brake
  • d)
    shoe brake
  • e)
    electric brake
Correct answer is option 'D'. Can you explain this answer?

Nandita Chakraborty answered
The correct answer to the question is option 'D', shoe brake. Now let's understand why the shoe brake is commonly used on train bogies.

Introduction to Shoe Brake:
A shoe brake, also known as a block brake, is a type of braking mechanism commonly used in railway applications. It consists of a pair of brake shoes, which are curved metal plates lined with friction material, that press against the rotating surface of a wheel to slow down or stop the train.

Working Principle of Shoe Brake:
The shoe brake operates on the principle of friction. When the brake is engaged, the brake shoes are forced against the rotating wheels of the train bogie. The friction between the brake shoes and the wheels generates a braking force, which opposes the motion of the train and eventually brings it to a stop.

Advantages of Shoe Brake:
There are several reasons why shoe brakes are commonly used on train bogies:

1. High Friction Coefficient: Shoe brakes offer a high friction coefficient, which allows them to provide excellent stopping power and control, especially for heavy trains.

2. Effective Heat Dissipation: The curved design of the brake shoes allows for effective heat dissipation, preventing the brakes from overheating during prolonged braking. This is crucial for maintaining the braking efficiency and ensuring the safety of the train.

3. Reliable Performance: Shoe brakes are known for their reliability and durability. They can withstand heavy loads and repeated braking cycles without significant wear and tear.

4. Easy Maintenance: Shoe brakes are relatively easy to maintain and replace. The brake shoes can be easily inspected and replaced when necessary, minimizing downtime and ensuring the continuous operation of the train.

5. Cost-Effective: Shoe brakes are cost-effective compared to other braking mechanisms, making them a popular choice for train bogies.

Conclusion:
In conclusion, the shoe brake is commonly used on train bogies due to its high friction coefficient, effective heat dissipation, reliable performance, easy maintenance, and cost-effectiveness. It provides the necessary braking force to slow down and stop the train, ensuring the safety and efficiency of railway operations.

Pitching of a ship produces forces on the bearings
  • a)
    in the direction of motion of ship
  • b)
    which act horizontally perpendicular to the motion of ship
  • c)
    in the plane of the pitching
  • d)
    Which act along the axis of the bearings
  • e)
    Which can be resolved into all the three components
Correct answer is option 'D'. Can you explain this answer?

Subhankar Malik answered
Pitching of a Ship and Forces on Bearings

Pitching of a ship refers to the motion of the ship's bow and stern as it moves through the water. This motion can produce forces on the ship's bearings, which are responsible for supporting and allowing the rotation of various ship components such as propellers and turbines. The direction of these forces and their effects on the bearings depend on several factors such as the ship's speed, size, and the design of the bearings themselves.

Forces on Bearings

The forces produced by pitching can be resolved into three components: axial, radial, and tangential. These forces act on the bearings in different directions and produce different effects. The correct option is 'D' which states that the forces act along the axis of the bearings.

Axis of Bearings

The axis of the bearings is the imaginary line that passes through the center of the bearing and is perpendicular to its surface. The forces acting along this axis are called axial forces. These forces can cause the bearing to move along its axis or rotate around it. They are responsible for maintaining the alignment of the bearing and preventing it from shifting or tilting.

Conclusion

In conclusion, the correct option is 'D' which states that the forces produced by pitching of a ship act along the axis of the bearings. These axial forces are responsible for maintaining the alignment and preventing the bearing from shifting or tilting. Understanding the effects of pitching on ship components such as bearings is crucial in ensuring the safe and efficient operation of the vessel.

The following is the inversion of slider crank chain mechanism
  • a)
    Whitworth quick return mechanism
  • b)
    hand pump
  • c)
    oscillating cylinder engine
  • d)
    all of the above
  • e)
    none of the above
Correct answer is option 'D'. Can you explain this answer?

Lekshmi Rane answered
Inversion of Slider Crank Chain Mechanism

The slider crank chain mechanism is a basic mechanical structure that converts rotary motion into reciprocating motion. It consists of a crank, connecting rod, and slider. When the crank rotates, the connecting rod moves the slider back and forth in a straight line.

Whitworth Quick Return Mechanism

The Whitworth quick return mechanism is an inversion of the slider crank chain mechanism. It is used to convert rotary motion into reciprocating motion with a quick return stroke and a slower forward stroke. In this mechanism, the crank and connecting rod are replaced with a slotted lever and a connecting rod.

Hand Pump

The hand pump is another inversion of the slider crank chain mechanism. It is used to pump fluids by converting rotary motion into reciprocating motion. In this mechanism, the crank and connecting rod are replaced with a handle and a piston.

Oscillating Cylinder Engine

The oscillating cylinder engine is yet another inversion of the slider crank chain mechanism. It is used to convert rotary motion into reciprocating motion with a rotating cylinder. In this mechanism, the crank and connecting rod are replaced with a rotating cylinder and a piston.

All of the Above

All of the above mechanisms are inversions of the slider crank chain mechanism. They are used to convert rotary motion into reciprocating motion for various applications.

Conclusion

In summary, the inversion of the slider crank chain mechanism is a fundamental concept in mechanical engineering. It is used to create various types of mechanisms that convert rotary motion into reciprocating motion. The Whitworth quick return mechanism, hand pump, and oscillating cylinder engine are some examples of such mechanisms.

The moment on the pulley which production rotation is called
  • a)
    inertia
  • b)
    momentum
  • c)
    moment of momentum
  • d)
    work
  • e)
    torque
Correct answer is option 'E'. Can you explain this answer?

Kalyan Chakraborty answered
The Moment on the Pulley Which Produces Rotation

The correct answer to the given question is option 'E', which is torque. Torque is the moment on the pulley that produces rotation. Let's understand this concept in detail.

1. Torque:
Torque is a measure of how much a force acting on an object causes that object to rotate. It is the rotational equivalent of force. Torque can be defined as the product of the force applied and the perpendicular distance from the axis of rotation to the line of action of the force. Mathematically, torque (τ) is given by the equation:

τ = r x F

Where τ is the torque, r is the distance from the axis of rotation to the line of action of the force, and F is the applied force.

2. Moment of Inertia:
The moment of inertia is a property of an object that describes its resistance to rotational motion about a particular axis. It depends on the mass distribution of the object and the axis of rotation. Moment of inertia is given by the equation:

I = ∑(m_i * r_i^2)

Where I is the moment of inertia, m_i is the mass of the ith particle, and r_i is the perpendicular distance of the ith particle from the axis of rotation.

3. Momentum:
Momentum is a property of an object that describes its motion. It is defined as the product of the mass and velocity of an object. Momentum is given by the equation:

p = m * v

Where p is the momentum, m is the mass of the object, and v is the velocity of the object.

4. Work:
Work is defined as the product of the force applied to an object and the displacement of the object in the direction of the force. Work done on an object can change its energy. The work (W) is given by the equation:

W = F * d * cosθ

Where W is the work done, F is the applied force, d is the displacement of the object, and θ is the angle between the force and displacement vectors.

5. Moment of Momentum:
Moment of momentum is not a well-defined term in physics. It does not represent any physical quantity or concept.

Therefore, the correct answer to the given question is torque (option 'E'), which is the moment on the pulley that produces rotation.

Length of open belt, in addition to centre length, depends
  • a)
    only on the sum of the radii of pulleys
  • b)
    on the sum and difference of the radii of the pulleys
  • c)
    square of difference of radii of pulleys
  • d)
    square of sum of radii of pulleys
  • e)
    none of the above
Correct answer is option 'B'. Can you explain this answer?

Prateek Mukherjee answered
Length of Open Belt

The length of an open belt is the total length of the belt when it is extended between the two pulleys. This length is required to calculate the size of the belt required for a particular application.

Factors Affecting Length of Open Belt

The length of an open belt depends on:

1. Centre Distance

The distance between the two pulleys is known as the centre distance. The length of the belt depends on the centre distance between the two pulleys.

2. Sum and Difference of Radii

The sum and difference of the radii of the pulleys also affect the length of the belt.

- When the radii of the two pulleys are equal, the centre distance is equal to twice the radius of the pulley.
- When the radii of the two pulleys are different, the centre distance will be greater than the sum of the radii and less than the difference of the radii.

3. Angle of Contact

The angle of contact is the angle between the belt and the pulley. The greater the angle of contact, the greater the length of the belt.

4. Thickness of Belt

The thickness of the belt also affects the length of the belt. The thicker the belt, the greater the length of the belt.

Conclusion

In conclusion, the length of an open belt depends on the centre distance between the two pulleys, the sum and difference of the radii of the pulleys, the angle of contact, and the thickness of the belt. Therefore, the correct answer is option B, which states that the length of an open belt depends on the sum and difference of the radii of the pulleys.

Intermediate gears are used for
  • a)
    obtaining rotation in desired direction
  • b)
    reducing the size of the individual gear
  • c)
    bridging the gap between the first and last wheels of the train
  • d)
    driving auxiliaries incidental to the main drive
  • e)
    any one of the above
Correct answer is option 'E'. Can you explain this answer?

Bhaskar Joshi answered
Intermediate gears are used for obtaining rotation in the desired direction, reducing the size of the individual gear, bridging the gap between the first and last wheels of the train, and driving auxiliaries incidental to the main drive.

1. Obtaining rotation in the desired direction:
Intermediate gears are often used in gear trains to change the direction of rotation. The rotation of the input gear is transmitted to an intermediate gear, which then transmits the rotation to the final output gear. By strategically placing intermediate gears, the direction of rotation can be manipulated to meet specific requirements.

2. Reducing the size of the individual gear:
In some cases, the size of the gear required to achieve a specific gear ratio may be too large. By introducing intermediate gears into the gear train, the overall gear ratio can be achieved using smaller individual gears. This helps to reduce the size and weight of the gear system, making it more compact and efficient.

3. Bridging the gap between the first and last wheels of the train:
In gear trains, the first and last gears may have significantly different sizes. Intermediate gears are used to bridge the gap between these gears and ensure a smooth transmission of rotation. They help to distribute the load evenly across the gears and prevent excessive wear and tear on any single gear.

4. Driving auxiliaries incidental to the main drive:
In many mechanical systems, there are auxiliary components or subsystems that need to be driven in addition to the main drive. Intermediate gears can be used to transmit power from the main drive to these auxiliary components. This allows for the simultaneous operation of multiple components using a single power source.

In summary, intermediate gears serve multiple purposes in mechanical systems. They help to obtain rotation in the desired direction, reduce the size of individual gears, bridge the gap between different-sized gears, and drive auxiliaries incidental to the main drive.

Flexible coupling is used because
  • a)
    it is easy to disassemble
  • b)
    it is easy to engage and disengage
  • c)
    it transmits shocks gradually
  • d)
    it prevents shock transmission and eliminates stress reversals.
  • e)
    it increase shaft life
Correct answer is option 'D'. Can you explain this answer?

Manasa Sen answered
Flexible Coupling - Importance and Working

Flexible Couplings are mechanical devices that transmit torque from one shaft to another when the two shafts are slightly misaligned. They are used to connect two shafts and compensate for misalignment, as well as to prevent shock transmission and eliminate stress reversals. In this article, we will discuss the importance of flexible couplings and how they work.

Importance of Flexible Coupling

Flexible Couplings have a wide range of applications in mechanical engineering and are used in various industries. They are essential for the smooth functioning of machines and equipment. The following are the reasons why flexible couplings are important:

1. Compensate for Misalignment

Flexible Couplings are designed to compensate for shaft misalignment, which can be caused by various factors such as thermal expansion, manufacturing tolerances, and dynamic loading. They can absorb shocks and vibrations, which reduces wear and tear on the equipment.

2. Prevent Shock Transmission

Flexible Couplings are essential in preventing shock transmission between two shafts. They can absorb and dampen the shockwaves that are generated due to sudden changes in load or torque. This reduces the stress on the equipment and increases its lifespan.

3. Eliminate Stress Reversals

Flexible Couplings can eliminate stress reversals that are generated due to misalignment or shock loads. Stress reversals can cause fatigue failure in the equipment, which can lead to costly repairs and downtime.

Working of Flexible Coupling

Flexible Couplings work by transmitting torque from one shaft to another while compensating for misalignment. They are designed to absorb and dampen shockwaves and vibrations, which reduces the stress on the equipment. The following are the types of flexible couplings:

1. Gear Couplings

Gear Couplings are used to transmit high torque between two shafts. They are made of two hubs with external teeth that are connected by a sleeve with internal teeth. Gear couplings are designed to compensate for angular, parallel, and axial misalignment.

2. Universal Couplings

Universal Couplings are used to transmit torque between two shafts with large angular misalignment. They are made of two yokes with a cross-shaped bearing that is connected by a center block. Universal couplings can compensate for angular, parallel, and axial misalignment.

3. Disc Couplings

Disc Couplings are used to transmit torque between two shafts with low to medium misalignment. They are made of two hubs with a flexible disc that is connected by a spacer. Disc couplings can absorb and dampen shockwaves and vibrations.

Conclusion

Flexible Couplings are essential in mechanical engineering as they compensate for misalignment, prevent shock transmission, and eliminate stress reversals. They are used in various industries and are designed to absorb and dampen shockwaves and vibrations, which reduces the stress on the equipment. There are different types of flexible couplings, and each is designed for a specific application.

The governor used in gramophone is of the following type
  • a)
    Pickening
  • b)
    Porter
  • c)
    hartnell
  • d)
    watt
  • e)
    hartung
Correct answer is option 'A'. Can you explain this answer?

Juhi Choudhary answered

Types of Governors in Gramophone

Governors used in gramophones are crucial components that help regulate the speed of rotation of the turntable, ensuring that the music plays at the correct speed. The type of governor commonly used in gramophones is the Pickering governor.

Pickering Governor
- The Pickering governor is a type of centrifugal governor that consists of two masses attached to a rotating shaft.
- As the shaft rotates, the centrifugal force acting on the masses causes them to move outwards, which in turn alters the position of the control mechanism.
- The control mechanism of the Pickering governor is designed to adjust the speed of the gramophone motor based on the position of the masses.
- By maintaining a constant speed of rotation, the Pickering governor ensures that the music plays accurately and does not sound distorted.

Other Types of Governors
- While the Pickering governor is commonly used in gramophones, there are other types of governors that can also be used in similar applications.
- Some examples of other types of governors include the Porter governor, Hartnell governor, Watt governor, and Hartung governor.
- Each type of governor has its unique design and mechanism for regulating speed, but the Pickering governor is specifically chosen for its effectiveness in gramophones.

In conclusion, the governor used in gramophones is typically the Pickering governor due to its ability to maintain consistent speed and ensure accurate playback of music.

The belting can transmit maximum power when maximum total tension in belt equals
  • a)
    twice the centrifugal tension
  • b)
    thrice the centrifugal tension
  • c)
    four times the centrifugal tension
  • d)
    half the centrifugal tension
Correct answer is option 'B'. Can you explain this answer?

Sanchita Pillai answered
Introduction:
In mechanical power transmission systems, belts are often used to transfer power between two rotating shafts. The efficiency of power transmission depends on the tension in the belt. The maximum power transmission occurs when the total tension in the belt is optimized. This can be achieved by considering the centrifugal tension in the belt.

Explanation:
To understand why the maximum total tension in the belt should be three times the centrifugal tension, we need to consider the different types of tensions acting on the belt during power transmission.

1. Tension in the tight side:
The tight side of the belt experiences tension due to the driving force applied to the belt. This tension is responsible for transmitting power from the driver shaft to the driven shaft.

2. Tension in the slack side:
The slack side of the belt experiences less tension compared to the tight side. This tension is necessary to maintain the belt's position on the pulleys and prevent slippage.

3. Centrifugal tension:
When the belt is in motion, it experiences centrifugal forces due to its own weight. These forces create tension in the belt, which opposes the driving force. The centrifugal tension increases with the speed of the belt.

4. Total tension:
The total tension in the belt is the sum of the tension in the tight side, tension in the slack side, and the centrifugal tension.

Maximizing power transmission:
To maximize power transmission, we need to optimize the tension in the belt. The tension in the tight side and slack side should be balanced to prevent excessive wear and slippage. Additionally, the centrifugal tension should be considered.

When the total tension is twice the centrifugal tension (as mentioned in option A), the belt may experience excessive wear and slippage. This can lead to reduced power transmission efficiency and potential belt failure.

On the other hand, when the total tension is thrice the centrifugal tension (as mentioned in option B), the tension in the belt is balanced, and the centrifugal tension is properly accounted for. This ensures efficient power transmission without excessive wear or slippage.

Therefore, the correct answer is option B - thrice the centrifugal tension.

According to Kennedy's theorem, if three bodes have plane motions, their instantaneous centres lie on
  • a)
    a triangle
  • b)
    a point
  • c)
    two lines
  • d)
    s straight line
  • e)
    a curve
Correct answer is option 'D'. Can you explain this answer?

Divya Banerjee answered
Kennedy's Theorem in Plane Motion

Kennedy's theorem is a fundamental theorem in the study of planar motion of rigid bodies. It relates the motion of three bodies in a plane to the instantaneous centers of rotation. According to Kennedy's theorem, if three bodies have plane motion, their instantaneous centers lie on a straight line.

Instantaneous Center of Rotation

The instantaneous center of rotation is the point about which a rigid body has pure rotation at a given instant. It is the point in the plane of motion that has zero velocity at a particular instant. For a rigid body with plane motion, every point on the body has a different instantaneous center of rotation.

Proof of Kennedy's Theorem

Consider three bodies A, B, and C in plane motion. Let P and Q be the instantaneous centers of rotation of A and B, respectively, with respect to C. Let the velocities of A and B with respect to C be vA and vB, respectively. Then, the velocity of A with respect to B is given by vA - vB. Similarly, the velocity of P with respect to B is vP - vB.

Since P is the instantaneous center of rotation of A with respect to C, the velocity of P with respect to A is zero. Therefore, the velocity of P with respect to B is equal to the velocity of A with respect to B, i.e., vA - vB = vP - vB. Simplifying this equation, we get vA = vP.

Similarly, since Q is the instantaneous center of rotation of B with respect to C, we can show that vB = vQ. Hence, vA = vP = vQ = vB. Therefore, P, Q, and C have the same velocity with respect to B. Since their velocities are collinear, they lie on a straight line.

Conclusion

Kennedy's theorem is a simple yet powerful tool for analyzing the planar motion of rigid bodies. It relates the motion of three bodies in a plane to the instantaneous centers of rotation, which lie on a straight line. This theorem has wide applications in many areas of engineering, including machine design, robotics, and biomechanics.

According to law of gearing
  • a)
    teeth should be of involute type
  • b)
    clearance between mating teeth should be provided
  • c)
    dedendum should be equal to 1.157 m
  • d)
    teeth should be of cycloidal type
  • e)
    none of the above
Correct answer is option 'E'. Can you explain this answer?

Atharva Majumdar answered
The correct answer to the question is option 'E' - none of the above. Let's discuss each option and explain why it is not correct:

a) Teeth should be of involute type: The law of gearing does not specify the type of teeth that should be used. However, involute teeth are commonly used in gear design due to their desirable characteristics such as smooth operation, constant angular velocity ratio, and ease of manufacturing.

b) Clearance between mating teeth should be provided: It is essential to provide a small amount of clearance between mating teeth to ensure smooth operation and prevent interference. However, the law of gearing does not specifically mention the provision of clearance.

c) Dedendum should be equal to 1.157 m: The dedendum is the distance between the bottom of the tooth and the pitch circle. It is determined based on the module or the diametral pitch of the gear. The value of 1.157 is associated with the addendum, and it is used to calculate the outside diameter of the gear. Therefore, it is not correct to state that the dedendum should be equal to 1.157 m.

d) Teeth should be of cycloidal type: Cycloidal teeth are another type of tooth profile used in gear design. They have the advantage of providing smooth contact between the teeth and low noise operation. However, the law of gearing does not specify the type of teeth that should be used.

Explanation:

The law of gearing, also known as the fundamental law of gearing, states that the angular velocity ratio of mating gears is equal to the inverse ratio of their pitch diameters. In other words, the ratio of the number of teeth on two gears determines their speed relationship.

The law of gearing does not provide specific guidelines regarding the type of tooth profile, clearance, or dedendum. These factors depend on various design considerations such as the application, load conditions, manufacturing capabilities, and desired performance characteristics.

Gear tooth profile selection is typically based on factors such as load capacity, smooth operation, noise level, manufacturing ease, and cost. Involute teeth are commonly used due to their favorable characteristics, but other profiles like cycloidal teeth can also be employed.

Clearance between mating teeth is necessary to prevent interference and ensure smooth meshing. The amount of clearance depends on factors such as the manufacturing tolerances, operating conditions, and backlash requirements. The specific value of clearance is not dictated by the law of gearing.

The dedendum is determined based on the module or diametral pitch of the gear and is selected to ensure proper clearance and tooth strength. The value of 1.157 is associated with the addendum and is used to calculate the outside diameter of the gear.

In conclusion, the law of gearing does not specify the type of tooth profile, the provision of clearance, or a specific value for the dedendum. These design factors are determined based on various considerations and requirements specific to each gear application.

Chapter doubts & questions for Theory of Machines (TOM) - Mechanical Engineering SSC JE (Technical) 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Theory of Machines (TOM) - Mechanical Engineering SSC JE (Technical) in English & Hindi are available as part of Mechanical Engineering exam. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.

Mechanical Engineering SSC JE (Technical)

6 videos|104 docs|59 tests

Top Courses Mechanical Engineering

© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup