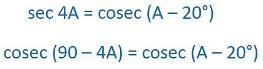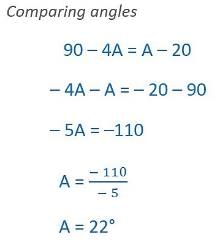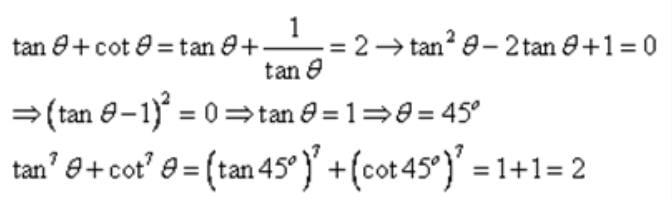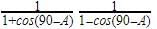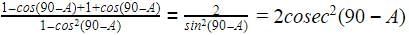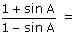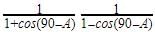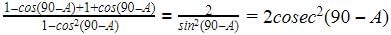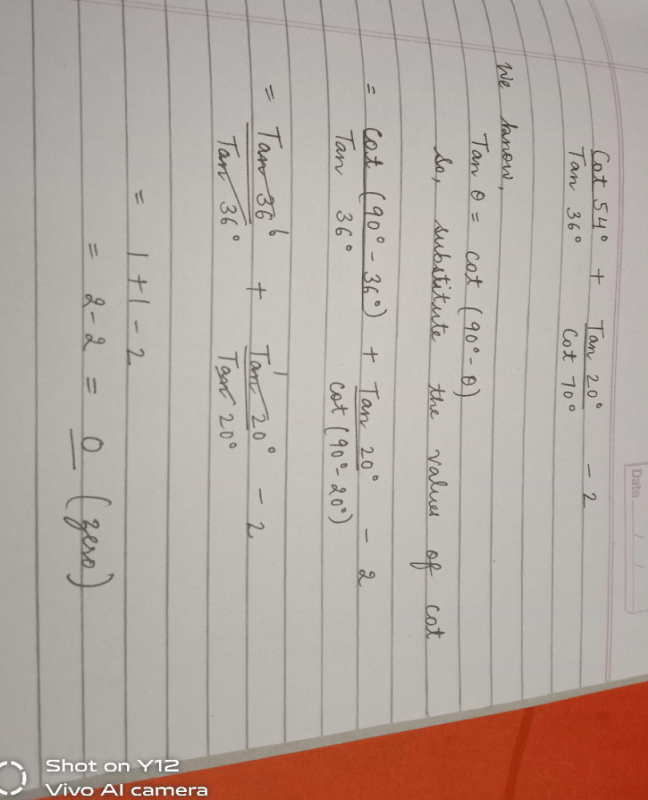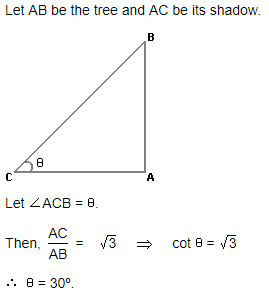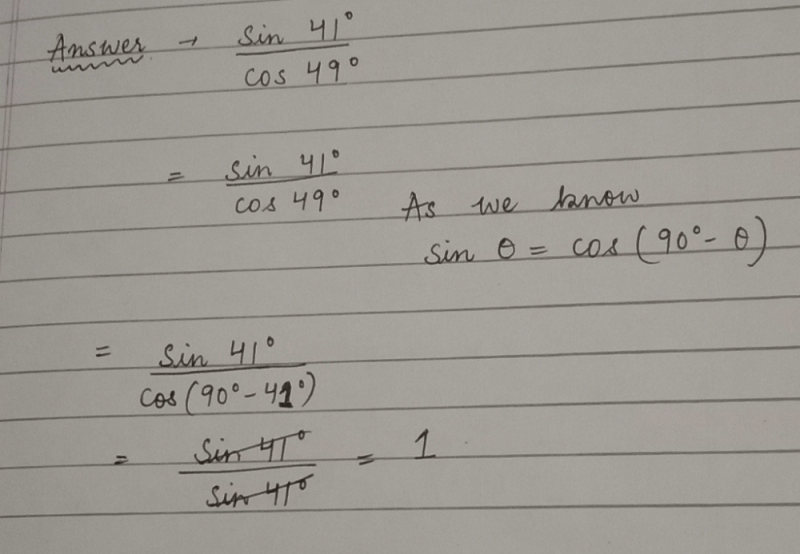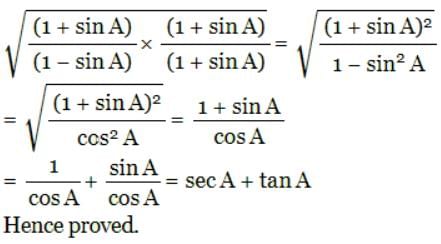All Exams >
BMAT >
Mathematics for BMAT (Section 2) >
All Questions
All questions of Trigonometry for BMAT Exam
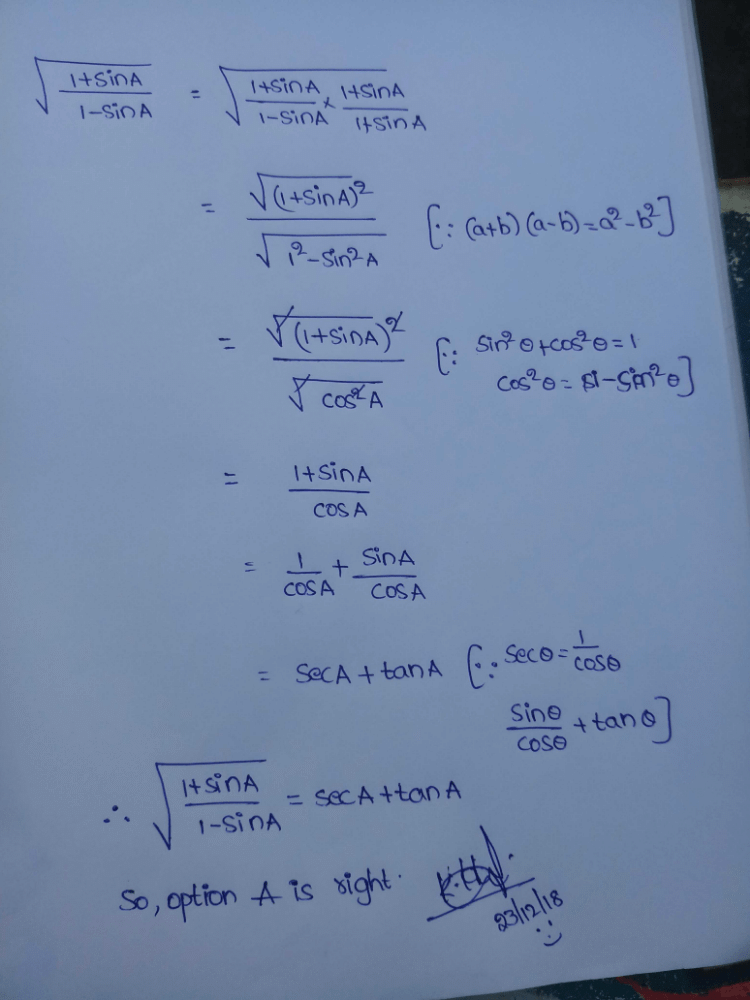
If tan 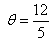 , then
, then 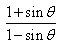 is equal to
is equal to- a)24
- b)12/13
- c)25
- d)9
Correct answer is option 'C'. Can you explain this answer?
If tan 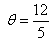 , then
, then 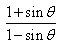 is equal to
is equal to
a)
24
b)
12/13
c)
25
d)
9

|
Vp Classes answered |
tanθ = 12/5
so sinθ = 12/13
so
(1 + 12/13)/(1-12/13)
= 25/1 = 25
Can you explain the answer of this question below:If 7sin2x + 3cos2x = 4 then , secx + cosecx =- A:
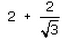
- B:
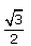
- C:
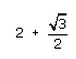
- D:
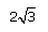
The answer is a.
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
A:
B:
C:
D:

|
Gunjan Lakhani answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=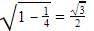
Sec x= 1/cos x=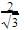
Cosec x + sec x=2+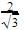
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
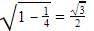
Sec x= 1/cos x=
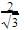
Cosec x + sec x=2+
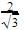
The value of tan1°.tan2°.tan3°………. tan89° is :- a)2
- b)1
- c)1/2
- d)0
Correct answer is option 'B'. Can you explain this answer?
The value of tan1°.tan2°.tan3°………. tan89° is :
a)
2
b)
1
c)
1/2
d)
0
|
|
Meera Rana answered |
tan 1.tan 2.tan 3...tan (90 - 3 ).tan ( 90 - 2 ).tan ( 90 - 1)
=tan 1.tan 2 .tan 3...cot 3.cot 2.cot 1
=tan 1.cot 1.tan 2.cot 2.tan 3.cot 3 ... tan 89.cot 89
1 x 1 x 1 x 1 x ... x 1 =1
=tan 1.tan 2 .tan 3...cot 3.cot 2.cot 1
=tan 1.cot 1.tan 2.cot 2.tan 3.cot 3 ... tan 89.cot 89
1 x 1 x 1 x 1 x ... x 1 =1
The value of 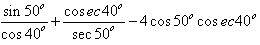 is
is- a)2
- b)0
- c)4
- d)-2
Correct answer is option 'D'. Can you explain this answer?
The value of 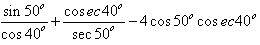 is
is
a)
2
b)
0
c)
4
d)
-2
|
|
Krishna Iyer answered |
we know sin(90 - a) = cos(a)
cos(90 - a) = sin(a)
sin(a) = 1/cosec(a)
sec(a) = 1/cos(a)
cos40 = cos(90-50) = sin50
cosec40 = cosec(90-50) = sec50
so our expression becomes
sin50/sin50 + sec50/sec50 - 4cos50 / sin40
= 1 + 1 - 4(1) since cos50 = sin40
= -2
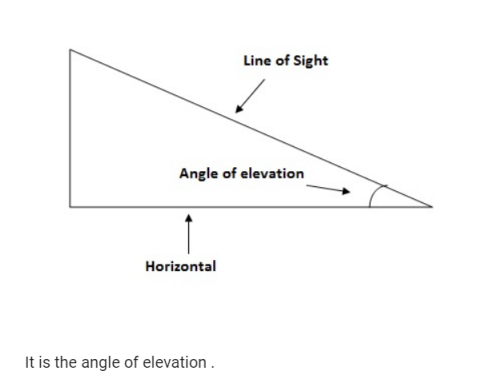
If the length of a shadow cast by a pole is √3 times the length of the pole, then the angle of elevation of the sun is- a)45°
- b)60°
- c)30°
- d)90°
Correct answer is option 'C'. Can you explain this answer?
If the length of a shadow cast by a pole is √3 times the length of the pole, then the angle of elevation of the sun is
a)
45°
b)
60°
c)
30°
d)
90°
|
|
Anjana Khatri answered |
Consider the height of tower be h
∴ height of shadow =√3h .
In a triangle ABC,
tan ∠ACB = h / √3h
tan ∠ACB = 1 / √3
∠ACB = 30degree.
Therefore, angle of elevation is 30degree .
If cos (40° + A) = sin 30°, the value of A is:
- a)60°
- b)20°
- c)40°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
If cos (40° + A) = sin 30°, the value of A is:
a)
60°
b)
20°
c)
40°
d)
30°

|
EduRev Class 10 answered |
cos(θ)=sin(90-θ)
so 40+A+30=90
A=20
so 40+A+30=90
A=20
If the angle of elevation of a cloud from a point 60 metres above a lake is 30o and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
- a)30 m
- b)120 m
- c)200 m
- d)500 m
Correct answer is option 'B'. Can you explain this answer?
If the angle of elevation of a cloud from a point 60 metres above a lake is 30o and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
a)
30 m
b)
120 m
c)
200 m
d)
500 m
|
|
Neha Patel answered |
Let AB be the surface of the lake and P be the point of observation such that AP = 60 m. Let C be the position of the cloud and C be its reflection in the lake.
Then CB =
Draw PM⊥CB
Let CM = h
∴ CB = h + 60 m


The value of cos θ cos(90° - θ) – sin θ sin (90° - θ) is:
- a)1
- b)0
- c)-1
- d)2
Correct answer is option 'B'. Can you explain this answer?
The value of cos θ cos(90° - θ) – sin θ sin (90° - θ) is:
a)
1
b)
0
c)
-1
d)
2
|
|
Vikas Kumar answered |
Explanation:
- Given expression: cos θ cos(90° - θ) – sin θ sin (90° - θ)
- We know that cos(90° - θ) = sin θ and sin(90° - θ) = cos θ
- Substitute these values into the expression:
= cos θ * sin θ - sin θ * cos θ
= sin θ cos θ - sin θ cos θ
= 0
- Therefore, the value of the expression is 0.
- Given expression: cos θ cos(90° - θ) – sin θ sin (90° - θ)
- We know that cos(90° - θ) = sin θ and sin(90° - θ) = cos θ
- Substitute these values into the expression:
= cos θ * sin θ - sin θ * cos θ
= sin θ cos θ - sin θ cos θ
= 0
- Therefore, the value of the expression is 0.
If A and B are the angles of a right angled triangle ABC, right angled at C, then 1+cot2A =- a)cot2B
- b)sec2B
- c)cos2B
- d)tan2B
Correct answer is option 'B'. Can you explain this answer?
If A and B are the angles of a right angled triangle ABC, right angled at C, then 1+cot2A =
a)
cot2B
b)
sec2B
c)
cos2B
d)
tan2B

|
Siddharth answered |
ABC is a Δ, right angle at c.
1 +cot^2 =?........
we know that.....
Cosec^2 - cot^2= 1...
So,
=> 1+ cot^2
=> cosec^2 A
=> (AB)^2/( CB)^2
= sec ^2B.
Out of the following options, the two angles that are together classified as complementary angles are- a)120° and 60°
- b)50° and 30°
- c)65° and 25°
- d)70° and 30°
Correct answer is option 'C'. Can you explain this answer?
Out of the following options, the two angles that are together classified as complementary angles are
a)
120° and 60°
b)
50° and 30°
c)
65° and 25°
d)
70° and 30°
|
|
Namita khanna answered |
B)90
c)45
The two angles that are together classified as complementary angles are b)90 and c)45.
c)45
The two angles that are together classified as complementary angles are b)90 and c)45.
The value of cos2 17° – sin2 73° is- a)0
- b)1
- c)-1
- d)3
Correct answer is 'A'. Can you explain this answer?
The value of cos2 17° – sin2 73° is
a)
0
b)
1
c)
-1
d)
3
|
|
Amit Sharma answered |
cos217-sin273
=cos217-sin2(90-17)
=cos217-cos217 (because sin(90-x)=cos x)
=0
=cos217-sin2(90-17)
=cos217-cos217 (because sin(90-x)=cos x)
=0
The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:- a)45°
- b)60°
- c)30°
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:
a)
45°
b)
60°
c)
30°
d)
None of these
|
|
Ananya Das answered |
Consider the diagram shown above where QR represents the tree and PQ represents its shadow
We have, QR = PQ
Let ∠QPR = θ
tan θ = QR/PQ = 1 (since QR = PQ)
⇒ θ = 45°
Let ∠QPR = θ
tan θ = QR/PQ = 1 (since QR = PQ)
⇒ θ = 45°
i,e., required angle of elevation = 45°
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45o. Then the height (in meters) of the tower is- a)25
- b)25√3
- c)12.5
- d)25√2
Correct answer is option 'A'. Can you explain this answer?
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45o. Then the height (in meters) of the tower is
a)
25
b)
25√3
c)
12.5
d)
25√2
|
|
Vikram Kapoor answered |
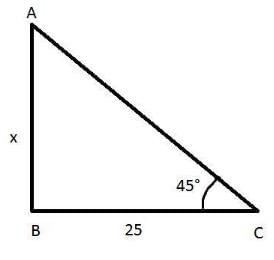
A point on the ground which is 25 m away from the foot of the tower i. BC= 25 m
Let the height of the tower be x
The angle of elevation of the tower is found to be 45 degree.i.e.∠ACB=45°
In ΔABC
Using trigonometric ratios
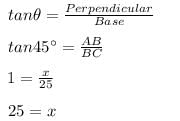
Hence the height of the tower is 25 m.
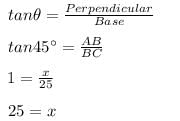
Hence the height of the tower is 25 m.
A 20 m long ladder touches the wall at a height of 10 m. The angle which the ladder makes with the horizontal is- a)450
- b)300
- c)900
- d)600
Correct answer is option 'B'. Can you explain this answer?
A 20 m long ladder touches the wall at a height of 10 m. The angle which the ladder makes with the horizontal is
a)
450
b)
300
c)
900
d)
600
|
|
Anjana Khatri answered |
ATQ , perpendicular /hypotenuse= 10/20
i.e sinθ = 10/ 20
sinθ= 1/2
so, sin 30 deg= 1/2
required angle = 30 Deg
Tree is broken by the wind the top struck the ground at 30° at a distance of 30m. away from the root. Find the height of the tree.
- a)45.9
- b)88.60
- c)54.63
- d) 51.96
Correct answer is option 'D'. Can you explain this answer?
Tree is broken by the wind the top struck the ground at 30° at a distance of 30m. away from the root. Find the height of the tree.
a)
45.9
b)
88.60
c)
54.63
d)
51.96
|
|
Neha Patel answered |
let ,
the height of standing part of the tree be = h
the height of fallen part (forms hypotenuse) be = x
then the total height of the tree will be = h + x
now,
tan 30 = h/30 m
1/√3 = h/30 m
30/√3 = h
⇒ h= 30/√3 m .... 1
similarly,
cos 30 = 30 m/ x
√3/2 = 30 / x
√3x = (30)2
√3x = 60 m
⇒ x = 60 / √3 m ....2
( we now have both value of h and x )
on adding equation1 & 2 :
⇒ h + x = 30 /√3 +60 /√3
=90 /√3 m
= 60√3 m
so , the total height of the tree is 60√3 m .
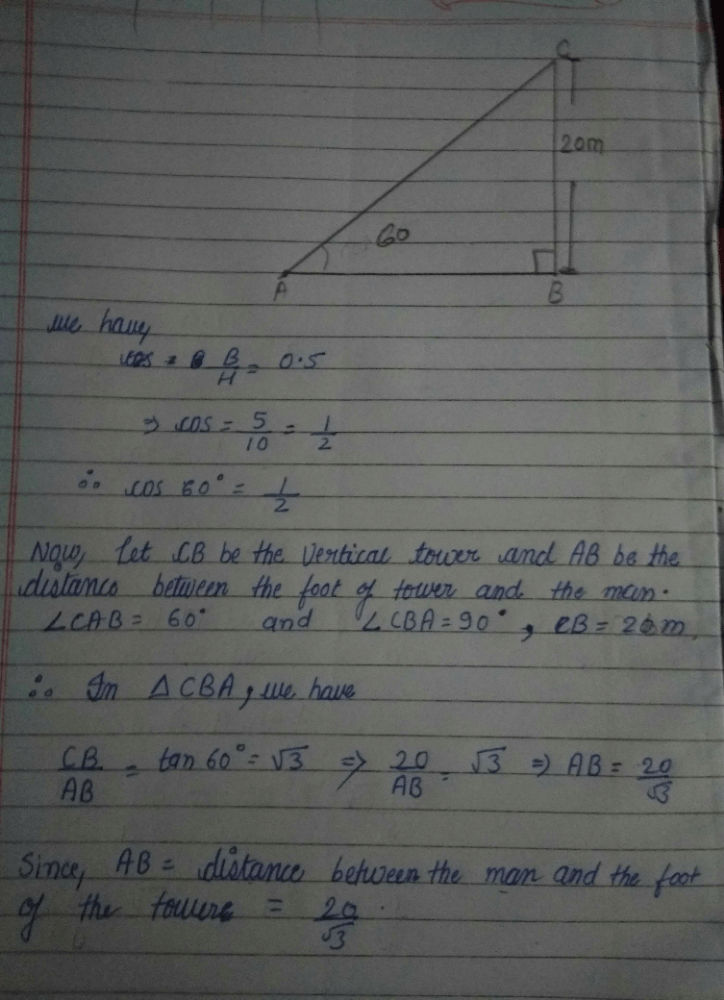
A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and angle of depression of the base of the hill as 30°. What is the height of the hill?- a)

- b)24 m
- c)32 m
- d)
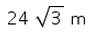
Correct answer is option 'C'. Can you explain this answer?
A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and angle of depression of the base of the hill as 30°. What is the height of the hill?
a)
b)
24 m
c)
32 m
d)
|
|
Mubeena Akhter answered |

A tree casts a shadow 4 m long on the ground, when the angle of elevation of the sun is 45o. The height of the tree is:- a)5.2 m
- b)4 m
- c)3 m
- d)4.5 m
Correct answer is option 'B'. Can you explain this answer?
A tree casts a shadow 4 m long on the ground, when the angle of elevation of the sun is 45o. The height of the tree is:
a)
5.2 m
b)
4 m
c)
3 m
d)
4.5 m
|
|
Nisha Choudhury answered |
In a triangle with one angle being 90 degrees (which the tree makes with the ground) and the other being 45 degrees (the angle of elevation), the 3rd angle is bound to be 45 degrees (180 - 90 - 45 = 45).
We also know that sides opposite to equal angles are equal.
Hence, the height of the tree will also be 4m.
Let AC be the rope whose length is 20 m, and AB be the vertical pole of height h m and the angle of elevation of A at point C on the ground is 30°.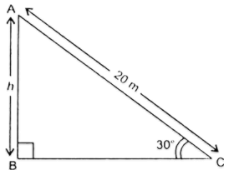
- a)10 m
- b)21 m
- c)19 m
- d)17 m
Correct answer is option 'A'. Can you explain this answer?
Let AC be the rope whose length is 20 m, and AB be the vertical pole of height h m and the angle of elevation of A at point C on the ground is 30°.
a)
10 m
b)
21 m
c)
19 m
d)
17 m
|
|
Ananya Das answered |
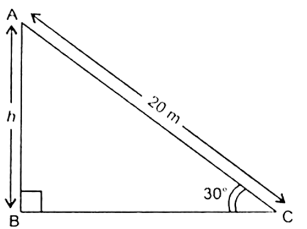
Fif. 9.11
i.e., ∠ACB = 30°
In right triangle ABC, we have
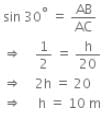
Hence, the height of the pole is 10 m.
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from his eyes is 45°. The height of the tower is- a)10 m
- b)40 m
- c)30 m
- d)20 m
Correct answer is option 'C'. Can you explain this answer?
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from his eyes is 45°. The height of the tower is
a)
10 m
b)
40 m
c)
30 m
d)
20 m

|
EduRev Class 10 answered |
To solve for the height of the tower, we use the tangent function. The angle of elevation is 45°, and the horizontal distance from the observer to the tower is 28.5 m.
Let the height of the tower be h. The observer's eye level is 1.5 m, so the difference in height between the top of the tower and the observer's eyes is h−1.5h.

The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30o. If the height of the second tower is 60 m then, the height of the first tower is- a)140.83 m
- b)135 m
- c)139.5 m
- d)142 m
Correct answer is option 'A'. Can you explain this answer?
The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30o. If the height of the second tower is 60 m then, the height of the first tower is
a)
140.83 m
b)
135 m
c)
139.5 m
d)
142 m
|
|
Amit Sharma answered |
The second tower is smaller than the first tower so let the height of the first tower is h So a part of it is equal to 60m so the remaining height is h-60 m
Tan 30=perpendicular/base
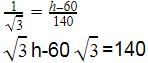
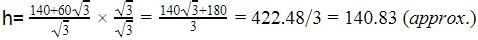
Tan 30=perpendicular/base
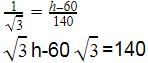
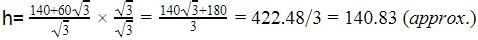
A tree is broken by wind and its upper part touches the ground at a point 10 metres from the foot of the tree and makes an angle of 45° with the ground. The entire length of the tree is- a)20 m
- b)10(1+√2)m
- c)10 m
- d)10√2 m
Correct answer is option 'B'. Can you explain this answer?
A tree is broken by wind and its upper part touches the ground at a point 10 metres from the foot of the tree and makes an angle of 45° with the ground. The entire length of the tree is
a)
20 m
b)
10(1+√2)m
c)
10 m
d)
10√2 m
|
|
Drishti Kumari answered |
Base = 10m
Angle of elevation = 45 degree
tan 45 ^ = P / b ( Let p supoose h )
1= h / 10
h = 10 m
height of half tree = 10 m
Now the length of broken part i.e, hypotenuse
H^2 = P ^2 + B ^2
H ^2 = 10^2 + 10 ^2
H ^2 = 100 +100
H = root under 100
H = 10 root 2
Hence , the length of entire tree = 10 + 10 root2
10 ( 1 + root 2 )
That's why B is the correct optipn .
Angle of elevation = 45 degree
tan 45 ^ = P / b ( Let p supoose h )
1= h / 10
h = 10 m
height of half tree = 10 m
Now the length of broken part i.e, hypotenuse
H^2 = P ^2 + B ^2
H ^2 = 10^2 + 10 ^2
H ^2 = 100 +100
H = root under 100
H = 10 root 2
Hence , the length of entire tree = 10 + 10 root2
10 ( 1 + root 2 )
That's why B is the correct optipn .
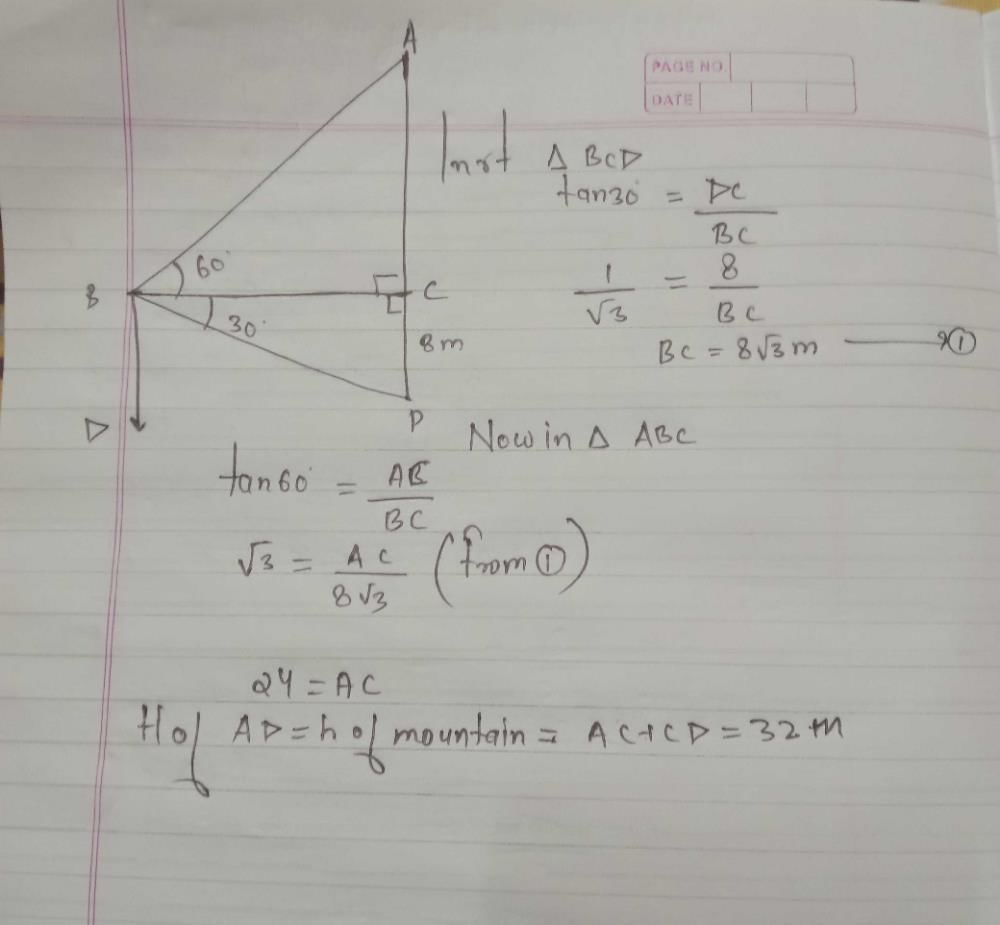
A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and angle of depression of the base of the hill as 30°. What is the height of the hill?- a)24√3 m
- b)24 m
- c)8√3 m
- d)32 m
Correct answer is option 'D'. Can you explain this answer?
A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and angle of depression of the base of the hill as 30°. What is the height of the hill?
a)
24√3 m
b)
24 m
c)
8√3 m
d)
32 m
|
|
Mysterio Man answered |
If the angles of depression from the top of a tower of height 40 m to the top and bottom of a tree are 45° and 60° respectively, then the height of the tree is- a)
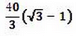
- b)
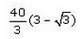
- c)
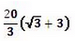
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
If the angles of depression from the top of a tower of height 40 m to the top and bottom of a tree are 45° and 60° respectively, then the height of the tree is
a)
b)
c)
d)
None of the above

|
EduRev Class 10 answered |
A tower of height 40 m is given, and the angles of depression from the top of the tower to:
- The top of the tree = 45°
- The bottom of the tree = 60°
We need to find the height of the tree (h).
Step 1: Use trigonometry for the angles of depression
Let:
Let:
- The distance between the base of the tower and the base of the tree = d
- The height of the tree = h
From the 45° angle (to the top of the tree):
The formula is:
tan(45°) = (Height of the tower - Height of the tree) / Distance (d)
Since tan(45°) = 1:
1 = (40 - h) / d
d = 40 - h (1)
From the 60° angle (to the bottom of the tree):
The formula is:
tan(60°) = Height of the tower / Distance (d)
Since tan(60°) = √3:
√3 = 40 / d
d = 40 / √3 (2)
Step 2: Solve the equations
Equate d from equations (1) and (2):
40 - h = 40 / √3
Rearrange to solve for h:
h = 40 - (40 / √3)
Rationalize the denominator:
h = 40 - (40√3 / 3)
h = (120 / 3) - (40√3 / 3)
h = (40 (3 - √3)) / 3
The height of the tree is:
b) (40 / 3) (3 - √3)
If 7sin2x + 3cos2x = 4 then , secx + cosecx =- a)
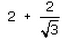
- b)
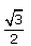
- c)
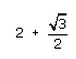
- d)
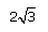
Correct answer is 'A'. Can you explain this answer?
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
a)
b)
c)
d)
|
|
Naina Sharma answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=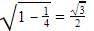
Sec x= 1/cos x=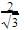
Cosec x + sec x=2+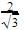
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
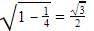
Sec x= 1/cos x=
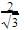
Cosec x + sec x=2+
A tower stands vertically on the ground. From a point C on the ground, which is 20 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45 degrees. The height of the tower is
- a)15 m
- b)8 m
- c)20 m
- d)10 m
Correct answer is option 'C'. Can you explain this answer?
A tower stands vertically on the ground. From a point C on the ground, which is 20 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45
degrees
. The height of the tower isa)
15 m
b)
8 m
c)
20 m
d)
10 m
|
|
Rohan Kapoor answered |
Angle of elevation =45 degrees
Base=20 m
Height of the tower=perpendicular
We have tan 45=P/B
1=P/20
P=20 m
Hence the height of the tower is 20 metres.
Base=20 m
Height of the tower=perpendicular
We have tan 45=P/B
1=P/20
P=20 m
Hence the height of the tower is 20 metres.
The angle of elevation from a point 30 feet from the base of a pole, of height h, as level ground to the top of the pole is 45o. Which equation can be used to find the height of the pole.- a)cos 45° = h/30
- b)tan 45° = 30/h
- c)tan 45° = h/30
- d)sin 45° = h/30
Correct answer is option 'C'. Can you explain this answer?
The angle of elevation from a point 30 feet from the base of a pole, of height h, as level ground to the top of the pole is 45o. Which equation can be used to find the height of the pole.
a)
cos 45° = h/30
b)
tan 45° = 30/h
c)
tan 45° = h/30
d)
sin 45° = h/30
|
|
Prabhat jha answered |
= h/30
b)sin 45 = h/30
c)tan 45 = h/30
d)sec 45 = h/30
Answer: b) sin 45 = h/30
Explanation:
The angle of elevation is the angle between the horizontal ground and the line of sight to the top of the pole. In this case, the angle of elevation is 45 degrees.
We can use the trigonometric ratio of sine to find the height of the pole. The sine of an angle is the ratio of the opposite side to the hypotenuse in a right triangle.
In this case, the opposite side is the height of the pole (h) and the hypotenuse is the distance from the point to the base of the pole (30 feet). Therefore, we have:
sin 45 = h/30
Solving for h, we get:
h = 30 sin 45
Using a calculator, we find that sin 45 is approximately 0.707. Therefore,
h = 30 x 0.707 = 21.21 feet
So the height of the pole is approximately 21.21 feet.
b)sin 45 = h/30
c)tan 45 = h/30
d)sec 45 = h/30
Answer: b) sin 45 = h/30
Explanation:
The angle of elevation is the angle between the horizontal ground and the line of sight to the top of the pole. In this case, the angle of elevation is 45 degrees.
We can use the trigonometric ratio of sine to find the height of the pole. The sine of an angle is the ratio of the opposite side to the hypotenuse in a right triangle.
In this case, the opposite side is the height of the pole (h) and the hypotenuse is the distance from the point to the base of the pole (30 feet). Therefore, we have:
sin 45 = h/30
Solving for h, we get:
h = 30 sin 45
Using a calculator, we find that sin 45 is approximately 0.707. Therefore,
h = 30 x 0.707 = 21.21 feet
So the height of the pole is approximately 21.21 feet.
Find AB in the given figure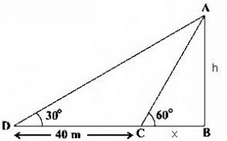
- a)√3
- b)30√3
- c)20√3
- d)10√3
Correct answer is option 'C'. Can you explain this answer?
Find AB in the given figure
a)
√3
b)
30√3
c)
20√3
d)
10√3

|
Kamna Science Academy answered |
Use tanθ formula in both the triangles ABC and ABD.
tan 60 =h/x
tan 30 =h/60+x
tan 60 =h/x
tan 30 =h/60+x
चित्तियों वाले केलों की क्या विशेषता होती हैं?- a)वे सुपाच्य होते हैं
- b)वे सस्ते होते हैं
- c)वे अधिक दिन तक नहीं रह सकते
- d)वे गर्मियों में ही मिलते हैं
Correct answer is option 'A'. Can you explain this answer?
चित्तियों वाले केलों की क्या विशेषता होती हैं?
a)
वे सुपाच्य होते हैं
b)
वे सस्ते होते हैं
c)
वे अधिक दिन तक नहीं रह सकते
d)
वे गर्मियों में ही मिलते हैं
|
|
Nilanjan Unni answered |
This question is incomplete as it does not provide any context or information to make a proper answer choice. Without any additional information, it is not possible to determine the correct answer for this question.
It is important to provide sufficient details or a complete question in order to accurately answer it. Please provide more information or context so that I can assist you better.
It is important to provide sufficient details or a complete question in order to accurately answer it. Please provide more information or context so that I can assist you better.
If cos X = a/b, then sin X is equal to:(- a)(b2-a2)/b
- b)(b-a)/b
- c)√(b2-a2)/b
- d)√(b-a)/b
Correct answer is option 'C'. Can you explain this answer?
If cos X = a/b, then sin X is equal to:(
a)
(b2-a2)/b
b)
(b-a)/b
c)
√(b2-a2)/b
d)
√(b-a)/b

|
Kds Coaching answered |
Answer: (c) √(b2-a2)/b
Explanation: cos X = a/b
By trigonometry identities, we know that:
sin2X + cos2X = 1
sin2X = 1 – cos2X = 1-(a/b)2
sin X = √(b2-a2)/b
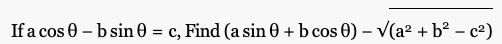
- a)0
- b)-ab
- c)c
- d)-c2
Correct answer is option 'A'. Can you explain this answer?
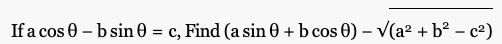
a)
0
b)
-ab
c)
c
d)
-c2

|
Kds Coaching answered |
We have,
a cos θ – b sin θ = c
a cos θ – b sin θ = c
Squaring both sides
⇒ a²cos²θ + b²sin²θ – 2ab sin θ cos θ = c²
⇒ a² (1 – sin²θ) + b² (1 – cos²θ) – 2ab sin θ cos θ = c²
⇒ a² – a²sin²θ + b² – b²cos²θ – 2ab sin θ cos θ = c²
⇒ a² + b² – c² = a²sin²θ + b²cos²θ + 2ab cos θ sin θ
⇒ a² + b² – c² = (a sin θ + b cos θ)²
⇒ (a sin θ + b cos θ) = ±√(a² + b² – c²) → (1)
⇒ a²cos²θ + b²sin²θ – 2ab sin θ cos θ = c²
⇒ a² (1 – sin²θ) + b² (1 – cos²θ) – 2ab sin θ cos θ = c²
⇒ a² – a²sin²θ + b² – b²cos²θ – 2ab sin θ cos θ = c²
⇒ a² + b² – c² = a²sin²θ + b²cos²θ + 2ab cos θ sin θ
⇒ a² + b² – c² = (a sin θ + b cos θ)²
⇒ (a sin θ + b cos θ) = ±√(a² + b² – c²) → (1)
So
(a sin θ + b cos θ) – √(a² + b² – c²) = 0
(a sin θ + b cos θ) – √(a² + b² – c²) = 0
Chapter doubts & questions for Trigonometry - Mathematics for BMAT (Section 2) 2025 is part of BMAT exam preparation. The chapters have been prepared according to the BMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for BMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Trigonometry - Mathematics for BMAT (Section 2) in English & Hindi are available as part of BMAT exam.
Download more important topics, notes, lectures and mock test series for BMAT Exam by signing up for free.
Mathematics for BMAT (Section 2)
52 videos|41 docs|34 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup