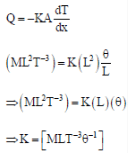All Exams >
Mechanical Engineering >
GATE Mechanical (ME) Mock Test Series 2026 >
All Questions
All questions of Heat Transfer for Mechanical Engineering Exam
Can you explain the answer of this question below:For a given heat flow and for the same thickness, the temperature drop across the material will be maximum for - A:Copper
- B:Steel
- C:Glass-wool
- D:Refractory brick
The answer is c.
For a given heat flow and for the same thickness, the temperature drop across the material will be maximum for
A:
Copper
B:
Steel
C:
Glass-wool
D:
Refractory brick

|
Swara Dasgupta answered |
Q = -kA (dT/dx)
Qdx/A = -kdT
therefore, kdT = constant or dT ∞ 1/k
The one which has minimum thermal conductivity, will give maximum temperature drop. So, Glass-wool will have maximum temperature drop.
A thermocouple in a thermo-well measures the temperature of hot gas flowing through the pipe. For the most accurate measurement of temperature, the thermo-well should be made of: - a)Steel
- b)Brass
- c)Copper
- d)Aluminium
Correct answer is option 'A'. Can you explain this answer?
A thermocouple in a thermo-well measures the temperature of hot gas flowing through the pipe. For the most accurate measurement of temperature, the thermo-well should be made of:
a)
Steel
b)
Brass
c)
Copper
d)
Aluminium

|
Bijoy Kapoor answered |
(tl - ta)/(t0-ta) = (1/coshmL)
Therefor Error = tl-ta = ((t0-ta)/cosh(mL))
Where m = √(hp/KAc)
t0 = temperature of pipe wall
ta = temperature of gas or air flowing through pipe
tl = temperature recorded by the thermometer at the bottom of the wall so to have better thermo well K should be minimum
Material - K(W/m2-K)
Steel - 16-20
Brass - 100
Copper - 380
Aluminimum - 225
So steel will be the better material for thermo well
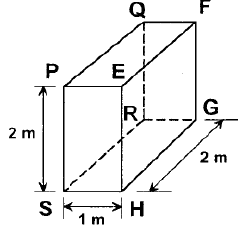
For the three-dimensional object shown in thefigure below, five faces are insulated. Thesixth face (PQRS), which is not insulated,interacts thermally with the ambient, with aconvective heat transfer coefficient of 10 W/m2.K. The ambient temperature is 30°C. Heatis uniformly generated inside the object at therate of 100 W/m3. Assuming the face PQRS tobe at uniform temperature, its steady statetemperature is:
- a)10°C
- b)20°C
- c)30°C
- d)40°C
Correct answer is option 'D'. Can you explain this answer?
For the three-dimensional object shown in thefigure below, five faces are insulated. Thesixth face (PQRS), which is not insulated,interacts thermally with the ambient, with aconvective heat transfer coefficient of 10 W/m2.K. The ambient temperature is 30°C. Heatis uniformly generated inside the object at therate of 100 W/m3. Assuming the face PQRS tobe at uniform temperature, its steady statetemperature is:
a)
10°C
b)
20°C
c)
30°C
d)
40°C

|
Bijoy Kapoor answered |

It is proposed to coat a 1 mm diameter wire with enamel paint (k = 0.1W/mK) to increase heat transfer with air. If the air side heat transfer coefficient is 100 W/m2K, then optimum thickness of enamel paint should be: - a)0.25 mm
- b)0.5 mm
- c)1 mm
- d)2 mm
Correct answer is option 'B'. Can you explain this answer?
It is proposed to coat a 1 mm diameter wire with enamel paint (k = 0.1W/mK) to increase heat transfer with air. If the air side heat transfer coefficient is 100 W/m2K, then optimum thickness of enamel paint should be:
a)
0.25 mm
b)
0.5 mm
c)
1 mm
d)
2 mm
|
|
Avik Yadav answered |
Ans. (b) Critical radius of insulation (rc) =
∴ Critical thickness of enamel point = 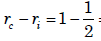 = 0.5 mm
= 0.5 mm
It is desired to increase the heat dissipation rate over the surface of anelectronic device of spherical shape of 5 mm radius exposed toconvection with h = 10 W/m2K by encasing it in a spherical sheath ofconductivity 0.04 W/mK, For maximum heat flow, the diameter of thesheath should be: - a)18 mm
- b)16 mm
- c)12 mm
- d)8 mm
Correct answer is option 'B'. Can you explain this answer?
It is desired to increase the heat dissipation rate over the surface of anelectronic device of spherical shape of 5 mm radius exposed toconvection with h = 10 W/m2K by encasing it in a spherical sheath ofconductivity 0.04 W/mK, For maximum heat flow, the diameter of thesheath should be:
a)
18 mm
b)
16 mm
c)
12 mm
d)
8 mm
|
|
Mainak Unni answered |
Ans. (b) The critical radius of insulation for ensuring maximum heat transfer by
conduction (r) =
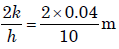 = 8mm.
= 8mm.
conduction (r) =
Therefore diameter should be 16 mm.
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe? - a)10 cm
- b)15 cm
- c)19.5 cm
- d)20 cm
Correct answer is option 'C'. Can you explain this answer?
A hollow pipe of 1 cm outer diameter is to be insulated by thick cylindrical insulation having thermal conductivity 1 W/mK. The surfaceheat transfer coefficient on the insulation surface is 5 W/m2K. What isthe minimum effective thickness of insulation for causing the reduction in heat leakage from the insulated pipe?
a)
10 cm
b)
15 cm
c)
19.5 cm
d)
20 cm
|
|
Avantika Chauhan answered |
Ans. (c) Critical radius of insulation 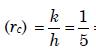 = 0.2m = 20cm
= 0.2m = 20cm
∴ Critical thickness of insulation ( Δr)C = rc − r1 = 20 - 0.5 = 19.5cm
∴ Critical thickness of insulation ( Δr)C = rc − r1 = 20 - 0.5 = 19.5cm
In descending order of magnitude, the thermal conductivity of
a. Pure iron,
b. Liquid water,
c. Saturated water vapour, and
d. Pure aluminium can be arranged as- a)a b c d
- b)b c a d
- c)d a b c
- d)d c b a
Correct answer is option 'C'. Can you explain this answer?
In descending order of magnitude, the thermal conductivity of
a. Pure iron,
b. Liquid water,
c. Saturated water vapour, and
d. Pure aluminium can be arranged as
a. Pure iron,
b. Liquid water,
c. Saturated water vapour, and
d. Pure aluminium can be arranged as
a)
a b c d
b)
b c a d
c)
d a b c
d)
d c b a
|
|
Siddharth Menon answered |
Thermal Conductivity of Different Substances
Thermal conductivity is the property of a material that determines how quickly it can transfer heat through it. It is usually measured in watts per meter per kelvin (W/m.K). In this question, we are given four substances, and we need to arrange them in descending order of thermal conductivity.
a. Pure Iron
Pure iron is a good conductor of heat, and its thermal conductivity is around 80 W/m.K. This means that it can transfer heat quite quickly through it.
b. Liquid Water
Liquid water has a thermal conductivity of around 0.6 W/m.K. This is much lower than that of pure iron, which means that water is not a good conductor of heat.
c. Saturated Water Vapour
Saturated water vapor has a thermal conductivity of around 0.03 W/m.K. This is much lower than that of liquid water, which means that water vapor is an even worse conductor of heat.
d. Pure Aluminium
Pure aluminium is an excellent conductor of heat, and its thermal conductivity is around 237 W/m.K. This is much higher than that of pure iron, which means that aluminium can transfer heat even more quickly than iron.
Arrangement of Thermal Conductivity in Descending Order
Based on the above information, we can arrange the substances in descending order of thermal conductivity as follows:
1. Pure Aluminium - 237 W/m.K
2. Pure Iron - 80 W/m.K
3. Liquid Water - 0.6 W/m.K
4. Saturated Water Vapour - 0.03 W/m.K
Therefore, option C, i.e., a-b-c-d, is the correct answer.
Thermal conductivity is the property of a material that determines how quickly it can transfer heat through it. It is usually measured in watts per meter per kelvin (W/m.K). In this question, we are given four substances, and we need to arrange them in descending order of thermal conductivity.
a. Pure Iron
Pure iron is a good conductor of heat, and its thermal conductivity is around 80 W/m.K. This means that it can transfer heat quite quickly through it.
b. Liquid Water
Liquid water has a thermal conductivity of around 0.6 W/m.K. This is much lower than that of pure iron, which means that water is not a good conductor of heat.
c. Saturated Water Vapour
Saturated water vapor has a thermal conductivity of around 0.03 W/m.K. This is much lower than that of liquid water, which means that water vapor is an even worse conductor of heat.
d. Pure Aluminium
Pure aluminium is an excellent conductor of heat, and its thermal conductivity is around 237 W/m.K. This is much higher than that of pure iron, which means that aluminium can transfer heat even more quickly than iron.
Arrangement of Thermal Conductivity in Descending Order
Based on the above information, we can arrange the substances in descending order of thermal conductivity as follows:
1. Pure Aluminium - 237 W/m.K
2. Pure Iron - 80 W/m.K
3. Liquid Water - 0.6 W/m.K
4. Saturated Water Vapour - 0.03 W/m.K
Therefore, option C, i.e., a-b-c-d, is the correct answer.
Assertion (A): Thermal diffusivity is a dimension less quantity.Reason (R): In M-L-T-Q system the dimensions of thermal diffusivityare [L2T-1] - a)Both A and R are individually true and R is the correct explanation of A
- b)Both A and R are individually true but R is not the correct explanation of A
- c)A is true but R is false
- d)A is false but R is true
Correct answer is option 'D'. Can you explain this answer?
Assertion (A): Thermal diffusivity is a dimension less quantity.
Reason (R): In M-L-T-Q system the dimensions of thermal diffusivityare [L2T-1]
a)
Both A and R are individually true and R is the correct explanation of A
b)
Both A and R are individually true but R is not the correct explanation of A
c)
A is true but R is false
d)
A is false but R is true
|
|
Kabir Verma answered |
Ans. (d)
subjected to symmetrical heat transfer from one face of each block. The other face of the block will be reaching to the same temperature at arate: - a)Faster in air block
- b)Faster in copper block
- c)Equal in air as well as copper block
- d)Cannot be predicted with the given information
Correct answer is option 'B'. Can you explain this answer?
subjected to symmetrical heat transfer from one face of each block. The other face of the block will be reaching to the same temperature at arate:
a)
Faster in air block
b)
Faster in copper block
c)
Equal in air as well as copper block
d)
Cannot be predicted with the given information

|
Kaavya Sengupta answered |
Copper has higher value of k than air and hence heat flow faster in copper.
A steel ball of mass 1kg and specific heat 0.4 kJ/kg is at a temperature of 60°C. It is dropped into 1kg water at 20°C. The final steady state temperature of water is: - a)23.5°C
- b)300°C
- c)35°C
- d)40°C
Correct answer is option 'A'. Can you explain this answer?
A steel ball of mass 1kg and specific heat 0.4 kJ/kg is at a temperature of 60°C. It is dropped into 1kg water at 20°C. The final steady state temperature of water is:
a)
23.5°C
b)
300°C
c)
35°C
d)
40°C
|
|
Sinjini Bose answered |
Given:
Mass of steel ball, m = 1 kg
Specific heat of steel, C_s = 0.4 kJ/kg
Initial temperature of steel ball, T_s1 = 60°C
Mass of water, M_w = 1 kg
Initial temperature of water, T_w1 = 20°C
Final steady state temperature of water, T_w2 = ?
To find:
Final steady state temperature of water
Solution:
1. Heat lost by steel ball = Heat gained by water
i.e., m × C_s × (T_s1 - T_w2) = M_w × C_w × (T_w2 - T_w1)
where, C_w is the specific heat of water (taken as 4.18 kJ/kg°C)
2. On solving the above equation, we get:
T_w2 = (m × C_s × T_s1 + M_w × C_w × T_w1) / (m × C_s + M_w × C_w)
Substituting the given values, we get:
T_w2 = (1 × 0.4 × 60 + 1 × 4.18 × 20) / (1 × 0.4 + 1 × 4.18)
T_w2 = 23.5°C
Therefore, the final steady state temperature of water is 23.5°C.
Mass of steel ball, m = 1 kg
Specific heat of steel, C_s = 0.4 kJ/kg
Initial temperature of steel ball, T_s1 = 60°C
Mass of water, M_w = 1 kg
Initial temperature of water, T_w1 = 20°C
Final steady state temperature of water, T_w2 = ?
To find:
Final steady state temperature of water
Solution:
1. Heat lost by steel ball = Heat gained by water
i.e., m × C_s × (T_s1 - T_w2) = M_w × C_w × (T_w2 - T_w1)
where, C_w is the specific heat of water (taken as 4.18 kJ/kg°C)
2. On solving the above equation, we get:
T_w2 = (m × C_s × T_s1 + M_w × C_w × T_w1) / (m × C_s + M_w × C_w)
Substituting the given values, we get:
T_w2 = (1 × 0.4 × 60 + 1 × 4.18 × 20) / (1 × 0.4 + 1 × 4.18)
T_w2 = 23.5°C
Therefore, the final steady state temperature of water is 23.5°C.
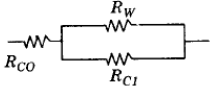
Solar energy is absorbed by the wall of a building as shown in the above figure. Assuming that the ambient temperature inside and outside are equal and considering steady-state, the equivalent circuit will be as shown in (Symbols: Rco = Rconvection,outside RCI = Rconvection,inside
and Rw = RWall)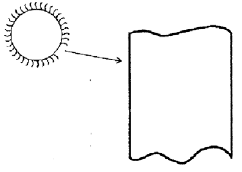
- a)
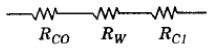
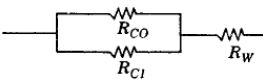
- b)
- c)
- d)

Correct answer is option 'A'. Can you explain this answer?
Solar energy is absorbed by the wall of a building as shown in the above figure. Assuming that the ambient temperature inside and outside are equal and considering steady-state, the equivalent circuit will be as shown in (Symbols: Rco = Rconvection,outside RCI = Rconvection,inside
and Rw = RWall)
and Rw = RWall)
a)
b)
c)
d)
|
|
Akshay Joshi answered |
Ans. (a) All resistances are in series.
Assertion (A): Hydrogen cooling is used for high capacity electrical generators.
Reason (R): Hydrogen is light and has high thermal conductivity ascompared to air - a)Both A and R are individually true and R is the correct explanation of A
- b)Both A and R are individually true but R is not the correct explanation of A
- c)A is true but R is false
- d)A is false but R is true
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): Hydrogen cooling is used for high capacity electrical generators.
Reason (R): Hydrogen is light and has high thermal conductivity ascompared to air
Reason (R): Hydrogen is light and has high thermal conductivity ascompared to air
a)
Both A and R are individually true and R is the correct explanation of A
b)
Both A and R are individually true but R is not the correct explanation of A
c)
A is true but R is false
d)
A is false but R is true

|
Dineshkumar M answered |
A
A furnace is made of a red brick wall of thickness 0.5 m and conductivity 0.7 W/mK. For the same heat loss and temperature drop,this can be replaced by a layer of diatomite earth of conductivity 0.14W/mK and thickness - a)0.05 m
- b)0.1 m
- c)0.2 m
- d)0.5 m
Correct answer is option 'B'. Can you explain this answer?
A furnace is made of a red brick wall of thickness 0.5 m and conductivity 0.7 W/mK. For the same heat loss and temperature drop,this can be replaced by a layer of diatomite earth of conductivity 0.14W/mK and thickness
a)
0.05 m
b)
0.1 m
c)
0.2 m
d)
0.5 m

|
Shivam Sharma answered |
k1/x1 = k2/x2,
0.7/0.5 = 0.14/x2,
= 0.07/0.7 = 0.1.
A copper wire of radius 0.5 mm is insulated with a sheathing ofthickness 1 mm having a thermal conductivity of 0.5 W/m – K. Theoutside surface convective heat transfer coefficient is 10 W/m2 – K. Ifthe thickness of insulation sheathing is raised by 10 mm, then theelectrical current-carrying capacity of the wire will: - a)Increase
- b)Decrease
- c)Remain the same
- d)Vary depending upon theelectrical conductivity of the wire
Correct answer is option 'A'. Can you explain this answer?
A copper wire of radius 0.5 mm is insulated with a sheathing ofthickness 1 mm having a thermal conductivity of 0.5 W/m – K. Theoutside surface convective heat transfer coefficient is 10 W/m2 – K. Ifthe thickness of insulation sheathing is raised by 10 mm, then theelectrical current-carrying capacity of the wire will:
a)
Increase
b)
Decrease
c)
Remain the same
d)
Vary depending upon theelectrical conductivity of the wire

|
Swara Dasgupta answered |
Given that:
ri = 0.5 mm
ro = 0.5 + 1 + 10
= 11.5 mm
κ = 0.5 W/mK
h = 10 W/m2K
Critical radius of insulation for wire is
rc = κ/ho = 0.5/10
= 0.05 m
= 5 mm
Since rc < ro, there will be decrease in rate of heat
transfer.
An oil cooler in a high performance engine has an outside surface area 0.12 m2 and a surface temperature of 65 degree Celsius. At any intermediate time air moves over the surface of the cooler at a temperature of 30 degree Celsius and gives rise to a surface coefficient equal to 45.4 W/ m 2 K. Find out the heat transfer rate?
- a)238.43 W
- b)190.68 W
- c)543.67 W
- d)675.98 W
Correct answer is option 'B'. Can you explain this answer?
An oil cooler in a high performance engine has an outside surface area 0.12 m2 and a surface temperature of 65 degree Celsius. At any intermediate time air moves over the surface of the cooler at a temperature of 30 degree Celsius and gives rise to a surface coefficient equal to 45.4 W/ m 2 K. Find out the heat transfer rate?
a)
238.43 W
b)
190.68 W
c)
543.67 W
d)
675.98 W
|
|
Asha Basu answered |
To find the heat transfer rate in the oil cooler, we can use the formula:
Q = h * A * ΔT
Where:
Q = Heat transfer rate (in watts)
h = Surface coefficient (in W/m2K)
A = Surface area (in m2)
ΔT = Temperature difference between the surface and the air (in K)
Given:
Surface area (A) = 0.12 m2
Surface temperature (T1) = 65 °C = 65 + 273.15 = 338.15 K
Air temperature (T2) = 30 °C = 30 + 273.15 = 303.15 K
Surface coefficient (h) = 45.4 W/m2K
Substituting the given values into the formula, we have:
ΔT = T1 - T2 = 338.15 K - 303.15 K = 35 K
Q = 45.4 W/m2K * 0.12 m2 * 35 K
Q = 190.68 W
Therefore, the heat transfer rate in the oil cooler is 190.68 W.
Hence, option B (190.68 W) is the correct answer.
Q = h * A * ΔT
Where:
Q = Heat transfer rate (in watts)
h = Surface coefficient (in W/m2K)
A = Surface area (in m2)
ΔT = Temperature difference between the surface and the air (in K)
Given:
Surface area (A) = 0.12 m2
Surface temperature (T1) = 65 °C = 65 + 273.15 = 338.15 K
Air temperature (T2) = 30 °C = 30 + 273.15 = 303.15 K
Surface coefficient (h) = 45.4 W/m2K
Substituting the given values into the formula, we have:
ΔT = T1 - T2 = 338.15 K - 303.15 K = 35 K
Q = 45.4 W/m2K * 0.12 m2 * 35 K
Q = 190.68 W
Therefore, the heat transfer rate in the oil cooler is 190.68 W.
Hence, option B (190.68 W) is the correct answer.
For an opaque plane surface the irradiation, radiosity and emissive power are respectively 20, 12 and 10 W/m2.What is the emissivity of the surface? - a)0.2
- b)0.4
- c)0.8
- d)1.0
Correct answer is option 'C'. Can you explain this answer?
For an opaque plane surface the irradiation, radiosity and emissive power are respectively 20, 12 and 10 W/m2.What is the emissivity of the surface?
a)
0.2
b)
0.4
c)
0.8
d)
1.0
|
|
Dishani Desai answered |
Given:
Irradiation = 20 W/m²
Radiosity = 12 W/m²
Emissive Power = 10 W/m²
To find: Emissivity of the surface
Formula used:
Emissivity (ε) = Emissive power (P) / Irradiation (I)
Calculation:
Substituting the given values in the formula,
ε = 10 / 20
ε = 0.5
Therefore, the emissivity of the surface is 0.5 or 50%.
Answer: Option (c) 0.8
Irradiation = 20 W/m²
Radiosity = 12 W/m²
Emissive Power = 10 W/m²
To find: Emissivity of the surface
Formula used:
Emissivity (ε) = Emissive power (P) / Irradiation (I)
Calculation:
Substituting the given values in the formula,
ε = 10 / 20
ε = 0.5
Therefore, the emissivity of the surface is 0.5 or 50%.
Answer: Option (c) 0.8
An electric cable of aluminium conductor (k = 240 W/mK) is to be insulated with rubber (k = 0.15 W/mK). The cable is to be located in air (h = 6 W/m2). The critical thickness of insulation will be
- a)25mm
- b)40 mm
- c)160 mm
- d)800 mm
Correct answer is option 'A'. Can you explain this answer?
An electric cable of aluminium conductor (k = 240 W/mK) is to be insulated with rubber (k = 0.15 W/mK). The cable is to be located in air (h = 6 W/m2). The critical thickness of insulation will be
a)
25mm
b)
40 mm
c)
160 mm
d)
800 mm

|
Gate Funda answered |

A plane wall is 25 cm thick with an area of 1 m2, and has a thermal conductivity of 0.5 W/mK. If a temperature difference of 60°C is imposed across it, what is the heat flow? - a)120W
- b)140W
- c)160W
- d)180W
Correct answer is 'A'. Can you explain this answer?
A plane wall is 25 cm thick with an area of 1 m2, and has a thermal conductivity of 0.5 W/mK. If a temperature difference of 60°C is imposed across it, what is the heat flow?
a)
120W
b)
140W
c)
160W
d)
180W
|
|
Aditya Deshmukh answered |
We know, Q = kA(dT/dx)
Where, k = thermal conductivity = 0.5,
A = area = 1 m^2,
dT = temperature difference = 60 deg C,
dx = thickness = 25 cm = 0.25 m
So, Q = 0.5 x 1 x (60/0.25) = 120 W
Hence Option (A) is correct
For Notes on Modes Of Heat Transfer click on the link given below:
A steam pipe is to be lined with two layers of insulating materials of different thermal conductivities. For minimum heat transfer- a)The better insulation must be put inside
- b)The better insulation must be put outside
- c)One could place either insulation on either side
- d)One should take into account the steam temperature before deciding as towhich insulation is put where.
Correct answer is option 'A'. Can you explain this answer?
A steam pipe is to be lined with two layers of insulating materials of different thermal conductivities. For minimum heat transfer
a)
The better insulation must be put inside
b)
The better insulation must be put outside
c)
One could place either insulation on either side
d)
One should take into account the steam temperature before deciding as towhich insulation is put where.
|
|
Arka Patel answered |
Ans. (a) For minimum heat transfer, the better insulation must be put inside.
Upto the critical radius of insulation: - a)Added insulation increases heat loss
- b)Added insulation decreases heat loss
- c)Convection heat loss is less than conduction heat loss
- d)Heat flux decreases
Correct answer is option 'A'. Can you explain this answer?
Upto the critical radius of insulation:
a)
Added insulation increases heat loss
b)
Added insulation decreases heat loss
c)
Convection heat loss is less than conduction heat loss
d)
Heat flux decreases
|
|
Rajeev Menon answered |
Up to the critical radius the heat transfer is increased and at the critical radius heat transfer is max. Beyond critical radius heat transfer decreases.
The earth receives at its surface radiation from the sun at the rate of 1400 W/m2. The distance of centre of sun from the surface of earth is1.5 × 108 m and the radius of sun is 7.0 × 108 m. What is approximately the surface temperature of the sun treating the sun as a black body? - a)3650 K
- b)4500 K
- c)5800 K
- d)6150 K
Correct answer is option 'C'. Can you explain this answer?
The earth receives at its surface radiation from the sun at the rate of 1400 W/m2. The distance of centre of sun from the surface of earth is1.5 × 108 m and the radius of sun is 7.0 × 108 m. What is approximately the surface temperature of the sun treating the sun as a black body?
a)
3650 K
b)
4500 K
c)
5800 K
d)
6150 K
|
|
Sravya Bajaj answered |
Ans. (c)
Can you explain the answer of this question below:Consider the following statements:
The Fourier heat conduction equation Q = 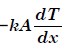 presumes
presumes
1. Steady-state conditions
2. Constant value of thermal conductivity.
3. Uniform temperatures at the wall surfaces
4. One-dimensional heat flow. Of these statements:
- A:
1, 2 and 3 are correct
- B:
1, 2 and 4 are correct
- C:
2, 3 and 4 are correct
- D:
1, 3 and 4 are correct
The answer is d.
Consider the following statements:
The Fourier heat conduction equation Q = presumes
1. Steady-state conditions
2. Constant value of thermal conductivity.
3. Uniform temperatures at the wall surfaces
4. One-dimensional heat flow. Of these statements:
1, 2 and 3 are correct
1, 2 and 4 are correct
2, 3 and 4 are correct
1, 3 and 4 are correct
|
|
Rajeev Sharma answered |
Assumptions of Fourier equation:1. Steady state heat conduction.2. One directional heat flow.3. Bounding surfaces are isothermal in character that is constant and uniform temperatures are maintained at the two faces.4. Isotropic and homogeneous material and thermal conductivity ‘k’ is constant.5. Constant temperature gradient and linear temperature profile.6. No internal heat generation.
Two rods, one of length L and the other of length 2L are made of thesame material and have the same diameter. The two ends of the longerrod are maintained at 100°C. One end of the shorter rod Is maintainedat 100°C while the other end is insulated. Both the rods are exposed tothe same environment at 40°C. The temperature at the insulated end ofthe shorter rod is measured to be 55°C. The temperature at the midpointof the longer rod would be: - a)40°C
- b)50°C
- c)55°C
- d)100°C
Correct answer is option 'C'. Can you explain this answer?
Two rods, one of length L and the other of length 2L are made of thesame material and have the same diameter. The two ends of the longerrod are maintained at 100°C. One end of the shorter rod Is maintainedat 100°C while the other end is insulated. Both the rods are exposed tothe same environment at 40°C. The temperature at the insulated end ofthe shorter rod is measured to be 55°C. The temperature at the midpointof the longer rod would be:
a)
40°C
b)
50°C
c)
55°C
d)
100°C
|
|
Avinash Mehta answered |

6.0 kJ of conduction heat transfer has to take place in 10 minutes from one end to other end of a metallic cylinder of 10 cm2 cross-sectional area, length 1 meter and thermal conductivity as 100 W/mK. What is the temperature difference between the two ends of the cylindrical bar? - a)80°C
- b)100°C
- c)120°C
- d)160°C
Correct answer is option 'B'. Can you explain this answer?
6.0 kJ of conduction heat transfer has to take place in 10 minutes from one end to other end of a metallic cylinder of 10 cm2 cross-sectional area, length 1 meter and thermal conductivity as 100 W/mK. What is the temperature difference between the two ends of the cylindrical bar?
a)
80°C
b)
100°C
c)
120°C
d)
160°C

|
Ananya Sharma answered |
Ans. (b)
or
or dt = 1000C
Assertion (A): The nose of aeroplane is painted black. Reason (R) Black body absorbs maximum heat which is generated byaerodynamic heating when the plane is flying. - a)Both A and R are individually true and R is the correct explanation of A
- b)Both A and R are individually true but R is not the correct explanation of A
- c)A is true but R is false
- d)A is false but R is true
Correct answer is option 'B'. Can you explain this answer?
Assertion (A): The nose of aeroplane is painted black. Reason (R) Black body absorbs maximum heat which is generated byaerodynamic heating when the plane is flying.
a)
Both A and R are individually true and R is the correct explanation of A
b)
Both A and R are individually true but R is not the correct explanation of A
c)
A is true but R is false
d)
A is false but R is true
|
|
Mrinalini Nambiar answered |
Ans. (b)
A composite hollow sphere with steady internal heating is made of 2layers of materials of equal thickness with thermal conductivities inthe ratio of 1 : 2 for inner to outer layers. Ratio of inside to outside diameter is 0.8. What is ratio of temperature drop across the inner andouter layers? - a)0.4
- b)1.6
- c)2 ln (0.8)
- d)2.5
Correct answer is option 'D'. Can you explain this answer?
A composite hollow sphere with steady internal heating is made of 2layers of materials of equal thickness with thermal conductivities inthe ratio of 1 : 2 for inner to outer layers. Ratio of inside to outside diameter is 0.8. What is ratio of temperature drop across the inner andouter layers?
a)
0.4
b)
1.6
c)
2 ln (0.8)
d)
2.5
|
|
Sagnik Desai answered |
Ans. (d)
For the same inlet and outlet temperatures of hot and cold fluids, theLog Mean Temperature Difference (LMTD) is:- a)Greater for parallel flow heat exchanger than for counter flow heatexchanger.
- b)Greater for counter flow heat exchanger than for parallel flow heatexchanger.
- c)Same for both parallel and counter flow heat exchangers.
- d)Dependent on the properties of the fluids.
Correct answer is option 'B'. Can you explain this answer?
For the same inlet and outlet temperatures of hot and cold fluids, theLog Mean Temperature Difference (LMTD) is:
a)
Greater for parallel flow heat exchanger than for counter flow heatexchanger.
b)
Greater for counter flow heat exchanger than for parallel flow heatexchanger.
c)
Same for both parallel and counter flow heat exchangers.
d)
Dependent on the properties of the fluids.
|
|
Mansi Rane answered |
Ans. (b)
The following figure was generated from experimental data relatingspectral black body emissive power to wavelength at threetemperatures T1, T2 and T3 (T1 > T2 > T3). The conclusion is that themeasurements are: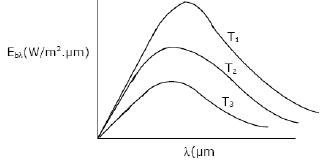
- a)Correct because the maximain Ebλ show the correct trend
- b)Correct because Planck's lawis satisfied
- c)Wrong because the StefanBoltzmann law is not satisfied
- d)Wrong because Wien's displacement law is not satisfied
Correct answer is option 'D'. Can you explain this answer?
The following figure was generated from experimental data relatingspectral black body emissive power to wavelength at threetemperatures T1, T2 and T3 (T1 > T2 > T3). The conclusion is that themeasurements are:
a)
Correct because the maximain Ebλ show the correct trend
b)
Correct because Planck's lawis satisfied
c)
Wrong because the StefanBoltzmann law is not satisfied
d)
Wrong because Wien's displacement law is not satisfied
|
|
Kabir Verma answered |
Ans. (d)
For natural convective flow over a vertical flat plate as shown in the given figure, the governing differential
equation for momentum is: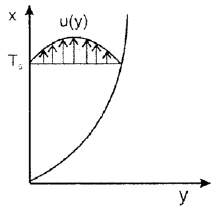
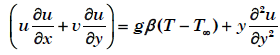 If equation is non-dimensionalized by
If equation is non-dimensionalized by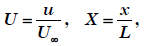
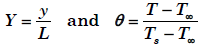 then the term gβ (T - T∞) , is equal to:
then the term gβ (T - T∞) , is equal to:- a)Grashof number
- b)Prandtl number
- c)Rayleigh number
- d)
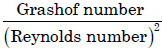
Correct answer is option 'D'. Can you explain this answer?
For natural convective flow over a vertical flat plate as shown in the given figure, the governing differential
equation for momentum is:
equation for momentum is:
If equation is non-dimensionalized by
then the term gβ (T - T∞) , is equal to:
a)
Grashof number
b)
Prandtl number
c)
Rayleigh number
d)
|
|
Ravi Singh answered |
Ans. (d)
gives dimensionless number which signifies whether flow is forced or free connection.
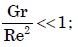 Forced convection
Forced convection
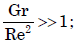 Natural convection
Natural convection
In order to substantially reduce leakage of heat from atmosphere intocold refrigerant flowing in small diameter copper tubes in a refrigerant system, the radial thickness of insulation, cylindrically wrapped around the tubes, must be: - a)Higher than critical radius of insulation
- b)Slightly lower than critical radius of insulation
- c)Equal to the critical radius of insulation
- d)Considerably higher than critical radius of insulation
Correct answer is option 'D'. Can you explain this answer?
In order to substantially reduce leakage of heat from atmosphere intocold refrigerant flowing in small diameter copper tubes in a refrigerant system, the radial thickness of insulation, cylindrically wrapped around the tubes, must be:
a)
Higher than critical radius of insulation
b)
Slightly lower than critical radius of insulation
c)
Equal to the critical radius of insulation
d)
Considerably higher than critical radius of insulation
|
|
Ravi Singh answered |
Ans. (d) At critical radius of insulation heat leakage is maximum if we add more
insulation then heat leakage will reduce.
insulation then heat leakage will reduce.
When α is absorbtivity, ρ is reflectivity and τ is transmisivity, then for diathermanous body, which of the following relation is valid? - a)α = 1, ρ = 0, τ = 0
- b)α = 0, ρ = 1, τ = 0
- c)α = 0, ρ = 0, τ = 1
- d)α + ρ = 1, τ = 0
Correct answer is option 'C'. Can you explain this answer?
When α is absorbtivity, ρ is reflectivity and τ is transmisivity, then for diathermanous body, which of the following relation is valid?
a)
α = 1, ρ = 0, τ = 0
b)
α = 0, ρ = 1, τ = 0
c)
α = 0, ρ = 0, τ = 1
d)
α + ρ = 1, τ = 0
|
|
Avinash Sharma answered |
Ans. (c)
A plane wall of thickness 2L has a uniform volumetric heat source q* (W/m3). It is exposed to local ambient temperature T∞ at both the ends (x = ± L). The surface temperature Ts of the wall under steady-state
condition (where h and k have their usual meanings) is given by: - a)
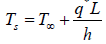
- b)
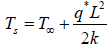
- c)
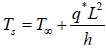
- d)
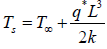
Correct answer is option 'A'. Can you explain this answer?
A plane wall of thickness 2L has a uniform volumetric heat source q* (W/m3). It is exposed to local ambient temperature T∞ at both the ends (x = ± L). The surface temperature Ts of the wall under steady-state
condition (where h and k have their usual meanings) is given by:
condition (where h and k have their usual meanings) is given by:
a)
b)
c)
d)
|
|
Ananya Shah answered |
Ans. (a)
A large concrete slab 1 m thick has one dimensional temperature distribution:
T = 4 – 10x + 20x2 + 10x3
Where T is temperature and x is distance from one face towards other face of wall. If the slab material has thermal diffusivity of 2 × 10-3 m2/hr,what is the rate of change of temperature at the other face of the wall?- a)0.1°C/h
- b)0.2°C/h
- c)0.3°C/h
- d)0.4°C/h
Correct answer is option 'B'. Can you explain this answer?
A large concrete slab 1 m thick has one dimensional temperature distribution:
T = 4 – 10x + 20x2 + 10x3
Where T is temperature and x is distance from one face towards other face of wall. If the slab material has thermal diffusivity of 2 × 10-3 m2/hr,what is the rate of change of temperature at the other face of the wall?
T = 4 – 10x + 20x2 + 10x3
Where T is temperature and x is distance from one face towards other face of wall. If the slab material has thermal diffusivity of 2 × 10-3 m2/hr,what is the rate of change of temperature at the other face of the wall?
a)
0.1°C/h
b)
0.2°C/h
c)
0.3°C/h
d)
0.4°C/h
|
|
Gitanjali Banerjee answered |
Ans. (b)
An electric cable of aluminium conductor (k = 240 W/mK) is to be insulated with rubber (k = 0.15 W/mK). The cable is to be located in air (h = 6W/m2). The critical thickness of insulation will be:- a)25mm
- b)40 mm
- c)160 mm
- d)800 mm
Correct answer is option 'A'. Can you explain this answer?
An electric cable of aluminium conductor (k = 240 W/mK) is to be insulated with rubber (k = 0.15 W/mK). The cable is to be located in air (h = 6W/m2). The critical thickness of insulation will be:
a)
25mm
b)
40 mm
c)
160 mm
d)
800 mm
|
|
Arshiya Dey answered |
Ans. (c)
Which one of the following modes of heat transfer would take placepredominantly, from boiler furnace to water wall? - a)Convection
- b)Conduction
- c)Radiation
- d)Conduction and convection
Correct answer is option 'C'. Can you explain this answer?
Which one of the following modes of heat transfer would take placepredominantly, from boiler furnace to water wall?
a)
Convection
b)
Conduction
c)
Radiation
d)
Conduction and convection
|
|
Yash Patel answered |
Ans. (c) In boiler, the energy from flame is transmitted mainly by radiation to water wall and radiant super heater.
Two large parallel grey plates with a small gap, exchange radiation atthe rate of 1000 W/m2 when their emissivities are 0.5 each. By coatingone plate, its emissivity is reduced to 0.25. Temperature remains unchanged. The new rate of heat exchange shall become: - a)500 W/m2
- b)600 W/m2
- c)700 W/m2
- d)800 W/m2
Correct answer is option 'B'. Can you explain this answer?
Two large parallel grey plates with a small gap, exchange radiation atthe rate of 1000 W/m2 when their emissivities are 0.5 each. By coatingone plate, its emissivity is reduced to 0.25. Temperature remains unchanged. The new rate of heat exchange shall become:
a)
500 W/m2
b)
600 W/m2
c)
700 W/m2
d)
800 W/m2
|
|
Atharva Majumdar answered |
Ans. (b)
Assertion (A): Cork is a good insulator.Reason (R): Good insulators are highly porous. - a)Both A and R are individually true and R is the correct explanation of A
- b)Both A and R individually true but R in not the correct explanation of A
- c)A is true but R is false
- d)A is false but R is true
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): Cork is a good insulator.
Reason (R): Good insulators are highly porous.
a)
Both A and R are individually true and R is the correct explanation of A
b)
Both A and R individually true but R in not the correct explanation of A
c)
A is true but R is false
d)
A is false but R is true

|
Rahul Chatterjee answered |
It is the air which fills the cells in the cork that makes it an excellent thermal insulator. The same protective principle can also be found in other natural products, such as wool and feathers, and in industry, such as double glazed windows, for example. However, none of these materials have such a high level of insulation as cork.
Temperature profiles for four cases are shown in the following figures and are labelled A, B, C and D.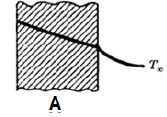
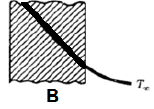
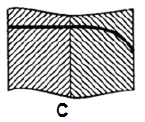
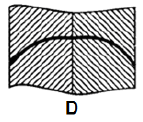 Match the above figures with
Match the above figures with
1. High conductivity fluid
2. Low conductivity fluid
3. Insulating body
4. Guard heaterSelect the correct answer using the codes given below:
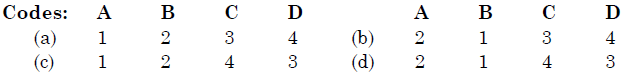
- a)(a)
- b)(b)
- c)(c)
- d)(d)
Correct answer is option 'A'. Can you explain this answer?
Temperature profiles for four cases are shown in the following figures and are labelled A, B, C and D.
Match the above figures with
1. High conductivity fluid
2. Low conductivity fluid
3. Insulating body
4. Guard heater
1. High conductivity fluid
2. Low conductivity fluid
3. Insulating body
4. Guard heater
Select the correct answer using the codes given below:
a)
(a)
b)
(b)
c)
(c)
d)
(d)

|
Pie Academy answered |
Ans. (a) Temperature slope is higher for low conducting and lower for high
conducting fluid. Thus A is for 1, B for 2. Temperature profile in C is for insulator. Temperature rise is possible only for heater and as such D is for guard heater.
conducting fluid. Thus A is for 1, B for 2. Temperature profile in C is for insulator. Temperature rise is possible only for heater and as such D is for guard heater.
A wall of thickness 0.6 m has width has a normal area 1.5 m2 and is made up of material of thermal conductivity 0.4 W/mK. The temperatures on the two sides are 800°C. What is the thermal resistance of the wall? - a)1 W/K
- b)1.8 W/K
- c)1 K/W
- d)1.8 K/W
Correct answer is option 'C'. Can you explain this answer?
A wall of thickness 0.6 m has width has a normal area 1.5 m2 and is made up of material of thermal conductivity 0.4 W/mK. The temperatures on the two sides are 800°C. What is the thermal resistance of the wall?
a)
1 W/K
b)
1.8 W/K
c)
1 K/W
d)
1.8 K/W

|
Anmol Nair answered |
Ans. (c)
Two spheres A and B of same material have radii 1 m and 4 m and temperature 4000 K and 2000 K respectively. Which one of the following statements is correct? The energy radiated by sphere A is: - a)Greater than that of sphere B
- b)Less than that of sphere B
- c)Equal to that of sphere B
- d)Equal to double that of sphere B
Correct answer is option 'C'. Can you explain this answer?
Two spheres A and B of same material have radii 1 m and 4 m and temperature 4000 K and 2000 K respectively. Which one of the following statements is correct? The energy radiated by sphere A is:
a)
Greater than that of sphere B
b)
Less than that of sphere B
c)
Equal to that of sphere B
d)
Equal to double that of sphere B
|
|
Ashutosh Sharma answered |
Understanding Blackbody Radiation
The energy radiated by a blackbody is described by the Stefan-Boltzmann Law, which states that the total energy radiated per unit surface area is proportional to the fourth power of its absolute temperature.
Stefan-Boltzmann Law
- The formula is given by:
E = σT^4
where E is the energy radiated per unit area, σ is the Stefan-Boltzmann constant, and T is the absolute temperature in Kelvin.
Calculating Energy for Sphere A and B
- Sphere A:
- Radius = 1 m
- Temperature = 4000 K
- Surface Area = 4π(1^2) = 4π m²
- Energy radiated (EA) = σ(4000^4) * 4π
- Sphere B:
- Radius = 4 m
- Temperature = 2000 K
- Surface Area = 4π(4^2) = 64π m²
- Energy radiated (EB) = σ(2000^4) * 64π
Comparing Energy Radiated
- Calculating EA and EB:
- EA = σ * 4π * (4000^4)
- EB = σ * 64π * (2000^4)
- Simplifying the comparison:
- 4000^4 = 256 * 1000^4
- 2000^4 = 16 * 1000^4
- Thus, EB becomes 64π * (16 * 1000^4) = 1024π * σ
- Final Comparison:
- EA = 1024π * σ
- EB = 1024π * σ
Conclusion
Both spheres radiate equal energy despite their different sizes and temperatures, hence the correct answer is option C: Equal to that of sphere B.
The energy radiated by a blackbody is described by the Stefan-Boltzmann Law, which states that the total energy radiated per unit surface area is proportional to the fourth power of its absolute temperature.
Stefan-Boltzmann Law
- The formula is given by:
E = σT^4
where E is the energy radiated per unit area, σ is the Stefan-Boltzmann constant, and T is the absolute temperature in Kelvin.
Calculating Energy for Sphere A and B
- Sphere A:
- Radius = 1 m
- Temperature = 4000 K
- Surface Area = 4π(1^2) = 4π m²
- Energy radiated (EA) = σ(4000^4) * 4π
- Sphere B:
- Radius = 4 m
- Temperature = 2000 K
- Surface Area = 4π(4^2) = 64π m²
- Energy radiated (EB) = σ(2000^4) * 64π
Comparing Energy Radiated
- Calculating EA and EB:
- EA = σ * 4π * (4000^4)
- EB = σ * 64π * (2000^4)
- Simplifying the comparison:
- 4000^4 = 256 * 1000^4
- 2000^4 = 16 * 1000^4
- Thus, EB becomes 64π * (16 * 1000^4) = 1024π * σ
- Final Comparison:
- EA = 1024π * σ
- EB = 1024π * σ
Conclusion
Both spheres radiate equal energy despite their different sizes and temperatures, hence the correct answer is option C: Equal to that of sphere B.
Assertion (A): Heat transfer at high temperature is dominated byradiation rather than convection.Reason (R): Radiation depends on fourth power of temperature while convection depends on unit power relationship. - a)Both A and R are individually true and R is the correct explanation of A
- b)Both A and R are individually true but R is not the of A
- c)A is true but R is false
- d)A is false but R is true
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): Heat transfer at high temperature is dominated byradiation rather than convection.
Reason (R): Radiation depends on fourth power of temperature while convection depends on unit power relationship.
a)
Both A and R are individually true and R is the correct explanation of A
b)
Both A and R are individually true but R is not the of A
c)
A is true but R is false
d)
A is false but R is true
|
|
Gaurav Kapoor answered |
Ans. (a)
When all the conditions are identical, in the case of flow through pipeswith heat transfer, the velocity profiles will be identical for: - a)Liquid heating and liquid cooling
- b)Gas heating and gas cooling
- c)Liquid heating and gas cooling
- d)Heating and cooling of any fluid
Correct answer is option 'A'. Can you explain this answer?
When all the conditions are identical, in the case of flow through pipeswith heat transfer, the velocity profiles will be identical for:
a)
Liquid heating and liquid cooling
b)
Gas heating and gas cooling
c)
Liquid heating and gas cooling
d)
Heating and cooling of any fluid
|
|
Sparsh Chakraborty answered |
Velocity Profiles in Flow Through Pipes with Heat Transfer
Introduction:
In the case of flow through pipes with heat transfer, the velocity profiles can vary depending on the conditions. However, when all the conditions are identical, the velocity profiles will be identical for liquid heating and liquid cooling.
Explanation:
1. Flow Through Pipes:
In flow through pipes, the velocity of the fluid can vary across the cross-section of the pipe. This variation is known as the velocity profile. The velocity profile is influenced by various factors such as fluid properties, pipe geometry, and boundary conditions.
2. Heat Transfer:
Heat transfer occurs when there is a temperature difference between the fluid and the pipe wall. This temperature difference can result in either heating or cooling of the fluid as it flows through the pipe.
3. Identical Conditions:
When all the conditions are identical, it means that the fluid properties, pipe geometry, and boundary conditions are the same for both heating and cooling scenarios. This includes factors such as pipe diameter, fluid viscosity, fluid density, and flow rate.
4. Velocity Profile:
The velocity profile in a pipe is governed by the Navier-Stokes equation, which describes the conservation of momentum. When all the conditions are identical, the velocity profile remains the same for both heating and cooling scenarios.
5. Liquid Heating and Liquid Cooling:
For liquid heating and liquid cooling, the fluid properties remain constant. The viscosity and density of the liquid do not change significantly with temperature. Therefore, the velocity profile will be the same for both heating and cooling of the liquid.
6. Gas Heating and Gas Cooling:
For gas heating and gas cooling, the fluid properties can vary significantly with temperature. The viscosity and density of the gas change with temperature, which can affect the velocity profile. Therefore, the velocity profiles will not be identical for gas heating and gas cooling.
Conclusion:
When all the conditions are identical, the velocity profiles will be identical for liquid heating and liquid cooling. This is because the fluid properties, pipe geometry, and boundary conditions remain constant for both heating and cooling scenarios. However, the velocity profiles will not be identical for gas heating and gas cooling due to the significant changes in fluid properties with temperature.
Introduction:
In the case of flow through pipes with heat transfer, the velocity profiles can vary depending on the conditions. However, when all the conditions are identical, the velocity profiles will be identical for liquid heating and liquid cooling.
Explanation:
1. Flow Through Pipes:
In flow through pipes, the velocity of the fluid can vary across the cross-section of the pipe. This variation is known as the velocity profile. The velocity profile is influenced by various factors such as fluid properties, pipe geometry, and boundary conditions.
2. Heat Transfer:
Heat transfer occurs when there is a temperature difference between the fluid and the pipe wall. This temperature difference can result in either heating or cooling of the fluid as it flows through the pipe.
3. Identical Conditions:
When all the conditions are identical, it means that the fluid properties, pipe geometry, and boundary conditions are the same for both heating and cooling scenarios. This includes factors such as pipe diameter, fluid viscosity, fluid density, and flow rate.
4. Velocity Profile:
The velocity profile in a pipe is governed by the Navier-Stokes equation, which describes the conservation of momentum. When all the conditions are identical, the velocity profile remains the same for both heating and cooling scenarios.
5. Liquid Heating and Liquid Cooling:
For liquid heating and liquid cooling, the fluid properties remain constant. The viscosity and density of the liquid do not change significantly with temperature. Therefore, the velocity profile will be the same for both heating and cooling of the liquid.
6. Gas Heating and Gas Cooling:
For gas heating and gas cooling, the fluid properties can vary significantly with temperature. The viscosity and density of the gas change with temperature, which can affect the velocity profile. Therefore, the velocity profiles will not be identical for gas heating and gas cooling.
Conclusion:
When all the conditions are identical, the velocity profiles will be identical for liquid heating and liquid cooling. This is because the fluid properties, pipe geometry, and boundary conditions remain constant for both heating and cooling scenarios. However, the velocity profiles will not be identical for gas heating and gas cooling due to the significant changes in fluid properties with temperature.
A spherical aluminium shell of inside diameter 2 m is evacuated andused as a radiation test chamber. If the inner surface is coated with carbon black and maintained at 600 K, the irradiation on a small test surface placed inside the chamber is:
(Stefan-Boltzmann constant σ = 5.67 × 10-8 W/m2K4)- a)1000 W/m2
- b)3400 W/m2
- c)5680 W/m2
- d)7348 W/m2
Correct answer is option 'D'. Can you explain this answer?
A spherical aluminium shell of inside diameter 2 m is evacuated andused as a radiation test chamber. If the inner surface is coated with carbon black and maintained at 600 K, the irradiation on a small test surface placed inside the chamber is:
(Stefan-Boltzmann constant σ = 5.67 × 10-8 W/m2K4)
(Stefan-Boltzmann constant σ = 5.67 × 10-8 W/m2K4)
a)
1000 W/m2
b)
3400 W/m2
c)
5680 W/m2
d)
7348 W/m2
|
|
Avik Ghosh answered |
Ans. (d) Irradiation on a small test surface placed inside a hollow black spherical chamber = σT4 = 5.67 × 10-8 × 6004 = 7348 W/m2
Which of the following would lead to a reduction in thermal resistance?
1. In conduction; reduction in the thickness of the material and an increase in the thermal conductivity.
2. In convection, stirring of the fluid and cleaning the heating surface.
3. In radiation, increasing the temperature and reducing theemissivity.
Codes:- a)1, 2 and 3
- b)1 and 2
- c)1 and 3
- d)2 and 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following would lead to a reduction in thermal resistance?
1. In conduction; reduction in the thickness of the material and an increase in the thermal conductivity.
2. In convection, stirring of the fluid and cleaning the heating surface.
3. In radiation, increasing the temperature and reducing theemissivity.
Codes:
1. In conduction; reduction in the thickness of the material and an increase in the thermal conductivity.
2. In convection, stirring of the fluid and cleaning the heating surface.
3. In radiation, increasing the temperature and reducing theemissivity.
Codes:
a)
1, 2 and 3
b)
1 and 2
c)
1 and 3
d)
2 and 3
|
|
Arshiya Dey answered |
Ans. (b) 1. In conduction, heat resistance = Δ x/kA
Thus reduction in thickness and increase in area result in reduction of thermal resistance.
2. Stirring of fluid and cleaning the heating surface increases value of h, and thus reduces thermal resistance.
3. In radiation, heat flow increases with increase in temperature and reduces with reduction in emissivity. Thus thermal resistance does not decrease.
Thus 1 and 2 are correct.
Thus reduction in thickness and increase in area result in reduction of thermal resistance.
2. Stirring of fluid and cleaning the heating surface increases value of h, and thus reduces thermal resistance.
3. In radiation, heat flow increases with increase in temperature and reduces with reduction in emissivity. Thus thermal resistance does not decrease.
Thus 1 and 2 are correct.
Chapter doubts & questions for Heat Transfer - GATE Mechanical (ME) Mock Test Series 2026 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Heat Transfer - GATE Mechanical (ME) Mock Test Series 2026 in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
GATE Mechanical (ME) Mock Test Series 2026
30 docs|220 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup