All questions of Practice Test: Full Length for Electronics and Communication Engineering (ECE) Exam
In the question given below, the sentence has a part printed in bold. That part may contain a grammatical error. Replace that part with four choices given below:The famous playwright has been in the sick bed from the last one week.- a)For the past
- b)For past
- c)Since past
- d)For last
Correct answer is option 'A'. Can you explain this answer?
In the question given below, the sentence has a part printed in bold. That part may contain a grammatical error. Replace that part with four choices given below:
The famous playwright has been in the sick bed from the last one week.
a)
For the past
b)
For past
c)
Since past
d)
For last
|
|
Yash Patel answered |
We use the present perfect continuous tense to talk about an action that started in the past and is continuing now. This is often used with 'for' (showing period of time) or since (showing point of time).
As the given sentence is one, the prepositional phrase 'from the last' must be replaced with 'for the past' to make it a grammatically correct sentence.
As the given sentence is one, the prepositional phrase 'from the last' must be replaced with 'for the past' to make it a grammatically correct sentence.
If  = log(a + b), then
= log(a + b), then - a)a + b = 1
- b)a – b = 1
- c)a = b
- d)

Correct answer is option 'A'. Can you explain this answer?
a)
a + b = 1
b)
a – b = 1
c)
a = b
d)
|
|
Yash Patel answered |
log a/b + logb/a = log ( a + b)
log ( a/b * b/a ) = log ( a + b )
log 1 = log ( a + b)
So, a + b = 1 .
a = 1 - b
b = 1 - a.
Therefore, If log a/b + log b/a = log (a + b), then a+ b = 1
log ( a/b * b/a ) = log ( a + b )
log 1 = log ( a + b)
So, a + b = 1 .
a = 1 - b
b = 1 - a.
Therefore, If log a/b + log b/a = log (a + b), then a+ b = 1
The solution of differential equation dy = (1-y) dx is- a)y = e-x c
- b)y = ex c
- c)y = 1 ce-x
- d)y = 1 cex
Correct answer is option 'C'. Can you explain this answer?
The solution of differential equation dy = (1-y) dx is
a)
y = e-x c
b)
y = ex c
c)
y = 1 ce-x
d)
y = 1 cex

|
Sanchita Pillai answered |
Understanding the Differential Equation
The given differential equation is:
dy = (1 - y) dx
This means we can rearrange it to find the relationship between y and x.
Rearranging the Equation
We can rewrite the equation as:
dy / (1 - y) = dx
This format allows us to separate variables, making it easier to integrate both sides.
Integrating Both Sides
Now, integrate both sides:
∫ dy / (1 - y) = ∫ dx
The left side integrates to -ln|1 - y|, and the right side integrates to x + C, where C is the integration constant. Thus, we have:
-ln|1 - y| = x + C
Solving for y
To solve for y, we exponentiate both sides:
|1 - y| = e^(-x - C)
This simplifies to:
1 - y = ±e^(-x - C)
Now isolate y:
y = 1 - ±e^(-x - C)
By setting a new constant K = ±e^(-C), we can express y as:
y = 1 - Ke^(-x)
Analyzing the Solutions
The form y = 1 - Ke^(-x) indicates that as x approaches infinity, y approaches 1 (the horizontal asymptote). Therefore, the solution of this differential equation approaches the line y = 1.
Conclusion
Thus, the correct answer is indeed option 'C', which indicates that the solution converges to the constant value:
y = 1.
The given differential equation is:
dy = (1 - y) dx
This means we can rearrange it to find the relationship between y and x.
Rearranging the Equation
We can rewrite the equation as:
dy / (1 - y) = dx
This format allows us to separate variables, making it easier to integrate both sides.
Integrating Both Sides
Now, integrate both sides:
∫ dy / (1 - y) = ∫ dx
The left side integrates to -ln|1 - y|, and the right side integrates to x + C, where C is the integration constant. Thus, we have:
-ln|1 - y| = x + C
Solving for y
To solve for y, we exponentiate both sides:
|1 - y| = e^(-x - C)
This simplifies to:
1 - y = ±e^(-x - C)
Now isolate y:
y = 1 - ±e^(-x - C)
By setting a new constant K = ±e^(-C), we can express y as:
y = 1 - Ke^(-x)
Analyzing the Solutions
The form y = 1 - Ke^(-x) indicates that as x approaches infinity, y approaches 1 (the horizontal asymptote). Therefore, the solution of this differential equation approaches the line y = 1.
Conclusion
Thus, the correct answer is indeed option 'C', which indicates that the solution converges to the constant value:
y = 1.
A signal is given by, γ(t) = s(t) n(t) where s(t) = 20 Cos2π4000t 40 Cos2π2000t and the noise n(t) is white with power spectral density η0 = 1 W/Hz. The total received signal is put through a band pass filter with pass band between 100 to 110 Hz. The value of SNR at the output of filter is- a)40 dB
- b)20 dB
- c)10 dB
- d)15 dB
Correct answer is option 'B'. Can you explain this answer?
A signal is given by,
γ(t) = s(t) n(t)
where s(t) = 20 Cos2π4000t 40 Cos2π2000t and the noise n(t) is white with power spectral density η0 = 1 W/Hz. The total received signal is put through a band pass filter with pass band between 100 to 110 Hz. The value of SNR at the output of filter is
a)
40 dB
b)
20 dB
c)
10 dB
d)
15 dB
|
|
Ravi Singh answered |
Signal power
= 200 800
= 1000
and noise power, Pn = n0 × (BW)
= 1 × 10
= 10W
So, SNR = 1000/10 = 100
In dB = 10log100 = 20dB
The digital circuit shown in the figure works as a 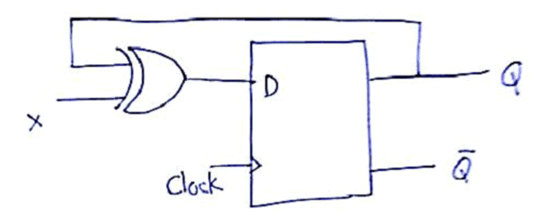
- a)JK flip-flop
- b)Clocked RS flip-flop
- c)Ring Counter
- d)T flip-flop
Correct answer is option 'D'. Can you explain this answer?
The digital circuit shown in the figure works as a
a)
JK flip-flop
b)
Clocked RS flip-flop
c)
Ring Counter
d)
T flip-flop

|
Telecom Tuners answered |
For D flip-flop
Qn 1 = D
Here, D = X  Qn
Qn
So Qn 1 = X  Qn
Qn
So it becomes T flip-flop
Statement: All bags are cakes. All lamps are cakes.
Conclusions:
I. Some lamps are bags.
II. No lamp is bag.
Deduce which of the above conclusion logically follows statements:- a)Only conclusion I follows
- b)Only conclusion II follows
- c)Either I or II follows
- d)Neither I or II follows
Correct answer is option 'C'. Can you explain this answer?
Conclusions:
I. Some lamps are bags.
II. No lamp is bag.
Deduce which of the above conclusion logically follows statements:
a)
Only conclusion I follows
b)
Only conclusion II follows
c)
Either I or II follows
d)
Neither I or II follows
|
|
Aditya Deshmukh answered |
Since the middle term 'cakes' is not distributed even once in the premises, no definite conclusion follows. However, I and II involve only the extreme terms and form a complementary pair. So, either I or II follows.
Can you explain the answer of this question below:Man does not live by __________ alone.- A:Food
- B: Bread
- C:Meals
- D:Diet
The answer is B.
|
|
Sanvi Kapoor answered |
Man does not live by bread alone.
Determine the z-parameter for the network shown below.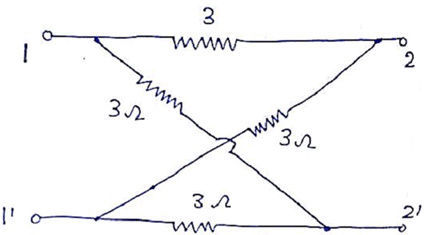
- a)
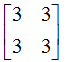
- b)
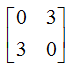
- c)
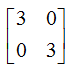
- d)
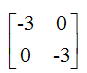
Correct answer is option 'C'. Can you explain this answer?
Determine the z-parameter for the network shown below.
a)
b)
c)
d)
|
|
Yash Patel answered |
Since it is symmetrical ladder network
A rectangular waveguide, in dominant TE mode, has dimensions 10 cm x 15 cm. The cut off frequency is- a)10 GHz
- b)15 GHz
- c)25 GHz
- d)1 GHz
Correct answer is option 'D'. Can you explain this answer?
A rectangular waveguide, in dominant TE mode, has dimensions 10 cm x 15 cm. The cut off frequency is
a)
10 GHz
b)
15 GHz
c)
25 GHz
d)
1 GHz
|
|
Harsh Joshi answered |
Rectangular Waveguide Dimensions
- Given dimensions of the rectangular waveguide: 10 cm x 15 cm
Dominant TE Mode
- The dominant TE mode is the lowest order mode that can propagate in a waveguide.
- In this mode, the electric field is purely transverse to the direction of propagation.
Cut-off Frequency
- The cut-off frequency is the frequency below which a particular mode cannot propagate in the waveguide.
- It depends on the dimensions of the waveguide.
Calculation
- The cut-off frequency for the dominant TE mode in a rectangular waveguide can be calculated using the formula:
fc = (c / 2) * sqrt((m / a)^2 + (n / b)^2)
where fc is the cut-off frequency, c is the speed of light in vacuum (3 x 10^8 m/s), m and n are the mode numbers, and a and b are the dimensions of the waveguide.
- In this case, the dimensions of the waveguide are given as 10 cm x 15 cm.
- Converting the dimensions to meters, we have a = 0.1 m and b = 0.15 m.
- For the dominant TE mode (m = 1, n = 0), substituting the values into the formula:
fc = (3 x 10^8 / 2) * sqrt((1 / 0.1)^2 + (0 / 0.15)^2)
= (1.5 x 10^8) * sqrt(100 + 0)
= 1.5 x 10^8 Hz
= 150 MHz
Correct Option
- Comparing the calculated value with the options given, we find that none of the options match the calculated value.
- However, the closest option is 1 GHz, which is equivalent to 1000 MHz.
- It is possible that the options provided in the question are incorrectly labeled.
- Therefore, the correct answer is option 'D' (1 GHz).
- Given dimensions of the rectangular waveguide: 10 cm x 15 cm
Dominant TE Mode
- The dominant TE mode is the lowest order mode that can propagate in a waveguide.
- In this mode, the electric field is purely transverse to the direction of propagation.
Cut-off Frequency
- The cut-off frequency is the frequency below which a particular mode cannot propagate in the waveguide.
- It depends on the dimensions of the waveguide.
Calculation
- The cut-off frequency for the dominant TE mode in a rectangular waveguide can be calculated using the formula:
fc = (c / 2) * sqrt((m / a)^2 + (n / b)^2)
where fc is the cut-off frequency, c is the speed of light in vacuum (3 x 10^8 m/s), m and n are the mode numbers, and a and b are the dimensions of the waveguide.
- In this case, the dimensions of the waveguide are given as 10 cm x 15 cm.
- Converting the dimensions to meters, we have a = 0.1 m and b = 0.15 m.
- For the dominant TE mode (m = 1, n = 0), substituting the values into the formula:
fc = (3 x 10^8 / 2) * sqrt((1 / 0.1)^2 + (0 / 0.15)^2)
= (1.5 x 10^8) * sqrt(100 + 0)
= 1.5 x 10^8 Hz
= 150 MHz
Correct Option
- Comparing the calculated value with the options given, we find that none of the options match the calculated value.
- However, the closest option is 1 GHz, which is equivalent to 1000 MHz.
- It is possible that the options provided in the question are incorrectly labeled.
- Therefore, the correct answer is option 'D' (1 GHz).
If x = ya , y = zb and z = xc then abc = ?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
If x = ya , y = zb and z = xc then abc = ?
a)
1
b)
2
c)
3
d)
4
|
|
Rajat Kapoor answered |
Explanation:
Given:
x = ya
y = zb
z = xc
We need to find the value of abc.
Step 1: Substitute the value of y from the second equation into the first equation:
x = (zb)a
Step 2: Substitute the value of z from the third equation into the equation obtained in Step 1:
x = (xc)(b)a
Step 3: Simplify the equation:
x = x(a)(b)(c)
Step 4: Divide both sides of the equation by x:
1 = (a)(b)(c)
Step 5: Rearrange the equation to find the value of abc:
abc = 1
Therefore, the value of abc is 1.
Final Answer: Option 'A' (1)
Given:
x = ya
y = zb
z = xc
We need to find the value of abc.
Step 1: Substitute the value of y from the second equation into the first equation:
x = (zb)a
Step 2: Substitute the value of z from the third equation into the equation obtained in Step 1:
x = (xc)(b)a
Step 3: Simplify the equation:
x = x(a)(b)(c)
Step 4: Divide both sides of the equation by x:
1 = (a)(b)(c)
Step 5: Rearrange the equation to find the value of abc:
abc = 1
Therefore, the value of abc is 1.
Final Answer: Option 'A' (1)
Fill in the blanks in the given sentence so as to make it logically and grammatically correct. Select the correct words from the answer choices and mark its number as your answer.Q.Owls can detect and ______________ prey in total darknesswith the help of sound.- a)follow
- b)kill
- c)catch
- d)hound
Correct answer is option 'C'. Can you explain this answer?
Fill in the blanks in the given sentence so as to make it logically and grammatically correct. Select the correct words from the answer choices and mark its number as your answer.
Q.
Owls can detect and ______________ prey in total darknesswith the help of sound.
a)
follow
b)
kill
c)
catch
d)
hound
|
|
Sarita Yadav answered |
Catch can fallow detection.
Calculate the hysteresis width (in Volts) for an inverting Schmitt trigger with feedback fraction 0.5. Assume the supply voltage to be 1Correct answer is '10'. Can you explain this answer?
Calculate the hysteresis width (in Volts) for an inverting Schmitt trigger with feedback fraction 0.5. Assume the supply voltage to be 1
|
|
Yash Patel answered |
For a inverting Schmitt trigger.
Given: β = 0.5, Vcc = 10V
Hysteresis Voltage VH = VUT - VLT
VUT = +β x Vcc
VLT = -β x Vcc
VH = 2 x β x Vcc
VH = 2 x 0.5 x 10
VH = 10V
Heat sinks are used in power amplifier circuits- a)to increase the out put power.
- b)to reduce the heat losses in the transistor.
- c)to increase the voltage gain of the power amplifier.
- d)to increase the collector dissipation rating of the transistor.
Correct answer is option 'D'. Can you explain this answer?
Heat sinks are used in power amplifier circuits
a)
to increase the out put power.
b)
to reduce the heat losses in the transistor.
c)
to increase the voltage gain of the power amplifier.
d)
to increase the collector dissipation rating of the transistor.

|
Arshiya Dasgupta answered |
A study of people who reduced the calories they consumed has found the strongest evidence yet that such restrictions slow down metabolism, raising hopes that a low calories lifestyle or treatments stimulating biological effects of restricted eating, could prolong health in old age. The report provides the most robust evidence to date that everything we have learnt in other animals can be applied to humans.Which of the following argument will prove that the above conclusion is flawed?- a)In a long-term study led by researchers at the University of Wisconsin, calorie restriction seemed to extend the lives of human-like rhesus monkeys.
- b)Your body needs a certain amount of calories to carry out vital functions and if it does not get those calories from the diet, it can start to break down its own tissues for energy.
- c)By putting people on a carefully reduced diet for two years, investigators hope to learn the biological mechanism that connects eating less to living longer.
- d)Like calorie restriction, intermittent fasting may slow down the aging process by reducing free radicals in the cells.
Correct answer is option 'B'. Can you explain this answer?
A study of people who reduced the calories they consumed has found the strongest evidence yet that such restrictions slow down metabolism, raising hopes that a low calories lifestyle or treatments stimulating biological effects of restricted eating, could prolong health in old age. The report provides the most robust evidence to date that everything we have learnt in other animals can be applied to humans.
Which of the following argument will prove that the above conclusion is flawed?
a)
In a long-term study led by researchers at the University of Wisconsin, calorie restriction seemed to extend the lives of human-like rhesus monkeys.
b)
Your body needs a certain amount of calories to carry out vital functions and if it does not get those calories from the diet, it can start to break down its own tissues for energy.
c)
By putting people on a carefully reduced diet for two years, investigators hope to learn the biological mechanism that connects eating less to living longer.
d)
Like calorie restriction, intermittent fasting may slow down the aging process by reducing free radicals in the cells.
|
|
Rhea Reddy answered |
The given passage gives the benefits of reducing calories to attain a healthier lifestyle and out of the given options, option B seems to give a contradictory fact stating that the lack of required calories may cause problems to the body. Hence, option B is correct.
Determine the region of operation of BJT in the given circuit.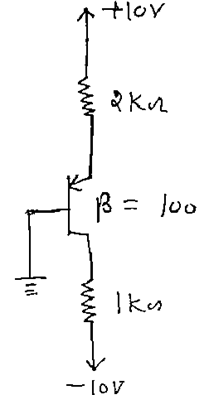
- a)Active region
- b)Saturation region
- c)Cut-off region
- d)Reverse active region
Correct answer is option 'A'. Can you explain this answer?
Determine the region of operation of BJT in the given circuit.
a)
Active region
b)
Saturation region
c)
Cut-off region
d)
Reverse active region

|
Gate Gurus answered |
Since, VEB = 0.7
Here VB = 0, So, VE = 0.7 V
So, VC = -10 4.6 × 1
= - 5.4 V
Since, VEC = 0.7 5.4 = 6.1V
That is greater than 0.2V So BJT is in active region.
The system of linear equations
3x + 4y = 6
2x + 3y = 5
has- a)A unique solution
- b)No solution
- c)Infinite solutions
- d)Exactly two distinct solution
Correct answer is option 'A'. Can you explain this answer?
3x + 4y = 6
2x + 3y = 5
has
a)
A unique solution
b)
No solution
c)
Infinite solutions
d)
Exactly two distinct solution
|
|
Sanya Agarwal answered |
Auguemented matrix,
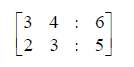
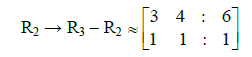
Since rank of matrix A as well as auguemented matrix is 2, therefore it has unique solution.
Since rank of matrix A as well as auguemented matrix is 2, therefore it has unique solution.
Which of the following is most similar in meaning to the given word
DIRE- a)Pessimistic
- b)Alarming
- c)Futile
- d)Fraudulent
Correct answer is option 'B'. Can you explain this answer?
DIRE
a)
Pessimistic
b)
Alarming
c)
Futile
d)
Fraudulent
|
|
Yash Patel answered |
DIRE means very serious
Alarming means something very serious.
So the correct answer is ALARMING
In the following figure, the J and K inputs of all the four Flip-Flops are made high. The frequency of the signal at output Y is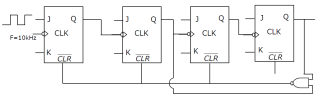
- a)0.833 KHz
- b)1.0 KHz
- c)0.91 KHz
- d)0.77 KHz
Correct answer is option 'B'. Can you explain this answer?
In the following figure, the J and K inputs of all the four Flip-Flops are made high. The frequency of the signal at output Y is

a)
0.833 KHz
b)
1.0 KHz
c)
0.91 KHz
d)
0.77 KHz

|
Telecom Tuners answered |
Output of NAND is zero when Q3Q2Q1Q0 have state 1010=(10), Dec. Therefore, the given figure represents mod- 10 up counter. And, frequency of the signal will be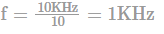
A class B push pull power amplifier is supplied with Vcc = 50V. The signal swings the collector voltage down to Vmin = 5V. The total dissipation in both transistors is 40W. Find conversion efficiency.- a)73.03%
- b)87.21%
- c)60.29%
- d)40.87%
Correct answer is option 'A'. Can you explain this answer?
A class B push pull power amplifier is supplied with Vcc = 50V. The signal swings the collector voltage down to Vmin = 5V. The total dissipation in both transistors is 40W. Find conversion efficiency.
a)
73.03%
b)
87.21%
c)
60.29%
d)
40.87%
|
|
Sarita Yadav answered |
The initial of MOD-16 down counter is 0110. After 37 clock pulses, the state of the counter will be:- a)0001
- b) 0010
- c)0000
- d) 0011
Correct answer is option 'A'. Can you explain this answer?
a)
0001
b)
0010
c)
0000
d)
0011

|
Ankit Mukherjee answered |
After 37 clock pulses, the state of MOD-16 DOWN counter will be five states below the present state.
The value of d/dt x(t) at t = 1.5 for x(t) = u(t) + r(t) - 2r(t - 1) + r(t - 2) - u(t - 2) isCorrect answer is '-1'. Can you explain this answer?
The value of d/dt x(t) at t = 1.5 for x(t) = u(t) + r(t) - 2r(t - 1) + r(t - 2) - u(t - 2) is
|
|
Sharmila Dasgupta answered |
Understanding x(t)
To evaluate d/dt x(t) at t = 1.5 for the given function, we first need to analyze the components of x(t):
- u(t): Unit step function, which is 0 for t < 0="" and="" 1="" for="" t="" />= 0.
- r(t): Ramp function, which is 0 for t < 0="" and="" increases="" linearly="" as="" t="" for="" t="" />= 0.
- r(t - 1) and r(t - 2): Ramp functions shifted to the right.
Expression Breakdown
The function x(t) is given as:
x(t) = u(t) + r(t) - 2r(t - 1) + r(t - 2) - u(t - 2)
Now, substitute the value of t = 1.5 into the expression:
1. u(1.5) = 1 (since 1.5 >= 0)
2. r(1.5) = 1.5 (since 1.5 >= 0)
3. r(1.5 - 1) = r(0.5) = 0.5
4. r(1.5 - 2) = r(-0.5) = 0 (since t < />
5. u(1.5 - 2) = 0 (since 1.5 < />
Calculating x(1.5)
Now, substituting these values into x(t):
x(1.5) = 1 + 1.5 - 2(0.5) + 0 - 0
x(1.5) = 1 + 1.5 - 1 = 1.5
Finding d/dt x(t)
To find d/dt x(t), we differentiate the components:
- u(t) contributes 0 for t > 0.
- r(t) contributes 1.
- -2r(t - 1) contributes -2 for t > 1.
- r(t - 2) contributes 0 for t < />
- -u(t - 2) contributes 0 for t < />
Thus, for t = 1.5:
- The only active components are r(t) and -2r(t - 1).
Therefore, d/dt x(t) = 1 - 2 = -1 at t = 1.5, confirming the given answer.
To evaluate d/dt x(t) at t = 1.5 for the given function, we first need to analyze the components of x(t):
- u(t): Unit step function, which is 0 for t < 0="" and="" 1="" for="" t="" />= 0.
- r(t): Ramp function, which is 0 for t < 0="" and="" increases="" linearly="" as="" t="" for="" t="" />= 0.
- r(t - 1) and r(t - 2): Ramp functions shifted to the right.
Expression Breakdown
The function x(t) is given as:
x(t) = u(t) + r(t) - 2r(t - 1) + r(t - 2) - u(t - 2)
Now, substitute the value of t = 1.5 into the expression:
1. u(1.5) = 1 (since 1.5 >= 0)
2. r(1.5) = 1.5 (since 1.5 >= 0)
3. r(1.5 - 1) = r(0.5) = 0.5
4. r(1.5 - 2) = r(-0.5) = 0 (since t < />
5. u(1.5 - 2) = 0 (since 1.5 < />
Calculating x(1.5)
Now, substituting these values into x(t):
x(1.5) = 1 + 1.5 - 2(0.5) + 0 - 0
x(1.5) = 1 + 1.5 - 1 = 1.5
Finding d/dt x(t)
To find d/dt x(t), we differentiate the components:
- u(t) contributes 0 for t > 0.
- r(t) contributes 1.
- -2r(t - 1) contributes -2 for t > 1.
- r(t - 2) contributes 0 for t < />
- -u(t - 2) contributes 0 for t < />
Thus, for t = 1.5:
- The only active components are r(t) and -2r(t - 1).
Therefore, d/dt x(t) = 1 - 2 = -1 at t = 1.5, confirming the given answer.
Select the pair that best expresses a relationship similar to that expressed in the pair:
LIGHT : BLIND- a)Speech : Dumb
- b)Language : Deaf
- c)Tongue : Sound
- d)Voice : Vibration
Correct answer is option 'A'. Can you explain this answer?
LIGHT : BLIND
a)
Speech : Dumb
b)
Language : Deaf
c)
Tongue : Sound
d)
Voice : Vibration
|
|
Zoya Sharma answered |
As a blind person cannot see light and a Dumb person cannot speak. So option (a) is the correct answer.
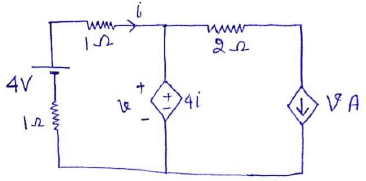
In the given circuit determine the value of current source
- a)2/3 A
- b)4/3 A
- c)8/3 A
- d)0 A
Correct answer is option 'C'. Can you explain this answer?
a)
2/3 A
b)
4/3 A
c)
8/3 A
d)
0 A

|
Akanksha . answered |
1. Apply KVL to 1st loop, 1i+4i+1i=4, 6i=4, i=4/6 2. voltage source=4i =V ( given in loop 1) 3. loop 2, current source= V amp. V=4i= 4*4/6 = 16/6= 8/3.
Gate function is defined as ______________- a)
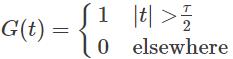 )
) - b)
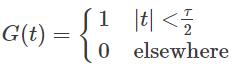
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
Gate function is defined as ______________
a)
b)
c)
d)

|
Gate Funda answered |
A gate function is a rectangular function defined as
Where τ is pulse width.
The value of k such that the system of equationx + ky + z = 0, x + 3y + kz = 0, 2x + y + z = 0 has non-trivial solution.Correct answer is '0.5'. Can you explain this answer?
The value of k such that the system of equation
x + ky + z = 0, x + 3y + kz = 0, 2x + y + z = 0 has non-trivial solution.
|
|
Sanya Agarwal answered |
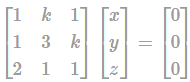
To find the value of K, we have to make rank of matrix less than unknown of the equation.
Apply R2 = R2 - R1
R3 = R3 - 2R1
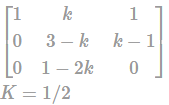
A system with an input x(t), and output y(t) is described by the relation y(t) = tx(t). The system is- a)linear, time invariant and stable
- b)linear, time varying, un stable
- c)non linear, time invariant, stable
- d)non linear, time varying, unstable
Correct answer is option 'B'. Can you explain this answer?
A system with an input x(t), and output y(t) is described by the relation y(t) = tx(t). The system is
a)
linear, time invariant and stable
b)
linear, time varying, un stable
c)
non linear, time invariant, stable
d)
non linear, time varying, unstable

|
Saikat Gupta answered |
If an electrical system is compared to a fluid system, the electrical current corresponds to the:
- a)Pressure
- b)Pump
- c)Water wheel
- d)Water flow
Correct answer is option 'D'. Can you explain this answer?
If an electrical system is compared to a fluid system, the electrical current corresponds to the:
a)
Pressure
b)
Pump
c)
Water wheel
d)
Water flow

|
Pavan Kumar answered |
Electric current is nothing but flow of charge
similarly in fluid system flow water is comparable with electric current
similarly in fluid system flow water is comparable with electric current
A speech signal, band limited to 5 KHz with peak to peak between +10 V to – 10 V and the signal is sampled at Nyquist rate and the bits 0 and 1 are transmitted using bipolar pulses. What is minimum bandwidth for distortion free transmission ….- a)40
- b)50
- c)60
- d)55
Correct answer is option 'A'. Can you explain this answer?
A speech signal, band limited to 5 KHz with peak to peak between +10 V to – 10 V and the signal is sampled at Nyquist rate and the bits 0 and 1 are transmitted using bipolar pulses. What is minimum bandwidth for distortion free transmission ….
a)
40
b)
50
c)
60
d)
55

|
Pioneer Academy answered |
While using polar pulses, the minimum bandwidth required is four times the theoretical bandwidth or nyquist bandwidth.
Required BW = 4 * Nyquist BW
= 4 × 2 fm = 4 × 2 × 5 KHz = 40 KHz
A signal m(t) = 5 cos(2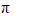 100t) is frequency modulated a carrier. The resulting FM signal is
100t) is frequency modulated a carrier. The resulting FM signal is
The approximate bandwidth of the FM signal would be 
The approximate bandwidth of the FM signal would be
- a)6.4 kHz
- b)1.6 kHz
- c)3.2 kHz
- d)100 kHz
Correct answer is option 'C'. Can you explain this answer?
The approximate bandwidth of the FM signal would be
The approximate bandwidth of the FM signal would be
a)
6.4 kHz
b)
1.6 kHz
c)
3.2 kHz
d)
100 kHz
|
|
Kabir Verma answered |
=
= 3.2 KHz
In the given circuit, the equivalent impedance of the circuit between terminals A-B is- a)(5+j3)Ω
- b)-3jΩ
- c)(5-3j)Ω
- d)5Ω
Correct answer is option 'D'. Can you explain this answer?
In the given circuit, the equivalent impedance of the circuit between terminals A-B is
a)
(5+j3)Ω
b)
-3jΩ
c)
(5-3j)Ω
d)
5Ω

|
Pie Academy answered |
To find out Thevenin’s equivalent, we put a test source between terminals A-B.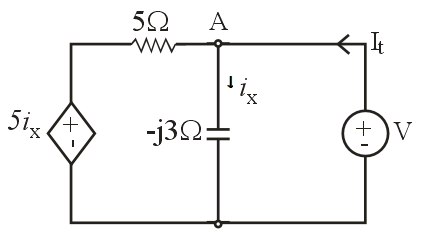
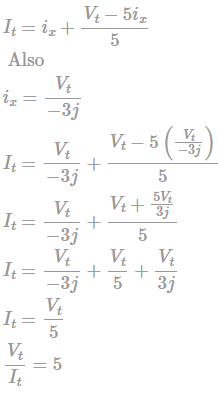

KCL at node A
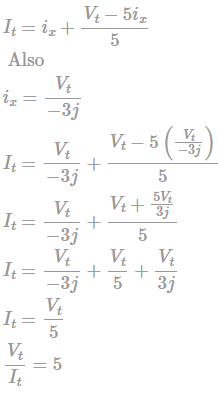
Given that D = z⋅ρ cos2ϕa2c/m2, Calculate the charge density at (1, π/4, 3) and then the total charge enclosed by the cylinder of radius 1m with −2 ≤ z ≤ 2m is?- a)
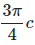
- b)
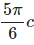
- c)
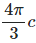
- d)

Correct answer is option 'C'. Can you explain this answer?
Given that D = z⋅ρ cos2ϕa2c/m2, Calculate the charge density at (1, π/4, 3) and then the total charge enclosed by the cylinder of radius 1m with −2 ≤ z ≤ 2m is?
a)
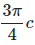
b)
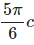
c)
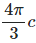
d)


|
Cstoppers Instructors answered |
Charge density ρv = ∇.D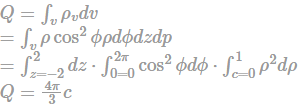
=∂Dz/∂z =ρ⋅cos2ϕ
Now charge enclosed is
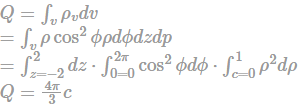
Hence option C is correct.
Which of the following signals is / are periodic?1. S(t) = Cos 2t + Cos 3t + Cos 5t2. S(t) = exp (j8π t)3. S(t) = exp (-7t) Sin 10πt4. S(t) = Cos 2t Cos 4t- a) Only 2 is periodic
- b) (1) and (2) are periodic
- c) (1), (2) and (3) are periodic
- d) (2) and (4) are periodic
Correct answer is option 'B'. Can you explain this answer?
Which of the following signals is / are periodic?
1. S(t) = Cos 2t + Cos 3t + Cos 5t
2. S(t) = exp (j8π t)
3. S(t) = exp (-7t) Sin 10πt
4. S(t) = Cos 2t Cos 4t
a)
Only 2 is periodic
b)
(1) and (2) are periodic
c)
(1), (2) and (3) are periodic
d)
(2) and (4) are periodic

|
Arya Kaur answered |
Only (1) and (2) satisfies S{t) = S(t + T).
Maximum number of Self Dual possible for 4-variable function.Correct answer is '256'. Can you explain this answer?
Maximum number of Self Dual possible for 4-variable function.
|
|
Kabir Verma answered |
For n variable Boolean function maximum number of self-dual possible is 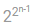
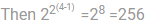
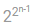
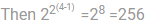
Chapter doubts & questions for Practice Test: Full Length - GATE ECE (Electronics) Mock Test Series 2026 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Practice Test: Full Length - GATE ECE (Electronics) Mock Test Series 2026 in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
GATE ECE (Electronics) Mock Test Series 2026
26 docs|263 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

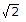 R1
R1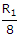


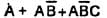 is equal to
is equal to











