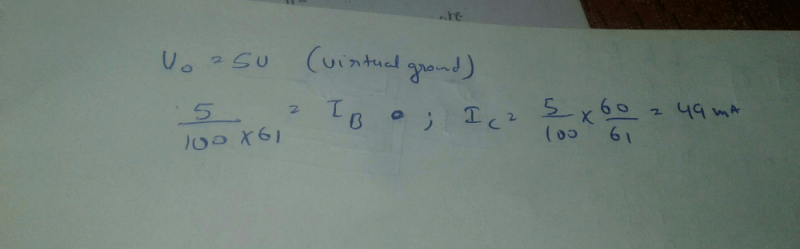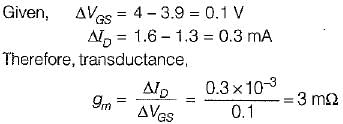All questions of Analog Electronics for Electrical Engineering (EE) Exam
Req = ?
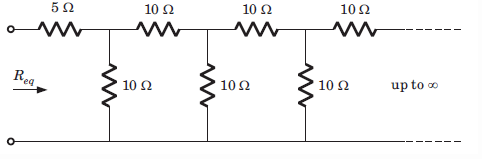
- a)11.86 ohm
- b)10 ohm
- c)25 ohm
- d)11.18 ohm
Correct answer is option 'D'. Can you explain this answer?
Req = ?
a)
11.86 ohm
b)
10 ohm
c)
25 ohm
d)
11.18 ohm
|
Ravi Singh answered |
- Req – 5 = 10(Req + 5)/(10 + 5 +Req).
- Solving for Req we have
Req = 11.18 ohm.
In the question a circuit and a waveform for the input voltage is given. The diode in circuit has cutin voltage Vγ = 0. Choose the option for the waveform of output voltage vo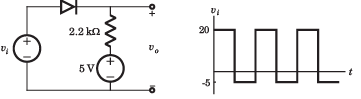 
- a)
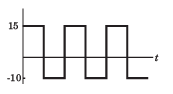
- b)
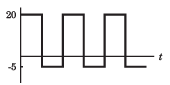
- c)
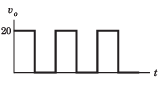
- d)
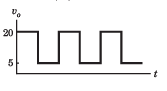
Correct answer is option 'D'. Can you explain this answer?
In the question a circuit and a waveform for the input voltage is given. The diode in circuit has cutin voltage Vγ = 0. Choose the option for the waveform of output voltage vo
a)
b)
c)
d)
|
Ankit Mukherjee answered |
Diode is off for vi < 5 V. Hence vo = 5 V.
For vi > 5 V, vo = vi .Therefore (D) is correct option.
The density and mobility of electrons in a conductor are respectively 1020/cm3 and 800 cm2/V-s. If a uniform electric field of 1 V/cm exists across this conductor, then the electron current density would be approximately- a)11 kA/cm2
- b)9 kA/cm2
- c)13 kA/cm2
- d)18 kA/cm2
Correct answer is option 'C'. Can you explain this answer?
The density and mobility of electrons in a conductor are respectively 1020/cm3 and 800 cm2/V-s. If a uniform electric field of 1 V/cm exists across this conductor, then the electron current density would be approximately
a)
11 kA/cm2
b)
9 kA/cm2
c)
13 kA/cm2
d)
18 kA/cm2
|
Pioneer Academy answered |
The current density is given by
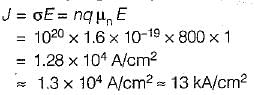
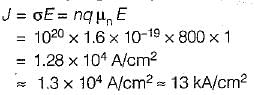
A solid copper sphere, 10 cm in diameter is deprived of 1020 electrons by a charging scheme. The charge on the sphere is- a)160.2 C
- b)-160.2 C
- c)16.02 C
- d)-16.02 C
Correct answer is option 'C'. Can you explain this answer?
A solid copper sphere, 10 cm in diameter is deprived of 1020 electrons by a charging scheme. The charge on the sphere is
a)
160.2 C
b)
-160.2 C
c)
16.02 C
d)
-16.02 C
|
Aditya Deshmukh answered |
n 10^20, Q = ne = e 10^20 = 16.02 C.
Charge on sphere will be positive.
Consider the circuit graph shown in figure below. Each branch of circuit graph represent a circuit element. The value of voltage V1 is
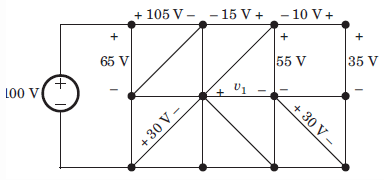
- a)30 V
- b)25 V
- c)20 V
- d)15 V
Correct answer is option 'D'. Can you explain this answer?
Consider the circuit graph shown in figure below. Each branch of circuit graph represent a circuit element. The value of voltage V1 is
a)
30 V
b)
25 V
c)
20 V
d)
15 V
|
Gate Gurus answered |
- 100 = 65 + V2 ⇒ V2 = 35 V
- V3 – 30 = V2 ⇒ V3 = 65 V
- 105 – V3 + V4 – 65 = 0 ⇒ V4 = 25 V
- V4 + 15 – 55 + V1 = 0 ⇒ V1 = 15 V.
A FET circuit has a transconductance of 2500 µ seconds and drain resistance equals to 10Kohms than voltage gain will be __________- a)20
- b)25
- c)30
- d)35
Correct answer is option 'B'. Can you explain this answer?
A FET circuit has a transconductance of 2500 µ seconds and drain resistance equals to 10Kohms than voltage gain will be __________
a)
20
b)
25
c)
30
d)
35
|
|
Pioneer Academy answered |
The transconductance, gm is defined as
gm = ΔID / ΔVGS
so gm = Voltage gain / RD
Therefore, voltage gain = gm x RD
= 2500 x 10-6 x 10 x 103
= 25.
gm = ΔID / ΔVGS
so gm = Voltage gain / RD
Therefore, voltage gain = gm x RD
= 2500 x 10-6 x 10 x 103
= 25.
If a current of 1.6 μA is flowing through a conductor, the number of electrons crossing a particular cross-section per second will be- a)1013
- b)1.6
- c)1019
- d)1.6 x 10-6
Correct answer is option 'A'. Can you explain this answer?
If a current of 1.6 μA is flowing through a conductor, the number of electrons crossing a particular cross-section per second will be
a)
1013
b)
1.6
c)
1019
d)
1.6 x 10-6
|
Lavanya Menon answered |
Given, I = 1.6 x 10-6 A
= 1.6 x 10-6 Coulomb/second
Charge crossing a particular cross-section per second = 1.6 x 10-6 C Hence, number of electrons crossing a particular cross-section per second
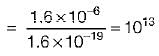
= 1.6 x 10-6 Coulomb/second
Charge crossing a particular cross-section per second = 1.6 x 10-6 C Hence, number of electrons crossing a particular cross-section per second
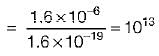
The energy required to charge a 10 µF capacitor to 100 V is- a)0.1 J
- b)0.05 J
- c) 5 x 10(-9) J
- d)10 x 10(-9) J
Correct answer is option 'B'. Can you explain this answer?
The energy required to charge a 10 µF capacitor to 100 V is
a)
0.1 J
b)
0.05 J
c)
5 x 10(-9) J
d)
10 x 10(-9) J
|
Sanjana Chopra answered |
Energy provided is equal to 0.5 CVxV.
With the increase in temperature, the resistivity of an intrinsic semiconductor decreases. This is because, with the increase of temperature- a)the carrier concentration decreases, but the mobility of carriers increases.
- b)the carrier concentration increases, but the mobility of carriers decreases.
- c)the carrier concentration remains the same but the mobility of carriers decreases.
- d)both the carrier concentration and mobility of carriers decreases
Correct answer is option 'B'. Can you explain this answer?
With the increase in temperature, the resistivity of an intrinsic semiconductor decreases. This is because, with the increase of temperature
a)
the carrier concentration decreases, but the mobility of carriers increases.
b)
the carrier concentration increases, but the mobility of carriers decreases.
c)
the carrier concentration remains the same but the mobility of carriers decreases.
d)
both the carrier concentration and mobility of carriers decreases
|
Malavika Nair answered |
In an intrinsic semiconductor, as the temperature increases mobility is slightly reduced since mobility of charge carrier is inversely proportional to temperature. This will slightly reduce the conductivity. But, due to temperature effect, large number of covalent bonds are broken which creates electrons and holes and this increases the conductivity by a larger value. As a result of this resistivity is decreased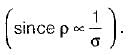 
Consider the circuit shown in fig.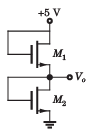
The both transistor have parameter as followsVTN = 0.8V, kn' = 30 μA/V2Que: If the width-to-length ratios of M1 and M2 are(W/L)1 = (W/L)2 = 40The output Vo is- a)2.5 V
- b)2.5 V
- c)5 V
- d)0 V
Correct answer is option 'B'. Can you explain this answer?
Consider the circuit shown in fig.
The both transistor have parameter as follows
VTN = 0.8V, kn' = 30 μA/V2
Que: If the width-to-length ratios of M1 and M2 are
(W/L)1 = (W/L)2 = 40
The output Vo is
a)
2.5 V
b)
2.5 V
c)
5 V
d)
0 V
|
Sanvi Kapoor answered |
For both transistor VDS = VGS ,
The LED in the circuit of fig. will be on if vi is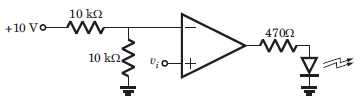
- a) > 10 V
- b)<10 V
- c) > 5 V
- d)< 5 V
Correct answer is option 'C'. Can you explain this answer?
The LED in the circuit of fig. will be on if vi is
a)
> 10 V
b)
<10 V
c)
> 5 V
d)
< 5 V
|
|
Anjana Khatri answered |
When v+ > 5 V, output will be positive and LED will be on. Hence (C) is correct.
In an n-p-n transistor biased in the active region, as the magnitude of the collector-base voltage is increased,- a)the base current increases because more electrons are injected from the emitter.
- b)the base current increases because more holes are injected from the base to the collector.
- c)the emitter current decreases because the base-emitter junction gets slightly less forward biased.
- d)the collector current increases slightly because the base width reduces.
Correct answer is option 'D'. Can you explain this answer?
In an n-p-n transistor biased in the active region, as the magnitude of the collector-base voltage is increased,
a)
the base current increases because more electrons are injected from the emitter.
b)
the base current increases because more holes are injected from the base to the collector.
c)
the emitter current decreases because the base-emitter junction gets slightly less forward biased.
d)
the collector current increases slightly because the base width reduces.
|
Mahesh Datta answered |
IC increases because base width reduces due to early effect.
In a Common Drain (CD) MOSFET amplifier with voltage divider bias with R1 and R2 equal to 1.5 MΩ and 1 MΩ respectively, the input impedance Zf is:- a)220 kΩ
- b)600 kΩ
- c)470 kΩ
- d)200 kΩ
Correct answer is option 'B'. Can you explain this answer?
In a Common Drain (CD) MOSFET amplifier with voltage divider bias with R1 and R2 equal to 1.5 MΩ and 1 MΩ respectively, the input impedance Zf is:
a)
220 kΩ
b)
600 kΩ
c)
470 kΩ
d)
200 kΩ
|
|
Sanjana Chopra answered |
Calculation of Input Impedance Zf:
- The input impedance Zf of a CD MOSFET amplifier with voltage divider bias can be calculated using the formula:
Zf = R1 || R2 + (1 + g_m * (R1 || R2))^-1
- Given that R1 = 1.5 MΩ and R2 = 1 MΩ, we can substitute these values into the formula.
Calculating R1 || R2:
- R1 || R2 = (R1 * R2) / (R1 + R2)
- R1 || R2 = (1.5 MΩ * 1 MΩ) / (1.5 MΩ + 1 MΩ)
- R1 || R2 = 1.5 MΩ * 1 MΩ / 2.5 MΩ
- R1 || R2 = 0.6 MΩ = 600 kΩ
Calculating g_m:
- Given parameters of the MOSFET and biasing conditions, the transconductance g_m is typically provided in the problem statement.
Substitute into the Input Impedance Formula:
- Zf = 600 kΩ + (1 + g_m * 600 kΩ)^-1
Final Calculation:
- Since we are given the options, we can calculate the input impedance for each option and find that the correct answer is option 'B' 600 kΩ.
Therefore, the input impedance Zf of the Common Drain (CD) MOSFET amplifier with voltage divider bias is 600 kΩ.
- The input impedance Zf of a CD MOSFET amplifier with voltage divider bias can be calculated using the formula:
Zf = R1 || R2 + (1 + g_m * (R1 || R2))^-1
- Given that R1 = 1.5 MΩ and R2 = 1 MΩ, we can substitute these values into the formula.
Calculating R1 || R2:
- R1 || R2 = (R1 * R2) / (R1 + R2)
- R1 || R2 = (1.5 MΩ * 1 MΩ) / (1.5 MΩ + 1 MΩ)
- R1 || R2 = 1.5 MΩ * 1 MΩ / 2.5 MΩ
- R1 || R2 = 0.6 MΩ = 600 kΩ
Calculating g_m:
- Given parameters of the MOSFET and biasing conditions, the transconductance g_m is typically provided in the problem statement.
Substitute into the Input Impedance Formula:
- Zf = 600 kΩ + (1 + g_m * 600 kΩ)^-1
Final Calculation:
- Since we are given the options, we can calculate the input impedance for each option and find that the correct answer is option 'B' 600 kΩ.
Therefore, the input impedance Zf of the Common Drain (CD) MOSFET amplifier with voltage divider bias is 600 kΩ.
Assertion (A): The drift velocity is in the direction opposite to that of the electric field.
Reason (R): At each inelastic collision with an ion, an electron loses energy, and a steady-state condition is reached where a finite value of drift speed is attained.- a)Both A and R are true and R is the correct explanation of A.
- b)Both A and R are true but R is not the correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'B'. Can you explain this answer?
Assertion (A): The drift velocity is in the direction opposite to that of the electric field.
Reason (R): At each inelastic collision with an ion, an electron loses energy, and a steady-state condition is reached where a finite value of drift speed is attained.
Reason (R): At each inelastic collision with an ion, an electron loses energy, and a steady-state condition is reached where a finite value of drift speed is attained.
a)
Both A and R are true and R is the correct explanation of A.
b)
Both A and R are true but R is not the correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Nikhil Iyer answered |
Assertion (A): The drift velocity is in the direction opposite to that of the electric field.
Reason (R): At each inelastic collision with an ion, an electron loses energy, and a steady-state condition is reached where a finite value of drift speed is attained.
Explanation:
The drift velocity is the average velocity at which charges (such as electrons) move in a conductor under the influence of an electric field. It is important to note that the drift velocity is in the opposite direction of the electric field.
Reason (R)
When an electric field is applied across a conductor, the electrons experience a force in the direction opposite to the electric field. This force causes the electrons to accelerate, gaining kinetic energy. However, due to collisions with ions and other impurities present in the conductor, the electrons lose some of their kinetic energy in each collision. As a result, the electrons do not achieve a constant acceleration, and their velocity does not increase indefinitely.
The collisions with ions and impurities cause the electrons to lose energy, and as a result, they lose velocity. However, the electric field continues to exert a force on the electrons, causing them to accelerate again. This cycle of acceleration followed by collision-induced deceleration continues until a steady-state condition is reached.
In the steady state, the acceleration due to the electric field is balanced by the deceleration due to collisions, resulting in a constant average drift velocity. This drift velocity is in the opposite direction of the electric field because the electrons lose energy and velocity in each collision.
Conclusion:
Both the assertion and the reason are true. The reason provides a correct explanation for the assertion. Therefore, option B is the correct answer.
Reason (R): At each inelastic collision with an ion, an electron loses energy, and a steady-state condition is reached where a finite value of drift speed is attained.
Explanation:
The drift velocity is the average velocity at which charges (such as electrons) move in a conductor under the influence of an electric field. It is important to note that the drift velocity is in the opposite direction of the electric field.
Reason (R)
When an electric field is applied across a conductor, the electrons experience a force in the direction opposite to the electric field. This force causes the electrons to accelerate, gaining kinetic energy. However, due to collisions with ions and other impurities present in the conductor, the electrons lose some of their kinetic energy in each collision. As a result, the electrons do not achieve a constant acceleration, and their velocity does not increase indefinitely.
The collisions with ions and impurities cause the electrons to lose energy, and as a result, they lose velocity. However, the electric field continues to exert a force on the electrons, causing them to accelerate again. This cycle of acceleration followed by collision-induced deceleration continues until a steady-state condition is reached.
In the steady state, the acceleration due to the electric field is balanced by the deceleration due to collisions, resulting in a constant average drift velocity. This drift velocity is in the opposite direction of the electric field because the electrons lose energy and velocity in each collision.
Conclusion:
Both the assertion and the reason are true. The reason provides a correct explanation for the assertion. Therefore, option B is the correct answer.
Consider a voltage series feedback network, where amplifier gain = 100, feedback factor = 5. For the basic amplifier, input voltage = 4V, input current=2mA. Find the input resistance of the network.- a)1.002kΩ
- b)1002kΩ
- c)2kΩ
- d)2000kΩ
Correct answer is option 'B'. Can you explain this answer?
Consider a voltage series feedback network, where amplifier gain = 100, feedback factor = 5. For the basic amplifier, input voltage = 4V, input current=2mA. Find the input resistance of the network.
a)
1.002kΩ
b)
1002kΩ
c)
2kΩ
d)
2000kΩ
|
Athul Das answered |
To find the input resistance of the network, we can use the formula:
Input resistance (Rin) = (Voltage gain / Current gain) * (Feedback factor / Amplifier gain)
Given:
Amplifier gain (Av) = 100
Feedback factor (β) = 5
The voltage gain (Av) can be calculated as the ratio of output voltage (Vo) to input voltage (Vi):
Av = Vo / Vi
Since it is a voltage series feedback network, the output voltage (Vo) and input voltage (Vi) are related by the formula:
Vo = Vi / (1 + β * Av)
Substituting the given values:
Av = 100
β = 5
Vo = Vi / (1 + 5 * 100)
Vo = Vi / 501
Now, we can calculate the output voltage (Vo) using the formula:
Vo = Av * Vi
Vo = 100 * 4V
Vo = 400V
Substituting the calculated values into the equation for Vo:
400V = Vi / 501
Solving for Vi:
Vi = 400V * 501
Vi = 200,400V
Now, we can substitute the calculated values into the formula for input resistance (Rin):
Rin = (Av / Ai) * (β / Av)
Rin = (100 / (2mA / 200,400V)) * (5 / 100)
Rin = (100 / (0.002A / 200,400V)) * (5 / 100)
Rin = (100 / (0.002A / 200,400V)) * (5 / 100)
Rin = (100 / (0.002A / 200,400V)) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = 1,000 * 0.05
Rin = 50
Therefore, the input resistance of the network is 50 ohms.
Input resistance (Rin) = (Voltage gain / Current gain) * (Feedback factor / Amplifier gain)
Given:
Amplifier gain (Av) = 100
Feedback factor (β) = 5
The voltage gain (Av) can be calculated as the ratio of output voltage (Vo) to input voltage (Vi):
Av = Vo / Vi
Since it is a voltage series feedback network, the output voltage (Vo) and input voltage (Vi) are related by the formula:
Vo = Vi / (1 + β * Av)
Substituting the given values:
Av = 100
β = 5
Vo = Vi / (1 + 5 * 100)
Vo = Vi / 501
Now, we can calculate the output voltage (Vo) using the formula:
Vo = Av * Vi
Vo = 100 * 4V
Vo = 400V
Substituting the calculated values into the equation for Vo:
400V = Vi / 501
Solving for Vi:
Vi = 400V * 501
Vi = 200,400V
Now, we can substitute the calculated values into the formula for input resistance (Rin):
Rin = (Av / Ai) * (β / Av)
Rin = (100 / (2mA / 200,400V)) * (5 / 100)
Rin = (100 / (0.002A / 200,400V)) * (5 / 100)
Rin = (100 / (0.002A / 200,400V)) * (5 / 100)
Rin = (100 / (0.002A / 200,400V)) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = (100 / 0.002A) * (5 / 100)
Rin = 1,000 * 0.05
Rin = 50
Therefore, the input resistance of the network is 50 ohms.
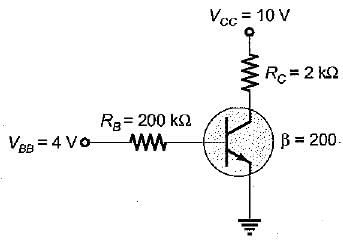
For the circuit shown below, the collector to emitter voltage is
- a)1.25 V
- b)3.40 V
- c)-2.30 V
- d)0 V
Correct answer is option 'B'. Can you explain this answer?
For the circuit shown below, the collector to emitter voltage is
a)
1.25 V
b)
3.40 V
c)
-2.30 V
d)
0 V
|
|
Sanya Agarwal answered |
Let the transistor be operating under active region.
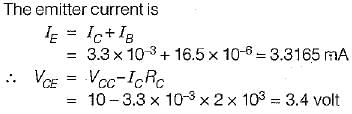
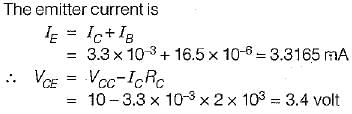
Compared to bipolar transistors, field effect transistors are NOT normally characterized by:- a)high input impedance
- b)a reverse-biased PN junction
- c)low input impedance
- d)low power consumption
Correct answer is option 'C'. Can you explain this answer?
Compared to bipolar transistors, field effect transistors are NOT normally characterized by:
a)
high input impedance
b)
a reverse-biased PN junction
c)
low input impedance
d)
low power consumption
|
|
Pioneer Academy answered |
The difference between FET and BJT is explained in the following table:
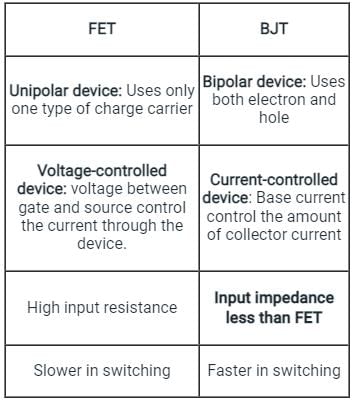
Hence, Option C is correct.
In a feedback network, input voltage is 14V, feedback voltage is 6V and source voltage is 20V. β is in ohms. What is its configuration?- a)Shunt-Shunt feedback
- b)Shunt-Series feedback
- c)Series-Series feedback
- d)Series-Shunt feedback
Correct answer is option 'C'. Can you explain this answer?
In a feedback network, input voltage is 14V, feedback voltage is 6V and source voltage is 20V. β is in ohms. What is its configuration?
a)
Shunt-Shunt feedback
b)
Shunt-Series feedback
c)
Series-Series feedback
d)
Series-Shunt feedback
|
|
Pioneer Academy answered |
Given that input is 14V, feedback is 6V and source is 20 V, we can see
VI = VS – VF, which is voltage mixing. Also, β is in ohms that is voltage/current.
Since output of feedback is voltage and input is current, the output has current sampling.
Thus, configuration is a series-series feedback/current – series feedback.
VI = VS – VF, which is voltage mixing. Also, β is in ohms that is voltage/current.
Since output of feedback is voltage and input is current, the output has current sampling.
Thus, configuration is a series-series feedback/current – series feedback.
What is the reverse transmission factor?- a)Ratio of output by input signal
- b)Ratio of feedback by input signal
- c)Ration of feedback by output signal
- d)Ratio of input by feedback signal
Correct answer is option 'C'. Can you explain this answer?
What is the reverse transmission factor?
a)
Ratio of output by input signal
b)
Ratio of feedback by input signal
c)
Ration of feedback by output signal
d)
Ratio of input by feedback signal
|
|
Athul Das answered |
The reverse transmission factor refers to the ratio of feedback by the output signal in a control system. It plays a crucial role in determining the stability and performance of the system. To understand this concept, let's break down the components of a control system and how they interact with each other.
1. Control system components:
a) Input signal: The desired or reference signal that the system aims to achieve.
b) Output signal: The measured or actual signal produced by the system.
c) Feedback signal: The portion of the output signal that is fed back to the system for comparison with the input signal.
d) Forward path: The path through which the input signal is processed to produce the output signal.
e) Feedback path: The path through which the feedback signal is combined with the input signal to generate an error signal.
2. Importance of feedback:
Feedback is essential in control systems as it allows for error correction and improves system performance. By comparing the output signal with the input signal, any discrepancies or errors can be detected, and appropriate adjustments can be made to minimize these errors.
3. Reverse transmission factor:
The reverse transmission factor, denoted as β, represents the ratio of feedback by the output signal. Mathematically, it can be expressed as:
β = Feedback signal / Output signal
4. Significance of the reverse transmission factor:
The reverse transmission factor influences the gain and stability of a control system. Here's why:
a) Gain: The gain of a system determines how much the output signal changes in response to a change in the input signal. The presence of feedback modifies the overall gain of the system. The reverse transmission factor affects the gain by determining the fraction of the output signal that is fed back into the system. A higher reverse transmission factor implies more feedback, leading to a reduction in the overall gain of the system.
b) Stability: Stability is a critical aspect of control systems. It refers to the ability of the system to maintain a steady output in the presence of disturbances or changes in the input signal. The reverse transmission factor plays a significant role in determining system stability. If the reverse transmission factor is too high, it can introduce instability into the system, causing oscillations or even system failure. Hence, it is crucial to carefully design the reverse transmission factor to ensure stability.
In summary, the reverse transmission factor represents the ratio of feedback by the output signal in a control system. It affects the gain and stability of the system and needs to be carefully considered during system design and analysis.
1. Control system components:
a) Input signal: The desired or reference signal that the system aims to achieve.
b) Output signal: The measured or actual signal produced by the system.
c) Feedback signal: The portion of the output signal that is fed back to the system for comparison with the input signal.
d) Forward path: The path through which the input signal is processed to produce the output signal.
e) Feedback path: The path through which the feedback signal is combined with the input signal to generate an error signal.
2. Importance of feedback:
Feedback is essential in control systems as it allows for error correction and improves system performance. By comparing the output signal with the input signal, any discrepancies or errors can be detected, and appropriate adjustments can be made to minimize these errors.
3. Reverse transmission factor:
The reverse transmission factor, denoted as β, represents the ratio of feedback by the output signal. Mathematically, it can be expressed as:
β = Feedback signal / Output signal
4. Significance of the reverse transmission factor:
The reverse transmission factor influences the gain and stability of a control system. Here's why:
a) Gain: The gain of a system determines how much the output signal changes in response to a change in the input signal. The presence of feedback modifies the overall gain of the system. The reverse transmission factor affects the gain by determining the fraction of the output signal that is fed back into the system. A higher reverse transmission factor implies more feedback, leading to a reduction in the overall gain of the system.
b) Stability: Stability is a critical aspect of control systems. It refers to the ability of the system to maintain a steady output in the presence of disturbances or changes in the input signal. The reverse transmission factor plays a significant role in determining system stability. If the reverse transmission factor is too high, it can introduce instability into the system, causing oscillations or even system failure. Hence, it is crucial to carefully design the reverse transmission factor to ensure stability.
In summary, the reverse transmission factor represents the ratio of feedback by the output signal in a control system. It affects the gain and stability of the system and needs to be carefully considered during system design and analysis.
The secondary transformer voltage of the rectifier circuit shown in fig. is vs = 60 sin 2π 60tV. Each diode has a cut in voltage of Vγ = 0.6 V. The ripple voltage is to be no more than Vrip = 2 V. The value of filter capacitor will be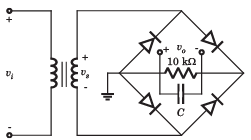
- a)48.8 μF
- b)24.4 μF
- c)32.2 μF
- d)16.1 μF
Correct answer is option 'B'. Can you explain this answer?
The secondary transformer voltage of the rectifier circuit shown in fig. is vs = 60 sin 2π 60tV. Each diode has a cut in voltage of Vγ = 0.6 V. The ripple voltage is to be no more than Vrip = 2 V. The value of filter capacitor will be
a)
48.8 μF
b)
24.4 μF
c)
32.2 μF
d)
16.1 μF
|
Zoya Sharma answered |
vs = 60 sin 2π 60tV
When a 1 V increase in the gate voltage changes the drain current 10 mA in a FET, its gm equals.- a)0.01 mho
- b)100 mho
- c)1000 mho
- d)10000 mho
Correct answer is option 'A'. Can you explain this answer?
When a 1 V increase in the gate voltage changes the drain current 10 mA in a FET, its gm equals.
a)
0.01 mho
b)
100 mho
c)
1000 mho
d)
10000 mho
|
Pooja Patel answered |
Concept:
Transconductance indicates the amount of control the gate has on the drain current.
Mathematically, the transconductance (gm) is defined as:
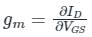
It is given the name transconductance because it gives the relationship between the input voltage and the output current.
Calculation:
Given: Δ VGS = 1 V and Δ ID = 10 mA
∴ 
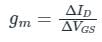
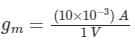
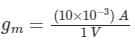
= 0.01 mho
Voltage gain of common drain amplifier is always slightly less than _____- a)0.5
- b)1
- c)1.5
- d)2
Correct answer is option 'B'. Can you explain this answer?
Voltage gain of common drain amplifier is always slightly less than _____
a)
0.5
b)
1
c)
1.5
d)
2
|
|
Pooja Patel answered |
In common drain amplifier
Writing KCL at the source node ;
Gm(vin – vout) – gmbs vout – gds vout = 0
vout vin = Gm / Gm + Gmbs + gds
Therefore gain is less than one.
Writing KCL at the source node ;
Gm(vin – vout) – gmbs vout – gds vout = 0
vout vin = Gm / Gm + Gmbs + gds
Therefore gain is less than one.
The gain of a FET amplifier can be changed by changing:- a)fm
- b)gm
- c)RL
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The gain of a FET amplifier can be changed by changing:
a)
fm
b)
gm
c)
RL
d)
None of these
|
Gate Funda answered |
Concept:
Voltage gain for a FET amplifier is given as:
AV = −gm(rd||RD)
Analysis:
Hence, The gain of a FET amplifier can be changed by changing gm
What is the value of thermal resistance for the 2N338 transistor for which the manufacturer specifies PC,max = 125 mW at 25°C free-air temperature and maximum junction temperature of 150°C?- a)1.0°C/mW
- b)1.45°C/mW
- c)1.2°C/mW
- d)0.2°C/mW
Correct answer is option 'A'. Can you explain this answer?
What is the value of thermal resistance for the 2N338 transistor for which the manufacturer specifies PC,max = 125 mW at 25°C free-air temperature and maximum junction temperature of 150°C?
a)
1.0°C/mW
b)
1.45°C/mW
c)
1.2°C/mW
d)
0.2°C/mW
|
Avik Saha answered |
Calculating Thermal Resistance for 2N338 Transistor:
In this case, we are given the maximum power dissipation (PC,max) of the 2N338 transistor as 125 mW at a free-air temperature of 25°C and a maximum junction temperature of 150°C. To calculate the thermal resistance of the transistor, we can use the formula:
Thermal Resistance (θ) = (Tj - Ta) / PC,max
Where:
- θ is the thermal resistance
- Tj is the junction temperature (150°C)
- Ta is the ambient temperature (25°C)
- PC,max is the maximum power dissipation (125 mW)
Now, substituting the given values into the formula:
θ = (150°C - 25°C) / 125 mW
θ = 125°C / 125 mW
θ = 1.0 °C/mW
Therefore, the thermal resistance of the 2N338 transistor is 1.0 °C/mW. This means that for every 1 mW of power dissipated by the transistor, the junction temperature will increase by 1.0°C above the ambient temperature.
In this case, we are given the maximum power dissipation (PC,max) of the 2N338 transistor as 125 mW at a free-air temperature of 25°C and a maximum junction temperature of 150°C. To calculate the thermal resistance of the transistor, we can use the formula:
Thermal Resistance (θ) = (Tj - Ta) / PC,max
Where:
- θ is the thermal resistance
- Tj is the junction temperature (150°C)
- Ta is the ambient temperature (25°C)
- PC,max is the maximum power dissipation (125 mW)
Now, substituting the given values into the formula:
θ = (150°C - 25°C) / 125 mW
θ = 125°C / 125 mW
θ = 1.0 °C/mW
Therefore, the thermal resistance of the 2N338 transistor is 1.0 °C/mW. This means that for every 1 mW of power dissipated by the transistor, the junction temperature will increase by 1.0°C above the ambient temperature.
Assertion (A): An emitter follower is widely used in electronic instruments.
Reason (R): The voltage gain of emitter follower is very high.- a)Both A and R are true and R is the correct explanation of A.
- b)Both A and R are true but R is not the correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'C'. Can you explain this answer?
Assertion (A): An emitter follower is widely used in electronic instruments.
Reason (R): The voltage gain of emitter follower is very high.
Reason (R): The voltage gain of emitter follower is very high.
a)
Both A and R are true and R is the correct explanation of A.
b)
Both A and R are true but R is not the correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Gaurav Chauhan answered |
The voltage gain of emitter follower (or common collector configuration) is less than unity i.e. a low value.
Hence, reason is not true.
Hence, reason is not true.
A FET can be used as a variable- a)Inductor
- b)Capacitor
- c)Resistor
- d)Voltage Source
Correct answer is option 'C'. Can you explain this answer?
A FET can be used as a variable
a)
Inductor
b)
Capacitor
c)
Resistor
d)
Voltage Source
|
|
Pooja Patel answered |
- FET is a device that is usually operated in the constant-current portion of its output characteristics. But if it is operated on the region prior to pinch-off (that is where VDS is small, say below 100 mV), it will behave as a voltage-variable resistor.
- It is due to the fact that in this region drain-to-source resistance RDS can be controlled by varying the bias voltage VGS.
- In such applications the FET is also referred to as a voltage-variable resistor or volatile dependent resistor. It finds applications in many areas where this property is useful.
The drain of FET is analogous to BJT- a)collector
- b)emitter
- c)base
- d)drain
Correct answer is option 'A'. Can you explain this answer?
The drain of FET is analogous to BJT
a)
collector
b)
emitter
c)
base
d)
drain
|
Nilesh Joshi answered |
Analogies between FET and BJT
An analogy between Field Effect Transistor (FET) and Bipolar Junction Transistor (BJT) can be drawn in the context of their functioning. Both of these electronic devices are used for amplifying signals, and they have a similar structure in terms of the presence of a source, gate, and drain in FET and collector, base, and emitter in BJT. However, the way they function is different, and the analogy is drawn between the specific parts of the devices.
The drain of FET and collector of BJT
In FET, the drain is the part where the current flows out of the device. Similarly, in BJT, the collector is the part where the current flows out of the device. The analogy between these two parts is drawn based on their functionality. The collector in BJT is responsible for collecting the majority carriers (either electrons or holes) that flow from the emitter and then move towards the base. Similarly, the drain in FET is responsible for collecting the majority carriers that flow from the channel to the drain.
The analogy between the drain of FET and collector of BJT is further strengthened by the fact that both of these parts are operated in the reverse-biased mode. In BJT, the collector-base junction is reverse-biased, while in FET, the gate-source junction is reverse-biased. In both cases, the reverse-biasing results in a depletion region, which helps to control the flow of current through the device.
Conclusion
In conclusion, the analogy between the drain of FET and the collector of BJT is drawn based on their functionality and the way they operate in the device. Both of these parts are responsible for collecting the majority carriers and are operated in the reverse-biased mode. However, it is important to note that this analogy is limited to specific parts of the devices and does not imply that FET and BJT are the same.
An analogy between Field Effect Transistor (FET) and Bipolar Junction Transistor (BJT) can be drawn in the context of their functioning. Both of these electronic devices are used for amplifying signals, and they have a similar structure in terms of the presence of a source, gate, and drain in FET and collector, base, and emitter in BJT. However, the way they function is different, and the analogy is drawn between the specific parts of the devices.
The drain of FET and collector of BJT
In FET, the drain is the part where the current flows out of the device. Similarly, in BJT, the collector is the part where the current flows out of the device. The analogy between these two parts is drawn based on their functionality. The collector in BJT is responsible for collecting the majority carriers (either electrons or holes) that flow from the emitter and then move towards the base. Similarly, the drain in FET is responsible for collecting the majority carriers that flow from the channel to the drain.
The analogy between the drain of FET and collector of BJT is further strengthened by the fact that both of these parts are operated in the reverse-biased mode. In BJT, the collector-base junction is reverse-biased, while in FET, the gate-source junction is reverse-biased. In both cases, the reverse-biasing results in a depletion region, which helps to control the flow of current through the device.
Conclusion
In conclusion, the analogy between the drain of FET and the collector of BJT is drawn based on their functionality and the way they operate in the device. Both of these parts are responsible for collecting the majority carriers and are operated in the reverse-biased mode. However, it is important to note that this analogy is limited to specific parts of the devices and does not imply that FET and BJT are the same.
In typical circuits, the stabilization factor S = (ΔICICO) is- a)< 1
- b)> 1
- c)= 1
- d)<< 1
Correct answer is option 'D'. Can you explain this answer?
In typical circuits, the stabilization factor S = (ΔICICO) is
a)
< 1
b)
> 1
c)
= 1
d)
<< 1
|
|
Kajal Yadav answered |
For better stability of the circuit, stability factor S must be as small as possible.
Applications of negative feedback to a certain amplifier reduced its gain from 200 to 100. If the gain with the same feedback is to be raised to 150, in the case of another such appliance, the gain of the amplifier without feedback must have been- a)400
- b)450
- c)500
- d)600
Correct answer is option 'D'. Can you explain this answer?
Applications of negative feedback to a certain amplifier reduced its gain from 200 to 100. If the gain with the same feedback is to be raised to 150, in the case of another such appliance, the gain of the amplifier without feedback must have been
a)
400
b)
450
c)
500
d)
600
|
|
Pooja Patel answered |
Concept:
A negative feedback network is shown below.
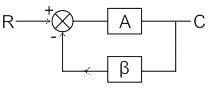
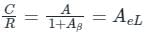
Where A is the gain of the amplifier without feedback and feedback gain = β
Calculation:
Case 1:
Gain without feedback, A = 200
Gain with feedback ACL = 100
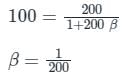
Case 2:
Gain with feedback, ACL = 150
Feedback,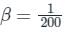 
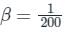
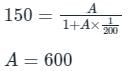
A device whose characteristics are very close to that of an ideal current source is- a)a BJT in CB mode
- b)a gas diode
- c)a triode
- d)a BJT in CE mode
Correct answer is option 'A'. Can you explain this answer?
A device whose characteristics are very close to that of an ideal current source is
a)
a BJT in CB mode
b)
a gas diode
c)
a triode
d)
a BJT in CE mode
|
Raj Singh answered |
The output characteristic of a CB transistor configuration is shown in figure below.
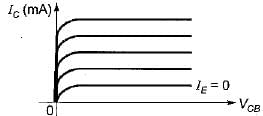
It is clear that for a constant value of IE, IC is independent of VCB and the curves are parallel to the axis of VCB.
Hence, a CB transistor acts as an ideal current source.
It is clear that for a constant value of IE, IC is independent of VCB and the curves are parallel to the axis of VCB.
Hence, a CB transistor acts as an ideal current source.
It is desired to reduce total harmonic of amplifier from 8% to 1% by use of 10% negative feedback. If the gain of the amplifier with original distortion and with reduced distortion is A1 and A2 then, A1 + A2 = −−−−−−
Correct answer is between '78.70,78.80'. Can you explain this answer?
It is desired to reduce total harmonic of amplifier from 8% to 1% by use of 10% negative feedback. If the gain of the amplifier with original distortion and with reduced distortion is A1 and A2 then, A1 + A2 = −−−−−−
|
|
Snehal Rane answered |
To solve this problem, we can use the formula for the reduction in distortion due to negative feedback:
Rd = 1 - (1 + β) * Hd
Where Rd is the reduction in distortion, β is the feedback factor, and Hd is the distortion without feedback.
Given that the reduction in distortion is desired to be from 8% to 1%, we can calculate the initial distortion without feedback (Hd) as:
Hd = 8% = 0.08
And the desired distortion with feedback (Hd') as:
Hd' = 1% = 0.01
We are also given that the feedback factor (β) is 10%.
Using the formula, we can calculate the reduction in distortion (Rd) as:
Rd = 1 - (1 + 0.1) * 0.08
= 1 - 1.08 * 0.08
= 1 - 0.0864
= 0.9136
Next, we can calculate the gain of the amplifier with reduced distortion (A2) using the formula:
A2 = A1 / (1 + β * A1 * Rd)
Where A1 is the gain of the amplifier with original distortion.
Since we want to find the relationship between A1 and A2, we can rearrange the formula to:
A2 = A1 / (1 + β * A1 * Rd)
A2 * (1 + β * A1 * Rd) = A1
A2 + β * A1 * Rd * A2 = A1
A2 - A1 = - β * A1 * Rd * A2
(A2 - A1) / (A1 * A2) = - β * Rd
(A2 - A1) / (A1 * A2 * Rd) = - β
Therefore, A1 * A2 = -(A2 - A1) / (β * Rd)
Substituting the values we have calculated:
A1 * A2 = -(A2 - A1) / (0.1 * 0.9136)
= -(A2 - A1) / 0.09136
Rd = 1 - (1 + β) * Hd
Where Rd is the reduction in distortion, β is the feedback factor, and Hd is the distortion without feedback.
Given that the reduction in distortion is desired to be from 8% to 1%, we can calculate the initial distortion without feedback (Hd) as:
Hd = 8% = 0.08
And the desired distortion with feedback (Hd') as:
Hd' = 1% = 0.01
We are also given that the feedback factor (β) is 10%.
Using the formula, we can calculate the reduction in distortion (Rd) as:
Rd = 1 - (1 + 0.1) * 0.08
= 1 - 1.08 * 0.08
= 1 - 0.0864
= 0.9136
Next, we can calculate the gain of the amplifier with reduced distortion (A2) using the formula:
A2 = A1 / (1 + β * A1 * Rd)
Where A1 is the gain of the amplifier with original distortion.
Since we want to find the relationship between A1 and A2, we can rearrange the formula to:
A2 = A1 / (1 + β * A1 * Rd)
A2 * (1 + β * A1 * Rd) = A1
A2 + β * A1 * Rd * A2 = A1
A2 - A1 = - β * A1 * Rd * A2
(A2 - A1) / (A1 * A2) = - β * Rd
(A2 - A1) / (A1 * A2 * Rd) = - β
Therefore, A1 * A2 = -(A2 - A1) / (β * Rd)
Substituting the values we have calculated:
A1 * A2 = -(A2 - A1) / (0.1 * 0.9136)
= -(A2 - A1) / 0.09136
The current gain of a common-emitter amplifier _____ as the load resistance is increased.- a)increases
- b)decreases
- c)in unchanged
- d)increase and then decreases
Correct answer is option 'B'. Can you explain this answer?
The current gain of a common-emitter amplifier _____ as the load resistance is increased.
a)
increases
b)
decreases
c)
in unchanged
d)
increase and then decreases
|
Prisha Iyer answered |
As the load resistance is increases, collector current reduces and hence current gain (β) is decreased.
If ‘V’ is the voltage phasor and ‘I’ is the current phasor, then VI represents- a)Apparent power
- b)Active power
- c)Reactive power
- d)Total power
Correct answer is option 'A'. Can you explain this answer?
If ‘V’ is the voltage phasor and ‘I’ is the current phasor, then VI represents
a)
Apparent power
b)
Active power
c)
Reactive power
d)
Total power
|
|
Sarita Yadav answered |
Apparent Power (S): It is defined as the product of r.m.s value of voltage (V) and current (1). It is denoted by S. S = V/I Volt Ampere
An amplifier has a Open Loop voltage gain of –500. This gain is reduced to –100 when negative feedback is applied. The reverse transmission factor,β of this system is:-- a)– 0.025
- b)– 0.008
- c)0.1
- d)– 0.2
Correct answer is option 'B'. Can you explain this answer?
An amplifier has a Open Loop voltage gain of –500. This gain is reduced to –100 when negative feedback is applied. The reverse transmission factor,β of this system is:-
a)
– 0.025
b)
– 0.008
c)
0.1
d)
– 0.2
|
Srishti Choudhary answered |
An amplifier has an open loop voltage gain of "A." The open loop voltage gain, also known as the gain without any feedback applied, is a measure of how much the amplifier amplifies the input voltage. It is typically expressed as a ratio or in decibels.
The open loop voltage gain can be calculated by dividing the output voltage by the input voltage:
Open Loop Voltage Gain (A) = Output Voltage / Input Voltage
For example, if an amplifier has an output voltage of 10V and an input voltage of 1V, the open loop voltage gain would be 10.
It is important to note that the open loop voltage gain is not a fixed value and can vary depending on the frequency of the input signal. Amplifiers often have a frequency response curve that shows how the gain changes with frequency.
Additionally, the open loop voltage gain is usually much higher than the closed loop voltage gain when feedback is applied. Feedback is commonly used to stabilize the amplifier's performance and reduce distortion.
The open loop voltage gain can be calculated by dividing the output voltage by the input voltage:
Open Loop Voltage Gain (A) = Output Voltage / Input Voltage
For example, if an amplifier has an output voltage of 10V and an input voltage of 1V, the open loop voltage gain would be 10.
It is important to note that the open loop voltage gain is not a fixed value and can vary depending on the frequency of the input signal. Amplifiers often have a frequency response curve that shows how the gain changes with frequency.
Additionally, the open loop voltage gain is usually much higher than the closed loop voltage gain when feedback is applied. Feedback is commonly used to stabilize the amplifier's performance and reduce distortion.
A lightning bolt carrying 15,000 A lasts for 100 s. If the lightning strikes an airplane flying at 2 km, the charge deposited on the plane is- a)13.33 C
- b)75 C
- c)1500 C
- d)1.5 C
Correct answer is option 'D'. Can you explain this answer?
A lightning bolt carrying 15,000 A lasts for 100 s. If the lightning strikes an airplane flying at 2 km, the charge deposited on the plane is
a)
13.33 C
b)
75 C
c)
1500 C
d)
1.5 C
|
Janhavi Roy answered |
To calculate the charge deposited on the plane when struck by a lightning bolt, we can use the equation Q = I * t, where Q is the charge, I is the current, and t is the time.
Given:
Current (I) = 15,000 A
Time (t) = 100 s
Calculating the Charge:
Using the formula Q = I * t, we can substitute the given values:
Q = 15,000 A * 100 s
Q = 1,500,000 C
Therefore, the charge deposited on the plane when struck by the lightning bolt is 1,500,000 Coulombs or 1.5 C.
In this case, the correct answer is option 'D'.
Given:
Current (I) = 15,000 A
Time (t) = 100 s
Calculating the Charge:
Using the formula Q = I * t, we can substitute the given values:
Q = 15,000 A * 100 s
Q = 1,500,000 C
Therefore, the charge deposited on the plane when struck by the lightning bolt is 1,500,000 Coulombs or 1.5 C.
In this case, the correct answer is option 'D'.
Primary trigger for oscillation is obtained from ___________- a)DC voltage
- b)Noise voltage
- c)External trigger voltage
- d)No trigger is required
Correct answer is option 'B'. Can you explain this answer?
Primary trigger for oscillation is obtained from ___________
a)
DC voltage
b)
Noise voltage
c)
External trigger voltage
d)
No trigger is required
|
|
Pooja Patel answered |
The primary trigger for oscillation is obtained from noise voltage.
When an electric field is applied across a semiconductor, free electrons in it will accelerate due to the applied field, and gain energy. This energy can be lost as heat when the electrons- a)recombine with holes
- b)collide with atoms in the crystal
- c)radiate energy while being accelerated
- d)collide with other electrons
Correct answer is option 'B'. Can you explain this answer?
When an electric field is applied across a semiconductor, free electrons in it will accelerate due to the applied field, and gain energy. This energy can be lost as heat when the electrons
a)
recombine with holes
b)
collide with atoms in the crystal
c)
radiate energy while being accelerated
d)
collide with other electrons
|
|
Nikhil Iyer answered |
Explanation:
When an electric field is applied across a semiconductor, the free electrons in the material experience a force due to the field. This force causes the electrons to accelerate and gain kinetic energy. However, this energy gained by the electrons is not permanently retained. Instead, it is lost as heat through collisions with atoms in the crystal lattice of the semiconductor material.
Collisions with Atoms in the Crystal:
- When the accelerated electrons collide with atoms in the crystal lattice, they transfer some of their kinetic energy to these atoms.
- These collisions cause the atoms to vibrate, increasing their thermal energy and consequently increasing the temperature of the material.
- This process is known as electron-phonon scattering, where phonons represent the lattice vibrations.
Reason for Choosing Option 'B':
- The other options listed (recombination with holes, radiation while being accelerated, and collision with other electrons) do not play a significant role in the loss of energy as heat in a semiconductor under an applied electric field.
- Recombination with holes refers to the combination of a free electron with an empty state (hole) in the valence band, resulting in the release of energy as light or heat. However, this process is not directly related to the loss of energy by accelerated electrons in an electric field.
- Radiation while being accelerated is more relevant in the context of charged particles moving close to the speed of light or in high-energy physics. In the case of electrons in a semiconductor under a typical electric field, the energy lost through radiation is negligible.
- Collisions with other electrons can lead to scattering and resistance in the material but do not directly result in the loss of energy as heat.
Conclusion:
When an electric field is applied across a semiconductor, the kinetic energy gained by the free electrons is lost primarily as heat through collisions with atoms in the crystal lattice. These collisions transfer energy to the lattice, increasing its thermal energy and causing the material to heat up. This phenomenon is an essential aspect of understanding the behavior of semiconductors under electric fields.
When an electric field is applied across a semiconductor, the free electrons in the material experience a force due to the field. This force causes the electrons to accelerate and gain kinetic energy. However, this energy gained by the electrons is not permanently retained. Instead, it is lost as heat through collisions with atoms in the crystal lattice of the semiconductor material.
Collisions with Atoms in the Crystal:
- When the accelerated electrons collide with atoms in the crystal lattice, they transfer some of their kinetic energy to these atoms.
- These collisions cause the atoms to vibrate, increasing their thermal energy and consequently increasing the temperature of the material.
- This process is known as electron-phonon scattering, where phonons represent the lattice vibrations.
Reason for Choosing Option 'B':
- The other options listed (recombination with holes, radiation while being accelerated, and collision with other electrons) do not play a significant role in the loss of energy as heat in a semiconductor under an applied electric field.
- Recombination with holes refers to the combination of a free electron with an empty state (hole) in the valence band, resulting in the release of energy as light or heat. However, this process is not directly related to the loss of energy by accelerated electrons in an electric field.
- Radiation while being accelerated is more relevant in the context of charged particles moving close to the speed of light or in high-energy physics. In the case of electrons in a semiconductor under a typical electric field, the energy lost through radiation is negligible.
- Collisions with other electrons can lead to scattering and resistance in the material but do not directly result in the loss of energy as heat.
Conclusion:
When an electric field is applied across a semiconductor, the kinetic energy gained by the free electrons is lost primarily as heat through collisions with atoms in the crystal lattice. These collisions transfer energy to the lattice, increasing its thermal energy and causing the material to heat up. This phenomenon is an essential aspect of understanding the behavior of semiconductors under electric fields.
Chapter doubts & questions for Analog Electronics - GATE Electrical Engineering (EE) Mock Test Series 2026 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Analog Electronics - GATE Electrical Engineering (EE) Mock Test Series 2026 in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
GATE Electrical Engineering (EE) Mock Test Series 2026
26 docs|257 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup