All Exams >
Class 10 >
Olympiad Preparation for Class 10 >
All Questions
All questions of Linear Equations in Two Variables for Class 10 Exam
Places M and N are 90 km apart from each other on a national highway. A truck starts from M and another from N at the same time. If they go in the same direction, then they meet in 9 hours and if they go in opposite directions they meet in 9/7 hours. The speed of the trucks are _______.- a)90 km/hr, 40 km/hr
- b)40 km/hr, 30 km/hr
- c)20 km/hr, 60 km/hr
- d)50 km/hr, 12 km/hr
Correct answer is option 'B'. Can you explain this answer?
Places M and N are 90 km apart from each other on a national highway. A truck starts from M and another from N at the same time. If they go in the same direction, then they meet in 9 hours and if they go in opposite directions they meet in 9/7 hours. The speed of the trucks are _______.
a)
90 km/hr, 40 km/hr
b)
40 km/hr, 30 km/hr
c)
20 km/hr, 60 km/hr
d)
50 km/hr, 12 km/hr
|
|
Prabhat mehta answered |
Given:
Distance between M and N = 90 km
When the trucks go in the same direction:
Time taken to meet = 9 hours
When the trucks go in opposite directions:
Time taken to meet = 9/7 hours
Let the speed of one truck be x km/hr and the speed of the other truck be y km/hr.
When the trucks go in the same direction:
Relative speed = (x - y) km/hr
Distance traveled = 90 km
Time taken = 9 hours
Using the formula:
Distance = Speed × Time
90 = (x - y) × 9
Simplifying the equation:
10 = x - y ...........(1)
When the trucks go in opposite directions:
Relative speed = (x + y) km/hr
Distance traveled = 90 km
Time taken = 9/7 hours
Using the formula:
Distance = Speed × Time
90 = (x + y) × (9/7)
Simplifying the equation:
10 = (x + y) × (1/7) ...........(2)
Solving equations (1) and (2) simultaneously:
x - y = 10
x + y = 70/7
Adding the two equations:
2x = 10 + 70/7
2x = (70 + 10/7)
2x = 80/7
Dividing by 2 on both sides:
x = (80/7) ÷ 2
x = 40/7
Substituting the value of x in equation (1):
40/7 - y = 10
Simplifying the equation:
y = 40/7 - 70/7
y = -30/7
Since speed cannot be negative, we take the positive value:
y = 30/7
Therefore, the speed of the trucks are:
Truck 1: x = 40/7 km/hr
Truck 2: y = 30/7 km/hr
So, the correct answer is option (b) 40 km/hr and 30 km/hr.
Distance between M and N = 90 km
When the trucks go in the same direction:
Time taken to meet = 9 hours
When the trucks go in opposite directions:
Time taken to meet = 9/7 hours
Let the speed of one truck be x km/hr and the speed of the other truck be y km/hr.
When the trucks go in the same direction:
Relative speed = (x - y) km/hr
Distance traveled = 90 km
Time taken = 9 hours
Using the formula:
Distance = Speed × Time
90 = (x - y) × 9
Simplifying the equation:
10 = x - y ...........(1)
When the trucks go in opposite directions:
Relative speed = (x + y) km/hr
Distance traveled = 90 km
Time taken = 9/7 hours
Using the formula:
Distance = Speed × Time
90 = (x + y) × (9/7)
Simplifying the equation:
10 = (x + y) × (1/7) ...........(2)
Solving equations (1) and (2) simultaneously:
x - y = 10
x + y = 70/7
Adding the two equations:
2x = 10 + 70/7
2x = (70 + 10/7)
2x = 80/7
Dividing by 2 on both sides:
x = (80/7) ÷ 2
x = 40/7
Substituting the value of x in equation (1):
40/7 - y = 10
Simplifying the equation:
y = 40/7 - 70/7
y = -30/7
Since speed cannot be negative, we take the positive value:
y = 30/7
Therefore, the speed of the trucks are:
Truck 1: x = 40/7 km/hr
Truck 2: y = 30/7 km/hr
So, the correct answer is option (b) 40 km/hr and 30 km/hr.
How many values of c, for which the system of equations 6x + 3y = c – 3, 12x + cy = c has infinitely many solutions?- a)1
- b)2
- c)3
- d)Infinite
Correct answer is option 'A'. Can you explain this answer?
How many values of c, for which the system of equations 6x + 3y = c – 3, 12x + cy = c has infinitely many solutions?
a)
1
b)
2
c)
3
d)
Infinite
|
|
Abhi verma answered |
The question seems to be incomplete. Could you please provide the complete system of equations?
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. What is the fraction?- a)2/7
- b)3/7
- c)5/7
- d)1/7
Correct answer is option 'C'. Can you explain this answer?
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. What is the fraction?
a)
2/7
b)
3/7
c)
5/7
d)
1/7
|
|
Ritu Saxena answered |
Let the fraction be x/y
then x + y = 12 .....(1)
and
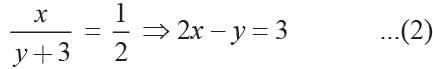
By solving eqn (1) and (2), we get x = 5, y = 7
x/y = 5/7
then x + y = 12 .....(1)
and
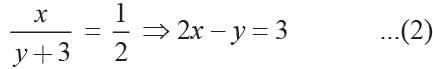
By solving eqn (1) and (2), we get x = 5, y = 7
x/y = 5/7
Rajesh scored 40 marks on a test getting 3 marks for each right answer and losing one mark for each wrong answer. If 4 marks have been awarded for each correct answer and 2 marks have been deducted for each incorrect answer then Rajesh will score 50 marks. What is the number of questions in the test?- a)30
- b)20
- c)15
- d)40
Correct answer is option 'B'. Can you explain this answer?
Rajesh scored 40 marks on a test getting 3 marks for each right answer and losing one mark for each wrong answer. If 4 marks have been awarded for each correct answer and 2 marks have been deducted for each incorrect answer then Rajesh will score 50 marks. What is the number of questions in the test?
a)
30
b)
20
c)
15
d)
40
|
|
Anjali rao answered |
Given:
- Rajesh scored 40 marks on the test.
- He gets 3 marks for each right answer and loses 1 mark for each wrong answer.
- If 4 marks were awarded for each correct answer and 2 marks were deducted for each incorrect answer, Rajesh would score 50 marks.
To find: The number of questions in the test.
Assumption:
Let's assume the number of questions in the test as 'x'.
Solution:
1. Calculating score based on the given information:
- According to the given information, Rajesh scored 40 marks on the test.
- For each right answer, he gets 3 marks, so the total marks scored for all the right answers would be 3 * (number of right answers).
- For each wrong answer, he loses 1 mark, so the total marks deducted for all the wrong answers would be 1 * (number of wrong answers).
- Therefore, we can write the equation as: 3 * (number of right answers) - 1 * (number of wrong answers) = 40.
2. Calculating score based on the alternative scenario:
- According to the alternative scenario, if 4 marks were awarded for each correct answer and 2 marks were deducted for each incorrect answer, Rajesh would score 50 marks.
- For each correct answer, he gets 4 marks, so the total marks scored for all the correct answers would be 4 * (number of correct answers).
- For each incorrect answer, he loses 2 marks, so the total marks deducted for all the incorrect answers would be 2 * (number of incorrect answers).
- Therefore, we can write the equation as: 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50.
3. Solving the equations:
- We have two equations:
1) 3 * (number of right answers) - 1 * (number of wrong answers) = 40
2) 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50
- If we simplify both equations, we get:
1) 3 * (number of right answers) - (number of wrong answers) = 40
2) 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50
- We can multiply equation 1 by 2 to eliminate the negative sign:
2 * (3 * (number of right answers) - (number of wrong answers)) = 2 * 40
Simplifying it, we get: 6 * (number of right answers) - 2 * (number of wrong answers) = 80
- Now, we have two equations:
1) 6 * (number of right answers) - 2 * (number of wrong answers) = 80
2) 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50
- If we compare both equations, we can see that they are the same.
- Therefore, we can conclude that the number of right answers is equal to the number of correct answers and the number of wrong answers is
- Rajesh scored 40 marks on the test.
- He gets 3 marks for each right answer and loses 1 mark for each wrong answer.
- If 4 marks were awarded for each correct answer and 2 marks were deducted for each incorrect answer, Rajesh would score 50 marks.
To find: The number of questions in the test.
Assumption:
Let's assume the number of questions in the test as 'x'.
Solution:
1. Calculating score based on the given information:
- According to the given information, Rajesh scored 40 marks on the test.
- For each right answer, he gets 3 marks, so the total marks scored for all the right answers would be 3 * (number of right answers).
- For each wrong answer, he loses 1 mark, so the total marks deducted for all the wrong answers would be 1 * (number of wrong answers).
- Therefore, we can write the equation as: 3 * (number of right answers) - 1 * (number of wrong answers) = 40.
2. Calculating score based on the alternative scenario:
- According to the alternative scenario, if 4 marks were awarded for each correct answer and 2 marks were deducted for each incorrect answer, Rajesh would score 50 marks.
- For each correct answer, he gets 4 marks, so the total marks scored for all the correct answers would be 4 * (number of correct answers).
- For each incorrect answer, he loses 2 marks, so the total marks deducted for all the incorrect answers would be 2 * (number of incorrect answers).
- Therefore, we can write the equation as: 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50.
3. Solving the equations:
- We have two equations:
1) 3 * (number of right answers) - 1 * (number of wrong answers) = 40
2) 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50
- If we simplify both equations, we get:
1) 3 * (number of right answers) - (number of wrong answers) = 40
2) 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50
- We can multiply equation 1 by 2 to eliminate the negative sign:
2 * (3 * (number of right answers) - (number of wrong answers)) = 2 * 40
Simplifying it, we get: 6 * (number of right answers) - 2 * (number of wrong answers) = 80
- Now, we have two equations:
1) 6 * (number of right answers) - 2 * (number of wrong answers) = 80
2) 4 * (number of correct answers) - 2 * (number of incorrect answers) = 50
- If we compare both equations, we can see that they are the same.
- Therefore, we can conclude that the number of right answers is equal to the number of correct answers and the number of wrong answers is
The length of a field exceeds its breadth by 3 meters. If the length is increased by 3 meters and the breadth is decreased by 2 meters. The area remains the same. What are the length and breadth respectively of the field?- a)15 m, 12 m
- b)12 m, 15 m
- c)18 m, 10 m
- d)10 m , 18 m
Correct answer is option 'B'. Can you explain this answer?
The length of a field exceeds its breadth by 3 meters. If the length is increased by 3 meters and the breadth is decreased by 2 meters. The area remains the same. What are the length and breadth respectively of the field?
a)
15 m, 12 m
b)
12 m, 15 m
c)
18 m, 10 m
d)
10 m , 18 m
|
|
Bhoomika patil answered |
Understanding the Problem
To solve the problem, we need to find the length and breadth of a field where:
- The length exceeds the breadth by 3 meters.
- If the length is increased by 3 meters and the breadth is decreased by 2 meters, the area remains the same.
Setting Up Equations
1. Let the breadth be 'b' meters.
2. Then, the length will be 'b + 3' meters.
Original Area Calculation
- The original area (A) of the field can be expressed as:
- A = Length × Breadth
- A = (b + 3) × b
Modified Area Calculation
- After the changes in dimensions, the new length and breadth become:
- New Length = (b + 3 + 3) = (b + 6) meters
- New Breadth = (b - 2) meters
- The area remains the same, so:
- A = (b + 6) × (b - 2)
Setting Areas Equal
Now, we set the original area equal to the modified area:
- (b + 3) × b = (b + 6) × (b - 2)
Expanding and Simplifying
1. Expanding both sides:
- b^2 + 3b = b^2 + 6b - 2b - 12
- b^2 + 3b = b^2 + 4b - 12
2. Cancel b^2 from both sides:
- 3b = 4b - 12
3. Rearranging gives:
- b = 12
Finding Length
- Now substituting b back to find the length:
- Length = b + 3 = 12 + 3 = 15 meters.
Final Dimensions
- Therefore, the length and breadth of the field are:
- Length = 15 m
- Breadth = 12 m
Thus, the correct answer is option 'B': 12 m (breadth) and 15 m (length).
To solve the problem, we need to find the length and breadth of a field where:
- The length exceeds the breadth by 3 meters.
- If the length is increased by 3 meters and the breadth is decreased by 2 meters, the area remains the same.
Setting Up Equations
1. Let the breadth be 'b' meters.
2. Then, the length will be 'b + 3' meters.
Original Area Calculation
- The original area (A) of the field can be expressed as:
- A = Length × Breadth
- A = (b + 3) × b
Modified Area Calculation
- After the changes in dimensions, the new length and breadth become:
- New Length = (b + 3 + 3) = (b + 6) meters
- New Breadth = (b - 2) meters
- The area remains the same, so:
- A = (b + 6) × (b - 2)
Setting Areas Equal
Now, we set the original area equal to the modified area:
- (b + 3) × b = (b + 6) × (b - 2)
Expanding and Simplifying
1. Expanding both sides:
- b^2 + 3b = b^2 + 6b - 2b - 12
- b^2 + 3b = b^2 + 4b - 12
2. Cancel b^2 from both sides:
- 3b = 4b - 12
3. Rearranging gives:
- b = 12
Finding Length
- Now substituting b back to find the length:
- Length = b + 3 = 12 + 3 = 15 meters.
Final Dimensions
- Therefore, the length and breadth of the field are:
- Length = 15 m
- Breadth = 12 m
Thus, the correct answer is option 'B': 12 m (breadth) and 15 m (length).
The student of a class are made to stand in rows. If 4 students are extra in each row, there would be 2 rows less. If 4 students are less to each row, there would be 4 rows more. What is the number of students in the class?- a)96
- b)106
- c)86
- d)116
Correct answer is option 'A'. Can you explain this answer?
The student of a class are made to stand in rows. If 4 students are extra in each row, there would be 2 rows less. If 4 students are less to each row, there would be 4 rows more. What is the number of students in the class?
a)
96
b)
106
c)
86
d)
116
|
|
Ritu Saxena answered |
Let the number of rows be x and the number of students in each row be y.
Total number of students = xy
(x - 2) (y + 4) = xy
⇒ xy + 4x - 2y - 8 = xy
⇒ 4x - 2y = 8 ...(1)
and (x + 4) (y - 4) = xy
xy - 4x + 4y - 16 = xy
⇒ -4x + 4y = 16 ...(2)
From eqn. (1) and (2)
4x - 2y - 4x + 4y = 24
2y = 24 ⇒ y = 12
and 4x - 2 × 12 = 8
⇒ 4x = 8 + 24 = 32 ⇒ x = 8
Total no. of students = 12 × 8 = 96.
Total number of students = xy
(x - 2) (y + 4) = xy
⇒ xy + 4x - 2y - 8 = xy
⇒ 4x - 2y = 8 ...(1)
and (x + 4) (y - 4) = xy
xy - 4x + 4y - 16 = xy
⇒ -4x + 4y = 16 ...(2)
From eqn. (1) and (2)
4x - 2y - 4x + 4y = 24
2y = 24 ⇒ y = 12
and 4x - 2 × 12 = 8
⇒ 4x = 8 + 24 = 32 ⇒ x = 8
Total no. of students = 12 × 8 = 96.
The sum of the digits of a two-digit number is 12. The number obtained by interchanging the two digits exceeds the given number by 18. Find the number.- a)57
- b)75
- c)85
- d)58
Correct answer is option 'A'. Can you explain this answer?
The sum of the digits of a two-digit number is 12. The number obtained by interchanging the two digits exceeds the given number by 18. Find the number.
a)
57
b)
75
c)
85
d)
58
|
|
Ritu Saxena answered |
Let the unit’s and ten’s digits in the number be y and x respectively.
So, the number be 10x + y.
According to the question, x + y = 12
Also, 10x + y + 18 = 10y + x
⇒ 9x – 9y = –18 ⇒ x – y = –2
Solving (1) and (2), we get x = 5 and y = 7
∴ Required number is 57.
So, the number be 10x + y.
According to the question, x + y = 12
Also, 10x + y + 18 = 10y + x
⇒ 9x – 9y = –18 ⇒ x – y = –2
Solving (1) and (2), we get x = 5 and y = 7
∴ Required number is 57.
At the end of the year 2002, Ram was half as old as his grandpa. The sum of the years in which they were born is 3854. Age of Ram at the end of year 2003 is _______.- a)50 years
- b)35 years
- c)51 years
- d)36 years
Correct answer is option 'C'. Can you explain this answer?
At the end of the year 2002, Ram was half as old as his grandpa. The sum of the years in which they were born is 3854. Age of Ram at the end of year 2003 is _______.
a)
50 years
b)
35 years
c)
51 years
d)
36 years
|
|
Subham Ghosh answered |
Given:
- At the end of the year 2002, Ram was half as old as his grandpa.
- The sum of the years in which they were born is 3854.
To find:
Age of Ram at the end of year 2003.
Solution:
Let's assume the current year is "x".
1. Age of Ram and his grandpa in the year 2002:
- In the year 2002, Ram's age = (x - 2002) years
- In the year 2002, Grandpa's age = (x - 2002) * 2 years (as Ram was half as old as his grandpa)
2. Year of Birth:
- Ram's year of birth = x - (x - 2002) = 2002
- Grandpa's year of birth = x - ((x - 2002) * 2) = 2002 - (x - 2002) = 4004 - x
3. Sum of the years in which they were born:
- Ram's year of birth + Grandpa's year of birth = 3854
- 2002 + (4004 - x) = 3854
- 6006 - x = 3854
- x = 6006 - 3854
- x = 2152
4. Age of Ram in the year 2003:
- Ram's age in the year 2003 = (x - 2003) - (x - 2002)
- Ram's age in the year 2003 = 2152 - 2003
- Ram's age in the year 2003 = 149 years
Therefore, the age of Ram at the end of the year 2003 is 149 years (Option B).
- At the end of the year 2002, Ram was half as old as his grandpa.
- The sum of the years in which they were born is 3854.
To find:
Age of Ram at the end of year 2003.
Solution:
Let's assume the current year is "x".
1. Age of Ram and his grandpa in the year 2002:
- In the year 2002, Ram's age = (x - 2002) years
- In the year 2002, Grandpa's age = (x - 2002) * 2 years (as Ram was half as old as his grandpa)
2. Year of Birth:
- Ram's year of birth = x - (x - 2002) = 2002
- Grandpa's year of birth = x - ((x - 2002) * 2) = 2002 - (x - 2002) = 4004 - x
3. Sum of the years in which they were born:
- Ram's year of birth + Grandpa's year of birth = 3854
- 2002 + (4004 - x) = 3854
- 6006 - x = 3854
- x = 6006 - 3854
- x = 2152
4. Age of Ram in the year 2003:
- Ram's age in the year 2003 = (x - 2003) - (x - 2002)
- Ram's age in the year 2003 = 2152 - 2003
- Ram's age in the year 2003 = 149 years
Therefore, the age of Ram at the end of the year 2003 is 149 years (Option B).
If the system of equations
2x + 3y = 7
2ax + (a + b)y = 28
has infinitely many solutions, then the values of a and b respectively are _______.- a)2, 5
- b)5, 8
- c)4, 8
- d)3, 6
Correct answer is option 'C'. Can you explain this answer?
If the system of equations
2x + 3y = 7
2ax + (a + b)y = 28
has infinitely many solutions, then the values of a and b respectively are _______.
2x + 3y = 7
2ax + (a + b)y = 28
has infinitely many solutions, then the values of a and b respectively are _______.
a)
2, 5
b)
5, 8
c)
4, 8
d)
3, 6
|
|
Vivek Bansal answered |
Given equations are
2x + 3y = 7 and 2ax + (a + b)y = 28
For infinitely many solutions, we have
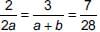
Taking first two members, we get 2a + 2b = 6a
⇒ 4a = 2b ⇒ 2a = b ...(1)
Also,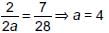 ...(2)
...(2)
From (1) and (2), we have
2(4) = b ⇒ b = 8
2x + 3y = 7 and 2ax + (a + b)y = 28
For infinitely many solutions, we have
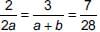
Taking first two members, we get 2a + 2b = 6a
⇒ 4a = 2b ⇒ 2a = b ...(1)
Also,
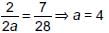 ...(2)
...(2)From (1) and (2), we have
2(4) = b ⇒ b = 8
Arun and Prabhat have some books with them. Once Prabhat said to Arun that, if Arun gives 3 books to Prabhat then Arun will have only 1/2 of the books that Prabhat will have with him. Then Arun asked frankly that if Prabhat gives him only two books (to Arun), then Prabhat will have as many books as Arun will have. The total number of books that Arun and Prabhat have with them is _______.- a)25
- b)56
- c)30
- d)Can’t be determined
Correct answer is option 'C'. Can you explain this answer?
Arun and Prabhat have some books with them. Once Prabhat said to Arun that, if Arun gives 3 books to Prabhat then Arun will have only 1/2 of the books that Prabhat will have with him. Then Arun asked frankly that if Prabhat gives him only two books (to Arun), then Prabhat will have as many books as Arun will have. The total number of books that Arun and Prabhat have with them is _______.
a)
25
b)
56
c)
30
d)
Can’t be determined
|
|
Prabhat mehta answered |
Let's assume Arun has A books and Prabhat has P books.
According to the first statement, if Arun gives 3 books to Prabhat, Arun will have 1/2 of the books that Prabhat will have. So we can write this as:
A - 3 = (1/2)(P + 3)
Simplifying this equation, we get:
2A - 6 = P + 3
2A - P = 9 ----(1)
According to the second statement, if Prabhat gives 2 books to Arun, Prabhat will have the same number of books as Arun. So we can write this as:
P - 2 = A
P = A + 2 ----(2)
Now we can substitute equation (2) into equation (1):
2A - (A + 2) = 9
A - 2 = 9
A = 11
Substituting A = 11 into equation (2), we get:
P = 11 + 2
P = 13
Therefore, Arun has 11 books and Prabhat has 13 books.
The total number of books they have is:
11 + 13 = 24
So the answer is not among the options given.
According to the first statement, if Arun gives 3 books to Prabhat, Arun will have 1/2 of the books that Prabhat will have. So we can write this as:
A - 3 = (1/2)(P + 3)
Simplifying this equation, we get:
2A - 6 = P + 3
2A - P = 9 ----(1)
According to the second statement, if Prabhat gives 2 books to Arun, Prabhat will have the same number of books as Arun. So we can write this as:
P - 2 = A
P = A + 2 ----(2)
Now we can substitute equation (2) into equation (1):
2A - (A + 2) = 9
A - 2 = 9
A = 11
Substituting A = 11 into equation (2), we get:
P = 11 + 2
P = 13
Therefore, Arun has 11 books and Prabhat has 13 books.
The total number of books they have is:
11 + 13 = 24
So the answer is not among the options given.
A three digit number abc is 459 more than the sum of its digits. What is the sum of the 2 digit number ab and the 1-digit number a?- a)37
- b)73
- c)51
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
A three digit number abc is 459 more than the sum of its digits. What is the sum of the 2 digit number ab and the 1-digit number a?
a)
37
b)
73
c)
51
d)
Cannot be determined
|
|
Arjun Rane answered |
Given: A three-digit number abc is 459 more than the sum of its digits.
Let's represent the number abc as 100a + 10b + c.
According to the given information, we have:
100a + 10b + c = a + b + c + 459
Simplifying this equation, we get:
99a + 9b = 459
Dividing both sides by 9, we get:
11a + b = 51
We can see that a and b are two-digit numbers that add up to 51. The only possible values for a and b are 4 and 7, respectively.
Therefore, ab = 47 and a = 4.
The sum of ab and a is 4 + 47 = 51.
Hence, the correct answer is option (c) 51.
Summary:
- We are given a three-digit number abc that is 459 more than the sum of its digits.
- Writing abc as 100a + 10b + c and simplifying the equation, we get 11a + b = 51.
- The only possible values for a and b are 4 and 7, respectively.
- Therefore, ab = 47 and a = 4.
- The sum of ab and a is 4 + 47 = 51.
- Hence, the correct answer is option (c) 51.
Let's represent the number abc as 100a + 10b + c.
According to the given information, we have:
100a + 10b + c = a + b + c + 459
Simplifying this equation, we get:
99a + 9b = 459
Dividing both sides by 9, we get:
11a + b = 51
We can see that a and b are two-digit numbers that add up to 51. The only possible values for a and b are 4 and 7, respectively.
Therefore, ab = 47 and a = 4.
The sum of ab and a is 4 + 47 = 51.
Hence, the correct answer is option (c) 51.
Summary:
- We are given a three-digit number abc that is 459 more than the sum of its digits.
- Writing abc as 100a + 10b + c and simplifying the equation, we get 11a + b = 51.
- The only possible values for a and b are 4 and 7, respectively.
- Therefore, ab = 47 and a = 4.
- The sum of ab and a is 4 + 47 = 51.
- Hence, the correct answer is option (c) 51.
Five years ago, Ram was thrice as old as Mohan. Ten years later Ram shall be twice as old as Mohan. What is the present age of Ram and Mohan?- a)50 years, 20 years
- b)56 years, 24 years
- c)50 years, 24 years
- d)56 years, 20 years
Correct answer is option 'A'. Can you explain this answer?
Five years ago, Ram was thrice as old as Mohan. Ten years later Ram shall be twice as old as Mohan. What is the present age of Ram and Mohan?
a)
50 years, 20 years
b)
56 years, 24 years
c)
50 years, 24 years
d)
56 years, 20 years
|
|
Akshara kulkarni answered |
Problem: Five years ago, Ram was thrice as old as Mohan. Ten years later Ram shall be twice as old as Mohan. What is the present age of Ram and Mohan?
Solution:
Let the present age of Ram and Mohan be R and M years respectively.
Five years ago,
Ram's age = R - 5,
Mohan's age = M - 5.
According to the problem,
(R - 5) = 3(M - 5) ...(1) [Five years ago, Ram was thrice as old as Mohan]
R + 10 = 2(M + 10) ...(2) [Ten years later Ram shall be twice as old as Mohan]
Solving equations (1) and (2), we get
R - 3M = -10 ...(3)
R - 2M = 10 ...(4)
Subtracting equation (4) from equation (3), we get
(-3M) - (-2M) = -10 - 10
-M = -20
Therefore, M = 20.
Putting this value of M in equation (4), we get
R - 2(20) = 10
R = 50
Hence, the present age of Ram is 50 years and the present age of Mohan is 20 years.
Therefore, the correct answer is option (a) 50 years, 20 years.
Solution:
Let the present age of Ram and Mohan be R and M years respectively.
Five years ago,
Ram's age = R - 5,
Mohan's age = M - 5.
According to the problem,
(R - 5) = 3(M - 5) ...(1) [Five years ago, Ram was thrice as old as Mohan]
R + 10 = 2(M + 10) ...(2) [Ten years later Ram shall be twice as old as Mohan]
Solving equations (1) and (2), we get
R - 3M = -10 ...(3)
R - 2M = 10 ...(4)
Subtracting equation (4) from equation (3), we get
(-3M) - (-2M) = -10 - 10
-M = -20
Therefore, M = 20.
Putting this value of M in equation (4), we get
R - 2(20) = 10
R = 50
Hence, the present age of Ram is 50 years and the present age of Mohan is 20 years.
Therefore, the correct answer is option (a) 50 years, 20 years.
What is the value of k except which the given system of equations has a unique solution?
2x + 3y - 5 = 0 and kx - 6y - 8 = 0- a)4
- b)-4
- c)2
- d)3
Correct answer is option 'B'. Can you explain this answer?
What is the value of k except which the given system of equations has a unique solution?
2x + 3y - 5 = 0 and kx - 6y - 8 = 0
2x + 3y - 5 = 0 and kx - 6y - 8 = 0
a)
4
b)
-4
c)
2
d)
3
|
|
Alisha nayar answered |
To find the value of k for which the given system of equations has a unique solution, we can use the concept of determinants.
The given system of equations is:
2x + 3y - 5 = 0
kx - 6y - 8 = 0
We can rewrite the equations in the form Ax + By + C = 0, where A, B, and C are the coefficients of x, y, and the constant term respectively.
The given system can be rewritten as:
2x + 3y = 5
kx - 6y = 8
Now, let's write the coefficients of x, y, and the constant term in matrix form.
The coefficient matrix, A, is:
| 2 3 |
| k -6 |
Next, we need to find the determinant of A, denoted as |A|.
|A| = (2)(-6) - (3)(k)
= -12 - 3k
= -3k - 12
For the given system of equations to have a unique solution, the determinant |A| must be non-zero. In other words, -3k - 12 ≠ 0.
Solving the inequality -3k - 12 ≠ 0, we have:
-3k ≠ 12
k ≠ -4
Therefore, the value of k except -4 will give the given system of equations a unique solution.
Hence, the correct answer is option B) -4.
The given system of equations is:
2x + 3y - 5 = 0
kx - 6y - 8 = 0
We can rewrite the equations in the form Ax + By + C = 0, where A, B, and C are the coefficients of x, y, and the constant term respectively.
The given system can be rewritten as:
2x + 3y = 5
kx - 6y = 8
Now, let's write the coefficients of x, y, and the constant term in matrix form.
The coefficient matrix, A, is:
| 2 3 |
| k -6 |
Next, we need to find the determinant of A, denoted as |A|.
|A| = (2)(-6) - (3)(k)
= -12 - 3k
= -3k - 12
For the given system of equations to have a unique solution, the determinant |A| must be non-zero. In other words, -3k - 12 ≠ 0.
Solving the inequality -3k - 12 ≠ 0, we have:
-3k ≠ 12
k ≠ -4
Therefore, the value of k except -4 will give the given system of equations a unique solution.
Hence, the correct answer is option B) -4.
If am = bl and bn ≠ cm, then the system of equations
ax + by = c
lx + my = n- a)Has a unique solution.
- b)Has no solution.
- c)Has infinitely many solutions.
- d)May or may not have a solution.
Correct answer is option 'B'. Can you explain this answer?
If am = bl and bn ≠ cm, then the system of equations
ax + by = c
lx + my = n
ax + by = c
lx + my = n
a)
Has a unique solution.
b)
Has no solution.
c)
Has infinitely many solutions.
d)
May or may not have a solution.
|
|
Vivek Bansal answered |
We have, ax + by = c and lx + my = n
Now,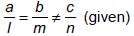
∴ The given system of equations has no solution.
Now,
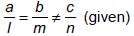
∴ The given system of equations has no solution.
On selling a tea-set at 5% loss and lemonset at 15% gain, a crockery seller gains ₹ 7. If he sells the tea-set at 5% gain and the lemon-set at 10% gain, he gains ₹ 13. Find the actual prices of the tea-set and the lemon-set.- a)₹ 100, ₹ 80
- b)₹ 90, ₹ 100
- c)₹ 120, ₹ 60
- d)₹ 150, ₹ 80
Correct answer is option 'A'. Can you explain this answer?
On selling a tea-set at 5% loss and lemonset at 15% gain, a crockery seller gains ₹ 7. If he sells the tea-set at 5% gain and the lemon-set at 10% gain, he gains ₹ 13. Find the actual prices of the tea-set and the lemon-set.
a)
₹ 100, ₹ 80
b)
₹ 90, ₹ 100
c)
₹ 120, ₹ 60
d)
₹ 150, ₹ 80
|
|
Aashi iyer answered |
Let's assume the cost price of the tea-set is x and the cost price of the lemon-set is y.
Selling at Loss and Gain
When the tea-set is sold at a 5% loss, the selling price becomes 0.95x. On the other hand, when the lemon-set is sold at a 15% gain, the selling price becomes 1.15y. The total gain from these sales is 7.
Selling at Gain and Gain
When the tea-set is sold at a 5% gain, the selling price becomes 1.05x. Similarly, when the lemon-set is sold at a 10% gain, the selling price becomes 1.10y. The total gain from these sales is 13.
Forming Equations
We can form the following equations based on the given information:
0.95x + 1.15y = x + y + 7 (Equation 1)
1.05x + 1.10y = x + y + 13 (Equation 2)
Simplifying the Equations
We can simplify Equation 1 by subtracting x and y from both sides:
0.95x - x + 1.15y - y = 7
-0.05x + 0.15y = 7 (Equation 3)
Similarly, we can simplify Equation 2 by subtracting x and y from both sides:
1.05x - x + 1.10y - y = 13
0.05x + 0.10y = 13 (Equation 4)
Solving the Equations
Now, we can solve Equations 3 and 4 simultaneously to find the values of x and y.
Multiplying Equation 3 by 20 and Equation 4 by 100 to eliminate decimals:
-1x + 3y = 140 (Equation 5)
5x + 10y = 1300 (Equation 6)
Multiplying Equation 5 by 5 and Equation 6 by 1 to make the coefficients of x equal:
-5x + 15y = 700 (Equation 7)
5x + 10y = 1300 (Equation 6)
Adding Equations 7 and 6:
25y = 2000
y = 80
Substituting the value of y in Equation 5:
-1x + 3(80) = 140
-1x + 240 = 140
-1x = -100
x = 100
Therefore, the cost price of the tea-set is 100 and the cost price of the lemon-set is 80. Thus, option A is correct.
Selling at Loss and Gain
When the tea-set is sold at a 5% loss, the selling price becomes 0.95x. On the other hand, when the lemon-set is sold at a 15% gain, the selling price becomes 1.15y. The total gain from these sales is 7.
Selling at Gain and Gain
When the tea-set is sold at a 5% gain, the selling price becomes 1.05x. Similarly, when the lemon-set is sold at a 10% gain, the selling price becomes 1.10y. The total gain from these sales is 13.
Forming Equations
We can form the following equations based on the given information:
0.95x + 1.15y = x + y + 7 (Equation 1)
1.05x + 1.10y = x + y + 13 (Equation 2)
Simplifying the Equations
We can simplify Equation 1 by subtracting x and y from both sides:
0.95x - x + 1.15y - y = 7
-0.05x + 0.15y = 7 (Equation 3)
Similarly, we can simplify Equation 2 by subtracting x and y from both sides:
1.05x - x + 1.10y - y = 13
0.05x + 0.10y = 13 (Equation 4)
Solving the Equations
Now, we can solve Equations 3 and 4 simultaneously to find the values of x and y.
Multiplying Equation 3 by 20 and Equation 4 by 100 to eliminate decimals:
-1x + 3y = 140 (Equation 5)
5x + 10y = 1300 (Equation 6)
Multiplying Equation 5 by 5 and Equation 6 by 1 to make the coefficients of x equal:
-5x + 15y = 700 (Equation 7)
5x + 10y = 1300 (Equation 6)
Adding Equations 7 and 6:
25y = 2000
y = 80
Substituting the value of y in Equation 5:
-1x + 3(80) = 140
-1x + 240 = 140
-1x = -100
x = 100
Therefore, the cost price of the tea-set is 100 and the cost price of the lemon-set is 80. Thus, option A is correct.
A railway half ticket cost half the full fare and the reservation charge is the same on a half ticket as on a full ticket. one reserved first-class ticket from Delhi to Patna costs ₹ 216. One full and one half reserved first-class ticket cost ₹ 328. What is the reservation charge?- a)₹ 16
- b)₹ 26
- c)₹ 6
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A railway half ticket cost half the full fare and the reservation charge is the same on a half ticket as on a full ticket. one reserved first-class ticket from Delhi to Patna costs ₹ 216. One full and one half reserved first-class ticket cost ₹ 328. What is the reservation charge?
a)
₹ 16
b)
₹ 26
c)
₹ 6
d)
None of these
|
|
Ritu Saxena answered |
Let ₹ x be the charge of full first-class ticket and ₹ y be reservation charge.
x + y = 216 ...(1)
x + y + x/2 + y = 327
⇒ 3x + 4y = 654 ...(2)
By solving eqns (1) and (2), we get
x = 210, y = 6
x + y = 216 ...(1)
x + y + x/2 + y = 327
⇒ 3x + 4y = 654 ...(2)
By solving eqns (1) and (2), we get
x = 210, y = 6
The denominator of a rational number is greater than its numerator by 3. If 3 is subtracted from the numerator and 2 is added to the denominator, the new number becomes 1/5. Then the original number was _______.- a)7/11
- b)3/5
- c)5/8
- d)4/7
Correct answer is option 'C'. Can you explain this answer?
The denominator of a rational number is greater than its numerator by 3. If 3 is subtracted from the numerator and 2 is added to the denominator, the new number becomes 1/5. Then the original number was _______.
a)
7/11
b)
3/5
c)
5/8
d)
4/7
|
|
Sudeep rane answered |
To solve this problem, let's first assign variables to the numerator and the denominator of the original rational number.
Let the numerator be x.
Then, the denominator is x + 3, as stated in the problem.
According to the given information, if 3 is subtracted from the numerator and 2 is added to the denominator, the new number becomes 1/5.
So, the new numerator is x - 3 and the new denominator is x + 3 + 2 = x + 5.
We can write this as an equation:
(x - 3)/(x + 5) = 1/5
To solve this equation, we can cross-multiply:
5(x - 3) = (x + 5)
Simplifying the equation:
5x - 15 = x + 5
Subtracting x from both sides:
4x - 15 = 5
Adding 15 to both sides:
4x = 20
Dividing both sides by 4:
x = 5
So, the numerator of the original rational number is 5.
Substituting this value back into the equation for the denominator:
x + 3 = 5 + 3 = 8
Therefore, the denominator of the original rational number is 8.
Hence, the original number is 5/8.
Therefore, the correct answer is option C) 5/8.
Let the numerator be x.
Then, the denominator is x + 3, as stated in the problem.
According to the given information, if 3 is subtracted from the numerator and 2 is added to the denominator, the new number becomes 1/5.
So, the new numerator is x - 3 and the new denominator is x + 3 + 2 = x + 5.
We can write this as an equation:
(x - 3)/(x + 5) = 1/5
To solve this equation, we can cross-multiply:
5(x - 3) = (x + 5)
Simplifying the equation:
5x - 15 = x + 5
Subtracting x from both sides:
4x - 15 = 5
Adding 15 to both sides:
4x = 20
Dividing both sides by 4:
x = 5
So, the numerator of the original rational number is 5.
Substituting this value back into the equation for the denominator:
x + 3 = 5 + 3 = 8
Therefore, the denominator of the original rational number is 8.
Hence, the original number is 5/8.
Therefore, the correct answer is option C) 5/8.
Value of x in pair of linear equations 36x + 24y = 702 and 24x + 36y = 558 is- a)33/2
- b)145/7
- c)16
- d)17
Correct answer is option 'A'. Can you explain this answer?
Value of x in pair of linear equations 36x + 24y = 702 and 24x + 36y = 558 is
a)
33/2
b)
145/7
c)
16
d)
17
|
|
Priyanka Kapoor answered |
We have, 36x + 24y = 702
and 24x + 36y = 558
Simplifying above equations, we get
6x + 4y = 117 ...(1) and 4x + 6y = 93 ...(2)
Multiplying eq. (1) by 3, eq. (2) by –2 and then adding, we get 18x + 12y – 8x – 12y = 351 – 186
⇒ 10x = 165 ⇒ x =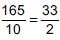
and 24x + 36y = 558
Simplifying above equations, we get
6x + 4y = 117 ...(1) and 4x + 6y = 93 ...(2)
Multiplying eq. (1) by 3, eq. (2) by –2 and then adding, we get 18x + 12y – 8x – 12y = 351 – 186
⇒ 10x = 165 ⇒ x =
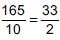
What are the values of m and n for which the system of linear equations has infinitely many solutions, 3x + 4y = 12, (m + n)x + 2(m - n)y = (5m - 1)?- a)m = 1, n = 1
- b)m = 5, n = +1
- c)m = 1, n = 5
- d)m = 5, n = 2
Correct answer is option 'B'. Can you explain this answer?
What are the values of m and n for which the system of linear equations has infinitely many solutions, 3x + 4y = 12, (m + n)x + 2(m - n)y = (5m - 1)?
a)
m = 1, n = 1
b)
m = 5, n = +1
c)
m = 1, n = 5
d)
m = 5, n = 2
|
|
Anjana shukla answered |
To determine the values of m and n for which the system of linear equations has infinitely many solutions, we need to solve the system of equations and analyze the conditions that lead to infinite solutions.
Given system of equations:
1) 3x + 4y = 12
2) (m - n)x + 2(m - n)y = (5m - 1)
Step 1: Simplify the equations
Equation 2 can be rewritten as:
(m - n)(x + 2y) = 5m - 1
Step 2: Check for parallel lines
For the system to have infinitely many solutions, the two equations must represent parallel lines. This means that their slopes should be equal. Since the given equations are in standard form, we can find the slopes by dividing the coefficients of x by the coefficients of y.
The slope of equation 1: m1 = -3/4
The slope of equation 2: m2 = (m - n)/2(m - n) = 1/2
Step 3: Set the slopes equal to each other
To find the values of m and n, we equate the slopes:
-3/4 = 1/2
Step 4: Solve for m and n
Cross multiply to solve for m and n:
-3 * 2 = 4 * 1
-6 = 4
Since -6 is not equal to 4, there is no solution for m and n that would make the slopes equal.
Step 5: Analyze the answer choices
Based on the analysis above, we can conclude that there are no values of m and n that would result in infinitely many solutions for the given system of equations. Therefore, none of the answer choices (A, B, C, D) are correct.
In conclusion, the correct answer is none of the above options.
Given system of equations:
1) 3x + 4y = 12
2) (m - n)x + 2(m - n)y = (5m - 1)
Step 1: Simplify the equations
Equation 2 can be rewritten as:
(m - n)(x + 2y) = 5m - 1
Step 2: Check for parallel lines
For the system to have infinitely many solutions, the two equations must represent parallel lines. This means that their slopes should be equal. Since the given equations are in standard form, we can find the slopes by dividing the coefficients of x by the coefficients of y.
The slope of equation 1: m1 = -3/4
The slope of equation 2: m2 = (m - n)/2(m - n) = 1/2
Step 3: Set the slopes equal to each other
To find the values of m and n, we equate the slopes:
-3/4 = 1/2
Step 4: Solve for m and n
Cross multiply to solve for m and n:
-3 * 2 = 4 * 1
-6 = 4
Since -6 is not equal to 4, there is no solution for m and n that would make the slopes equal.
Step 5: Analyze the answer choices
Based on the analysis above, we can conclude that there are no values of m and n that would result in infinitely many solutions for the given system of equations. Therefore, none of the answer choices (A, B, C, D) are correct.
In conclusion, the correct answer is none of the above options.
If three times the larger of two numbers is divided by the smaller one, we get 4 as quotient and 3 as remainder. If seven times the smaller number is divided by the larger one, we get 5 as the quotient and 1 as the remainder. What is the smaller number?- a)15
- b)20
- c)18
- d)25
Correct answer is option 'C'. Can you explain this answer?
If three times the larger of two numbers is divided by the smaller one, we get 4 as quotient and 3 as remainder. If seven times the smaller number is divided by the larger one, we get 5 as the quotient and 1 as the remainder. What is the smaller number?
a)
15
b)
20
c)
18
d)
25

|
Palak Roy answered |
Let's assume the two numbers as follows:
Smaller number = x
Larger number = y
According to the given information:
1) "Three times the larger of two numbers is divided by the smaller one, we get 4 as quotient and 3 as remainder."
This can be expressed as:
3y ÷ x = 4 + 3/x
2) "Seven times the smaller number is divided by the larger one, we get 5 as quotient and 1 as remainder."
This can be expressed as:
7x ÷ y = 5 + 1/y
To solve this problem, we will solve the two equations simultaneously.
Equation 1:
3y ÷ x = 4 + 3/x
Multiplying both sides by x:
3y = 4x + 3
Equation 2:
7x ÷ y = 5 + 1/y
Multiplying both sides by y:
7x = 5y + 1
Now, we have two equations:
3y = 4x + 3
7x = 5y + 1
Solving the two equations:
Multiply equation 1 by 5 and equation 2 by 4 to eliminate the coefficients of x and y:
15y = 20x + 15
28x = 20y + 4
Now, let's solve for x:
From equation 1, we have:
15y - 20x = 15 (Equation 3)
From equation 2, we have:
20y - 28x = -4 (Equation 4)
Multiply equation 3 by 2 and equation 4 by 3 to eliminate the coefficients of y and x:
30y - 40x = 30
60y - 84x = -12
Subtract equation 3 from equation 4:
60y - 84x - (30y - 40x) = -12 - 30
30y - 44x = -42 (Equation 5)
Now, let's solve equation 5 for x:
30y - 44x = -42
-44x = -30y - 42
44x = 30y + 42
11x = 7.5y + 10.5
Since the coefficients of x and y are not integers, we can conclude that this system of equations does not have an integer solution. Therefore, the given problem does not have a valid solution.
Smaller number = x
Larger number = y
According to the given information:
1) "Three times the larger of two numbers is divided by the smaller one, we get 4 as quotient and 3 as remainder."
This can be expressed as:
3y ÷ x = 4 + 3/x
2) "Seven times the smaller number is divided by the larger one, we get 5 as quotient and 1 as remainder."
This can be expressed as:
7x ÷ y = 5 + 1/y
To solve this problem, we will solve the two equations simultaneously.
Equation 1:
3y ÷ x = 4 + 3/x
Multiplying both sides by x:
3y = 4x + 3
Equation 2:
7x ÷ y = 5 + 1/y
Multiplying both sides by y:
7x = 5y + 1
Now, we have two equations:
3y = 4x + 3
7x = 5y + 1
Solving the two equations:
Multiply equation 1 by 5 and equation 2 by 4 to eliminate the coefficients of x and y:
15y = 20x + 15
28x = 20y + 4
Now, let's solve for x:
From equation 1, we have:
15y - 20x = 15 (Equation 3)
From equation 2, we have:
20y - 28x = -4 (Equation 4)
Multiply equation 3 by 2 and equation 4 by 3 to eliminate the coefficients of y and x:
30y - 40x = 30
60y - 84x = -12
Subtract equation 3 from equation 4:
60y - 84x - (30y - 40x) = -12 - 30
30y - 44x = -42 (Equation 5)
Now, let's solve equation 5 for x:
30y - 44x = -42
-44x = -30y - 42
44x = 30y + 42
11x = 7.5y + 10.5
Since the coefficients of x and y are not integers, we can conclude that this system of equations does not have an integer solution. Therefore, the given problem does not have a valid solution.
Which of the following linear equation coincide with the line 4x + 5y = 15?- a)8x + 10y = 25
- b)2x + 3y = 7
- c)7x + 14y = 17
- d)12x + 15y = 45
Correct answer is option 'D'. Can you explain this answer?
Which of the following linear equation coincide with the line 4x + 5y = 15?
a)
8x + 10y = 25
b)
2x + 3y = 7
c)
7x + 14y = 17
d)
12x + 15y = 45
|
|
Prabhat mehta answered |
To determine which of the given linear equations coincides with the line 4x + 5y = 15, we need to compare the equations by rearranging them into the standard form (Ax + By = C) and checking if the coefficients A, B, and C are the same.
Given equation: 4x + 5y = 15
Let's rearrange the equation:
4x + 5y = 15
5y = -4x + 15
y = (-4/5)x + 3
Now, let's compare this equation with the given options:
a) 8x + 10y = 25
Comparing the coefficients, we see that A = 8, B = 10, and C = 25. These coefficients are not the same as in the given equation, so option a) does not coincide with the line.
b) 2x + 3y = 7
Comparing the coefficients, we see that A = 2, B = 3, and C = 7. These coefficients are not the same as in the given equation, so option b) does not coincide with the line.
c) 7x + 14y = 17
Comparing the coefficients, we see that A = 7, B = 14, and C = 17. These coefficients are not the same as in the given equation, so option c) does not coincide with the line.
d) 12x + 15y = 45
Comparing the coefficients, we see that A = 12, B = 15, and C = 45. These coefficients are the same as in the given equation, so option d) coincides with the line.
Therefore, the correct answer is option d) 12x + 15y = 45.
Given equation: 4x + 5y = 15
Let's rearrange the equation:
4x + 5y = 15
5y = -4x + 15
y = (-4/5)x + 3
Now, let's compare this equation with the given options:
a) 8x + 10y = 25
Comparing the coefficients, we see that A = 8, B = 10, and C = 25. These coefficients are not the same as in the given equation, so option a) does not coincide with the line.
b) 2x + 3y = 7
Comparing the coefficients, we see that A = 2, B = 3, and C = 7. These coefficients are not the same as in the given equation, so option b) does not coincide with the line.
c) 7x + 14y = 17
Comparing the coefficients, we see that A = 7, B = 14, and C = 17. These coefficients are not the same as in the given equation, so option c) does not coincide with the line.
d) 12x + 15y = 45
Comparing the coefficients, we see that A = 12, B = 15, and C = 45. These coefficients are the same as in the given equation, so option d) coincides with the line.
Therefore, the correct answer is option d) 12x + 15y = 45.
A chemist has one solution containing 50% acid and a second one containing 25% acid. How much of each should be used respectively to make 10 litres of a 40% acid solution?- a)6 litres, 4 litres
- b)2 litres, 6 litres
- c)4 litres, 6 litres
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A chemist has one solution containing 50% acid and a second one containing 25% acid. How much of each should be used respectively to make 10 litres of a 40% acid solution?
a)
6 litres, 4 litres
b)
2 litres, 6 litres
c)
4 litres, 6 litres
d)
None of these
|
|
Sarangi sharma answered |
Understanding the Problem
To create a 10-litre solution with 40% acid, we need to combine two solutions: one that has 50% acid and another with 25% acid. We need to determine how much of each solution to mix.
Let’s Define the Variables
- Let x = litres of the 50% acid solution.
- Let y = litres of the 25% acid solution.
We know that:
- The total volume of the mixture: x + y = 10 litres.
Setting Up the Equations
To find the amount of acid in each solution:
- Acid from 50% solution: 0.50x
- Acid from 25% solution: 0.25y
We want the total acid to equal 40% of the final solution:
- Total acid in the mixture: 0.40 * 10 = 4 litres.
Thus, we can set up the second equation:
- 0.50x + 0.25y = 4 litres.
Solving the Equations
Now we have a system of equations:
1. x + y = 10
2. 0.50x + 0.25y = 4
We can solve the first equation for y:
- y = 10 - x.
Now substitute y in the second equation:
- 0.50x + 0.25(10 - x) = 4
This simplifies to:
- 0.50x + 2.5 - 0.25x = 4
Combine like terms:
- 0.25x + 2.5 = 4
Subtract 2.5 from both sides:
- 0.25x = 1.5
Multiply both sides by 4:
- x = 6 litres.
Now substitute back to find y:
- y = 10 - 6 = 4 litres.
Conclusion
Thus, the chemist should use:
- 6 litres of the 50% acid solution.
- 4 litres of the 25% acid solution.
The correct option is a) 6 litres, 4 litres.
To create a 10-litre solution with 40% acid, we need to combine two solutions: one that has 50% acid and another with 25% acid. We need to determine how much of each solution to mix.
Let’s Define the Variables
- Let x = litres of the 50% acid solution.
- Let y = litres of the 25% acid solution.
We know that:
- The total volume of the mixture: x + y = 10 litres.
Setting Up the Equations
To find the amount of acid in each solution:
- Acid from 50% solution: 0.50x
- Acid from 25% solution: 0.25y
We want the total acid to equal 40% of the final solution:
- Total acid in the mixture: 0.40 * 10 = 4 litres.
Thus, we can set up the second equation:
- 0.50x + 0.25y = 4 litres.
Solving the Equations
Now we have a system of equations:
1. x + y = 10
2. 0.50x + 0.25y = 4
We can solve the first equation for y:
- y = 10 - x.
Now substitute y in the second equation:
- 0.50x + 0.25(10 - x) = 4
This simplifies to:
- 0.50x + 2.5 - 0.25x = 4
Combine like terms:
- 0.25x + 2.5 = 4
Subtract 2.5 from both sides:
- 0.25x = 1.5
Multiply both sides by 4:
- x = 6 litres.
Now substitute back to find y:
- y = 10 - 6 = 4 litres.
Conclusion
Thus, the chemist should use:
- 6 litres of the 50% acid solution.
- 4 litres of the 25% acid solution.
The correct option is a) 6 litres, 4 litres.
In a cyclic quadrilateral ABCD, ∠A = 2x - 1, ∠B = y + 5, ∠C = 2y + 15, ∠D = 4x - 7. Which is the greatest angle of quadrilateral.- a)115°
- b)120°
- c)125°
- d)85°
Correct answer is option 'C'. Can you explain this answer?
In a cyclic quadrilateral ABCD, ∠A = 2x - 1, ∠B = y + 5, ∠C = 2y + 15, ∠D = 4x - 7. Which is the greatest angle of quadrilateral.
a)
115°
b)
120°
c)
125°
d)
85°
|
|
Arnab Yadav answered |
Explanation:
Finding the greatest angle:
- To find the greatest angle of the cyclic quadrilateral, we need to compare the given angles.
Given angles:
- ∠A = 2x - 1
- ∠B = y + 5
- ∠C = 2y + 15
- ∠D = 4x - 7
Comparing the angles:
- To find the greatest angle, we need to compare the expressions for the angles given in terms of x and y.
- Given the expressions:
- ∠A = 2x - 1
- ∠B = y + 5
- ∠C = 2y + 15
- ∠D = 4x - 7
- To compare the angles, we need to find the values of x and y that would make the corresponding expressions largest.
- By comparing the expressions, we find that the largest expression is for ∠C = 2y + 15.
Therefore, the greatest angle of the quadrilateral is 2y + 15.
- We need to find the value of y that would make this expression largest.
- Since the value of y that makes the expression largest is the greatest angle of the quadrilateral, we need to solve for y.
- Comparing the expressions for ∠C = 2y + 15 with ∠B = y + 5:
- 2y + 15 > y + 5
- y > -10
- Therefore, the value of y that makes the expression 2y + 15 largest is y > -10.
- Substituting y = -10 into the expression 2y + 15:
- 2(-10) + 15 = -20 + 15 = -5
- Therefore, the greatest angle of the cyclic quadrilateral is 2y + 15 = 2(-5) + 15 = 10 + 15 = 25 degrees.
Hence, the greatest angle of the quadrilateral is 125 degrees (option C).
Finding the greatest angle:
- To find the greatest angle of the cyclic quadrilateral, we need to compare the given angles.
Given angles:
- ∠A = 2x - 1
- ∠B = y + 5
- ∠C = 2y + 15
- ∠D = 4x - 7
Comparing the angles:
- To find the greatest angle, we need to compare the expressions for the angles given in terms of x and y.
- Given the expressions:
- ∠A = 2x - 1
- ∠B = y + 5
- ∠C = 2y + 15
- ∠D = 4x - 7
- To compare the angles, we need to find the values of x and y that would make the corresponding expressions largest.
- By comparing the expressions, we find that the largest expression is for ∠C = 2y + 15.
Therefore, the greatest angle of the quadrilateral is 2y + 15.
- We need to find the value of y that would make this expression largest.
- Since the value of y that makes the expression largest is the greatest angle of the quadrilateral, we need to solve for y.
- Comparing the expressions for ∠C = 2y + 15 with ∠B = y + 5:
- 2y + 15 > y + 5
- y > -10
- Therefore, the value of y that makes the expression 2y + 15 largest is y > -10.
- Substituting y = -10 into the expression 2y + 15:
- 2(-10) + 15 = -20 + 15 = -5
- Therefore, the greatest angle of the cyclic quadrilateral is 2y + 15 = 2(-5) + 15 = 10 + 15 = 25 degrees.
Hence, the greatest angle of the quadrilateral is 125 degrees (option C).
Swathi starts her job with a certain monthly salary and earns a fixed increment every year. If her salary was ₹ 22500 per month after 6 years of service and ₹ 30000 per month after 11 years of service. Find her salary in rupees after 8 years of service.- a)24000
- b)25500
- c)26000
- d)24500
Correct answer is option 'B'. Can you explain this answer?
Swathi starts her job with a certain monthly salary and earns a fixed increment every year. If her salary was ₹ 22500 per month after 6 years of service and ₹ 30000 per month after 11 years of service. Find her salary in rupees after 8 years of service.
a)
24000
b)
25500
c)
26000
d)
24500
|
|
Vivek Bansal answered |
Let Swathi's first salary is Rs. x & fixed increment is Rs. y
∴ Swathi's salary after 6 years = Rs. (x + 6y)
Swathi's salary after 11 years = Rs. (x + 11y)
Swathi's salary after 8 years = Rs. (x + 8y)
∴ x + 6y = 22500 ......(1)
& x + 11y = 30000 .......(2)
From (1) & (2), we get
22500 - 6y + 11y = 30000
⇒ 5y = 30000 - 22500
= 7500
⇒ y = 7500/5 = 1500
∴∴ From (1), we get
x = 22500 - 6y
= 22500 - 6 × 1500
= 22500 - 9000
= 13500
∴∴ Swathi's salary after 8 years of service = Rs. (x + 8y)
= Rs. (13500 + 8 × 1500)
= Rs. (13500 + 12000)
= Rs. 25500
∴ Swathi's salary after 6 years = Rs. (x + 6y)
Swathi's salary after 11 years = Rs. (x + 11y)
Swathi's salary after 8 years = Rs. (x + 8y)
∴ x + 6y = 22500 ......(1)
& x + 11y = 30000 .......(2)
From (1) & (2), we get
22500 - 6y + 11y = 30000
⇒ 5y = 30000 - 22500
= 7500
⇒ y = 7500/5 = 1500
∴∴ From (1), we get
x = 22500 - 6y
= 22500 - 6 × 1500
= 22500 - 9000
= 13500
∴∴ Swathi's salary after 8 years of service = Rs. (x + 8y)
= Rs. (13500 + 8 × 1500)
= Rs. (13500 + 12000)
= Rs. 25500
The value of k, for which the system of equations kx – 3y + 6 = 0, 4x – 6y + 15 = 0 represent parallel lines, is _______.- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
The value of k, for which the system of equations kx – 3y + 6 = 0, 4x – 6y + 15 = 0 represent parallel lines, is _______.
a)
1
b)
2
c)
3
d)
4
|
|
Vivek Bansal answered |
It is given that, kx – 3y + 6 = 0 and 4x – 6y + 15 = 0 are two parallel lines.
i.e., The given lines has no solution or
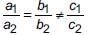
⇒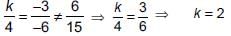
i.e., The given lines has no solution or
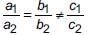
⇒
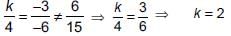
The sum of two numbers is 8 and the sum of their reciprocals is 8/15. Find the numbers.- a)5, 3
- b)7, 1
- c)4, 4
- d)2, 6
Correct answer is option 'A'. Can you explain this answer?
The sum of two numbers is 8 and the sum of their reciprocals is 8/15. Find the numbers.
a)
5, 3
b)
7, 1
c)
4, 4
d)
2, 6
|
|
Damini singhania answered |
To solve this problem, we can set up a system of equations based on the given information.
Let's assume that the two numbers are x and y.
Given:
1) The sum of two numbers is 8:
x + y = 8
2) The sum of their reciprocals is 8/15:
1/x + 1/y = 8/15
We can solve this system of equations to find the values of x and y.
Solving the System of Equations:
To solve this system of equations, we can use the method of substitution.
1) Solve the first equation for one variable in terms of the other. Let's solve for y in terms of x:
y = 8 - x
2) Substitute this value of y in the second equation:
1/x + 1/(8 - x) = 8/15
3) Multiply through by 15x(8 - x) to eliminate fractions:
15(8 - x) + 15x = 8x(8 - x)
4) Simplify and rearrange the equation:
120 - 15x + 15x = 64x - 8x^2
120 = 64x - 8x^2
5) Rewrite the equation in standard form:
8x^2 - 64x + 120 = 0
6) Factor the quadratic equation:
4(x^2 - 8x + 15) = 0
4(x - 3)(x - 5) = 0
From this equation, we can see that the possible values for x are 3 and 5.
7) Substitute each value of x back into the first equation to find the corresponding value of y:
For x = 3:
y = 8 - 3
y = 5
For x = 5:
y = 8 - 5
y = 3
Therefore, the numbers are 3 and 5, which corresponds to option A: 5, 3.
Let's assume that the two numbers are x and y.
Given:
1) The sum of two numbers is 8:
x + y = 8
2) The sum of their reciprocals is 8/15:
1/x + 1/y = 8/15
We can solve this system of equations to find the values of x and y.
Solving the System of Equations:
To solve this system of equations, we can use the method of substitution.
1) Solve the first equation for one variable in terms of the other. Let's solve for y in terms of x:
y = 8 - x
2) Substitute this value of y in the second equation:
1/x + 1/(8 - x) = 8/15
3) Multiply through by 15x(8 - x) to eliminate fractions:
15(8 - x) + 15x = 8x(8 - x)
4) Simplify and rearrange the equation:
120 - 15x + 15x = 64x - 8x^2
120 = 64x - 8x^2
5) Rewrite the equation in standard form:
8x^2 - 64x + 120 = 0
6) Factor the quadratic equation:
4(x^2 - 8x + 15) = 0
4(x - 3)(x - 5) = 0
From this equation, we can see that the possible values for x are 3 and 5.
7) Substitute each value of x back into the first equation to find the corresponding value of y:
For x = 3:
y = 8 - 3
y = 5
For x = 5:
y = 8 - 5
y = 3
Therefore, the numbers are 3 and 5, which corresponds to option A: 5, 3.
A boat goes 32 km upstream and 36 km downstream in 7 hours. In 9 hours, it can go 40 km upstream and 48 km downstream. If x represents the speed of the boat in still water in km/hr and y represents the speed of the stream in km/hr, then_______.- a)x + y = 12, x – y = 8
- b)x + y = 5, x – y = 11
- c)x + y = 6, x – y = 10
- d)x + y = 10, x – y = 6
Correct answer is option 'A'. Can you explain this answer?
A boat goes 32 km upstream and 36 km downstream in 7 hours. In 9 hours, it can go 40 km upstream and 48 km downstream. If x represents the speed of the boat in still water in km/hr and y represents the speed of the stream in km/hr, then_______.
a)
x + y = 12, x – y = 8
b)
x + y = 5, x – y = 11
c)
x + y = 6, x – y = 10
d)
x + y = 10, x – y = 6
|
|
Leena kumar answered |
Understanding the Problem:
To solve this problem, we need to use the concept of relative speed of the boat with respect to the stream. The boat's speed in still water is represented by x km/hr, and the speed of the stream is represented by y km/hr.
Setting Up Equations:
1. For the first scenario (7 hours):
- Upstream speed = x - y km/hr
- Downstream speed = x + y km/hr
- Time taken to go 32 km upstream + Time taken to go 36 km downstream = 7 hours
- 32/(x-y) + 36/(x+y) = 7
2. For the second scenario (9 hours):
- Upstream speed = x - y km/hr
- Downstream speed = x + y km/hr
- Time taken to go 40 km upstream + Time taken to go 48 km downstream = 9 hours
- 40/(x-y) + 48/(x+y) = 9
Solving the Equations:
By solving the above two equations simultaneously, we get:
x + y = 12
x - y = 8
Conclusion:
Therefore, the correct answer is option A: x + y = 12, x - y = 8. This implies that the speed of the boat in still water is 10 km/hr and the speed of the stream is 2 km/hr.
To solve this problem, we need to use the concept of relative speed of the boat with respect to the stream. The boat's speed in still water is represented by x km/hr, and the speed of the stream is represented by y km/hr.
Setting Up Equations:
1. For the first scenario (7 hours):
- Upstream speed = x - y km/hr
- Downstream speed = x + y km/hr
- Time taken to go 32 km upstream + Time taken to go 36 km downstream = 7 hours
- 32/(x-y) + 36/(x+y) = 7
2. For the second scenario (9 hours):
- Upstream speed = x - y km/hr
- Downstream speed = x + y km/hr
- Time taken to go 40 km upstream + Time taken to go 48 km downstream = 9 hours
- 40/(x-y) + 48/(x+y) = 9
Solving the Equations:
By solving the above two equations simultaneously, we get:
x + y = 12
x - y = 8
Conclusion:
Therefore, the correct answer is option A: x + y = 12, x - y = 8. This implies that the speed of the boat in still water is 10 km/hr and the speed of the stream is 2 km/hr.
Five years ago, Ravi was thrice as old as Shashi. Ten years later Ravi will be twice as old as Shashi. What is the age of Shashi?- a)20 years
- b)30 years
- c)35 years
- d)50 years
Correct answer is option 'A'. Can you explain this answer?
Five years ago, Ravi was thrice as old as Shashi. Ten years later Ravi will be twice as old as Shashi. What is the age of Shashi?
a)
20 years
b)
30 years
c)
35 years
d)
50 years
|
|
Ritu Saxena answered |
Let Shashi’s present age be x and Ravi’s present age be y.
y - 5 = 3 (x - 5) ⇒ 3x - y = 10 ...(1)
y + 10 = 2 (x + 10) ⇒ 2x - y = 10 ...(2)
Solving eqns (1) and (2), we get
x = 20, y = 50
y - 5 = 3 (x - 5) ⇒ 3x - y = 10 ...(1)
y + 10 = 2 (x + 10) ⇒ 2x - y = 10 ...(2)
Solving eqns (1) and (2), we get
x = 20, y = 50
Sum of tw o n umb ers is 6 4 an d the ir difference is 22. Find the numbers.- a)42, 22
- b)43, 21
- c)40, 24
- d)50, 28
Correct answer is option 'B'. Can you explain this answer?
Sum of tw o n umb ers is 6 4 an d the ir difference is 22. Find the numbers.
a)
42, 22
b)
43, 21
c)
40, 24
d)
50, 28
|
|
Priyanka Kapoor answered |
Let the two numbers be x and y.
Then, x + y = 64 ...(1)
Also, x – y = 22 ...(2)
or y – x = 22 ...(3)
(i) If x – y = 22, from (1) and (2), we have 2x = 86
⇒ x = 43 and y = 21
(ii) If y – x = 22, from (1) and (3), we have 2y = 86 ⇒ y = 43 and x = 21
∴ Numbers are 43 and 21.
Then, x + y = 64 ...(1)
Also, x – y = 22 ...(2)
or y – x = 22 ...(3)
(i) If x – y = 22, from (1) and (2), we have 2x = 86
⇒ x = 43 and y = 21
(ii) If y – x = 22, from (1) and (3), we have 2y = 86 ⇒ y = 43 and x = 21
∴ Numbers are 43 and 21.
What are the values of x and y if x + y = a + b ax - by = a2 - b2?- a)a, b
- b)-a, -b
- c)a, 0
- d)0, b
Correct answer is option 'A'. Can you explain this answer?
What are the values of x and y if x + y = a + b ax - by = a2 - b2?
a)
a, b
b)
-a, -b
c)
a, 0
d)
0, b
|
|
Ritu Saxena answered |
Here
bx + by = ab + b2 ...(1)
and ax - by = a2 - b2 ...(2)
Adding, x (a + b) = a (b + a) ⇒ x = a
Putting x = a in eqn (2), we have
a2 - by = a2 - b2
⇒ by = - b2 ⇒ y = b
Hence x = a, y = b
bx + by = ab + b2 ...(1)
and ax - by = a2 - b2 ...(2)
Adding, x (a + b) = a (b + a) ⇒ x = a
Putting x = a in eqn (2), we have
a2 - by = a2 - b2
⇒ by = - b2 ⇒ y = b
Hence x = a, y = b
The sum of two numbers is 16 and the sum of their reciprocals is 1/3. What are the numbers?- a)12, 4
- b)8, 8
- c)10, 6
- d)14, 2
Correct answer is option 'A'. Can you explain this answer?
The sum of two numbers is 16 and the sum of their reciprocals is 1/3. What are the numbers?
a)
12, 4
b)
8, 8
c)
10, 6
d)
14, 2
|
|
Ritu Saxena answered |
Let the numbers be x and y.
x + y = 16 ...(1)
and
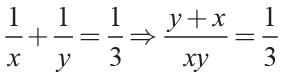
Now
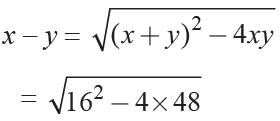
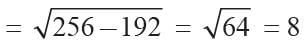
⇒ x - y = 8 ...(2)
From (1) and (2), we get x = 12, y = 4.
x + y = 16 ...(1)
and
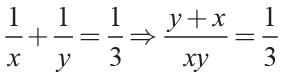
Now
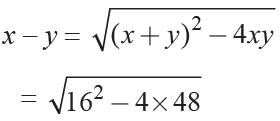
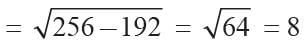
⇒ x - y = 8 ...(2)
From (1) and (2), we get x = 12, y = 4.
What are the values of x and y, if 2(ax - by) + (a + 4b) = 0 and 2 (bx + ay) + (b - 4a) = 0- a)x = 2, y = -1
- b)x = -1/2, y/2
- c)y = -1/2, x = 1
- d)x = 2, y = -1/2
Correct answer is option 'B'. Can you explain this answer?
What are the values of x and y, if 2(ax - by) + (a + 4b) = 0 and 2 (bx + ay) + (b - 4a) = 0
a)
x = 2, y = -1
b)
x = -1/2, y/2
c)
y = -1/2, x = 1
d)
x = 2, y = -1/2
|
|
Ritu Saxena answered |
We have
2ax - 2by = - a - 4b ...(1)
and 2bx + 2ay = 4a - b ...(2)
2a2x - 2aby = -a2 - 4ab ...(3)
Now 2b2x + 2aby = 4ab - b2
2x (a2 + b2) = - (a2 +b2) ⇒ x = -1/2
Now putting the value of 2aby from eqn. (3), we get
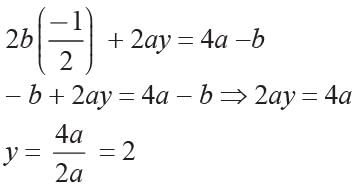
2ax - 2by = - a - 4b ...(1)
and 2bx + 2ay = 4a - b ...(2)
2a2x - 2aby = -a2 - 4ab ...(3)
Now 2b2x + 2aby = 4ab - b2
2x (a2 + b2) = - (a2 +b2) ⇒ x = -1/2
Now putting the value of 2aby from eqn. (3), we get
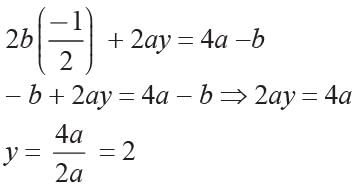
The sum of the digits of a two digits number is 12. The number obtained by interchanging the digits exceeds the given number by 18. What is that number?- a)84
- b)48
- c)57
- d)75
Correct answer is option 'C'. Can you explain this answer?
The sum of the digits of a two digits number is 12. The number obtained by interchanging the digits exceeds the given number by 18. What is that number?
a)
84
b)
48
c)
57
d)
75
|
|
Ritu Saxena answered |
L et unit’s digit be x and ten’s digit be y.
Then number = 10y + x
x + y = 12 ...(1)
10x + y - (10y + x) = 18
9x - 9y = 18 ⇒ x - y = 2 ...(2)
Solving (1) and (2), we get x = 7, y = 5.
∴ number = 10 × 5 + 7 = 50 + 7 = 57
Then number = 10y + x
x + y = 12 ...(1)
10x + y - (10y + x) = 18
9x - 9y = 18 ⇒ x - y = 2 ...(2)
Solving (1) and (2), we get x = 7, y = 5.
∴ number = 10 × 5 + 7 = 50 + 7 = 57
In a triangle ΔABC, 3∠B = ∠C = 2 (∠A + ∠B). Which angle is the largest and what is its value?- a)∠C, 120°
- b)∠C, 80°
- c)∠B, 40°
- d)∠B, 100°
Correct answer is option 'A'. Can you explain this answer?
In a triangle ΔABC, 3∠B = ∠C = 2 (∠A + ∠B). Which angle is the largest and what is its value?
a)
∠C, 120°
b)
∠C, 80°
c)
∠B, 40°
d)
∠B, 100°
|
|
Ritu Saxena answered |
L et ∠A = x°, ∠B = y°, ∠C = 3∠B = 3y°
In ΔABC, ∠A + ∠B + ∠C = 180°
x° + y° +3y° = 180°
x° + 4y° = 180 ...(1)
∠C = 2(∠A + ∠B) ⇒ 3y = 2 (x° + y°)
2x° - y° = 0 ...(2)
From (1) and (2)
x = 20 , y = 40
∴ ∠A = 20°, ∠B = 40°, ∠C = 3 × 40 = 120°
In ΔABC, ∠A + ∠B + ∠C = 180°
x° + y° +3y° = 180°
x° + 4y° = 180 ...(1)
∠C = 2(∠A + ∠B) ⇒ 3y = 2 (x° + y°)
2x° - y° = 0 ...(2)
From (1) and (2)
x = 20 , y = 40
∴ ∠A = 20°, ∠B = 40°, ∠C = 3 × 40 = 120°
The larger of the two supplementary angles exceeds the smaller by 18º. What is the Value of a larger angle?- a)81°
- b)99°
- c)109°
- d)89°
Correct answer is option 'B'. Can you explain this answer?
The larger of the two supplementary angles exceeds the smaller by 18º. What is the Value of a larger angle?
a)
81°
b)
99°
c)
109°
d)
89°
|
|
Ritu Saxena answered |
Let x be the larger angle and y be smaller angle.
then x + y = 180° ...(1)
and x - y = 18°
Solving eqns (1) and (2), we get
x = 99°, y = 81°
then x + y = 180° ...(1)
and x - y = 18°
Solving eqns (1) and (2), we get
x = 99°, y = 81°
If a pair of linear equations in two variables is consistent, then the lines represented by two equations are- a)Always intersecting
- b)Parallel
- c)Always coincident
- d)Intersecting or coincident
Correct answer is option 'D'. Can you explain this answer?
If a pair of linear equations in two variables is consistent, then the lines represented by two equations are
a)
Always intersecting
b)
Parallel
c)
Always coincident
d)
Intersecting or coincident
|
|
Ritu Saxena answered |
Two lines can have solution in two different cases,
Case 1: When they intersect at one point (unique solution)
Case 2: When the lines are coincident (infinite solutions)
Thus, if a pair of linear equations is consistent, then the lines will be intersecting or coincident.
Case 1: When they intersect at one point (unique solution)
Case 2: When the lines are coincident (infinite solutions)
Thus, if a pair of linear equations is consistent, then the lines will be intersecting or coincident.
ax + by + c = 0 does not represent an equation of line when _______.- a)a = c = 0, b ≠ 0
- b)b = c = 0, a ≠ 0
- c)a = b = 0
- d)a = b ≠ 0
Correct answer is option 'C'. Can you explain this answer?
ax + by + c = 0 does not represent an equation of line when _______.
a)
a = c = 0, b ≠ 0
b)
b = c = 0, a ≠ 0
c)
a = b = 0
d)
a = b ≠ 0
|
|
Vivek Bansal answered |
ax + by + c = 0
When a and b are equal to zero, then the above linear equation does not represent an equation of line.
When a and b are equal to zero, then the above linear equation does not represent an equation of line.
The solution of the system of equations 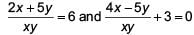 (where x ≠ 0, y ≠ 0), is _______.
(where x ≠ 0, y ≠ 0), is _______.- a)1, 2
- b)0, 0
- c)–1, 2
- d)1, –2
Correct answer is option 'A'. Can you explain this answer?
The solution of the system of equations 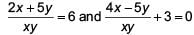 (where x ≠ 0, y ≠ 0), is _______.
(where x ≠ 0, y ≠ 0), is _______.
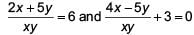 (where x ≠ 0, y ≠ 0), is _______.
(where x ≠ 0, y ≠ 0), is _______.a)
1, 2
b)
0, 0
c)
–1, 2
d)
1, –2
|
|
Priyanka Kapoor answered |
We have, 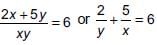 ......(1)
......(1)
Also,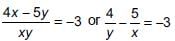 ...(2)
...(2)
Let 1/y = a and 1/x = b
So, (1) and (2) become
2a + 5b = 6 ...(3)
and, 4a – 5b = –3 ...(4)
Adding (3) and (4), we get
a = 1/2 and b = 1 [From (3)]
∴ x = 1 and y = 2
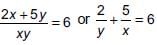 ......(1)
......(1)Also,
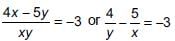 ...(2)
...(2)Let 1/y = a and 1/x = b
So, (1) and (2) become
2a + 5b = 6 ...(3)
and, 4a – 5b = –3 ...(4)
Adding (3) and (4), we get
a = 1/2 and b = 1 [From (3)]
∴ x = 1 and y = 2
What is the value of K for which the system has no solution?
2x - ky + 3 = 0; 3x + 2y - 1 = 0- a)-4/3
- b)3/4
- c)-3/4
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
What is the value of K for which the system has no solution?
2x - ky + 3 = 0; 3x + 2y - 1 = 0
2x - ky + 3 = 0; 3x + 2y - 1 = 0
a)
-4/3
b)
3/4
c)
-3/4
d)
None of these
|
|
Ritu Saxena answered |
Given
2x - ky + 3 = 0
3x + 2y - 1 = 0
For no solution, we have
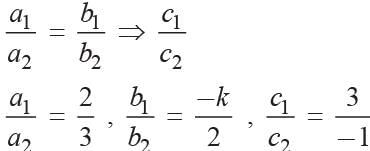
Now
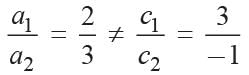
So,

2x - ky + 3 = 0
3x + 2y - 1 = 0
For no solution, we have
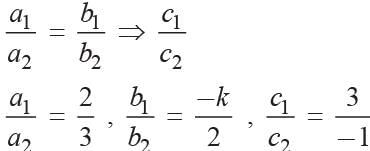
Now
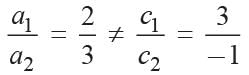
So,

The ratio of a 2-digit number to the sum of digits of that number is 4 : 1. If the digit in the unit place is 3 more than the digit in the tens place, what is the number?- a)63
- b)36
- c)24
- d)40
Correct answer is option 'B'. Can you explain this answer?
The ratio of a 2-digit number to the sum of digits of that number is 4 : 1. If the digit in the unit place is 3 more than the digit in the tens place, what is the number?
a)
63
b)
36
c)
24
d)
40
|
|
Vivek Bansal answered |
Let the digit at unit place be x and the digit at tens place be y, then the number = 10y + x
Now, according to the question,
⇒ 10y + x = 4y + 4x
⇒ 6y = 3x ⇒ x = 2y ...(1)
Also, x = 3 + y ⇒ 2y = 3 + y [From (1)]
⇒ y = 3 and x = 6 \ Number = 36
Now, according to the question,
⇒ 10y + x = 4y + 4x
⇒ 6y = 3x ⇒ x = 2y ...(1)
Also, x = 3 + y ⇒ 2y = 3 + y [From (1)]
⇒ y = 3 and x = 6 \ Number = 36
What are the values of x and y, if
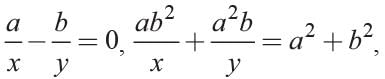
where x ≠ 0, y ≠ 0?- a)x = b, y = 1
- b)x = a, y = b
- c)x = 1, y = b
- d)x = a, y = 1
Correct answer is option 'B'. Can you explain this answer?
What are the values of x and y, if
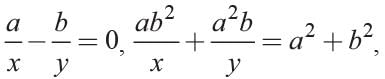
where x ≠ 0, y ≠ 0?
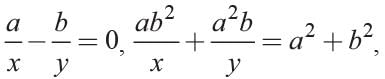
where x ≠ 0, y ≠ 0?
a)
x = b, y = 1
b)
x = a, y = b
c)
x = 1, y = b
d)
x = a, y = 1
|
|
Ritu Saxena answered |
Let
1/x = m, 1/y = n
Then am - bn = 0 ...(1)
ab2m + a2bn = a2 + b2 ...(2)
Now am - bn + 0 = 0
ab2m + a2bn - (a2 + b2) = 0
By cross multiplication,
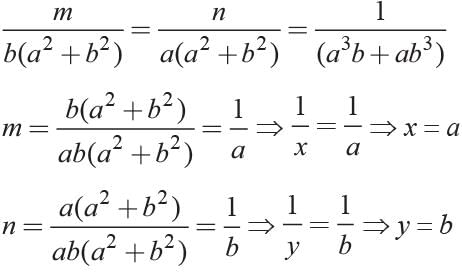
1/x = m, 1/y = n
Then am - bn = 0 ...(1)
ab2m + a2bn = a2 + b2 ...(2)
Now am - bn + 0 = 0
ab2m + a2bn - (a2 + b2) = 0
By cross multiplication,
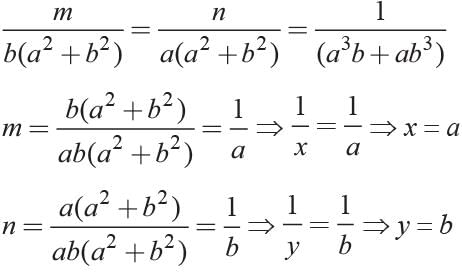
In a ΔABC, ∠C = 3 ∠B = 2 (∠A + ∠B). The three angles will be _______.- a)20°, 40°, 120°
- b)30°, 60°, 90°
- c)45°, 45°, 90°
- d)90°, 40°, 50°
Correct answer is option 'A'. Can you explain this answer?
In a ΔABC, ∠C = 3 ∠B = 2 (∠A + ∠B). The three angles will be _______.
a)
20°, 40°, 120°
b)
30°, 60°, 90°
c)
45°, 45°, 90°
d)
90°, 40°, 50°
|
|
Vivek Bansal answered |
In a triangle, sum of angles is 180°.
∴ ∠A + ∠B + ∠C = 180° ...(1)
∠C = 3∠B ...(2)
and 3∠B = 2∠A + 2∠B
∴ ∠A = ∠B/2 ...(3)
From (1), (2) and (3), we get
∠B/2+ ∠B +3∠B = 180°
⇒ (9/2)∠B = 180° ⇒ ∠B = 40°
∴ ∠C = 120° and ∠A = 20°
∴ ∠A + ∠B + ∠C = 180° ...(1)
∠C = 3∠B ...(2)
and 3∠B = 2∠A + 2∠B
∴ ∠A = ∠B/2 ...(3)
From (1), (2) and (3), we get
∠B/2+ ∠B +3∠B = 180°
⇒ (9/2)∠B = 180° ⇒ ∠B = 40°
∴ ∠C = 120° and ∠A = 20°
What are the values of x and y if
- a)x = 11, y = 8
- b)x = 8, y = 11
- c)x = -8, y = 11
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
What are the values of x and y if
a)
x = 11, y = 8
b)
x = 8, y = 11
c)
x = -8, y = 11
d)
None of these
|
|
Ritu Saxena answered |
Let
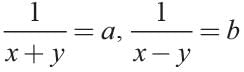
then 57a + 6b = 5 ...(1)
38a + 21b = 9 ...(2)
Solving (1) and (2) we get a = 1/19, b = 1/3
Hence
x + y = 19 ...(4)
x - y = 3 ...(5)
Solving (4) and (5), we get x = 11, y = 8
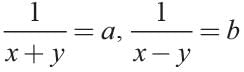
then 57a + 6b = 5 ...(1)
38a + 21b = 9 ...(2)
Solving (1) and (2) we get a = 1/19, b = 1/3
Hence
x + y = 19 ...(4)
x - y = 3 ...(5)
Solving (4) and (5), we get x = 11, y = 8
Chapter doubts & questions for Linear Equations in Two Variables - Olympiad Preparation for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Linear Equations in Two Variables - Olympiad Preparation for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily