All Exams >
Class 10 >
Olympiad Preparation for Class 10 >
All Questions
All questions of Probability for Class 10 Exam
What is the probability of getting 53 Tuesday in a leap year?- a)
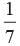
- b)
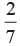
- c)

- d)None of these
Correct answer is option 'B'. Can you explain this answer?
What is the probability of getting 53 Tuesday in a leap year?
a)
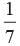
b)
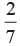
c)

d)
None of these
|
|
Ritu Saxena answered |
In a leap year, there are 52 weeks and 2 days.
These two days may be (Monday, Tuesday) (Tuesday, Wednesday), (Wednesday, Thursday) (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday), (Sunday, Monday).
These two days may be (Monday, Tuesday) (Tuesday, Wednesday), (Wednesday, Thursday) (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday), (Sunday, Monday).
A box contains 6 green balls, 4 red balls and some white balls. If the probability of not drawing a white ball in one draw is 2/3, what is the number of white balls?- a)5
- b)6
- c)7
- d)4
Correct answer is option 'A'. Can you explain this answer?
A box contains 6 green balls, 4 red balls and some white balls. If the probability of not drawing a white ball in one draw is 2/3, what is the number of white balls?
a)
5
b)
6
c)
7
d)
4
|
|
Vivek Bansal answered |
Let no. of white balls = x
Total no. of balls = 6 + 4 + x = 10 + x
Probability of drawing not a white ball
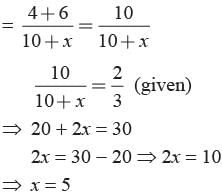
Total no. of balls = 6 + 4 + x = 10 + x
Probability of drawing not a white ball
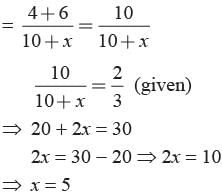
250 lottery tickets were sold and there are 5 prizes on these tickets. If Kunal has purchased one lottery ticket, what is the probability that he wins a prize?- a)1/50
- b)1/125
- c)3/125
- d)3/50
Correct answer is option 'A'. Can you explain this answer?
250 lottery tickets were sold and there are 5 prizes on these tickets. If Kunal has purchased one lottery ticket, what is the probability that he wins a prize?
a)
1/50
b)
1/125
c)
3/125
d)
3/50
|
|
Vivek Bansal answered |
Total number of outcomes = 250
Number of favourable outcomes = 5
∴ Probability that Kunal wins the prize = 5/250 = 1/50
Number of favourable outcomes = 5
∴ Probability that Kunal wins the prize = 5/250 = 1/50
Five cards-the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. If the queen is drawn and put aside, one card is then picked up at random. what is the probability that the second card picked up is
(i) a king and
(ii) a queen?- a)1/4, 0
- b)1/2, 0
- c)1/3, 0
- d)1/3, 1/2
Correct answer is option 'A'. Can you explain this answer?
Five cards-the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. If the queen is drawn and put aside, one card is then picked up at random. what is the probability that the second card picked up is
(i) a king and
(ii) a queen?
(i) a king and
(ii) a queen?
a)
1/4, 0
b)
1/2, 0
c)
1/3, 0
d)
1/3, 1/2
|
|
Radha sengupta answered |
To solve this problem, we need to consider the total number of cards remaining in the deck and the number of favorable outcomes for each case.
Total number of cards remaining in the deck = 4 (10, jack, king, and ace of diamonds)
Total number of favorable outcomes for picking a king = 1 (king of diamonds)
Total number of favorable outcomes for picking a queen = 0 (as the queen has already been put aside)
(i) Probability of picking a king:
The probability of picking a king can be calculated as the ratio of the number of favorable outcomes to the total number of possible outcomes.
Probability = Number of favorable outcomes / Total number of possible outcomes
= 1 / 4
= 1/4
(ii) Probability of picking a queen:
Since the queen has already been put aside, there are no favorable outcomes for picking a queen. Therefore, the probability of picking a queen is 0.
Probability = Number of favorable outcomes / Total number of possible outcomes
= 0 / 4
= 0
Therefore, the probability of picking a king as the second card is 1/4 and the probability of picking a queen as the second card is 0. Hence, the correct answer is option 'A' - 1/4, 0.
Total number of cards remaining in the deck = 4 (10, jack, king, and ace of diamonds)
Total number of favorable outcomes for picking a king = 1 (king of diamonds)
Total number of favorable outcomes for picking a queen = 0 (as the queen has already been put aside)
(i) Probability of picking a king:
The probability of picking a king can be calculated as the ratio of the number of favorable outcomes to the total number of possible outcomes.
Probability = Number of favorable outcomes / Total number of possible outcomes
= 1 / 4
= 1/4
(ii) Probability of picking a queen:
Since the queen has already been put aside, there are no favorable outcomes for picking a queen. Therefore, the probability of picking a queen is 0.
Probability = Number of favorable outcomes / Total number of possible outcomes
= 0 / 4
= 0
Therefore, the probability of picking a king as the second card is 1/4 and the probability of picking a queen as the second card is 0. Hence, the correct answer is option 'A' - 1/4, 0.
A game consists of tossing a one rupee coin three times and noting its outcome each time. Hanif wins if all the tosses give the same result, i.e., three heads or three tails and loses otherwise. Calculate the probability that Hanif will lose the game.- a)1/4
- b)1/2
- c)3/4
- d)5/8
Correct answer is option 'C'. Can you explain this answer?
A game consists of tossing a one rupee coin three times and noting its outcome each time. Hanif wins if all the tosses give the same result, i.e., three heads or three tails and loses otherwise. Calculate the probability that Hanif will lose the game.
a)
1/4
b)
1/2
c)
3/4
d)
5/8
|
|
Uma shukla answered |
Probability of Losing the Game
To calculate the probability that Hanif will lose the game, we need to consider all the possible outcomes when tossing a one rupee coin three times.
Possible Outcomes
- When tossing a coin three times, there are a total of 2 x 2 x 2 = 8 possible outcomes.
- These outcomes are: HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
Winning Outcomes
- Hanif wins the game if all tosses give the same result (three heads or three tails).
- The winning outcomes are HHH and TTT, which are 2 out of the 8 possible outcomes.
Probability of Winning
- The probability of winning the game is given by the number of winning outcomes divided by the total number of possible outcomes.
- Probability of winning = 2/8 = 1/4
Probability of Losing
- Since the probability of winning is 1/4, the probability of losing the game is the complement of winning.
- Probability of losing = 1 - 1/4 = 3/4
Therefore, the probability that Hanif will lose the game is 3/4.
To calculate the probability that Hanif will lose the game, we need to consider all the possible outcomes when tossing a one rupee coin three times.
Possible Outcomes
- When tossing a coin three times, there are a total of 2 x 2 x 2 = 8 possible outcomes.
- These outcomes are: HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
Winning Outcomes
- Hanif wins the game if all tosses give the same result (three heads or three tails).
- The winning outcomes are HHH and TTT, which are 2 out of the 8 possible outcomes.
Probability of Winning
- The probability of winning the game is given by the number of winning outcomes divided by the total number of possible outcomes.
- Probability of winning = 2/8 = 1/4
Probability of Losing
- Since the probability of winning is 1/4, the probability of losing the game is the complement of winning.
- Probability of losing = 1 - 1/4 = 3/4
Therefore, the probability that Hanif will lose the game is 3/4.
A black die, a red die and a green die are thrown at the same time. What is the probability that the sum of three numbers that turn up is 15?- a)11/216
- b)5/108
- c)9/216
- d)12 x 1/18
Correct answer is option 'B'. Can you explain this answer?
A black die, a red die and a green die are thrown at the same time. What is the probability that the sum of three numbers that turn up is 15?
a)
11/216
b)
5/108
c)
9/216
d)
12 x 1/18
|
|
Ritu Saxena answered |
Total number o f outcom es when three dice are thrown = 6 x 6 x 6 = 216
For sum of numbers to be 15, possible ways are, (6, 6, 3), (6, 3, 6), (3, 6, 6), (6, 5, 4), (6, 4, 5), (5, 4, 6), (5, 6, 4), (4, 5, 6), (4, 6, 5), (5, 5, 5)
∴ Number of favorable outcomes = 10
∴ Required probability = 10/216 = 5/108
For sum of numbers to be 15, possible ways are, (6, 6, 3), (6, 3, 6), (3, 6, 6), (6, 5, 4), (6, 4, 5), (5, 4, 6), (5, 6, 4), (4, 5, 6), (4, 6, 5), (5, 5, 5)
∴ Number of favorable outcomes = 10
∴ Required probability = 10/216 = 5/108
A jar contains 54 marbles each of which is blue, green or white. The probability of selecting a blue marble at random from the jar is 1/3,and the probability of selecting a green marble at random is 4/9. How many white marbles does the jar contain?- a)12
- b)6
- c)9
- d)11
Correct answer is option 'A'. Can you explain this answer?
A jar contains 54 marbles each of which is blue, green or white. The probability of selecting a blue marble at random from the jar is 1/3,and the probability of selecting a green marble at random is 4/9. How many white marbles does the jar contain?
a)
12
b)
6
c)
9
d)
11
|
|
Ritu Saxena answered |
Let there be b blue, g green and w white marbles in the jar. Then, b + g + w = 54 ...(i)
∴ P (Selecting a blue marble) = b/54
It is given that the probability of selecting a blue marble is 1/3
∴ 1/3 = b/54
⇒ b = 18
We have, P (Selecting a green marble) = 4/9(given)
⇒ g/54 = 4/9
⇒ g = 24
Substituting the values of b and g in (i), we get 18 + 24 + w = 54 ⇒ w = 1 2 Hence, the jar contains 12 white marbles.
∴ P (Selecting a blue marble) = b/54
It is given that the probability of selecting a blue marble is 1/3
∴ 1/3 = b/54
⇒ b = 18
We have, P (Selecting a green marble) = 4/9(given)
⇒ g/54 = 4/9
⇒ g = 24
Substituting the values of b and g in (i), we get 18 + 24 + w = 54 ⇒ w = 1 2 Hence, the jar contains 12 white marbles.
There are 100 cards in a bag on which numbers from 1 to 100 are written. A card is taken out from the bag at random. Find the probability that the number on the selected card is divisible by 9 and is a perfect square.- a)9/100
- b)1/25
- c)7/100
- d)3/100
Correct answer is option 'D'. Can you explain this answer?
There are 100 cards in a bag on which numbers from 1 to 100 are written. A card is taken out from the bag at random. Find the probability that the number on the selected card is divisible by 9 and is a perfect square.
a)
9/100
b)
1/25
c)
7/100
d)
3/100

|
Anmol Chatterjee answered |
Problem:
There are 100 cards in a bag on which numbers from 1 to 100 are written. A card is taken out from the bag at random. Find the probability that the number on the selected card is divisible by 9 and is a perfect square.
Solution:
To find the probability that the number on the selected card is divisible by 9 and is a perfect square, we need to determine the number of cards that satisfy both conditions and divide it by the total number of cards.
Step 1: Determine the number of cards that are divisible by 9:
To find the number of cards that are divisible by 9, we need to determine the number of multiples of 9 between 1 and 100.
The first multiple of 9 between 1 and 100 is 9 itself. The last multiple of 9 between 1 and 100 is 99. So, the number of cards that are divisible by 9 is 99 / 9 = 11.
Step 2: Determine the number of perfect square cards:
To find the number of perfect square cards, we need to determine the number of perfect squares between 1 and 100.
The perfect squares between 1 and 100 are 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100. So, the number of perfect square cards is 10.
Step 3: Determine the number of cards that satisfy both conditions:
To find the number of cards that are divisible by 9 and are perfect squares, we need to find the common elements between the two sets.
The common elements between the multiples of 9 and perfect squares are 9, 36, and 81. So, the number of cards that satisfy both conditions is 3.
Step 4: Calculate the probability:
The probability is given by the number of favorable outcomes divided by the total number of outcomes.
Number of favorable outcomes = 3
Total number of outcomes = 100
Probability = 3 / 100 = 0.03 = 3/100
Therefore, the correct answer is option 'D', 3/100.
There are 100 cards in a bag on which numbers from 1 to 100 are written. A card is taken out from the bag at random. Find the probability that the number on the selected card is divisible by 9 and is a perfect square.
Solution:
To find the probability that the number on the selected card is divisible by 9 and is a perfect square, we need to determine the number of cards that satisfy both conditions and divide it by the total number of cards.
Step 1: Determine the number of cards that are divisible by 9:
To find the number of cards that are divisible by 9, we need to determine the number of multiples of 9 between 1 and 100.
The first multiple of 9 between 1 and 100 is 9 itself. The last multiple of 9 between 1 and 100 is 99. So, the number of cards that are divisible by 9 is 99 / 9 = 11.
Step 2: Determine the number of perfect square cards:
To find the number of perfect square cards, we need to determine the number of perfect squares between 1 and 100.
The perfect squares between 1 and 100 are 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100. So, the number of perfect square cards is 10.
Step 3: Determine the number of cards that satisfy both conditions:
To find the number of cards that are divisible by 9 and are perfect squares, we need to find the common elements between the two sets.
The common elements between the multiples of 9 and perfect squares are 9, 36, and 81. So, the number of cards that satisfy both conditions is 3.
Step 4: Calculate the probability:
The probability is given by the number of favorable outcomes divided by the total number of outcomes.
Number of favorable outcomes = 3
Total number of outcomes = 100
Probability = 3 / 100 = 0.03 = 3/100
Therefore, the correct answer is option 'D', 3/100.
When two dice are thrown, the probability of getting a number always greater than 4 on the second dice is _____- a)1/6
- b)1/3
- c)1/36
- d)5/36
Correct answer is option 'B'. Can you explain this answer?
When two dice are thrown, the probability of getting a number always greater than 4 on the second dice is _____
a)
1/6
b)
1/3
c)
1/36
d)
5/36
|
|
Ritu Saxena answered |
Total number o f outcomes when two dice are thrown = 36.
Let A be the event of getting a number always greater than 4 on second dice.
∴ A = {(1,5), (1,6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6),
(5, 5), (5, 6), (6, 5), (6, 6)}
∴ Number of possible outcomes = 12
∴ P(A) = 12/36 = 1/3
Let A be the event of getting a number always greater than 4 on second dice.
∴ A = {(1,5), (1,6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6),
(5, 5), (5, 6), (6, 5), (6, 6)}
∴ Number of possible outcomes = 12
∴ P(A) = 12/36 = 1/3
Cards marked wit h numbers 13, 14, 15,.......,60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that number on the drawn card is
(i) divisible by 5.
(ii) a number which is a perfect square.- a)5/24, 1/24
- b)5/24, 1/12
- c)1/12, 5/12
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Cards marked wit h numbers 13, 14, 15,.......,60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that number on the drawn card is
(i) divisible by 5.
(ii) a number which is a perfect square.
(i) divisible by 5.
(ii) a number which is a perfect square.
a)
5/24, 1/24
b)
5/24, 1/12
c)
1/12, 5/12
d)
None of these
|
|
Vivek Bansal answered |
Outcomes are 13, 14, 15,.......,60.
Total number of possible outcomes = 60 - 12 = 48
(i) The numbers divisible by 5 are 15, 20, 25, 30, 35, 40, 45, 50, 55, 60.
Thus, the number of numbers divisible by 5 = 10
Required probability = 10/48 = 5/24
(ii) Perfect square numbers are 16, 25, 36, 49
Thus, the number of perfect square number = 4
Required probability = 4/48 = 1/12
Total number of possible outcomes = 60 - 12 = 48
(i) The numbers divisible by 5 are 15, 20, 25, 30, 35, 40, 45, 50, 55, 60.
Thus, the number of numbers divisible by 5 = 10
Required probability = 10/48 = 5/24
(ii) Perfect square numbers are 16, 25, 36, 49
Thus, the number of perfect square number = 4
Required probability = 4/48 = 1/12
A man calculates that the probability of his winning the first prize in a lottery is 0.08. If 6000 tickets are sold, how many tickets has he bought?- a)480
- b)720
- c)240
- d)140
Correct answer is option 'A'. Can you explain this answer?
A man calculates that the probability of his winning the first prize in a lottery is 0.08. If 6000 tickets are sold, how many tickets has he bought?
a)
480
b)
720
c)
240
d)
140
|
|
Anmol tiwari answered |
To find the number of tickets the man has bought, we can use the formula:
Number of tickets bought = Probability of winning × Total number of tickets
Given that the probability of winning the first prize is 0.08 and the total number of tickets sold is 6000, we can substitute these values into the formula:
Number of tickets bought = 0.08 × 6000
Simplifying the calculation:
Number of tickets bought = 480
Therefore, the man has bought 480 tickets.
Explanation:
Let's break down the problem into the following components:
1. Probability of winning: The probability of winning the first prize is given as 0.08. This means that out of every 100 tickets sold, he is expected to win the first prize in 8 tickets.
2. Total number of tickets sold: The total number of tickets sold is given as 6000.
By multiplying the probability of winning by the total number of tickets sold, we can calculate the number of tickets the man has bought. This is because the probability represents the ratio of favorable outcomes (winning tickets) to the total number of outcomes (total tickets sold).
In this case, the calculation is as follows:
Number of tickets bought = 0.08 × 6000 = 480
Therefore, the man has bought 480 tickets.
Number of tickets bought = Probability of winning × Total number of tickets
Given that the probability of winning the first prize is 0.08 and the total number of tickets sold is 6000, we can substitute these values into the formula:
Number of tickets bought = 0.08 × 6000
Simplifying the calculation:
Number of tickets bought = 480
Therefore, the man has bought 480 tickets.
Explanation:
Let's break down the problem into the following components:
1. Probability of winning: The probability of winning the first prize is given as 0.08. This means that out of every 100 tickets sold, he is expected to win the first prize in 8 tickets.
2. Total number of tickets sold: The total number of tickets sold is given as 6000.
By multiplying the probability of winning by the total number of tickets sold, we can calculate the number of tickets the man has bought. This is because the probability represents the ratio of favorable outcomes (winning tickets) to the total number of outcomes (total tickets sold).
In this case, the calculation is as follows:
Number of tickets bought = 0.08 × 6000 = 480
Therefore, the man has bought 480 tickets.
A lot of 24 bulbs contains 25% defective. A bulb is drawn at random from the lot. It is found to be not defective and it is not put back. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?- a)
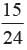
- b)
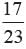
- c)
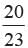
- d)
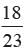
Correct answer is option 'B'. Can you explain this answer?
A lot of 24 bulbs contains 25% defective. A bulb is drawn at random from the lot. It is found to be not defective and it is not put back. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
a)
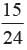
b)
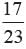
c)
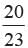
d)
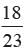
|
|
Vivek Bansal answered |
Total no. of bulbs = 24
No. of defective bulbs = 25% of 24

Now a bulb is drawn at random from the 10%. It is found to be not defective and it is not put back. Now one bulb is drawn at random from the rest. Hence the probability that this bulb is not defective =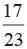
No. of defective bulbs = 25% of 24

Now a bulb is drawn at random from the 10%. It is found to be not defective and it is not put back. Now one bulb is drawn at random from the rest. Hence the probability that this bulb is not defective =
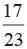
A card is drawn at random from a well shuffled deck of 52 cards. What is the probability that the card drawn is neither a king nor a queen?- a)
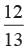
- b)
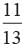
- c)
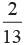
- d)
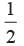
Correct answer is option 'B'. Can you explain this answer?
A card is drawn at random from a well shuffled deck of 52 cards. What is the probability that the card drawn is neither a king nor a queen?
a)
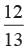
b)
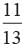
c)
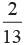
d)
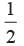
|
|
Deepak trivedi answered |
To find the probability that the card drawn is neither a king nor a queen, we first need to determine the total number of cards in the deck that are neither kings nor queens.
Total Number of Kings and Queens:
There are 4 kings and 4 queens in a deck of 52 cards.
Total Number of Cards:
There are 52 cards in a standard deck.
Calculating the Total Number of Cards that are neither Kings nor Queens:
To find the total number of cards that are neither kings nor queens, we subtract the number of kings and queens from the total number of cards.
Total Number of Cards that are neither Kings nor Queens = Total Number of Cards - Total Number of Kings - Total Number of Queens
= 52 - 4 - 4
= 44
Therefore, there are 44 cards in the deck that are neither kings nor queens.
Calculating the Probability:
The probability of drawing a card that is neither a king nor a queen can be calculated by dividing the number of favorable outcomes (44 cards that are neither kings nor queens) by the total number of possible outcomes (52 cards in the deck).
Probability = Number of Favorable Outcomes / Total Number of Possible Outcomes
= 44 / 52
= 11 / 13
Thus, the probability that the card drawn is neither a king nor a queen is 11/13, which corresponds to option B.
Total Number of Kings and Queens:
There are 4 kings and 4 queens in a deck of 52 cards.
Total Number of Cards:
There are 52 cards in a standard deck.
Calculating the Total Number of Cards that are neither Kings nor Queens:
To find the total number of cards that are neither kings nor queens, we subtract the number of kings and queens from the total number of cards.
Total Number of Cards that are neither Kings nor Queens = Total Number of Cards - Total Number of Kings - Total Number of Queens
= 52 - 4 - 4
= 44
Therefore, there are 44 cards in the deck that are neither kings nor queens.
Calculating the Probability:
The probability of drawing a card that is neither a king nor a queen can be calculated by dividing the number of favorable outcomes (44 cards that are neither kings nor queens) by the total number of possible outcomes (52 cards in the deck).
Probability = Number of Favorable Outcomes / Total Number of Possible Outcomes
= 44 / 52
= 11 / 13
Thus, the probability that the card drawn is neither a king nor a queen is 11/13, which corresponds to option B.
Find the probability of getting 52 sunday in a leap year.- a)
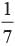
- b)

- c)
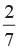
- d)
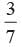
Correct answer is option 'B'. Can you explain this answer?
Find the probability of getting 52 sunday in a leap year.
a)
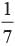
b)

c)
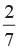
d)
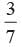
|
|
Sparsh Ghoshal answered |
Probability of Getting 52 Sundays in a Leap Year
A leap year has 366 days instead of the usual 365 days. This extra day is added to keep our calendar in alignment with the Earth's revolutions around the Sun.
In order to find the probability of getting 52 Sundays in a leap year, we need to consider the following factors:
1. Understanding Leap Years:
- A leap year occurs every 4 years.
- Leap years are divisible by 4, but not divisible by 100, unless they are divisible by 400.
2. Number of Days in a Week:
- There are 7 days in a week: Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, and Saturday.
3. Number of Sundays in a Leap Year:
- To find the number of Sundays in a leap year, we need to determine the number of days that fall on a Sunday.
- Since there are 7 days in a week, every 7th day will be a Sunday.
- Therefore, there will be a total of 52 Sundays in a leap year.
4. Calculating the Probability:
- Probability is defined as the number of desired outcomes divided by the total number of possible outcomes.
- In this case, the desired outcome is getting 52 Sundays in a leap year.
- The total number of possible outcomes is the total number of days in a leap year, which is 366.
- Therefore, the probability of getting 52 Sundays in a leap year is:
Desired Outcomes / Total Outcomes
= 52 / 366
= 13 / 91
= 1 / 7
≈ 0.143
Conclusion:
The probability of getting 52 Sundays in a leap year is 1/7 or approximately 0.143. This means that there is a 1 in 7 chance of any given day in a leap year being a Sunday.
A leap year has 366 days instead of the usual 365 days. This extra day is added to keep our calendar in alignment with the Earth's revolutions around the Sun.
In order to find the probability of getting 52 Sundays in a leap year, we need to consider the following factors:
1. Understanding Leap Years:
- A leap year occurs every 4 years.
- Leap years are divisible by 4, but not divisible by 100, unless they are divisible by 400.
2. Number of Days in a Week:
- There are 7 days in a week: Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, and Saturday.
3. Number of Sundays in a Leap Year:
- To find the number of Sundays in a leap year, we need to determine the number of days that fall on a Sunday.
- Since there are 7 days in a week, every 7th day will be a Sunday.
- Therefore, there will be a total of 52 Sundays in a leap year.
4. Calculating the Probability:
- Probability is defined as the number of desired outcomes divided by the total number of possible outcomes.
- In this case, the desired outcome is getting 52 Sundays in a leap year.
- The total number of possible outcomes is the total number of days in a leap year, which is 366.
- Therefore, the probability of getting 52 Sundays in a leap year is:
Desired Outcomes / Total Outcomes
= 52 / 366
= 13 / 91
= 1 / 7
≈ 0.143
Conclusion:
The probability of getting 52 Sundays in a leap year is 1/7 or approximately 0.143. This means that there is a 1 in 7 chance of any given day in a leap year being a Sunday.
500 tickets of a lottery were sold. There are 15 prizes on these tickets. If Mohan has purchased one ticket, what is the probability that he will win a price?- a)0.03
- b)0.01
- c)0.05
- d)0.04
Correct answer is option 'A'. Can you explain this answer?
500 tickets of a lottery were sold. There are 15 prizes on these tickets. If Mohan has purchased one ticket, what is the probability that he will win a price?
a)
0.03
b)
0.01
c)
0.05
d)
0.04
|
|
Vivek Bansal answered |
Total no. of tickets = 500
Total no. of prizes = 15
P (win a prize) =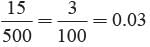
Total no. of prizes = 15
P (win a prize) =
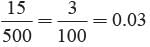
The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well-shuffled. One card is selected from the remaining cards. The probability of getting a club is ______- a)13/49
- b)10/49
- c)3/49
- d)1/49
Correct answer is option 'B'. Can you explain this answer?
The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well-shuffled. One card is selected from the remaining cards. The probability of getting a club is ______
a)
13/49
b)
10/49
c)
3/49
d)
1/49
|
|
Jay Choudhary answered |
The total number of cards in a deck is 52. After removing the king, queen, and jack of clubs, we are left with 49 cards. We want to find the probability of selecting a club from these 49 cards.
To calculate the probability, we need to determine the number of favorable outcomes (selecting a club) and the total number of possible outcomes (selecting any card from the remaining 49).
Favorable outcomes:
- There are 13 clubs in a deck, but we removed the king, queen, and jack of clubs, so we are left with 10 clubs.
Total possible outcomes:
- After removing the king, queen, and jack of clubs, we are left with 49 cards.
Therefore, the probability of selecting a club is:
Probability = (Number of favorable outcomes) / (Total number of possible outcomes)
Probability = 10 / 49
Hence, the correct answer is option B) 10/49.
To calculate the probability, we need to determine the number of favorable outcomes (selecting a club) and the total number of possible outcomes (selecting any card from the remaining 49).
Favorable outcomes:
- There are 13 clubs in a deck, but we removed the king, queen, and jack of clubs, so we are left with 10 clubs.
Total possible outcomes:
- After removing the king, queen, and jack of clubs, we are left with 49 cards.
Therefore, the probability of selecting a club is:
Probability = (Number of favorable outcomes) / (Total number of possible outcomes)
Probability = 10 / 49
Hence, the correct answer is option B) 10/49.
T hree c ards of spades are los t f r om a pack of 52 playing cards. The remaining cards were well shuffled and then a card was drawn at random from them. Find the probability that the drawn cards is of black colour.- a)26/49
- b)23/49
- c)13/26
- d)23/52
Correct answer is option 'B'. Can you explain this answer?
T hree c ards of spades are los t f r om a pack of 52 playing cards. The remaining cards were well shuffled and then a card was drawn at random from them. Find the probability that the drawn cards is of black colour.
a)
26/49
b)
23/49
c)
13/26
d)
23/52
|
|
Ritu Saxena answered |
No. of cards left = 52 - 3 = 49
No. of cards of spade left = 13 - 3 = 10
No. of black cards left = 13 + 10 = 23
[∵ Spade is of black colour]
Total no. of ways to draw a card = 49 No. of ways to draw a black card = 23
∴ Required probability = 23/49
No. of cards of spade left = 13 - 3 = 10
No. of black cards left = 13 + 10 = 23
[∵ Spade is of black colour]
Total no. of ways to draw a card = 49 No. of ways to draw a black card = 23
∴ Required probability = 23/49
A bag contains 12 balls of two different colours, out of which x are white. One ball is drawn at random. If 6 more white balls are put in the bag, the probability of drawing a white ball now will be double to that of the previous probability of drawing a white ball. Then, the value of x is _____.- a)3
- b)4
- c)5
- d)6
Correct answer is option 'A'. Can you explain this answer?
A bag contains 12 balls of two different colours, out of which x are white. One ball is drawn at random. If 6 more white balls are put in the bag, the probability of drawing a white ball now will be double to that of the previous probability of drawing a white ball. Then, the value of x is _____.
a)
3
b)
4
c)
5
d)
6

|
Jhanvi Pillai answered |
Understanding the Problem
To solve the problem, we need to establish the initial conditions and the subsequent changes in the bag's contents.
Initial Setup
- Total balls in the bag = 12
- White balls = x
- Therefore, non-white balls = 12 - x
Initial Probability of Drawing a White Ball
The probability (P1) of drawing a white ball initially is calculated as:
- P1 = Number of white balls / Total number of balls = x / 12
After Adding More White Balls
When 6 more white balls are added:
- New number of white balls = x + 6
- New total number of balls = 12 + 6 = 18
New Probability of Drawing a White Ball
The new probability (P2) of drawing a white ball becomes:
- P2 = (x + 6) / 18
Setting Up the Equation
According to the problem, the new probability is double the initial probability:
- P2 = 2 * P1
Substituting the probabilities:
- (x + 6) / 18 = 2 * (x / 12)
Solving the Equation
Cross-multiplying gives:
- 12(x + 6) = 36x
- 12x + 72 = 36x
- 72 = 36x - 12x
- 72 = 24x
- x = 72 / 24
- x = 3
Conclusion
Thus, the value of x, the number of white balls initially in the bag, is 3. The correct answer is option 'A'.
To solve the problem, we need to establish the initial conditions and the subsequent changes in the bag's contents.
Initial Setup
- Total balls in the bag = 12
- White balls = x
- Therefore, non-white balls = 12 - x
Initial Probability of Drawing a White Ball
The probability (P1) of drawing a white ball initially is calculated as:
- P1 = Number of white balls / Total number of balls = x / 12
After Adding More White Balls
When 6 more white balls are added:
- New number of white balls = x + 6
- New total number of balls = 12 + 6 = 18
New Probability of Drawing a White Ball
The new probability (P2) of drawing a white ball becomes:
- P2 = (x + 6) / 18
Setting Up the Equation
According to the problem, the new probability is double the initial probability:
- P2 = 2 * P1
Substituting the probabilities:
- (x + 6) / 18 = 2 * (x / 12)
Solving the Equation
Cross-multiplying gives:
- 12(x + 6) = 36x
- 12x + 72 = 36x
- 72 = 36x - 12x
- 72 = 24x
- x = 72 / 24
- x = 3
Conclusion
Thus, the value of x, the number of white balls initially in the bag, is 3. The correct answer is option 'A'.
Two dice are thrown at a time. The probability that the difference of the numbers shown on the dice is 1 is _____. - a)5/18
- b)1/36
- c)1/6
- d)1/18
Correct answer is option 'A'. Can you explain this answer?
Two dice are thrown at a time. The probability that the difference of the numbers shown on the dice is 1 is _____.
a)
5/18
b)
1/36
c)
1/6
d)
1/18
|
|
Govind sekhar answered |
Calculation:
When two dice are thrown, the sample space consists of all possible outcomes. For each dice, there are 6 possible outcomes (numbers 1 to 6). Therefore, the total number of outcomes when two dice are thrown is 6 x 6 = 36.
Favorable Outcomes:
To find the favorable outcomes, we need to determine the pairs of numbers whose difference is 1. We can list these pairs as follows:
(1, 2), (2, 1)
(2, 3), (3, 2)
(3, 4), (4, 3)
(4, 5), (5, 4)
(5, 6), (6, 5)
There are 10 favorable outcomes in total.
Probability:
The probability is defined as the ratio of favorable outcomes to the total number of outcomes. Therefore, the probability of getting a difference of 1 when two dice are thrown is:
Probability = Number of favorable outcomes / Total number of outcomes
= 10 / 36
= 5 / 18
Therefore, the correct answer is option A) 5/18.
When two dice are thrown, the sample space consists of all possible outcomes. For each dice, there are 6 possible outcomes (numbers 1 to 6). Therefore, the total number of outcomes when two dice are thrown is 6 x 6 = 36.
Favorable Outcomes:
To find the favorable outcomes, we need to determine the pairs of numbers whose difference is 1. We can list these pairs as follows:
(1, 2), (2, 1)
(2, 3), (3, 2)
(3, 4), (4, 3)
(4, 5), (5, 4)
(5, 6), (6, 5)
There are 10 favorable outcomes in total.
Probability:
The probability is defined as the ratio of favorable outcomes to the total number of outcomes. Therefore, the probability of getting a difference of 1 when two dice are thrown is:
Probability = Number of favorable outcomes / Total number of outcomes
= 10 / 36
= 5 / 18
Therefore, the correct answer is option A) 5/18.
The probability that it will rain today is 0.76. What is the probability that it will not rain today?- a)0.24
- b)0.2
- c)0.5
- d)1
Correct answer is option 'A'. Can you explain this answer?
The probability that it will rain today is 0.76. What is the probability that it will not rain today?
a)
0.24
b)
0.2
c)
0.5
d)
1
|
|
Vivek Bansal answered |
Let E be the event that it will rain today.
P(E) = 0.76
P (That it will not rain today) = 1 - 0.76
= 0.24
P(E) = 0.76
P (That it will not rain today) = 1 - 0.76
= 0.24
A bag contains 5 red balls and some black balls. If the probability of drawing a black ball from the bag is twice that of a red ball. Find the number of black balls in the bag.- a)7
- b)12
- c)10
- d)15
Correct answer is option 'C'. Can you explain this answer?
A bag contains 5 red balls and some black balls. If the probability of drawing a black ball from the bag is twice that of a red ball. Find the number of black balls in the bag.
a)
7
b)
12
c)
10
d)
15
|
|
Ritu Saxena answered |
Let the no. of black balls = x
Total no. of balls = x + 5
Probability of drawing a black ball =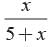
Probability of drawing a red ball =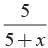
According to question,
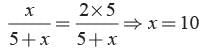
Total no. of balls = x + 5
Probability of drawing a black ball =
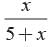
Probability of drawing a red ball =
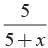
According to question,
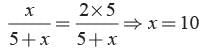
Find the probability of getting 53 Fridays in a leap year.- a)3/7
- b)4/7
- c)2/7
- d)5/7
Correct answer is option 'C'. Can you explain this answer?
Find the probability of getting 53 Fridays in a leap year.
a)
3/7
b)
4/7
c)
2/7
d)
5/7
|
|
Varsha das answered |
To find the probability of getting 53 Fridays in a leap year, we need to consider the total number of possible outcomes and the number of favorable outcomes.
Total number of outcomes:
In a leap year, there are 366 days.
Number of favorable outcomes:
To have 53 Fridays in a leap year, we need to have 53 days that fall on a Friday. There are 7 possible days of the week, so we can choose any 53 days out of the 366 days to be Fridays.
Using the combination formula, the number of ways to choose 53 days out of 366 is given by:
C(366, 53) = 366! / (53! * (366-53)!)
= (366 * 365 * 364 * ... * 315) / (53 * 52 * 51 * ... * 3 * 2 * 1)
Simplifying this expression would give us a very large number, but we don't need the exact value. We only need the probability, which is the ratio of the number of favorable outcomes to the total number of outcomes.
Calculating the probability:
The probability can be calculated as:
P = Number of favorable outcomes / Total number of outcomes
Since we have already determined that the total number of outcomes is 366 and the number of favorable outcomes is C(366, 53), we can substitute these values into the formula:
P = C(366, 53) / 366
Calculating this expression would give us a decimal value. To convert it into a fraction, we can simplify the expression by dividing both the numerator and denominator by their greatest common divisor.
After simplification, the probability can be written as a fraction, and the corresponding option is the correct answer.
Total number of outcomes:
In a leap year, there are 366 days.
Number of favorable outcomes:
To have 53 Fridays in a leap year, we need to have 53 days that fall on a Friday. There are 7 possible days of the week, so we can choose any 53 days out of the 366 days to be Fridays.
Using the combination formula, the number of ways to choose 53 days out of 366 is given by:
C(366, 53) = 366! / (53! * (366-53)!)
= (366 * 365 * 364 * ... * 315) / (53 * 52 * 51 * ... * 3 * 2 * 1)
Simplifying this expression would give us a very large number, but we don't need the exact value. We only need the probability, which is the ratio of the number of favorable outcomes to the total number of outcomes.
Calculating the probability:
The probability can be calculated as:
P = Number of favorable outcomes / Total number of outcomes
Since we have already determined that the total number of outcomes is 366 and the number of favorable outcomes is C(366, 53), we can substitute these values into the formula:
P = C(366, 53) / 366
Calculating this expression would give us a decimal value. To convert it into a fraction, we can simplify the expression by dividing both the numerator and denominator by their greatest common divisor.
After simplification, the probability can be written as a fraction, and the corresponding option is the correct answer.
Two dice are thrown simultaneously. The probability of getting a doublet or a total of 4 is _____.- a)2/9
- b)3/7
- c)4/9
- d)5/9
Correct answer is option 'A'. Can you explain this answer?
Two dice are thrown simultaneously. The probability of getting a doublet or a total of 4 is _____.
a)
2/9
b)
3/7
c)
4/9
d)
5/9
|
|
Renuka shah answered |
To find the probability of getting a doublet or a total of 4 when two dice are thrown simultaneously, we need to determine the number of favorable outcomes and the total number of possible outcomes.
Number of favorable outcomes:
1. Doublet: A doublet means both dice show the same number. There are six possible outcomes for a doublet - (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), and (6, 6).
2. Total of 4: To get a total of 4, there are three possible outcomes - (1, 3), (2, 2), and (3, 1).
Therefore, the number of favorable outcomes is 6 (for doublets) + 3 (for a total of 4) = 9.
Total number of possible outcomes:
When two dice are thrown simultaneously, each die has 6 possible outcomes. Since both dice are thrown together, the total number of possible outcomes is 6 x 6 = 36.
Probability:
Probability = Number of favorable outcomes / Total number of possible outcomes
Therefore, the probability of getting a doublet or a total of 4 is 9/36, which simplifies to 1/4.
To convert 1/4 into a multiple of 9, we can multiply both the numerator and denominator by 9.
1/4 * 9/9 = 9/36
So, the probability of getting a doublet or a total of 4 is 9/36, which is equal to 2/9.
Hence, the correct answer is option A, 2/9.
Number of favorable outcomes:
1. Doublet: A doublet means both dice show the same number. There are six possible outcomes for a doublet - (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), and (6, 6).
2. Total of 4: To get a total of 4, there are three possible outcomes - (1, 3), (2, 2), and (3, 1).
Therefore, the number of favorable outcomes is 6 (for doublets) + 3 (for a total of 4) = 9.
Total number of possible outcomes:
When two dice are thrown simultaneously, each die has 6 possible outcomes. Since both dice are thrown together, the total number of possible outcomes is 6 x 6 = 36.
Probability:
Probability = Number of favorable outcomes / Total number of possible outcomes
Therefore, the probability of getting a doublet or a total of 4 is 9/36, which simplifies to 1/4.
To convert 1/4 into a multiple of 9, we can multiply both the numerator and denominator by 9.
1/4 * 9/9 = 9/36
So, the probability of getting a doublet or a total of 4 is 9/36, which is equal to 2/9.
Hence, the correct answer is option A, 2/9.
A bag contains tickets marked with numbers 179, 180, 172, 127, 115, 115, 122, 143, 175, 222, 232, 162, 112, 132, 192, 182, 174, 132, 32, 131. A ticket is drawn at random. Find the probability that the ticket drawn has an even digit at 10’s place.- a)
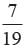
- b)
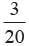
- c)
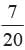
- d)
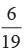
Correct answer is option 'C'. Can you explain this answer?
A bag contains tickets marked with numbers 179, 180, 172, 127, 115, 115, 122, 143, 175, 222, 232, 162, 112, 132, 192, 182, 174, 132, 32, 131. A ticket is drawn at random. Find the probability that the ticket drawn has an even digit at 10’s place.
a)
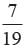
b)
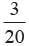
c)
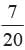
d)
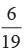
|
|
Vivek Bansal answered |
Total no. of tickets = 20
Let E = The ticket drawn has an even digit at 10’s place
E = 180, 127, 122, 143, 222, 162, 182,
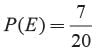
Let E = The ticket drawn has an even digit at 10’s place
E = 180, 127, 122, 143, 222, 162, 182,
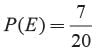
A box contains 5 red marbles, 7 black marbles and 3 white marbles. One marble is taken out from the box at random what is the probability that the marble taken out will be black or white?- a)
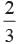
- b)

- c)
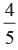
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A box contains 5 red marbles, 7 black marbles and 3 white marbles. One marble is taken out from the box at random what is the probability that the marble taken out will be black or white?
a)
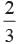
b)

c)
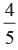
d)
None of these
|
|
Vivek Bansal answered |
No. of possible outcomes = 5 + 7 + 3 = 15
Probability of black marble =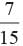
Probability of white marble =
Probability that the marble taken out will be black or white =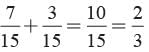
Probability of black marble =
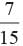
Probability of white marble =

Probability that the marble taken out will be black or white =
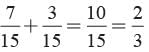
There are 35 tickets numbered 1, 2, 3, . . . 35. One ticket is drawn at random. What is the probability that the number on the ticket is a multiple of 3 or 5.- a)
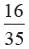
- b)
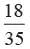
- c)
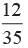
- d)

Correct answer is option 'A'. Can you explain this answer?
There are 35 tickets numbered 1, 2, 3, . . . 35. One ticket is drawn at random. What is the probability that the number on the ticket is a multiple of 3 or 5.
a)
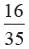
b)
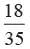
c)
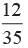
d)

|
|
Vivek Bansal answered |
1, 2, 3, . . . . 35
The multiples of 3 or 5 = 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30, 33, 35
P (ticket is a multiple of 3 or 5) =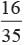
The multiples of 3 or 5 = 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30, 33, 35
P (ticket is a multiple of 3 or 5) =
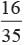
A Jar contains 54 marbles each of which is blue, green or white. The probability of getting a blue marble at random from the Jar is 1/3 and the probability of getting a green marble at random is 4/9. What is the number of white marbles?- a)12
- b)10
- c)21
- d)15
Correct answer is option 'A'. Can you explain this answer?
A Jar contains 54 marbles each of which is blue, green or white. The probability of getting a blue marble at random from the Jar is 1/3 and the probability of getting a green marble at random is 4/9. What is the number of white marbles?
a)
12
b)
10
c)
21
d)
15
|
|
Vivek Bansal answered |
Let there are b blue, g green and w white marbles.
b + g + w = 54
P (getting a blue marble) = b/54
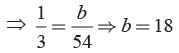
P (getting a green marble)
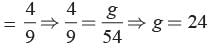
No. of while marbles = 54 - (18 + 24) = 54 - 42 = 12
b + g + w = 54
P (getting a blue marble) = b/54
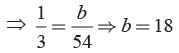
P (getting a green marble)
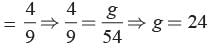
No. of while marbles = 54 - (18 + 24) = 54 - 42 = 12
What is the probability that a number selected at random from the numbers 1, 2, . . . . . 35 is not a multiple of 7?- a)
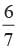
- b)
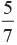
- c)
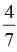
- d)
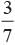
Correct answer is option 'A'. Can you explain this answer?
What is the probability that a number selected at random from the numbers 1, 2, . . . . . 35 is not a multiple of 7?
a)
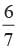
b)
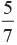
c)
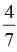
d)
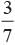
|
|
Ritu Saxena answered |
Numbers are 1, 2, 3, .......... 35
Total no. of possible outcomes = 35
E = The number which is multiple of 7
= 7, 14, 21, 28, 35
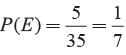
P (Not multiple of 7) =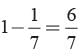
Total no. of possible outcomes = 35
E = The number which is multiple of 7
= 7, 14, 21, 28, 35
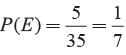
P (Not multiple of 7) =
A bag contains three green, four blue and two orange marbles. If a marble is picked at random, then the probability that it is not an orange marble, is ______ .- a)1/4
- b)1/3
- c)4/9
- d)7/9
Correct answer is option 'D'. Can you explain this answer?
A bag contains three green, four blue and two orange marbles. If a marble is picked at random, then the probability that it is not an orange marble, is ______ .
a)
1/4
b)
1/3
c)
4/9
d)
7/9
|
|
Vivek Bansal answered |
Total number of marbles = 3 + 4 + 2 = 9
No. of green and blue marbles = 3 + 4 = 7.
∴ Probability of not getting an orange marble = 7/9
No. of green and blue marbles = 3 + 4 = 7.
∴ Probability of not getting an orange marble = 7/9
One card is drawn from a well-shuffled deck of 52 cards. The probability of drawing an ace is _____.- a)1/12
- b)1/13
- c)1/50
- d)3/10
Correct answer is option 'B'. Can you explain this answer?
One card is drawn from a well-shuffled deck of 52 cards. The probability of drawing an ace is _____.
a)
1/12
b)
1/13
c)
1/50
d)
3/10
|
|
Vivek Bansal answered |
Total number of cards = 52
Total number of aces present in a deck of cards = 4
∴ Probability of drawing an ace = 4/52 = 1/13
Total number of aces present in a deck of cards = 4
∴ Probability of drawing an ace = 4/52 = 1/13
It is know that a box of 600 electric bulbs contains 12 defective bulbs. One bulb is taken out at random from this box. What is the probability that it is a non-defective bulb?- a)0.45
- b)0.98
- c)0.57
- d)0.85
Correct answer is option 'B'. Can you explain this answer?
It is know that a box of 600 electric bulbs contains 12 defective bulbs. One bulb is taken out at random from this box. What is the probability that it is a non-defective bulb?
a)
0.45
b)
0.98
c)
0.57
d)
0.85
|
|
Priyanka Kapoor answered |
Out of 600 electric bulbs one bulb can be chosen in 600 ways.
∴ Total number of elementary events = 600
There are 588 (= 600 - 12) non-defective bulbs out of which one bulb can be chosen in 588 ways.
∴ Favorable number of elementary events = 588
Hence. P (getting a non-defective bulb) = 588/600
= 49/50
= 0.98
∴ Total number of elementary events = 600
There are 588 (= 600 - 12) non-defective bulbs out of which one bulb can be chosen in 588 ways.
∴ Favorable number of elementary events = 588
Hence. P (getting a non-defective bulb) = 588/600
= 49/50
= 0.98
A letter is chosen at random from the letter of word concentration. What is the probability that the chosen letter is a consonant?- a)
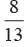
- b)
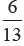
- c)
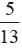
- d)
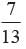
Correct answer is option 'A'. Can you explain this answer?
A letter is chosen at random from the letter of word concentration. What is the probability that the chosen letter is a consonant?
a)
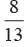
b)
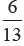
c)
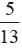
d)
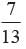
|
|
Ritu Saxena answered |
Total no. of letters = 13
No. of consonant letters = 8
Required probability =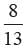
No. of consonant letters = 8
Required probability =
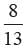
A letter is chosen at random from the letter of word communication. What is the probability that the chosen letter is a vowel?- a)
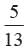
- b)

- c)
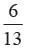
- d)
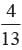
Correct answer is option 'C'. Can you explain this answer?
A letter is chosen at random from the letter of word communication. What is the probability that the chosen letter is a vowel?
a)
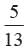
b)

c)
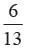
d)
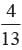
|
|
Ritu Saxena answered |
Total no. of letters = 13
No. of vowel letters = 6
Requited probability =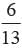
No. of vowel letters = 6
Requited probability =
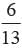
A die is thrown 350 times and the score of 6 obtained 28 times. Find the probability of getting a score under 6.- a)
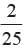
- b)
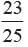
- c)
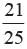
- d)
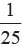
Correct answer is option 'B'. Can you explain this answer?
A die is thrown 350 times and the score of 6 obtained 28 times. Find the probability of getting a score under 6.
a)
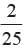
b)
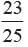
c)
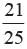
d)
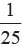
|
|
Vivek Bansal answered |
Total number of outcomes = 350 No. of score of 6 obtained = 28 No. of score under 6 obtained = 350 - 28 = 322
Probability of getting the score of under 6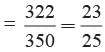
Probability of getting the score of under 6
A card is drawn from a well shuffled pack of 52 cards. Find the probability that the card drawn is a non ace.- a)
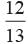
- b)
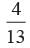
- c)
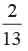
- d)
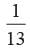
Correct answer is option 'A'. Can you explain this answer?
A card is drawn from a well shuffled pack of 52 cards. Find the probability that the card drawn is a non ace.
a)
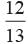
b)
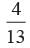
c)
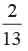
d)
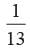
|
|
Ritu Saxena answered |
Total no. of outcomes = 52
No. of ace cards = 4
No. of Non ace cards = 52 - 4 = 48
P (getting a non-ace card) =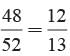
No. of ace cards = 4
No. of Non ace cards = 52 - 4 = 48
P (getting a non-ace card) =
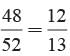
There are 25 cards numbered from 1 to 25. One card is drawn at random. What is the probability that the number on this card is not divisible by 4?- a)
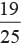
- b)
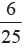
- c)
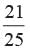
- d)
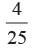
Correct answer is option 'A'. Can you explain this answer?
There are 25 cards numbered from 1 to 25. One card is drawn at random. What is the probability that the number on this card is not divisible by 4?
a)
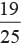
b)
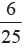
c)
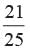
d)
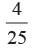
|
|
Vivek Bansal answered |
1, 2, 3, . . . . 35
The numbers which are divisible by 4. 4, 8, 12, 16, 20, 24
P (Number divisible by 4) =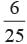
P (Number not divisible by 4) =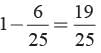
The numbers which are divisible by 4. 4, 8, 12, 16, 20, 24
P (Number divisible by 4) =
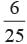
P (Number not divisible by 4) =
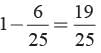
A bag contains 19 balls having numbers 1, 2, 3, . . . . . . . 19 respectively. A ball is drawn at random from the bag, what is the probability that the number on the ball is a prime number?- a)

- b)
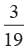
- c)

- d)
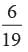
Correct answer is option 'A'. Can you explain this answer?
A bag contains 19 balls having numbers 1, 2, 3, . . . . . . . 19 respectively. A ball is drawn at random from the bag, what is the probability that the number on the ball is a prime number?
a)

b)
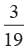
c)

d)
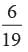
|
|
Vivek Bansal answered |
Total number of possible outcomes = 19 Out of the given numbers, prime numbers are –2, 3, 5, 7, 11, 13, 17, 19
P (the number on the ball is a prime) =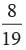
P (the number on the ball is a prime) =
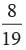
In a pack of 52 playing cards, the king, the queen, the Jack and 10 are lost, All these cards are of spade. A card is drawn from the remaining well shuffled back. Find the probability of getting a king.- a)
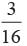
- b)
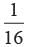
- c)

- d)
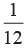
Correct answer is option 'B'. Can you explain this answer?
In a pack of 52 playing cards, the king, the queen, the Jack and 10 are lost, All these cards are of spade. A card is drawn from the remaining well shuffled back. Find the probability of getting a king.
a)
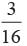
b)
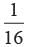
c)

d)
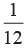
|
|
Vivek Bansal answered |
Remaining cards = 52 - 4 = 48
There are 3 kings
∴ P (getting a king) =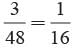
There are 3 kings
∴ P (getting a king) =
Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any one day as on another.
What is the probability that both will visit the shop on different days?- a)3/5
- b)4/5
- c)12/25
- d)1/5
Correct answer is option 'B'. Can you explain this answer?
Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any one day as on another.
What is the probability that both will visit the shop on different days?
What is the probability that both will visit the shop on different days?
a)
3/5
b)
4/5
c)
12/25
d)
1/5
|
|
Ritu Saxena answered |
Shyam and Ekta are visiting a shop from Tuesday to Saturday.
Total possible ways of visiting the shop by them = 5 x 5 = 25.
Possible ways of visiting the shop on same day = 5
∴ Possible ways of visiting the shop on different days = 25 - 5 = 20
∴ Probability o f visiting the shop on different days = 20/25 = 4/5
Total possible ways of visiting the shop by them = 5 x 5 = 25.
Possible ways of visiting the shop on same day = 5
∴ Possible ways of visiting the shop on different days = 25 - 5 = 20
∴ Probability o f visiting the shop on different days = 20/25 = 4/5
A let t er is chosen at random f rom t he letters of the word ‘ASSOCIATION’. Find the probability that the chosen letter is a vowel.- a)3/11
- b)5/11
- c)6/11
- d)7/11
Correct answer is option 'C'. Can you explain this answer?
A let t er is chosen at random f rom t he letters of the word ‘ASSOCIATION’. Find the probability that the chosen letter is a vowel.
a)
3/11
b)
5/11
c)
6/11
d)
7/11
|
|
Ritu Saxena answered |
Total number of letters in 'ASSOCIATION' = 11 Vowels are A, O, I, A, I, O, i.e, 6 in numbers.
∴ Probability of getting a vowel = 6/11
∴ Probability of getting a vowel = 6/11
A bag contains 6 blue and 4 green marbles. If a marble is drawn at random from the bag, the probability that the marble drawn is green, is ____.- a)2/5
- b)1/5
- c)4/5
- d)1/10
Correct answer is option 'A'. Can you explain this answer?
A bag contains 6 blue and 4 green marbles. If a marble is drawn at random from the bag, the probability that the marble drawn is green, is ____.
a)
2/5
b)
1/5
c)
4/5
d)
1/10
|
|
Ritu Saxena answered |
Total number of marbles = 10
∴ Probability of drawing a green marble = 4/10
= 2/5
∴ Probability of drawing a green marble = 4/10
= 2/5
In a bag, there are 70, Rs.1 coin, 30, Rs. 2 coin and 50, Rs. 5 coin. One coin is drawn at random. What is the probability that it will not be a Rs. 5 coin?- a)
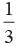
- b)
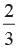
- c)
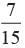
- d)
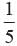
Correct answer is option 'B'. Can you explain this answer?
In a bag, there are 70, Rs.1 coin, 30, Rs. 2 coin and 50, Rs. 5 coin. One coin is drawn at random. What is the probability that it will not be a Rs. 5 coin?
a)
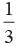
b)
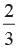
c)
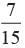
d)
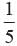
|
|
Vivek Bansal answered |
Total no. of possible outcomes
= 70 + 30 + 50
= 150
No. of Rs. 5 coin = 50
No. of coins of Rs. 1 & Rs. 2 coin = 70 + 30 = 100
P (will not be Rs. 5 coin) =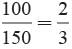
= 70 + 30 + 50
= 150
No. of Rs. 5 coin = 50
No. of coins of Rs. 1 & Rs. 2 coin = 70 + 30 = 100
P (will not be Rs. 5 coin) =
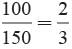
In a class, there are 35 boys and 15 girls. What is the probability of a randomly selected student of the class to be a girl?- a)
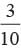
- b)
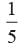
- c)
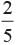
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In a class, there are 35 boys and 15 girls. What is the probability of a randomly selected student of the class to be a girl?
a)
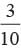
b)
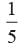
c)
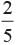
d)
None of these
|
|
Ritu Saxena answered |
Total no. of students = 35 + 15 = 50 Probability that selected student is a girl 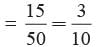
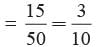
Two dice are thrown simultaneously. Who is the probability of getting 9 as the sum of two numbers that turn up?- a)
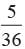
- b)

- c)
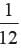
- d)
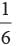
Correct answer is option 'B'. Can you explain this answer?
Two dice are thrown simultaneously. Who is the probability of getting 9 as the sum of two numbers that turn up?
a)
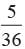
b)

c)
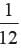
d)
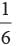
|
|
Vivek Bansal answered |
Total number of possible outcomes = 36 E = The sum of two numbers be 9 is as (3, 6), (6, 3), (4, 5), (5, 4)
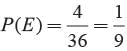
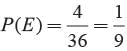
A bag contains 6 red balls, 8 white balls, 5 green balls and 3 black balls. One ball is drawn at random from the bag. Find the probability that the ball drawn is not white.- a)
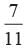
- b)
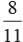
- c)
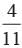
- d)
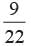
Correct answer is option 'A'. Can you explain this answer?
A bag contains 6 red balls, 8 white balls, 5 green balls and 3 black balls. One ball is drawn at random from the bag. Find the probability that the ball drawn is not white.
a)
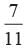
b)
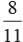
c)
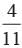
d)
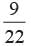
|
|
Vivek Bansal answered |
Total no. of balls = 6 + 8 + 5 + 3 = 22 Probability that ball drawn is not white
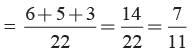
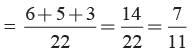
Chapter doubts & questions for Probability - Olympiad Preparation for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - Olympiad Preparation for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









