All Exams >
Mechanical Engineering >
Engineering Mechanics for Mechanical Engineering >
All Questions
All questions of Free Body Diagrams & Equilibrium Equations for Mechanical Engineering Exam
What is not the condition for the equilibrium in three dimensional system of axis?- a)∑Fx=0
- b)∑Fy=0
- c)∑Fz=0
- d)∑F≠0
Correct answer is option 'D'. Can you explain this answer?
What is not the condition for the equilibrium in three dimensional system of axis?
a)
∑Fx=0
b)
∑Fy=0
c)
∑Fz=0
d)
∑F≠0

|
Kritika Shah answered |
For the equilibrium in the three dimensional system of axis we have all the conditions true as, ∑Fx=0, ∑Fy=0 and ∑Fz=0. Also we have the summation of the forces equal to zero. Which is not a non-zero value.
Which of the following is correct?- a)The application of the conditions of the equilibrium of the body is valid only if the forces are collinear
- b)The application of the conditions of the equilibrium of the body is valid only if the forces are parallel
- c)The application of the conditions of the equilibrium of the body is valid only if the forces are perpendicular
- d)The application of the conditions of the equilibrium of the body is valid throughout
Correct answer is option 'D'. Can you explain this answer?
Which of the following is correct?
a)
The application of the conditions of the equilibrium of the body is valid only if the forces are collinear
b)
The application of the conditions of the equilibrium of the body is valid only if the forces are parallel
c)
The application of the conditions of the equilibrium of the body is valid only if the forces are perpendicular
d)
The application of the conditions of the equilibrium of the body is valid throughout
|
|
Bhargavi Chauhan answered |
The application of the conditions of the equilibrium of the body is valid throughout. This means that the conditions are irrespective of the types of forces. The conditions are the basic rules that defines the equilibrium of the body and thus are applicable in any type of forces of the real axis.
If five forces are acting on the single particle and having an angle of 72˚ between each and are collinear, then:- a)The net force acting on the body is zero
- b)The net force acting on the body is horizontal
- c)The net force acting on the body is vertical
- d)The net force acting on the body is at an angle of 45
Correct answer is option 'A'. Can you explain this answer?
If five forces are acting on the single particle and having an angle of 72˚ between each and are collinear, then:
a)
The net force acting on the body is zero
b)
The net force acting on the body is horizontal
c)
The net force acting on the body is vertical
d)
The net force acting on the body is at an angle of 45

|
Moumita Chopra answered |
Explanation:
To determine the net force acting on a particle, we need to consider the magnitude and direction of each force.
Given:
- Five forces are acting on the single particle.
- The forces have an angle of 72 degrees between each other.
- The forces are collinear.
Collinear Forces:
Collinear forces are forces that have the same line of action. This means that all the forces are acting along a straight line.
Angle between Forces:
The angle between each force is given as 72 degrees. Since the forces are collinear, this angle represents the angle between the directions of adjacent forces.
Net Force:
The net force is the vector sum of all the forces acting on the particle. If the net force is zero, it means that the forces are balanced and the particle will remain in equilibrium.
Analysis:
In this case, since the forces are collinear, they will add up algebraically to determine the net force. The angle between each force is 72 degrees, which means that each force contributes to the net force in the same direction.
If we consider the forces clockwise or counterclockwise, we can see that the forces cancel each other out. For every force in one direction, there is an equal and opposite force in the opposite direction.
Conclusion:
Since the forces are collinear and have an angle of 72 degrees between each other, they will cancel each other out when added algebraically. Therefore, the net force acting on the body is zero.
Answer:
The correct answer is option 'A': The net force acting on the body is zero.
To determine the net force acting on a particle, we need to consider the magnitude and direction of each force.
Given:
- Five forces are acting on the single particle.
- The forces have an angle of 72 degrees between each other.
- The forces are collinear.
Collinear Forces:
Collinear forces are forces that have the same line of action. This means that all the forces are acting along a straight line.
Angle between Forces:
The angle between each force is given as 72 degrees. Since the forces are collinear, this angle represents the angle between the directions of adjacent forces.
Net Force:
The net force is the vector sum of all the forces acting on the particle. If the net force is zero, it means that the forces are balanced and the particle will remain in equilibrium.
Analysis:
In this case, since the forces are collinear, they will add up algebraically to determine the net force. The angle between each force is 72 degrees, which means that each force contributes to the net force in the same direction.
If we consider the forces clockwise or counterclockwise, we can see that the forces cancel each other out. For every force in one direction, there is an equal and opposite force in the opposite direction.
Conclusion:
Since the forces are collinear and have an angle of 72 degrees between each other, they will cancel each other out when added algebraically. Therefore, the net force acting on the body is zero.
Answer:
The correct answer is option 'A': The net force acting on the body is zero.
A cantilever beam is one which is -- a)Fixed at one end and free at the other end
- b)Fixed at both ends
- c)Supported at its ends
- d)Supported at more than two points
Correct answer is option 'A'. Can you explain this answer?
A cantilever beam is one which is -
a)
Fixed at one end and free at the other end
b)
Fixed at both ends
c)
Supported at its ends
d)
Supported at more than two points

|
Nilanjan Rane answered |
Definition of Cantilever Beam:
A cantilever beam is a type of beam that is fixed at one end and free at the other end. This means that one end of the beam is securely anchored or supported, while the other end is left unsupported and extends into space.
Characteristics of Cantilever Beams:
- Fixed at one end: The fixed end of the beam is typically anchored to a wall, column, or other structure to provide stability and support.
- Free at the other end: The free end of the beam is not supported, which allows it to extend outwards without any additional support.
- Unidirectional loading: Cantilever beams are designed to carry loads in one direction, typically perpendicular to the fixed end of the beam.
Applications of Cantilever Beams:
Cantilever beams are commonly used in various structures and engineering applications, such as:
- Overhanging balconies and decks
- Diving boards
- Cantilever bridges
- Shelves and bookcases
- Crane arms
Analysis of Cantilever Beams:
When analyzing a cantilever beam, engineers consider factors such as the material properties, load distribution, and support conditions to ensure the beam can safely support the applied loads without failing. Various theories and equations, such as Euler-Bernoulli beam theory and moment-curvature relationships, are used to calculate the deflection, stress, and deformation of cantilever beams under different loading conditions.
A cantilever beam is a type of beam that is fixed at one end and free at the other end. This means that one end of the beam is securely anchored or supported, while the other end is left unsupported and extends into space.
Characteristics of Cantilever Beams:
- Fixed at one end: The fixed end of the beam is typically anchored to a wall, column, or other structure to provide stability and support.
- Free at the other end: The free end of the beam is not supported, which allows it to extend outwards without any additional support.
- Unidirectional loading: Cantilever beams are designed to carry loads in one direction, typically perpendicular to the fixed end of the beam.
Applications of Cantilever Beams:
Cantilever beams are commonly used in various structures and engineering applications, such as:
- Overhanging balconies and decks
- Diving boards
- Cantilever bridges
- Shelves and bookcases
- Crane arms
Analysis of Cantilever Beams:
When analyzing a cantilever beam, engineers consider factors such as the material properties, load distribution, and support conditions to ensure the beam can safely support the applied loads without failing. Various theories and equations, such as Euler-Bernoulli beam theory and moment-curvature relationships, are used to calculate the deflection, stress, and deformation of cantilever beams under different loading conditions.
Statically indeterminacy means?- a)There will be less equations available for equilibrium than the unknown loadings
- b)There will be more equations available for equilibrium than the unknown loadings
- c)There will be equal equations available for equilibrium as the unknown loadings
- d)The support reactions are opposite to each other
Correct answer is option 'A'. Can you explain this answer?
Statically indeterminacy means?
a)
There will be less equations available for equilibrium than the unknown loadings
b)
There will be more equations available for equilibrium than the unknown loadings
c)
There will be equal equations available for equilibrium as the unknown loadings
d)
The support reactions are opposite to each other
|
|
Athul Kumar answered |
Statically indeterminacy is the condition when less equations are available for equilibrium than the unknown loadings. This not only creates a problem in achieving the equilibrium but also affects the calculation of the equilibrium. Thus this is the stuff which one needs to prevent from happening.
If the body is in equilibrium, but it having a rotational curled ray shown in the free body diagram then:- a)The diagram is wrong
- b)Such rotations can’t be shown in the fbds(free body diagrams)
- c)The ray shown may be correct, but the body is not said to be in equilibrium
- d)The body is said to be in equilibrium only, as the other forces will cancel out that rotation
Correct answer is option 'D'. Can you explain this answer?
If the body is in equilibrium, but it having a rotational curled ray shown in the free body diagram then:
a)
The diagram is wrong
b)
Such rotations can’t be shown in the fbds(free body diagrams)
c)
The ray shown may be correct, but the body is not said to be in equilibrium
d)
The body is said to be in equilibrium only, as the other forces will cancel out that rotation
|
|
Sharmila Chauhan answered |
The body having equilibrium will not rotate at any cost. Yes, the diagram may contain the rotational array showing the couple being acted over the structure. But the thing is that the forces, i.e. the other forces which are outside the dependency of this rotation will cancel out this rotation and thus the body is in equilibrium.
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the total net force to zero.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the total net force to zero.
a)
True
b)
False
|
|
Stuti Bajaj answered |
Understanding the Concept
In mechanics, the analysis of forces acting on a system can often be complex, especially in three dimensions (3D). When dealing with intricate 3D scenarios, simplifying the problem to a two-dimensional (2D) representation can be beneficial.
Why Use 2D Instead of 3D?
- Simplification: Reducing the problem to 2D allows for easier calculations and visualization. Many scenarios can effectively be modeled in a plane without losing critical information about the forces involved.
- Net Force Equilibrium: In both 2D and 3D, the principle of equilibrium states that the total net force acting on a system must equal zero for the system to be in a state of rest or uniform motion. This can be expressed as:
- For 2D: ΣF_x = 0 and ΣF_y = 0
- For 3D: ΣF_x = 0, ΣF_y = 0, and ΣF_z = 0
Practical Application
- Vector Resolution: In 3D problems, forces can be resolved into their components along the x, y, and z axes. When solving in 2D, one can focus on just the x and y components, simplifying calculations.
- Cross-Verification: After solving the 2D system, one can verify the results by checking if the forces balance out in the third dimension, ensuring that the solution is robust.
Conclusion
Thus, if solving a 3D problem proves challenging, utilizing a 2D approach to equate total net forces to zero is a valid and often effective strategy. This method enhances understanding and simplifies the analysis without significantly compromising accuracy.
In mechanics, the analysis of forces acting on a system can often be complex, especially in three dimensions (3D). When dealing with intricate 3D scenarios, simplifying the problem to a two-dimensional (2D) representation can be beneficial.
Why Use 2D Instead of 3D?
- Simplification: Reducing the problem to 2D allows for easier calculations and visualization. Many scenarios can effectively be modeled in a plane without losing critical information about the forces involved.
- Net Force Equilibrium: In both 2D and 3D, the principle of equilibrium states that the total net force acting on a system must equal zero for the system to be in a state of rest or uniform motion. This can be expressed as:
- For 2D: ΣF_x = 0 and ΣF_y = 0
- For 3D: ΣF_x = 0, ΣF_y = 0, and ΣF_z = 0
Practical Application
- Vector Resolution: In 3D problems, forces can be resolved into their components along the x, y, and z axes. When solving in 2D, one can focus on just the x and y components, simplifying calculations.
- Cross-Verification: After solving the 2D system, one can verify the results by checking if the forces balance out in the third dimension, ensuring that the solution is robust.
Conclusion
Thus, if solving a 3D problem proves challenging, utilizing a 2D approach to equate total net forces to zero is a valid and often effective strategy. This method enhances understanding and simplifies the analysis without significantly compromising accuracy.
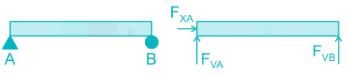
Determine the vertical components of the reaction on the beam caused by the pin at P. The force 60N is multiplied by 10 and then is applied.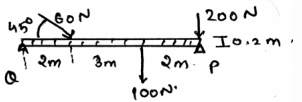
- a)405N
- b)445N
- c)45N
- d)40N
Correct answer is option 'A'. Can you explain this answer?
Determine the vertical components of the reaction on the beam caused by the pin at P. The force 60N is multiplied by 10 and then is applied.
a)
405N
b)
445N
c)
45N
d)
40N
|
|
Mahi Kaur answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
What is partially constrained?- a)There will be less equations available for equilibrium than the reactive forces
- b)There will be more equations available for equilibrium than the reactive forces
- c)There will be equal equations available for equilibrium as the reactive forces
- d)The support reactions are opposite to each other
Correct answer is option 'B'. Can you explain this answer?
What is partially constrained?
a)
There will be less equations available for equilibrium than the reactive forces
b)
There will be more equations available for equilibrium than the reactive forces
c)
There will be equal equations available for equilibrium as the reactive forces
d)
The support reactions are opposite to each other
|
|
Siddharth Menon answered |
The situation may arise when there will be more equations available for equilibrium than the reactive forces. This condition is known as partially constrained. This is also one of the factor which is giving instability to the structure.
When the body is in equilibrium then which of the following is true?- a)We equate all the components of the forces acting on the body equal to their resultant vector’s magnitude
- b)We equate all the components of the forces acting on the body equal to their resultant vector’s magnitude square
- c)We equate all the components of the forces acting on the body equal to their resultant vector’s magnitude square root
- d)We equate all the components of the forces acting on the body equal to zero
Correct answer is option 'D'. Can you explain this answer?
When the body is in equilibrium then which of the following is true?
a)
We equate all the components of the forces acting on the body equal to their resultant vector’s magnitude
b)
We equate all the components of the forces acting on the body equal to their resultant vector’s magnitude square
c)
We equate all the components of the forces acting on the body equal to their resultant vector’s magnitude square root
d)
We equate all the components of the forces acting on the body equal to zero
|
|
Pankaj Joshi answered |
A) We equate all the components of the forces acting on the body equal to their resultant vector.
An electromagnet crane is carrying the electromagnet with the help of the three cables. But the electromagnet is not stable because of the wind. What is science behind the cause?- a)The wind is making the net force of the body equal to a non-zero value
- b)The wind is making the net force of the body equal to zero value
- c)The wind is making the net force of the body equal to a non-zero value but is supporting the equilibrium
- d)The wind is making the net force of the body equal to zero value and supporting equilibrium
Correct answer is option 'A'. Can you explain this answer?
An electromagnet crane is carrying the electromagnet with the help of the three cables. But the electromagnet is not stable because of the wind. What is science behind the cause?
a)
The wind is making the net force of the body equal to a non-zero value
b)
The wind is making the net force of the body equal to zero value
c)
The wind is making the net force of the body equal to a non-zero value but is supporting the equilibrium
d)
The wind is making the net force of the body equal to zero value and supporting equilibrium
|
|
Ashish Pillai answered |
Any body is in equilibrium only if the net force along the three axis is zero. But in this case the wind is not helping the body to do so. The science behind this is that the resultant forces are being equated to a non-zero value by the wind. Hence unstable.
A simply supported laterally loaded beam was found to deflect more than a specified value. Which of the following measures will reduce the deflection?- a)Increase the area moment of inertia
- b)Increase the span of the beam
- c)Select a different material having lesser modulus of elasticity
- d)Magnitude of the load to be increased
Correct answer is option 'A'. Can you explain this answer?
A simply supported laterally loaded beam was found to deflect more than a specified value. Which of the following measures will reduce the deflection?
a)
Increase the area moment of inertia
b)
Increase the span of the beam
c)
Select a different material having lesser modulus of elasticity
d)
Magnitude of the load to be increased

|
Bhaskar Rane answered |
Increasing the area moment of inertia will reduce the deflection of a simply supported laterally loaded beam. This is because the area moment of inertia is a measure of the beam's resistance to bending, and a higher value indicates a stiffer beam.
Increasing the area moment of inertia can be achieved by:
- Using a beam with a larger cross-sectional area: This will increase the stiffness of the beam and reduce the deflection under a given load.
- Changing the shape of the beam to one with a greater area moment of inertia: For example, using an I-beam instead of a rectangular beam.
By increasing the area moment of inertia of the beam, the beam will be better able to resist bending and therefore deflect less under the same load. This is a common strategy used in structural engineering to reduce deflections in beams.
Increasing the area moment of inertia can be achieved by:
- Using a beam with a larger cross-sectional area: This will increase the stiffness of the beam and reduce the deflection under a given load.
- Changing the shape of the beam to one with a greater area moment of inertia: For example, using an I-beam instead of a rectangular beam.
By increasing the area moment of inertia of the beam, the beam will be better able to resist bending and therefore deflect less under the same load. This is a common strategy used in structural engineering to reduce deflections in beams.
If three forces, acting at a point, be in equilibrium then each force is proportional to the sine of the angle between the other two. This theorem is called- a)Law of triangle of forces
- b)Law of parallelogram of forces
- c)Lami's theorem
- d)Trigonometrical theorem
Correct answer is option 'C'. Can you explain this answer?
If three forces, acting at a point, be in equilibrium then each force is proportional to the sine of the angle between the other two. This theorem is called
a)
Law of triangle of forces
b)
Law of parallelogram of forces
c)
Lami's theorem
d)
Trigonometrical theorem

|
Alok Iyer answered |
The Concept of Lami's Theorem
Lami's Theorem is a fundamental principle in mechanics that applies to three forces acting at a single point. This theorem states that if three forces are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.
Understanding the Theorem
- The theorem is mathematically represented as:
\[
\frac{F_1}{\sin A} = \frac{F_2}{\sin B} = \frac{F_3}{\sin C}
\]
where:
- \(F_1, F_2, F_3\) are the magnitudes of the three forces.
- \(A, B, C\) are the angles opposite to the respective forces.
Conditions for Equilibrium
- For Lami's Theorem to hold true:
- The forces must be concurrent, meaning they all act at the same point.
- The forces must be in equilibrium, which means the net force acting on the point is zero.
Applications of Lami's Theorem
- Lami's Theorem is widely used in mechanical engineering to analyze structures and systems where multiple forces act at a point.
- It simplifies the calculations required to determine unknown forces and their angles.
Conclusion
- Option 'C', Lami's Theorem, provides a practical method for solving problems involving three forces in equilibrium.
- This theorem is essential for engineers and physicists when dealing with statics and dynamics in mechanical systems.
Lami's Theorem is a fundamental principle in mechanics that applies to three forces acting at a single point. This theorem states that if three forces are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.
Understanding the Theorem
- The theorem is mathematically represented as:
\[
\frac{F_1}{\sin A} = \frac{F_2}{\sin B} = \frac{F_3}{\sin C}
\]
where:
- \(F_1, F_2, F_3\) are the magnitudes of the three forces.
- \(A, B, C\) are the angles opposite to the respective forces.
Conditions for Equilibrium
- For Lami's Theorem to hold true:
- The forces must be concurrent, meaning they all act at the same point.
- The forces must be in equilibrium, which means the net force acting on the point is zero.
Applications of Lami's Theorem
- Lami's Theorem is widely used in mechanical engineering to analyze structures and systems where multiple forces act at a point.
- It simplifies the calculations required to determine unknown forces and their angles.
Conclusion
- Option 'C', Lami's Theorem, provides a practical method for solving problems involving three forces in equilibrium.
- This theorem is essential for engineers and physicists when dealing with statics and dynamics in mechanical systems.
The main condition for the rigid body is that the distance between various particles of the body does change.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
The main condition for the rigid body is that the distance between various particles of the body does change.
a)
True
b)
False
|
|
Ruchi Ahuja answered |
The main condition for the rigid body is that the distance between various particles of the body does not change. If the distance does change the body is not to be called as rigid. Thus the fix distance of the particles is very much required for the equilibrium of the rigid body.
Cantilever beams are always in equilibrium, whether you form the equilibrium equations or not.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Cantilever beams are always in equilibrium, whether you form the equilibrium equations or not.
a)
True
b)
False
|
|
Sahil Majumdar answered |
The thing is that the formation of the conditions only verifies that the body is in equilibrium or not. Thus if the cantilever is in equilibrium then also the condition needs to be applied. It will be wrong to justify the equilibrium only on the basis of structure.
Which of the following is correct?- a)The application of the conditions of the equilibrium of the body is valid only in the 2D
- b)The application of the conditions of the equilibrium of the body is valid only in the 3D
- c)The application of the conditions of the equilibrium of the body is valid only in the 1D
- d)The application of the conditions of the equilibrium of the body is valid throughout
Correct answer is option 'D'. Can you explain this answer?
Which of the following is correct?
a)
The application of the conditions of the equilibrium of the body is valid only in the 2D
b)
The application of the conditions of the equilibrium of the body is valid only in the 3D
c)
The application of the conditions of the equilibrium of the body is valid only in the 1D
d)
The application of the conditions of the equilibrium of the body is valid throughout
|
|
Nisha Singh answered |
The application of the conditions of the equilibrium of the body is valid throughout. This means that the conditions are irrespective of the dimensions. The conditions are the basic rules that defines the equilibrium of the body and thus are applicable in any dimension of the real axis.
Free body diagrams doesn’t play any role in making the calculations on the conditions of the equilibrium of the body.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Free body diagrams doesn’t play any role in making the calculations on the conditions of the equilibrium of the body.
a)
True
b)
False
|
|
Ishaan Malik answered |
't have any actual mass or weight, as they are simply visual representations used to analyze the forces acting on an object. They typically consist of a simple sketch of the object with arrows pointing in the direction of each force acting on it, along with labels indicating the type of force and its magnitude. Free body diagrams are an important tool in physics and engineering to help solve problems involving forces and motion.
For equilibrium the net force acting on the body is zero.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
For equilibrium the net force acting on the body is zero.
a)
True
b)
False
|
|
Mahi Kaur answered |
The equilibrium is only attained if the net force on the body tends to be equal to zero. Thus the forces cancels out. If this happens there is no motion of the body along any direction and hence the body is said to be in equilibrium. The body here is a rigid body.
According to Lami’s theorem, if three coplanar forces are acting at a point b in equilibrium, then each force is proportional to the ______ of the angle between the other two.- a)sine
- b)tangent
- c)sec
- d)cosine
Correct answer is option 'A'. Can you explain this answer?
According to Lami’s theorem, if three coplanar forces are acting at a point b in equilibrium, then each force is proportional to the ______ of the angle between the other two.
a)
sine
b)
tangent
c)
sec
d)
cosine
|
|
Avinash Sharma answered |
Lami's theorem:
It states that if three forces acting at a point are in equilibrium, each force is proportional to the sine of the angle between the other two forces.
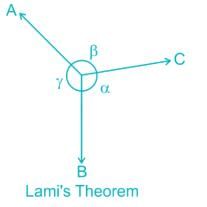
Consider three forces FA, FB, FC acting on a particle or rigid body making angles α, β and γ with each other.
Then from Lami's theorem,
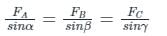
It states that if three forces acting at a point are in equilibrium, each force is proportional to the sine of the angle between the other two forces.
Consider three forces FA, FB, FC acting on a particle or rigid body making angles α, β and γ with each other.

Then from Lami's theorem,
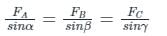
Determine the vertical components of the reaction on the beam caused by the pin at Q. The force 60N is multiplied by 10 and then is applied.- a)319N
- b)445N
- c)45N
- d)40N
Correct answer is option 'A'. Can you explain this answer?
Determine the vertical components of the reaction on the beam caused by the pin at Q. The force 60N is multiplied by 10 and then is applied.
a)
319N
b)
445N
c)
45N
d)
40N
|
|
Nandini Basak answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
Impact load is an example of - a)uniform load
- b)static load
- c)dynamic load
- d)fatigue load
Correct answer is option 'C'. Can you explain this answer?
Impact load is an example of
a)
uniform load
b)
static load
c)
dynamic load
d)
fatigue load
|
|
Sarita Yadav answered |
Load: A load is an external effort acting on the structure.
Uniform loading: The load that is either equal or varies uniformly along the element length is given as uniform load.
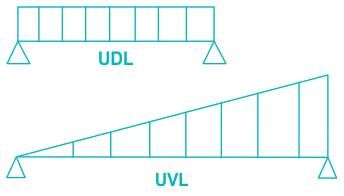
Where, UDL = uniformly distributed load, UVL = uniformly variable load
Static loading: Static load is a load that doesn't change over time and there will be no vibrations and no dynamic effects on the member.
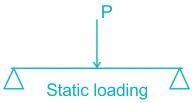
Dynamic loading: If the load increases rapidly and changes over time it is known as dynamic loading
⇒ Impact loading is an example of dynamic loading
Fatigue load: Fatigue loading is primarily the type of loading which causes cyclic variations in the applied stress or strain on a component. Thus any variable loading is basically a fatigue loading.
Under fatigue load, the material fails due to sudden propagation of cracks and fractures
Uniform loading: The load that is either equal or varies uniformly along the element length is given as uniform load.

Where, UDL = uniformly distributed load, UVL = uniformly variable load
Static loading: Static load is a load that doesn't change over time and there will be no vibrations and no dynamic effects on the member.

Dynamic loading: If the load increases rapidly and changes over time it is known as dynamic loading
⇒ Impact loading is an example of dynamic loading
Fatigue load: Fatigue loading is primarily the type of loading which causes cyclic variations in the applied stress or strain on a component. Thus any variable loading is basically a fatigue loading.
Under fatigue load, the material fails due to sudden propagation of cracks and fractures
If anybody is tied to three or more ropes, and then is allowed to achieve its equilibrium. Then the equilibrium achieved is achieved w.r.t what?- a)The ground
- b)The three axis of the body
- c)The ropes direction
- d)The weight direction
Correct answer is option 'A'. Can you explain this answer?
If anybody is tied to three or more ropes, and then is allowed to achieve its equilibrium. Then the equilibrium achieved is achieved w.r.t what?
a)
The ground
b)
The three axis of the body
c)
The ropes direction
d)
The weight direction
|
|
Neha Joshi answered |
Yes, the equilibrium is being achieved w.r.t the ground. Like the motion, w.r.t ground need be zero. That is the relative velocity of the object or the body must be zero w.r.t the ground. This means motion is in equilibrium.
What does the Newton’s second law states?- a)The rate of change of momentum is equal to the force applied
- b)For every reaction there is an opposite reaction
- c)The body is tend to be rotated if the force is applied tangentially
- d)The body is rest until a force is applied
Correct answer is option 'A'. Can you explain this answer?
What does the Newton’s second law states?
a)
The rate of change of momentum is equal to the force applied
b)
For every reaction there is an opposite reaction
c)
The body is tend to be rotated if the force is applied tangentially
d)
The body is rest until a force is applied
|
|
Anuj Chauhan answered |
The requirement of the second law is important in the equilibrium of the body. Specially the rigid bodies. The rigid body particles are if are in motion then this law helps in making the conditions for the equilibrium of the body. As when the body will leave its state of motion and come in rest, etc.
For equilibrium the net moment acting on the body by various forces is zero.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
For equilibrium the net moment acting on the body by various forces is zero.
a)
True
b)
False
|
|
Sagarika Mukherjee answered |
The equilibrium is only attained if the net moment on the body tends to be equal to zero. Thus the moments caused by different forces cancels out. If this happens there is no motion of the body along any direction and hence the body is said to be in equilibrium. The body here is a rigid body.
Determine the horizontal components of the reaction on the beam caused by the pin at P. The force 60N is multiplied by 10 and then is applied.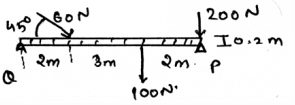
- a)424N
- b)24N
- c)44N
- d)441N
Correct answer is option 'A'. Can you explain this answer?
Determine the horizontal components of the reaction on the beam caused by the pin at P. The force 60N is multiplied by 10 and then is applied.
a)
424N
b)
24N
c)
44N
d)
441N

|
Nayanika Joshi answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
The net force of the body is zero that means the force are not being applied to the body at all and hence the body is in equilibrium.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'C'. Can you explain this answer?
The net force of the body is zero that means the force are not being applied to the body at all and hence the body is in equilibrium.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Rashi Chauhan answered |
Understanding Net Force and Equilibrium
When analyzing forces acting on a body, two key concepts are crucial: net force and equilibrium.
Net Force Equals Zero
- A net force of zero implies that all the forces acting on the body balance each other out.
- This can occur when:
- The body is at rest.
- The body is moving at a constant velocity.
Equilibrium Defined
- A body is said to be in equilibrium when it experiences no net force acting on it.
- There are two types of equilibrium:
- Static Equilibrium: The body is at rest.
- Dynamic Equilibrium: The body is in motion with a constant speed in a straight line.
Analyzing the Statement
- The statement claims that "the net force of the body is zero" and concludes "the body is in equilibrium."
- The first part of the statement is true because a net force of zero indeed indicates balanced forces.
- The second part is also true, as a body with no net force is, by definition, in equilibrium.
Conclusion
- Therefore, the correct option is C: "The first part of the statement is true and the other part is true too."
- This reflects the fundamental principles of mechanics where balance of forces leads to equilibrium.
Understanding these concepts is essential in mechanical engineering, as they form the basis for analyzing structures, machines, and dynamic systems.
When analyzing forces acting on a body, two key concepts are crucial: net force and equilibrium.
Net Force Equals Zero
- A net force of zero implies that all the forces acting on the body balance each other out.
- This can occur when:
- The body is at rest.
- The body is moving at a constant velocity.
Equilibrium Defined
- A body is said to be in equilibrium when it experiences no net force acting on it.
- There are two types of equilibrium:
- Static Equilibrium: The body is at rest.
- Dynamic Equilibrium: The body is in motion with a constant speed in a straight line.
Analyzing the Statement
- The statement claims that "the net force of the body is zero" and concludes "the body is in equilibrium."
- The first part of the statement is true because a net force of zero indeed indicates balanced forces.
- The second part is also true, as a body with no net force is, by definition, in equilibrium.
Conclusion
- Therefore, the correct option is C: "The first part of the statement is true and the other part is true too."
- This reflects the fundamental principles of mechanics where balance of forces leads to equilibrium.
Understanding these concepts is essential in mechanical engineering, as they form the basis for analyzing structures, machines, and dynamic systems.
Which of the following needs to zero for the perfect equilibrium?- a)∑F=0, ∑M=0 and ∑θ = 0
- b)∑F=0, ∑M≠0 and ∑θ = 0
- c)∑F≠0, ∑M=0 and ∑θ = 0
- d)∑F=0, ∑M=0 and ∑θ≠0
Correct answer is option 'D'. Can you explain this answer?
Which of the following needs to zero for the perfect equilibrium?
a)
∑F=0, ∑M=0 and ∑θ = 0
b)
∑F=0, ∑M≠0 and ∑θ = 0
c)
∑F≠0, ∑M=0 and ∑θ = 0
d)
∑F=0, ∑M=0 and ∑θ≠0
|
|
Ameya Kaur answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
What is redundant support?- a)The supports consisting of hinge and a roller
- b)The supports consisting of hinge only
- c)The supports consisting of roller only
- d)The supports more than necessary to hold the structure
Correct answer is option 'D'. Can you explain this answer?
What is redundant support?
a)
The supports consisting of hinge and a roller
b)
The supports consisting of hinge only
c)
The supports consisting of roller only
d)
The supports more than necessary to hold the structure
|
|
Ruchi Ahuja answered |
The supports if are more than the supports required to hold the structure are termed as the reductant supports. It becomes statically indeterminate. This not only creates a problem in achieving the equilibrium but also affects the calculation of the equilibrium.
Which of the following is correct?- a)There is only one type of support for the beams
- b)There are only two types of support for the beams
- c)There are only three types of support for the beams
- d)There are various types of support for the beams and they are countless
Correct answer is option 'D'. Can you explain this answer?
Which of the following is correct?
a)
There is only one type of support for the beams
b)
There are only two types of support for the beams
c)
There are only three types of support for the beams
d)
There are various types of support for the beams and they are countless
|
|
Prateek Mukherjee answered |
The support is the thing which a human decides. That can be anything. That is the support can be given in any way. The type of support also is important as different types of supports have different conditions for the equilibrium.
For the conditions of the equilibrium of the body, i.e. the rigid body only the external forces defines the equilibrium. And the support reactions only cancels out the rotation part of the body.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'C'. Can you explain this answer?
For the conditions of the equilibrium of the body, i.e. the rigid body only the external forces defines the equilibrium. And the support reactions only cancels out the rotation part of the body.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too

|
Shreya Choudhary answered |
**Explanation:**
**External Forces and Equilibrium:**
- The first part of the statement, which says that only external forces define the equilibrium of a rigid body, is **false**. In addition to external forces, internal forces within the body also play a crucial role in determining the equilibrium conditions.
- Internal forces such as tension, compression, and shear forces also need to be considered when analyzing the equilibrium of a rigid body. These internal forces contribute to the overall state of equilibrium of the body.
**Support Reactions and Equilibrium:**
- The second part of the statement, which mentions that support reactions only cancel out the rotation part of the body, is **false** as well. Support reactions are essential for maintaining both translational and rotational equilibrium of a rigid body.
- Support reactions not only counteract the rotational tendencies of a body but also help in balancing the external forces acting on the body. These reactions provide the necessary constraints that prevent the body from moving in any direction.
**Conclusion:**
- In conclusion, both parts of the statement are false. The equilibrium of a rigid body is influenced by both external and internal forces, and support reactions are crucial for maintaining both translational and rotational equilibrium.
**External Forces and Equilibrium:**
- The first part of the statement, which says that only external forces define the equilibrium of a rigid body, is **false**. In addition to external forces, internal forces within the body also play a crucial role in determining the equilibrium conditions.
- Internal forces such as tension, compression, and shear forces also need to be considered when analyzing the equilibrium of a rigid body. These internal forces contribute to the overall state of equilibrium of the body.
**Support Reactions and Equilibrium:**
- The second part of the statement, which mentions that support reactions only cancel out the rotation part of the body, is **false** as well. Support reactions are essential for maintaining both translational and rotational equilibrium of a rigid body.
- Support reactions not only counteract the rotational tendencies of a body but also help in balancing the external forces acting on the body. These reactions provide the necessary constraints that prevent the body from moving in any direction.
**Conclusion:**
- In conclusion, both parts of the statement are false. The equilibrium of a rigid body is influenced by both external and internal forces, and support reactions are crucial for maintaining both translational and rotational equilibrium.
Determine the horizontal components of the reaction on the beam caused by the pin at Q.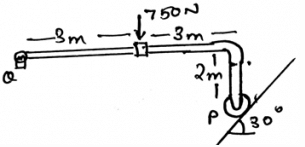
- a)268N
- b)68N
- c)28N
- d)288N
Correct answer is option 'A'. Can you explain this answer?
Determine the horizontal components of the reaction on the beam caused by the pin at Q.
a)
268N
b)
68N
c)
28N
d)
288N
|
|
Prateek Mukherjee answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
Which of the following is CORRECT for indeterminate beam condition?- a)Number of unknown components should be equal to the number of equilibrium equations
- b)Number of unknown components should be less than the number of equilibrium equations
- c)Number of unknown components should be greater than the number of equilibrium equations
- d)Number of unknown components should be zero
Correct answer is option 'C'. Can you explain this answer?
Which of the following is CORRECT for indeterminate beam condition?
a)
Number of unknown components should be equal to the number of equilibrium equations
b)
Number of unknown components should be less than the number of equilibrium equations
c)
Number of unknown components should be greater than the number of equilibrium equations
d)
Number of unknown components should be zero
|
|
Avinash Sharma answered |
A beam is said to be in static equilibrium when the beam is initially at rest and remains at rest when subjected to a system of forces and couples.
Generally, there are 3 equilibrium equations for a planer structure.
The conditions of zero resultant force and zero resultant couple can be expressed as:
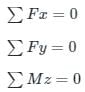
where Fx represents forces along the horizontal or x-axis, Fy represents forces along the vertical or y-axis, and Mz represents the sum of moments taken around any point on the beam.
Degree of indeterminacy = Total number of unknown forces - Total number of equilibrium equations
Eg. Statically indeterminate structure

Here, the total number of unknown forces = 7
total number of equilibrium equations = 3
So, the degree of indeterminacy = 7 - 3 = 4, which is greater than zero so it is a statically indeterminate structure.
Eg. Statically determinate structure
Here, the total number of unknown forces = 3
Total number of equilibrium equations = 3
So, the degree of indeterminacy = 3 - 3 = 0, so it is a statically determinate structure.
Generally, there are 3 equilibrium equations for a planer structure.
The conditions of zero resultant force and zero resultant couple can be expressed as:
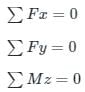
where Fx represents forces along the horizontal or x-axis, Fy represents forces along the vertical or y-axis, and Mz represents the sum of moments taken around any point on the beam.
Degree of indeterminacy = Total number of unknown forces - Total number of equilibrium equations

Eg. Statically indeterminate structure

Here, the total number of unknown forces = 7
total number of equilibrium equations = 3
So, the degree of indeterminacy = 7 - 3 = 4, which is greater than zero so it is a statically indeterminate structure.
Eg. Statically determinate structure

Here, the total number of unknown forces = 3
Total number of equilibrium equations = 3
So, the degree of indeterminacy = 3 - 3 = 0, so it is a statically determinate structure.
The improper constraining leading to instability occurs when ___________________- a)The reactive forces are parallel
- b)The reactive forces are perpendicular
- c)The reactive forces are equal
- d)The reactive forces are rotational
Correct answer is option 'A'. Can you explain this answer?
The improper constraining leading to instability occurs when ___________________
a)
The reactive forces are parallel
b)
The reactive forces are perpendicular
c)
The reactive forces are equal
d)
The reactive forces are rotational
|
|
Mrinalini Sharma answered |
If the forces are parallel (the reactive forces) then this creates an instability. That is this is also a type of improper constraining which is resulting in instability of the structure. Thus reactive forces are parallel are resulting in the instability of the body.
The generation of equal equations available for equilibrium as the unknown loadings always guarantees the stability of the body.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
The generation of equal equations available for equilibrium as the unknown loadings always guarantees the stability of the body.
a)
True
b)
False
|
|
Ashutosh Sharma answered |
The generation of equal equations available for equilibrium as the unknown loadings doesn’t always guarantees the stability of the body. It is defined on the basis of the supports that are their supporting the body. Or it also depends on the types of the forces that are acting, i.e. the three or two force system.
Determine the horizontal components of the reaction on the beam caused by the roller at P.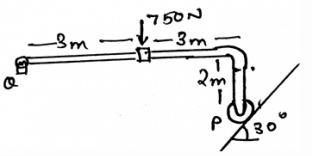
- a)536N
- b)536cos30N
- c)536sin30N
- d)536tan30N
Correct answer is option 'C'. Can you explain this answer?
Determine the horizontal components of the reaction on the beam caused by the roller at P.
a)
536N
b)
536cos30N
c)
536sin30N
d)
536tan30N
|
|
Anu Deshpande answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
Determine the vertical components of the reaction on the beam caused by the roller at P.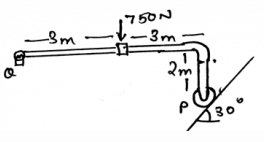
- a)536N
- b)536cos30N
- c)536sin30N
- d)536tan30N
Correct answer is option 'B'. Can you explain this answer?
Determine the vertical components of the reaction on the beam caused by the roller at P.
a)
536N
b)
536cos30N
c)
536sin30N
d)
536tan30N
|
|
Gaurav Kapoor answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
The shown here has a mass of 100kg. What is missing here in the diagram?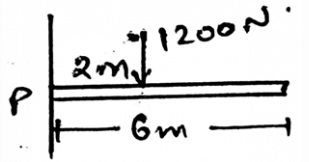
- a)The weight of the body is not shown
- b)The moment of the force is not shown
- c)The body cant be held like this
- d)The body diagonal is not shown
Correct answer is option 'A'. Can you explain this answer?
The shown here has a mass of 100kg. What is missing here in the diagram?
a)
The weight of the body is not shown
b)
The moment of the force is not shown
c)
The body cant be held like this
d)
The body diagonal is not shown
|
|
Saikat Choudhary answered |
The main condition for the rigid body is that the distance between various particles of the body does not change. If the distance does change the body is not to be called as rigid. Thus the fix distance of the particles is very much required for the equilibrium of the rigid body.
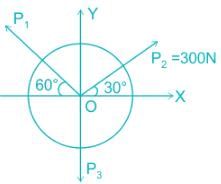
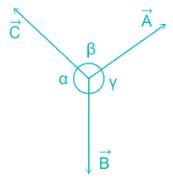
A body acted upon by three coplanar forces P1, P2 and P3 (as shown in figure) is in equilibrium. Which of the following is correct? [where, "O" is the point of concurrency of the forces]
- a)P3 = 600 N
- b)P1 = P3 = 400 N
- c)P1 = P2 = P3 = 300 N
- d)P1 = 350 N
Correct answer is option 'A'. Can you explain this answer?
A body acted upon by three coplanar forces P1, P2 and P3 (as shown in figure) is in equilibrium. Which of the following is correct? [where, "O" is the point of concurrency of the forces]


a)
P3 = 600 N
b)
P1 = P3 = 400 N
c)
P1 = P2 = P3 = 300 N
d)
P1 = 350 N
|
|
Yash Patel answered |
LAMI’S THEOREM:
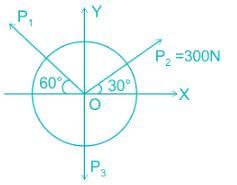
- If a system of Three forces is in equilibrium, then, each force of the system is proportional to sine of the angle between the other two forces (and constant of proportionality is the same for all the forces). Thus, we have,
The formula for Lami's Theorem:
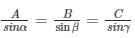
Calculation:
Given:
A = P1, B = P2 = 300N, C = P3, and
α = 90° + 30° = 120°, β = 90° + 60° = 150° and γ = 360° - 120° - 150° = 90°
on salving
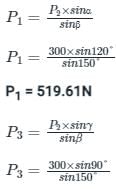
P3 = 600N
only option 1 is correct.
State true or false. We first make equilibrium equations and then the free body diagram and then solve the question?- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
State true or false. We first make equilibrium equations and then the free body diagram and then solve the question?
a)
True
b)
False
|
|
Anu Deshpande answered |
We first make the free body diagram and then we make the equilibrium equations to satisfy the given conditions. This helps us to solve the question easily. As this reduces the part of imagination and increases accuracy too.
Determine the horizontal components of the reaction on the beam caused by the pin at Q.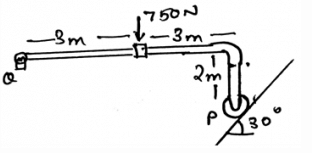
- a)268N
- b)68N
- c)28N
- d)288N
Correct answer is option 'A'. Can you explain this answer?
Determine the horizontal components of the reaction on the beam caused by the pin at Q.
a)
268N
b)
68N
c)
28N
d)
288N
|
|
Pritam Jain answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
To satisfy the conditions of the equilibrium, the must not only be having a net force zero, but also be properly held or constrained on its supports.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
To satisfy the conditions of the equilibrium, the must not only be having a net force zero, but also be properly held or constrained on its supports.
a)
True
b)
False
|
|
Saikat Choudhary answered |
To satisfy the conditions of the equilibrium, the must not only be having a net force zero, but also be properly held or constrained on its supports. The more the stable are the supports the more the stable is the equilibrium, that is the more easily is the equilibrium is achived.
Consider a beam sustaining a load of "L" kN at its center. Which of the following options gives the maximum bending moment of the given beam? (where I is length of beam)- a)L × l/4 kNm
- b)L × l/2 kNm
- c)L/l kNm
- d)L × l kNm
Correct answer is option 'A'. Can you explain this answer?
Consider a beam sustaining a load of "L" kN at its center. Which of the following options gives the maximum bending moment of the given beam? (where I is length of beam)
a)
L × l/4 kNm
b)
L × l/2 kNm
c)
L/l kNm
d)
L × l kNm
|
|
Avinash Sharma answered |
When a simply supported beam is subjected to a point load, L at the center of the length of the beam then there will be the generation of two equal vertical reactions, L/2 at the ends.
By drawing a bending moment diagram of this beam, it is clearly indicated that the maximum bending moment in the beam occurs at the center of beam length and its value is [(L/2) × (l/2)] or L × l/4 kN-m
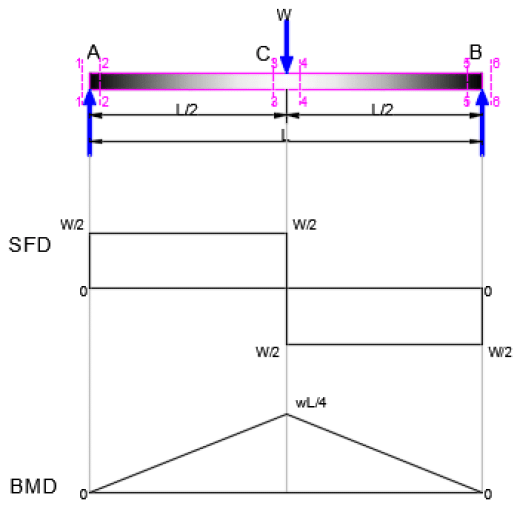
By drawing a bending moment diagram of this beam, it is clearly indicated that the maximum bending moment in the beam occurs at the center of beam length and its value is [(L/2) × (l/2)] or L × l/4 kN-m

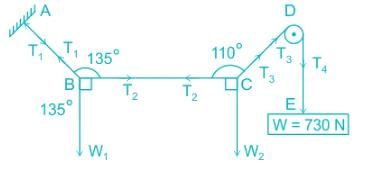
A string whose extreme A is fixed has weights W1 and W2 attached to it at B and C, respectively, and passes around a smooth peg D carrying a weight of 730 N at the free end E. If in a state of equilibrium, BC is horizontal and AB and CD make angles of 135° and 110°, respectively, with BC, the weights W1 and W2 will be ______ and ______, respectively.
- a)353 N; 685.9 N
- b)353 N; 730 N
- c)249.67 N; 353 N
- d)249.67 N; 685.9 N
Correct answer is option 'D'. Can you explain this answer?
A string whose extreme A is fixed has weights W1 and W2 attached to it at B and C, respectively, and passes around a smooth peg D carrying a weight of 730 N at the free end E. If in a state of equilibrium, BC is horizontal and AB and CD make angles of 135° and 110°, respectively, with BC, the weights W1 and W2 will be ______ and ______, respectively.


a)
353 N; 685.9 N
b)
353 N; 730 N
c)
249.67 N; 353 N
d)
249.67 N; 685.9 N
|
|
Avinash Sharma answered |
Lami's theorem:
It states that if three forces acting at a point are in equilibrium, each force is proportional to the sine of the angle between the other two forces.
Consider three forces FA, FB, and FC acting on a particle or rigid body making angles α, β, and γ with each other.
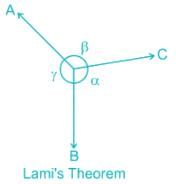
Then from Lami's theorem,
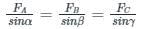
Calculation:
Given:
W = 730 N, And the pulley is smooth.
First string ABCD is split into two parts and consider the joints B and C separately.
Let, T1 = Tension in String AB, T2 = Tension in String BC, T3 = Tension in String CD, T4 = Tension in String DE
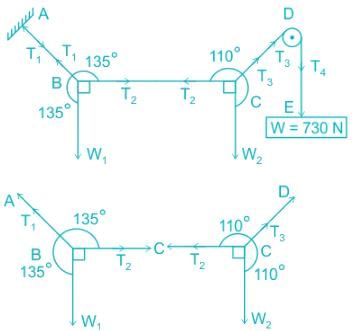
Since at joint B and C, three forces are acting on both points. But at B all three forces are unknown and at point C only two forces are unknown. So Apply Lami's theorem first at joint C:
∵ Pulley is smooth, T3 = T4 = 730 N
Apply Lami's theorem first at joint C:
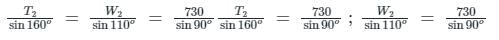
⇒ T2 = 249.674 N And W2 = 685.98 N
Now, the value of T2 is known at point B.
Apply Lami's theorem first at joint B:
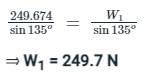
It states that if three forces acting at a point are in equilibrium, each force is proportional to the sine of the angle between the other two forces.
Consider three forces FA, FB, and FC acting on a particle or rigid body making angles α, β, and γ with each other.

Then from Lami's theorem,
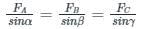
Calculation:
Given:
W = 730 N, And the pulley is smooth.
First string ABCD is split into two parts and consider the joints B and C separately.
Let, T1 = Tension in String AB, T2 = Tension in String BC, T3 = Tension in String CD, T4 = Tension in String DE

Since at joint B and C, three forces are acting on both points. But at B all three forces are unknown and at point C only two forces are unknown. So Apply Lami's theorem first at joint C:
∵ Pulley is smooth, T3 = T4 = 730 N
Apply Lami's theorem first at joint C:
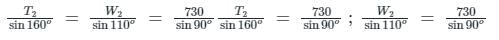
⇒ T2 = 249.674 N And W2 = 685.98 N
Now, the value of T2 is known at point B.
Apply Lami's theorem first at joint B:
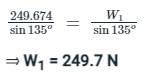
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the sum of all the vertical forces at the supports.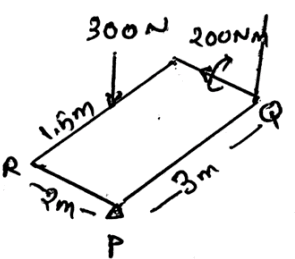
- a)1280N
- b)80N
- c)200N
- d)100N
Correct answer is option 'A'. Can you explain this answer?
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the sum of all the vertical forces at the supports.
a)
1280N
b)
80N
c)
200N
d)
100N
|
|
Ruchi Ahuja answered |
As the vertical force means that the force is going from the outer to the inner section of the plate and the horizontal force means that the force is travelling along the plane of the surface. Thus by applying the conditions for the equilibrium we get the above answer.
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the vertical reaction at the support P.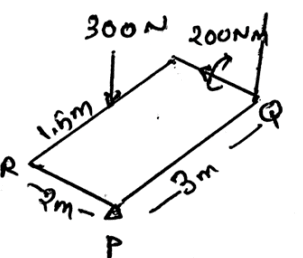
- a)-217N
- b)80N
- c)700N
- d)-250N
Correct answer is option 'A'. Can you explain this answer?
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the vertical reaction at the support P.
a)
-217N
b)
80N
c)
700N
d)
-250N
|
|
Mrinalini Sharma answered |
As the vertical force means that the force is going from the outer to the inner section of the plate and the horizontal force means that the force is travelling along the plane of the surface. Thus by applying the conditions for the equilibrium we get the above answer.
For the conditions of the equilibrium of the body, i.e. the rigid body only the external forces defines the equilibrium. Because the internal forces cancels out so not to be considered.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'C'. Can you explain this answer?
For the conditions of the equilibrium of the body, i.e. the rigid body only the external forces defines the equilibrium. Because the internal forces cancels out so not to be considered.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Debolina Menon answered |
The application of the internal forces does affect the conditions of the equilibrium of the body. Not only the external but the internal forces that are developed by the sake of external forces does develop a tending effect on the equilibrium of the body. Thus the internal forces doesn’t cancels out.
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the vertical reaction at the support Q.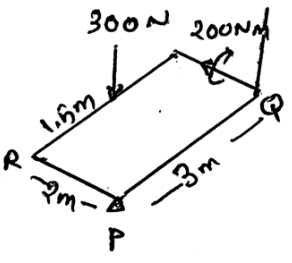
- a)707N
- b)80N
- c)200N
- d)100N
Correct answer is option 'A'. Can you explain this answer?
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the vertical reaction at the support Q.
a)
707N
b)
80N
c)
200N
d)
100N
|
|
Athul Kumar answered |
As the vertical force means that the force is going from the outer to the inner section of the plate and the horizontal force means that the force is travelling along the plane of the surface. Thus by applying the conditions for the equilibrium we get the above answer.
In 3D the body will be improperly constrained if the axis is intersected by the reaction forces.- a)The statement is right
- b)The statement is wrong
- c)The statement is right if there is ‘2D’
- d)The statement is right if there is ‘support reaction’
Correct answer is option 'A'. Can you explain this answer?
In 3D the body will be improperly constrained if the axis is intersected by the reaction forces.
a)
The statement is right
b)
The statement is wrong
c)
The statement is right if there is ‘2D’
d)
The statement is right if there is ‘support reaction’
|
|
Stuti Mishra answered |
In 3D the body will be improperly constrained if the axis is intersected by the reaction forces. This is because there will be small moments which will occur in the real situations. But they will not be matched in the calculations done for determining the equilibrium. Thus the statement is right.
The additional equations invented in the statically indeterminacy condition is solved by __________- a)Deformation conditions at the point of supports
- b)Rotational equations
- c)Translation equations
- d)Linear rotation equations
Correct answer is option 'A'. Can you explain this answer?
The additional equations invented in the statically indeterminacy condition is solved by __________
a)
Deformation conditions at the point of supports
b)
Rotational equations
c)
Translation equations
d)
Linear rotation equations
|
|
Ruchi Ahuja answered |
The additional equations invented in the statically indeterminacy condition is solved by deformation conditions at the point of supports. This are the conditions which are based on the physical and the chemical properties of the body. A different study for this is done in mechanics of material.
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the vertical reaction at the support R.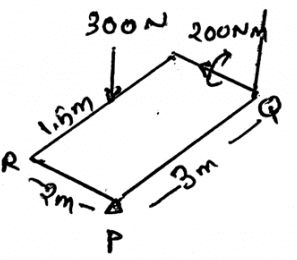
- a)790N
- b)80N
- c)200N
- d)100N
Correct answer is option 'A'. Can you explain this answer?
A homogeneous plate is shown has a mass of 100kg and is subjected to a force and a system of couple along its edge. If it is supported by a horizontal plane and a roller at R a ball and socket joint at P and a cord at Q, determine the vertical reaction at the support R.
a)
790N
b)
80N
c)
200N
d)
100N
|
|
Ruchi Ahuja answered |
As the vertical force means that the force is going from the outer to the inner section of the plate and the horizontal force means that the force is travelling along the plane of the surface. Thus by applying the conditions for the equilibrium we get the above answer.
Chapter doubts & questions for Free Body Diagrams & Equilibrium Equations - Engineering Mechanics for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Free Body Diagrams & Equilibrium Equations - Engineering Mechanics for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Engineering Mechanics for Mechanical Engineering
33 videos|78 docs|44 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









