All Exams >
Mechanical Engineering >
Engineering Mechanics for Mechanical Engineering >
All Questions
All questions of Kinematics of Point Mass & Rigid Bodies for Mechanical Engineering Exam
The centre of mass for the composite body is the ratio of ________ to _________- a)The product of centroid and mass to the total weight
- b)The addition of centroid and weight to the total weight
- c)The subtraction of centroid and weight to the total weight
- d)The product of centroid and mass to the total mass
Correct answer is option 'D'. Can you explain this answer?
The centre of mass for the composite body is the ratio of ________ to _________
a)
The product of centroid and mass to the total weight
b)
The addition of centroid and weight to the total weight
c)
The subtraction of centroid and weight to the total weight
d)
The product of centroid and mass to the total mass

|
Pratap Singh answered |
A
The total of all the weights of small particles adds up to give the total body weight. This weight is the force vector which is being passed by ________- a)Axis of rotation
- b)Axis of rolling
- c)Centre of Gravity
- d)Centre of mass
Correct answer is option 'C'. Can you explain this answer?
The total of all the weights of small particles adds up to give the total body weight. This weight is the force vector which is being passed by ________
a)
Axis of rotation
b)
Axis of rolling
c)
Centre of Gravity
d)
Centre of mass

|
Akinware Breakthrough answered |
The total weight passes through the center of gravity
When a particle moves along a straight path, then the particle has- a)tangential acceleration only
- b)centripetal acceleration only
- c)both tangential and centripetal acceleration
- d)none of the mentioned
Correct answer is option 'A'. Can you explain this answer?
When a particle moves along a straight path, then the particle has
a)
tangential acceleration only
b)
centripetal acceleration only
c)
both tangential and centripetal acceleration
d)
none of the mentioned
|
|
Neha Joshi answered |
The acceleration of a particle at any instant moving along a circular path in a direction tangential to that instant, is known as tangential component of acceleration or tangential acceleration.
What is the mass MOI of a hollow circular cylinder if R is the outer diameter and r is the inner diameter?- a)M(R + r)/4
- b)M(R – r )/4
- c)M(R+ r)/2
- d)M(R – r)/2
Correct answer is option 'A'. Can you explain this answer?
What is the mass MOI of a hollow circular cylinder if R is the outer diameter and r is the inner diameter?
a)
M(R + r)/4
b)
M(R – r )/4
c)
M(R+ r)/2
d)
M(R – r)/2
|
|
Sarita Yadav answered |
The mass MOI of a hollow circular cylinder is M(R + r)/4 where R is the outer diameter and r is the inner diameter.
The x axis coordinate and the y axis coordinate of the centroid are having different types of calculations to calculate them.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
The x axis coordinate and the y axis coordinate of the centroid are having different types of calculations to calculate them.
a)
True
b)
False

|
Shounak Saini answered |
False
The x-axis and y-axis coordinates of the centroid are calculated using the same method and formula. The centroid, also known as the center of mass or center of gravity, is the point at which the entire mass of a body is considered to be concentrated.
Calculation of x-coordinate of the centroid:
To calculate the x-coordinate of the centroid, we need to consider the sum of the products of the individual masses and their corresponding x-coordinates. This can be represented by the formula:
x̄ = (m₁x₁ + m₂x₂ + ... + mₙxₙ) / (m₁ + m₂ + ... + mₙ)
Where:
x̄ - x-coordinate of the centroid
m₁, m₂, ..., mₙ - masses of individual points or sections
x₁, x₂, ..., xₙ - x-coordinates of individual points or sections
Calculation of y-coordinate of the centroid:
Similarly, to calculate the y-coordinate of the centroid, we consider the sum of the products of the individual masses and their corresponding y-coordinates. This can be represented by the formula:
ȳ = (m₁y₁ + m₂y₂ + ... + mₙyₙ) / (m₁ + m₂ + ... + mₙ)
Where:
ȳ - y-coordinate of the centroid
m₁, m₂, ..., mₙ - masses of individual points or sections
y₁, y₂, ..., yₙ - y-coordinates of individual points or sections
Conclusion:
Both the x-coordinate and y-coordinate of the centroid are calculated using similar formulas. The only difference lies in the consideration of the x-coordinates and y-coordinates of the individual points or sections. Thus, the statement that the x-axis and y-axis coordinates of the centroid have different types of calculations to calculate them is false.
The x-axis and y-axis coordinates of the centroid are calculated using the same method and formula. The centroid, also known as the center of mass or center of gravity, is the point at which the entire mass of a body is considered to be concentrated.
Calculation of x-coordinate of the centroid:
To calculate the x-coordinate of the centroid, we need to consider the sum of the products of the individual masses and their corresponding x-coordinates. This can be represented by the formula:
x̄ = (m₁x₁ + m₂x₂ + ... + mₙxₙ) / (m₁ + m₂ + ... + mₙ)
Where:
x̄ - x-coordinate of the centroid
m₁, m₂, ..., mₙ - masses of individual points or sections
x₁, x₂, ..., xₙ - x-coordinates of individual points or sections
Calculation of y-coordinate of the centroid:
Similarly, to calculate the y-coordinate of the centroid, we consider the sum of the products of the individual masses and their corresponding y-coordinates. This can be represented by the formula:
ȳ = (m₁y₁ + m₂y₂ + ... + mₙyₙ) / (m₁ + m₂ + ... + mₙ)
Where:
ȳ - y-coordinate of the centroid
m₁, m₂, ..., mₙ - masses of individual points or sections
y₁, y₂, ..., yₙ - y-coordinates of individual points or sections
Conclusion:
Both the x-coordinate and y-coordinate of the centroid are calculated using similar formulas. The only difference lies in the consideration of the x-coordinates and y-coordinates of the individual points or sections. Thus, the statement that the x-axis and y-axis coordinates of the centroid have different types of calculations to calculate them is false.
Centroid determination involves the calculations of various forces. In that forces are having various properties. That is force is developed by a support that not allows the ________ of its attached member.- a)Translation
- b)Rotation
- c)Addition
- d)Subtraction
Correct answer is option 'A'. Can you explain this answer?
Centroid determination involves the calculations of various forces. In that forces are having various properties. That is force is developed by a support that not allows the ________ of its attached member.
a)
Translation
b)
Rotation
c)
Addition
d)
Subtraction

|
Jithin Choudhury answered |
Centroid Determination and Forces
Centroid determination is an important process in mechanics and engineering, which involves the calculation of various forces and their properties. One key property of forces is their ability to either allow or restrict the translation and rotation of attached members. In the context of this question, the force developed by a support does not allow the translation of its attached member.
Translation and Rotation
When a force is applied to an object, it can cause the object to move or translate. Translation refers to the linear motion of an object from one point to another without any change in its orientation. For example, when a force is applied to push a box across the floor, the box translates from one location to another without rotating.
On the other hand, rotation refers to the circular or angular motion of an object around a fixed point. When a force is applied in a way that causes an object to rotate, the object will pivot around a specific point or axis. For instance, when a force is applied to one end of a seesaw, the seesaw rotates around its support point.
Force and Support
A support is a structure or component that provides stability and resistance to external forces acting on an object. In the context of centroid determination, a support restricts the translation of its attached member. This means that the support prevents the attached member from moving or translating in any direction.
Example
Consider a simple example of a beam supported by two fixed supports at both ends. When a force is applied to the beam, it cannot translate or move in any direction because of the support. The supports provide a reaction force that counteracts the applied force, creating an equilibrium and preventing any translation.
However, it is important to note that while the support restricts translation, it does not restrict rotation. The beam is free to rotate around the supports, allowing for angular movement.
Conclusion
In centroid determination, the calculation of forces and their properties is crucial. The force developed by a support restricts the translation of its attached member, ensuring that the object remains in equilibrium and does not move in any direction. This understanding of forces and their effects on objects is fundamental in mechanical engineering and other related fields.
The total of all the masses of small particles adds up to give the total body mass of the composite body. This mass lies along with gravity gives a force vector which is being passed by ________- a)Axis of rotation
- b)Axis of rolling
- c)Centre of Gravity
- d)Centre of mass
Correct answer is option 'C'. Can you explain this answer?
The total of all the masses of small particles adds up to give the total body mass of the composite body. This mass lies along with gravity gives a force vector which is being passed by ________
a)
Axis of rotation
b)
Axis of rolling
c)
Centre of Gravity
d)
Centre of mass
|
|
Mrinalini Sharma answered |
The total body mass along with the product of gravity always passes through the centre of gravity. All the forces are parallel is the right answer. Thus the total sum of all these small weights add up to the total weight of the body. Which passes through the centre of gravity.
The centre of ____________ is the ratio of the product of centroid and volume to the total volume.- a)Centroid axis
- b)Density
- c)Mass
- d)Volume
Correct answer is option 'D'. Can you explain this answer?
The centre of ____________ is the ratio of the product of centroid and volume to the total volume.
a)
Centroid axis
b)
Density
c)
Mass
d)
Volume
|
|
Gopal Choudhury answered |
The product of the centroid of the section to its volume to the total volume of the body is the centre of volume. Thus the answer. The ratio is generally used to locate the coordinate of the centroid or the centre of volume.
The axis about which moment of area is taken is known as _____- a)Axis of area
- b)Axis of moment
- c)Axis of reference
- d)Axis of rotation
Correct answer is option 'C'. Can you explain this answer?
The axis about which moment of area is taken is known as _____
a)
Axis of area
b)
Axis of moment
c)
Axis of reference
d)
Axis of rotation
|
|
Mansi Rane answered |
Axis of reference is the correct answer.
Explanation:
- Moment of area is a property of a shape that measures its ability to resist bending or twisting under an applied load.
- When calculating the moment of area, we need to specify the axis about which the moment is taken.
- The axis of reference is the axis about which the moment of area is taken.
- This axis is used as a reference point to calculate the moment of area for a given shape.
- The choice of the axis of reference is arbitrary and can be chosen based on convenience or the specific problem at hand.
- The axis of reference is usually chosen to simplify the calculations and make them easier to solve.
- It is important to note that the choice of the axis of reference does not affect the physical properties of the shape itself, but only affects the calculations.
- The axis of reference can be any line passing through the shape, and it can be horizontal, vertical, or inclined.
- Once the axis of reference is chosen, the moment of area can be calculated using the appropriate formulas and integration techniques.
- The moment of area provides valuable information about the shape's resistance to bending and twisting, which is crucial in structural analysis and design.
- By choosing the appropriate axis of reference, engineers can accurately determine the moment of area and design structures that can withstand the applied loads.
- Therefore, the axis of reference is a critical concept in the field of mechanics and engineering.
Explanation:
- Moment of area is a property of a shape that measures its ability to resist bending or twisting under an applied load.
- When calculating the moment of area, we need to specify the axis about which the moment is taken.
- The axis of reference is the axis about which the moment of area is taken.
- This axis is used as a reference point to calculate the moment of area for a given shape.
- The choice of the axis of reference is arbitrary and can be chosen based on convenience or the specific problem at hand.
- The axis of reference is usually chosen to simplify the calculations and make them easier to solve.
- It is important to note that the choice of the axis of reference does not affect the physical properties of the shape itself, but only affects the calculations.
- The axis of reference can be any line passing through the shape, and it can be horizontal, vertical, or inclined.
- Once the axis of reference is chosen, the moment of area can be calculated using the appropriate formulas and integration techniques.
- The moment of area provides valuable information about the shape's resistance to bending and twisting, which is crucial in structural analysis and design.
- By choosing the appropriate axis of reference, engineers can accurately determine the moment of area and design structures that can withstand the applied loads.
- Therefore, the axis of reference is a critical concept in the field of mechanics and engineering.
If any external force also is applied on the distributed loading on the composite body then?- a)The net force will act at the centroid of the structure only
- b)The net load will not be formed as all the forces will be cancelled
- c)The net force will act on the base of the loading horizontally
- d)The net force will not to be considered, there would be a net force of the distribution, and rest will be the external forces
Correct answer is option 'D'. Can you explain this answer?
If any external force also is applied on the distributed loading on the composite body then?
a)
The net force will act at the centroid of the structure only
b)
The net load will not be formed as all the forces will be cancelled
c)
The net force will act on the base of the loading horizontally
d)
The net force will not to be considered, there would be a net force of the distribution, and rest will be the external forces
|
|
Sanskriti Basu answered |
The external forces are treated differently. They are not added by the force of the distributed loading. That is the force not only acts at the centroid always. It can be shifted also. Depending on the external forces. Thus the use of centroid or centre of mass.
Determine the y coordinate of centroid of the wire in the shape of circle as shown.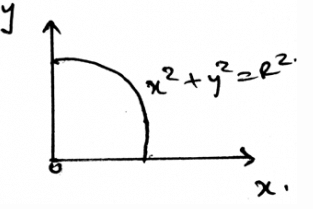
- a)2R/π
- b)2/π
- c)2R/3
- d)2R/5
Correct answer is option 'A'. Can you explain this answer?
Determine the y coordinate of centroid of the wire in the shape of circle as shown.
a)
2R/π
b)
2/π
c)
2R/3
d)
2R/5

|
Nidhi Tiwari answered |
The weight of the body is the sum of the all the small weights that are been applied by all the particles. The smaller the particle the smaller the weight it applies. Thus the total weight of the body is the summation of all the infinite number of small weights applied to the body.
Mass is best given by _______- a)Ratio of density to volume
- b)Product of volume and density
- c)Addition of mass and density
- d)Subtraction of mass and density
Correct answer is option 'B'. Can you explain this answer?
Mass is best given by _______
a)
Ratio of density to volume
b)
Product of volume and density
c)
Addition of mass and density
d)
Subtraction of mass and density

|
Sai Prathap answered |
We know that density = mass/volume
then mass = density ×volume
then mass = density ×volume
The centre of mass is the ratio of ________ to _________- a)The product of centroid and mass to the total weight
- b)The addition of centroid and weight to the total weight
- c)The subtraction of centroid and weight to the total weight
- d)The product of centroid and mass to the total mass
Correct answer is option 'D'. Can you explain this answer?
The centre of mass is the ratio of ________ to _________
a)
The product of centroid and mass to the total weight
b)
The addition of centroid and weight to the total weight
c)
The subtraction of centroid and weight to the total weight
d)
The product of centroid and mass to the total mass
|
|
Mahi Kaur answered |
The centre of mass is the ratio of the product of centroid and mass to the total mass. This can be explained in detail as follows:
1. Understanding the Centre of Mass:
- The centre of mass is a point in an object or system that represents the average position of all the mass.
- It is the point where the object or system can be balanced, as if all the mass is concentrated at that point.
- The centre of mass is a crucial concept in physics and engineering, as it helps in analyzing the motion and stability of objects.
2. Definition of Centroid:
- The centroid is a geometric property of a shape or object.
- It represents the average position of all the points in the shape or object.
- In simpler terms, it is the point at which a shape or object would balance if it were placed on a pin.
3. Relationship between Centre of Mass and Centroid:
- The centre of mass and centroid are related to each other, but they are not the same thing.
- For simple and regular objects with uniform mass distribution, the centre of mass and centroid coincide.
- However, for irregular objects or objects with non-uniform mass distribution, the centre of mass and centroid may not coincide.
4. Calculation of Centre of Mass:
- To calculate the centre of mass of an object or system, we need to consider the mass and position of each individual component.
- The centre of mass is calculated by taking the sum of the products of the mass and position of each component, divided by the total mass of the object or system.
- Mathematically, the centre of mass (CM) can be represented as CM = (m1r1 + m2r2 + m3r3 + ... + mnrn) / (m1 + m2 + m3 + ... + mn), where m represents the mass of each component and r represents the position vector of each component.
5. Relationship to the Total Mass:
- The centre of mass is a ratio of the product of centroid and mass to the total mass.
- This means that the position of the centre of mass is influenced by both the mass of each component and its position relative to the centroid.
- The total mass of the object or system is taken into account to determine the overall distribution of mass and its effect on the centre of mass.
Overall, the correct answer is option D, which states that the centre of mass is the ratio of the product of centroid and mass to the total mass. This relationship helps in understanding and calculating the position of the centre of mass in objects or systems with non-uniform mass distribution.
1. Understanding the Centre of Mass:
- The centre of mass is a point in an object or system that represents the average position of all the mass.
- It is the point where the object or system can be balanced, as if all the mass is concentrated at that point.
- The centre of mass is a crucial concept in physics and engineering, as it helps in analyzing the motion and stability of objects.
2. Definition of Centroid:
- The centroid is a geometric property of a shape or object.
- It represents the average position of all the points in the shape or object.
- In simpler terms, it is the point at which a shape or object would balance if it were placed on a pin.
3. Relationship between Centre of Mass and Centroid:
- The centre of mass and centroid are related to each other, but they are not the same thing.
- For simple and regular objects with uniform mass distribution, the centre of mass and centroid coincide.
- However, for irregular objects or objects with non-uniform mass distribution, the centre of mass and centroid may not coincide.
4. Calculation of Centre of Mass:
- To calculate the centre of mass of an object or system, we need to consider the mass and position of each individual component.
- The centre of mass is calculated by taking the sum of the products of the mass and position of each component, divided by the total mass of the object or system.
- Mathematically, the centre of mass (CM) can be represented as CM = (m1r1 + m2r2 + m3r3 + ... + mnrn) / (m1 + m2 + m3 + ... + mn), where m represents the mass of each component and r represents the position vector of each component.
5. Relationship to the Total Mass:
- The centre of mass is a ratio of the product of centroid and mass to the total mass.
- This means that the position of the centre of mass is influenced by both the mass of each component and its position relative to the centroid.
- The total mass of the object or system is taken into account to determine the overall distribution of mass and its effect on the centre of mass.
Overall, the correct answer is option D, which states that the centre of mass is the ratio of the product of centroid and mass to the total mass. This relationship helps in understanding and calculating the position of the centre of mass in objects or systems with non-uniform mass distribution.
During elastic impact, the relative velocity of the two bodies after impact is _______ the relative velocity of the two bodies before impact.- a)equal to
- b)equal and opposite to
- c)less than
- d)greater than
Correct answer is option 'B'. Can you explain this answer?
During elastic impact, the relative velocity of the two bodies after impact is _______ the relative velocity of the two bodies before impact.
a)
equal to
b)
equal and opposite to
c)
less than
d)
greater than
|
|
Keerthana Joshi answered |
Elastic Impact and Relative Velocity
In an elastic impact, two bodies collide and then separate without any permanent deformation or loss of kinetic energy. The relative velocity of the two bodies refers to the velocity of one body with respect to the other. Before the impact, the two bodies can either be moving towards each other or in the same direction.
Conservation of Momentum
During an elastic impact, the principle of conservation of momentum applies. According to this principle, the total momentum of a system before the impact is equal to the total momentum after the impact, provided no external forces are acting on the system.
Initial Relative Velocity
Before the impact, the relative velocity of the two bodies can be calculated by subtracting the velocity of one body from the velocity of the other. For example, if one body is moving towards the other with a velocity of 5 m/s and the other body is stationary, the initial relative velocity would be 5 m/s.
Effect of Elastic Impact
During the elastic impact, the two bodies exert forces on each other that cause a change in their velocities. These forces depend on the nature of the collision and the properties of the bodies involved. However, in an elastic impact, the total kinetic energy of the system is conserved.
Final Relative Velocity
After the elastic impact, the two bodies separate, and their velocities change. The relative velocity of the two bodies after the impact can be calculated in the same way as before the impact by subtracting the velocity of one body from the velocity of the other.
Equal and Opposite Relative Velocity
In an elastic impact, the relative velocity of the two bodies after the impact is equal and opposite to the relative velocity before the impact. This means that if the bodies were moving towards each other before the impact, they will move away from each other after the impact with the same magnitude of velocity.
Conclusion
In conclusion, during an elastic impact, the relative velocity of the two bodies after the impact is equal and opposite to the relative velocity before the impact. This principle is based on the conservation of momentum and the conservation of kinetic energy.
In an elastic impact, two bodies collide and then separate without any permanent deformation or loss of kinetic energy. The relative velocity of the two bodies refers to the velocity of one body with respect to the other. Before the impact, the two bodies can either be moving towards each other or in the same direction.
Conservation of Momentum
During an elastic impact, the principle of conservation of momentum applies. According to this principle, the total momentum of a system before the impact is equal to the total momentum after the impact, provided no external forces are acting on the system.
Initial Relative Velocity
Before the impact, the relative velocity of the two bodies can be calculated by subtracting the velocity of one body from the velocity of the other. For example, if one body is moving towards the other with a velocity of 5 m/s and the other body is stationary, the initial relative velocity would be 5 m/s.
Effect of Elastic Impact
During the elastic impact, the two bodies exert forces on each other that cause a change in their velocities. These forces depend on the nature of the collision and the properties of the bodies involved. However, in an elastic impact, the total kinetic energy of the system is conserved.
Final Relative Velocity
After the elastic impact, the two bodies separate, and their velocities change. The relative velocity of the two bodies after the impact can be calculated in the same way as before the impact by subtracting the velocity of one body from the velocity of the other.
Equal and Opposite Relative Velocity
In an elastic impact, the relative velocity of the two bodies after the impact is equal and opposite to the relative velocity before the impact. This means that if the bodies were moving towards each other before the impact, they will move away from each other after the impact with the same magnitude of velocity.
Conclusion
In conclusion, during an elastic impact, the relative velocity of the two bodies after the impact is equal and opposite to the relative velocity before the impact. This principle is based on the conservation of momentum and the conservation of kinetic energy.
The unit of linear acceleration is- a)kg-m
- b)m/s
- c)m/s2
- d)rad/s2
Correct answer is option 'C'. Can you explain this answer?
The unit of linear acceleration is
a)
kg-m
b)
m/s
c)
m/s2
d)
rad/s2
|
|
Avinash Sharma answered |
Linear acceleration is defined as the rate of change of linear velocity of a body with respect to the time.
i.e a = v/t
and unit of velocity is m/s
so, unit of linear acceleration becomes m/s2.
i.e a = v/t
and unit of velocity is m/s
so, unit of linear acceleration becomes m/s2.
Composite materials can be of __________ shapes.- a)Any
- b)Circular only
- c)Rectangular only
- d)Oval only
Correct answer is option 'A'. Can you explain this answer?
Composite materials can be of __________ shapes.
a)
Any
b)
Circular only
c)
Rectangular only
d)
Oval only

|
Rahul Chauhan answered |
Composite materials can be of Any shapes.
Composite materials are a combination of two or more different materials, each with its own distinct properties, to create a material with enhanced performance characteristics. These materials can be made into a wide variety of shapes depending on the specific application and manufacturing process.
There are several reasons why composite materials can be of any shape:
1. Flexibility in Manufacturing Process: Composite materials can be manufactured using various techniques such as hand layup, filament winding, pultrusion, and autoclave molding. These processes allow for the fabrication of complex shapes, including curved, contoured, and irregular shapes.
2. Customization: Composite materials can be tailored to meet specific design requirements. By adjusting the composition, fiber orientation, and stacking sequence, the mechanical properties of the material can be optimized for a particular application. This flexibility allows for the creation of composite components in various shapes to suit different needs.
3. Moldability: Composite materials can be molded into different shapes using molds or tooling. The molds can be designed to have the desired shape and dimensions of the final product. The composite material is then placed in the mold and cured or solidified to take on the shape of the mold. This allows for the production of composite parts with intricate geometries.
4. Layering: Composite materials are typically made up of multiple layers or plies of reinforcement materials, such as fibers or fabrics, embedded in a matrix material. These layers can be stacked and arranged in different ways to create complex shapes. By varying the number, orientation, and arrangement of the layers, the shape of the composite material can be controlled.
In conclusion, composite materials can be of any shape due to the flexibility in the manufacturing process, the ability to customize the material properties, the moldability of the material, and the layering technique used in composite fabrication. These factors allow for the production of composite components in a wide range of shapes to meet the specific requirements of different applications.
Composite materials are a combination of two or more different materials, each with its own distinct properties, to create a material with enhanced performance characteristics. These materials can be made into a wide variety of shapes depending on the specific application and manufacturing process.
There are several reasons why composite materials can be of any shape:
1. Flexibility in Manufacturing Process: Composite materials can be manufactured using various techniques such as hand layup, filament winding, pultrusion, and autoclave molding. These processes allow for the fabrication of complex shapes, including curved, contoured, and irregular shapes.
2. Customization: Composite materials can be tailored to meet specific design requirements. By adjusting the composition, fiber orientation, and stacking sequence, the mechanical properties of the material can be optimized for a particular application. This flexibility allows for the creation of composite components in various shapes to suit different needs.
3. Moldability: Composite materials can be molded into different shapes using molds or tooling. The molds can be designed to have the desired shape and dimensions of the final product. The composite material is then placed in the mold and cured or solidified to take on the shape of the mold. This allows for the production of composite parts with intricate geometries.
4. Layering: Composite materials are typically made up of multiple layers or plies of reinforcement materials, such as fibers or fabrics, embedded in a matrix material. These layers can be stacked and arranged in different ways to create complex shapes. By varying the number, orientation, and arrangement of the layers, the shape of the composite material can be controlled.
In conclusion, composite materials can be of any shape due to the flexibility in the manufacturing process, the ability to customize the material properties, the moldability of the material, and the layering technique used in composite fabrication. These factors allow for the production of composite components in a wide range of shapes to meet the specific requirements of different applications.
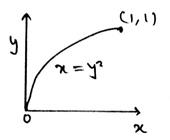
Determine the x coordinate of centroid of the line in the shape of parabola as shown.
- a) 0.410m
- b) 1.410m
- c) 2.410m
- d) 0.10m
Correct answer is option 'A'. Can you explain this answer?
Determine the x coordinate of centroid of the line in the shape of parabola as shown.
a)
0.410mb)
1.410mc)
2.410md)
0.10m

|
Saikat Gupta answered |
The weight of the body is the sum of the all the small weights that are been applied by all the particles. The smaller the particle the smaller the weight it applies. Thus the total weight of the body is the summation of all the infinite number of small weights applied to the body.
Density is best given by _______- a)Product of volume and density
- b)Ratio of mass to Volume
- c)Addition of mass and density
- d)Subtraction of mass and density
Correct answer is option 'B'. Can you explain this answer?
Density is best given by _______
a)
Product of volume and density
b)
Ratio of mass to Volume
c)
Addition of mass and density
d)
Subtraction of mass and density
|
|
Priyanka Tiwari answered |
The density is the ratio of the mass to the volume of the body. Thus arranging them and the volume is said to be as ratio of mass to density. This equation is generally used in the calculations of the centroid of the body.
The all small weights that are being applied by all the infinite particles of the body act __________ to each other.- a)Parallel
- b)Perpendicular
- c)Collinear
- d)Divergent
Correct answer is option 'A'. Can you explain this answer?
The all small weights that are being applied by all the infinite particles of the body act __________ to each other.
a)
Parallel
b)
Perpendicular
c)
Collinear
d)
Divergent

|
Sreemoyee Joshi answered |
Explanation:
When considering the weights applied by the infinite particles of a body, it is important to understand the concept of weight and its direction. Weight is a force that is exerted by an object due to gravity.
Parallel:
The option 'A' states that the weights applied by all the infinite particles of the body act parallel to each other. This means that the direction of the weight is the same for all particles.
Perpendicular:
If the weights were acting perpendicular to each other, it would mean that the particles are being pulled in different directions. This is not the case with the weights applied by the particles of a body.
Collinear:
If the weights were acting collinearly, it would mean that the particles are being pulled towards the same line of action. However, the particles in a body are distributed in three-dimensional space and therefore their weights do not act collinearly.
Divergent:
If the weights were acting divergently, it would mean that the particles are being pulled away from each other. However, the weights applied by the particles of a body act in the same direction and therefore they are not divergent.
Therefore, the correct answer is option 'A' - parallel. The weights applied by all the infinite particles of the body act parallel to each other. This is because gravity acts uniformly on all particles, and their weights are directed towards the center of the Earth.
When considering the weights applied by the infinite particles of a body, it is important to understand the concept of weight and its direction. Weight is a force that is exerted by an object due to gravity.
Parallel:
The option 'A' states that the weights applied by all the infinite particles of the body act parallel to each other. This means that the direction of the weight is the same for all particles.
Perpendicular:
If the weights were acting perpendicular to each other, it would mean that the particles are being pulled in different directions. This is not the case with the weights applied by the particles of a body.
Collinear:
If the weights were acting collinearly, it would mean that the particles are being pulled towards the same line of action. However, the particles in a body are distributed in three-dimensional space and therefore their weights do not act collinearly.
Divergent:
If the weights were acting divergently, it would mean that the particles are being pulled away from each other. However, the weights applied by the particles of a body act in the same direction and therefore they are not divergent.
Therefore, the correct answer is option 'A' - parallel. The weights applied by all the infinite particles of the body act parallel to each other. This is because gravity acts uniformly on all particles, and their weights are directed towards the center of the Earth.
Point, where the total volume of the body is assumed to be concentrated is ______- a)Center of area
- b)Centroid of volume
- c)Centroid of mass
- d)All of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Point, where the total volume of the body is assumed to be concentrated is ______
a)
Center of area
b)
Centroid of volume
c)
Centroid of mass
d)
All of the mentioned

|
Shraddha Datta answered |
Centroid of Volume
The centroid of a three-dimensional object is the point where the total volume of the body is assumed to be concentrated. It is a geometric center of the object and is used in the calculation of various physical properties such as moment of inertia and center of mass. In the case of a two-dimensional object, the centroid is called the center of area.
Calculation of Centroid of Volume
The centroid of a volume can be calculated using the following formula:
x = (1/V)∫∫∫ x dV
y = (1/V)∫∫∫ y dV
z = (1/V)∫∫∫ z dV
where x, y, and z are the coordinates of the centroid, V is the volume of the object, and the integrals are taken over the entire volume of the object.
Applications of Centroid of Volume
The centroid of volume is used in various engineering applications such as:
1. Calculation of moment of inertia: The moment of inertia of an object about any axis can be calculated using the parallel axis theorem and the centroid of volume.
2. Analysis of structures: The centroid of volume is used in the analysis of structures to determine the location of the center of gravity and the distribution of loads.
3. Design of machinery: The centroid of volume is used in the design of machinery to ensure that the weight is evenly distributed and the machine is balanced.
Conclusion
The centroid of volume is a crucial concept in engineering and is used in various calculations and analysis. It is the point where the total volume of the body is assumed to be concentrated and is used in the calculation of various physical properties.
The centroid of a three-dimensional object is the point where the total volume of the body is assumed to be concentrated. It is a geometric center of the object and is used in the calculation of various physical properties such as moment of inertia and center of mass. In the case of a two-dimensional object, the centroid is called the center of area.
Calculation of Centroid of Volume
The centroid of a volume can be calculated using the following formula:
x = (1/V)∫∫∫ x dV
y = (1/V)∫∫∫ y dV
z = (1/V)∫∫∫ z dV
where x, y, and z are the coordinates of the centroid, V is the volume of the object, and the integrals are taken over the entire volume of the object.
Applications of Centroid of Volume
The centroid of volume is used in various engineering applications such as:
1. Calculation of moment of inertia: The moment of inertia of an object about any axis can be calculated using the parallel axis theorem and the centroid of volume.
2. Analysis of structures: The centroid of volume is used in the analysis of structures to determine the location of the center of gravity and the distribution of loads.
3. Design of machinery: The centroid of volume is used in the design of machinery to ensure that the weight is evenly distributed and the machine is balanced.
Conclusion
The centroid of volume is a crucial concept in engineering and is used in various calculations and analysis. It is the point where the total volume of the body is assumed to be concentrated and is used in the calculation of various physical properties.
One of the use of the centre of mass or centroid is as in the simplification of the loading system the net force acts at the ___________ of the loading body.- a)Centroid
- b)The centre axis
- c)The corner
- d)The base
Correct answer is option 'A'. Can you explain this answer?
One of the use of the centre of mass or centroid is as in the simplification of the loading system the net force acts at the ___________ of the loading body.
a)
Centroid
b)
The centre axis
c)
The corner
d)
The base
|
|
Shreya Choudhury answered |
In the simplification of the loading system the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then the at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading.
A thin rod of length L and mass M will have what moment of inertia about an axis passing through one of its edge and perpendicular to the rod?- a)ML2/12
- b)ML2/6
- c)ML2/3
- d)ML2/9
Correct answer is option 'C'. Can you explain this answer?
A thin rod of length L and mass M will have what moment of inertia about an axis passing through one of its edge and perpendicular to the rod?
a)
ML2/12
b)
ML2/6
c)
ML2/3
d)
ML2/9

|
Nidhi Tiwari answered |
Calculating Moment of Inertia
To calculate the moment of inertia of a thin rod about an axis passing through one of its edges and perpendicular to the rod, we can use the formula for the moment of inertia of a rod about an axis perpendicular to the rod and passing through its center. The moment of inertia of a rod of length L and mass M about an axis passing through its center and perpendicular to the rod is given by the formula:
I = (1/12) * M * L^2
Shifting the Axis
When the axis is shifted to one of the edges of the rod, we can use the parallel axis theorem to calculate the moment of inertia about the new axis. The parallel axis theorem states that the moment of inertia about an axis parallel to and at a distance d from the original axis is given by:
I' = I + M * d^2
In this case, since the axis is shifted to one of the edges, the distance d is equal to L/2. Substituting the values in the formula, we get:
I' = (1/12) * M * L^2 + M * (L/2)^2
I' = (1/12) * M * L^2 + (1/4) * M * L^2
I' = (1/3) * M * L^2
Therefore, the moment of inertia of the thin rod about an axis passing through one of its edges and perpendicular to the rod is given by:
I' = (1/3) * M * L^2
Thus, the correct answer is option C - ML^2/3.
We use sometimes the measures to know the direction of moment in the calculations of the centre of mass. It is done by right handed coordinate system. Which is right about it(consider the mentioned axis to be positive)?- a)Thumb is z-axis, fingers curled from x-axis to y-axis
- b)Thumb is x-axis, fingers curled from z-axis to y-axis
- c)Thumb is y-axis, fingers curled from x-axis to z-axis
- d)Thumb is z-axis, fingers curled from y-axis to x-axis
Correct answer is option 'A'. Can you explain this answer?
We use sometimes the measures to know the direction of moment in the calculations of the centre of mass. It is done by right handed coordinate system. Which is right about it(consider the mentioned axis to be positive)?
a)
Thumb is z-axis, fingers curled from x-axis to y-axis
b)
Thumb is x-axis, fingers curled from z-axis to y-axis
c)
Thumb is y-axis, fingers curled from x-axis to z-axis
d)
Thumb is z-axis, fingers curled from y-axis to x-axis

|
Jhanvi Choudhary answered |
As right handed coordinate system means that you are curling your fingers from positive x-axis towards y-axis and the thumb which is projected is pointed to the positive z-axis. Thus visualizing the same and knowing the basic members of axis will not create much problem.
A Particle is dropped from a height of 3 m on a horizantal floor, which has a coefficient of restitution with the ball of 1/2. The height to which the hall will rebound after striking the floor is- a)0.5 m
- b)0.75 m
- c)1.0 m
- d)1.5 m
Correct answer is option 'B'. Can you explain this answer?
A Particle is dropped from a height of 3 m on a horizantal floor, which has a coefficient of restitution with the ball of 1/2. The height to which the hall will rebound after striking the floor is
a)
0.5 m
b)
0.75 m
c)
1.0 m
d)
1.5 m
|
|
Kajal Tiwari answered |
Given:
- Initial height of the particle = 3 m
- Coefficient of restitution of the ball with the floor = 1/2
To find:
- The height to which the ball will rebound after striking the floor
Explanation:
1. Coefficient of restitution:
The coefficient of restitution (e) is a measure of the ability of a ball to bounce back after a collision. It is defined as the ratio of the relative velocity of separation to the relative velocity of approach between two colliding bodies.
Mathematically, e = (v2f - v1f) / (v1i - v2i)
Where,
- v1i and v2i are the initial velocities of the two bodies before collision
- v1f and v2f are the final velocities of the two bodies after collision
In this case, the ball is dropped from a height, so its initial velocity is zero.
2. Calculation:
When the ball is dropped from a height of 3 m, it falls freely under the influence of gravity. As it hits the floor, it comes to a stop momentarily and then rebounds.
The rebound height can be calculated using the equation:
h = e^2 * H
Where,
- h is the rebound height
- e is the coefficient of restitution
- H is the initial height
Substituting the given values:
h = (1/2)^2 * 3
h = 1/4 * 3
h = 3/4
h = 0.75 m
3. Answer:
The height to which the ball will rebound after striking the floor is 0.75 m. Therefore, the correct answer is option B.
- Initial height of the particle = 3 m
- Coefficient of restitution of the ball with the floor = 1/2
To find:
- The height to which the ball will rebound after striking the floor
Explanation:
1. Coefficient of restitution:
The coefficient of restitution (e) is a measure of the ability of a ball to bounce back after a collision. It is defined as the ratio of the relative velocity of separation to the relative velocity of approach between two colliding bodies.
Mathematically, e = (v2f - v1f) / (v1i - v2i)
Where,
- v1i and v2i are the initial velocities of the two bodies before collision
- v1f and v2f are the final velocities of the two bodies after collision
In this case, the ball is dropped from a height, so its initial velocity is zero.
2. Calculation:
When the ball is dropped from a height of 3 m, it falls freely under the influence of gravity. As it hits the floor, it comes to a stop momentarily and then rebounds.
The rebound height can be calculated using the equation:
h = e^2 * H
Where,
- h is the rebound height
- e is the coefficient of restitution
- H is the initial height
Substituting the given values:
h = (1/2)^2 * 3
h = 1/4 * 3
h = 3/4
h = 0.75 m
3. Answer:
The height to which the ball will rebound after striking the floor is 0.75 m. Therefore, the correct answer is option B.
When a particle moves with a uniform velocity along a circular path, then the particle has- a)tangential acceleration only
- b)centripetal acceleration only
- c)both tangential and centripetal acceleration
- d)none of the mentioned
Correct answer is option 'B'. Can you explain this answer?
When a particle moves with a uniform velocity along a circular path, then the particle has
a)
tangential acceleration only
b)
centripetal acceleration only
c)
both tangential and centripetal acceleration
d)
none of the mentioned
|
|
Mansi Kulkarni answered |
Explanation:
When a particle moves with uniform velocity along a circular path, it means that the speed of the particle is constant. However, the direction of the particle is constantly changing as it moves around the circle. This means that the particle is accelerating, as acceleration is defined as any change in velocity, including a change in direction.
The acceleration of a particle moving in a circle can be broken down into two components: tangential and centripetal acceleration.
Tangential Acceleration: This component of acceleration is parallel to the velocity vector of the particle, and it results from any change in the speed of the particle. When a particle moves with uniform velocity along a circular path, its speed is constant, so there is no tangential acceleration.
Centripetal Acceleration: This component of acceleration is perpendicular to the velocity vector of the particle, and it is responsible for keeping the particle moving in a circular path. The centripetal acceleration is always directed towards the center of the circle, and its magnitude is given by the formula a = v^2/r, where v is the speed of the particle and r is the radius of the circle.
Since the particle is moving with uniform velocity along a circular path, its speed is constant, but its direction is constantly changing due to the centripetal acceleration. Therefore, the particle has only centripetal acceleration and no tangential acceleration.
Conclusion:
Hence, option B- "Centripetal acceleration only" is the correct answer.
When a particle moves with uniform velocity along a circular path, it means that the speed of the particle is constant. However, the direction of the particle is constantly changing as it moves around the circle. This means that the particle is accelerating, as acceleration is defined as any change in velocity, including a change in direction.
The acceleration of a particle moving in a circle can be broken down into two components: tangential and centripetal acceleration.
Tangential Acceleration: This component of acceleration is parallel to the velocity vector of the particle, and it results from any change in the speed of the particle. When a particle moves with uniform velocity along a circular path, its speed is constant, so there is no tangential acceleration.
Centripetal Acceleration: This component of acceleration is perpendicular to the velocity vector of the particle, and it is responsible for keeping the particle moving in a circular path. The centripetal acceleration is always directed towards the center of the circle, and its magnitude is given by the formula a = v^2/r, where v is the speed of the particle and r is the radius of the circle.
Since the particle is moving with uniform velocity along a circular path, its speed is constant, but its direction is constantly changing due to the centripetal acceleration. Therefore, the particle has only centripetal acceleration and no tangential acceleration.
Conclusion:
Hence, option B- "Centripetal acceleration only" is the correct answer.
The body is sometimes acted by two or three force members. The difference between the two and the three force members is ________________- a)The former is collinear and the latter is parallel
- b)The former is parallel and the latter is perpendicular
- c)The former is perpendicular and the latter is collinear
- d)The former is acting on two points in the body while the latter is on three points
Correct answer is option 'D'. Can you explain this answer?
The body is sometimes acted by two or three force members. The difference between the two and the three force members is ________________
a)
The former is collinear and the latter is parallel
b)
The former is parallel and the latter is perpendicular
c)
The former is perpendicular and the latter is collinear
d)
The former is acting on two points in the body while the latter is on three points
|
|
Ameya Kaur answered |
The definition of the two force member only defines that the forces are being acted on the two points on the body. So does is the definition of the three forces members. The points of action of the three forces are three.
The all small masses that are being applied by all the infinite particles of the body act __________ to each other.- a)Parallel
- b)Perpendicular
- c)Collinear
- d)Divergent
Correct answer is option 'A'. Can you explain this answer?
The all small masses that are being applied by all the infinite particles of the body act __________ to each other.
a)
Parallel
b)
Perpendicular
c)
Collinear
d)
Divergent
|
|
Kritika Joshi answered |
All the small masses that are being applied by all the particles are being applied by them parallel to themselves. Thus the parallel is the right answer. Thus the total sum of all these small weights add up to the total weight of the body.
The centre of volume is the ratio of ________ to _________- a)The product of centroid and mass to the total weight
- b)The addition of centroid and weight to the total weight
- c)The subtraction of centroid and volume to the total weight
- d)The product of centroid and volume to the total volume
Correct answer is option 'D'. Can you explain this answer?
The centre of volume is the ratio of ________ to _________
a)
The product of centroid and mass to the total weight
b)
The addition of centroid and weight to the total weight
c)
The subtraction of centroid and volume to the total weight
d)
The product of centroid and volume to the total volume
|
|
Anshu Patel answered |
The product of the centroid of the section to its volume to the total volume of the body is the centre of volume. Thus the answer. The ratio is generally used to locate the coordinate of the centroid or the centre of volume.
We first make equilibrium equations of the body by considering all the three dimensional forces and then the free body diagram is made and then equations are made to be applied so as to calculate the centre of mass.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'D'. Can you explain this answer?
We first make equilibrium equations of the body by considering all the three dimensional forces and then the free body diagram is made and then equations are made to be applied so as to calculate the centre of mass.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Raj Kumar answered |
We first make the free body diagram and then we make the equilibrium equations to satisfy the given conditions. This helps us to solve the question easily. As this reduces the part of imagination and increases accuracy too.
Volume is best given by ___________- a)Product of mass and density
- b)Ratio of mass to density
- c)Addition of mass and density
- d)Subtraction of mass and density
Correct answer is option 'B'. Can you explain this answer?
Volume is best given by ___________
a)
Product of mass and density
b)
Ratio of mass to density
c)
Addition of mass and density
d)
Subtraction of mass and density
|
|
Nishanth Basu answered |
The density is the ration of the mass to the volume of the body. Thus arranging them and the volume is said to be as ratio of mass to density. This equation is generally used in the calculations of the centroid of the body or the centre of gravity.
Moment of inertia of a thin spherical shell of mass M and radius R, about its diameter is- a)MR2
- b)(1/2)MR2
- c)(2/5)MR2
- d)(2/3)MR2
Correct answer is option 'D'. Can you explain this answer?
Moment of inertia of a thin spherical shell of mass M and radius R, about its diameter is
a)
MR2
b)
(1/2)MR2
c)
(2/5)MR2
d)
(2/3)MR2
|
|
Neha Joshi answered |
Moment of inertia:
Moment of inertia is a measure of the resistance of a body to angular acceleration about a given axis that is equal to the sum of the products of each element of mass in the body and the square of the element’s distance from the axis.
Moment of inertia of a thin spherical shell of mass M and radius R about its diameter.
I = (2/3)MR2
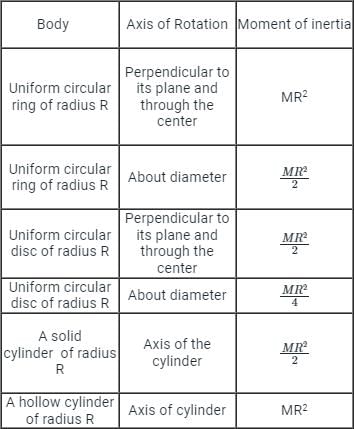
Additional Information
Moment of inertia of some important shapes:
Moment of inertia is a measure of the resistance of a body to angular acceleration about a given axis that is equal to the sum of the products of each element of mass in the body and the square of the element’s distance from the axis.
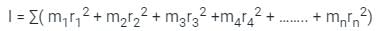
Moment of inertia of a thin spherical shell of mass M and radius R about its diameter.
I = (2/3)MR2
Additional Information
Moment of inertia of some important shapes:

What is the mass MOI of right circular cone of radius R and height H about its axis?- a)4MR2/10
- b)MR2/10
- c)3MR2/10
- d)MR2/12
Correct answer is option 'C'. Can you explain this answer?
What is the mass MOI of right circular cone of radius R and height H about its axis?
a)
4MR2/10
b)
MR2/10
c)
3MR2/10
d)
MR2/12
|
|
Ameya Kaur answered |
Mass Moment of Inertia of Right Circular Cone
The mass moment of inertia of an object is a measure of its resistance to rotational motion around a particular axis. The mass moment of inertia depends on the mass distribution of the object and the axis of rotation.
For a right circular cone with radius R and height H, the mass moment of inertia about its axis can be calculated as follows:
1. Divide the cone into infinitesimal discs.
2. Calculate the mass of each disc using the formula:
Mass of disc = density x volume of disc
The density of the cone can be assumed to be constant, so the mass of each disc will be proportional to its volume.
The volume of each disc can be calculated using the formula for the volume of a cylinder:
Volume of disc = πr2h, where r is the radius and h is the thickness of the disc.
For a cone, the radius of each disc will vary depending on its position along the height of the cone. The thickness of each disc will also vary, but it can be assumed to be infinitesimal.
Therefore, the mass of each disc can be expressed as:
dm = ρπr2dh, where ρ is the density of the cone, r is the radius of the disc, and dh is the thickness of the disc.
3. Use the parallel axis theorem to calculate the mass moment of inertia of each disc about the axis passing through its center.
The parallel axis theorem states that the mass moment of inertia of an object about any axis is equal to the mass moment of inertia of the object about a parallel axis passing through its center of mass, plus the product of the mass of the object and the square of the distance between the two axes.
Therefore, the mass moment of inertia of each disc about the axis passing through its center can be expressed as:
I = (1/2)mr2 + (1/4)mh2, where m is the mass of the disc, r is the radius of the disc, and h is the distance between the center of the disc and the axis passing through the center of the cone.
4. Integrate the mass moment of inertia of each disc over the entire volume of the cone to obtain the total mass moment of inertia of the cone about its axis.
The integral can be expressed as:
I = ∫(1/2)ρπr4dr + ∫(1/4)ρπr2h2dh, where the limits of integration are from 0 to R for r and from 0 to H for h.
Solving this integral yields:
I = (1/10)ρπR2H(R2 + 3H2)
Substituting the mass of the cone, M = (1/3)ρπR2H, yields the final expression for the mass moment of inertia:
I = (3/10)MR2
The mass moment of inertia of an object is a measure of its resistance to rotational motion around a particular axis. The mass moment of inertia depends on the mass distribution of the object and the axis of rotation.
For a right circular cone with radius R and height H, the mass moment of inertia about its axis can be calculated as follows:
1. Divide the cone into infinitesimal discs.
2. Calculate the mass of each disc using the formula:
Mass of disc = density x volume of disc
The density of the cone can be assumed to be constant, so the mass of each disc will be proportional to its volume.
The volume of each disc can be calculated using the formula for the volume of a cylinder:
Volume of disc = πr2h, where r is the radius and h is the thickness of the disc.
For a cone, the radius of each disc will vary depending on its position along the height of the cone. The thickness of each disc will also vary, but it can be assumed to be infinitesimal.
Therefore, the mass of each disc can be expressed as:
dm = ρπr2dh, where ρ is the density of the cone, r is the radius of the disc, and dh is the thickness of the disc.
3. Use the parallel axis theorem to calculate the mass moment of inertia of each disc about the axis passing through its center.
The parallel axis theorem states that the mass moment of inertia of an object about any axis is equal to the mass moment of inertia of the object about a parallel axis passing through its center of mass, plus the product of the mass of the object and the square of the distance between the two axes.
Therefore, the mass moment of inertia of each disc about the axis passing through its center can be expressed as:
I = (1/2)mr2 + (1/4)mh2, where m is the mass of the disc, r is the radius of the disc, and h is the distance between the center of the disc and the axis passing through the center of the cone.
4. Integrate the mass moment of inertia of each disc over the entire volume of the cone to obtain the total mass moment of inertia of the cone about its axis.
The integral can be expressed as:
I = ∫(1/2)ρπr4dr + ∫(1/4)ρπr2h2dh, where the limits of integration are from 0 to R for r and from 0 to H for h.
Solving this integral yields:
I = (1/10)ρπR2H(R2 + 3H2)
Substituting the mass of the cone, M = (1/3)ρπR2H, yields the final expression for the mass moment of inertia:
I = (3/10)MR2
A composite body is consisted of __________ number of particles.- a)Infinite
- b)Finite
- c)Hundreds
- d)Thousands
Correct answer is option 'A'. Can you explain this answer?
A composite body is consisted of __________ number of particles.
a)
Infinite
b)
Finite
c)
Hundreds
d)
Thousands
|
|
Hiral Jain answered |
A composite body is a physical object that is composed of multiple particles. These particles can be atoms, molecules, or even smaller particles, depending on the scale of the composite body. The number of particles in a composite body can vary depending on the size and composition of the body itself.
In the case of a composite body, the number of particles is generally considered to be infinite. This is because a composite body is made up of an extremely large number of particles that are densely packed together. Even if the body is relatively small in size, there are still a vast number of particles within it.
One way to understand this concept is to consider a solid object, such as a piece of metal. At the atomic level, the metal is made up of a lattice structure, with each lattice point representing an atom. The number of atoms in even a small piece of metal is on the order of Avogadro's number, which is approximately 6.022 x 10^23. This is an extremely large number and can be considered to be infinite for practical purposes.
Furthermore, the composite body may also contain other types of particles, such as molecules or ions. These particles can also contribute to the overall number of particles in the body. For example, in a composite body made of a polymer material, there are not only atoms but also polymer chains that consist of many repeating units. Each repeating unit can be considered as a particle, adding to the total number of particles in the composite body.
In summary, a composite body is comprised of a vast number of particles, which can be considered to be infinite for practical purposes. The number of particles in a composite body depends on the size, composition, and structure of the body itself.
In the case of a composite body, the number of particles is generally considered to be infinite. This is because a composite body is made up of an extremely large number of particles that are densely packed together. Even if the body is relatively small in size, there are still a vast number of particles within it.
One way to understand this concept is to consider a solid object, such as a piece of metal. At the atomic level, the metal is made up of a lattice structure, with each lattice point representing an atom. The number of atoms in even a small piece of metal is on the order of Avogadro's number, which is approximately 6.022 x 10^23. This is an extremely large number and can be considered to be infinite for practical purposes.
Furthermore, the composite body may also contain other types of particles, such as molecules or ions. These particles can also contribute to the overall number of particles in the body. For example, in a composite body made of a polymer material, there are not only atoms but also polymer chains that consist of many repeating units. Each repeating unit can be considered as a particle, adding to the total number of particles in the composite body.
In summary, a composite body is comprised of a vast number of particles, which can be considered to be infinite for practical purposes. The number of particles in a composite body depends on the size, composition, and structure of the body itself.
Moment of inertia of a thin spherical shell of mass M and radius R, about its diameter is- a)MR2
- b)(1/2)MR2
- c)(2/5)MR2
- d)(2/3)MR2
Correct answer is option 'D'. Can you explain this answer?
Moment of inertia of a thin spherical shell of mass M and radius R, about its diameter is
a)
MR2
b)
(1/2)MR2
c)
(2/5)MR2
d)
(2/3)MR2
|
|
Stuti Mishra answered |
Understanding Moment of Inertia
The moment of inertia (I) quantifies the rotational inertia of an object about a given axis. For a thin spherical shell, this is calculated based on its mass distribution relative to the axis of rotation.
Moment of Inertia of a Thin Spherical Shell
For a thin spherical shell of mass M and radius R, the moment of inertia about its diameter can be derived from the principles of integration or by using standard formulas for common shapes.
Key Formula
- The moment of inertia for a thin spherical shell about an axis through its center (diameter) is given by:
- I = (2/3)MR²
Explanation of the Result
- The spherical shell is uniform, meaning its mass is evenly distributed across its surface.
- When rotating about the diameter:
- Each mass element contributes to the total inertia based on its distance from the axis.
- The integration over the shell's surface leads to the factor of (2/3), which considers the geometry of a sphere.
Comparison with Other Shapes
- For comparison:
- A solid sphere has a moment of inertia of (2/5)MR².
- A solid cylinder has a moment of inertia of (1/2)MR².
- The spherical shell's unique geometry results in its specific inertia value.
Conclusion
- Thus, the moment of inertia of a thin spherical shell about its diameter is indeed (2/3)MR², confirming that the correct answer is option 'D'. This demonstrates how mass distribution and geometry significantly influence rotational characteristics.
The moment of inertia (I) quantifies the rotational inertia of an object about a given axis. For a thin spherical shell, this is calculated based on its mass distribution relative to the axis of rotation.
Moment of Inertia of a Thin Spherical Shell
For a thin spherical shell of mass M and radius R, the moment of inertia about its diameter can be derived from the principles of integration or by using standard formulas for common shapes.
Key Formula
- The moment of inertia for a thin spherical shell about an axis through its center (diameter) is given by:
- I = (2/3)MR²
Explanation of the Result
- The spherical shell is uniform, meaning its mass is evenly distributed across its surface.
- When rotating about the diameter:
- Each mass element contributes to the total inertia based on its distance from the axis.
- The integration over the shell's surface leads to the factor of (2/3), which considers the geometry of a sphere.
Comparison with Other Shapes
- For comparison:
- A solid sphere has a moment of inertia of (2/5)MR².
- A solid cylinder has a moment of inertia of (1/2)MR².
- The spherical shell's unique geometry results in its specific inertia value.
Conclusion
- Thus, the moment of inertia of a thin spherical shell about its diameter is indeed (2/3)MR², confirming that the correct answer is option 'D'. This demonstrates how mass distribution and geometry significantly influence rotational characteristics.
Centroid of a body does depends upon the small weights of tiny particles. Which statement is right for force acting by the small particles of the body having it’s vector form as = Ai + Bj + Ck?- a)In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
- b)In rectangular components representation of any vector we have vector F = Ax + By + Cz
- c)In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
- d)In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
Correct answer is option 'C'. Can you explain this answer?
Centroid of a body does depends upon the small weights of tiny particles. Which statement is right for force acting by the small particles of the body having it’s vector form as = Ai + Bj + Ck?
a)
In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
b)
In rectangular components representation of any vector we have vector F = Ax + By + Cz
c)
In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
d)
In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
|
|
Priyanka Tiwari answered |
As given the vector is F = Ai + Bj + Ck, this implies that the x ,y and z-axis components of this vector is A, B and C respectively. But, in rectangular components representation of any vector, the vector is written as F = Fx + Fy + Fz.
A body is consisted of __________ number of particles.- a)Infinite
- b)Finite
- c)Hundreds
- d)Thousands
Correct answer is option 'A'. Can you explain this answer?
A body is consisted of __________ number of particles.
a)
Infinite
b)
Finite
c)
Hundreds
d)
Thousands
|
|
Pritam Jain answered |
The various bodies are composed of infinite number of particles. They are very small in size. They cant be seen by our naked eyes. Thus the number of particles is not thousands nor hundreds. But it is uncountable.
What is the unit of mass moment of inertia?
- a)m4
- b)kg.m2
- c)N
- d)m2
Correct answer is option 'B'. Can you explain this answer?
What is the unit of mass moment of inertia?
a)
m4
b)
kg.m2
c)
N
d)
m2
|
|
Avinash Sharma answered |
The mass moment of inertia is the product of moment of inertia and area. So L4 x L2 = L6. so its unit will be m6.
One of the use of the centroid is as in the simplification of the loading system the net force acts at the ___________ of the loading body.- a)Centroid
- b)The centre axis
- c)The corner
- d)The base
Correct answer is option 'A'. Can you explain this answer?
One of the use of the centroid is as in the simplification of the loading system the net force acts at the ___________ of the loading body.
a)
Centroid
b)
The centre axis
c)
The corner
d)
The base
|
|
Anshul Sharma answered |
In the simplification of the loading system the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then the at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading.
The ratio of moment of inertia of a circular plate to that of a square plate for equal depth is- a)less than one
- b)equal to one
- c)greater than one
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
The ratio of moment of inertia of a circular plate to that of a square plate for equal depth is
a)
less than one
b)
equal to one
c)
greater than one
d)
none of the above
|
|
Atharva Majumdar answered |
The moment of inertia is a property of an object that measures its resistance to rotational motion. It depends on the mass distribution of the object and the axis of rotation. For a circular plate and a square plate of equal depth, the mass is distributed differently, leading to different moment of inertia values.
The moment of inertia of a circular plate is given by the formula:
I_circular = (1/4) * m * r^2
where m is the mass of the plate and r is the radius of the plate.
The moment of inertia of a square plate is given by the formula:
I_square = (1/12) * m * h^2
where m is the mass of the plate and h is the side length of the square plate.
To compare the two moment of inertia values, we can take the ratio of I_circular to I_square:
I_circular / I_square = [(1/4) * m * r^2] / [(1/12) * m * h^2]
The mass cancels out in the ratio, so we are left with:
I_circular / I_square = (r^2) / (3 * h^2)
From the equation, we can see that the ratio of the moment of inertia of a circular plate to that of a square plate depends on the ratio of r^2 to h^2.
Now, let's consider a circular plate and a square plate with equal depth. This means that the height of the square plate is equal to the diameter of the circular plate (h = 2r). Substituting this into the ratio equation:
I_circular / I_square = (r^2) / (3 * (2r)^2) = (r^2) / (12r^2) = 1/12
So, the ratio of moment of inertia of a circular plate to that of a square plate for equal depth is 1/12, which is less than one. Therefore, the correct answer is option A: less than one.
The moment of inertia of a circular plate is given by the formula:
I_circular = (1/4) * m * r^2
where m is the mass of the plate and r is the radius of the plate.
The moment of inertia of a square plate is given by the formula:
I_square = (1/12) * m * h^2
where m is the mass of the plate and h is the side length of the square plate.
To compare the two moment of inertia values, we can take the ratio of I_circular to I_square:
I_circular / I_square = [(1/4) * m * r^2] / [(1/12) * m * h^2]
The mass cancels out in the ratio, so we are left with:
I_circular / I_square = (r^2) / (3 * h^2)
From the equation, we can see that the ratio of the moment of inertia of a circular plate to that of a square plate depends on the ratio of r^2 to h^2.
Now, let's consider a circular plate and a square plate with equal depth. This means that the height of the square plate is equal to the diameter of the circular plate (h = 2r). Substituting this into the ratio equation:
I_circular / I_square = (r^2) / (3 * (2r)^2) = (r^2) / (12r^2) = 1/12
So, the ratio of moment of inertia of a circular plate to that of a square plate for equal depth is 1/12, which is less than one. Therefore, the correct answer is option A: less than one.
A particle moves in a straight line. Its position is defined by the equation x = 6t2 − t3 where t in seconds and x is in meters. The maximum velocity of the particle during its motion will be- a)12 m/s
- b)6 m/s
- c)24 m/s
- d)48 m/s
Correct answer is option 'A'. Can you explain this answer?
A particle moves in a straight line. Its position is defined by the equation x = 6t2 − t3 where t in seconds and x is in meters. The maximum velocity of the particle during its motion will be
a)
12 m/s
b)
6 m/s
c)
24 m/s
d)
48 m/s

|
Ameya Deshpande answered |
The equation x = 6t^2 describes the position of the particle in terms of time, t.
In this equation, x represents the position of the particle and t represents the time elapsed. The position of the particle changes as time progresses. The function 6t^2 describes how the position changes with time.
To find the position of the particle at a specific time, substitute the value of t into the equation. For example, if t = 2, then x = 6(2)^2 = 6(4) = 24. This means that the particle's position at t = 2 is 24.
The equation x = 6t^2 describes the motion of the particle in a straight line. As time increases, the position of the particle increases quadratically. This means that the particle is accelerating, as the position changes at an increasing rate.
In this equation, x represents the position of the particle and t represents the time elapsed. The position of the particle changes as time progresses. The function 6t^2 describes how the position changes with time.
To find the position of the particle at a specific time, substitute the value of t into the equation. For example, if t = 2, then x = 6(2)^2 = 6(4) = 24. This means that the particle's position at t = 2 is 24.
The equation x = 6t^2 describes the motion of the particle in a straight line. As time increases, the position of the particle increases quadratically. This means that the particle is accelerating, as the position changes at an increasing rate.
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the ratio of the product of the centroid of the section to its mass to the total mass of the body to the centroid.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the ratio of the product of the centroid of the section to its mass to the total mass of the body to the centroid.
a)
True
b)
False
|
|
Soumya Basak answered |
The answer is obviously no. Still if we are having any difficulty in making the vector components, then we can go in 2D. As if the particle is in equilibrium, the net force will be zero. No matter where you see first. Net force is zero. But the statement here is not correct about the centroid.
Moment of inertia of a square of side 'b' about an axis through its centre of gravity is- a)b3/3
- b)b4/3
- c)b4/12
- d)b4/8
Correct answer is option 'C'. Can you explain this answer?
Moment of inertia of a square of side 'b' about an axis through its centre of gravity is
a)
b3/3
b)
b4/3
c)
b4/12
d)
b4/8
|
|
Stuti Mishra answered |
Moment of inertia is a measure of an object's resistance to rotational motion. It depends on the mass distribution of the object and the axis of rotation. In this case, we are calculating the moment of inertia of a square about an axis through its center of gravity.
The moment of inertia of a square about an axis through its center of gravity can be calculated using the parallel axis theorem. According to this theorem, the moment of inertia about an axis parallel to and a distance 'd' from an axis through the center of gravity is given by the sum of the moment of inertia about the center of gravity and the product of the mass and the square of the distance 'd'.
Let's calculate the moment of inertia of a square about an axis through its center of gravity.
1. Define the axis of rotation:
- The axis of rotation is passing through the center of gravity of the square.
2. Calculate the moment of inertia about the center of gravity:
- The moment of inertia of a square about an axis through its center of gravity is given by the equation: I = (1/12) * m * (a^2 + b^2), where 'm' is the mass of the square and 'a' and 'b' are the side lengths of the square.
- In this case, since the square has equal side lengths, 'a' and 'b' are both equal to 'b'.
- Therefore, the moment of inertia about the center of gravity is given by: I_center = (1/12) * m * (b^2 + b^2) = (1/12) * m * (2b^2) = (1/6) * m * b^2.
3. Apply the parallel axis theorem:
- The distance between the center of gravity and the axis of rotation is half of the side length of the square, which is 'b/2'.
- Using the parallel axis theorem, the moment of inertia about the axis through the center of gravity is given by: I_axis = I_center + m * (b/2)^2.
- Substituting the value of I_center, we get: I_axis = (1/6) * m * b^2 + m * (b/2)^2 = (1/6) * m * b^2 + (1/4) * m * b^2 = (1/6 + 1/4) * m * b^2 = (2/12 + 3/12) * m * b^2 = (5/12) * m * b^2.
Therefore, the moment of inertia of a square of side 'b' about an axis through its center of gravity is (5/12) * m * b^2, which is option 'C'.
The moment of inertia of a square about an axis through its center of gravity can be calculated using the parallel axis theorem. According to this theorem, the moment of inertia about an axis parallel to and a distance 'd' from an axis through the center of gravity is given by the sum of the moment of inertia about the center of gravity and the product of the mass and the square of the distance 'd'.
Let's calculate the moment of inertia of a square about an axis through its center of gravity.
1. Define the axis of rotation:
- The axis of rotation is passing through the center of gravity of the square.
2. Calculate the moment of inertia about the center of gravity:
- The moment of inertia of a square about an axis through its center of gravity is given by the equation: I = (1/12) * m * (a^2 + b^2), where 'm' is the mass of the square and 'a' and 'b' are the side lengths of the square.
- In this case, since the square has equal side lengths, 'a' and 'b' are both equal to 'b'.
- Therefore, the moment of inertia about the center of gravity is given by: I_center = (1/12) * m * (b^2 + b^2) = (1/12) * m * (2b^2) = (1/6) * m * b^2.
3. Apply the parallel axis theorem:
- The distance between the center of gravity and the axis of rotation is half of the side length of the square, which is 'b/2'.
- Using the parallel axis theorem, the moment of inertia about the axis through the center of gravity is given by: I_axis = I_center + m * (b/2)^2.
- Substituting the value of I_center, we get: I_axis = (1/6) * m * b^2 + m * (b/2)^2 = (1/6) * m * b^2 + (1/4) * m * b^2 = (1/6 + 1/4) * m * b^2 = (2/12 + 3/12) * m * b^2 = (5/12) * m * b^2.
Therefore, the moment of inertia of a square of side 'b' about an axis through its center of gravity is (5/12) * m * b^2, which is option 'C'.
What is the product of the mass and the square of the distance of the center of gravity of the mass from an axis?- a)Moment of inertia
- b)Mass moment of inertia
- c)Center of gravity
- d)Product of inertia
Correct answer is option 'B'. Can you explain this answer?
What is the product of the mass and the square of the distance of the center of gravity of the mass from an axis?
a)
Moment of inertia
b)
Mass moment of inertia
c)
Center of gravity
d)
Product of inertia
|
|
Rashi Chauhan answered |
Mass Moment of Inertia:
The product of the mass and the square of the distance of the center of gravity of the mass from an axis is known as the mass moment of inertia. It is a physical property of an object that measures its resistance to rotational motion around a particular axis. The mass moment of inertia is denoted by the symbol "I" and is given by the equation:
I = m * r^2
where:
- I is the mass moment of inertia
- m is the mass of the object
- r is the distance between the center of gravity of the mass and the axis of rotation
Explanation:
The mass moment of inertia is a measure of how the mass of an object is distributed around a given axis of rotation. It takes into account both the mass of the object and its distribution with respect to the axis. The farther the mass is from the axis, the greater the mass moment of inertia.
The concept of mass moment of inertia is important in various engineering applications, particularly in the design and analysis of rotating machinery, such as engines, turbines, and flywheels. It helps determine how the object will respond to rotational forces and torques.
The mass moment of inertia depends on the shape and mass distribution of the object. For simple shapes, such as cylinders or spheres, there are formulas that can be used to calculate the mass moment of inertia. For more complex shapes, numerical methods or computer simulations may be required.
The mass moment of inertia has several important properties:
1. It is always positive or zero, as it is a measure of the object's resistance to rotation.
2. The mass moment of inertia of a point mass is zero, as the mass is concentrated at a single point and has no distribution.
3. The mass moment of inertia is additive. For a system of particles, the total mass moment of inertia is the sum of the individual mass moments of inertia.
In conclusion, the product of the mass and the square of the distance of the center of gravity of the mass from an axis is known as the mass moment of inertia. It is a fundamental property of an object that characterizes its rotational behavior.
The product of the mass and the square of the distance of the center of gravity of the mass from an axis is known as the mass moment of inertia. It is a physical property of an object that measures its resistance to rotational motion around a particular axis. The mass moment of inertia is denoted by the symbol "I" and is given by the equation:
I = m * r^2
where:
- I is the mass moment of inertia
- m is the mass of the object
- r is the distance between the center of gravity of the mass and the axis of rotation
Explanation:
The mass moment of inertia is a measure of how the mass of an object is distributed around a given axis of rotation. It takes into account both the mass of the object and its distribution with respect to the axis. The farther the mass is from the axis, the greater the mass moment of inertia.
The concept of mass moment of inertia is important in various engineering applications, particularly in the design and analysis of rotating machinery, such as engines, turbines, and flywheels. It helps determine how the object will respond to rotational forces and torques.
The mass moment of inertia depends on the shape and mass distribution of the object. For simple shapes, such as cylinders or spheres, there are formulas that can be used to calculate the mass moment of inertia. For more complex shapes, numerical methods or computer simulations may be required.
The mass moment of inertia has several important properties:
1. It is always positive or zero, as it is a measure of the object's resistance to rotation.
2. The mass moment of inertia of a point mass is zero, as the mass is concentrated at a single point and has no distribution.
3. The mass moment of inertia is additive. For a system of particles, the total mass moment of inertia is the sum of the individual mass moments of inertia.
In conclusion, the product of the mass and the square of the distance of the center of gravity of the mass from an axis is known as the mass moment of inertia. It is a fundamental property of an object that characterizes its rotational behavior.
A thin disc and a thin ring, both have mass M and radius R. Both rotate about axes through their centre of mass and are perpendicular to their surfaces at the same angular velocity. Which of the following is true?- a)The ring has higher kinetic energy
- b)The disc has higher kinetic energy
- c)The ring and the disc have the same kinetic energy
- d)Kinetic energies of both the bodies are zero since they are not in linear motion
Correct answer is option 'A'. Can you explain this answer?
A thin disc and a thin ring, both have mass M and radius R. Both rotate about axes through their centre of mass and are perpendicular to their surfaces at the same angular velocity. Which of the following is true?
a)
The ring has higher kinetic energy
b)
The disc has higher kinetic energy
c)
The ring and the disc have the same kinetic energy
d)
Kinetic energies of both the bodies are zero since they are not in linear motion
|
|
Aman Ghosh answered |
Explanation:
When a disc and a ring rotate about axes passing through their centers of mass and perpendicular to their surfaces, they have the same angular velocity. However, their moments of inertia are different due to their different shapes.
Moment of Inertia:
The moment of inertia of an object is a measure of its resistance to rotational motion about a particular axis. It depends on the mass distribution of the object and the axis of rotation.
The moment of inertia for a thin disc rotating about an axis through its center is given by the formula:
I_disc = (1/2) * MR^2
The moment of inertia for a thin ring rotating about an axis through its center is given by the formula:
I_ring = MR^2
Kinetic Energy:
Kinetic energy is the energy an object possesses due to its motion. The kinetic energy of a rotating object depends on its moment of inertia and its angular velocity.
The kinetic energy of a rotating object is given by the formula:
KE = (1/2) * I * ω^2
where KE is the kinetic energy, I is the moment of inertia, and ω is the angular velocity.
Comparison:
Now, let's compare the kinetic energies of the disc and the ring using the formulas above.
The kinetic energy of the disc is given by:
KE_disc = (1/2) * (1/2) * MR^2 * ω^2 = (1/4) * MR^2 * ω^2
The kinetic energy of the ring is given by:
KE_ring = (1/2) * MR^2 * ω^2
Comparing the two expressions, we can see that the kinetic energy of the disc is (1/4) times the kinetic energy of the ring. Therefore, option 'A' is correct - the ring has a higher kinetic energy than the disc.
Summary:
In summary, when a thin disc and a thin ring with the same mass and radius rotate about axes passing through their centers of mass and perpendicular to their surfaces at the same angular velocity, the ring has a higher kinetic energy than the disc. This is due to the difference in their moments of inertia, with the moment of inertia of the disc being half that of the ring.
When a disc and a ring rotate about axes passing through their centers of mass and perpendicular to their surfaces, they have the same angular velocity. However, their moments of inertia are different due to their different shapes.
Moment of Inertia:
The moment of inertia of an object is a measure of its resistance to rotational motion about a particular axis. It depends on the mass distribution of the object and the axis of rotation.
The moment of inertia for a thin disc rotating about an axis through its center is given by the formula:
I_disc = (1/2) * MR^2
The moment of inertia for a thin ring rotating about an axis through its center is given by the formula:
I_ring = MR^2
Kinetic Energy:
Kinetic energy is the energy an object possesses due to its motion. The kinetic energy of a rotating object depends on its moment of inertia and its angular velocity.
The kinetic energy of a rotating object is given by the formula:
KE = (1/2) * I * ω^2
where KE is the kinetic energy, I is the moment of inertia, and ω is the angular velocity.
Comparison:
Now, let's compare the kinetic energies of the disc and the ring using the formulas above.
The kinetic energy of the disc is given by:
KE_disc = (1/2) * (1/2) * MR^2 * ω^2 = (1/4) * MR^2 * ω^2
The kinetic energy of the ring is given by:
KE_ring = (1/2) * MR^2 * ω^2
Comparing the two expressions, we can see that the kinetic energy of the disc is (1/4) times the kinetic energy of the ring. Therefore, option 'A' is correct - the ring has a higher kinetic energy than the disc.
Summary:
In summary, when a thin disc and a thin ring with the same mass and radius rotate about axes passing through their centers of mass and perpendicular to their surfaces at the same angular velocity, the ring has a higher kinetic energy than the disc. This is due to the difference in their moments of inertia, with the moment of inertia of the disc being half that of the ring.
What is not the condition for the equilibrium in calculations involved in the determination of the centre of mass?- a)∑Fx=0
- b)∑Fy=0
- c)∑Fz=0
- d)∑F≠0
Correct answer is option 'D'. Can you explain this answer?
What is not the condition for the equilibrium in calculations involved in the determination of the centre of mass?
a)
∑Fx=0
b)
∑Fy=0
c)
∑Fz=0
d)
∑F≠0

|
Anand Mehta answered |
Explanation:
Conditions for equilibrium in calculations involved in the determination of the centre of mass:
- ∑Fx=0: This condition states that the sum of all forces acting in the x-direction must be zero for equilibrium. This ensures that there is no net force causing any acceleration in the x-direction.
- ∑Fy=0: This condition states that the sum of all forces acting in the y-direction must be zero for equilibrium. This ensures that there is no net force causing any acceleration in the y-direction.
- ∑Fz=0: This condition states that the sum of all forces acting in the z-direction must be zero for equilibrium. This ensures that there is no net force causing any acceleration in the z-direction.
Not a condition for equilibrium:
- ∑F≠0: This statement is not a condition for equilibrium. In fact, the sum of all forces acting on an object must be zero for equilibrium, not unequal to zero. If the sum of forces is not zero, the object will accelerate in the direction of the resultant force.
Therefore, the correct answer is option 'D' as it does not represent a condition for equilibrium in calculations involved in the determination of the centre of mass.
Conditions for equilibrium in calculations involved in the determination of the centre of mass:
- ∑Fx=0: This condition states that the sum of all forces acting in the x-direction must be zero for equilibrium. This ensures that there is no net force causing any acceleration in the x-direction.
- ∑Fy=0: This condition states that the sum of all forces acting in the y-direction must be zero for equilibrium. This ensures that there is no net force causing any acceleration in the y-direction.
- ∑Fz=0: This condition states that the sum of all forces acting in the z-direction must be zero for equilibrium. This ensures that there is no net force causing any acceleration in the z-direction.
Not a condition for equilibrium:
- ∑F≠0: This statement is not a condition for equilibrium. In fact, the sum of all forces acting on an object must be zero for equilibrium, not unequal to zero. If the sum of forces is not zero, the object will accelerate in the direction of the resultant force.
Therefore, the correct answer is option 'D' as it does not represent a condition for equilibrium in calculations involved in the determination of the centre of mass.
The centre of gravity is the ratio of ________ to _________- a)The product of centroid and weight to the total weight
- b)The addition of centroid and weight to the total weight
- c)The subtraction of centroid and weight to the total weight
- d)The product of centroid and weight to the total mass
Correct answer is option 'A'. Can you explain this answer?
The centre of gravity is the ratio of ________ to _________
a)
The product of centroid and weight to the total weight
b)
The addition of centroid and weight to the total weight
c)
The subtraction of centroid and weight to the total weight
d)
The product of centroid and weight to the total mass
|
|
Mansi Rane answered |
The product of the centroid of the section to its weight to the total weight of the body is the centre of gravity. Thus the answer. The ratio is generally used to locate the coordinate of the centroid or the centre of gravity.
The co-efficient of restitution of a perfectly plastic impact is- a)0
- b)1
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
The co-efficient of restitution of a perfectly plastic impact is
a)
0
b)
1
c)
2
d)
3
|
|
Pankaj Joshi answered |
Co-efficient of Restitution in Perfectly Plastic Impact
The co-efficient of restitution (e) is a measure of how much kinetic energy is conserved during a collision. In the case of a perfectly plastic impact, the objects stick together after the collision, meaning there is no rebound or loss of energy.
Explanation of the Correct Answer
a) 0
In a perfectly plastic impact, the value of the co-efficient of restitution is 0. This is because all kinetic energy is lost during the collision, and the objects deform and stick together. This results in no rebound and no energy being conserved.
Comparison with Other Options
- Option b) 1: A co-efficient of restitution of 1 signifies a perfectly elastic collision where all kinetic energy is conserved. This is not the case in a perfectly plastic impact.
- Option c) 2: A co-efficient of restitution greater than 1 implies energy gain after the collision, which is not possible in a perfectly plastic impact.
- Option d) 3: Similarly, a co-efficient of restitution greater than 1 is not applicable to a perfectly plastic impact.
In conclusion, the correct answer for the co-efficient of restitution of a perfectly plastic impact is 0, as all kinetic energy is lost during the collision.
The linear velocity of a body rotating at ω rad/s along a circular path of radius r is given by- a)ω.r
- b)ω/r
- c)ωs2.r
- d)ωs2/r
Correct answer is option 'A'. Can you explain this answer?
The linear velocity of a body rotating at ω rad/s along a circular path of radius r is given by
a)
ω.r
b)
ω/r
c)
ωs2.r
d)
ωs2/r
|
|
Kritika Joshi answered |
A given angular velocity depends on the distance from the axis of rotation. This relationship is described by the formula:
v = r x ω
where:
v = linear velocity
r = distance from the axis of rotation
ω = angular velocity
This formula applies to any object rotating around an axis, such as a wheel, a spinning top, or the Earth. The linear velocity is directly proportional to the distance from the axis of rotation, which means that the farther away an object is from the axis, the faster it moves.
For example, consider a wheel with a radius of 0.5 meters that is rotating at a rate of 10 revolutions per second. The angular velocity of the wheel is:
ω = 10 x 2π = 62.83 radians per second
Using the formula above, we can calculate the linear velocity of a point on the edge of the wheel:
v = 0.5 x 62.83 = 31.42 meters per second
This means that a point on the edge of the wheel is moving at a speed of 31.42 meters per second, or approximately 112.5 kilometers per hour. Note that the linear velocity is highest at the edge of the wheel, where the distance from the axis is greatest.
v = r x ω
where:
v = linear velocity
r = distance from the axis of rotation
ω = angular velocity
This formula applies to any object rotating around an axis, such as a wheel, a spinning top, or the Earth. The linear velocity is directly proportional to the distance from the axis of rotation, which means that the farther away an object is from the axis, the faster it moves.
For example, consider a wheel with a radius of 0.5 meters that is rotating at a rate of 10 revolutions per second. The angular velocity of the wheel is:
ω = 10 x 2π = 62.83 radians per second
Using the formula above, we can calculate the linear velocity of a point on the edge of the wheel:
v = 0.5 x 62.83 = 31.42 meters per second
This means that a point on the edge of the wheel is moving at a speed of 31.42 meters per second, or approximately 112.5 kilometers per hour. Note that the linear velocity is highest at the edge of the wheel, where the distance from the axis is greatest.
Chapter doubts & questions for Kinematics of Point Mass & Rigid Bodies - Engineering Mechanics for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Kinematics of Point Mass & Rigid Bodies - Engineering Mechanics for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Engineering Mechanics for Mechanical Engineering
33 videos|78 docs|44 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









