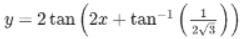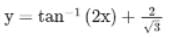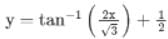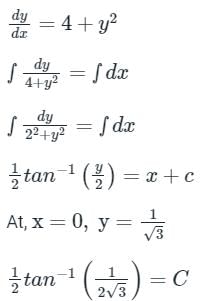All Exams >
Civil Engineering (CE) >
Engineering Mathematics for Civil Engineering >
All Questions
All questions of Ordinary Differential Equations for Civil Engineering (CE) Exam
The solution of differential equation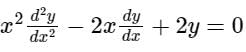 will be ___________, where c1 and c2 are arbitrary constants.
will be ___________, where c1 and c2 are arbitrary constants.- a)y = c1x + c2x2
- b)y = c1 log x + c2x
- c)y = c1 + c2x
- d)y = c1x2 + c2x3
Correct answer is option 'A'. Can you explain this answer?
The solution of differential equation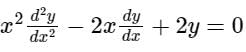 will be ___________, where c1 and c2 are arbitrary constants.
will be ___________, where c1 and c2 are arbitrary constants.
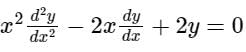 will be ___________, where c1 and c2 are arbitrary constants.
will be ___________, where c1 and c2 are arbitrary constants.a)
y = c1x + c2x2
b)
y = c1 log x + c2x
c)
y = c1 + c2x
d)
y = c1x2 + c2x3

|
Gate Gurus answered |
Concept:
Linear differential equations with variable coefficients can be reduced to linear differential equations with constant coefficients by suitable substitutions.
Euler Cauchy Homogeneous linear equation:
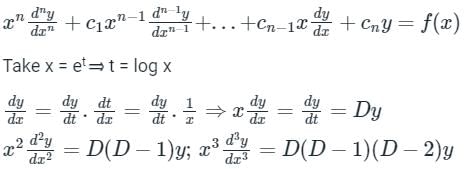
Calculation:
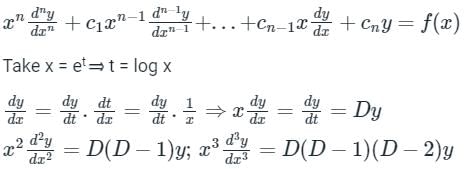
Calculation:
Given:
Euler Cauchy equation:
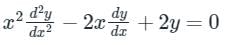
Now, the above differential equation becomes
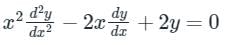
Now, the above differential equation becomes
D (D – 1) y – 2 D y + 2 y = 0
⇒ D2 y – D y – 2 D y + 2 y = 0
⇒ (D2 – 3 D + 2) y = 0
Auxiliary equation:
(D2 – 3 D + 2) = 0
⇒ (D - 2) (D - 1) = 0
⇒ D = 2, 1
Now the roots are real and different, and the general solution of given equation is
y = c1 e2t + c2 et
⇒ y = c1x + c2x2
General solution of the Cauchy-Euler equation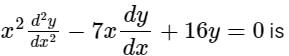
- a)y = c1x2 + c2x4
- b)y = c1x2 + c2x-4
- c)y = (c1 + c2 In x) x4
- d)y = c1x4 + c2x-4 In x
Correct answer is option 'C'. Can you explain this answer?
General solution of the Cauchy-Euler equation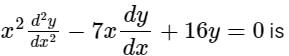
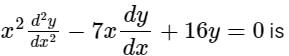
a)
y = c1x2 + c2x4
b)
y = c1x2 + c2x-4
c)
y = (c1 + c2 In x) x4
d)
y = c1x4 + c2x-4 In x

|
Gate Gurus answered |
Concept:
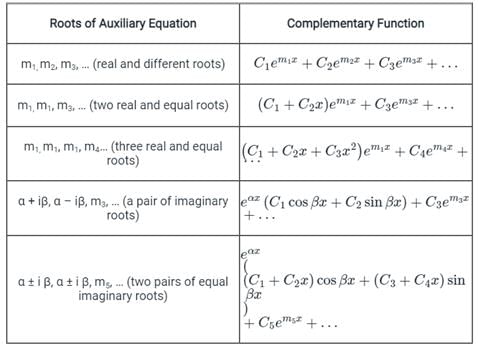
For different roots of the auxiliary equation, the solution (complementary function) of the differential equation is as shown below.
Calculation:

Calculation:
Given:

Put x = et

Put x = et
⇒ t = ln x
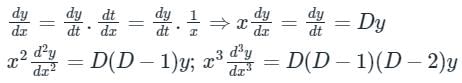
Now, the above differential equation becomes
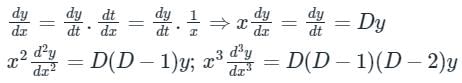
Now, the above differential equation becomes
D(D – 1)y – 7Dy + 16y = 0
⇒ D2y – Dy – 7Dy + 16y = 0
⇒ (D2 – 8D + 16)y = 0
Auxiliary equation:
(D2 – 8 D + 16) = 0
⇒ D = 4
The solutions for the above roots of auxiliary equations are:
y(t) = (c1 + c2 t) e4t
⇒ y(x) = (c1 + c2 ln x) x4
A solution which does not contain any arbitrary constants is called a general solution.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
A solution which does not contain any arbitrary constants is called a general solution.
a)
True
b)
False

|
Rahul Chauhan answered |
The answer is True.
Explanation:
In mathematics and engineering, a solution that does not contain any arbitrary constants is referred to as a general solution. This means that the solution represents all possible solutions to a given problem or equation, without any additional constraints or specific values.
Definition of a General Solution:
A general solution is a solution in which all possible solutions to a problem or equation are included. It does not contain any arbitrary constants, which means that it represents the complete set of solutions without any additional restrictions or specific values.
Characteristics of a General Solution:
1. Contains No Arbitrary Constants: A general solution does not involve any arbitrary constants. It represents the complete set of solutions without imposing any specific values or restrictions.
2. Represents All Possible Solutions: A general solution encompasses all possible solutions to a problem or equation. It includes all valid solutions without any additional constraints.
3. Allows for Flexibility: Since a general solution does not involve any arbitrary constants, it allows for flexibility in determining specific solutions. It provides a framework within which specific solutions can be derived by assigning suitable values to the constants.
4. Can Be Modified: A general solution can be modified or refined by adding specific constraints or conditions. By introducing additional information or requirements, a more specific solution can be obtained.
5. Applies to a Range of Problems: The concept of a general solution is applicable to various mathematical and engineering problems. It is a fundamental concept in differential equations, linear algebra, and other branches of mathematics.
In conclusion, a general solution is a solution that represents all possible solutions to a problem or equation without any arbitrary constants. It offers flexibility and can be modified or refined to obtain more specific solutions.
Explanation:
In mathematics and engineering, a solution that does not contain any arbitrary constants is referred to as a general solution. This means that the solution represents all possible solutions to a given problem or equation, without any additional constraints or specific values.
Definition of a General Solution:
A general solution is a solution in which all possible solutions to a problem or equation are included. It does not contain any arbitrary constants, which means that it represents the complete set of solutions without any additional restrictions or specific values.
Characteristics of a General Solution:
1. Contains No Arbitrary Constants: A general solution does not involve any arbitrary constants. It represents the complete set of solutions without imposing any specific values or restrictions.
2. Represents All Possible Solutions: A general solution encompasses all possible solutions to a problem or equation. It includes all valid solutions without any additional constraints.
3. Allows for Flexibility: Since a general solution does not involve any arbitrary constants, it allows for flexibility in determining specific solutions. It provides a framework within which specific solutions can be derived by assigning suitable values to the constants.
4. Can Be Modified: A general solution can be modified or refined by adding specific constraints or conditions. By introducing additional information or requirements, a more specific solution can be obtained.
5. Applies to a Range of Problems: The concept of a general solution is applicable to various mathematical and engineering problems. It is a fundamental concept in differential equations, linear algebra, and other branches of mathematics.
In conclusion, a general solution is a solution that represents all possible solutions to a problem or equation without any arbitrary constants. It offers flexibility and can be modified or refined to obtain more specific solutions.
Consider the following statements about the linear dependence of the real valued functions y1 = 1, y2 = x and y3 = x2, over the field of real numbers.I. y1, y2 and y3 are linearly independent on – 1 ≤ x ≤ 0II. y1, y2 and y3 are linearly dependent on 0 ≤ x ≤ 1III. y1, y2 and y3 are linearly independent on 0 ≤ x ≤ 1IV. y1, y2 and y3 are linearly dependent on – 1 ≤ x ≤ 0Which one among the following is correct?- a)Both I and II are true
- b)Both I and III are true
- c)Both II and IV are true
- d)Both III and IV are true
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements about the linear dependence of the real valued functions y1 = 1, y2 = x and y3 = x2, over the field of real numbers.
I. y1, y2 and y3 are linearly independent on – 1 ≤ x ≤ 0
II. y1, y2 and y3 are linearly dependent on 0 ≤ x ≤ 1
III. y1, y2 and y3 are linearly independent on 0 ≤ x ≤ 1
IV. y1, y2 and y3 are linearly dependent on – 1 ≤ x ≤ 0
Which one among the following is correct?
a)
Both I and II are true
b)
Both I and III are true
c)
Both II and IV are true
d)
Both III and IV are true
|
|
Sanya Agarwal answered |
Concept:
The linear dependency or Independency of function fi can be found using Wronskion Matrix.
An analytic function is linearly dependent if:
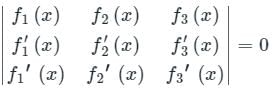
Application:
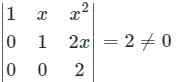
Determinant ≠ 0
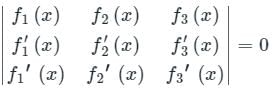
Application:
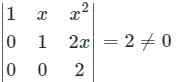
Determinant ≠ 0
Function y1, y2, y3 are linearly independent.
A function y(t) such that y(0) = 1 and y(1) = 3e-1, is a solution of the differential equation 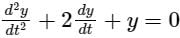 . Then y(2) is
. Then y(2) is- a)5e−1
- b)5e−2
- c)7e−1
- d)7e−2
Correct answer is option 'B'. Can you explain this answer?
A function y(t) such that y(0) = 1 and y(1) = 3e-1, is a solution of the differential equation 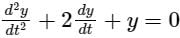 . Then y(2) is
. Then y(2) is
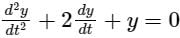 . Then y(2) is
. Then y(2) isa)
5e−1
b)
5e−2
c)
7e−1
d)
7e−2

|
Pioneer Academy answered |

By applying the Laplace transform,
s2Y(s) − sy(0) − y′(0) + 2sY(s) − 2y(0) + Y(s) = 0
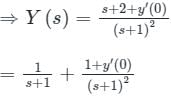
By applying the inverse Laplace transform
y(t) = e−t + (1 + y′(0))te−t
y(1) = 3 e-1
⇒ y(1) = e-1 + (1 + y’(0)) e-1 = 3 e-1
⇒ y’(0) = 1
Now the equation of y(t) becomes
y(t) = (1 + 2t) e-t
At t = 2,
y(2) = 5 e-2
In fluid kinematics, the approach of the Lagrangian method for analysis is:- a)tracing the behaviour of each and every particle of the flow
- b)tracing the simultaneous behaviour of all particles through a section
- c)by tracing only inlet particles' behaviour
- d)by tracing only outlet particles' behaviour
Correct answer is option 'A'. Can you explain this answer?
In fluid kinematics, the approach of the Lagrangian method for analysis is:
a)
tracing the behaviour of each and every particle of the flow
b)
tracing the simultaneous behaviour of all particles through a section
c)
by tracing only inlet particles' behaviour
d)
by tracing only outlet particles' behaviour

|
Simran Dasgupta answered |
Tracing Behaviour of Each Particle
The Lagrangian method in fluid kinematics involves tracing the behavior of each and every particle of the flow. This means that instead of looking at the flow as a whole, individual particles are followed throughout their movements.
Advantages of Lagrangian Method
1. Precision: By tracking the behavior of each particle, the Lagrangian method allows for a detailed and precise analysis of fluid flow. This can be especially useful in complex flow situations.
2. Individual Particle Insights: By focusing on individual particles, the method provides insights into how each particle interacts with its surroundings and how it contributes to the overall flow behavior.
3. Dynamic Analysis: The Lagrangian method is well-suited for analyzing dynamic flow situations where particles may have varying velocities and trajectories.
4. Particle Tracking: By tracing the path of each particle, researchers can gain a better understanding of phenomena such as turbulence, mixing, and diffusion in fluid flows.
Application in Engineering
The Lagrangian method is commonly used in various engineering applications, such as in the design of turbomachinery, optimization of chemical processes, and simulation of environmental flows. By considering the behavior of individual particles, engineers can make more informed decisions and improve the efficiency and performance of fluid systems.
In conclusion, the Lagrangian method for fluid kinematics involves tracing the behavior of each particle in the flow, providing a detailed and insightful analysis of fluid dynamics.
The Lagrangian method in fluid kinematics involves tracing the behavior of each and every particle of the flow. This means that instead of looking at the flow as a whole, individual particles are followed throughout their movements.
Advantages of Lagrangian Method
1. Precision: By tracking the behavior of each particle, the Lagrangian method allows for a detailed and precise analysis of fluid flow. This can be especially useful in complex flow situations.
2. Individual Particle Insights: By focusing on individual particles, the method provides insights into how each particle interacts with its surroundings and how it contributes to the overall flow behavior.
3. Dynamic Analysis: The Lagrangian method is well-suited for analyzing dynamic flow situations where particles may have varying velocities and trajectories.
4. Particle Tracking: By tracing the path of each particle, researchers can gain a better understanding of phenomena such as turbulence, mixing, and diffusion in fluid flows.
Application in Engineering
The Lagrangian method is commonly used in various engineering applications, such as in the design of turbomachinery, optimization of chemical processes, and simulation of environmental flows. By considering the behavior of individual particles, engineers can make more informed decisions and improve the efficiency and performance of fluid systems.
In conclusion, the Lagrangian method for fluid kinematics involves tracing the behavior of each particle in the flow, providing a detailed and insightful analysis of fluid dynamics.
A particle undergoes forced vibrations according to the law xn(t) + 25x(t) = 21 sin t. If the particle starts from rest at t = 0, find the displacement at any time t > 0. - a)

- b)
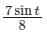
- c)
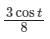
- d)
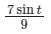
Correct answer is option 'B'. Can you explain this answer?
A particle undergoes forced vibrations according to the law xn(t) + 25x(t) = 21 sin t. If the particle starts from rest at t = 0, find the displacement at any time t > 0.
a)

b)
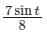
c)
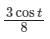
d)
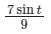

|
Pioneer Academy answered |
Concept:
The solution of the linear differential equation is of the form:
y = C.F + P.I
where C.F is the complementary function and P.I is the particular integral.
The 2nd order linear differential equation in the symbolic form is represented as:
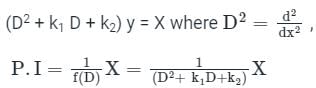
When X = Sin(ax)
f(-a2) is calculated by replacing D2 with a2 in f(D)
In the case of a forced damped system, the vibration equation:
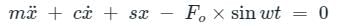 The solution of x is (CF + PI)
The solution of x is (CF + PI)Where CF is complimentary function and PI is particular integral
But after some time CF becomes zero.
∴ x = P.I
Calculation:
Given:
xn(t) + 25x(t) = 21 sin t
The above equation can be written as:
D2 + 25x = 21 × Sin (t)
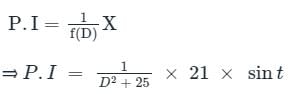
Here, a = 1, So putting -a2 = D2 = -1 in the above equation

∴ The displacement at any time t > 0 = 

A particular solution for an equation is derived by substituting particular values to the arbitrary constants in the complete solution.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
A particular solution for an equation is derived by substituting particular values to the arbitrary constants in the complete solution.
a)
True
b)
False
|
|
Sanya Agarwal answered |
A solution which does not contain any arbitrary constants is called a general solution whereas a particular solution is derived by substituting particular values to the arbitrary constants in this solution.
If f(Z) is an analytical function and (r, θ) denotes the polar co-ordinates, then:- a)
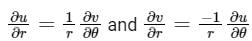
- b)

- c)

- d)
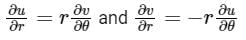
Correct answer is option 'A'. Can you explain this answer?
If f(Z) is an analytical function and (r, θ) denotes the polar co-ordinates, then:
a)
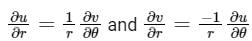
b)

c)

d)
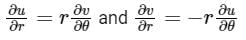
|
|
Sanya Agarwal answered |
Cauchy Riemann Equation in Polar Form:
A function f(z) which is single-valued and possesses a unique derivative with respect to z at all points of a region R, is called an analytic function of z in that region.
If f = u + iv is differentiable at z = reiθ then the Polar Cauchy Riemann equations at (r, θ) and x = rcos θ and y = rsin θ is given by,

Important Point:

Important Point:
Cauchy Riemann Equation in Rectangular Form:
If f(z) = u (x, y) + iv (x,y) is differentiable at z = x + iy. Then at z the first order patial derivatives of u and v exist and satisfy:
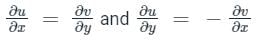
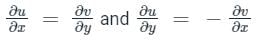
The ordinary differential equation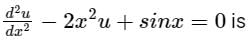
- a)linear and homogeneous
- b)linear and non-homogeneous
- c)non-linear and homogeneous
- d)non-linear and non-homogeneous
Correct answer is option 'B'. Can you explain this answer?
The ordinary differential equation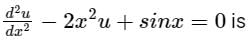
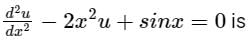
a)
linear and homogeneous
b)
linear and non-homogeneous
c)
non-linear and homogeneous
d)
non-linear and non-homogeneous

|
Vertex Academy answered |
Concept:
Identification of Non-linear Differential Equation:
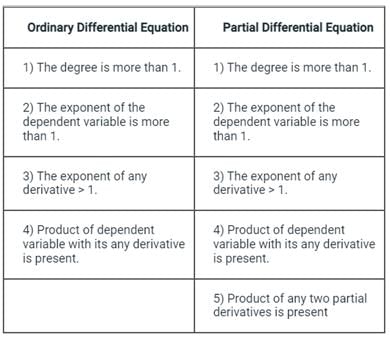
If any differential equation consists at least one of the above properties, then it is called non-linear differential equation and if any differential equation is free from all the above properties, then it is a linear differential equation.

If any differential equation consists at least one of the above properties, then it is called non-linear differential equation and if any differential equation is free from all the above properties, then it is a linear differential equation.
Given:
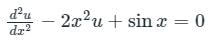
It is free from all the four characteristics described in the table. Hence it is a linear differential equation.
Product of dependent and independent variable i.e. x and u is present. Hence it is a non-homogenous equation.
Singular solution of a differential equation is one that cannot be obtained from the general solution gotten by the usual method of solving the differential equation.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Singular solution of a differential equation is one that cannot be obtained from the general solution gotten by the usual method of solving the differential equation.
a)
True
b)
False
|
|
Sanya Agarwal answered |
A differential equation is said to have a singular solution if in all points in the domain of the equation the uniqueness of the solution is violated. Hence, this solution cannot be obtained from the general solution.
The differential equation representing the family of circles touching y-axis at origin is:- a)Linear & of first order
- b)Linear & of second order
- c)Non-linear & of first order
- d)Non-linear & of second order
Correct answer is option 'C'. Can you explain this answer?
The differential equation representing the family of circles touching y-axis at origin is:
a)
Linear & of first order
b)
Linear & of second order
c)
Non-linear & of first order
d)
Non-linear & of second order

|
Jay Sharma answered |
Understanding the Family of Circles
The family of circles that touch the y-axis at the origin can be represented by the general equation of a circle. The equation can be described as:
- (x - h)² + (y - k)² = r²
Here, for circles touching the y-axis at the origin, the center (h, k) will be (r, k) where r is the radius and k can take any value.
Equation of the Circles
The specific equation becomes:
- (x - r)² + (y - k)² = r²
This can be expanded and rearranged as:
- x² - 2xr + r² + y² - 2yk + k² = r²
This simplifies to:
- x² + y² - 2xr - 2yk + k² = 0
Deriving the Differential Equation
To find the differential equation, we differentiate this equation with respect to x:
- 2x + 2y(dy/dx) - 2r - 2(dy/dx)k = 0
Rearranging gives us a first-order differential equation in terms of dy/dx.
Nature of the Differential Equation
- The equation is non-linear because of the presence of the terms involving (dy/dx) in a multiplicative form.
- It is of first order since it involves the first derivative but not higher derivatives.
Conclusion
Thus, the correct classification of the differential equation representing the family of circles touching the y-axis at the origin is:
- Non-linear & of first order (Option C).
The family of circles that touch the y-axis at the origin can be represented by the general equation of a circle. The equation can be described as:
- (x - h)² + (y - k)² = r²
Here, for circles touching the y-axis at the origin, the center (h, k) will be (r, k) where r is the radius and k can take any value.
Equation of the Circles
The specific equation becomes:
- (x - r)² + (y - k)² = r²
This can be expanded and rearranged as:
- x² - 2xr + r² + y² - 2yk + k² = r²
This simplifies to:
- x² + y² - 2xr - 2yk + k² = 0
Deriving the Differential Equation
To find the differential equation, we differentiate this equation with respect to x:
- 2x + 2y(dy/dx) - 2r - 2(dy/dx)k = 0
Rearranging gives us a first-order differential equation in terms of dy/dx.
Nature of the Differential Equation
- The equation is non-linear because of the presence of the terms involving (dy/dx) in a multiplicative form.
- It is of first order since it involves the first derivative but not higher derivatives.
Conclusion
Thus, the correct classification of the differential equation representing the family of circles touching the y-axis at the origin is:
- Non-linear & of first order (Option C).
Which of the following is one of the criterions for linearity of an equation?- a)The dependent variable and its derivatives should be of second order
- b)The dependent variable and its derivatives should not be of same order
- c)Each coefficient does not depend on the independent variable
- d)Each coefficient depends only on the independent variable
Correct answer is option 'D'. Can you explain this answer?
Which of the following is one of the criterions for linearity of an equation?
a)
The dependent variable and its derivatives should be of second order
b)
The dependent variable and its derivatives should not be of same order
c)
Each coefficient does not depend on the independent variable
d)
Each coefficient depends only on the independent variable

|
Rajat Patel answered |
Linearity of an equation:
Linearity refers to the property of an equation where the dependent variable and its derivatives have a linear relationship with the independent variable. In other words, a linear equation is one that can be expressed in the form of a straight line on a graph.
Criterion for linearity:
The criterion for linearity of an equation is that each coefficient in the equation depends only on the independent variable. This means that the coefficients should not be dependent on the dependent variable or any of its derivatives.
Explanation:
Linearity is determined by the relationship between the dependent variable and the independent variable. If an equation is linear, it means that the dependent variable and its derivatives have a linear relationship with the independent variable.
In a linear equation, each coefficient represents the slope or rate of change of the dependent variable with respect to the independent variable. These coefficients determine how the dependent variable and its derivatives vary with changes in the independent variable.
If each coefficient in the equation depends only on the independent variable, it implies that the rate of change of the dependent variable and its derivatives is constant and does not depend on the values of the dependent variable or its derivatives. This is a characteristic of a linear equation.
On the other hand, if the coefficients depend on the dependent variable or its derivatives, the rate of change of the dependent variable and its derivatives will vary with changes in the values of the dependent variable or its derivatives. This violates the criterion for linearity.
Therefore, the correct criterion for linearity of an equation is that each coefficient depends only on the independent variable (option D). This ensures that the equation represents a linear relationship between the dependent variable and the independent variable.
Linearity refers to the property of an equation where the dependent variable and its derivatives have a linear relationship with the independent variable. In other words, a linear equation is one that can be expressed in the form of a straight line on a graph.
Criterion for linearity:
The criterion for linearity of an equation is that each coefficient in the equation depends only on the independent variable. This means that the coefficients should not be dependent on the dependent variable or any of its derivatives.
Explanation:
Linearity is determined by the relationship between the dependent variable and the independent variable. If an equation is linear, it means that the dependent variable and its derivatives have a linear relationship with the independent variable.
In a linear equation, each coefficient represents the slope or rate of change of the dependent variable with respect to the independent variable. These coefficients determine how the dependent variable and its derivatives vary with changes in the independent variable.
If each coefficient in the equation depends only on the independent variable, it implies that the rate of change of the dependent variable and its derivatives is constant and does not depend on the values of the dependent variable or its derivatives. This is a characteristic of a linear equation.
On the other hand, if the coefficients depend on the dependent variable or its derivatives, the rate of change of the dependent variable and its derivatives will vary with changes in the values of the dependent variable or its derivatives. This violates the criterion for linearity.
Therefore, the correct criterion for linearity of an equation is that each coefficient depends only on the independent variable (option D). This ensures that the equation represents a linear relationship between the dependent variable and the independent variable.
Solve: (x2D2 - 4xD + 6)y = x2
where D = d/dx - a)y = c1 x2 + c2 x2 - x2 logx2
- b)y = c1 x2 + c2 x3 - xlogx2
- c)y = c1 x2 + c2 x3 - x2logx2
- d)y = c1 x2 + c2 x2 - x logx2
Correct answer is option 'C'. Can you explain this answer?
Solve: (x2D2 - 4xD + 6)y = x2
where D = d/dx
where D = d/dx
a)
y = c1 x2 + c2 x2 - x2 logx2
b)
y = c1 x2 + c2 x3 - xlogx2
c)
y = c1 x2 + c2 x3 - x2logx2
d)
y = c1 x2 + c2 x2 - x logx2
|
|
Sanya Agarwal answered |
Cauchy's Equation MCQ Question 2 Detailed Solution
Concept:
If the derivation power and the variable power are the same, then the equation is Cauchy - Euler equation.
Now,
It can be solved by putting x = ez and log x = z and hence d/dz = θ
Analysis:
(x2D2 - 4xD + 6)y = x2 ---(1)
xD = θ
x2D2 = θ (θ - 1)
substitute in equation (1):
[(θ2 - θ) - 4θ + 6]y = e2z ---(2)
It becomes linear differential equation with real constants.
f(θ) y = ϕ (z)
f(θ) = θ2 - 5θ + 6, ϕ (z) = e2z
C.F:
θ2 - 5θ + 6 = 0
m2 - 5m + 6 = 0
(m - 2) (m - 3) = 0
∴ C.F = C1e2z + C2e3z
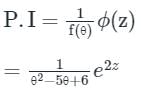
putting θ = 2, f(θ) = 0
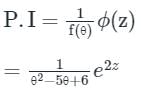
putting θ = 2, f(θ) = 0
hence,
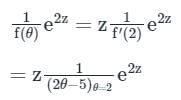
= -ze2z
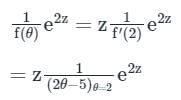
= -ze2z
∴ y = c1e2z + c2e3z - ze2z
putting, x = ez
∴ y = c1 x2 + c2 x3 - x2logx2
Solve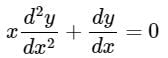 Which of the following is the solution of above equation, when x = 0?
Which of the following is the solution of above equation, when x = 0?- a)Can be any constant
- b)Undefined
- c)Zero
- d)1
Correct answer is option 'B'. Can you explain this answer?
Solve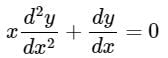
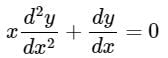
Which of the following is the solution of above equation, when x = 0?
a)
Can be any constant
b)
Undefined
c)
Zero
d)
1
|
|
Sanya Agarwal answered |
Concept:
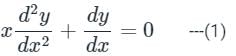
The given equation is multiplied with x to make it a equation of Cauchy Euler type.
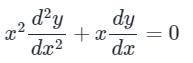
The given equation is of Cauchy Euler type. Cauchy Euler equation is homogenous linear equation with variable coefficient.
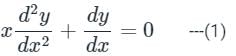
The given equation is multiplied with x to make it a equation of Cauchy Euler type.
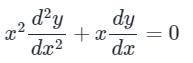
The given equation is of Cauchy Euler type. Cauchy Euler equation is homogenous linear equation with variable coefficient.
They can be reduced to linear equations with constant coefficients
Calculation:
Given:
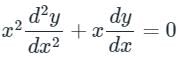
Put x = et
log x = t
The given equation is written as
[x2D2 + xD]y = 0 ---(1)
Put xD = D’, x2D2 = D’(D’ - 1)
[D’(D’ - 1) + D’]y = 0
D’2 y = 0
The auxiliary equation is D’2 = 0
The roots of this equation are 0, 0
C.F = (At + B) e0t
y = (At + B)
Put t = log x
y = A log x + B
At x = 0; y is undefined as log 0 is undefined.
Every Cauchy sequence is- a)Unbounded
- b)Bounded
- c)Infinite
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Every Cauchy sequence is
a)
Unbounded
b)
Bounded
c)
Infinite
d)
None of these

|
Gate Gurus answered |
Basic properties of Cauchy sequences:
(i) Every convergent sequence is a Cauchy sequence,
(ii) Every Cauchy sequence of real (or complex) numbers is bounded,
(iii) If in a metric space, a Cauchy sequence possessing a convergent subsequence with limit is itself convergent and has the same limit.
∴ Every Cauchy sequence is bounded
Which of the following is an example of non-linear differential equation?- a)y = mx + c
- b)x + x’ = 0
- c)x + x2 = 0
- d)x” + 2x = 0
Correct answer is option 'C'. Can you explain this answer?
Which of the following is an example of non-linear differential equation?
a)
y = mx + c
b)
x + x’ = 0
c)
x + x2 = 0
d)
x” + 2x = 0

|
Prerna Menon answered |
The example of a non-linear differential equation is a) y = mx^c.
Cauchy’s linear differential equation 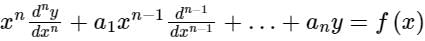 can be reduced to a linear differential equation with constant coefficient by using substitution
can be reduced to a linear differential equation with constant coefficient by using substitution- a)x = ez
- b)y = ez
- c)z = ex
- d)z = ey
Correct answer is option 'A'. Can you explain this answer?
Cauchy’s linear differential equation 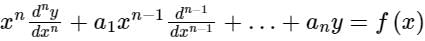 can be reduced to a linear differential equation with constant coefficient by using substitution
can be reduced to a linear differential equation with constant coefficient by using substitution
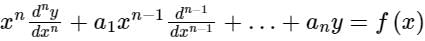 can be reduced to a linear differential equation with constant coefficient by using substitution
can be reduced to a linear differential equation with constant coefficient by using substitutiona)
x = ez
b)
y = ez
c)
z = ex
d)
z = ey

|
Gate Gurus answered |
Concept:
Any linear equation of the following form:
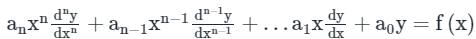 is considered as Cauchy’s differential equation. The equation has variable coefficients so its solution becomes tedious but we can convert the above equation into the linear differential equation with constant coefficients
is considered as Cauchy’s differential equation. The equation has variable coefficients so its solution becomes tedious but we can convert the above equation into the linear differential equation with constant coefficientsBy taking,
log x = z or x = ez
Proof:
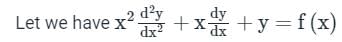
log x = z
Taking differentiation on both sides we get,
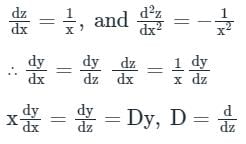
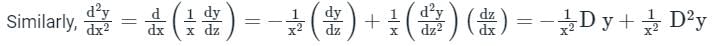

Now, it can be solved by finding C.F and P.I just like we solve linear differential equations with constant coefficients.
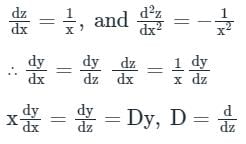
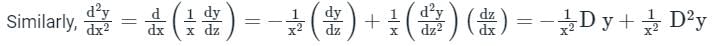

Now, it can be solved by finding C.F and P.I just like we solve linear differential equations with constant coefficients.
The complementary function of the differential equation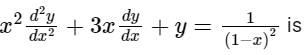
- a)
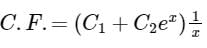
- b)
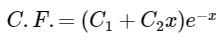
- c)
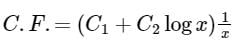
- d)
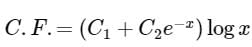
Correct answer is option 'C'. Can you explain this answer?
The complementary function of the differential equation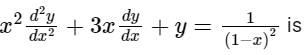
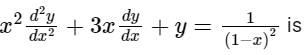
a)
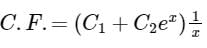
b)
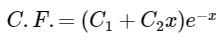
c)
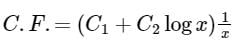
d)
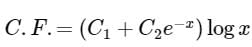
|
|
Sanya Agarwal answered |
Concept:
Linear differential equations with variable coefficients can be reduced to linear differential equations with constant coefficients by suitable substitutions.
Euler Cauchy Homogeneous linear equation:

Calculation:

Calculation:
Given:
Euler Cauchy equation:

Put x = et

Put x = et
⇒ t = log x
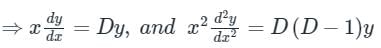
Now the equation becomes,
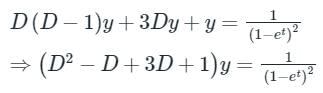
Auxillary equation is D2 + 2D + 1 = 0
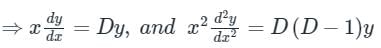
Now the equation becomes,
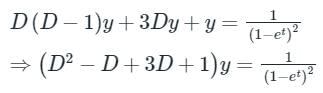
Auxillary equation is D2 + 2D + 1 = 0
⇒ (D + 1)2 = 0
⇒ D = -1, -1
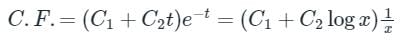
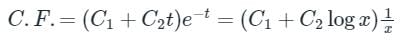
The solution to the differential equation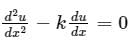 where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is
where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is- a)

- b)

- c)
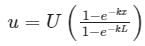
- d)
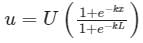
Correct answer is option 'B'. Can you explain this answer?
The solution to the differential equation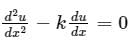 where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is
where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is
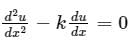 where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is
where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, isa)

b)

c)
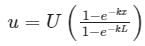
d)
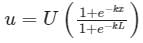

|
Naroj Boda answered |
Concept:
If roots are real and different then
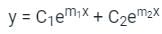
Calculation:
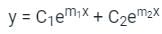
Calculation:
Given:
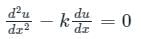
D2 – kD = 0
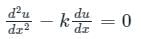
D2 – kD = 0
m(m - k) = 0
m1 = 0, m2 = k
Roots are real and different
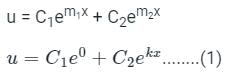
u(0) = 0
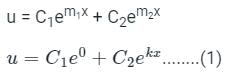
u(0) = 0
∴ C1 + C2 = 0 .................... (2)
u(L) = U
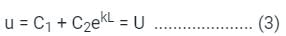
solving (2) and (3), we get
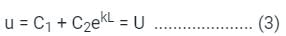
solving (2) and (3), we get
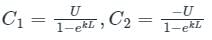
Putting values fo C1 and C2 in eqn 1
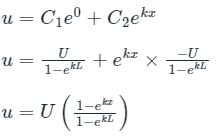
The solution of the differential equation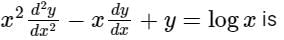
- a)y = (c1 + c2x) log x + 2 log x + 3
- b)y = (c1 + c2x2) log x + log x + 2
- c)y = (c1 + c2x) log x + log x + 2
- d)y = (c1 + c2 log x) x + log x + 2
Correct answer is option 'D'. Can you explain this answer?
The solution of the differential equation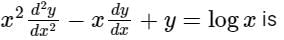
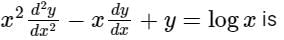
a)
y = (c1 + c2x) log x + 2 log x + 3
b)
y = (c1 + c2x2) log x + log x + 2
c)
y = (c1 + c2x) log x + log x + 2
d)
y = (c1 + c2 log x) x + log x + 2

|
Gate Gurus answered |
We are given DE shown below;
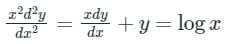
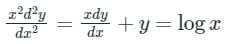
By putting x = ez we can replace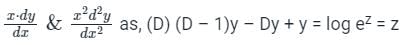
⇒ (D2 – 2D + 1)y = z (Here F(D) = (D - 1)2
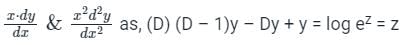
⇒ (D2 – 2D + 1)y = z (Here F(D) = (D - 1)2
⇒ F(D) = (D - 1)2 = (1 - D)2 has two equal roots Q = 1, 1
So its C⋅F = (C1 + C2z)ez
⇒ C⋅F = (C1 + C2 log x)x (∵ x = ez)
& its P⋅I = [F(D)]-1⋅z = (1 - D)-2⋅ z
Since expansion of (1 - D)-2 = (1 + 2D + 3D2 + 4D3 + …)
⇒ P⋅I = [1 + 2D + 3D2 + 4D3 + …](z)
P⋅I = (1 + 2D + 3D2 + 4D3 + …)(z)

⇒ P⋅I = z + 2

⇒ P⋅I = z + 2
⇒ P⋅I = log x + 2 (since x = ez)
So net solution of QE will be P⋅I + C⋅F
⇒ y = C⋅F + P⋅I = (C1 + C2 log x)x + log x + 2
⇒ y = (C1 + C2 log x) x + log x + 2
Solve
- a)y = (c1 + c2logx)x + logx + 2
- b)y = (c1 + c2logx)x + ex + 2
- c)y = (c1 + c2logx)x + ex logx + 2
- d)y = (c1 + c2x)log x + log x + 2
Correct answer is option 'A'. Can you explain this answer?
Solve

a)
y = (c1 + c2logx)x + logx + 2
b)
y = (c1 + c2logx)x + ex + 2
c)
y = (c1 + c2logx)x + ex logx + 2
d)
y = (c1 + c2x)log x + log x + 2
|
|
Sanya Agarwal answered |
Explanation:
Linear differential equations with variable coefficients which can be reduced to linear differential equations with constant coefficients by suitable substitution.
Euler Cauchy's homogeneous linear equation:
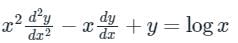
This is a Cauchy’s homogenous linear equation
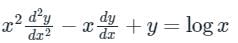
This is a Cauchy’s homogenous linear equation
Put x = et
⇒ t = log x
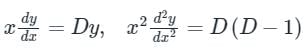
Now, the equation becomes,
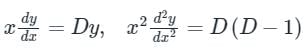
Now, the equation becomes,
(D(D − 1) − D + 1)y = t ⇒ (D − 1)2y = t
A.E. is (D – 1)2 = 0
⇒ D = 1, 1
C.F. = (c1 + c2 t) et
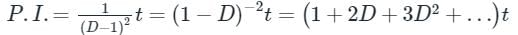
= t + 2
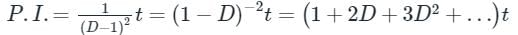
= t + 2
Complete solution is
y = (c1 + c2 t) et + t + 2
Putting t = log x
⇒ y = (c1 + c2 log x) x + log x + 2
Which of the following is the property of error function?- a)erf (0) = 1
- b)erf (∞) = 1
- c)erf (0) = ∞
- d)erf (∞) = 0
Correct answer is option 'B'. Can you explain this answer?
Which of the following is the property of error function?
a)
erf (0) = 1
b)
erf (∞) = 1
c)
erf (0) = ∞
d)
erf (∞) = 0
|
|
Sanvi Kapoor answered |
Error Function is given by, 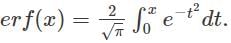
Some of its properties are:
erf (0) = 0
erf (∞) = 1
erf (-x) = -erf(x)
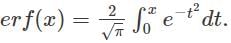
Some of its properties are:
erf (0) = 0
erf (∞) = 1
erf (-x) = -erf(x)
Which of the following is a type of Iterative method of solving non-linear equations?- a)Graphical method
- b)Interpolation method
- c)Trial and Error methods
- d)Direct Analytical methods
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a type of Iterative method of solving non-linear equations?
a)
Graphical method
b)
Interpolation method
c)
Trial and Error methods
d)
Direct Analytical methods
|
|
Sanya Agarwal answered |
There are 2 types of Iterative methods, (i) Interpolation methods (or Bracketing methods) and (ii) Extrapolation methods (or Open-end methods).
A differential equation is given as:
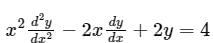
The solution of the differential equation in terms of arbitrary constants C1 and C2 is- a)y = C2x2 + C1x + 2
- b)
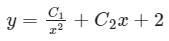
- c)y = C1x2 + C2x + 4
- d)
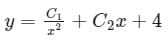
Correct answer is option 'A'. Can you explain this answer?
A differential equation is given as:
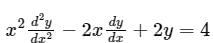
The solution of the differential equation in terms of arbitrary constants C1 and C2 is
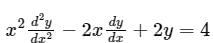
The solution of the differential equation in terms of arbitrary constants C1 and C2 is
a)
y = C2x2 + C1x + 2
b)
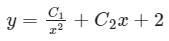
c)
y = C1x2 + C2x + 4
d)
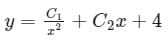
|
|
Sanya Agarwal answered |
Given differential equation:
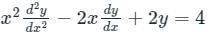
is the standard form of Euler-Cauchy DE.
So, let x = ez
⇒ dx = ezdz = x.dz
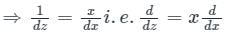
Similarly, we can obtain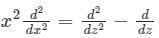
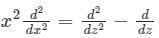
⇒ xD = θ
⇒ x2D2 = θ (θ - 1)
Making these substitutions in given DE, we get
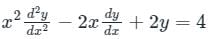
(θ (θ - 1) – 2θ + 2) y = 4
θ (θ - 1) – 2(θ – 1) = 0
⇒ Solution for this will constitute of CF & PI.
⇒ CF = (θ – 1) (θ – 2) = 0 ⇒ θ = 1 & θ = 2
⇒ y = c1ez + c2e2z = c1x + c2x2
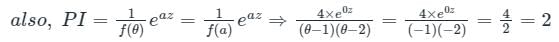
⇒ y = CF + PI = c2x2 + c1x + 2
{We can also solve this problem by differentiating option also, if we don’t remember the process.}
The particular integral of (D + 3)2 y = 5x - log 2, is- a)
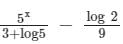
- b)
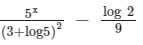
- c)
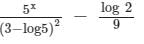
- d)
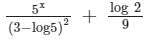
Correct answer is option 'B'. Can you explain this answer?
The particular integral of (D + 3)2 y = 5x - log 2, is
a)
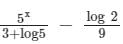
b)
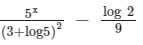
c)
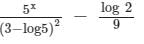
d)
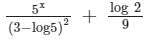
|
|
Sanya Agarwal answered |
Given:
(D + 3)2y = 5x - log 2
Formula Used:
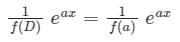
e log x = x
Calculation:
We have,
⇒ (D + 3)2y = 5x - log 2
Particular Integral of the differential equation is
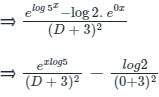
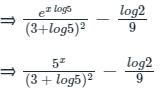
∴ The particular integral of (D + 3)2y = 5x - log 2 is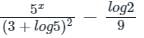
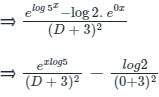
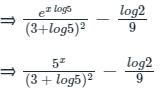
∴ The particular integral of (D + 3)2y = 5x - log 2 is
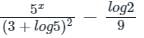
The solution to x2y’’ + xy’ – y = 0 is- a)y = c1x2 + c2x-3
- b)y = c1 + c2x-2
- c)
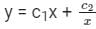
- d)y = c1x + c2x4
Correct answer is option 'C'. Can you explain this answer?
The solution to x2y’’ + xy’ – y = 0 is
a)
y = c1x2 + c2x-3
b)
y = c1 + c2x-2
c)
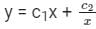
d)
y = c1x + c2x4
|
|
Sanya Agarwal answered |
Concept:
For different roots of the auxiliary equation, the solution (complementary function) of the differential equation is as shown below.
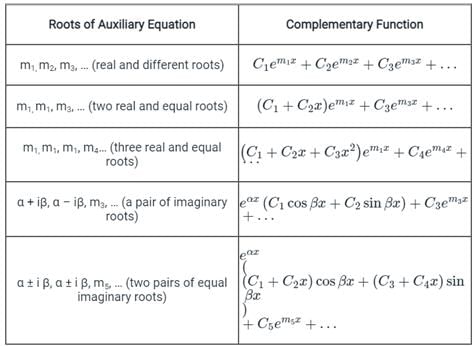
Calculation:

Calculation:
Given:
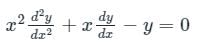
Put x = et
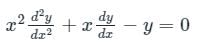
Put x = et
⇒ t = ln x
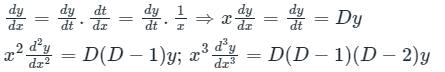
Now, the above differential equation becomes
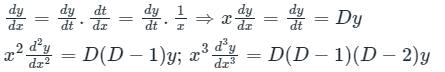
Now, the above differential equation becomes
D(D – 1)y + Dy - y = 0
⇒ D2y – Dy + Dy - y = 0
⇒ (D2 -1)y = 0
Auxiliary equation:
(m2 – 1) = 0
⇒ m = ±1
The solutions for the above roots of auxiliary equations are:
y(t) = c1 et + c2 e-t
y(x) = c1 x + c2 x-1
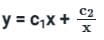
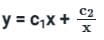
Euler's equation of motion is a statement of- a)linear momentum conservation for the flow of an inviscid fluid
- b)mass conservation
- c)energy conservation
- d)linear momentum conservation for a real fluid
Correct answer is option 'A'. Can you explain this answer?
Euler's equation of motion is a statement of
a)
linear momentum conservation for the flow of an inviscid fluid
b)
mass conservation
c)
energy conservation
d)
linear momentum conservation for a real fluid

|
Engineers Adda answered |
Euler's equation of motion:
The Euler's equation for a steady flow of an ideal fluid along a streamline is a relation between the velocity, pressure and density of a moving fluid. It is based on the Newton's Second Law of Motion which states that if the external force is zero, linear momentum is conserved. The integration of the equation gives Bernoulli's equation in the form of energy per unit weight of the following fluid.
It is based on the following assumptions:
- The fluid is non-viscous (i,e.,inviscid fluid or the frictional losses are zero)
- The fluid is homogeneous and incompressible (i.e., the mass density of the fluid is constant)
- The flow is continuous, steady and along the streamline.
- The velocity of the flow is uniform over the section.
- No energy or force (except gravity and pressure forces) is involved in the flow.
As there is no external force applied (Non-viscous flow), therefore linear momentum will be conserved.
The solution ex, e-x, and e2x of 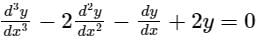 will be:
will be:- a)linearly dependent for x ϵ [-2, 2] and linearly independent elsewhere.
- b)linearly independent for x ϵ [-1, 1] and linearly independent elsewhere.
- c)linearly independent on every real interval.
- d)linearly dependent for all real x.
Correct answer is option 'C'. Can you explain this answer?
The solution ex, e-x, and e2x of 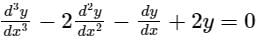 will be:
will be:
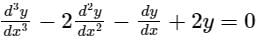 will be:
will be:a)
linearly dependent for x ϵ [-2, 2] and linearly independent elsewhere.
b)
linearly independent for x ϵ [-1, 1] and linearly independent elsewhere.
c)
linearly independent on every real interval.
d)
linearly dependent for all real x.
|
|
Sanya Agarwal answered |
Concept:
Write auxillary equation by replacing
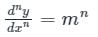
Equate to 0 and solve for (m) (f(m) = 0)
for m1, m2, m3, … (real and different roots)
Complementary function (CF) is given as:
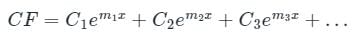
Calculation:
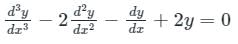
The above expression is in the form f(D)y = X and can be written as:
D3 y - 2D2y - Dy + 2y = 0
y(D3 - 2 × D2 - D + 2) = 0
D3 - 2D2 - D + 2 = 0
The auxiliary equation is f(m) = 0
m3 - 2m2 - m + 2 = 0
(m - 1)(m + 1)(m - 2) = 0
So, the roots the auxiliary equation are m1 = 1, m2 = -1, m3 = 2.
The characteristics of the roots are real and distinct.
C.F = yc = c1em1x + c2em2x + c3em3x
yc = c1ex + c2e-x + c3e2x
So the solution will be linearly independent on every real interval.
A simple mass-spring oscillatory system consists of a mass m, suspended from a spring of stiffness k. Considering z as the displacement of the system at any time t, the equation of motion for the free vibration of the system is 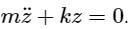 The natural frequency of the system is
The natural frequency of the system is- a)k/m
- b)
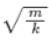
- c)
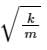
- d)m/k
Correct answer is option 'C'. Can you explain this answer?
A simple mass-spring oscillatory system consists of a mass m, suspended from a spring of stiffness k. Considering z as the displacement of the system at any time t, the equation of motion for the free vibration of the system is 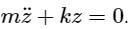 The natural frequency of the system is
The natural frequency of the system is
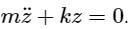 The natural frequency of the system is
The natural frequency of the system isa)
k/m
b)
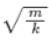
c)
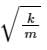
d)
m/k
|
|
Sanvi Kapoor answered |

Comparing with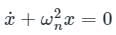 (Standard Differential Equation for Spring)
(Standard Differential Equation for Spring)
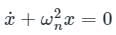 (Standard Differential Equation for Spring)
(Standard Differential Equation for Spring)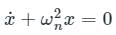
Natural frequency,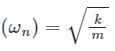
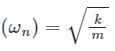
If roots of the auxiliary equation of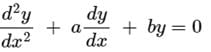 are real and equal, the general solution of the differential equation is
are real and equal, the general solution of the differential equation is- a)
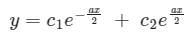
- b)
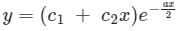
- c)
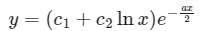
- d)
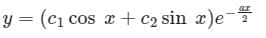
Correct answer is option 'B'. Can you explain this answer?
If roots of the auxiliary equation of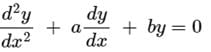 are real and equal, the general solution of the differential equation is
are real and equal, the general solution of the differential equation is
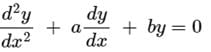 are real and equal, the general solution of the differential equation is
are real and equal, the general solution of the differential equation isa)
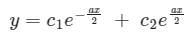
b)
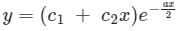
c)
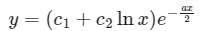
d)
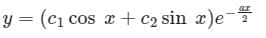
|
|
Sanya Agarwal answered |
Concept:
For different roots of the auxiliary equation, the solution (complementary function) of the differential equations is shown below.
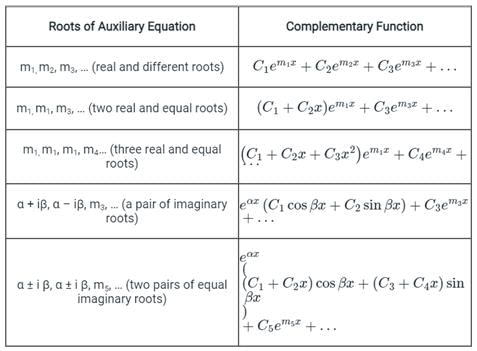
Calculation:

Calculation:
Given:
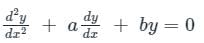
⇒ (D2 + aD + b)y = 0
Auxiliary equation:
m2 + am + b = 0
Roots of the auxiliary equation are:
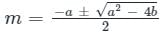
Given that, the roots of the auxiliary equation are real and equal.
⇒ m = -a/2 [∵ a2 - 4ab = 0]
The general solution of the differential equation is:
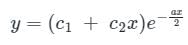
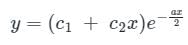
The general solution of the differential equation 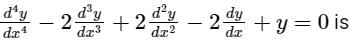
- a)y = (c1 – c2x) ex + c3 cos x + c4 sin x
- b)y = (c1 + c2x) ex – c3 cos x + c4 sin x
- c)y = (c1 + c2x) ex + c3 cos x + c4 sin x
- d)y = (c1 + c2x) ex + c3 cos x – c4 sin x
Correct answer is option 'C'. Can you explain this answer?
The general solution of the differential equation 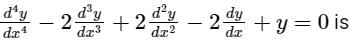
a)
y = (c1 – c2x) ex + c3 cos x + c4 sin x
b)
y = (c1 + c2x) ex – c3 cos x + c4 sin x
c)
y = (c1 + c2x) ex + c3 cos x + c4 sin x
d)
y = (c1 + c2x) ex + c3 cos x – c4 sin x
|
|
Sanya Agarwal answered |
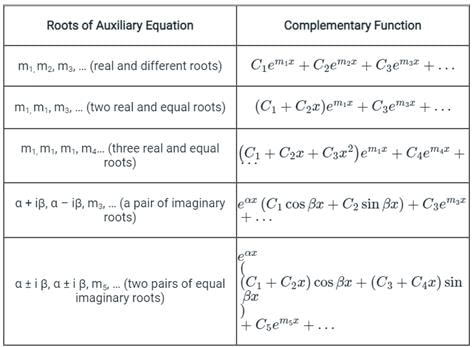
Concept:
General equation for DE:
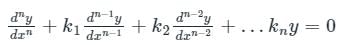
Then its corresponding Auxiliary equation will be
AE: Dn + k1 Dn-1 + … kn = 0
Then the solution of above DE will be as follows:

Calculation:
Given:

Its Auxillary equations:

Its Auxillary equations:
(D4 – 2D3 + 2D2 – 2D + D) = 0
(D - 1)(D3 - D2 + D - 1) = 0
(D - 1)(D - 1)(D2 + 1) = 0
It roots = 1, 1, i, -i
Then it has two equal roots and one pair of imaginary roots.
Therefore, the solution is:
(c1 + c2x) ex + c3 cos x + c4 sin x = 0
Consider the differential equation with y(0) = 1. Then the value of y(1) is
with y(0) = 1. Then the value of y(1) is- a)e + e−1
- b)1/2 [e - e−1]
- c)1/2 [e + e−1]
- d)2 [e - e−1]
Correct answer is option 'C'. Can you explain this answer?
Consider the differential equation with y(0) = 1. Then the value of y(1) is
with y(0) = 1. Then the value of y(1) is
 with y(0) = 1. Then the value of y(1) is
with y(0) = 1. Then the value of y(1) isa)
e + e−1
b)
1/2 [e - e−1]
c)
1/2 [e + e−1]
d)
2 [e - e−1]
|
|
Sanya Agarwal answered |
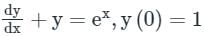
Integrating factor, IF = e∫dx = ex
y(IF) = ∫(IF)exdx + C
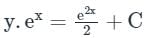
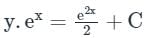
At x = 0, y = 1
∴ C = 1/2

∴ C = 1/2

Solve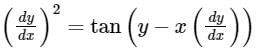
- a)y = cx + tan−1c2
- b)y = cx2 + tan−1c
- c)y = cx2 − tan−1c
- d)y = cx − tan−1c2
Correct answer is option 'A'. Can you explain this answer?
Solve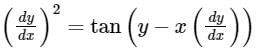
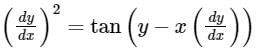
a)
y = cx + tan−1c2
b)
y = cx2 + tan−1c
c)
y = cx2 − tan−1c
d)
y = cx − tan−1c2
|
|
Sanvi Kapoor answered |
dy/dx = p
p2 = tan(y − xp)
tan−1p2 = y − xp
y = xp + tan−1p2
p2 = tan(y − xp)
tan−1p2 = y − xp
y = xp + tan−1p2
y = px + f(p)
Which is clairaut’s equation.
So equation is:
y = cx + tan−1c2
y = cx + tan−1c2
Which one of the following equation are considered gravity and pressure force only?- a)Stokes equation
- b)Euler equation
- c)Both a and b
- d)Neither a nor b
Correct answer is option 'B'. Can you explain this answer?
Which one of the following equation are considered gravity and pressure force only?
a)
Stokes equation
b)
Euler equation
c)
Both a and b
d)
Neither a nor b

|
Bayshore Academy answered |
Concept
Euler's equation of Motion
- Euler's equation for a steady flow of an ideal fluid along a streamline is a relation between the velocity, pressure, and density of a moving fluid.
- It is based on Newton's Second Law of Motion.
- The integration of the equation gives Bernoulli's equation in the form of energy per unit weight of the following fluid.
- Euler equation of motion in which the forces due to gravity and pressure are taken into consideration
Assumptions:
- The fluid is non-viscous (i,e., the frictional losses are zero)
- The fluid is homogeneous and incompressible (i.e., the mass density of the fluid is constant)
- The flow is continuous, steady and along the streamline
- The velocity of the flow is uniform over the section
- No energy or force (except gravity and pressure forces) is involved in the flow
Stokes Law:
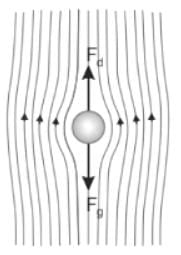
- According to Stokes law, the backward viscous force acting on a small spherical body of radius 'r' moving with uniform velocity V through the fluid of viscosity η is given by
F = 6 π η r V
Where η = Coefficient of viscosity, r = radius of the sphere, and V= Velocity
From above it is clear that, the viscous drag force as F = – 6πηav called Stokes' Law. Therefore option 3 is correct.
- From the figure, it is clear that the drag force fd is in the opposite direction fg
- Stoke's law is applicable for spherical particles only. The fine clay particles are not spherical in shape.
- While applying Stoke's law, the concept of equivalent diameter is used. The equivalent diameter of a soil particle is defined as the diameter of an imaginary sphere that has the same specific gravity as the soil particle and settles with the same terminal velocity as that of the soil particle.
Applications of Stoke's Law
- To calculate the terminal velocity of a falling sphere and hence the viscosity of the fluid.
- Desilting river flow
- Separating the coolant from metal chips in machining operations
- Sanitary engineering - treatment of raw water and sewerage etc.
Important Points
Reynolds equation is given by
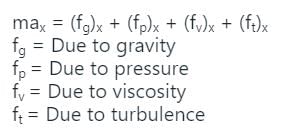
Note: By neglecting viscous force and force due to turbulence,
Euler’s equation, max = (fg)x + (fp)x
Euler’s equation, max = (fg)x + (fp)x
The Euler’s equation for steady flow of an ideal fluid along a stream line is based on Newton’s- a)First law of motion
- b)Second law of motion
- c)Third law of momentum
- d)Law of friction
Correct answer is option 'B'. Can you explain this answer?
The Euler’s equation for steady flow of an ideal fluid along a stream line is based on Newton’s
a)
First law of motion
b)
Second law of motion
c)
Third law of momentum
d)
Law of friction

|
Bayshore Academy answered |
Euler's equation of motion:
The Euler's equation for a steady flow of an ideal fluid along a streamline is a relation between the velocity, pressure and density of a moving fluid. It is based on the Newton's Second Law of Motion which states that if the external force is zero, linear momentum is conserved. The integration of the equation gives Bernoulli's equation in the form of energy per unit weight of the following fluid.
It is based on the following assumptions:
The fluid is non-viscous (i,e., the frictional losses are zero)
The fluid is homogeneous and incompressible (i.e., the mass density of the fluid is constant)
The flow is continuous, steady and along the streamline.
The velocity of the flow is uniform over the section.
No energy or force (except gravity and pressure forces) is involved in the flow.
As there is no external force applied (Non-viscous flow), therefore linear momentum will be conserved.
The fluid is homogeneous and incompressible (i.e., the mass density of the fluid is constant)
The flow is continuous, steady and along the streamline.
The velocity of the flow is uniform over the section.
No energy or force (except gravity and pressure forces) is involved in the flow.
As there is no external force applied (Non-viscous flow), therefore linear momentum will be conserved.
For the equation ay/dx 7x2y = 0, if y(0) = 3/7, then the value of y(1) is- a)
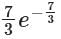
- b)
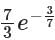
- c)
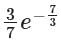
- d)
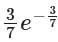
Correct answer is option 'C'. Can you explain this answer?
For the equation ay/dx 7x2y = 0, if y(0) = 3/7, then the value of y(1) is
a)
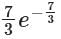
b)
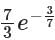
c)
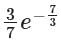
d)
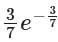

|
Engineers Adda answered |
Concept:
For solving first order, first-degree differential equations always first inspect with variable separation method.
Calculation:
Given the differential equation is,
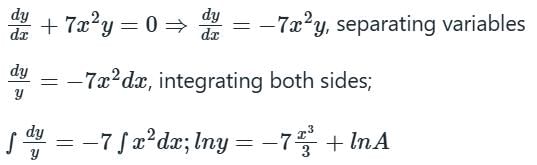
Where A is a constant.
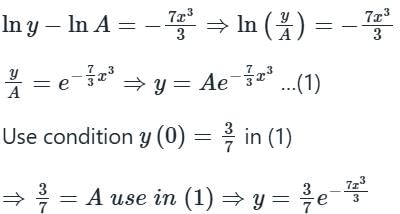
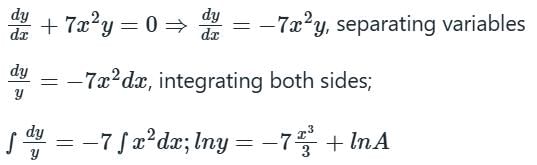
Where A is a constant.
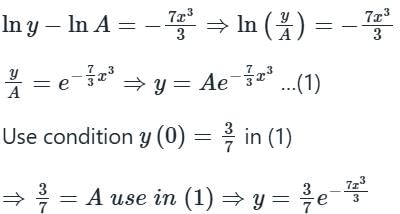
The general solution of the differential equation  in terms of arbitrary constants K1 and K2 is:
in terms of arbitrary constants K1 and K2 is:- a)
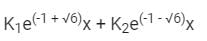
- b)
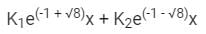
- c)
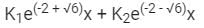
- d)

Correct answer is option 'A'. Can you explain this answer?
The general solution of the differential equation  in terms of arbitrary constants K1 and K2 is:
in terms of arbitrary constants K1 and K2 is:
 in terms of arbitrary constants K1 and K2 is:
in terms of arbitrary constants K1 and K2 is:a)
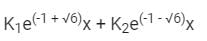
b)
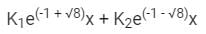
c)
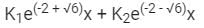
d)

|
|
Sanvi Kapoor answered |
Given Differential equation:
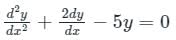
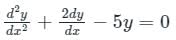
Auxillary equation = D2 + 2D – 5 = 0
Solving, we get roots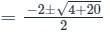
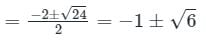
Therefore the general solution is;
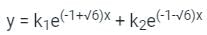
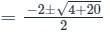
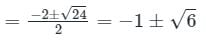
Therefore the general solution is;
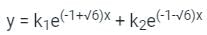
An integrating factor for the differential equation 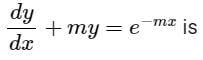
- a)em
- b)e-m
- c)e-mx
- d)emx
Correct answer is option 'D'. Can you explain this answer?
An integrating factor for the differential equation 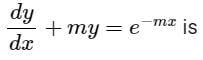
a)
em
b)
e-m
c)
e-mx
d)
emx
|
|
Sanya Agarwal answered |
Concept:
If a first-order linear differential equation can be expressed as,
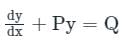
where P and Q are either function of x or constant
And integrating factor (I.F.) is given by
I.F = e∫Pdx
Then, The solution of the differential equation is given by,
y × e∫Pdx = ∫Q × e∫Pdxdx + c
where c is an integrating constant.
Calculation:
Given:
The given differential equation,
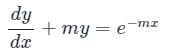
Here, P = m, Q = e−mx
I.F = e∫Pdx
= e∫mdx
= emx
The complete solution of the linear differential equation
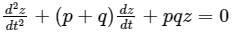
- a)c1 e-pt + c2 e-qt
- b)c1 ept - c2 eqt
- c)c1 e-pt + c2 eqt
- d)c1 ept + c2 eqt
Correct answer is option 'A'. Can you explain this answer?
The complete solution of the linear differential equation
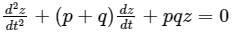
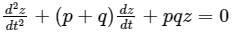
a)
c1 e-pt + c2 e-qt
b)
c1 ept - c2 eqt
c)
c1 e-pt + c2 eqt
d)
c1 ept + c2 eqt
|
|
Sanvi Kapoor answered |
For the given differential equation:

(D2 + (p + q)D + pq)z = 0
⇒ f(D)z = 0
Where f(D) = D2 + (p + q)D + pq
Consider in terms of M ⇒ f(m) = 0
M2 + (p + q)m + pq = 0
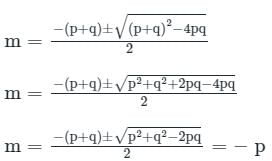
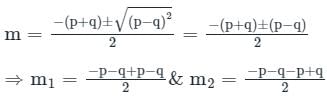
M1 = -q & m2 = -p
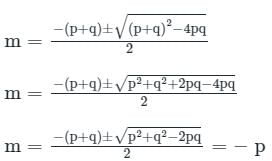
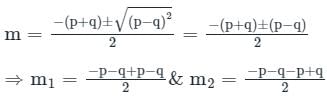
M1 = -q & m2 = -p
Hence, its solution is
Z = C1e-pt + C2e-qt
∴ Complete solution of the linear differential equation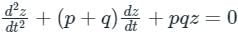 is c1 e-pt + c2 e-qt
is c1 e-pt + c2 e-qt
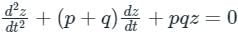 is c1 e-pt + c2 e-qt
is c1 e-pt + c2 e-qtParticular integral of 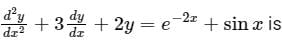
- a)
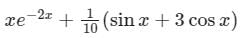
- b)
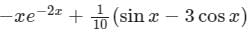
- c)
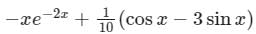
- d)
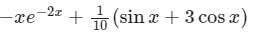
Correct answer is option 'B'. Can you explain this answer?
Particular integral of 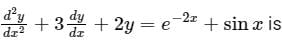
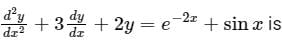
a)
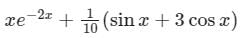
b)
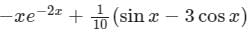
c)
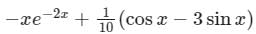
d)
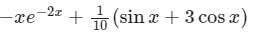
|
|
Sanya Agarwal answered |
Concept:
When Φ(x) = eax + V(x)
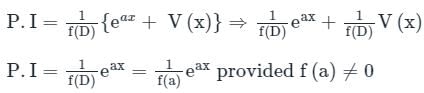
If f(a) = 0
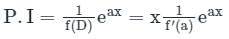
Calculation:

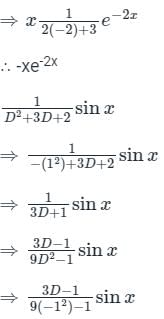
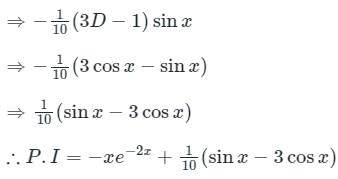
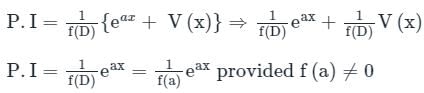
If f(a) = 0
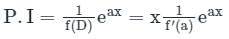
Calculation:

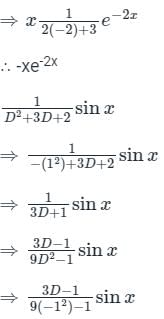
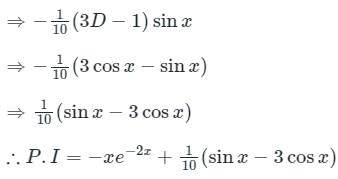
The Euler’s equation of motion:- a)Is a statement of energy balance
- b)Is a moment of momentum equation
- c)Relates various force with changes in momentum
- d)Is a preliminary step to drive Navier Stoke's equation
Correct answer is option 'B'. Can you explain this answer?
The Euler’s equation of motion:
a)
Is a statement of energy balance
b)
Is a moment of momentum equation
c)
Relates various force with changes in momentum
d)
Is a preliminary step to drive Navier Stoke's equation

|
Engineers Adda answered |
- Euler’s equation of motion of an ideal fluid, for a steady flow along a streamline, is basically a relation between velocity, pressure, and density of a moving fluid.
- Euler’s equation of motion is based on the basic concept of Newton’s second law of motion.
- The Euler’s equation of motion is a moment of momentum equation.
Solve the differential equation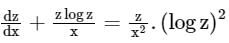
- a)
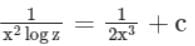
- b)

- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
Solve the differential equation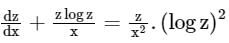
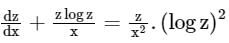
a)
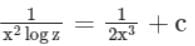
b)

c)

d)

|
|
Sanya Agarwal answered |
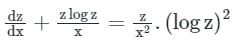
Dividing both sides by z (logz)2

Integrating Factor

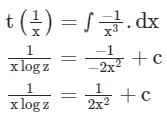
The singular solution of is/are
is/are- a)y = ± x2
- b)y = 2x + 3
- c)y = x2 – 2x
- d)y = ± 2x
Correct answer is option 'D'. Can you explain this answer?
The singular solution of is/are
is/are
 is/are
is/area)
y = ± x2
b)
y = 2x + 3
c)
y = x2 – 2x
d)
y = ± 2x
|
|
Sanya Agarwal answered |
The given differential equation is
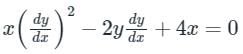
xD2 – 2y D + 4x = 0
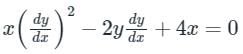
xD2 – 2y D + 4x = 0
The discriminant of this equation is
(-2y)2 – 4x.4x = 0 ⇒ y2 – 4x2 = 0
Differentiating with respect to x,


⇒ yD = 4x ⇒ D = 4x/y
Substituting D = 4x/y

⇒ y2 – 4x2 = 0
Hence y2 = 4x2 satisfies the given differential equation. The singular solution is
y2 – 4x2 = 0 ⇒ y = ±2x
For the Ordinary Differential Equation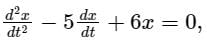 with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution is
with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution is- a)-5e2t + 6e3t
- b)5e2t = + 6e3t
- c)-10e2t + 10e3t
- d)10e2t + 10e+3t
Correct answer is option 'C'. Can you explain this answer?
For the Ordinary Differential Equation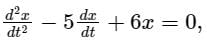 with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution is
with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution is
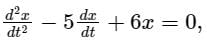 with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution is
with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution isa)
-5e2t + 6e3t
b)
5e2t = + 6e3t
c)
-10e2t + 10e3t
d)
10e2t + 10e+3t
|
|
Sanya Agarwal answered |
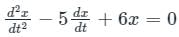
Above given equation is a linear differential equation of order = 2. Such equations are solved using CF + PI method.
Let D = dx/dt
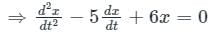
⇒ D2x – 5Dx + 6x = 0
⇒ (D2 – 5D + 6)x = 0
Thus auxiliary equation (obtained by replacing D with m) is m2 – 5D + 6 = 0.
Roots of above obtained auxiliary equation are-
m2 – 5D + 6 = 0
⇒ (m – 2) (m - 3) = 0
⇒ m1 = 2 or m2 = 3
When both roots of auxiliary equation are real and distinct
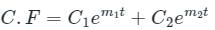
Thus general solution of above D.E is
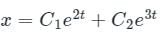
Applying boundary conditions, x(0) = 0
⇒ O = C1 + C2
⇒ C1 = -C2 ---(i)
Using initial condition dx/dt(0) = 10
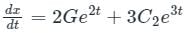
⇒ 10 = 2C1 + 3C2 ---(ii)
Solving equation (i) & (ii) simultaneously,
C1 = -10 and C2 = 10
Thus, x = -10e2t + 10e3t
Which of the following represents Lagrange’s linear equation?- a)P + Q = R
- b)Pp + Qq = R
- c)p + q = R
- d)Pp + Qq = P + Q
Correct answer is option 'B'. Can you explain this answer?
Which of the following represents Lagrange’s linear equation?
a)
P + Q = R
b)
Pp + Qq = R
c)
p + q = R
d)
Pp + Qq = P + Q
|
|
Sanya Agarwal answered |
Equations of the form, Pp + Qq = R are known as Lagrange’s linear equations, named after Franco-Italian mathematician, Joseph-Louis Lagrange (1736-1813).
The solution of differential equation un+3 - 4un+2 + un+1 + 6un = 0 will be:- a)un = C1(1)n + C2(2)n + C3(3)n, where C1, C2, C3 are constants.
- b)un = C1(-1)n +C2(-2)n + C3(-3)n, where C1, C2, C3 are constants.
- c)un = C1(1)n + C2(-2)n + C3(3)n, where C1, C2, C3 are constants.
- d)un = C1 (-1)n + C2(2)n + C3(3)n, where C1, C2, C3 are constants.
Correct answer is option 'D'. Can you explain this answer?
The solution of differential equation un+3 - 4un+2 + un+1 + 6un = 0 will be:
a)
un = C1(1)n + C2(2)n + C3(3)n, where C1, C2, C3 are constants.
b)
un = C1(-1)n +C2(-2)n + C3(-3)n, where C1, C2, C3 are constants.
c)
un = C1(1)n + C2(-2)n + C3(3)n, where C1, C2, C3 are constants.
d)
un = C1 (-1)n + C2(2)n + C3(3)n, where C1, C2, C3 are constants.
|
|
Sanya Agarwal answered |
Concept:
For solving a homogeneous linear differential equation with constant coefficients,
As a solution, we try un = A mn, where A and m are constants.
This choice has been made because un = kn uo was the solution to the equation un = k un-1.
After substituting and solving the auxiliary equation, say m1, m2, m3 ... mn be the roots, then the general solution will be
un = A(m1)n + B(m2)n + ... where A, B ... are constants
Calculation:
Given Differential equation is:
un+3 - 4n+2 + un+1 + 6un = 0
Substituting:
un+3 = A mn+3;
un+2 = A mn+2;
un+1 = A mn+1;
un = A mn;
A mn+3 - 4 A mn+2 + A mn+1 + 6 A mn = 0
A mn (m3 - 4m2 + m + 6) = 0
m3 - 4m2 + m + 6 = 0
This is called auxiliary equation.
The roots of the auxiliary equation are -1, 2, and 3, i.e.
m1 = -1, m2 = 2, m3 = 3;
The general solution will be:
un = A(-1)n + B(2)n + C(3)n
Chapter doubts & questions for Ordinary Differential Equations - Engineering Mathematics for Civil Engineering 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Ordinary Differential Equations - Engineering Mathematics for Civil Engineering in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Engineering Mathematics for Civil Engineering
62 videos|105 docs|59 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup


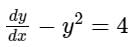 satisfying the condition y(0) = 1/√3
satisfying the condition y(0) = 1/√3