All Exams >
Computer Science Engineering (CSE) >
Theory of Computation >
All Questions
All questions of Introduction to Grammars, Languages & Automata for Computer Science Engineering (CSE) Exam
Over the alphabet , {0,1} consider the language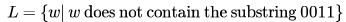 Which of the following is true about L.
Which of the following is true about L.- a)L is not context free
- b)L is regular
- c)L is not regular but it is context free
- d)L is context free but not recursively enumerable
Correct answer is option 'B'. Can you explain this answer?
Over the alphabet , {0,1} consider the language
Which of the following is true about L.
a)
L is not context free
b)
L is regular
c)
L is not regular but it is context free
d)
L is context free but not recursively enumerable
|
|
Raj Sen answered |
L is regular.
The language 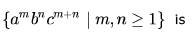
- a)regular
- b)context-free but not regular
- c)context-sensitive but not context free
- d)type-0 but not context sensitive
Correct answer is option 'B'. Can you explain this answer?
The language 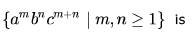
a)
regular
b)
context-free but not regular
c)
context-sensitive but not context free
d)
type-0 but not context sensitive
|
|
Pallavi Reddy answered |
Language is not regular bcoz we need to match count of c's is equal to count of b's + count of a's
and that can implement by PDA
∂(q0,a,^)= (q0,a) [ push a in stack, as per language a comes first]
∂(q0,a,a)= (q0,aa) [push all a's into stack]
∂(q0,b,a) = (q1,ba) [push b in stack, state change to q1 that sure b comes after a]
∂(q1,b,b)=(q1,bb) [push all b's in stack]
∂(q1,c,b) = (q2,^) [ pop one b for one c]
∂(q0,b,a) = (q1,ba) [push b in stack, state change to q1 that sure b comes after a]
∂(q1,b,b)=(q1,bb) [push all b's in stack]
∂(q1,c,b) = (q2,^) [ pop one b for one c]
∂(q2,c,b) = (q2,c) [ pop one b's for each c and continue same ]
∂(q2,c,a) = (q3,^) [ pop one a for one c , when there is no more b in stack]
∂(q3,c,a) = (q3,^) [pop one a for each c and continue same]
∂(q3,^,^) = (qf,^) [ if sum of c's is sum of a's and b's then stack will be empty when there is no c in input]
∂(q2,c,a) = (q3,^) [ pop one a for one c , when there is no more b in stack]
∂(q3,c,a) = (q3,^) [pop one a for each c and continue same]
∂(q3,^,^) = (qf,^) [ if sum of c's is sum of a's and b's then stack will be empty when there is no c in input]
Note :1. state changes make sure b's comes after a and c's comes after b's]
Let denote the languages generated by the grammar S→ 0S0 I 00.Which of the following is TRUE?- a)L=0+
- b)L is regular but not 0+
- c) L is context free but not regular
- d)L is not context free
Correct answer is option 'B'. Can you explain this answer?
Let denote the languages generated by the grammar S→ 0S0 I 00.
Which of the following is TRUE?
a)
L=0+
b)
L is regular but not 0+
c)
L is context free but not regular
d)
L is not context free
|
|
Aditya Deshmukh answered |
Option A : L is not 0+ , because 0+ will contain any arbitrary string over alphabet 0 with any no of 0’s ( except empty string ), for ex: {0, 00, 000,00000}, but L will only have the strings as { 00, 0000, 000000,…}, i.e only even no of 0’s ( excluding empty string}.
Option D : L is a Context Free Language, because the Grammar G which generates the language L is Context Free Grammar. A Grammar G is CFG if all of its productions are of the form A->α, where A is a single non-terminal and α belongs to (V∪ T)* , i.e α can be a string of terminals and/or Non-terminals. (V represents a non-terminal and T represents a terminal)
Option C : L is a Regular Language, Because we are able to write a regular expression for it ( and also able to make a Finite Automaton), which is (00)+.
Option B : Hence This option is Correct, because L is Regular but not 0+, as we proved above.
Let denote the languages generated by the grammar S→ 0S0 I 00.Which of the following is TRUE?- a)L=0+
- b)L is regular but not 0+
- c) L is context free but not regular
- d)L is not context free
Correct answer is 'B'. Can you explain this answer?
Let denote the languages generated by the grammar S→ 0S0 I 00.
Which of the following is TRUE?
a)
L=0+
b)
L is regular but not 0+
c)
L is context free but not regular
d)
L is not context free
|
|
Avinash Mehta answered |
Explaining all the options:
Option A : L is not 0+ , because 0+ will contain any arbitrary string over alphabet 0 with any no of 0’s ( except empty string ), for ex: {0, 00, 000,00000}, but L will only have the strings as { 00, 0000, 000000,…}, i.e only even no of 0’s ( excluding empty string}.
Option D : L is a Context Free Language, because the Grammar G which generates the language L is Context Free Grammar. A Grammar G is CFG if all of its productions are of the form A->α, where A is a single non-terminal and α belongs to (V∪ T)* , i.e α can be a string of terminals and/or Non-terminals. (V represents a non-terminal and T represents a terminal)
Option C : L is a Regular Language, Because we are able to write a regular expression for it ( and also able to make a Finite Automaton), which is (00)+.
Hence This option is Correct, because L is Regular but not 0+, as we proved above.
Let L be a regular language and M be a context-free language, both over the alphabet 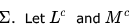 denote the complements of L and M respectively. Which of the following statements about the language
denote the complements of L and M respectively. Which of the following statements about the language 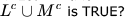
- a)It is necessarily regular but not necessarily context-free.
- b)It is necessarily context-free.
- c)It is necessarily non-regular.
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
Let L be a regular language and M be a context-free language, both over the alphabet 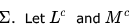 denote the complements of L and M respectively. Which of the following statements about the language
denote the complements of L and M respectively. Which of the following statements about the language 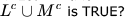
a)
It is necessarily regular but not necessarily context-free.
b)
It is necessarily context-free.
c)
It is necessarily non-regular.
d)
None of the above

|
Anirban Khanna answered |
Proposition:
L is a regular language
M is a context free language
Derivation:
L_c union M_c = complement{L intersection M}
Now, L intersection M is a CFL according to closure laws of CFLs, i.e. intersection of a CFL with RL is always a CFL.
But, complement{L intersection M} might not be a CFL because complement over CFL doesn’t guarantee a CFL. It can even be a RL or it might even lie outside the CFL circle. It will be a context-sensitive language certainly, but nothing else can be said about it.
Conclusion:
Considering the above derivation, none of the statements are true. Hence correct answer would be (D) None of the above.
The language accepted by a Pushdown Automaton in which the stack is limited to 10 items is best described as- a)Context free
- b)Regular
- c)Deterministic Context free
- d)Recursive
Correct answer is option 'B'. Can you explain this answer?
The language accepted by a Pushdown Automaton in which the stack is limited to 10 items is best described as
a)
Context free
b)
Regular
c)
Deterministic Context free
d)
Recursive
|
|
Rajeev Menon answered |
Pushdown automata is used for context free languages, i.e., languages in which the length of elements is unrestricted and length of one element is related to other. To resolve this problem, we use a stack with no restrictions on length.
But in the given case, length of stack is restricted. Thus, this pushdown automata can only accept languages which can also be accepted by finite state automata and a finite state automata accepts only regular languages.
If L1 is context free language and L2 is a regular language which of the following is/are false?
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular- a)Both a and c
- b) Both b and c
- c)Only b
- d)Only c
Correct answer is option 'A'. Can you explain this answer?
If L1 is context free language and L2 is a regular language which of the following is/are false?
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular
a)
Both a and c
b)
Both b and c
c)
Only b
d)
Only c
|
|
Kabir Verma answered |
- Given L1 is a context free language and L2 as a regular language then L1-L2 is context free language and
- ~L1(complement of context free) is not context free because context free is not closed under complement.
- Complement of regular language i.e. ~L2 is also regular ( so d is correct ) since statements a and c are false.
Hence,Option (C) is correct.
Consider the languages: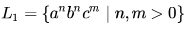 and
and 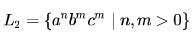 Which one of the following statements is FALSE?
Which one of the following statements is FALSE?- a)

- b)

- c)

- d)
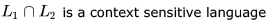
Correct answer is option 'A'. Can you explain this answer?
Consider the languages:
Which one of the following statements is FALSE?
a)
b)
c)
d)
|
|
Nikhil Roy answered |
L1 is CFL [ put a's in stack , and pop a with each b]]
L2 is CFL [put b's in stack and pop b with each c ]
c) is True.
L2 is CFL [put b's in stack and pop b with each c ]
c) is True.
b) is True CFL is closed under Union [ S-> S1 | S2 where S1 is grammar for L1 and S2 for L2]
CFL is not closed under Intersection, so intersection of two CFLs may or may not be CFL. Lets examine:
CFL is not closed under Intersection, so intersection of two CFLs may or may not be CFL. Lets examine:
L1 ∩ L2 = { aibici , i>0 } which is Context sensitive but not context free [can't match a's,b's and c's with one stack]
So a) is False
So a) is False
d) is True
For 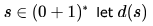 denote the decimal value of
denote the decimal value of 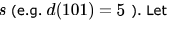
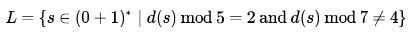 Which one of the following statements is true?
Which one of the following statements is true?- a)L is recursively enumerable, but not recursive
- b)L is recursive, but not context-free
- c)L is context-free, but not regular
- d)L is regular
Correct answer is option 'D'. Can you explain this answer?
For 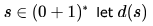 denote the decimal value of
denote the decimal value of 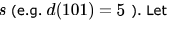
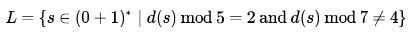
Which one of the following statements is true?
a)
L is recursively enumerable, but not recursive
b)
L is recursive, but not context-free
c)
L is context-free, but not regular
d)
L is regular
|
|
Rajveer Sharma answered |
L1 = { s∈(0+1)* ∣ d(s) mod 5=2 } is regular
having 2 as final state out of {0,1,2,3,4} states
as given in example in posted link [in same DFA , final state will be 2 instead of 0 ]
as given in example in posted link [in same DFA , final state will be 2 instead of 0 ]
similarly L2 = { s∈(0+1)* ∣ d(s) mod 7≠4 } is also regular
having states {0,1,2,3,4,5,6} and all are final state except 4
L1 ∩ L2 is L (given problem ) is also regular
As regular languages are closed under intersection. D is correct option.
having states {0,1,2,3,4,5,6} and all are final state except 4
L1 ∩ L2 is L (given problem ) is also regular
As regular languages are closed under intersection. D is correct option.
The language 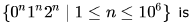
- a)regular
- b)context-free but not regular
- c)context-free but its complement is not context-free
- d)not context-free
Correct answer is option 'A'. Can you explain this answer?
The language 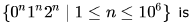
a)
regular
b)
context-free but not regular
c)
context-free but its complement is not context-free
d)
not context-free
|
|
Gauri Banerjee answered |
Regular (in fact finite). Since n is finite, we have a finite set of strings satisfying the given conditions. So, we can easily
make a finite automata for those strings.
make a finite automata for those strings.
Let L1 be a regular language L2, be a deterministic context-free language and L3 a recursively enumerable, but not recursive, language. Which one of the following statements is false?- a)

- b)
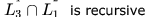
- c)
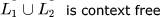
- d)
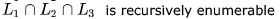
Correct answer is option 'B'. Can you explain this answer?
Let L1 be a regular language L2, be a deterministic context-free language and L3 a recursively enumerable, but not recursive, language. Which one of the following statements is false?
a)
b)
c)
d)

|
Baishali Bajaj answered |
(A) This statement is true because deterministic context free languages are closed under intersection with regular languages.
(B) This statement is false because L1 is recursive and every recursive language is decidable. L3 is recursively enumerable but not recursive. So, L3 is undecidable. Intersection of recursive language and recursive enumerable language is recursively enumerable .
(C) This statement is true because L1 is regular. Every regular language is also a context free languages. L2 is a deterministic context free language and every DCFL is also a context free languages. Every context free language is closed under Union.
(D) This statement is true beacuse L1 is regular hence it is also recursively enumerable. L2 is deterministic context free language so, it is also recursively enumerable . Recursively enumerable languages are closed under intersection.
Thus, problem mentioned in option (A) is undecidable.
Chapter doubts & questions for Introduction to Grammars, Languages & Automata - Theory of Computation 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Introduction to Grammars, Languages & Automata - Theory of Computation in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Theory of Computation
18 videos|88 docs|44 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









