All Exams >
Electrical Engineering (EE) >
Digital Electronics >
All Questions
All questions of Number System & Representation for Electrical Engineering (EE) Exam
What is the 1’s complement of (-011012)?- a)010102
- b)100112
- c)100102
- d)010112
Correct answer is option 'C'. Can you explain this answer?
What is the 1’s complement of (-011012)?
a)
010102
b)
100112
c)
100102
d)
010112
|
|
Pooja Patel answered |
Concept:
1’s complement:
- 1’s complement simply inverted every bit of input.
- Can be implemented using only NOT gate for each bit of binary number input.
When the value 37H is divided by 17H, the remainder is- a)C0H
- b)03H
- c)07H
- d)09H
Correct answer is option 'D'. Can you explain this answer?
When the value 37H is divided by 17H, the remainder is
a)
C0H
b)
03H
c)
07H
d)
09H
|
|
Alok Roy answered |
To find the remainder when the value 37H is divided by 17H, we can perform long division.
Step 1: Convert the hexadecimal values to decimal.
37H = 3 * 16^1 + 7 * 16^0 = 48
17H = 1 * 16^1 + 7 * 16^0 = 23
Step 2: Perform long division.
_______
23 | 48
- 46
_______
2
Step 3: The remainder is 2 in decimal. We need to convert it back to hexadecimal.
2 = 2 * 16^0 = 02H
Therefore, the remainder when 37H is divided by 17H is 02H, which corresponds to option D.
Step 1: Convert the hexadecimal values to decimal.
37H = 3 * 16^1 + 7 * 16^0 = 48
17H = 1 * 16^1 + 7 * 16^0 = 23
Step 2: Perform long division.
_______
23 | 48
- 46
_______
2
Step 3: The remainder is 2 in decimal. We need to convert it back to hexadecimal.
2 = 2 * 16^0 = 02H
Therefore, the remainder when 37H is divided by 17H is 02H, which corresponds to option D.
What is the Radix of octal Number system- a)16
- b)4
- c)8
- d)2
Correct answer is option 'C'. Can you explain this answer?
What is the Radix of octal Number system
a)
16
b)
4
c)
8
d)
2
|
|
Prasad Saini answered |
Radix of Octal Number System
Definition: Radix of a number system is the number of digits or symbols used to represent the values of the numbers in that system. For example, in the decimal number system, the radix is 10 because it uses 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) to represent the values of the numbers.
Octal Number System: The octal number system is a base-8 number system that uses 8 digits (0, 1, 2, 3, 4, 5, 6, 7) to represent the values of the numbers.
Calculation of Radix: To calculate the radix of a number system, we need to find the base of the number system. The base of the number system is the smallest number that can be represented with a single digit in that system.
In the octal number system, the smallest number that can be represented with a single digit is 0. The next highest number that can be represented with a single digit is 1. Therefore, the base of the octal number system is 8.
Conclusion: Hence, the radix of the octal number system is 8.
Definition: Radix of a number system is the number of digits or symbols used to represent the values of the numbers in that system. For example, in the decimal number system, the radix is 10 because it uses 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) to represent the values of the numbers.
Octal Number System: The octal number system is a base-8 number system that uses 8 digits (0, 1, 2, 3, 4, 5, 6, 7) to represent the values of the numbers.
Calculation of Radix: To calculate the radix of a number system, we need to find the base of the number system. The base of the number system is the smallest number that can be represented with a single digit in that system.
In the octal number system, the smallest number that can be represented with a single digit is 0. The next highest number that can be represented with a single digit is 1. Therefore, the base of the octal number system is 8.
Conclusion: Hence, the radix of the octal number system is 8.
The decimal equivalent of the binary number (1101)2 is- a)9
- b)11
- c)13
- d)15
Correct answer is option 'C'. Can you explain this answer?
The decimal equivalent of the binary number (1101)2 is
a)
9
b)
11
c)
13
d)
15
|
|
Sanskriti Bajaj answered |
Converting Binary to Decimal:
To convert a binary number to a decimal number, you can use the positional notation system. Each digit in a binary number represents a power of 2, starting from 2^0 on the rightmost digit.
Binary Number (1101)2:
In the binary number (1101)2, from right to left:
- The rightmost digit is 1 * 2^0 = 1
- The next digit is 0 * 2^1 = 0
- The next digit is 1 * 2^2 = 4
- The leftmost digit is 1 * 2^3 = 8
Calculating Decimal Equivalent:
To find the decimal equivalent, add up the values of each digit:
1 + 0 + 4 + 8 = 13
Therefore, the decimal equivalent of the binary number (1101)2 is 13.
So, the correct answer is option 'C'.
Code is a symbolic representation of __________ information.- a)Continuous
- b)Discrete
- c)Analog
- d)Both continuous and discrete
Correct answer is option 'B'. Can you explain this answer?
Code is a symbolic representation of __________ information.
a)
Continuous
b)
Discrete
c)
Analog
d)
Both continuous and discrete
|
|
Poulomi Ahuja answered |
Code is a symbolic representation of Discrete information.
Code is a method of representing information using symbols or signals. It is used in various fields, including computer programming, communication systems, and electrical engineering. The purpose of coding is to convert information into a format that can be easily processed, transmitted, or stored.
Continuous vs. Discrete Information:
To understand why code is a symbolic representation of discrete information, let's first define continuous and discrete information.
Continuous information refers to data that can take on any value within a certain range. It is represented by analog signals, which are continuous and can have infinite possible values. For example, the temperature in a room can vary continuously between 20 to 25 degrees Celsius.
Discrete information, on the other hand, can only take on specific values within a certain set. It is represented by digital signals, which are discrete and can only have a finite number of possible values. For example, the number of people in a room can only be a whole number, such as 10 or 15.
The Nature of Code:
Code is a symbolic representation of discrete information because it uses discrete symbols to represent data. In computer programming, for example, code consists of a series of instructions written using a specific set of symbols, such as letters, numbers, and punctuation marks. Each symbol represents a specific command, operation, or value.
When a computer program is executed, the code is interpreted or compiled into machine language, which consists of binary digits (0s and 1s). These binary digits, also known as bits, represent the fundamental units of discrete information in computing. Each bit can have a value of either 0 or 1, making it a discrete representation.
Advantages of Discrete Representation:
Using discrete representation in coding has several advantages:
1. Precision: Discrete representation allows for precise and accurate representation of information. Each symbol or bit carries a specific meaning, making it easier to interpret and process the data.
2. Storage Efficiency: Discrete representation requires less storage space compared to continuous representation. In digital systems, data can be stored using binary digits, which are compact and efficient for storage and transmission.
3. Error Detection and Correction: Discrete representation allows for error detection and correction techniques. By using error detection codes, it is possible to identify and correct errors that may occur during transmission or storage of data.
In conclusion, code is a symbolic representation of discrete information because it uses discrete symbols or bits to represent data. This allows for precise representation, efficient storage, and error detection and correction in various fields such as computer programming and communication systems.
Code is a method of representing information using symbols or signals. It is used in various fields, including computer programming, communication systems, and electrical engineering. The purpose of coding is to convert information into a format that can be easily processed, transmitted, or stored.
Continuous vs. Discrete Information:
To understand why code is a symbolic representation of discrete information, let's first define continuous and discrete information.
Continuous information refers to data that can take on any value within a certain range. It is represented by analog signals, which are continuous and can have infinite possible values. For example, the temperature in a room can vary continuously between 20 to 25 degrees Celsius.
Discrete information, on the other hand, can only take on specific values within a certain set. It is represented by digital signals, which are discrete and can only have a finite number of possible values. For example, the number of people in a room can only be a whole number, such as 10 or 15.
The Nature of Code:
Code is a symbolic representation of discrete information because it uses discrete symbols to represent data. In computer programming, for example, code consists of a series of instructions written using a specific set of symbols, such as letters, numbers, and punctuation marks. Each symbol represents a specific command, operation, or value.
When a computer program is executed, the code is interpreted or compiled into machine language, which consists of binary digits (0s and 1s). These binary digits, also known as bits, represent the fundamental units of discrete information in computing. Each bit can have a value of either 0 or 1, making it a discrete representation.
Advantages of Discrete Representation:
Using discrete representation in coding has several advantages:
1. Precision: Discrete representation allows for precise and accurate representation of information. Each symbol or bit carries a specific meaning, making it easier to interpret and process the data.
2. Storage Efficiency: Discrete representation requires less storage space compared to continuous representation. In digital systems, data can be stored using binary digits, which are compact and efficient for storage and transmission.
3. Error Detection and Correction: Discrete representation allows for error detection and correction techniques. By using error detection codes, it is possible to identify and correct errors that may occur during transmission or storage of data.
In conclusion, code is a symbolic representation of discrete information because it uses discrete symbols or bits to represent data. This allows for precise representation, efficient storage, and error detection and correction in various fields such as computer programming and communication systems.
If (110)x = (132)4, then x =- a)8
- b)5
- c)4
- d)9
Correct answer is option 'B'. Can you explain this answer?
If (110)x = (132)4, then x =
a)
8
b)
5
c)
4
d)
9
|
|
Pooja Patel answered |
Concept:
Another number system to Decimal
In each and every representation of numbers with different bases, the maximum value in a number system with the base ‘r’ is r – 1. Since numbers vary from 0 to r – 1.
To convert any number which is in the different base to decimal number system we use binary-weighted representation.
Eg: let the number be ( abc⋯ ⋯ yz)r
Now to convert the above number into the decimal number system
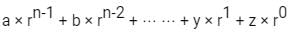
If we convert all numbers into decimal then we can perform normal addition and subtraction etc.
In each and every representation of numbers with different bases, the maximum value in a number system with the base ‘r’ is r – 1. Since numbers vary from 0 to r – 1.
To convert any number which is in the different base to decimal number system we use binary-weighted representation.
Eg: let the number be ( abc⋯ ⋯ yz)r
Now to convert the above number into the decimal number system
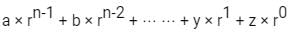
If we convert all numbers into decimal then we can perform normal addition and subtraction etc.
Application:
Given:
(110)x = (132)4,
The decimal equivalent of this number will be: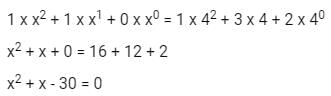
On solving this quadratic equation we'll get:
x = 5, -6
Base can't be a negative so;
x = 5
Given:
(110)x = (132)4,
The decimal equivalent of this number will be:
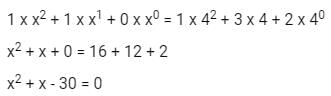
On solving this quadratic equation we'll get:
x = 5, -6
Base can't be a negative so;
x = 5
The hexadecimal representation of 6578 is
- a)D78
- b)1AF
- c)D71
- d)32F
Correct answer is option 'B'. Can you explain this answer?
The hexadecimal representation of 6578 is
a)
D78
b)
1AF
c)
D71
d)
32F

|
Cstoppers Instructors answered |
Concept:
Hexadecimal number: In this, value of the base is 16. Each digit is represented by 4-bit binary no.
Octal number: For octal number, value of base is 8. Each digit of an octal number is represented by 3-bit binary no.
Hexadecimal number: In this, value of the base is 16. Each digit is represented by 4-bit binary no.
Octal number: For octal number, value of base is 8. Each digit of an octal number is represented by 3-bit binary no.
Explanation:
Octal number = 657
Binary representation for this number (each digit of a octal number is converted into 3 binary bits)
So, 657 in binary is equivalent to 110 101 111
Now group this binary number into 4 bits starting from right to left.
i.e. 0001 1010 1111
Hexadecimal representation for this number is : 1AF
Octal number = 657
Binary representation for this number (each digit of a octal number is converted into 3 binary bits)
So, 657 in binary is equivalent to 110 101 111
Now group this binary number into 4 bits starting from right to left.
i.e. 0001 1010 1111
Hexadecimal representation for this number is : 1AF
The number 149 in octal code is- a)154
- b)178
- c)254
- d)225
Correct answer is option 'D'. Can you explain this answer?
The number 149 in octal code is
a)
154
b)
178
c)
254
d)
225
|
|
Pooja Patel answered |
Concept:
Steps to convert decimal number to octal:
1) Write the given decimal number.
2) If the given decimal number is less than 8 the octal number is the same.
3) If the decimal number is greater than 7 then divide the number by 8.
4) Note the remainder, we get after division.
5) Repeat steps 3 and 4 with the quotient till it is less than 8.
6) Now, write the remainders in reverse order (bottom to top).
7) The resultant is the equivalent octal number to the given decimal number.
Steps to convert decimal number to octal:
1) Write the given decimal number.
2) If the given decimal number is less than 8 the octal number is the same.
3) If the decimal number is greater than 7 then divide the number by 8.
4) Note the remainder, we get after division.
5) Repeat steps 3 and 4 with the quotient till it is less than 8.
6) Now, write the remainders in reverse order (bottom to top).
7) The resultant is the equivalent octal number to the given decimal number.
Calculation:
Given decimal number = 149
The long division method is as shown:
Given decimal number = 149
The long division method is as shown:
∴ The correct octal equivalent of 149 is 225
On addition of -33 and -40 using 2’s complement, we get ____________- a)1001110
- b)-110101
- c)0110001
- d)-1001001
Correct answer is option 'D'. Can you explain this answer?
On addition of -33 and -40 using 2’s complement, we get ____________
a)
1001110
b)
-110101
c)
0110001
d)
-1001001
|
|
Tanishq Majumdar answered |
When adding -33 and -40 using 2's complement, we follow these steps:
1. Convert -33 and -40 to their 2's complement representation.
-33 in 2's complement: 00100001
-40 in 2's complement: 00101000
2. Add the two numbers together, including any carry from the previous bit.
00100001
+ 00101000
__________
01001001
3. Check if the result is negative by looking at the leftmost bit. If it is 1, the result is negative.
In this case, the result is 01001001, which is positive. Therefore, the addition of -33 and -40 using 2's complement is 73.
1. Convert -33 and -40 to their 2's complement representation.
-33 in 2's complement: 00100001
-40 in 2's complement: 00101000
2. Add the two numbers together, including any carry from the previous bit.
00100001
+ 00101000
__________
01001001
3. Check if the result is negative by looking at the leftmost bit. If it is 1, the result is negative.
In this case, the result is 01001001, which is positive. Therefore, the addition of -33 and -40 using 2's complement is 73.
The Octal equivalent of the hexadecimal number 100 is _____.- a)400
- b)600
- c)300
- d)200
Correct answer is option 'A'. Can you explain this answer?
The Octal equivalent of the hexadecimal number 100 is _____.
a)
400
b)
600
c)
300
d)
200
|
|
Pooja Patel answered |
The given hexadecimal number is: 100
To convert the given Hexadecimal number, first, we need to convert it into binary and then into octal.
Hexadecimal to binary: 0001 0000 0000
Binary to octal: To convert a binary number into octal, we need to make a group of three digits from right to left before the decimal pointer and left to right after the decimal pointer.
= 000 100 000 000
= 0400 = 400
Hexadecimal to binary: 0001 0000 0000
Binary to octal: To convert a binary number into octal, we need to make a group of three digits from right to left before the decimal pointer and left to right after the decimal pointer.
= 000 100 000 000
= 0400 = 400
Which of the following is not a valid hexadecimal number?- a)ACED
- b)GFAB
- c)DFFC
- d)1508
Correct answer is option 'B'. Can you explain this answer?
Which of the following is not a valid hexadecimal number?
a)
ACED
b)
GFAB
c)
DFFC
d)
1508
|
|
Pooja Patel answered |
Concept:
The radix or base of a number system is defined as the number of different digits which can occur in each position in the number system
Application:
For hexadecimal number system base is 16 hence there are 16 different digits from (0 - F)
Any number containing digit greater than F is invalid hexadecimal number.
So, GFAB is invalid hexadecimal number
Any number containing digit greater than F is invalid hexadecimal number.
So, GFAB is invalid hexadecimal number
X = 00110 and Y = 10011 are two binary numbers represented in 2's complement format. The sum of X and Y represented in 2's complement format using 5 bits is _____- a)11001
- b)01001
- c)10100
- d)10010
Correct answer is option 'A'. Can you explain this answer?
X = 00110 and Y = 10011 are two binary numbers represented in 2's complement format. The sum of X and Y represented in 2's complement format using 5 bits is _____
a)
11001
b)
01001
c)
10100
d)
10010
|
|
Bijoy Mehta answered |
To find the sum of X and Y represented in 2's complement format, we need to follow these steps:
1. Convert the binary representation of X and Y to their decimal equivalent:
- X = 00110 = 2^1 + 2^2 = 6
- Y = 10011 = -2^0 + 2^1 + 2^4 = -1 + 2 + 16 = 17
2. Add the decimal values of X and Y:
- 6 + 17 = 23
3. Convert the decimal sum back to binary representation:
- If the sum is positive (greater than or equal to 0), convert it to binary normally:
- 23 = 2^4 + 2^3 + 2^2 + 2^1 + 2^0 = 16 + 8 + 4 + 2 + 1 = 10111
- If the sum is negative (less than 0), convert the absolute value to binary and take the 2's complement:
- Absolute value of -23 = 23 = 10111
- Take the 2's complement by inverting all the bits and adding 1:
- Inverting: 10111 -> 01000
- Adding 1: 01000 + 1 = 01001
4. If the binary representation of the sum has more bits than the desired number of bits, truncate the most significant bits until the desired number of bits is reached. In this case, the desired number of bits is 5, so we can keep only the last 5 bits.
Therefore, the sum of X and Y represented in 2's complement format using 5 bits is 11001.
1. Convert the binary representation of X and Y to their decimal equivalent:
- X = 00110 = 2^1 + 2^2 = 6
- Y = 10011 = -2^0 + 2^1 + 2^4 = -1 + 2 + 16 = 17
2. Add the decimal values of X and Y:
- 6 + 17 = 23
3. Convert the decimal sum back to binary representation:
- If the sum is positive (greater than or equal to 0), convert it to binary normally:
- 23 = 2^4 + 2^3 + 2^2 + 2^1 + 2^0 = 16 + 8 + 4 + 2 + 1 = 10111
- If the sum is negative (less than 0), convert the absolute value to binary and take the 2's complement:
- Absolute value of -23 = 23 = 10111
- Take the 2's complement by inverting all the bits and adding 1:
- Inverting: 10111 -> 01000
- Adding 1: 01000 + 1 = 01001
4. If the binary representation of the sum has more bits than the desired number of bits, truncate the most significant bits until the desired number of bits is reached. In this case, the desired number of bits is 5, so we can keep only the last 5 bits.
Therefore, the sum of X and Y represented in 2's complement format using 5 bits is 11001.
The decimal number (57.375)10 when converted to binary number takes the form:- a)(111001.011)2
- b)(100111.110)2
- c)(110011.101)2
- d)(111011.011)2
Correct answer is option 'A'. Can you explain this answer?
The decimal number (57.375)10 when converted to binary number takes the form:
a)
(111001.011)2
b)
(100111.110)2
c)
(110011.101)2
d)
(111011.011)2
|
|
Mansi Datta answered |
To convert a decimal number to a binary number, we can use the method of successive division by 2. Here's how we can convert the decimal number (57.375)10 to its binary equivalent:
1. Convert the integer part:
- Divide 57 by 2: 57 ÷ 2 = 28, remainder 1
- Divide 28 by 2: 28 ÷ 2 = 14, remainder 0
- Divide 14 by 2: 14 ÷ 2 = 7, remainder 0
- Divide 7 by 2: 7 ÷ 2 = 3, remainder 1
- Divide 3 by 2: 3 ÷ 2 = 1, remainder 1
- Divide 1 by 2: 1 ÷ 2 = 0, remainder 1
Reading the remainders from bottom to top, the binary equivalent of the integer part is 111001.
2. Convert the fractional part:
- Multiply the fractional part (0.375) by 2: 0.375 × 2 = 0.75
- Multiply the fractional part (0.75) by 2: 0.75 × 2 = 1.5
- Multiply the fractional part (0.5) by 2: 0.5 × 2 = 1.0
Reading the whole numbers from left to right, the binary equivalent of the fractional part is 011.
3. Combine the integer and fractional parts:
Putting the integer part and the fractional part together, we get the binary representation of (57.375)10 as 111001.011.
Therefore, the correct answer is option A, (111001.011)2.
1. Convert the integer part:
- Divide 57 by 2: 57 ÷ 2 = 28, remainder 1
- Divide 28 by 2: 28 ÷ 2 = 14, remainder 0
- Divide 14 by 2: 14 ÷ 2 = 7, remainder 0
- Divide 7 by 2: 7 ÷ 2 = 3, remainder 1
- Divide 3 by 2: 3 ÷ 2 = 1, remainder 1
- Divide 1 by 2: 1 ÷ 2 = 0, remainder 1
Reading the remainders from bottom to top, the binary equivalent of the integer part is 111001.
2. Convert the fractional part:
- Multiply the fractional part (0.375) by 2: 0.375 × 2 = 0.75
- Multiply the fractional part (0.75) by 2: 0.75 × 2 = 1.5
- Multiply the fractional part (0.5) by 2: 0.5 × 2 = 1.0
Reading the whole numbers from left to right, the binary equivalent of the fractional part is 011.
3. Combine the integer and fractional parts:
Putting the integer part and the fractional part together, we get the binary representation of (57.375)10 as 111001.011.
Therefore, the correct answer is option A, (111001.011)2.
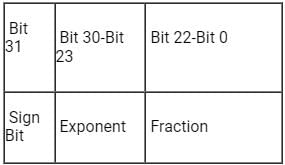
The difference in the dynamic range of 32-bit binary number(B) and floating-point number(F) is?
Standard Format for B and F as given below :B=

F=
- a)6.02(27 - 30) dB
- b)6.02(28 - 31) dB
- c)6.02(27 - 31) dB
- d)6.02(28 - 30) dB
Correct answer is option 'B'. Can you explain this answer?
The difference in the dynamic range of 32-bit binary number(B) and floating-point number(F) is?
Standard Format for B and F as given below :
Standard Format for B and F as given below :
B=

F=


F=

a)
6.02(27 - 30) dB
b)
6.02(28 - 31) dB
c)
6.02(27 - 31) dB
d)
6.02(28 - 30) dB
|
|
Pooja Patel answered |
The dynamic range in 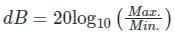
In fixed point, unsigned integer representation using N-bit, the range of Max to Min is 2N to 1
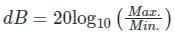
In fixed point, unsigned integer representation using N-bit, the range of Max to Min is 2N to 1
In fixed-point signed integer representation using N-bit, the range of Max to Min number is 2N-1 to 1
Calculation:
The dynamic range of a 32-bit binary number B is:

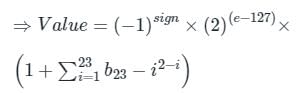
The dynamic range of a 32-bit binary number B is:

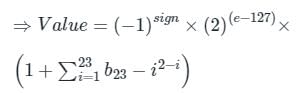
Exponent = e – 127 varies from –127 to 128,
e = 0 = all bits (b30 ---- b23) are zero.
Now, the dynamic range is determined by the size of the exponent, which is
1 × 2-127(min) to 2128 (max).
Dynamic range:
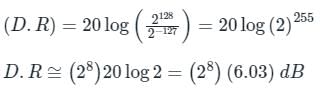
Difference in Dynamic Ranges = 6.03 (28 – 31)
So, Option (2) is correct.
e = 0 = all bits (b30 ---- b23) are zero.
Now, the dynamic range is determined by the size of the exponent, which is
1 × 2-127(min) to 2128 (max).
Dynamic range:
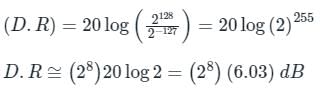
Difference in Dynamic Ranges = 6.03 (28 – 31)
So, Option (2) is correct.
The binary code of (21.125)10 is- a)10101.001
- b)10100.001
- c)10101.010
- d)10100.111
Correct answer is option 'A'. Can you explain this answer?
The binary code of (21.125)10 is
a)
10101.001
b)
10100.001
c)
10101.010
d)
10100.111
|
|
Janhavi Roy answered |
Binary Code of (21.125)10
To convert a decimal number to binary, we need to divide the decimal number by 2 repeatedly until the quotient becomes zero. The binary representation is obtained by writing the remainders in reverse order. In this case, we need to convert the decimal number 21.125 to binary.
Step 1: Integer Part Conversion
To convert the integer part of the decimal number (21), we divide it by 2 repeatedly until the quotient becomes zero.
21 ÷ 2 = 10 with a remainder of 1
10 ÷ 2 = 5 with a remainder of 0
5 ÷ 2 = 2 with a remainder of 1
2 ÷ 2 = 1 with a remainder of 0
1 ÷ 2 = 0 with a remainder of 1
The remainders in reverse order are 10101, which is the binary representation of the integer part of the decimal number.
Step 2: Fractional Part Conversion
To convert the fractional part of the decimal number (0.125), we multiply it by 2 repeatedly until it becomes zero or until the desired number of binary places are obtained.
0.125 × 2 = 0.25 (0)
0.25 × 2 = 0.5 (0)
0.5 × 2 = 1.0 (1)
The binary representation of the fractional part is 001. Therefore, the binary representation of the decimal number 21.125 is 10101.001.
Answer: Option A - 10101.001
To convert a decimal number to binary, we need to divide the decimal number by 2 repeatedly until the quotient becomes zero. The binary representation is obtained by writing the remainders in reverse order. In this case, we need to convert the decimal number 21.125 to binary.
Step 1: Integer Part Conversion
To convert the integer part of the decimal number (21), we divide it by 2 repeatedly until the quotient becomes zero.
21 ÷ 2 = 10 with a remainder of 1
10 ÷ 2 = 5 with a remainder of 0
5 ÷ 2 = 2 with a remainder of 1
2 ÷ 2 = 1 with a remainder of 0
1 ÷ 2 = 0 with a remainder of 1
The remainders in reverse order are 10101, which is the binary representation of the integer part of the decimal number.
Step 2: Fractional Part Conversion
To convert the fractional part of the decimal number (0.125), we multiply it by 2 repeatedly until it becomes zero or until the desired number of binary places are obtained.
0.125 × 2 = 0.25 (0)
0.25 × 2 = 0.5 (0)
0.5 × 2 = 1.0 (1)
The binary representation of the fractional part is 001. Therefore, the binary representation of the decimal number 21.125 is 10101.001.
Answer: Option A - 10101.001
The I's complement of the binary number (101100)2 is:- a)(001100)2
- b)(010011)2
- c)(101101)2
- d)(110011)2
Correct answer is option 'B'. Can you explain this answer?
The I's complement of the binary number (101100)2 is:
a)
(001100)2
b)
(010011)2
c)
(101101)2
d)
(110011)2
|
|
Pooja Patel answered |
Concept:
1's complement of Binary: 1's complement of a Binary number is defined by the value obtained by inverting all the bit, i.e, 0 as 1 and 1 as 0.
1's complement of Binary: 1's complement of a Binary number is defined by the value obtained by inverting all the bit, i.e, 0 as 1 and 1 as 0.
Calculation:
The 1's complement of the given binary digit will be:
(101100) → (010011)
The 1's complement of the given binary digit will be:
(101100) → (010011)
Find the Hexadecimal equivalent of (82.25)10- a)52.4
- b)56.0
- c)58.0
- d)56.4
Correct answer is option 'A'. Can you explain this answer?
Find the Hexadecimal equivalent of (82.25)10
a)
52.4
b)
56.0
c)
58.0
d)
56.4
|
|
Pooja Patel answered |
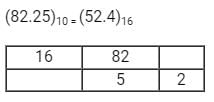
Convert Decimal to Hex:
- Decimal to hexadecimal conversion can be achieved by applying the repeated division and remainder algorithm.
- Decimal to Hex step by step Method:
- If the given decimal number is less than 16, the hex equivalent is the same. Remember that the letters A, B, C, D, E, and F are used for the values 10, 11, 12, 13, 14, and 15, convert accordingly
- For example, the decimal number 15 will be F in Hex.
- If the given decimal number is 16 or greater, divide the number by 16.
- Write down the remainder.
- Divide the part before the decimal point of your quotient by 16 again. Write down the remainder.
- Continue this process of dividing by 16 and noting the remainders until the last decimal digit you are left with is less than 16.
- When the last decimal digit is less than 16, the quotient will be less than 0 and the remainder will be the digit itself.
- The last remainder you get will be the most significant digit of Hex value while the first remainder from Step 3 is the least significant digit.

The 4-bit Gray code for decimal number 5 is:- a)0111
- b)1010
- c)1110
- d)1000
Correct answer is option 'A'. Can you explain this answer?
The 4-bit Gray code for decimal number 5 is:
a)
0111
b)
1010
c)
1110
d)
1000
|
|
Amar Sengupta answered |
Explanation:
Gray code is a binary numeral system where two successive values differ in only one bit. This is also known as the reflected binary code. The 4-bit Gray code can be represented as:
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
To find the Gray code for decimal number 5, we need to convert 5 into its binary equivalent which is 0101.
Steps to convert binary to Gray code:
1. Write the most significant bit of the binary number to the Gray code.
2. Write the next bit of the binary number XOR with the previous bit of the binary number to the Gray code.
3. Repeat step 2 for all remaining bits of the binary number.
Conversion of 0101 to Gray code:
Step 1: Write the most significant bit of the binary number to the Gray code.
0
Step 2: Write the next bit of the binary number XOR with the previous bit of the binary number to the Gray code.
01
Step 3: Repeat step 2 for all remaining bits of the binary number.
011
0111
Hence, the 4-bit Gray code for decimal number 5 is 0111 which is option A.
Gray code is a binary numeral system where two successive values differ in only one bit. This is also known as the reflected binary code. The 4-bit Gray code can be represented as:
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
To find the Gray code for decimal number 5, we need to convert 5 into its binary equivalent which is 0101.
Steps to convert binary to Gray code:
1. Write the most significant bit of the binary number to the Gray code.
2. Write the next bit of the binary number XOR with the previous bit of the binary number to the Gray code.
3. Repeat step 2 for all remaining bits of the binary number.
Conversion of 0101 to Gray code:
Step 1: Write the most significant bit of the binary number to the Gray code.
0
Step 2: Write the next bit of the binary number XOR with the previous bit of the binary number to the Gray code.
01
Step 3: Repeat step 2 for all remaining bits of the binary number.
011
0111
Hence, the 4-bit Gray code for decimal number 5 is 0111 which is option A.
On subtracting (01010)2 from (11110)2 using 1’s complement, we get ____________- a)01001
- b)11010
- c)10101
- d)10100
Correct answer is option 'D'. Can you explain this answer?
On subtracting (01010)2 from (11110)2 using 1’s complement, we get ____________
a)
01001
b)
11010
c)
10101
d)
10100
|
|
Pooja Patel answered |
Steps For Subtraction using 1’s complement are:
→ 1’s complement of the subtrahend is determined and added to the minuend.
→ If the result has a carry, then it is dropped and 1 is added to the last bit of the result.
→ Else, if there is no carry, then 1’s complement of the result is found out and a ‘-’ sign preceeds the result.

→ 1’s complement of the subtrahend is determined and added to the minuend.
→ If the result has a carry, then it is dropped and 1 is added to the last bit of the result.
→ Else, if there is no carry, then 1’s complement of the result is found out and a ‘-’ sign preceeds the result.

The decimal equivalent of the excess-3 number 110010100011.01110101 is _____________- a)970.42
- b)1253.75
- c)861.75
- d)1132.87
Correct answer is option 'A'. Can you explain this answer?
The decimal equivalent of the excess-3 number 110010100011.01110101 is _____________
a)
970.42
b)
1253.75
c)
861.75
d)
1132.87
|
|
Debanshi Basak answered |
Decimal Equivalent of Excess-3 Number 110010100011.01110101
To find the decimal equivalent of the given excess-3 number, we need to understand the concept of excess-3 code and convert it to decimal representation.
1. Excess-3 Code
Excess-3 code is a binary-coded decimal (BCD) representation of decimal digits. In this code, each decimal digit is represented by a 4-bit binary code. The excess-3 code is obtained by adding 3 to the corresponding BCD code.
For example, the BCD representation of decimal 0 is 0000. In excess-3 code, it becomes 0011 (0000 + 0011 = 0011). Similarly, the BCD representation of decimal 1 is 0001, and in excess-3 code, it becomes 0100 (0001 + 0011 = 0100).
2. Conversion Steps
To convert the given excess-3 number to decimal, we can follow these steps:
Step 1: Split the number into integer and fraction parts.
The given number is 110010100011.01110101. Splitting it into integer and fraction parts, we get:
Integer part: 110010100011
Fraction part: 01110101
Step 2: Convert the integer part to decimal.
To convert the integer part of the excess-3 number to decimal, we need to convert each group of 4 bits to its corresponding decimal digit. We can use the following table for reference:
Excess-3 Code | Decimal
0000 | 3
0001 | 4
0010 | 5
0011 | 6
0100 | 7
0101 | 8
0110 | 9
0111 | 10
1000 | 11
1001 | 12
1010 | 13
1011 | 14
1100 | 15
1101 | 16
1110 | 17
1111 | 18
Converting the integer part of the given number:
1100 1010 0011 -> 15 8 6 -> 1586
Step 3: Convert the fraction part to decimal.
To convert the fraction part of the excess-3 number to decimal, we can use the place value method. Each bit in the fraction part represents a negative power of 2.
0111 0101 -> (0*1/2) + (1*1/4) + (1*1/8) + (1*1/16) + (0*1/32) + (1*1/64) + (0*1/128) + (1*1/256)
-> 0 + 0.25 + 0.125 + 0.0625 + 0 + 0.015625 + 0 + 0.00390625
-> 0.45703125
Step 4: Combine the integer and fraction parts.
Combining the integer and fraction parts, we get:
1586.45703125
3. Final Answer
The decimal
To find the decimal equivalent of the given excess-3 number, we need to understand the concept of excess-3 code and convert it to decimal representation.
1. Excess-3 Code
Excess-3 code is a binary-coded decimal (BCD) representation of decimal digits. In this code, each decimal digit is represented by a 4-bit binary code. The excess-3 code is obtained by adding 3 to the corresponding BCD code.
For example, the BCD representation of decimal 0 is 0000. In excess-3 code, it becomes 0011 (0000 + 0011 = 0011). Similarly, the BCD representation of decimal 1 is 0001, and in excess-3 code, it becomes 0100 (0001 + 0011 = 0100).
2. Conversion Steps
To convert the given excess-3 number to decimal, we can follow these steps:
Step 1: Split the number into integer and fraction parts.
The given number is 110010100011.01110101. Splitting it into integer and fraction parts, we get:
Integer part: 110010100011
Fraction part: 01110101
Step 2: Convert the integer part to decimal.
To convert the integer part of the excess-3 number to decimal, we need to convert each group of 4 bits to its corresponding decimal digit. We can use the following table for reference:
Excess-3 Code | Decimal
0000 | 3
0001 | 4
0010 | 5
0011 | 6
0100 | 7
0101 | 8
0110 | 9
0111 | 10
1000 | 11
1001 | 12
1010 | 13
1011 | 14
1100 | 15
1101 | 16
1110 | 17
1111 | 18
Converting the integer part of the given number:
1100 1010 0011 -> 15 8 6 -> 1586
Step 3: Convert the fraction part to decimal.
To convert the fraction part of the excess-3 number to decimal, we can use the place value method. Each bit in the fraction part represents a negative power of 2.
0111 0101 -> (0*1/2) + (1*1/4) + (1*1/8) + (1*1/16) + (0*1/32) + (1*1/64) + (0*1/128) + (1*1/256)
-> 0 + 0.25 + 0.125 + 0.0625 + 0 + 0.015625 + 0 + 0.00390625
-> 0.45703125
Step 4: Combine the integer and fraction parts.
Combining the integer and fraction parts, we get:
1586.45703125
3. Final Answer
The decimal
The logic XOR operation of (4AC0)16 and (B53F)16 results________- a)AACB
- b)0000
- c)FFFF
- d)ABCD
Correct answer is option 'C'. Can you explain this answer?
The logic XOR operation of (4AC0)16 and (B53F)16 results________
a)
AACB
b)
0000
c)
FFFF
d)
ABCD
|
|
Bijoy Nair answered |
Logic XOR of hexadecimal numbers
XOR or exclusive OR is a logical operation that outputs true only when the two binary inputs are different. XOR operation is represented by the symbol ⊕. When used with hexadecimal numbers, the XOR operation is performed on each pair of corresponding bits.
Given hexadecimal numbers (4AC0)16 and (B53F)16, the XOR operation can be performed as follows:
4AC0 = 0100 1010 1100 0000
B53F = 1011 0101 0011 1111
XOR = 1111 1111 1111 1111
The result of the XOR operation is (FFFF)16, which is option C.
Explanation
- XOR operation: The XOR operation is a binary operation that takes two binary inputs and outputs true only if the inputs are different. The XOR operation is represented by the symbol ⊕.
- Conversion to binary: To perform the XOR operation on hexadecimal numbers, we need to convert them to binary. Each hexadecimal digit represents four binary digits or bits. For example, (4AC0)16 is equivalent to (0100 1010 1100 0000)2 in binary.
- Performing XOR: Once the numbers are in binary form, we can perform the XOR operation on each pair of corresponding bits. If both bits are the same, the result is 0. If the bits are different, the result is 1.
- Result: After performing the XOR operation on each pair of bits, we get the binary result of (1111 1111 1111 1111)2, which is equivalent to (FFFF)16 in hexadecimal form.
Conclusion
The logic XOR operation of (4AC0)16 and (B53F)16 results in (FFFF)16. This result is obtained by converting the hexadecimal numbers to binary, performing the XOR operation on each pair of corresponding bits, and converting the binary result back to hexadecimal form.
XOR or exclusive OR is a logical operation that outputs true only when the two binary inputs are different. XOR operation is represented by the symbol ⊕. When used with hexadecimal numbers, the XOR operation is performed on each pair of corresponding bits.
Given hexadecimal numbers (4AC0)16 and (B53F)16, the XOR operation can be performed as follows:
4AC0 = 0100 1010 1100 0000
B53F = 1011 0101 0011 1111
XOR = 1111 1111 1111 1111
The result of the XOR operation is (FFFF)16, which is option C.
Explanation
- XOR operation: The XOR operation is a binary operation that takes two binary inputs and outputs true only if the inputs are different. The XOR operation is represented by the symbol ⊕.
- Conversion to binary: To perform the XOR operation on hexadecimal numbers, we need to convert them to binary. Each hexadecimal digit represents four binary digits or bits. For example, (4AC0)16 is equivalent to (0100 1010 1100 0000)2 in binary.
- Performing XOR: Once the numbers are in binary form, we can perform the XOR operation on each pair of corresponding bits. If both bits are the same, the result is 0. If the bits are different, the result is 1.
- Result: After performing the XOR operation on each pair of bits, we get the binary result of (1111 1111 1111 1111)2, which is equivalent to (FFFF)16 in hexadecimal form.
Conclusion
The logic XOR operation of (4AC0)16 and (B53F)16 results in (FFFF)16. This result is obtained by converting the hexadecimal numbers to binary, performing the XOR operation on each pair of corresponding bits, and converting the binary result back to hexadecimal form.
Octal equivalent of 111010 is:- a)84
- b)70
- c)72
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Octal equivalent of 111010 is:
a)
84
b)
70
c)
72
d)
None of these
|
|
Sparsh Saini answered |
Octal is a numeral system that uses a base of 8, meaning it only includes the digits 0-7. To convert a binary number to octal, we need to group the binary digits into sets of three from right to left and assign an octal digit to each group.
Given binary number: 111010
To convert this binary number to octal, we will group the digits into sets of three from right to left:
1 1 1 0 1 0
Now let's assign an octal digit to each group:
Group 1: 1 1 1 -> The octal digit equivalent of binary 111 is 7.
Group 2: 0 1 0 -> The octal digit equivalent of binary 010 is 2.
So the octal equivalent of 111010 is 72.
Therefore, the correct answer is option C) 72.
Given binary number: 111010
To convert this binary number to octal, we will group the digits into sets of three from right to left:
1 1 1 0 1 0
Now let's assign an octal digit to each group:
Group 1: 1 1 1 -> The octal digit equivalent of binary 111 is 7.
Group 2: 0 1 0 -> The octal digit equivalent of binary 010 is 2.
So the octal equivalent of 111010 is 72.
Therefore, the correct answer is option C) 72.
Which of the following is the smallest 4-bit negative number stored in its 2's complement representation?- a)1000
- b)0000
- c)1111
- d)0111
Correct answer is option 'A'. Can you explain this answer?
Which of the following is the smallest 4-bit negative number stored in its 2's complement representation?
a)
1000
b)
0000
c)
1111
d)
0111
|
|
Pooja Patel answered |
The smallest negative number is the largest binary value.
1111 is -1, 1110 is -2, 1101 is -3, etc down to 1000 which represents -8.
The range of numbers represented by an 8-bit two’s complement representation is- a)-128 to +127
- b)-127 to +128
- c)-128 to +128
- d)0 to 255
Correct answer is option 'A'. Can you explain this answer?
The range of numbers represented by an 8-bit two’s complement representation is
a)
-128 to +127
b)
-127 to +128
c)
-128 to +128
d)
0 to 255
|
|
Mihir Khanna answered |
The range of numbers represented by an 8-bit two's complement system is -128 to 127. This means that the system can represent both positive and negative integers within this range. The most significant bit (MSB) is used as the sign bit, with 0 indicating a positive number and 1 indicating a negative number. The remaining 7 bits are used to represent the magnitude of the number.
In sign-magnitude numbers- a)ms bit always 1
- b)ms bit 0 stands for the positive numbers
- c)ms bit 0 stands for the negative numbers
- d)ms bit 1 stand for the positive numbers
Correct answer is option 'B'. Can you explain this answer?
In sign-magnitude numbers
a)
ms bit always 1
b)
ms bit 0 stands for the positive numbers
c)
ms bit 0 stands for the negative numbers
d)
ms bit 1 stand for the positive numbers
|
|
Pooja Patel answered |
Signed magnitude representation uses the most significant bit (MSB) a sign bit.
- If the sign bit is ‘0’ then the number is positive.
- If the sign bit is ‘1’ then the number is negative.
The remaining bits represent the magnitude of the binary number.
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:- a)(1100010.11)2 (246.6)8 and (62.C)16
- b)(0100011.11)2 (142.6)8 and (62.C)16
- c)(0100011.11)2 (242.6)8 and (62.12)16
- d)(1100010.11)2 (142.6)8 and (62.C)16
Correct answer is option 'D'. Can you explain this answer?
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:
a)
(1100010.11)2 (246.6)8 and (62.C)16
b)
(0100011.11)2 (142.6)8 and (62.C)16
c)
(0100011.11)2 (242.6)8 and (62.12)16
d)
(1100010.11)2 (142.6)8 and (62.C)16
|
|
Aniket Choudhury answered |
Conversion of Decimal to Binary
To convert the decimal number (98.75)10 into binary:
1. Whole Number Part (98)10
- Divide by 2 and keep track of the remainders:
- 98 ÷ 2 = 49 remainder 0
- 49 ÷ 2 = 24 remainder 1
- 24 ÷ 2 = 12 remainder 0
- 12 ÷ 2 = 6 remainder 0
- 6 ÷ 2 = 3 remainder 0
- 3 ÷ 2 = 1 remainder 1
- 1 ÷ 2 = 0 remainder 1
- Reading from bottom to top gives (1100010)2.
2. Fractional Part (0.75)10
- Multiply by 2 and take the integer part:
- 0.75 × 2 = 1.5 (integer part 1)
- 0.5 × 2 = 1.0 (integer part 1)
- Thus, (0.75)10 = (0.11)2.
- Combined: (1100010.11)2.
Conversion of Decimal to Octal
To convert (98.75)10 to octal:
1. Whole Number Part (98)10
- Divide by 8:
- 98 ÷ 8 = 12 remainder 2
- 12 ÷ 8 = 1 remainder 4
- 1 ÷ 8 = 0 remainder 1
- Reading from bottom to top gives (142)8.
2. Fractional Part (0.75)10
- Multiply by 8:
- 0.75 × 8 = 6.0 (integer part 6)
- Thus, (0.75)10 = (0.6)8.
- Combined: (142.6)8.
Conversion of Decimal to Hexadecimal
To convert (98.75)10 to hexadecimal:
1. Whole Number Part (98)10
- Divide by 16:
- 98 ÷ 16 = 6 remainder 2
- Thus, (62)16.
2. Fractional Part (0.75)10
- Multiply by 16:
- 0.75 × 16 = 12.0 (integer part 12, which is C in hex)
- Thus, (0.75)10 = (0.C)16.
Final Results
- Binary: (1100010.11)2
- Octal: (142.6)8
- Hexadecimal: (62.C)16
Thus, the correct answer is option 'D'.
To convert the decimal number (98.75)10 into binary:
1. Whole Number Part (98)10
- Divide by 2 and keep track of the remainders:
- 98 ÷ 2 = 49 remainder 0
- 49 ÷ 2 = 24 remainder 1
- 24 ÷ 2 = 12 remainder 0
- 12 ÷ 2 = 6 remainder 0
- 6 ÷ 2 = 3 remainder 0
- 3 ÷ 2 = 1 remainder 1
- 1 ÷ 2 = 0 remainder 1
- Reading from bottom to top gives (1100010)2.
2. Fractional Part (0.75)10
- Multiply by 2 and take the integer part:
- 0.75 × 2 = 1.5 (integer part 1)
- 0.5 × 2 = 1.0 (integer part 1)
- Thus, (0.75)10 = (0.11)2.
- Combined: (1100010.11)2.
Conversion of Decimal to Octal
To convert (98.75)10 to octal:
1. Whole Number Part (98)10
- Divide by 8:
- 98 ÷ 8 = 12 remainder 2
- 12 ÷ 8 = 1 remainder 4
- 1 ÷ 8 = 0 remainder 1
- Reading from bottom to top gives (142)8.
2. Fractional Part (0.75)10
- Multiply by 8:
- 0.75 × 8 = 6.0 (integer part 6)
- Thus, (0.75)10 = (0.6)8.
- Combined: (142.6)8.
Conversion of Decimal to Hexadecimal
To convert (98.75)10 to hexadecimal:
1. Whole Number Part (98)10
- Divide by 16:
- 98 ÷ 16 = 6 remainder 2
- Thus, (62)16.
2. Fractional Part (0.75)10
- Multiply by 16:
- 0.75 × 16 = 12.0 (integer part 12, which is C in hex)
- Thus, (0.75)10 = (0.C)16.
Final Results
- Binary: (1100010.11)2
- Octal: (142.6)8
- Hexadecimal: (62.C)16
Thus, the correct answer is option 'D'.
Find the decimal equivalent of the 6-bit binary number (101.101)2- a)5.2510
- b)5.12510
- c)5.62510
- d)6.62510
Correct answer is option 'C'. Can you explain this answer?
Find the decimal equivalent of the 6-bit binary number (101.101)2
a)
5.2510
b)
5.12510
c)
5.62510
d)
6.62510
|
|
Pooja Patel answered |
The decimal equivalent of the binary number 101.101 is,
= 1 x 22 + 0 x 21 + 1 x 20 + 1 x 2-1 + 0 x 2-2 + 1 × 2-3
= 4 + 0 + 1 + 0.5 + 0 + 0.125
= 5.625
= 4 + 0 + 1 + 0.5 + 0 + 0.125
= 5.625
1’s complement of 1011101 is ____________- a)0101110
- b)1001101
- c)0100010
- d)1100101
Correct answer is option 'C'. Can you explain this answer?
1’s complement of 1011101 is ____________
a)
0101110
b)
1001101
c)
0100010
d)
1100101
|
|
Rajesh Saha answered |
One possible way to answer this question is by providing a personal example of a time when you faced a difficult situation and how you overcame it. Here is an example response:
One difficult situation I faced was during my sophomore year of college when I was struggling with a particularly challenging math course. I had always considered myself to be strong in math, but this class was proving to be a real struggle for me. I was spending hours studying and trying to understand the material, but it just wasn't clicking.
Instead of giving up, I decided to seek help. I visited my professor during office hours and explained my difficulties. He was very understanding and offered to set up weekly one-on-one tutoring sessions with a graduate student who specialized in the subject matter. I also formed a study group with some classmates who were also struggling.
Through these tutoring sessions and study group meetings, I was able to gain a better understanding of the material. I learned different study techniques and approaches that helped me grasp the concepts. I also found that teaching others helped solidify my own understanding of the material.
By the end of the semester, I was able to improve my grades and pass the course. This experience taught me the importance of seeking help and not being afraid to ask for assistance when facing a difficult situation. It also showed me the value of collaboration and working with others to overcome challenges.
One difficult situation I faced was during my sophomore year of college when I was struggling with a particularly challenging math course. I had always considered myself to be strong in math, but this class was proving to be a real struggle for me. I was spending hours studying and trying to understand the material, but it just wasn't clicking.
Instead of giving up, I decided to seek help. I visited my professor during office hours and explained my difficulties. He was very understanding and offered to set up weekly one-on-one tutoring sessions with a graduate student who specialized in the subject matter. I also formed a study group with some classmates who were also struggling.
Through these tutoring sessions and study group meetings, I was able to gain a better understanding of the material. I learned different study techniques and approaches that helped me grasp the concepts. I also found that teaching others helped solidify my own understanding of the material.
By the end of the semester, I was able to improve my grades and pass the course. This experience taught me the importance of seeking help and not being afraid to ask for assistance when facing a difficult situation. It also showed me the value of collaboration and working with others to overcome challenges.
The decimal number 10 is represented in its BCD form as __________- a)10100000
- b)01010111
- c)00010000
- d)00101011
Correct answer is option 'C'. Can you explain this answer?
The decimal number 10 is represented in its BCD form as __________
a)
10100000
b)
01010111
c)
00010000
d)
00101011
|
|
Shivam Das answered |
BCD stands for Binary Coded Decimal. It is a binary representation of decimal numbers where each decimal digit is represented by a four-bit binary code.
To convert the decimal number 10 into its BCD form, we need to represent each digit (1 and 0) in binary using four bits each.
- Converting the first digit 1 into binary:
- The binary representation of 1 is 0001.
- Converting the second digit 0 into binary:
- The binary representation of 0 is 0000.
Therefore, the BCD representation of the decimal number 10 is obtained by concatenating the binary representations of each digit:
BCD representation = 0001 0000
So, the correct answer is option C: 00010000.
To convert the decimal number 10 into its BCD form, we need to represent each digit (1 and 0) in binary using four bits each.
- Converting the first digit 1 into binary:
- The binary representation of 1 is 0001.
- Converting the second digit 0 into binary:
- The binary representation of 0 is 0000.
Therefore, the BCD representation of the decimal number 10 is obtained by concatenating the binary representations of each digit:
BCD representation = 0001 0000
So, the correct answer is option C: 00010000.
On subtracting +28 from +29 using 2’s complement, we get ____________- a)11111010
- b)111111001
- c)100001
- d)1
Correct answer is option 'D'. Can you explain this answer?
On subtracting +28 from +29 using 2’s complement, we get ____________
a)
11111010
b)
111111001
c)
100001
d)
1
|
|
Anuj Rane answered |
To subtract 28 from 29 using 2, you would start with 29 and subtract 2 repeatedly until you reach 28.
29 - 2 = 27
27 - 2 = 25
25 - 2 = 23
23 - 2 = 21
21 - 2 = 19
19 - 2 = 17
17 - 2 = 15
15 - 2 = 13
13 - 2 = 11
11 - 2 = 9
9 - 2 = 7
7 - 2 = 5
5 - 2 = 3
3 - 2 = 1
So, subtracting 28 from 29 using 2 results in 1.
29 - 2 = 27
27 - 2 = 25
25 - 2 = 23
23 - 2 = 21
21 - 2 = 19
19 - 2 = 17
17 - 2 = 15
15 - 2 = 13
13 - 2 = 11
11 - 2 = 9
9 - 2 = 7
7 - 2 = 5
5 - 2 = 3
3 - 2 = 1
So, subtracting 28 from 29 using 2 results in 1.
Convert the binary number 10101110 to octal. - a)128
- b)184
- c)256
- d)312
Correct answer is option 'C'. Can you explain this answer?
Convert the binary number 10101110 to octal.
a)
128
b)
184
c)
256
d)
312
|
|
Pooja Patel answered |
Concept:
There are only 8 digits (from 0 to 7) in the octal number system, so we can represent any digit of octal number system using only 3 bits as following below:
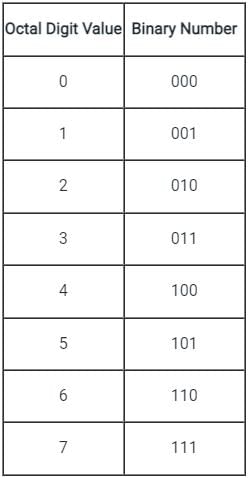
Follow below-mentioned steps to convert from Binary to Octal:
Step I: Select Binary Number.
Step II: Divide the binary digits into a group of three (starting from right) for the Integer part and start from left for the Fraction part.
Step III: Convert each group of three binary digits into an octal digit referring to the above table.

Follow below-mentioned steps to convert from Binary to Octal:
Step I: Select Binary Number.
Step II: Divide the binary digits into a group of three (starting from right) for the Integer part and start from left for the Fraction part.
Step III: Convert each group of three binary digits into an octal digit referring to the above table.
Calculation
Step I: Binary Number: 110101110
Step II: Divide the binary digits into the group of three (starting from the right) for the Integer part:
(010 101 110)
Step III: Convert each group of three binary digits into an octal digit referring to the above table:
Step I: Binary Number: 110101110
Step II: Divide the binary digits into the group of three (starting from the right) for the Integer part:
(010 101 110)
Step III: Convert each group of three binary digits into an octal digit referring to the above table:
(010 101 110)2 = (256)8
On addition of +38 and -20 using 2’s complement, we get ____________- a)11110001
- b)100001110
- c)010010
- d)110101011
Correct answer is option 'C'. Can you explain this answer?
On addition of +38 and -20 using 2’s complement, we get ____________
a)
11110001
b)
100001110
c)
010010
d)
110101011
|
|
Pooja Patel answered |
Steps for Binary Addition Using 2’s complement:
→ The 2’s complement of the addend is found out and added to the first number.
→ The result is the 2’s complement of the sum obtained.
→ The 2’s complement of the addend is found out and added to the first number.
→ The result is the 2’s complement of the sum obtained.

On addition of -46 and +28 using 2’s complement, we get ____________- a)-10010
- b)-00101
- c)01011
- d)0100101
Correct answer is option 'A'. Can you explain this answer?
On addition of -46 and +28 using 2’s complement, we get ____________
a)
-10010
b)
-00101
c)
01011
d)
0100101
|
|
Amar Sengupta answered |
's complement method, we get:
-46 = 1101 0010 (in 8-bit binary)
To get its 2's complement, we need to invert all bits and add 1:
0010 1110 + 1 = 0010 1111
28 = 0001 1100 (in 8-bit binary)
Now we can add these two numbers using binary addition:
0010 1111 (2's complement of -46)
+ 0001 1100 (28)
-----------
0100 1011
The result in binary is 0100 1011, which is equal to 75 in decimal. However, since we used the 2's complement method to represent negative numbers, we need to check if the result is negative by looking at the leftmost bit (the sign bit). If it is 1, the result is negative. In this case, the leftmost bit is 0, so the result is positive. Therefore, the final answer is 75.
-46 = 1101 0010 (in 8-bit binary)
To get its 2's complement, we need to invert all bits and add 1:
0010 1110 + 1 = 0010 1111
28 = 0001 1100 (in 8-bit binary)
Now we can add these two numbers using binary addition:
0010 1111 (2's complement of -46)
+ 0001 1100 (28)
-----------
0100 1011
The result in binary is 0100 1011, which is equal to 75 in decimal. However, since we used the 2's complement method to represent negative numbers, we need to check if the result is negative by looking at the leftmost bit (the sign bit). If it is 1, the result is negative. In this case, the leftmost bit is 0, so the result is positive. Therefore, the final answer is 75.
The number of 1’s in the 8-bit unsigned representation of 127 in its 2’s complement form is m and that in 1’s complement form is n. What is the value of m : n?- a)2 : 1
- b)1 : 2
- c)3 : 1
- d)1 : 3
Correct answer is option 'A'. Can you explain this answer?
The number of 1’s in the 8-bit unsigned representation of 127 in its 2’s complement form is m and that in 1’s complement form is n. What is the value of m : n?
a)
2 : 1
b)
1 : 2
c)
3 : 1
d)
1 : 3
|
|
Harshad Singh answered |
The number of 1 can refer to different things depending on the context. It could refer to:
- The quantity of the digit 1: In this case, the number of 1 would simply mean the count or total number of occurrences of the digit 1.
- The value of 1: This could refer to a specific number or quantity represented by the digit 1. For example, if we're talking about a specific number like 111, then the number of 1 would be 3.
- A placeholder or position in a number system: In a positional number system like decimal or binary, the number of 1 in a specific position represents its value. For example, in the decimal number 123, the number of 1 in the hundreds place is 1.
Without further information or context, it is not possible to determine the specific meaning of "the number of 1."
- The quantity of the digit 1: In this case, the number of 1 would simply mean the count or total number of occurrences of the digit 1.
- The value of 1: This could refer to a specific number or quantity represented by the digit 1. For example, if we're talking about a specific number like 111, then the number of 1 would be 3.
- A placeholder or position in a number system: In a positional number system like decimal or binary, the number of 1 in a specific position represents its value. For example, in the decimal number 123, the number of 1 in the hundreds place is 1.
Without further information or context, it is not possible to determine the specific meaning of "the number of 1."
Add the two BCD numbers: 1001 + 0100 = ?- a)10101111
- b)01010000
- c)00010011
- d)00101011
Correct answer is option 'C'. Can you explain this answer?
Add the two BCD numbers: 1001 + 0100 = ?
a)
10101111
b)
01010000
c)
00010011
d)
00101011
|
|
Pooja Patel answered |
Firstly, Add the 1001 and 0100. We get 1101 as output but it’s not in BCD form. So, we add 0110 (i.e. 6) with 1101. As a result we get 10011 and it’s BCD form is 0001 0011.
On subtracting (010110)2 from (1011001)2 using 2’s complement, we get ____________- a)0111001
- b)1100101
- c)0110110
- d)1000011
Correct answer is option 'D'. Can you explain this answer?
On subtracting (010110)2 from (1011001)2 using 2’s complement, we get ____________
a)
0111001
b)
1100101
c)
0110110
d)
1000011
|
|
Kajal Mukherjee answered |
To subtract (010110)2 from (1011001)2, we can use the binary subtraction method.
```
1 0 1 1 0 0 1 (carry)
- 0 1 0 1 1 0 (010110)
--------------
1 0 0 0 1 1 (1011001 - 010110 = 100011)
```
Therefore, (1011001)2 - (010110)2 = (100011)2.
```
1 0 1 1 0 0 1 (carry)
- 0 1 0 1 1 0 (010110)
--------------
1 0 0 0 1 1 (1011001 - 010110 = 100011)
```
Therefore, (1011001)2 - (010110)2 = (100011)2.
A register contains a 2’s complement no 10100. Find the value of a register if it is divided by 2- a)11010
- b)10110
- c)11100
- d)10101
Correct answer is option 'A'. Can you explain this answer?
A register contains a 2’s complement no 10100. Find the value of a register if it is divided by 2
a)
11010
b)
10110
c)
11100
d)
10101
|
|
Pooja Patel answered |
Given Number is 10100
The Right shift of the content in register is same as the content divided by 2
Apply Right Shift ⇒ 11010
Operation right shift is equivalent to divided by 2
The Right shift of the content in register is same as the content divided by 2
Apply Right Shift ⇒ 11010
Operation right shift is equivalent to divided by 2
Binary coded decimal is a combination of __________- a)Two binary digits
- b)Three binary digits
- c)Four binary digits
- d)Five binary digits
Correct answer is option 'C'. Can you explain this answer?
Binary coded decimal is a combination of __________
a)
Two binary digits
b)
Three binary digits
c)
Four binary digits
d)
Five binary digits
|
|
Pooja Patel answered |
Binary coded decimal is a combination of 4 binary digits. For example-8421.
Convert the octal number (471)8 into equivalent binary number.- a)(100111101)2
- b)(100011101)2
- c)(100111001)2
- d)(100111011)2
Correct answer is option 'C'. Can you explain this answer?
Convert the octal number (471)8 into equivalent binary number.
a)
(100111101)2
b)
(100011101)2
c)
(100111001)2
d)
(100111011)2
|
|
Pooja Patel answered |
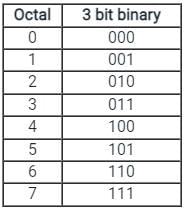
Octal to Binary Conversion:
- Every octal number is represented by a 3-bit binary equivalent.
- The table of binary representation for octal numbers (0 to 7) is given below:
Explanation:
- From the above table, the binary equivalent of 4 is 100.
- The binary equivalent of 7 is 111.
- The binary equivalent of 1 is 000
.
Hence, the binary equivalent of octal number 471 is (100111001)2
Hence, the binary equivalent of octal number 471 is (100111001)2
State the octal equivalent of hexa decimal number (B34)16.- a)(6454)8
- b)(4564)8
- c)(5464)8
- d)(5645)8
Correct answer is option 'C'. Can you explain this answer?
State the octal equivalent of hexa decimal number (B34)16.
a)
(6454)8
b)
(4564)8
c)
(5464)8
d)
(5645)8
|
|
Pooja Patel answered |
Concept:
A number system includes the number of independent digits used in the number system (the base), the place values of the different digits constituting the number, and the maximum numbers that can be written with the given number of digits.
Octal numbers: These numbers use digits from 0 to 7, total of 8 digits, and hence they are called octal number system. Octal numbers have base 8.
Hexadecimal numbers: The numbers which have base 16. It uses 16 different digits to represent the numbers. It is denoted as h16, where h is a hexadecimal number. It may be a combination of alphabets and numbers. Thus, it includes numbers from 0 to 9 and alphabets A to F.
A number system includes the number of independent digits used in the number system (the base), the place values of the different digits constituting the number, and the maximum numbers that can be written with the given number of digits.
Octal numbers: These numbers use digits from 0 to 7, total of 8 digits, and hence they are called octal number system. Octal numbers have base 8.
Hexadecimal numbers: The numbers which have base 16. It uses 16 different digits to represent the numbers. It is denoted as h16, where h is a hexadecimal number. It may be a combination of alphabets and numbers. Thus, it includes numbers from 0 to 9 and alphabets A to F.
Calculation:
Hexadecimal to Octal Conversion:
Given, B3416 is a hexadecimal number.
B → 1011, 3 → 0011, 4 → 0100
1011 0011 0100
Now group them from right to left, each having 3 digits.
101, 100, 110, 100
101 → 5, 100 → 4, 110 → 6, 100 → 4
Hence, B3416 = 54648
Hexadecimal to Octal Conversion:
Given, B3416 is a hexadecimal number.
B → 1011, 3 → 0011, 4 → 0100
1011 0011 0100
Now group them from right to left, each having 3 digits.
101, 100, 110, 100
101 → 5, 100 → 4, 110 → 6, 100 → 4
Hence, B3416 = 54648
Determine the octal equivalent of (432267)10?- a)(432267)8
- b)(346731)8
- c)(2164432)8
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
Determine the octal equivalent of (432267)10?
a)
(432267)8
b)
(346731)8
c)
(2164432)8
d)
None of the above
|
|
Pooja Patel answered |
Concept:
Following are the steps to convert decimal to octal:
- If the provided decimal number is less than the number 8 then the octal number is the same.
- If the provided decimal number is larger than 7 then divide it by number 8.
- take a note of the remainder, received after division
- Repeat step 2 and 3 with the quotient until it is less than 8
- Now, note the remainders in the reverse order (bottom to top)
- The resultant thus received is the equivalent octal number to the provided decimal number.
Explanation:
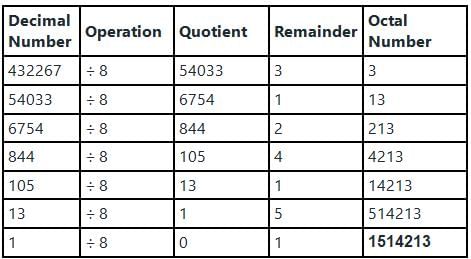
Hence, (432267)10 = (1514213)8

Hence, (432267)10 = (1514213)8
Which of the following is not an invalid BCD Code?- a)1011
- b)1010
- c)1001
- d)1100
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not an invalid BCD Code?
a)
1011
b)
1010
c)
1001
d)
1100
|
|
Tarun Chawla answered |
Understanding BCD Code
Binary-Coded Decimal (BCD) is a class of binary encodings for decimal numbers where each digit is represented by its own binary sequence. In standard BCD, each digit from 0 to 9 is represented using four bits.
Valid and Invalid BCD Codes
In BCD, only the binary representations of decimal digits 0 to 9 are valid. Therefore:
- Valid BCD Codes (0-9):
- 0000 (0)
- 0001 (1)
- 0010 (2)
- 0011 (3)
- 0100 (4)
- 0101 (5)
- 0110 (6)
- 0111 (7)
- 1000 (8)
- 1001 (9)
- Invalid BCD Codes:
- 1010 (A in hex)
- 1011 (B in hex)
- 1100 (C in hex)
- 1101 (D in hex)
- 1110 (E in hex)
- 1111 (F in hex)
Analysis of the Options
Given the options:
- a) 1011: Invalid BCD (represents 11)
- b) 1010: Invalid BCD (represents 10)
- c) 1001: Valid BCD (represents 9)
- d) 1100: Invalid BCD (represents 12)
Conclusion
The correct answer is option C (1001), as it is the only valid BCD representation among the given options. It represents the decimal digit 9 and adheres to the rules of BCD encoding. The other options (1010, 1011, and 1100) represent values outside the valid range for BCD.
Binary-Coded Decimal (BCD) is a class of binary encodings for decimal numbers where each digit is represented by its own binary sequence. In standard BCD, each digit from 0 to 9 is represented using four bits.
Valid and Invalid BCD Codes
In BCD, only the binary representations of decimal digits 0 to 9 are valid. Therefore:
- Valid BCD Codes (0-9):
- 0000 (0)
- 0001 (1)
- 0010 (2)
- 0011 (3)
- 0100 (4)
- 0101 (5)
- 0110 (6)
- 0111 (7)
- 1000 (8)
- 1001 (9)
- Invalid BCD Codes:
- 1010 (A in hex)
- 1011 (B in hex)
- 1100 (C in hex)
- 1101 (D in hex)
- 1110 (E in hex)
- 1111 (F in hex)
Analysis of the Options
Given the options:
- a) 1011: Invalid BCD (represents 11)
- b) 1010: Invalid BCD (represents 10)
- c) 1001: Valid BCD (represents 9)
- d) 1100: Invalid BCD (represents 12)
Conclusion
The correct answer is option C (1001), as it is the only valid BCD representation among the given options. It represents the decimal digit 9 and adheres to the rules of BCD encoding. The other options (1010, 1011, and 1100) represent values outside the valid range for BCD.
A three digit decimal number requires ________ for representation in the conventional BCD format.- a)3 bits
- b)6 bits
- c)12 bits
- d)24 bits
Correct answer is option 'C'. Can you explain this answer?
A three digit decimal number requires ________ for representation in the conventional BCD format.
a)
3 bits
b)
6 bits
c)
12 bits
d)
24 bits
|
|
Pooja Patel answered |
The number of bits needed to represent a given decimal number is always greater than the number of bits required for a straight binary encoding of the same. Hence, a three digit decimal number requires 12 bits for representation in BCD format.
Convert the 127 decimal number into binary.- a)1100111
- b)1111111
- c)1111011
- d)111111
Correct answer is option 'B'. Can you explain this answer?
Convert the 127 decimal number into binary.
a)
1100111
b)
1111111
c)
1111011
d)
111111
|
|
Ashwin Kapoor answered |
Understanding the Conversion of Decimal to Binary
To convert a decimal number into binary, we need to understand the binary number system, which is base 2, using only the digits 0 and 1. Each binary digit represents a power of 2, starting from the rightmost digit (which represents 2^0).
Step-by-Step Conversion of 127 to Binary
1. Identify the Largest Power of 2
The largest power of 2 less than or equal to 127 is 2^6, which is 64.
2. Subtract and Find Remaining Value
- 127 - 64 = 63
- The next largest power of 2 less than or equal to 63 is 2^5 (32).
- 63 - 32 = 31
- Next, 2^4 (16) gives 31 - 16 = 15.
- Next, 2^3 (8) gives 15 - 8 = 7.
- Next, 2^2 (4) gives 7 - 4 = 3.
- Next, 2^1 (2) gives 3 - 2 = 1.
- Finally, 2^0 (1) gives 1 - 1 = 0.
3. Write the Binary Representation
Since we used powers of 2 from 2^0 to 2^6, we can represent 127 in binary as:
- 2^6 (1), 2^5 (1), 2^4 (1), 2^3 (1), 2^2 (1), 2^1 (1), 2^0 (1) → 1111111
Final Answer Evaluation
Among the options provided:
- a) 1100111: This is 103 in decimal.
- b) 1111111: This is 127 in decimal (Correct Answer).
- c) 1111011: This is 123 in decimal.
- d) 111111: This is 63 in decimal.
Thus, option 'b' (1111111) is the accurate binary representation of the decimal number 127.
To convert a decimal number into binary, we need to understand the binary number system, which is base 2, using only the digits 0 and 1. Each binary digit represents a power of 2, starting from the rightmost digit (which represents 2^0).
Step-by-Step Conversion of 127 to Binary
1. Identify the Largest Power of 2
The largest power of 2 less than or equal to 127 is 2^6, which is 64.
2. Subtract and Find Remaining Value
- 127 - 64 = 63
- The next largest power of 2 less than or equal to 63 is 2^5 (32).
- 63 - 32 = 31
- Next, 2^4 (16) gives 31 - 16 = 15.
- Next, 2^3 (8) gives 15 - 8 = 7.
- Next, 2^2 (4) gives 7 - 4 = 3.
- Next, 2^1 (2) gives 3 - 2 = 1.
- Finally, 2^0 (1) gives 1 - 1 = 0.
3. Write the Binary Representation
Since we used powers of 2 from 2^0 to 2^6, we can represent 127 in binary as:
- 2^6 (1), 2^5 (1), 2^4 (1), 2^3 (1), 2^2 (1), 2^1 (1), 2^0 (1) → 1111111
Final Answer Evaluation
Among the options provided:
- a) 1100111: This is 103 in decimal.
- b) 1111111: This is 127 in decimal (Correct Answer).
- c) 1111011: This is 123 in decimal.
- d) 111111: This is 63 in decimal.
Thus, option 'b' (1111111) is the accurate binary representation of the decimal number 127.
On addition of 28 and 18 using 2’s complement, we get ____________- a)00101110
- b)0101110
- c)00101111
- d)1001111
Correct answer is option 'B'. Can you explain this answer?
On addition of 28 and 18 using 2’s complement, we get ____________
a)
00101110
b)
0101110
c)
00101111
d)
1001111
|
|
Harshad Singh answered |
To add 28 and 18 using base 2 (binary), we can convert the numbers to their binary representations and then perform the addition.
28 in binary is 11100.
18 in binary is 10010.
Now let's add them:
11100
+10010
_______
101010
Therefore, 28 + 18 in base 2 is equal to 101010.
28 in binary is 11100.
18 in binary is 10010.
Now let's add them:
11100
+10010
_______
101010
Therefore, 28 + 18 in base 2 is equal to 101010.
The excess-3 code for 597 is given by __________- a)100011001010
- b)100010100111
- c)010110010111
- d)010110101101
Correct answer is option 'A'. Can you explain this answer?
The excess-3 code for 597 is given by __________
a)
100011001010
b)
100010100111
c)
010110010111
d)
010110101101
|
|
Pooja Patel answered |
The addition of ‘3’ to each digit yields the three new digits ‘8’, ’12’ and ’10’. Hence, the corresponding four-bit binary equivalents are 100011001010, in accordance to 8421 format.
The 2’s complement of 1010101 is ______.- a)0101010
- b)1110011
- c)0101011
- d)1101010
Correct answer is option 'C'. Can you explain this answer?
The 2’s complement of 1010101 is ______.
a)
0101010
b)
1110011
c)
0101011
d)
1101010
|
|
Pooja Patel answered |
Tips and Tricks:
Steps to writing 2’s complement to any binary number:
- Start from right to left and search for the first ‘1’
- Write down the bits until that first ‘1’ as it is.
- Write down the remaining left bits with their respective complement.
2’s complement of 11001011 is ____________- a)01010111
- b)11010100
- c)00110101
- d)11100010
Correct answer is option 'C'. Can you explain this answer?
2’s complement of 11001011 is ____________
a)
01010111
b)
11010100
c)
00110101
d)
11100010
|
|
Prerna Tiwari answered |
2's complement of 11001011
To find the 2's complement of a binary number, we have to first find the 1's complement (flipping all the bits) and then add 1 to the result.
- 1's complement of 11001011
- The 1's complement of 11001011 is obtained by flipping all the bits: 00110100
- Adding 1 to the 1's complement
- To get the 2's complement, we add 1 to the 1's complement:
00110100
+ 00000001
00110101
Therefore, the 2's complement of 11001011 is 00110101, which corresponds to option C.
To find the 2's complement of a binary number, we have to first find the 1's complement (flipping all the bits) and then add 1 to the result.
- 1's complement of 11001011
- The 1's complement of 11001011 is obtained by flipping all the bits: 00110100
- Adding 1 to the 1's complement
- To get the 2's complement, we add 1 to the 1's complement:
00110100
+ 00000001
00110101
Therefore, the 2's complement of 11001011 is 00110101, which corresponds to option C.
Which of the following statement is NOT correct?- a)Hexadecimal number uses sixteen distinct counting digits 0 through 9 and A through F
- b)The 1’s complement of a binary number is obtained by changing its each 0 into a 1
- c)Octal number has a base of 7
- d)Excess-3 Code is an unweighted code
Correct answer is option 'C'. Can you explain this answer?
Which of the following statement is NOT correct?
a)
Hexadecimal number uses sixteen distinct counting digits 0 through 9 and A through F
b)
The 1’s complement of a binary number is obtained by changing its each 0 into a 1
c)
Octal number has a base of 7
d)
Excess-3 Code is an unweighted code
|
|
Pooja Patel answered |
Hexadecimal Number System:
- It has a base of 16. Hence, it uses sixteen distinct counting digits 0 through 9 and A through F
- Place value (or weight) for each digit is in ascending powers of 16 for integers and descending powers of 16 for fractions.
- The chief use of this system is in connection with byte-organized machines.
- It is used for specifying addresses of different binary numbers stored in computer memory.
Complement of a Number: In digital work, two types of complements of a binary number are used for complemental sub-traction:
1’s complement:
- The 1’s complement of a binary number is obtained by changing each 0 into a 1 and each 1 into a 0.
- It is also called radix-minus-one complement.
- For example, 1’s complement of 1002 is 0112, and 0112 is 00012.
2’s complement:
- The 2’s complement of a binary number is obtained by adding 1 to its 1’s complement.
- 2’s complement = 1’s complement + 1
- It is also known as a true complement.
Octal Number System:
- It has a base of 8 which means that it has eight distinct counting digits: 0, 1, 2, 3, 4, 5, 6, and 7
- These digits 0 through 7, have precisely the same physical meaning as in the decimal system.
- For counting beyond 7, 2-digit combinations are formed taking the second digit followed by the first, then the second followed by the second, and so on.
- Hence, after 7, the next octal number is 10 (second digit followed by first), then 11 (second digit followed by second), and so on.
Excess-3 Code:
- It is an unweighted code and is a modified form of BCD.
- It is widely used to represent numerical data in digital equipment.
- It is abbreviated as XS-3. As its name implies, each coded number in XS-3 is three larger than in the BCD code.
Convert BCD 0001 0010 0110 to binary- a)1111110
- b)1111100
- c)1111000
- d)1111111
Correct answer is option 'A'. Can you explain this answer?
Convert BCD 0001 0010 0110 to binary
a)
1111110
b)
1111100
c)
1111000
d)
1111111
|
|
Naveen Mukherjee answered |
Conversion of BCD to Binary
To convert BCD (Binary-Coded Decimal) to binary, we need to understand the BCD representation and the corresponding binary values.
BCD Representation:
BCD is a binary encoding of decimal numbers, where each decimal digit is represented by a 4-bit binary code. The BCD representation of decimal digits from 0 to 9 is as follows:
Decimal | BCD
--------|-----
0 | 0000
1 | 0001
2 | 0010
3 | 0011
4 | 0100
5 | 0101
6 | 0110
7 | 0111
8 | 1000
9 | 1001
Given BCD:
BCD 0001 0010 0110
Conversion Process:
To convert BCD to binary, we need to convert each BCD digit to its corresponding binary value and concatenate them.
Step 1:
Convert the first BCD digit (0001) to binary. Looking at the BCD table, we find that 0001 corresponds to the binary value 0001.
Step 2:
Convert the second BCD digit (0010) to binary. According to the BCD table, 0010 corresponds to the binary value 0010.
Step 3:
Convert the third BCD digit (0110) to binary. Referring to the BCD table, 0110 corresponds to the binary value 0110.
Concatenation:
Concatenate the binary values obtained from each BCD digit.
Binary value after concatenation: 0001 0010 0110
Therefore, the binary representation of the given BCD (0001 0010 0110) is 0001 0010 0110.
Conclusion:
The correct answer is option 'A' (1111110).
To convert BCD (Binary-Coded Decimal) to binary, we need to understand the BCD representation and the corresponding binary values.
BCD Representation:
BCD is a binary encoding of decimal numbers, where each decimal digit is represented by a 4-bit binary code. The BCD representation of decimal digits from 0 to 9 is as follows:
Decimal | BCD
--------|-----
0 | 0000
1 | 0001
2 | 0010
3 | 0011
4 | 0100
5 | 0101
6 | 0110
7 | 0111
8 | 1000
9 | 1001
Given BCD:
BCD 0001 0010 0110
Conversion Process:
To convert BCD to binary, we need to convert each BCD digit to its corresponding binary value and concatenate them.
Step 1:
Convert the first BCD digit (0001) to binary. Looking at the BCD table, we find that 0001 corresponds to the binary value 0001.
Step 2:
Convert the second BCD digit (0010) to binary. According to the BCD table, 0010 corresponds to the binary value 0010.
Step 3:
Convert the third BCD digit (0110) to binary. Referring to the BCD table, 0110 corresponds to the binary value 0110.
Concatenation:
Concatenate the binary values obtained from each BCD digit.
Binary value after concatenation: 0001 0010 0110
Therefore, the binary representation of the given BCD (0001 0010 0110) is 0001 0010 0110.
Conclusion:
The correct answer is option 'A' (1111110).
Chapter doubts & questions for Number System & Representation - Digital Electronics 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Number System & Representation - Digital Electronics in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Digital Electronics
115 videos|71 docs|58 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup










