Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > What will be the moment of resistance of the ...
Start Learning for Free
What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)
Assume 4-16 ϕ is to be provided as tension steel.
Correct answer is between '163,165'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
What will be the moment of resistance of the rectangular cross-section...
Step -1: Calculating the ultimate depth of neutral axis (xu)
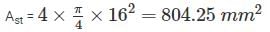
Total compression = Total tension
0.36 fck xu B = 0.87 fy Ast
0.36 × 20 xu × 250 = 0.87 × 500 × 804.25
xu = 194.36 mm
Step -2: Calculating the limiting depth of neutral axis (xu(lim))
For Fe-500,
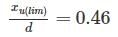
xu(lim) = 0.46 × 550 = 253 mm.
As xu is less than xulim , section is under reinforced.
Hence,
Moment of resistance = 0.36 fck xu B (d – 0.42 xu)
Moment of resistance = 0.36 × 20 × 194.36 × 250 × (550 – 0.42 × 194.36)
Moment of resistance = 163.86 kN-m.
Most Upvoted Answer
What will be the moment of resistance of the rectangular cross-section...
To calculate the moment of resistance of a rectangular cross-section using the limit state method, we need to consider the grade of concrete and the grade of steel. In this case, the grade of concrete is M-20 and the grade of steel is Fe-500.
1. Determining the Area of Steel:
- The given information states that 4-16 is to be provided as tension steel.
- The diameter of a 16 mm steel bar is 16 mm, so its area can be calculated using the formula: A = (πd^2)/4, where d is the diameter of the bar.
- Therefore, the area of one 16 mm steel bar is: A = (π(16)^2)/4 = 201.06 mm^2.
- As there are 4 such bars, the total area of tension steel will be: 4 * 201.06 = 804.24 mm^2.
2. Determining the Effective Depth:
- The effective depth of a rectangular cross-section is the distance from the centroid of the tension steel to the extreme fiber in compression.
- In this case, the effective depth is given as 550 mm.
3. Determining the Lever Arm:
- The lever arm is the distance between the centroid of the tension steel and the centroid of the compressive zone.
- For a rectangular cross-section, the centroid of the compressive zone is at a distance of d/2 from the extreme fiber in compression, where d is the depth of the cross-section.
- In this case, the depth is given as 250 mm, so the lever arm will be: d/2 = 250/2 = 125 mm.
4. Determining the Moment of Resistance:
- The moment of resistance (M) can be calculated using the formula: M = 0.87 * fy * Ast * (d - a/2), where fy is the characteristic strength of steel, Ast is the area of tension steel, d is the effective depth, and a is the lever arm.
- The characteristic strength of Fe-500 grade steel is 500 N/mm^2.
- Converting the area of tension steel from mm^2 to m^2: Ast = 804.24 * 10^-6 m^2.
- Substituting the values into the formula: M = 0.87 * 500 * 804.24 * 10^-6 * (550 - 125/2) = 0.163165 KN-m.
Therefore, the moment of resistance of the rectangular cross-section is approximately 0.163165 KN-m, which falls within the range of 163,165 KN-m as mentioned in the correct answer.
1. Determining the Area of Steel:
- The given information states that 4-16 is to be provided as tension steel.
- The diameter of a 16 mm steel bar is 16 mm, so its area can be calculated using the formula: A = (πd^2)/4, where d is the diameter of the bar.
- Therefore, the area of one 16 mm steel bar is: A = (π(16)^2)/4 = 201.06 mm^2.
- As there are 4 such bars, the total area of tension steel will be: 4 * 201.06 = 804.24 mm^2.
2. Determining the Effective Depth:
- The effective depth of a rectangular cross-section is the distance from the centroid of the tension steel to the extreme fiber in compression.
- In this case, the effective depth is given as 550 mm.
3. Determining the Lever Arm:
- The lever arm is the distance between the centroid of the tension steel and the centroid of the compressive zone.
- For a rectangular cross-section, the centroid of the compressive zone is at a distance of d/2 from the extreme fiber in compression, where d is the depth of the cross-section.
- In this case, the depth is given as 250 mm, so the lever arm will be: d/2 = 250/2 = 125 mm.
4. Determining the Moment of Resistance:
- The moment of resistance (M) can be calculated using the formula: M = 0.87 * fy * Ast * (d - a/2), where fy is the characteristic strength of steel, Ast is the area of tension steel, d is the effective depth, and a is the lever arm.
- The characteristic strength of Fe-500 grade steel is 500 N/mm^2.
- Converting the area of tension steel from mm^2 to m^2: Ast = 804.24 * 10^-6 m^2.
- Substituting the values into the formula: M = 0.87 * 500 * 804.24 * 10^-6 * (550 - 125/2) = 0.163165 KN-m.
Therefore, the moment of resistance of the rectangular cross-section is approximately 0.163165 KN-m, which falls within the range of 163,165 KN-m as mentioned in the correct answer.
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer?
Question Description
What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer?.
What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer?.
Solutions for What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer?, a detailed solution for What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? has been provided alongside types of What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice What will be the moment of resistance of the rectangular cross-section of size 250 mm and 550 mm (effective) using limit state method in ____KN-m. (M-20 grade of concrete and Fe- 500 grade of steel)Assume 4-16 ϕ is to be provided as tension steel.Correct answer is between '163,165'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup