NEET Exam > NEET Questions > Light of intensity I is incident on perfectly...
Start Learning for Free
Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring?
Most Upvoted Answer
Light of intensity I is incident on perfectly reflecting plate of area...
Problem: Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space. If the photon strikes the plate symmetrically and initially the spring was at its natural length, find the maximum compression in the spring?
Solution:
Introduction: In this problem, we have to find the maximum compression in the spring when a photon strikes the perfectly reflecting plate kept in a gravity-free space. We will use the concept of the conservation of momentum and conservation of energy to solve this problem.
Assumptions: We will make the following assumptions to simplify the problem:
- The plate is perfectly reflecting, which means it reflects the photon without any loss.
- The photon strikes the plate symmetrically, which means it strikes at the center of the plate.
- The spring is ideal, which means it is massless and has no damping or friction.
- The spring is initially at its natural length, which means it is neither compressed nor stretched.
Conservation of Momentum: When the photon strikes the plate, it exerts a force on the plate. As a result, the plate starts moving in the opposite direction. According to the conservation of momentum, the momentum of the photon before the collision is equal to the momentum of the plate and the photon after the collision. Since the photon has negligible mass, we can write:
Momentum of photon before collision = Momentum of photon and plate after collision
p = p'
Where p is the momentum of the photon before the collision and p' is the momentum of the photon and plate after the collision.
Conservation of Energy: When the photon strikes the plate, it imparts some energy to the plate. This energy is converted into the potential energy of the spring when the plate compresses the spring. According to the conservation of energy, the energy of the photon before the collision is equal to the energy of the photon and plate after the collision. Since the photon has negligible mass, we can write:
Energy of photon before collision = Energy of photon and plate after collision
E = E'
Where E is the energy of the photon before the collision and E' is the energy of the photon and plate after the collision.
Calculation of Maximum Compression: We can use the above equations to calculate the maximum compression in the spring. Since the photon strikes the plate symmetrically, the momentum of the photon and plate after the collision is zero. Therefore, we can write:
p' = 0
Using this in the conservation of momentum equation, we get:
p = 0
Since the energy of the photon is proportional to its frequency, we can write:
E = hf
Where h is the Planck's constant and f is the frequency of the photon.
Using this in the conservation of energy equation, we get:
hf = 1/2 mv^2
Where m is the mass of the plate and v is its velocity after the collision.
We can now use the above equations to find the velocity of the plate after the collision. Once we know the velocity, we can calculate the kinetic energy of the plate and use it to find the maximum compression in the spring using the formula:
1/2 kx^2 = 1/2 mv^2
Where k is the spring constant and x is the maximum compression in the spring.
Conclusion: In this problem,
Solution:
Introduction: In this problem, we have to find the maximum compression in the spring when a photon strikes the perfectly reflecting plate kept in a gravity-free space. We will use the concept of the conservation of momentum and conservation of energy to solve this problem.
Assumptions: We will make the following assumptions to simplify the problem:
- The plate is perfectly reflecting, which means it reflects the photon without any loss.
- The photon strikes the plate symmetrically, which means it strikes at the center of the plate.
- The spring is ideal, which means it is massless and has no damping or friction.
- The spring is initially at its natural length, which means it is neither compressed nor stretched.
Conservation of Momentum: When the photon strikes the plate, it exerts a force on the plate. As a result, the plate starts moving in the opposite direction. According to the conservation of momentum, the momentum of the photon before the collision is equal to the momentum of the plate and the photon after the collision. Since the photon has negligible mass, we can write:
Momentum of photon before collision = Momentum of photon and plate after collision
p = p'
Where p is the momentum of the photon before the collision and p' is the momentum of the photon and plate after the collision.
Conservation of Energy: When the photon strikes the plate, it imparts some energy to the plate. This energy is converted into the potential energy of the spring when the plate compresses the spring. According to the conservation of energy, the energy of the photon before the collision is equal to the energy of the photon and plate after the collision. Since the photon has negligible mass, we can write:
Energy of photon before collision = Energy of photon and plate after collision
E = E'
Where E is the energy of the photon before the collision and E' is the energy of the photon and plate after the collision.
Calculation of Maximum Compression: We can use the above equations to calculate the maximum compression in the spring. Since the photon strikes the plate symmetrically, the momentum of the photon and plate after the collision is zero. Therefore, we can write:
p' = 0
Using this in the conservation of momentum equation, we get:
p = 0
Since the energy of the photon is proportional to its frequency, we can write:
E = hf
Where h is the Planck's constant and f is the frequency of the photon.
Using this in the conservation of energy equation, we get:
hf = 1/2 mv^2
Where m is the mass of the plate and v is its velocity after the collision.
We can now use the above equations to find the velocity of the plate after the collision. Once we know the velocity, we can calculate the kinetic energy of the plate and use it to find the maximum compression in the spring using the formula:
1/2 kx^2 = 1/2 mv^2
Where k is the spring constant and x is the maximum compression in the spring.
Conclusion: In this problem,
Community Answer
Light of intensity I is incident on perfectly reflecting plate of area...
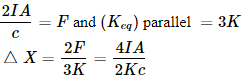

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring?
Question Description
Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring?.
Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring?.
Solutions for Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? defined & explained in the simplest way possible. Besides giving the explanation of
Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring?, a detailed solution for Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? has been provided alongside types of Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? theory, EduRev gives you an
ample number of questions to practice Light of intensity I is incident on perfectly reflecting plate of area A kept in a gravity free space .If the photon strikes the plate symmetrically and initially the spring was it's natural length, find the maximum compression in the spring? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























