GMAT Exam > GMAT Questions > Triplets Adam, Bruce, and Charlie enter a tri...
Start Learning for Free
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?
- a)3/14
- b)19/84
- c)11/42
- d)15/28
- e)3/4
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 co...
For probability, we always want to find the number of ways the requested event could happen and divide it by the total number of ways that any event could happen.
For this complicated problem, it is easiest to use combinatorics to find our two values. First, we find the total number of outcomes for the triathlon. There are 9 competitors; three will win medals and six will not. We can use the Combinatorics Grid, a counting method that allows us to determine the number of combinations without writing out every possible combination.

Out of our 9 total places, the first three, A, B, and C, win medals, so we label these with a "Y." The final six places (D, E, F, G, H, and I) do not win medals, so we label these with an "N." We translate this into math: 9! / 3!6! = 84. So our total possible number of combinations is 84. (Remember that ! means factorial; for example, 6! = 6 × 5 × 4 × 3 × 2 × 1.)
Note that although the problem seemed to make a point of differentiating the first, second, and third places, our question asks only whether the brothers will medal, not which place they will win. This is why we don't need to worry about labeling first, second, and third place distinctly.
Now, we need to determine the number of instances when at least two brothers win a medal. Practically speaking, this means we want to add the number of instances two brothers win to the number of instances three brothers win.
Let's start with all three brothers winning medals, where B represents a brother.

Since all the brothers win medals, we can ignore the part of the counting grid that includes those who don't win medals. We have 3! / 3! = 1. That is, there is only one instance when all three brothers win medals.
Next, let's calculate the instances when exactly two brothers win medals.
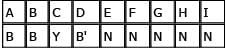
Since brothers both win and don't win medals in this scenario, we need to consider both sides of the grid (i.e. the ABC side and the DEFGHI side). First, for the three who win medals, we have 3! / 2! = 3. For the six who don't win medals, we have 6! / 5! = 6. We multiply these two numbers to get our total number: 3 × 6 = 18.
Another way to consider the instances of at least two brothers medaling would be to think of simple combinations with restrictions. If you are choosing 3 people out of 9 to be winners, how many different ways are there to chose a specific set of 3 from the 9 (i.e. all the brothers)? Just one. Therefore, there is only one scenario of all three brothers medaling.
If you are choosing 3 people out of 9 to be winners, if 2 specific people of the 9 have to be a member of the winning group, how many possible groups are there? It is best to think of this as a problem of choosing 1 out of 7 (2 must be chosen). Choosing 1 out of 7 can be represented as 7! / 1!6! = 7. However, if 1 of the remaining 7 can not be a member of this group (in this case the 3rd brother) there are actually only 6 such scenarios. Since there are 3 different sets of exactly two brothers (B1B2, B1B3, B2B3), we would have to multiply this 6 by 3 to get 18 scenarios of only two brothers medaling. The brothers win at least two medals in 18 + 1 = 19 circumstances. Our total number of circumstances is 84, so our probability is 19 / 84.
For this complicated problem, it is easiest to use combinatorics to find our two values. First, we find the total number of outcomes for the triathlon. There are 9 competitors; three will win medals and six will not. We can use the Combinatorics Grid, a counting method that allows us to determine the number of combinations without writing out every possible combination.

Out of our 9 total places, the first three, A, B, and C, win medals, so we label these with a "Y." The final six places (D, E, F, G, H, and I) do not win medals, so we label these with an "N." We translate this into math: 9! / 3!6! = 84. So our total possible number of combinations is 84. (Remember that ! means factorial; for example, 6! = 6 × 5 × 4 × 3 × 2 × 1.)
Note that although the problem seemed to make a point of differentiating the first, second, and third places, our question asks only whether the brothers will medal, not which place they will win. This is why we don't need to worry about labeling first, second, and third place distinctly.
Now, we need to determine the number of instances when at least two brothers win a medal. Practically speaking, this means we want to add the number of instances two brothers win to the number of instances three brothers win.
Let's start with all three brothers winning medals, where B represents a brother.

Since all the brothers win medals, we can ignore the part of the counting grid that includes those who don't win medals. We have 3! / 3! = 1. That is, there is only one instance when all three brothers win medals.
Next, let's calculate the instances when exactly two brothers win medals.

Since brothers both win and don't win medals in this scenario, we need to consider both sides of the grid (i.e. the ABC side and the DEFGHI side). First, for the three who win medals, we have 3! / 2! = 3. For the six who don't win medals, we have 6! / 5! = 6. We multiply these two numbers to get our total number: 3 × 6 = 18.
Another way to consider the instances of at least two brothers medaling would be to think of simple combinations with restrictions. If you are choosing 3 people out of 9 to be winners, how many different ways are there to chose a specific set of 3 from the 9 (i.e. all the brothers)? Just one. Therefore, there is only one scenario of all three brothers medaling.
If you are choosing 3 people out of 9 to be winners, if 2 specific people of the 9 have to be a member of the winning group, how many possible groups are there? It is best to think of this as a problem of choosing 1 out of 7 (2 must be chosen). Choosing 1 out of 7 can be represented as 7! / 1!6! = 7. However, if 1 of the remaining 7 can not be a member of this group (in this case the 3rd brother) there are actually only 6 such scenarios. Since there are 3 different sets of exactly two brothers (B1B2, B1B3, B2B3), we would have to multiply this 6 by 3 to get 18 scenarios of only two brothers medaling. The brothers win at least two medals in 18 + 1 = 19 circumstances. Our total number of circumstances is 84, so our probability is 19 / 84.
Most Upvoted Answer
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 co...
To solve this problem, we need to determine the probability that at least two of the triplets (Adam, Bruce, and Charlie) will win a medal in a triathlon with 9 competitors.
Total Possible Outcomes
-----------------------
The total number of possible outcomes is the number of ways to award the medals to any three of the 9 competitors. This can be calculated using combinations notation: C(9, 3) = 84.
Number of Outcomes with Only One Triplet Winning
------------------------------------------------
If only one triplet wins a medal, we need to determine which triplet wins and which medal they receive. There are 3 options for the winning triplet and 3 options for the medal they receive.
Therefore, the number of outcomes with only one triplet winning is: 3 * 3 = 9.
Number of Outcomes with No Triplets Winning
------------------------------------------
If no triplets win a medal, we need to determine which three competitors out of the remaining 6 win the medals. This can be calculated using combinations notation: C(6, 3) = 20.
Number of Outcomes with Two Triplets Winning
--------------------------------------------
If two triplets win a medal, we need to determine which two triplets win and which medals they receive. There are 3 options for the first winning triplet, 2 options for the second winning triplet, and 3 options for the medals they receive.
Therefore, the number of outcomes with two triplets winning is: 3 * 2 * 3 = 18.
Number of Outcomes with Three Triplets Winning
----------------------------------------------
If all three triplets win a medal, there is only one way this can happen.
Probability Calculation
-----------------------
To calculate the probability that at least two of the triplets will win a medal, we need to consider the number of favorable outcomes (outcomes with at least two triplets winning) divided by the total possible outcomes.
Number of Favorable Outcomes = Number of Outcomes with Only One Triplet Winning + Number of Outcomes with No Triplets Winning + Number of Outcomes with Two Triplets Winning + Number of Outcomes with Three Triplets Winning
= 9 + 20 + 18 + 1
= 48
Probability = Number of Favorable Outcomes / Total Possible Outcomes
= 48 / 84
= 19/84
Therefore, the probability that at least two of the triplets will win a medal is 19/84, which corresponds to option B.
Total Possible Outcomes
-----------------------
The total number of possible outcomes is the number of ways to award the medals to any three of the 9 competitors. This can be calculated using combinations notation: C(9, 3) = 84.
Number of Outcomes with Only One Triplet Winning
------------------------------------------------
If only one triplet wins a medal, we need to determine which triplet wins and which medal they receive. There are 3 options for the winning triplet and 3 options for the medal they receive.
Therefore, the number of outcomes with only one triplet winning is: 3 * 3 = 9.
Number of Outcomes with No Triplets Winning
------------------------------------------
If no triplets win a medal, we need to determine which three competitors out of the remaining 6 win the medals. This can be calculated using combinations notation: C(6, 3) = 20.
Number of Outcomes with Two Triplets Winning
--------------------------------------------
If two triplets win a medal, we need to determine which two triplets win and which medals they receive. There are 3 options for the first winning triplet, 2 options for the second winning triplet, and 3 options for the medals they receive.
Therefore, the number of outcomes with two triplets winning is: 3 * 2 * 3 = 18.
Number of Outcomes with Three Triplets Winning
----------------------------------------------
If all three triplets win a medal, there is only one way this can happen.
Probability Calculation
-----------------------
To calculate the probability that at least two of the triplets will win a medal, we need to consider the number of favorable outcomes (outcomes with at least two triplets winning) divided by the total possible outcomes.
Number of Favorable Outcomes = Number of Outcomes with Only One Triplet Winning + Number of Outcomes with No Triplets Winning + Number of Outcomes with Two Triplets Winning + Number of Outcomes with Three Triplets Winning
= 9 + 20 + 18 + 1
= 48
Probability = Number of Favorable Outcomes / Total Possible Outcomes
= 48 / 84
= 19/84
Therefore, the probability that at least two of the triplets will win a medal is 19/84, which corresponds to option B.

|
Explore Courses for GMAT exam
|

|
Similar GMAT Doubts
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer?
Question Description
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer?.
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer?.
Solutions for Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?a)3/14b)19/84c)11/42d)15/28e)3/4Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice GMAT tests.

|
Explore Courses for GMAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























