GMAT Exam > GMAT Questions > There are y different travelers who each have...
Start Learning for Free
There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination?
- a)1/n!
- b)n/n!
- c)1/ny
- d)1/ny -1
- e)n/yn
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
There are y different travelers who each have a choice of vacationing ...
The easiest way to attack this problem is to pick some real, easy numbers as values for y and n . Let's assume there are 3 travelers (A, B, C) and 2 different destinations (1, 2). We can chart out the possibilities as follows:
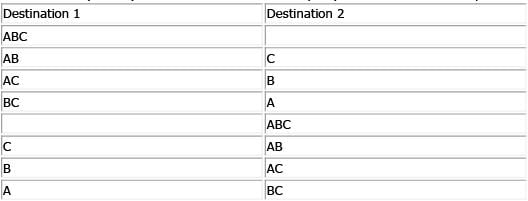
Thus there are 8 possibilities and in 2 of them all travelers end up at the same destination. Thus the probability is 2/8 or 1/4. By plugging in y = 3 and n = 2 into each answer choice, we see that only answer choice D yields a probability of 1/4. Alternatively, consider that each traveler can end up at any one of n destinations. Thus, for each traveler there are n possibilities. Therefore, for y travelers, there are possible outcomes. Additionally, the "winning" outcomes are those where all travelers end up at the same destination. Since there are n destinations there are n "winning" outcomes.
Thus, the probability =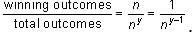

Thus there are 8 possibilities and in 2 of them all travelers end up at the same destination. Thus the probability is 2/8 or 1/4. By plugging in y = 3 and n = 2 into each answer choice, we see that only answer choice D yields a probability of 1/4. Alternatively, consider that each traveler can end up at any one of n destinations. Thus, for each traveler there are n possibilities. Therefore, for y travelers, there are possible outcomes. Additionally, the "winning" outcomes are those where all travelers end up at the same destination. Since there are n destinations there are n "winning" outcomes.
Thus, the probability =
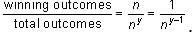
Most Upvoted Answer
There are y different travelers who each have a choice of vacationing ...
Probability of all travelers vacationing at the same destination
To solve this problem, let's break it down step by step.
1. Total number of outcomes:
- Each traveler has a choice of n different destinations, so the total number of outcomes for one traveler is n.
- Since there are y travelers, the total number of outcomes for all y travelers is n^y.
2. Number of favorable outcomes:
- In order for all y travelers to end up vacationing at the same destination, there is only 1 favorable outcome.
- This means that all y travelers need to choose the same destination out of the n available destinations.
3. Probability calculation:
- Probability is defined as the number of favorable outcomes divided by the total number of outcomes.
- Therefore, the probability that all y travelers will end up vacationing at the same destination is 1 favorable outcome divided by n^y total outcomes.
- Mathematically, this can be represented as: P = 1/n^y
4. Simplification:
- To simplify the expression further, we can rewrite n^y as (n^n)^(y/n), since y/n is the number of groups of size n that can be formed from y travelers.
- Using the property (a^b)^c = a^(b*c), we can simplify it as n^(y/n * n) = n^y.
- Therefore, the probability can be further simplified as: P = 1/n^y
- This matches option 'D' which states that the probability is 1/ny.
- Hence, the correct answer is option 'D' - 1/ny.
To solve this problem, let's break it down step by step.
1. Total number of outcomes:
- Each traveler has a choice of n different destinations, so the total number of outcomes for one traveler is n.
- Since there are y travelers, the total number of outcomes for all y travelers is n^y.
2. Number of favorable outcomes:
- In order for all y travelers to end up vacationing at the same destination, there is only 1 favorable outcome.
- This means that all y travelers need to choose the same destination out of the n available destinations.
3. Probability calculation:
- Probability is defined as the number of favorable outcomes divided by the total number of outcomes.
- Therefore, the probability that all y travelers will end up vacationing at the same destination is 1 favorable outcome divided by n^y total outcomes.
- Mathematically, this can be represented as: P = 1/n^y
4. Simplification:
- To simplify the expression further, we can rewrite n^y as (n^n)^(y/n), since y/n is the number of groups of size n that can be formed from y travelers.
- Using the property (a^b)^c = a^(b*c), we can simplify it as n^(y/n * n) = n^y.
- Therefore, the probability can be further simplified as: P = 1/n^y
- This matches option 'D' which states that the probability is 1/ny.
- Hence, the correct answer is option 'D' - 1/ny.

|
Explore Courses for GMAT exam
|

|
Question Description
There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer?.
There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer?.
Solutions for There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? a)1/n!b)n/n!c)1/nyd)1/ny -1e)n/ynCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice GMAT tests.

|
Explore Courses for GMAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















