GMAT Exam > GMAT Questions > Kate and Danny each have $10. Together, they ...
Start Learning for Free
Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?
- a)5/16
- b)1/2
- c)12/30
- d)15/32
- e)3/8
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
Kate and Danny each have $10. Together, they flip a fair coin 5 times....
Let's consider the different scenarios: If Kate wins all five flips, she ends up with $15.
If Kate wins four flips, and Danny wins one flip, Kate is left with $13.
If Kate wins three flips, and Danny wins two flips, Kate is left with $11.
If Kate wins two flips, and Danny wins three flips, Kate is left with $9.
If Kate wins one flip, and Danny wins four flips, Kate is left with $7.
If Kate loses all five flips, she ends up with $5.
The question asks for the probability that Kate will end up with more than $10 but less than $15. In other words, we need to determine the probability that Kate is left with $11 or $13 (since there is no way Kate can end up with $12 or $14).
The probability that Kate ends up with $11 after the five flips:
Since there are 2 possible outcomes on each flip, and there are 5 flips, the total number of possible outcomes is 2*2*2*2*2=32. Thus, the five flips of the coin yield 32 different outcomes.
To determine the probability that Kate will end up with $11, we need to determine how many of these 32 outcomes include a combination of exactly three winning flips for Kate.
We can create a systematic list of combinations that include three wins for Kate and two wins for Danny: DKKKD, DKKDK, DKDKK, DDKKK, KDKKD, KDKDK, KDDKK, KKDKD, KKDDK, KKKDD = 10 ways.
Alternatively, we can consider each of the five flips as five spots. There are 5 potential spots for Kate's first win. There are 4 potential spots for Kate's second win (because one spot has already been taken by Kate's first win). There are 3 potential spots for Kate's third win. Thus, there are 5*4*3=60 ways for Kate's three victories to be ordered. However, since we are interested only in unique winning combinations, this number must be reduced due to overcounting. Consider the winning combination KKKDD: This one winning combination has actually been counted 6 times (this is 3! or three factorial) because there are 6 different orderings of this one combination: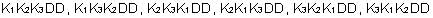
This overcounting by 6 is true for all of Kate's three-victory combinations. Therefore, there are only 60/6 =10, ways for Kate to have three wins and end up with $11 (as we had discovered earlier from our systematic list).
The probability that Kate ends up with $13 after the five flips: To determine the probability that Kate will end up with $13, we need to determine how many of the 32 total possible outcomes include a combination of exactly four winning flips for Kate.
Again, we can create a systematic list of combinations that include four wins for Kate and one win for Danny: KKKKD, KKKDK, KKDKK, KDKKK, DKKKK = 5 ways.
Alternatively, using the same reasoning as above, we can determine that there are 5*4*3*2 = 120 ays for Kate's four victories to be ordered. Then, reduce this by 4! (four factorial) or 24 due to overcounting. Thus, there are 120/24 = 5ways for Kate to have four wins and end up with $13 (the same answer we found using the systematic list).
The total probability that Kate ends up with either $11 or $13 after the five flips: There are 10 ways that Kate is left with $11. There are 5 ways that Kate is left with $13. Therefore, there are 15 ways that Kate is left with more than $10 but less than $15.
Since there are 32 possible outcomes, is 15/32.
If Kate wins four flips, and Danny wins one flip, Kate is left with $13.
If Kate wins three flips, and Danny wins two flips, Kate is left with $11.
If Kate wins two flips, and Danny wins three flips, Kate is left with $9.
If Kate wins one flip, and Danny wins four flips, Kate is left with $7.
If Kate loses all five flips, she ends up with $5.
The question asks for the probability that Kate will end up with more than $10 but less than $15. In other words, we need to determine the probability that Kate is left with $11 or $13 (since there is no way Kate can end up with $12 or $14).
The probability that Kate ends up with $11 after the five flips:
Since there are 2 possible outcomes on each flip, and there are 5 flips, the total number of possible outcomes is 2*2*2*2*2=32. Thus, the five flips of the coin yield 32 different outcomes.
To determine the probability that Kate will end up with $11, we need to determine how many of these 32 outcomes include a combination of exactly three winning flips for Kate.
We can create a systematic list of combinations that include three wins for Kate and two wins for Danny: DKKKD, DKKDK, DKDKK, DDKKK, KDKKD, KDKDK, KDDKK, KKDKD, KKDDK, KKKDD = 10 ways.
Alternatively, we can consider each of the five flips as five spots. There are 5 potential spots for Kate's first win. There are 4 potential spots for Kate's second win (because one spot has already been taken by Kate's first win). There are 3 potential spots for Kate's third win. Thus, there are 5*4*3=60 ways for Kate's three victories to be ordered. However, since we are interested only in unique winning combinations, this number must be reduced due to overcounting. Consider the winning combination KKKDD: This one winning combination has actually been counted 6 times (this is 3! or three factorial) because there are 6 different orderings of this one combination:
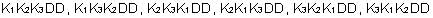
This overcounting by 6 is true for all of Kate's three-victory combinations. Therefore, there are only 60/6 =10, ways for Kate to have three wins and end up with $11 (as we had discovered earlier from our systematic list).
The probability that Kate ends up with $13 after the five flips: To determine the probability that Kate will end up with $13, we need to determine how many of the 32 total possible outcomes include a combination of exactly four winning flips for Kate.
Again, we can create a systematic list of combinations that include four wins for Kate and one win for Danny: KKKKD, KKKDK, KKDKK, KDKKK, DKKKK = 5 ways.
Alternatively, using the same reasoning as above, we can determine that there are 5*4*3*2 = 120 ays for Kate's four victories to be ordered. Then, reduce this by 4! (four factorial) or 24 due to overcounting. Thus, there are 120/24 = 5ways for Kate to have four wins and end up with $13 (the same answer we found using the systematic list).
The total probability that Kate ends up with either $11 or $13 after the five flips: There are 10 ways that Kate is left with $11. There are 5 ways that Kate is left with $13. Therefore, there are 15 ways that Kate is left with more than $10 but less than $15.
Since there are 32 possible outcomes, is 15/32.
Most Upvoted Answer
Kate and Danny each have $10. Together, they flip a fair coin 5 times....
Problem Analysis:
We need to find the probability that Kate has more than $10 but less than $15 after 5 coin flips. Kate and Danny start with $10 each, so the minimum amount Kate can have is $10 and the maximum amount she can have is $15. Let's consider the various scenarios that can lead to Kate having more than $10 but less than $15.
Possible Scenarios:
1. Kate wins all 5 coin flips: In this scenario, Kate will have $15 and Danny will have $5.
2. Kate wins 4 coin flips: In this scenario, Kate will have $14 and Danny will have $6.
3. Kate wins 3 coin flips: In this scenario, Kate will have $13 and Danny will have $7.
4. Kate wins 2 coin flips: In this scenario, Kate will have $12 and Danny will have $8.
5. Kate wins 1 coin flip: In this scenario, Kate will have $11 and Danny will have $9.
Calculating the Probability:
The probability of each scenario happening depends on the number of ways it can occur and the probability of each individual coin flip. Since the coin flips are fair, the probability of a head or a tail is 1/2.
1. Kate wins all 5 coin flips:
- Number of ways: 1
- Probability: (1/2)^5 = 1/32
2. Kate wins 4 coin flips:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
3. Kate wins 3 coin flips:
- Number of ways: 10 (Kate can win any 3 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
4. Kate wins 2 coin flips:
- Number of ways: 10 (Kate can win any 2 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
5. Kate wins 1 coin flip:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
Final Probability:
To find the probability that Kate has more than $10 but less than $15, we need to add up the probabilities of the scenarios 2, 3, 4, and 5:
Probability = (5/32) + (10/32) + (10/32) + (5/32) = 30/32 = 15/16
Therefore, the correct answer is option D) 15/32.
We need to find the probability that Kate has more than $10 but less than $15 after 5 coin flips. Kate and Danny start with $10 each, so the minimum amount Kate can have is $10 and the maximum amount she can have is $15. Let's consider the various scenarios that can lead to Kate having more than $10 but less than $15.
Possible Scenarios:
1. Kate wins all 5 coin flips: In this scenario, Kate will have $15 and Danny will have $5.
2. Kate wins 4 coin flips: In this scenario, Kate will have $14 and Danny will have $6.
3. Kate wins 3 coin flips: In this scenario, Kate will have $13 and Danny will have $7.
4. Kate wins 2 coin flips: In this scenario, Kate will have $12 and Danny will have $8.
5. Kate wins 1 coin flip: In this scenario, Kate will have $11 and Danny will have $9.
Calculating the Probability:
The probability of each scenario happening depends on the number of ways it can occur and the probability of each individual coin flip. Since the coin flips are fair, the probability of a head or a tail is 1/2.
1. Kate wins all 5 coin flips:
- Number of ways: 1
- Probability: (1/2)^5 = 1/32
2. Kate wins 4 coin flips:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
3. Kate wins 3 coin flips:
- Number of ways: 10 (Kate can win any 3 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
4. Kate wins 2 coin flips:
- Number of ways: 10 (Kate can win any 2 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
5. Kate wins 1 coin flip:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
Final Probability:
To find the probability that Kate has more than $10 but less than $15, we need to add up the probabilities of the scenarios 2, 3, 4, and 5:
Probability = (5/32) + (10/32) + (10/32) + (5/32) = 30/32 = 15/16
Therefore, the correct answer is option D) 15/32.
|
Explore Courses for GMAT exam
|
|
Similar GMAT Doubts
Top Courses for GMATView all
Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer?
Question Description
Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer?.
Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer?.
Solutions for Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?a)5/16b)1/2c)12/30d)15/32e)3/8Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice GMAT tests.
|
|
Explore Courses for GMAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup