GMAT Exam > GMAT Questions > It takes the high-speed train x hours to trav...
Start Learning for Free
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?
- a)
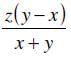
- b)
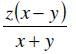
- c)
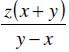
- d)
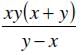
- e)

Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
It takes the high-speed train x hours to travel the z miles from Town ...
A question with variables in the answer choices (VIC) can be solved by picking values for the variables.
Let's pick the following values for x, y and z:

When picking values for a VIC question, it is best to pick numbers that are easy to work with (i.e., 12 is divisible by 4 and 6 here), but that don't have any extraneous relationships between them. For example x = 4, y = 3, z = 12 would be a less favorable set of numbers because xy would equal z in that case and there is no need for the product of the two times to equal the distance. Picking variables with extraneous relationships can lead to false positives when checking the answer choices.
Let's pick the following values for x, y and z:

When picking values for a VIC question, it is best to pick numbers that are easy to work with (i.e., 12 is divisible by 4 and 6 here), but that don't have any extraneous relationships between them. For example x = 4, y = 3, z = 12 would be a less favorable set of numbers because xy would equal z in that case and there is no need for the product of the two times to equal the distance. Picking variables with extraneous relationships can lead to false positives when checking the answer choices.
Now let's solve the question according to the values we selected.
If the high-speed train travels the 12 miles from A to B in 4 hours, it is traveling at 3 mph.
If the regular train travels the 12 miles from A to B in 6 hours, it is traveling at 2 mph.
If the high-speed train travels the 12 miles from A to B in 4 hours, it is traveling at 3 mph.
If the regular train travels the 12 miles from A to B in 6 hours, it is traveling at 2 mph.
To evaluate how far each train travels when they move toward each other starting at opposite ends, let's set up an RTD chart.
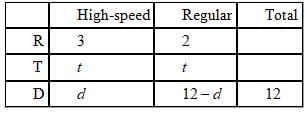
We can set-up two equations with two unknowns and solve
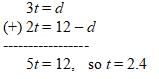

We can set-up two equations with two unknowns and solve
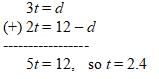
In the 2.4 hours it takes for the two trains to meet,
the high speed train will have traveled 3(2.4) = 7.2 miles,
and the regular train will have traveled 2(2.4) = 4.8 miles.
Therefore the high speed train will have traveled 7.2 – 4.8 = 2.4 miles farther than the regular train.
2.4 is our target number.
the high speed train will have traveled 3(2.4) = 7.2 miles,
and the regular train will have traveled 2(2.4) = 4.8 miles.
Therefore the high speed train will have traveled 7.2 – 4.8 = 2.4 miles farther than the regular train.
2.4 is our target number.
Let's see which of the five answer choices give us 2.4 when we plug in our values for x, y and z:
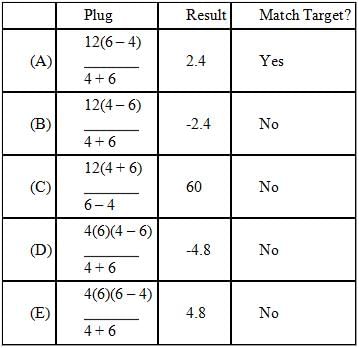

Only A matches the target.
This question can also be solved algebraically.
Since the trains traveled the z miles in x and y hours, their speeds can be represented as z/x and z/y respectively.
Since the trains traveled the z miles in x and y hours, their speeds can be represented as z/x and z/y respectively.
We can again use an RTD chart to evaluate how far each train travels when they move toward each other starting at opposite ends. Instead of using another variable d here, let's express the two distances in terms of their respective rates and times.
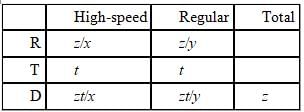

Since the two distances sum to the total when the two trains meet, we can set up the following equation:
zt/x + zt/y = z - divide both sides of the equation by z
t/x + t/y = 1 - multiply both sides of the equation by xy
ty + tx = xy - factor out a t on the left side
t(x + y) = xy - divide both sides by x + y
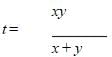
t/x + t/y = 1 - multiply both sides of the equation by xy
ty + tx = xy - factor out a t on the left side
t(x + y) = xy - divide both sides by x + y
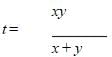
To find how much further the high-speed train went in this time:
(ratehigh × time) – (ratereg × time)
(ratehigh – ratereg) × time
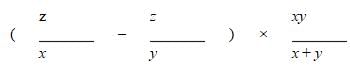
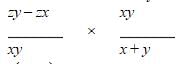
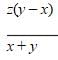
The correct answer is A.
(ratehigh × time) – (ratereg × time)
(ratehigh – ratereg) × time
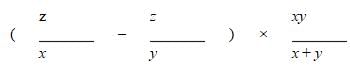
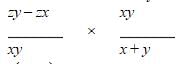
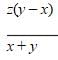
The correct answer is A.

|
Explore Courses for GMAT exam
|

|
Similar GMAT Doubts
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer?
Question Description
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? for GMAT 2024 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GMAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer?.
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? for GMAT 2024 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GMAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer?.
Solutions for It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer?, a detailed solution for It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?a)b)c)d)e)Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice GMAT tests.

|
Explore Courses for GMAT exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















