GMAT Exam > GMAT Questions > Guests at a recent party ate a total of fifte...
Start Learning for Free
Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor a
vegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, a
vegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?
(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate for
non-vegetarians.
(2) 30% of the guests were vegetarian non-students.
vegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, a
vegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?
(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate for
non-vegetarians.
(2) 30% of the guests were vegetarian non-students.
- a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.
- b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficient
- c)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficient
- d)EACH stetement ALONE is sufficient
- e)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Guests at a recent party ate a total of fifteen hamburgers. Each guest...
For this overlapping set problem, we want to set up a two-set table to test our possibilities. Our first set is vegetarians vs. non-vegetarians; our second set is students vs. non-students.
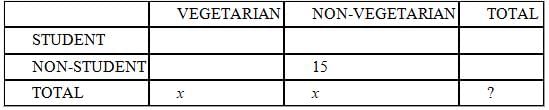
We are told that each non-vegetarian non-student ate exactly one of the 15 hamburgers, and that nobody else ate any of the 15 hamburgers. This means that there were exactly 15 people in the non-vegetarian non-student category. We are also told that the total number of vegetarians was equal to the total number of non-vegetarians; we represent this by putting the same variable in both boxes of the chart.
The question is asking us how many people attended the party; in other words, we are being asked for the number that belongs in the bottom-right box, where we have placed a question mark.
The second statement is easier than the first statement, so we'll start with statement (2).
(2) INSUFFICIENT: This statement gives us information only about the cell labeled "vegetarian non-student"; further it only tells us the number of these guests as a percentage of the total guests. The 30% figure does not allow us to calculate the actual number of any of the categories.
SUFFICIENT: This statement provides two pieces of information. First, the vegetarians attended at the rate, or in the ratio, of 2:3 students to non-students. We're also told that this 2:3 rate is half the rate for non-vegetarians. In order to double a rate, we double the first number; the rate for non-vegetarians is 4:3 We can represent the actual numbers of non-vegetarians as 4a and 3a and add this to the chart below. Since we know that there were 15 non-vegetarian non-students, we know the missing common multiple, a, is 15/3 = 5. Therefore, there were (4)(5) = 20 non-vegetarian students and 20 + 15 = 35 total non-vegetarians (see the chart below). Since the same number of vegetarians and non-vegetarians attended the party, there were also 35 vegetarians, for a total of 70 guests.
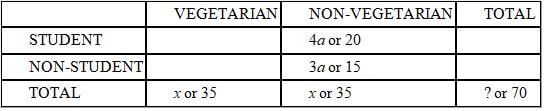
The correct answer is A
We are told that each non-vegetarian non-student ate exactly one of the 15 hamburgers, and that nobody else ate any of the 15 hamburgers. This means that there were exactly 15 people in the non-vegetarian non-student category. We are also told that the total number of vegetarians was equal to the total number of non-vegetarians; we represent this by putting the same variable in both boxes of the chart.
The question is asking us how many people attended the party; in other words, we are being asked for the number that belongs in the bottom-right box, where we have placed a question mark.
The second statement is easier than the first statement, so we'll start with statement (2).
(2) INSUFFICIENT: This statement gives us information only about the cell labeled "vegetarian non-student"; further it only tells us the number of these guests as a percentage of the total guests. The 30% figure does not allow us to calculate the actual number of any of the categories.
SUFFICIENT: This statement provides two pieces of information. First, the vegetarians attended at the rate, or in the ratio, of 2:3 students to non-students. We're also told that this 2:3 rate is half the rate for non-vegetarians. In order to double a rate, we double the first number; the rate for non-vegetarians is 4:3 We can represent the actual numbers of non-vegetarians as 4a and 3a and add this to the chart below. Since we know that there were 15 non-vegetarian non-students, we know the missing common multiple, a, is 15/3 = 5. Therefore, there were (4)(5) = 20 non-vegetarian students and 20 + 15 = 35 total non-vegetarians (see the chart below). Since the same number of vegetarians and non-vegetarians attended the party, there were also 35 vegetarians, for a total of 70 guests.
The correct answer is A
Most Upvoted Answer
Guests at a recent party ate a total of fifteen hamburgers. Each guest...
Given that half of the guests were vegetarians and that each guest who was neither a student nor a vegetarian ate exactly one hamburger, we need to determine the total number of guests at the party.
Statement 1: The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate for non-vegetarians.
This statement provides information about the ratio of vegetarian students to non-student vegetarians. However, it does not provide any information about the total number of vegetarians or non-vegetarians. Therefore, statement 1 alone is not sufficient to answer the question.
Statement 2: 30% of the guests were vegetarian non-students.
This statement provides information about the proportion of vegetarian non-students among the guests. However, it does not provide any information about the total number of vegetarians or non-vegetarians, or the total number of guests. Therefore, statement 2 alone is not sufficient to answer the question.
Statements 1 and 2 together:
Combining the information from both statements, we know that the vegetarians attended the party at a rate of 2 students to every 3 non-students, and that 30% of the guests were vegetarian non-students.
From statement 2, we can infer that the remaining 70% of the guests were either vegetarian students or non-vegetarian guests.
Let's assume there were a total of 100 guests:
- 30% of the guests (30 guests) were vegetarian non-students.
- The remaining 70% of the guests (70 guests) were either vegetarian students or non-vegetarian guests.
From statement 1, we know that the vegetarians attended at a rate of 2 students to every 3 non-students. If we assume that the ratio of vegetarian students to non-student vegetarians is 2:3, we can calculate the number of vegetarian students and non-student vegetarians as follows:
- Vegetarian students: (2/5) * 70 = 28 students
- Non-student vegetarians: (3/5) * 70 = 42 non-students
Adding up the number of vegetarian non-students, vegetarian students, and non-student vegetarians, we get:
30 + 28 + 42 = 100 guests
Therefore, both statements together are sufficient to determine the total number of guests at the party.
Hence, the correct answer is option A.
Statement 1: The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate for non-vegetarians.
This statement provides information about the ratio of vegetarian students to non-student vegetarians. However, it does not provide any information about the total number of vegetarians or non-vegetarians. Therefore, statement 1 alone is not sufficient to answer the question.
Statement 2: 30% of the guests were vegetarian non-students.
This statement provides information about the proportion of vegetarian non-students among the guests. However, it does not provide any information about the total number of vegetarians or non-vegetarians, or the total number of guests. Therefore, statement 2 alone is not sufficient to answer the question.
Statements 1 and 2 together:
Combining the information from both statements, we know that the vegetarians attended the party at a rate of 2 students to every 3 non-students, and that 30% of the guests were vegetarian non-students.
From statement 2, we can infer that the remaining 70% of the guests were either vegetarian students or non-vegetarian guests.
Let's assume there were a total of 100 guests:
- 30% of the guests (30 guests) were vegetarian non-students.
- The remaining 70% of the guests (70 guests) were either vegetarian students or non-vegetarian guests.
From statement 1, we know that the vegetarians attended at a rate of 2 students to every 3 non-students. If we assume that the ratio of vegetarian students to non-student vegetarians is 2:3, we can calculate the number of vegetarian students and non-student vegetarians as follows:
- Vegetarian students: (2/5) * 70 = 28 students
- Non-student vegetarians: (3/5) * 70 = 42 non-students
Adding up the number of vegetarian non-students, vegetarian students, and non-student vegetarians, we get:
30 + 28 + 42 = 100 guests
Therefore, both statements together are sufficient to determine the total number of guests at the party.
Hence, the correct answer is option A.
Attention GMAT Students!
To make sure you are not studying endlessly, EduRev has designed GMAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in GMAT.
|
Explore Courses for GMAT exam
|
|
Similar GMAT Doubts
Top Courses for GMATView all
Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer?
Question Description
Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? for GMAT 2024 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GMAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer?.
Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? for GMAT 2024 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GMAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer?.
Solutions for Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor avegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, avegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate fornon-vegetarians.(2) 30% of the guests were vegetarian non-students.a)Statement ( 1 ) ALONE is sufficient but statement ( 2 ) alone is not sufficient.b)Statemrnt ( 2 ) ALONE is sufficient but statement ( 1 ) is not sufficientc)Both Stement TOGETHER are sufficient, but Neither statement ALONE is sufficientd)EACH stetement ALONE is sufficiente)Statement ( 1 ) and ( 2 ) TOGETHER are NOT Sufficient.Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice GMAT tests.
|
|
Explore Courses for GMAT exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup