Physics Exam > Physics Questions > A bullet is fired horizontally in the north d...
Start Learning for Free
A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:
- a)0.36m/sec2
- b)0.036m/sec2
- c)0.24m/sec2
- d)7.2m/sec2
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A bullet is fired horizontally in the north direction with a velocity ...
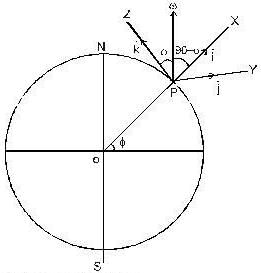
If X- axis is taken vertically, Z-axis towards north and Y-axis along east, then the velocity of the bulled is v = 500km/sec. and angular velocity w = w 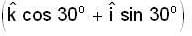 because the angular velocity vector w of the earth is directed parallel to its axis and is inclined at 300 to the horizontal
because the angular velocity vector w of the earth is directed parallel to its axis and is inclined at 300 to the horizontal
Here,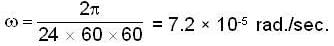
Hence Coriolis acceleration
= 2w x v
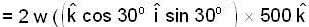
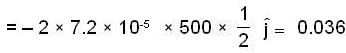 m/sec2 towards west.
m/sec2 towards west.
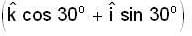 because the angular velocity vector w of the earth is directed parallel to its axis and is inclined at 300 to the horizontal
because the angular velocity vector w of the earth is directed parallel to its axis and is inclined at 300 to the horizontalHere,
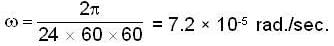

Hence Coriolis acceleration
= 2w x v
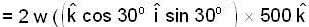
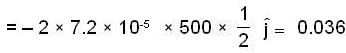 m/sec2 towards west.
m/sec2 towards west.Most Upvoted Answer
A bullet is fired horizontally in the north direction with a velocity ...
Coriolis effect and Coriolis acceleration:
The Coriolis effect is a phenomenon that occurs due to the rotation of the Earth. It causes moving objects to be deflected to the right in the northern hemisphere and to the left in the southern hemisphere. The Coriolis effect is responsible for the rotation of weather systems, such as cyclones and anticyclones.
Coriolis acceleration is the acceleration experienced by an object moving in a rotating reference frame, such as the Earth. It is perpendicular to the velocity vector of the object and is given by the equation:
a_c = -2v_0ωsin(φ)
where a_c is the Coriolis acceleration, v_0 is the velocity of the object, ω is the angular velocity of the Earth, and φ is the latitude.
Calculating the Coriolis acceleration:
Given:
Velocity of the bullet (v_0) = 500 m/s
Latitude (φ) = 300N
To calculate the Coriolis acceleration, we need to know the angular velocity of the Earth (ω). The angular velocity of the Earth can be calculated as the ratio of the Earth's rotational period to the circumference of the Earth:
ω = 2π/T
where T is the rotational period of the Earth.
The rotational period of the Earth is approximately 24 hours, which is equivalent to 86,400 seconds. The circumference of the Earth at the equator is approximately 40,075 km, which is equivalent to 40,075,000 meters.
Plugging in these values, we can calculate the angular velocity of the Earth:
ω = 2π/86,400 ≈ 7.27 × 10^(-5) rad/s
Now, we can calculate the Coriolis acceleration using the equation mentioned earlier:
a_c = -2v_0ωsin(φ)
a_c = -2(500)(7.27 × 10^(-5))sin(30°)
a_c ≈ -0.036 m/s^2
Since the Coriolis acceleration is perpendicular to the velocity vector, its direction is horizontal. Therefore, the horizontal component of the Coriolis acceleration is 0.036 m/s^2.
Hence, the correct answer is option 'B': 0.036 m/s^2.
The Coriolis effect is a phenomenon that occurs due to the rotation of the Earth. It causes moving objects to be deflected to the right in the northern hemisphere and to the left in the southern hemisphere. The Coriolis effect is responsible for the rotation of weather systems, such as cyclones and anticyclones.
Coriolis acceleration is the acceleration experienced by an object moving in a rotating reference frame, such as the Earth. It is perpendicular to the velocity vector of the object and is given by the equation:
a_c = -2v_0ωsin(φ)
where a_c is the Coriolis acceleration, v_0 is the velocity of the object, ω is the angular velocity of the Earth, and φ is the latitude.
Calculating the Coriolis acceleration:
Given:
Velocity of the bullet (v_0) = 500 m/s
Latitude (φ) = 300N
To calculate the Coriolis acceleration, we need to know the angular velocity of the Earth (ω). The angular velocity of the Earth can be calculated as the ratio of the Earth's rotational period to the circumference of the Earth:
ω = 2π/T
where T is the rotational period of the Earth.
The rotational period of the Earth is approximately 24 hours, which is equivalent to 86,400 seconds. The circumference of the Earth at the equator is approximately 40,075 km, which is equivalent to 40,075,000 meters.
Plugging in these values, we can calculate the angular velocity of the Earth:
ω = 2π/86,400 ≈ 7.27 × 10^(-5) rad/s
Now, we can calculate the Coriolis acceleration using the equation mentioned earlier:
a_c = -2v_0ωsin(φ)
a_c = -2(500)(7.27 × 10^(-5))sin(30°)
a_c ≈ -0.036 m/s^2
Since the Coriolis acceleration is perpendicular to the velocity vector, its direction is horizontal. Therefore, the horizontal component of the Coriolis acceleration is 0.036 m/s^2.
Hence, the correct answer is option 'B': 0.036 m/s^2.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer?
Question Description
A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer?.
A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer?.
Solutions for A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:a)0.36m/sec2b)0.036m/sec2c)0.24m/sec2d)7.2m/sec2Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.













