Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > The sequent depth ratio in a hydraulic jump t...
Start Learning for Free
The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream is
- a)3.33
- b)3.87
- c)4.33
- d)4.87
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
The sequent depth ratio in a hydraulic jump termed in a horizontal rec...
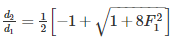
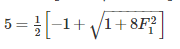
F1 = 3.87
Most Upvoted Answer
The sequent depth ratio in a hydraulic jump termed in a horizontal rec...
To explain the answer to this question, let's break it down into the following sections:
1. Introduction to hydraulic jump:
- A hydraulic jump occurs when a high-velocity, supercritical flow transitions into a low-velocity, subcritical flow.
- It typically occurs in open channels with a sudden change in water velocity, such as when water flows over a weir or a spillway.
2. Sequent Depth Ratio:
- The sequent depth ratio (y2/y1) is the ratio of the downstream depth (y2) to the upstream depth (y1) in a hydraulic jump.
- It is a measure of the energy dissipation that occurs during the jump.
- The larger the sequent depth ratio, the greater the energy dissipation.
3. Froude Number:
- The Froude number (Fr) is a dimensionless parameter that describes the flow regime.
- It is defined as the ratio of the flow velocity (V) to the square root of the product of gravity (g) and the flow depth (y).
- Mathematically, Fr = V / √(g * y).
- A Froude number less than 1 indicates subcritical flow, while a Froude number greater than 1 indicates supercritical flow.
4. Relationship between sequent depth ratio and Froude number:
- There is a relationship between the sequent depth ratio and the Froude number for a hydraulic jump.
- The relationship is given by the equation: Fr2 = (5/4) * (Fr1^2 - 1), where Fr2 is the Froude number downstream of the jump and Fr1 is the Froude number upstream of the jump.
- In this case, the sequent depth ratio is given as 5, so we can rewrite the equation as: 5 = (5/4) * (Fr1^2 - 1).
- Solving this equation, we find that Fr1 is approximately 3.87.
5. Determining the Froude number of the supercritical stream:
- The question asks for the Froude number of the supercritical stream, which is Fr1.
- From the previous calculation, we found that Fr1 is approximately 3.87.
- Therefore, the correct answer is option 'B', which states that the Froude number of the supercritical stream is 3.87.
1. Introduction to hydraulic jump:
- A hydraulic jump occurs when a high-velocity, supercritical flow transitions into a low-velocity, subcritical flow.
- It typically occurs in open channels with a sudden change in water velocity, such as when water flows over a weir or a spillway.
2. Sequent Depth Ratio:
- The sequent depth ratio (y2/y1) is the ratio of the downstream depth (y2) to the upstream depth (y1) in a hydraulic jump.
- It is a measure of the energy dissipation that occurs during the jump.
- The larger the sequent depth ratio, the greater the energy dissipation.
3. Froude Number:
- The Froude number (Fr) is a dimensionless parameter that describes the flow regime.
- It is defined as the ratio of the flow velocity (V) to the square root of the product of gravity (g) and the flow depth (y).
- Mathematically, Fr = V / √(g * y).
- A Froude number less than 1 indicates subcritical flow, while a Froude number greater than 1 indicates supercritical flow.
4. Relationship between sequent depth ratio and Froude number:
- There is a relationship between the sequent depth ratio and the Froude number for a hydraulic jump.
- The relationship is given by the equation: Fr2 = (5/4) * (Fr1^2 - 1), where Fr2 is the Froude number downstream of the jump and Fr1 is the Froude number upstream of the jump.
- In this case, the sequent depth ratio is given as 5, so we can rewrite the equation as: 5 = (5/4) * (Fr1^2 - 1).
- Solving this equation, we find that Fr1 is approximately 3.87.
5. Determining the Froude number of the supercritical stream:
- The question asks for the Froude number of the supercritical stream, which is Fr1.
- From the previous calculation, we found that Fr1 is approximately 3.87.
- Therefore, the correct answer is option 'B', which states that the Froude number of the supercritical stream is 3.87.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer?
Question Description
The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer?.
The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer?.
Solutions for The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer?, a detailed solution for The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The sequent depth ratio in a hydraulic jump termed in a horizontal rectangular channel is 5. The Froude number of the supercritical stream isa)3.33b)3.87c)4.33d)4.87Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























