Chemistry Exam > Chemistry Questions > The relative population of the state of a two...
Start Learning for Free
The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature is
- a)The upper level is more populated
- b)The lower level is more population
- c)The two levels are equally populated
- d)The upper level is not populated at all
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The relative population of the state of a two-level system, non-degene...
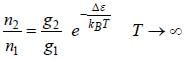
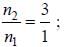
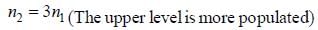
Most Upvoted Answer
The relative population of the state of a two-level system, non-degene...
Explanation:
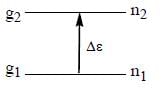
- A two-level system is a system that has only two possible energy states, such as a spin-up or spin-down electron, or an excited or ground state of an atom.
- If the two levels are non-degenerate, it means that they have different energy levels, but there is no additional degeneracy within each level.
- If the two levels are non-degenerate and separated by a finite energy gap, the population of the upper level will be less than that of the lower level at any finite temperature. However, if the temperature is increased to infinity, the population of the two levels will approach each other.
- If the two levels are non-degenerate to triply degenerate, it means that one of the levels has three possible states with the same energy, while the other level has only one state. This can occur, for example, when a spin-1/2 particle interacts with a magnetic field, resulting in three possible spin states in the higher energy level and one spin state in the lower level.
- At infinite temperature, all energy levels are equally accessible, regardless of their energy. Therefore, the relative population of the two levels will depend only on their degeneracy.
- In the case of a non-degenerate to triply degenerate system at infinite temperature, the upper level will be more populated than the lower level because it has three possible states compared to the lower level's one state.
Therefore, the correct answer is option 'A' - the upper level is more populated.
- A two-level system is a system that has only two possible energy states, such as a spin-up or spin-down electron, or an excited or ground state of an atom.
- If the two levels are non-degenerate, it means that they have different energy levels, but there is no additional degeneracy within each level.
- If the two levels are non-degenerate and separated by a finite energy gap, the population of the upper level will be less than that of the lower level at any finite temperature. However, if the temperature is increased to infinity, the population of the two levels will approach each other.
- If the two levels are non-degenerate to triply degenerate, it means that one of the levels has three possible states with the same energy, while the other level has only one state. This can occur, for example, when a spin-1/2 particle interacts with a magnetic field, resulting in three possible spin states in the higher energy level and one spin state in the lower level.
- At infinite temperature, all energy levels are equally accessible, regardless of their energy. Therefore, the relative population of the two levels will depend only on their degeneracy.
- In the case of a non-degenerate to triply degenerate system at infinite temperature, the upper level will be more populated than the lower level because it has three possible states compared to the lower level's one state.
Therefore, the correct answer is option 'A' - the upper level is more populated.

|
Explore Courses for Chemistry exam
|

|
Similar Chemistry Doubts
The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer?
Question Description
The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer?.
The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer?.
Solutions for The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Chemistry.
Download more important topics, notes, lectures and mock test series for Chemistry Exam by signing up for free.
Here you can find the meaning of The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The relative population of the state of a two-level system, non-degenerate to triply degenerate at infinite temperature isa)The upper level is more populatedb)The lower level is more populationc)The two levels are equally populatedd)The upper level is not populated at allCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Chemistry tests.

|
Explore Courses for Chemistry exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















