Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Mala has the colouring book in which each Eng...
Start Learning for Free
Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?
- a)9
- b)8
- c)7
- d)6
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Mala has the colouring book in which each English letter is drawn two ...
This question is slightly ambigous. So first let us understand what question is asking. So in a book, we have letters A-Z and each letter is printed twice, so there are 52 letters. Now we have to color each letter, so we need a pair of colors for that, because each letter is printed twice. Also in a pair, both colors can be same. Now condition is that a pair of colors can't be used more than once.
So suppose Mala has 3 colors : Red, Blue, Green. She can color as follows : 1:(Red,Red), 2:(Blue,Blue), 3:(Green,Green), 4: (Red,Blue), 5: (Red,Green),
6 : (Blue,Green).
Now we don't have more pairs of colors left, we have used all pairs, but could color only 6 letters out of 26. So question is to find minimum no. of colors, so that we could color all 26 letters.
So if Mala has k colors, she can have k pairs of same colors, thus coloring k letters, then kC2 other pairs of colors, thus coloring kC2 more letters.
So suppose Mala has 3 colors : Red, Blue, Green. She can color as follows : 1:(Red,Red), 2:(Blue,Blue), 3:(Green,Green), 4: (Red,Blue), 5: (Red,Green),
6 : (Blue,Green).
Now we don't have more pairs of colors left, we have used all pairs, but could color only 6 letters out of 26. So question is to find minimum no. of colors, so that we could color all 26 letters.
So if Mala has k colors, she can have k pairs of same colors, thus coloring k letters, then kC2 other pairs of colors, thus coloring kC2 more letters.
So total no. of letters colored 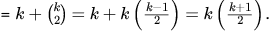
So we want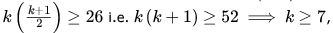
So we want
so option (C) is correct.
Most Upvoted Answer
Mala has the colouring book in which each English letter is drawn two ...
Problem Analysis:
Mala has a coloring book with 52 prints, each representing an English letter. There are two prints of each letter. Mala wants to color each print with one of k colors, such that the color pairs used to color any two letters are different. The goal is to find the minimum value of k that satisfies this requirement.
Solution:
To solve this problem, we need to consider the worst-case scenario, where we need to use the maximum number of distinct color pairs for different letters. Let's analyze this scenario:
Worst-case scenario:
In the worst-case scenario, each letter print needs to be colored with a different color pair. Since there are 52 prints, we need to find the maximum number of distinct color pairs required for 52 prints.
Calculating the maximum number of distinct color pairs:
To calculate the maximum number of distinct color pairs required for 52 prints, we can use the formula for the sum of the first n natural numbers: sum = n * (n + 1) / 2.
Let's assume the maximum number of color pairs required is x. Therefore, we have the equation:
x = 1 + 2 + 3 + ... + n
Using the formula for the sum of the first n natural numbers, we have:
x = n * (n + 1) / 2
Now, we need to find the minimum value of n that satisfies the equation:
x = n * (n + 1) / 2 >= 52
Simplifying the equation:
n * (n + 1) >= 104
n^2 + n - 104 >= 0
Solving this quadratic inequality, we find that n >= 10.2 (approximately).
Since n must be an integer, we can conclude that the minimum value of n is 11.
Calculating the minimum value of k:
Now that we have the maximum number of distinct color pairs required (11), we need to find the minimum value of k, which represents the number of colors needed.
Since each color pair consists of two colors, the total number of colors needed is 11 * 2 = 22.
Therefore, the minimum value of k is 22.
However, we need to consider that both prints of a letter can also be colored with the same color. In this case, we can use the same color pair for both prints of a letter.
Therefore, the minimum value of k is reduced to 11.
Final Answer:
The minimum value of k that satisfies the requirement is 11, which corresponds to option 'C'.
Mala has a coloring book with 52 prints, each representing an English letter. There are two prints of each letter. Mala wants to color each print with one of k colors, such that the color pairs used to color any two letters are different. The goal is to find the minimum value of k that satisfies this requirement.
Solution:
To solve this problem, we need to consider the worst-case scenario, where we need to use the maximum number of distinct color pairs for different letters. Let's analyze this scenario:
Worst-case scenario:
In the worst-case scenario, each letter print needs to be colored with a different color pair. Since there are 52 prints, we need to find the maximum number of distinct color pairs required for 52 prints.
Calculating the maximum number of distinct color pairs:
To calculate the maximum number of distinct color pairs required for 52 prints, we can use the formula for the sum of the first n natural numbers: sum = n * (n + 1) / 2.
Let's assume the maximum number of color pairs required is x. Therefore, we have the equation:
x = 1 + 2 + 3 + ... + n
Using the formula for the sum of the first n natural numbers, we have:
x = n * (n + 1) / 2
Now, we need to find the minimum value of n that satisfies the equation:
x = n * (n + 1) / 2 >= 52
Simplifying the equation:
n * (n + 1) >= 104
n^2 + n - 104 >= 0
Solving this quadratic inequality, we find that n >= 10.2 (approximately).
Since n must be an integer, we can conclude that the minimum value of n is 11.
Calculating the minimum value of k:
Now that we have the maximum number of distinct color pairs required (11), we need to find the minimum value of k, which represents the number of colors needed.
Since each color pair consists of two colors, the total number of colors needed is 11 * 2 = 22.
Therefore, the minimum value of k is 22.
However, we need to consider that both prints of a letter can also be colored with the same color. In this case, we can use the same color pair for both prints of a letter.
Therefore, the minimum value of k is reduced to 11.
Final Answer:
The minimum value of k that satisfies the requirement is 11, which corresponds to option 'C'.
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer?
Question Description
Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer?.
Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer?.
Solutions for Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?a)9b)8c)7d)6Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























